Study on the Classification of Metal Objects by a Fluxgate Magnetometer Cube Structure
Abstract
:1. Introduction
2. Methods
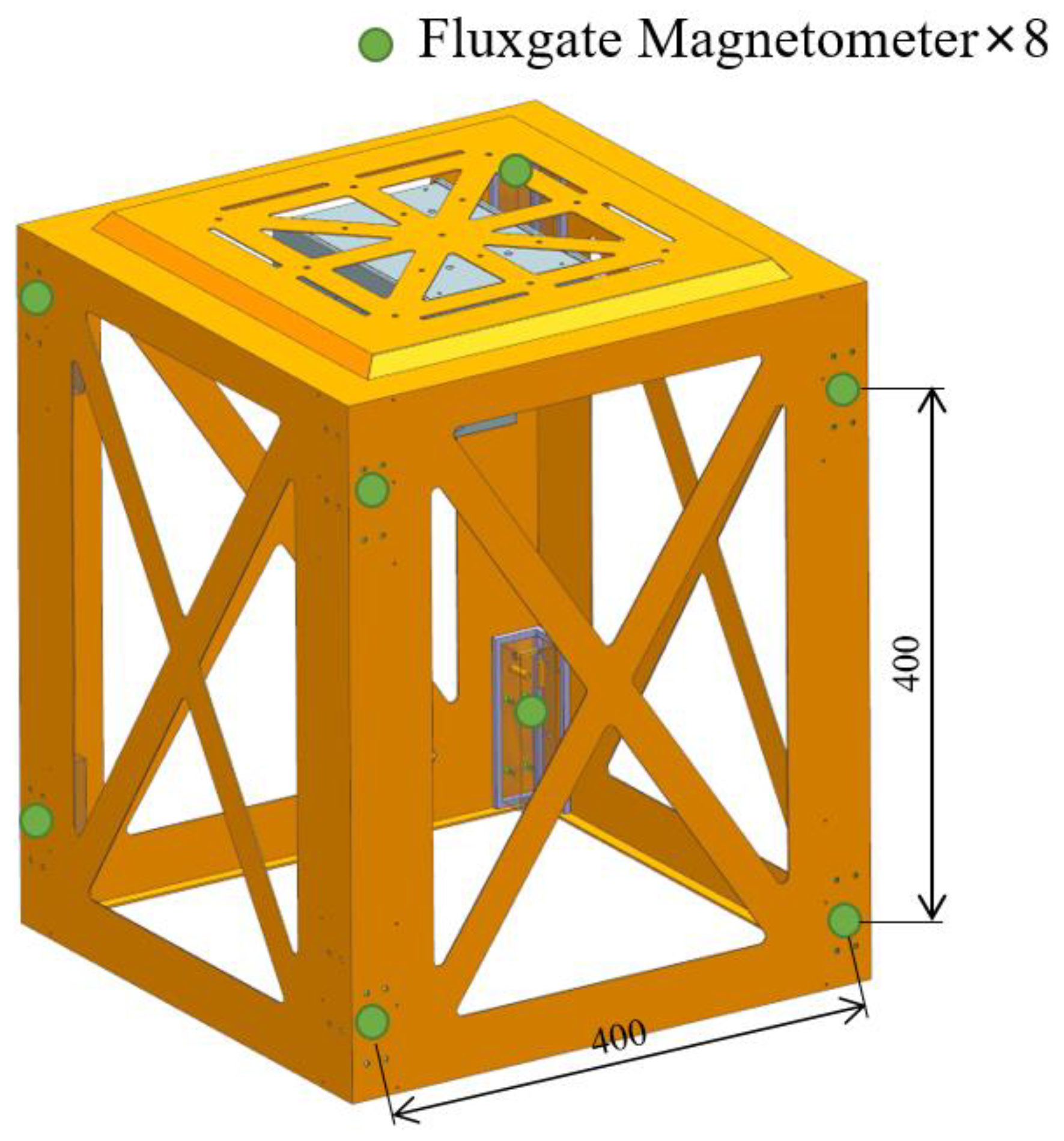
2.1. Space Magnetic Flux Density Acquisition
2.2. ResNet-18
3. Training ResNet-18 Model
3.1. Dataset Generation
3.2. Uncertainty Analysis
3.3. Training the Recognition Network
4. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
Greek Symbols
Subscripts
Glossary
References
- Mandea, M.; Chambodut, A. Geomagnetic field processes and their implications for space weather. Surv. Geophys. 2020, 41, 1611–1627. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Q.; Sohail, A.; Kumam, P.; Thounthong, P.; Muhammad, T. Mechanical aspects of Maxwell nanofluid in dynamic system with irreversible analysis. ZAMM-J. Appl. Math. Mech./Zeitschrift für Angewandte Mathematik und Mechanik 2021, 101, e202000212. [Google Scholar] [CrossRef]
- Buschow, K.H.J.; Boer, F.R. Physics of Magnetism and Magnetic Materials; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2003. [Google Scholar]
- Pang, H.; Luo, S.; Zhang, Q.; Li, J.; Chen, D.; Pan, M.; Luo, F. Calibration of a fluxgate magnetometer array and its application in magnetic object localization. Meas. Sci. Technol. 2013, 24, 075102. [Google Scholar] [CrossRef]
- Han, S.; Rong, X.; Bian, L.; Zhong, M.; Zhang, L. The application of magnetometers and electromagnetic induction sensors in UXO detection. E3S Web Conf. 2019, 131, 01045. [Google Scholar] [CrossRef]
- Shan, S.; Zhang, H.; Zhou, S.; Dai, Z. On Real-time Tracking for Underwater Magnetic Target with Extension Considerations. In Proceedings of the2020 7th International Forum on Electrical Engineering and Automation, Hefei, China, 25–27 September 2020; pp. 775–784. [Google Scholar]
- Obiora, D.N.; Oha, I.A.; Ihedike, A.O.; Igwe, E. Comparative depth estimates and modeling of magnetic anomalies over the Nkalagu area, Southeastern Nigeria. Model. Earth Syst. Environ. 2022, 8, 1291–1309. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, C.; Wang, X.; Wang, Z.; Ge, J.; Dong, H. A multi-magneto-inductive sensor array system for real-time magnetic field imaging of ferromagnetic targets. Rev. Sci. Instrum. 2021, 92, 035113. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Zhang, Y.; Fan, H.; Yin, G. Integrated compensation and rotation alignment for three-axis magnetic sensors array. IEEE Trans. Magn. 2018, 54, 1–11. [Google Scholar] [CrossRef]
- Yin, G.; Li, P.; Wei, Z.; Liu, G.; Yang, Z.; Zhao, L. Magnetic dipole localization and magnetic moment estimation method based on normalized source strength. J. Magn. Magn. Mater. 2020, 502, 166450. [Google Scholar] [CrossRef]
- Han, S.T.; Zhang, B.; Rong, X.L.; Bian, L.X.; Zhang, G.K.; Wen, Z. A Calculation Method of Magnetic Anomaly Field Distribution of Ellipsoid with Arbitrary Posture. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2154031. [Google Scholar] [CrossRef]
- Jin, H.; Zhuang, Z.; Fu, M.; Guo, J.; Wang, H. Modeling method using simplest multiple magnetic dipoles equivalence. Syst. Eng. Electron. Technol. 2021, 43, 2066–2075. (In Chinese) [Google Scholar]
- Nara, T.; Suzuki, S.; Ando, S. A closed-form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients. IEEE Trans. Magn. 2006, 42, 3291–3293. [Google Scholar]
- Kasatkin, S.I.; Polyakov, O.P.; Rusakova, N.E.; Rusakov, A.E. On uniqueness of solution of a reverse problem of magnetic location. J. Magn. Magn. Mater. 2006, 305, 361–364. [Google Scholar] [CrossRef]
- Birsan, M. Recursive Bayesian method for magnetic dipole tracking with a tensor gradiometer. IEEE Trans. Magn. 2010, 47, 409–415. [Google Scholar] [CrossRef]
- Fan, L.; Kang, X.; Zheng, Q.; Zhang, X.; Liu, X.; Chen, C.; Kang, C. A fast linear algorithm for magnetic dipole localization using total magnetic field gradient. IEEE Sens. J. 2017, 18, 1032–1038. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Zeng, X. A real-time magnetic dipole localization method based on cube magnetometer array. IEEE Trans. Magn. 2019, 55, 1–9. [Google Scholar] [CrossRef]
- Yin, G.; Zhang, L.; Jiang, H.; Wei, Z.; Xie, Y. A closed-form formula for magnetic dipole localization by measurement of its magnetic field vector and magnetic gradient tensor. J. Magn. Magn. Mater. 2020, 499, 166274. [Google Scholar] [CrossRef]
- Billings, S.D.; Pasion, C.; Walker, S.; Beran, L. Magnetic models of unexploded ordnance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2115–2124. [Google Scholar] [CrossRef]
- Oruç, B. Location and depth estimation of point-dipole and line of dipoles using analytic signals of the magnetic gradient tensor and magnitude of vector components. J. Appl. Geophys. 2010, 70, 27–37. [Google Scholar] [CrossRef]
- Hart, S.J.; Shaffer, R.E.; Rose-Pehrsson, S.L.; McDonald, J.R. Using physics-based modeler outputs to train probabilistic neural networks for unexploded ordnance (UXO) classification in magnetometry surveys. IEEE Trans. Geosci. Remote Sens. 2001, 39, 797–804. [Google Scholar] [CrossRef]
- Nelson, H.H.; Steinhurst, D.A.; Barrow, B.; Bell, T.; Khadar, N.; SanFilipo, B.; Won, I.J. Enhanced UXO Discrimination Using Frequency-Domain Electromagnetic Induction; Environmental Security Technology Certification Program Office (DOD): Arlington, VA, USA, 2007. [Google Scholar]
- Shamatava, I.; Shubitidze, F.; Fernandez, J.P.; Bijamov, A.; Barrowes, B.E.; O’Neill, K. Live-site UXO classification studies using advanced EMI and statistical models. Detect. Sens. Mines Explos. Objects Obs. Targets XVI SPIE 2011, 8017, 92–103. [Google Scholar]
- Bijamov, A.; Fernández, J.P.; Barrowes, B.E.; Shamatava, I.; O’Neill, K.; Shubitidze, F. Camp Butner live-site UXO classification using hierarchical clustering and Gaussian mixture modeling. IEEE Trans. Geosci. Remote Sens. 2013, 52, 5218–5229. [Google Scholar] [CrossRef]
- Billings, S.D.; Pasion, L.R.; Oldenburg, D.W. Inversion of magnetics for UXO discrimination and identification. In Proceedings of the 2002 UXO Forum, Orlando, FL, USA, 3–6 September 2002. [Google Scholar]
- Beran, L.; Billings, S.; Oldenburg, D. Incorporating uncertainty in unexploded ordnance discrimination. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3071–3080. [Google Scholar] [CrossRef]
- Wigh, M.D.; Hansen, T.M.; Døssing, A. Inference of unexploded ordnance (UXO) by probabilistic inversion of magnetic data. Geophys. J. Int. 2020, 220, 37–58. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Zhang, M.; Chen, J.; Wu, X. Detection and classification of multi-magnetic targets using mask-RCNN. IEEE Access 2020, 8, 187202–187207. [Google Scholar] [CrossRef]
- Walter, T., Jr. Introduction to Electrodynamics and Radiation; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Wiegert, R.; Lee, K.; Oeschger, J. Improved magnetic STAR methods for real-time, point-by-point localization of unexploded ordnance and buried mines. In Proceedings of the OCEANS 2008, Quebec City, QC, Canada, 15–18 September 2008; pp. 1–7. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 September 2015; pp. 1026–1034. [Google Scholar]
- Saxe, A.M.; McClelland, J.L.; Ganguli, S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv 2013, arXiv:1312.6120. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hulot, G.; Sabaka, T.J.; Olsen, N.; Fournier, A. The present and future geomagnetic field. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 33–78. [Google Scholar]
- Schubert, G. Treatise on Geophysics; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Zaporozhan, V.; Ponomarenko, A. Mechanisms of geomagnetic field influence on gene expression using influenza as a model system: Basics of physical epidemiology. Int. J. Environ. Res. Public Health 2010, 7, 938–965. [Google Scholar] [CrossRef] [PubMed] [Green Version]














| Performance Name | Range | Bandwidth | Noise |
|---|---|---|---|
| Parameter | −100 uT∼+100 uT | DC∼30 Hz | ≤15 pT@1 Hz |
| Layer Name | Output Size | 18-Layer | 50-Layer |
|---|---|---|---|
| conv1 | 112 × 112 | 7 × 7, 64, stride 2 | |
| conv2_x | 56 × 56 | 3 × 3 max pool, stride 2 | |
| conv3_x | 28 × 28 | ||
| conv4_x | 14 × 14 | ||
| conv5_x | 7 × 7 | ||
| 1 × 1 | average pool, 1000-d fc, softmax | ||
| Detection Target | Properties (Radius/mm) | Valid Data (Groups) | Invalid Data (Groups) |
|---|---|---|---|
| No. 1 iron ball | 51 | 1238 | 0 |
| No. 2 iron ball | 56.5 | 1223 | 0 |
| No. 3 iron ball | 67.5 | 1240 | 1 |
| Direction | Mean | Standard Deviation | Maximum | Minimum |
|---|---|---|---|---|
| z | 36,884.2 | 3.3 | 36,898.9 | 36,878.0 |
| x | 30,121.8 | 3.6 | 30,131.6 | 30,114.7 |
| y | 15,367.2 | 5.7 | 15,374.4 | 15,341.8 |
| Detection Target | Valid Data (Groups) |
|---|---|
| No. 1 iron ball | 40 |
| No. 2 iron ball | 32 |
| No. 3 iron ball | 28 |
| No see | 7 |
| Precision | Recall | Acc Single | F1-Score | |
|---|---|---|---|---|
| No. 1 iron ball | 88.2% | 75% | 86.9% | 0.81 |
| No. 2 iron ball | 87.5% | 87.5% | 92.5% | 0.87 |
| No. 3 iron ball | 96.4% | 96.4% | 96.3% | 0.96 |
| No see | 38.5% | 71.4% | 90.6% | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S.; Zhang, B.; Wen, Z.; Zhang, C.; He, Y. Study on the Classification of Metal Objects by a Fluxgate Magnetometer Cube Structure. Sensors 2022, 22, 7653. https://doi.org/10.3390/s22197653
Han S, Zhang B, Wen Z, Zhang C, He Y. Study on the Classification of Metal Objects by a Fluxgate Magnetometer Cube Structure. Sensors. 2022; 22(19):7653. https://doi.org/10.3390/s22197653
Chicago/Turabian StyleHan, Songtong, Bo Zhang, Zhu Wen, Chunwei Zhang, and Yong He. 2022. "Study on the Classification of Metal Objects by a Fluxgate Magnetometer Cube Structure" Sensors 22, no. 19: 7653. https://doi.org/10.3390/s22197653
APA StyleHan, S., Zhang, B., Wen, Z., Zhang, C., & He, Y. (2022). Study on the Classification of Metal Objects by a Fluxgate Magnetometer Cube Structure. Sensors, 22(19), 7653. https://doi.org/10.3390/s22197653







