Functionalization of Internal Resonance in Magnetically Coupled Resonators for Highly Efficient and Wideband Hybrid Vibration Energy Harvesting
Abstract
1. Introduction
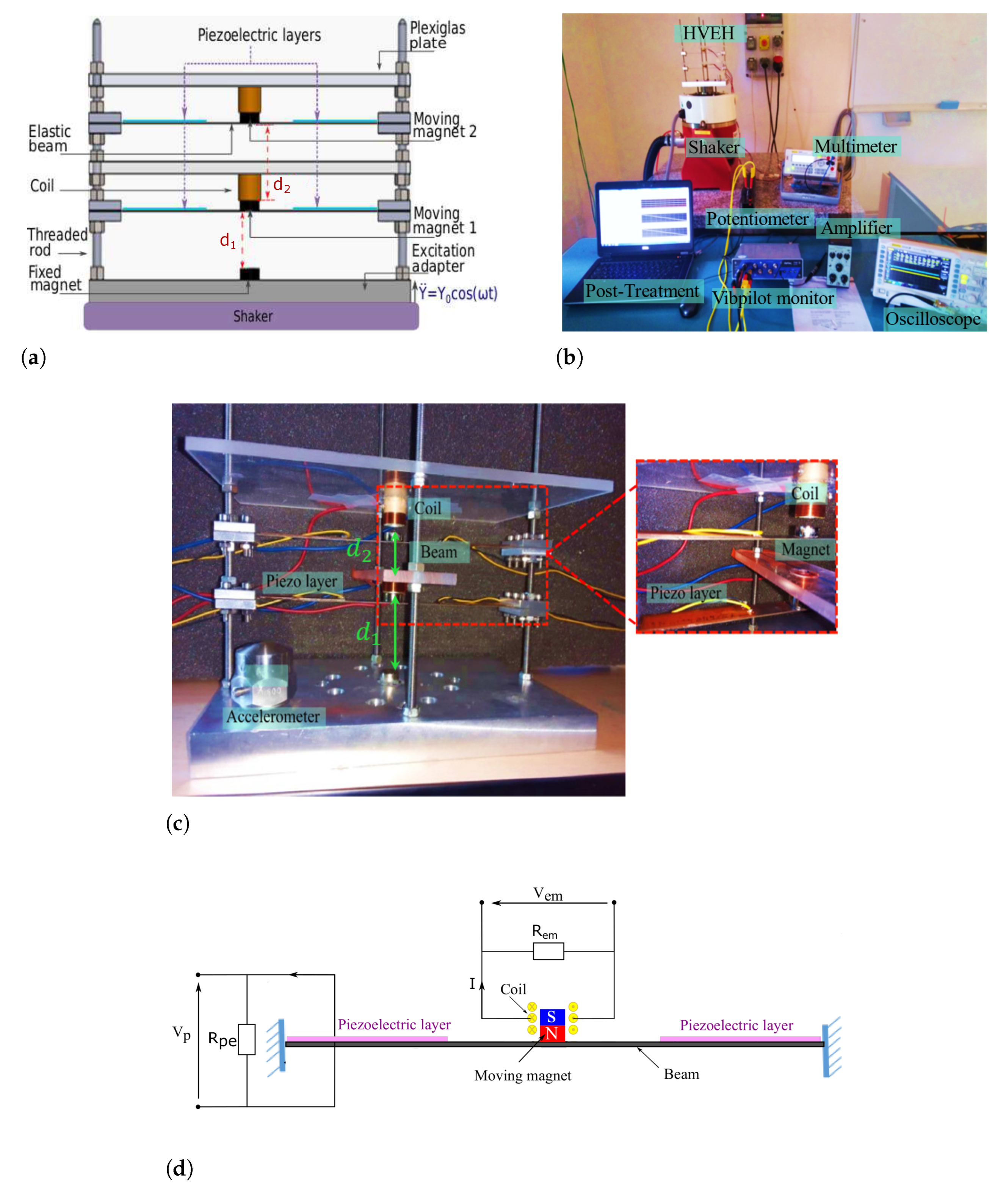
2. Model and Experimental Setup
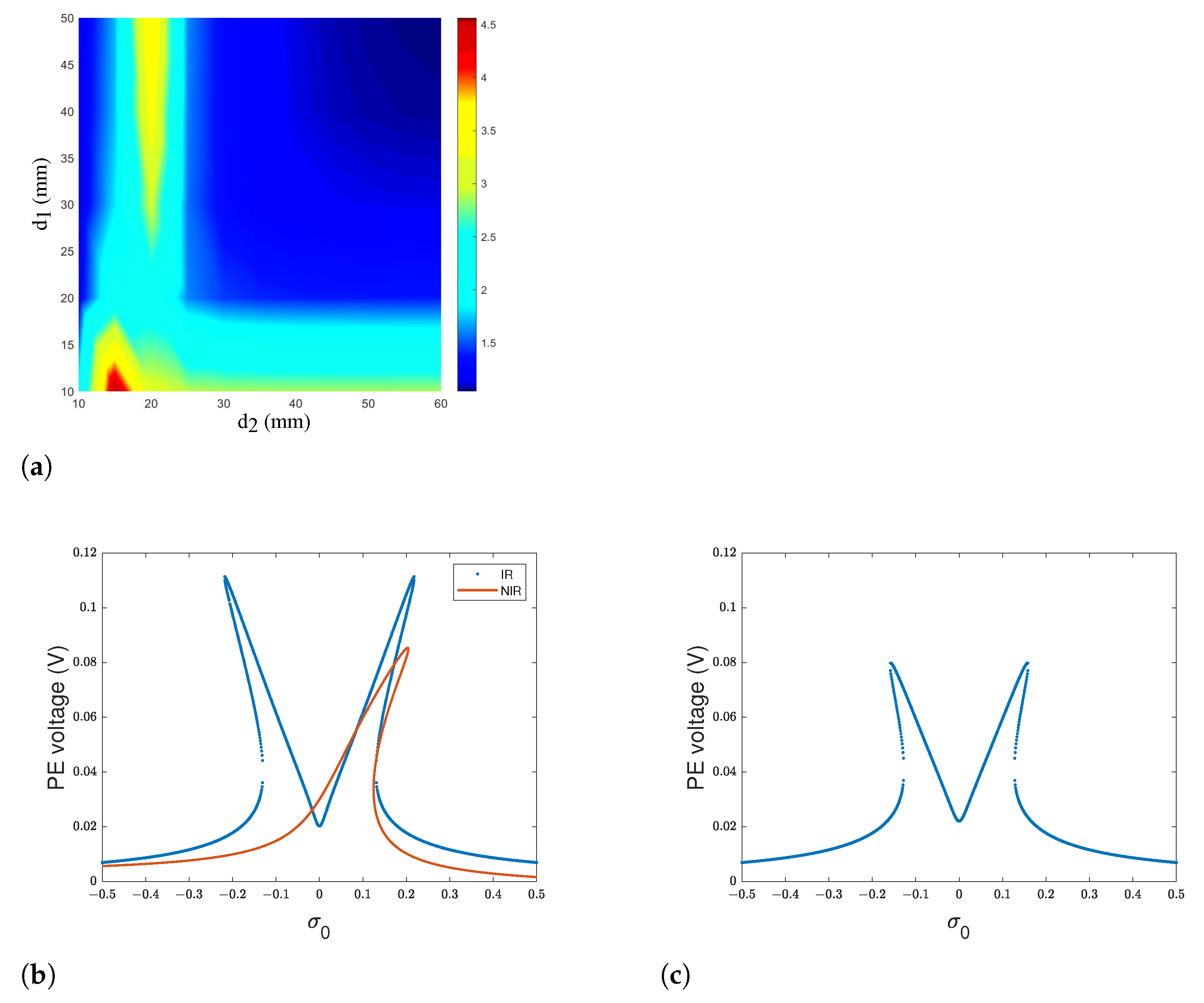
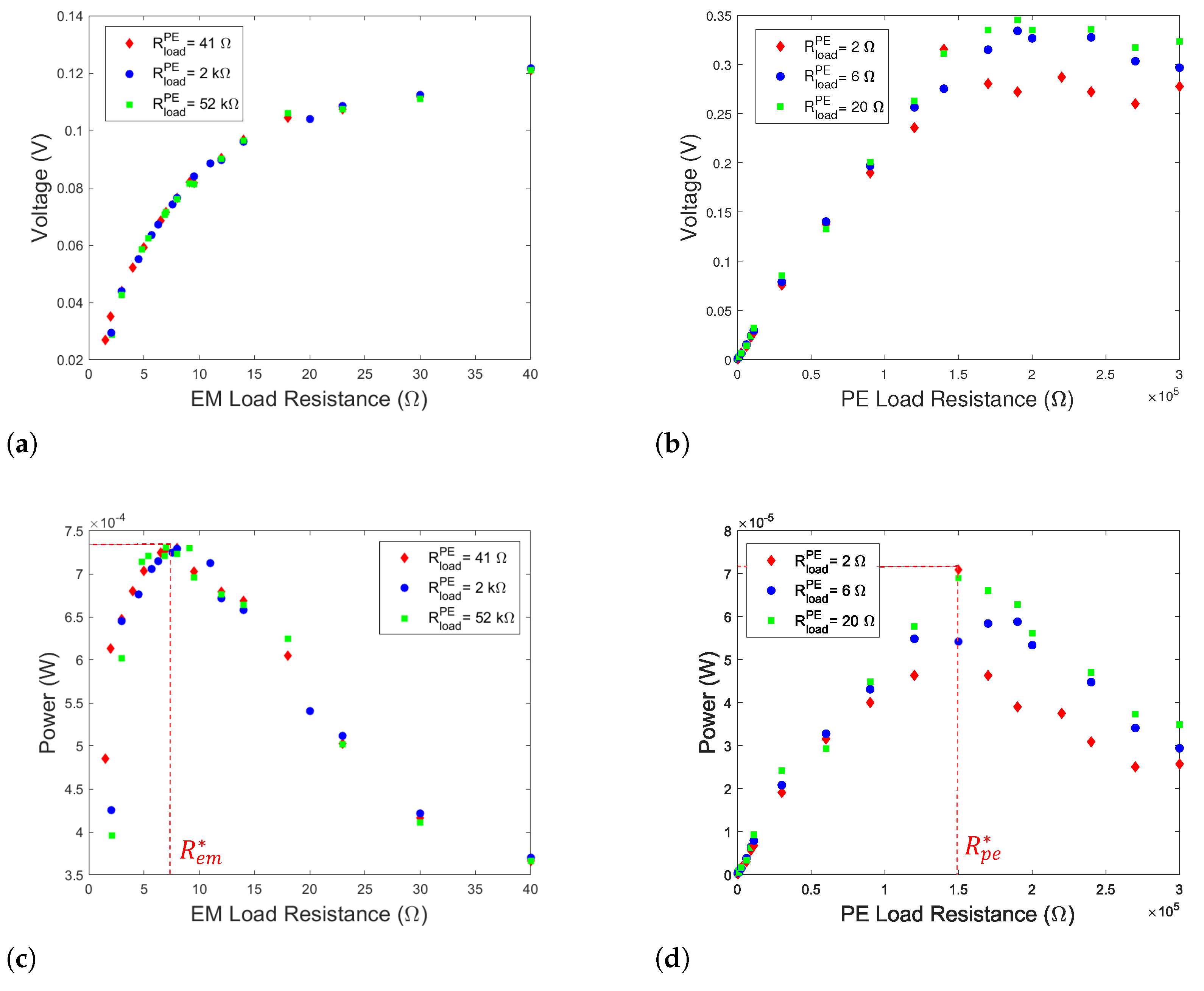
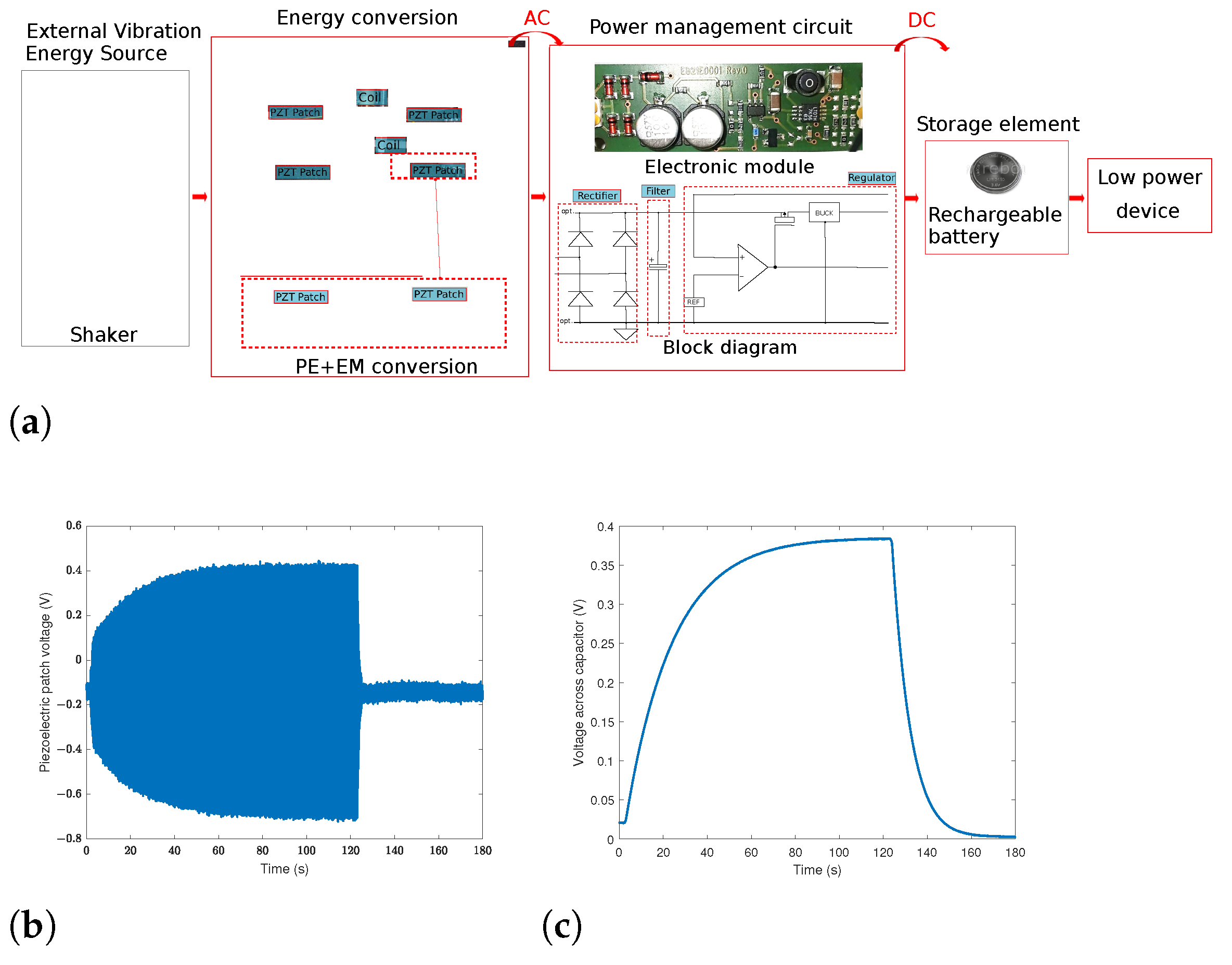
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Resolution Procedure with the Method of Multiple Scales (MMS)
References
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131–1142. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Soh, C.K. Toward broadband vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1867–1897. [Google Scholar] [CrossRef]
- Zhu, D.; Tudor, M.J.; Beeby, S. Strategies for increasing the operating frequency range of vibration energy harvesters: A review. Meas. Sci. Technol. 2009, 21, 022001. [Google Scholar] [CrossRef]
- Twiefel, J.; Westermann, H. Survey on broadband techniques for vibration energy harvesting. J. Intell. Mater. Syst. Struct. 2013, 24, 1291–1302. [Google Scholar] [CrossRef]
- Ibrahim, S.W.; Ali, W.G. A review on frequency tuning methods for piezoelectric energy harvesting systems. J. Renew. Sustain. Energy 2012, 4, 062703. [Google Scholar] [CrossRef]
- Hu, Y.; Xue, H.; Hu, H. A piezoelectric power harvester with adjustable frequency through axial preloads. Smart Mater. Struct. 2007, 16, 1961–1966. [Google Scholar] [CrossRef]
- Eichhorn, C.; Goldschmidtboeing, F.; Woias, P. A frequency tunable piezoelectric energy converter based on a cantilever beam. Proc. PowerMEMS 2008, 9, 309–312. [Google Scholar]
- Morris, D.J.; Youngsman, J.M.; Anderson, M.J.; Bahr, D. A resonant frequency tunable, extensional mode piezoelectric vibration harvesting mechanism. Smart Mater. Struct. 2008, 17, 065021. [Google Scholar] [CrossRef]
- Loverich, J.; Geiger, R.; Frank, J. Stiffness nonlinearity as a means for resonance frequency tuning and enhancing mechanical robustness of vibration power harvesters. In Active and Passive Smart Structures and Integrated Systems; International Society for Optics and Photonics: Bellingham, WA, USA, 2008; Volume 6928. [Google Scholar]
- Karadag, C.V.; Topaloglu, N. A Self-Sufficient and Frequency Tunable Piezoelectric Vibration Energy Harvester. J. Vib. Acoust. 2016, 139, 011013. [Google Scholar] [CrossRef]
- Hsu, J.-C.; Tseng, C.-T.; Chen, Y.-S. Analysis and experiment of self-frequency-tuning piezoelectric energy harvesters for rotational motion. Smart Mater. Struct. 2014, 23, 075013. [Google Scholar] [CrossRef]
- Priya, S.; Inman, D.J. (Eds.) Energy Harvesting Technologies; Springer: New York, NY, USA, 2009; Volume 21. [Google Scholar]
- Tadesse, Y.; Zhang, S.; Priya, S. Multimodal Energy Harvesting System: Piezoelectric and Electromagnetic. J. Intell. Mater. Syst. Struct. 2008, 20, 625–632. [Google Scholar] [CrossRef]
- Ahmad, M.M.; Khan, N.M.; Khan, F.U. Multi-degrees of freedom energy harvesting for broad-band vibration frequency range: A review. Sens. Actuators A Phys. 2022, 344, 113690. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, C.; Dai, K. A Multi-Mode Broadband Vibration Energy Harvester Composed of Symmetrically Distributed U-Shaped Cantilever Beams. Micromachines 2021, 12, 203. [Google Scholar] [CrossRef] [PubMed]
- Thong, L.W.; Kok, S.L.; Ramlan, R. Modeling of Multiple Cantilevers System for Broadband Vibration Energy Harvester. In Proceedings of the 2021 4th International Seminar on Research of Information Technology and Intelligent Systems (ISRITI), Yogyakarta, Indonesia, 16–17 December 2021. [Google Scholar]
- Nabavi, S.; Zhang, L. Nonlinear Multi-Mode Wideband Piezoelectric MEMS Vibration Energy Harvester. IEEE Sens. J. 2019, 19, 4837–4848. [Google Scholar] [CrossRef]
- Shahruz, S. Design of mechanical band-pass filters for energy scavenging. J. Sound Vib. 2006, 292, 987–998. [Google Scholar] [CrossRef]
- Oyabur, R.; Salauddin, M.; Cho, H.; Park, J.Y. A multimodal hybrid energy harvester based on piezoelectric-electromagnetic mechanisms for low-frequency ambient vibrations. Energy Convers. Manag. 2018, 168, 454–466. [Google Scholar]
- Yang, B.; Lee, C.; Xiang, W.; Xie, J.; He, J.H.; Kotlanka, R.K.; Low, S.P.; Feng, H. Electromagnetic energy harvesting from vibrations of multiple frequencies. J. Micromech. Microeng. 2009, 19, 035001. [Google Scholar] [CrossRef]
- Roundy, S.; Leland, E.S.; Baker, J.; Carleton, E.; Reilly, E.; Lai, E.; Otis, B.; Rabaey, J.M.; Wright, P.K.; Sundararajan, V. Improving Power Output for Vibration-Based Energy Scavengers. IEEE Pervasive Comput. 2005, 4, 28–36. [Google Scholar] [CrossRef]
- Qin, H.; Mo, S.; Jiang, X.; Shang, S.; Wang, P.; Liu, Y. Multimodal Multidirectional Piezoelectric Vibration Energy Harvester by U-Shaped Structure with Cross-Connected Beams. Micromachines 2022, 13, 396. [Google Scholar] [CrossRef]
- Eshtehardiha, R.; Tikani, R.; Ziaei-Rad, S. Experimental and numerical investigation of energy harvesting from double cantilever beams with internal resonance. J. Sound Vib. 2021, 500, 116022. [Google Scholar] [CrossRef]
- Yu, N.; Ma, H.; Wu, C.; Yu, G.; Yan, B. Modeling and experimental investigation of a novel bistable two-degree-of-freedom electromagnetic energy harvester. Mech. Syst. Signal Process. 2021, 156, 107608. [Google Scholar] [CrossRef]
- Jia, Y. Review of nonlinear vibration energy harvesting: Duffing, bistability, parametric, stochastic and others. J. Intell. Mater. Syst. Struct. 2020, 31, 921–944. [Google Scholar] [CrossRef]
- Jia, Y.; Du, S.; Arroyo, E.; Seshia, A.A. Autoparametric resonance in a piezoelectric MEMS vibration energy harvester. In Proceedings of the IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018. [Google Scholar]
- Maamer, B.; Boughamoura, A.; El-Bab, A.M.F.; Francis, L.A.; Tounsi, F. A review on design improvements and techniques for mechanical energy harvesting using piezoelectric and electromagnetic schemes. Energy Convers. Manag. 2019, 199, 111973. [Google Scholar] [CrossRef]
- Amri, M.; Basset, P.; Cottone, F.; Galayko, D.; Najar, F. Novel nonlinear spring design for wideband vibration energy harvesters. In Proceedings of the 11th International Workshop on Micro and Nanotechnology for Power Generation and Energy Conversion Applications, PowerMEMS 2011, Seoul, Korea, 15–18 November 2011. [Google Scholar]
- Engel, E.; Wei, J.; Lee, C.L. Enhanced vibration energy harvesting using nonlinear oscillations. In Energy Harvesting and Storage: Materials, Devices, and Applications; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9493. [Google Scholar]
- Mann, B.; Sims, N. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef]
- Sathyamoorthy, M. Nonlinear Vibrations of Plates: An Update of Recent Research Developments. Appl. Mech. Rev. 1996, 49, S55–S62. [Google Scholar] [CrossRef]
- Abed, I.; Kacem, N.; Bouhaddi, N.; Bouazizi, M.L. Multi-modal vibration energy harvesting approach based on nonlinear oscillator arrays under magnetic levitation. Smart Mater. Struct. 2016, 25, 025018. [Google Scholar] [CrossRef]
- Drezet, C.; Kacem, N.; Bouhaddi, N. Design of a nonlinear energy harvester based on high static low dynamic stiffness for low frequency random vibrations. Sens. Actuators A Phys. 2018, 283, 54–64. [Google Scholar] [CrossRef]
- Lyu, M.; Zhao, J.; Kacem, N.; Liu, P.; Tang, B.; Xiong, Z.; Wang, H.; Huang, Y. Exploiting nonlinearity to enhance the sensitivity of mode-localized mass sensor based on electrostatically coupled MEMS resonators. Int. J. Non-Linear Mech. 2020, 121, 103455. [Google Scholar] [CrossRef]
- Mahmoudi, S.; Kacem, N.; Bouhaddi, N. Enhancement of the performance of a hybrid nonlinear vibration energy harvester based on piezoelectric and electromagnetic transductions. Smart Mater. Struct. 2014, 23, 075024. [Google Scholar] [CrossRef]
- Liu, H.; Koh, K.H.; Lee, C.; Liu, H.; Koh, K.H.; Lee, C. Ultra-wide frequency broadening mechanism for micro-scale electromagnetic energy harvester. Appl. Phys. Lett. 2014, 104, 053901. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Phys. D Nonlinear Phenom. 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Experimental Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 102001. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S.; Fan, K.; Ji, H.; Qiu, J. Investigation of an ultra-low frequency piezoelectric energy harvester with high frequency up-conversion factor caused by internal resonance mechanism. Mech. Syst. Signal Process. 2021, 162, 108038. [Google Scholar] [CrossRef]
- Chen, L.-Q.; Jiang, W.-A. Internal Resonance Energy Harvesting. J. Appl. Mech. 2015, 82, 031004. [Google Scholar] [CrossRef]
- Cao, D.; Leadenham, S.; Erturk, A. Internal resonance for nonlinear vibration energy harvesting. Eur. Phys. J. Spec. Top. 2015, 224, 2867–2880. [Google Scholar] [CrossRef]
- Jiang, W.-A.; Ma, X.-D.; Han, X.-J.; Chen, L.-Q.; Bi, Q.-S. Broadband energy harvesting based on one-to-one internal resonance. Chin. Phys. B 2020, 29, 100503. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Nie, X.; Tan, T.; Yan, Z.; Yan, Z.; Hajj, M.R. Broadband and high-efficient L-shaped piezoelectric energy harvester based on internal resonance. Int. J. Mech. Sci. 2019, 159, 287–305. [Google Scholar] [CrossRef]
- Rocha, R.T.; Balthazar, J.M.; Tusset, A.M.; Piccirillo, V.; Felix, J.L.P. Nonlinear piezoelectric vibration energy harvesting from a portal frame with two-to-one internal resonance. Meccanica 2017, 52, 2583–2602. [Google Scholar] [CrossRef]
- Hou, S.; Teng, Y.-Y.; Zhang, Y.-W.; Zang, J. Enhanced Energy Harvesting of a Nonlinear Energy Sink by Internal Resonance. Int. J. Appl. Mech. 2019, 11, 1950100. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, L. Investigation on the characteristics of a novel internal resonance galloping oscillator for concurrent aeroelastic and base vibratory energy harvesting. Mech. Syst. Signal Process. 2022, 173, 109022. [Google Scholar] [CrossRef]
- Yang, W.; Towfighian, S. A hybrid nonlinear vibration energy harvester. Mech. Syst. Signal Process. 2017, 90, 317–333. [Google Scholar] [CrossRef]
- Xiong, L.; Tang, L.; Mace, B.R. Internal resonance with commensurability induced by an auxiliary oscillator for broadband energy harvesting. Appl. Phys. Lett. 2016, 108, 203901. [Google Scholar] [CrossRef]
- Liu, W.; Badel, A.; Formosa, F.; Wu, Y.; Bencheikh, N.; Agbossou, A. A wideband integrated piezoelectric bistable generator: Experimental performance evaluation and potential for real environmental vibrations. J. Intell. Mater. Syst. Struct. 2014, 26, 872–877. [Google Scholar] [CrossRef]
- Xiong, L.; Tang, L.; Mace, B.R. A comprehensive study of 2:1 internal-resonance-based piezoelectric vibration energy harvesting. Nonlinear Dyn. 2017, 91, 1817–1834. [Google Scholar] [CrossRef]
- Yang, W.; Towfighian, S. Internal resonance and low frequency vibration energy harvesting. Smart Mater. Struct. 2017, 26, 095008. [Google Scholar] [CrossRef]
- Chen, L.-Q.; Jiang, W.-A.; Panyam, M.; Daqaq, M.F. A Broadband Internally Resonant Vibratory Energy Harvester. J. Vib. Acoust. 2016, 138, 061007. [Google Scholar] [CrossRef]
- Foisal, A.R.; Hong, C.; Chung, G.-S. Multi-frequency electromagnetic energy harvester using a magnetic spring cantilever. Sens. Actuators A Phys. 2012, 182, 106–113. [Google Scholar] [CrossRef]
- Aouali, K.; Kacem, N.; Bouhaddi, N.; Mrabet, E.; Haddar, M. Efficient broadband vibration energy harvesting based on tuned nonlinearity and energy localization. Smart Mater. Struct. 2020, 29, 10LT01. [Google Scholar] [CrossRef]
- Liu, W.; Badel, A.; Formosa, F.; Wu, Y.P. A new figure of merit for wideband vibration energy harvesters. Smart Mater. Struct. 2015, 24, 125012. [Google Scholar] [CrossRef]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Simulation of a Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 075022. [Google Scholar] [CrossRef]
- Masana, R.; Daqaq, M.F. Relative performance of a vibratory energy harvester in mono- and bi-stable potentials. J. Sound Vib. 2011, 330, 6036–6052. [Google Scholar] [CrossRef]
- Mann, B.; Owens, B. Investigations of a nonlinear energy harvester with a bistable potential well. J. Sound Vib. 2010, 329, 1215–1226. [Google Scholar] [CrossRef]
- Aktakka, E.E.; Peterson, R.L.; Najafi, K. Thinned-PZT on SOI process and design optimization for piezoelectric inertial energy harvesting. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011. [Google Scholar]
- Beato-López, J.J.; Royo-Silvestre, I.; Algueta-Miguel, J.M.; Gómez-Polo, C. A Combination of a Vibrational Electromagnetic Energy Harvester and a Giant Magnetoimpedance (GMI) Sensor. Sensors 2020, 20, 1873. [Google Scholar] [CrossRef]
- Kecik, K.; Mitura, A. Theoretical and Experimental Investigations of a Pseudo-Magnetic Levitation System for Energy Harvesting. Sensors 2020, 20, 1623. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Design of a structure-based bistable piezoelectric energy harvester for scavenging vibration energy in gravity direction. Mech. Syst. Signal Process. 2022, 162, 108043. [Google Scholar] [CrossRef]
- Nan, W.; He, Y.; Fu, J. Bistable energy harvester using easy snap-through performance to increase output power. Energy 2021, 226, 120414. [Google Scholar] [CrossRef]
- Rabenimanana, T.; Walter, V.; Kacem, N.; Le Moal, P.; Bourbon, G.; Lardiès, J. Functionalization of electrostatic nonlinearities to overcome mode aliasing limitations in the sensitivity of mass microsensors based on energy localization. Appl. Phys. Lett. 2020, 117, 033502. [Google Scholar] [CrossRef]
- Majak, J.; Pohlak, M. Decomposition method for solving optimal material orientation problems. Compos. Struct. 2010, 92, 1839–1845. [Google Scholar] [CrossRef]
- Nabavi, S.; Zhang, L. Design and Optimization of a Low-Resonant-Frequency Piezoelectric MEMS Energy Harvester Based on Artificial Intelligence. Multidiscip. Digit. Publ. Inst. Proc. 2018, 2, 930. [Google Scholar]
- Jallouli, A.; Kacem, N.; Bouhaddi, N. Stabilization of solitons in coupled nonlinear pendulums with simultaneous external and parametric excitations. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 1–11. [Google Scholar] [CrossRef]


| Parameter | Designation/Value | Unity |
|---|---|---|
| Magnet Type | Neodymium magnet | – |
| Magnetization | N45 | — |
| Magnet diameter | 12 | mm |
| Magnet height | 4 | mm |
| Residual magnetic field | T | |
| Type of coil | Copper coil | — |
| Diameter of coil | 14 | mm |
| Number of coil turns N | 73 | — |
| Internal resistance |
| Designation | Value | Unity |
|---|---|---|
| Piezoelectric coupling coefficient | ||
| Piezoelectric permittivity | ||
| Vacuum permittivity | ||
| Piezoelectric density | 7500 | |
| Piezoelectric poisson ratio | — | |
| Piezoelectric layer length | 49 | mm |
| Piezoelectric layer width | 11 | mm |
| Piezolectric layer Young modulus | GPa | |
| Thickness of the piezoelectric layer | mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aouali, K.; Kacem, N.; Bouhaddi, N. Functionalization of Internal Resonance in Magnetically Coupled Resonators for Highly Efficient and Wideband Hybrid Vibration Energy Harvesting. Sensors 2022, 22, 7657. https://doi.org/10.3390/s22197657
Aouali K, Kacem N, Bouhaddi N. Functionalization of Internal Resonance in Magnetically Coupled Resonators for Highly Efficient and Wideband Hybrid Vibration Energy Harvesting. Sensors. 2022; 22(19):7657. https://doi.org/10.3390/s22197657
Chicago/Turabian StyleAouali, Kaouthar, Najib Kacem, and Noureddine Bouhaddi. 2022. "Functionalization of Internal Resonance in Magnetically Coupled Resonators for Highly Efficient and Wideband Hybrid Vibration Energy Harvesting" Sensors 22, no. 19: 7657. https://doi.org/10.3390/s22197657
APA StyleAouali, K., Kacem, N., & Bouhaddi, N. (2022). Functionalization of Internal Resonance in Magnetically Coupled Resonators for Highly Efficient and Wideband Hybrid Vibration Energy Harvesting. Sensors, 22(19), 7657. https://doi.org/10.3390/s22197657








