Payload Identification and Gravity/Inertial Compensation for Six-Dimensional Force/Torque Sensor with a Fast and Robust Trajectory Design Approach
Abstract
:1. Introduction
2. Gravity Compensation Algorithm
2.1. Analysis of the Influence of Load Gravity
2.2. Force and Torque of Six-Dimensional Force Sensor
2.3. Load Center of Gravity Coordinate Calculation
2.4. Calculation of Base Mounting Inclination, Sensor Zero Point, and Load Gravity
2.5. Calculation of External Force Perception
3. Inertial Force Compensation Algorithm
3.1. Analysis of the Influence of Load Inertia Force
3.2. Inertial Force Models and Compensation Algorithms
4. Fast Gravity/Inertial Force Identification Method Based on Excitation Trajectories
4.1. The Combined Forces of Gravity and Inertia Are Expressed
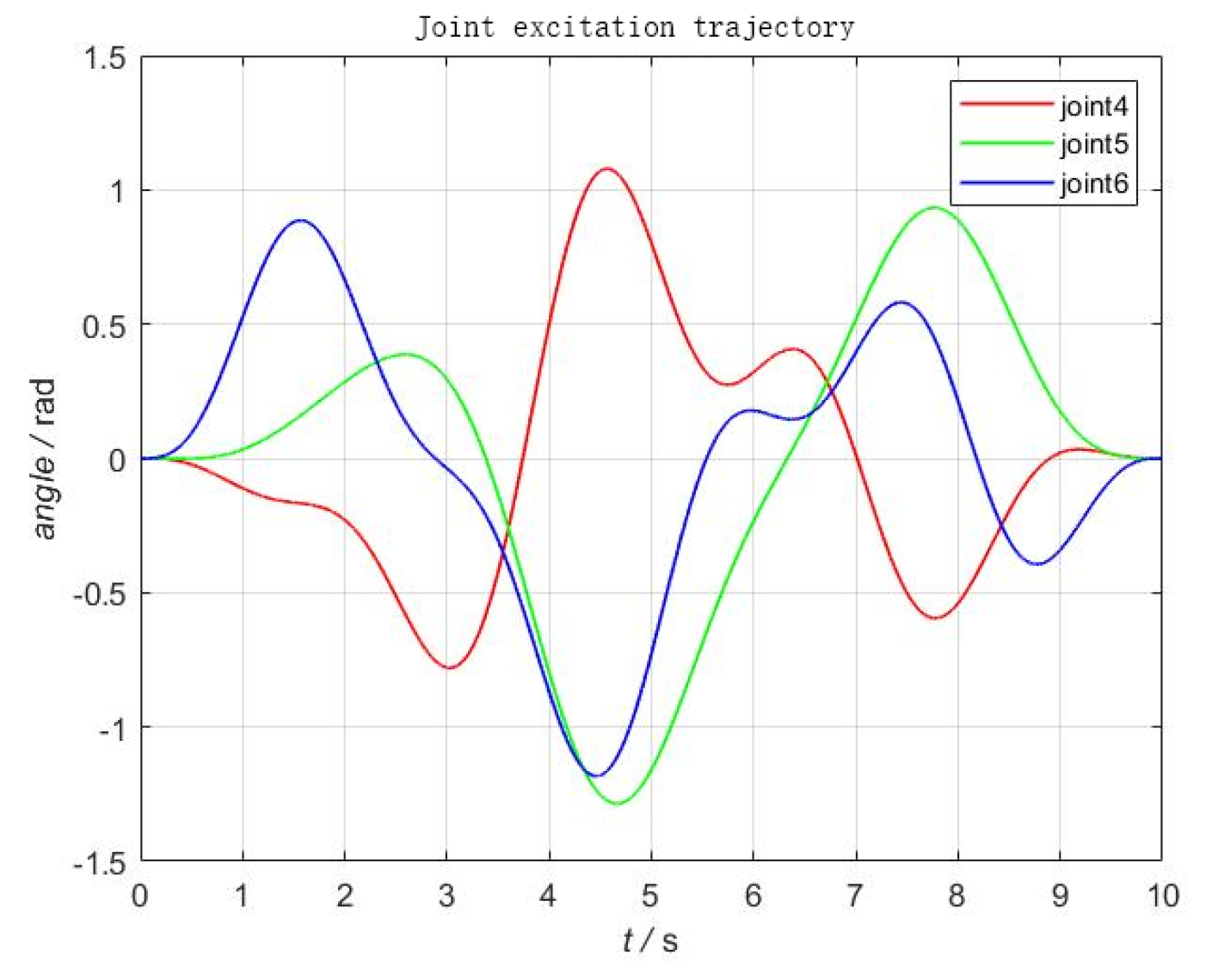
4.2. Excitation Trajectory Design
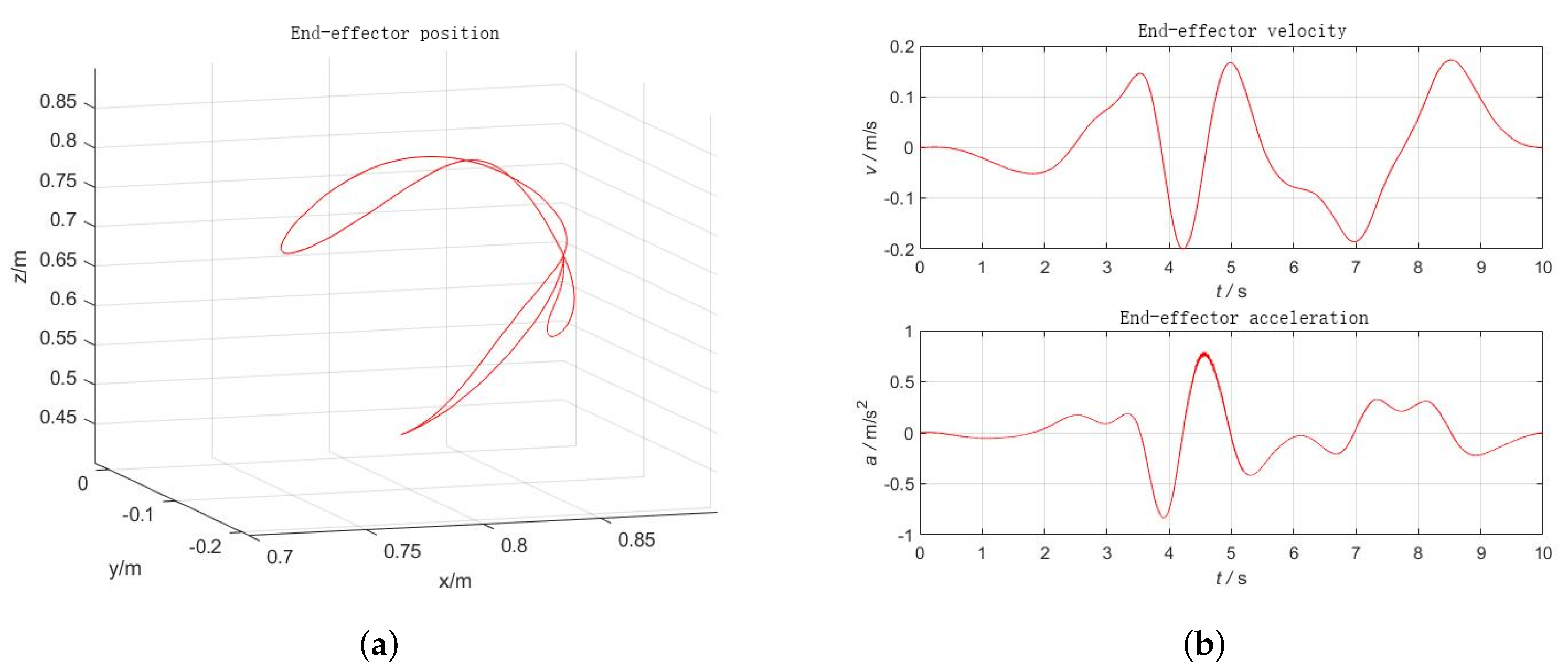
4.3. Excitation Trajectory Curve
5. Experimental Verification and Results
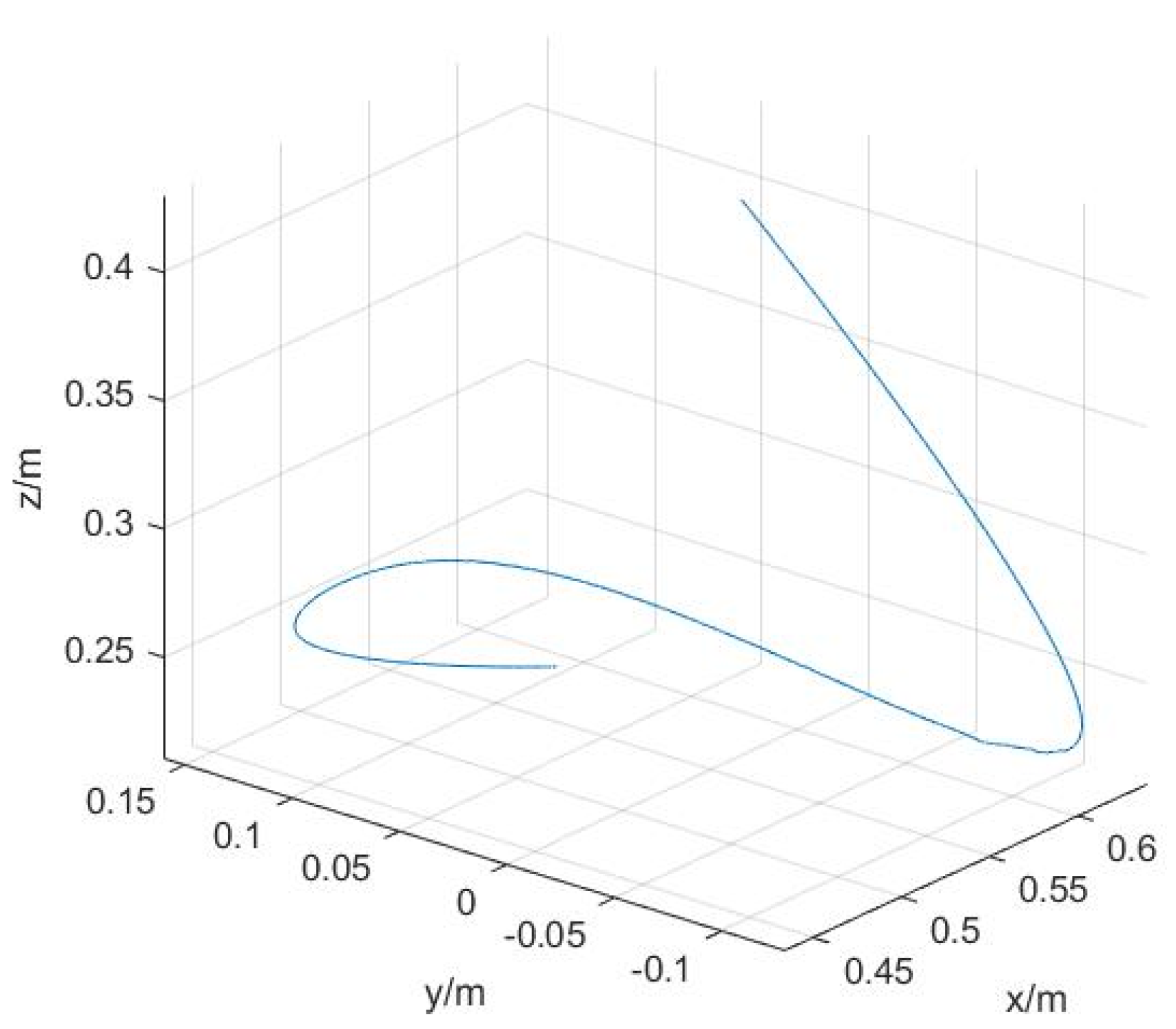
5.1. Experimental Platform Introduction and Verification
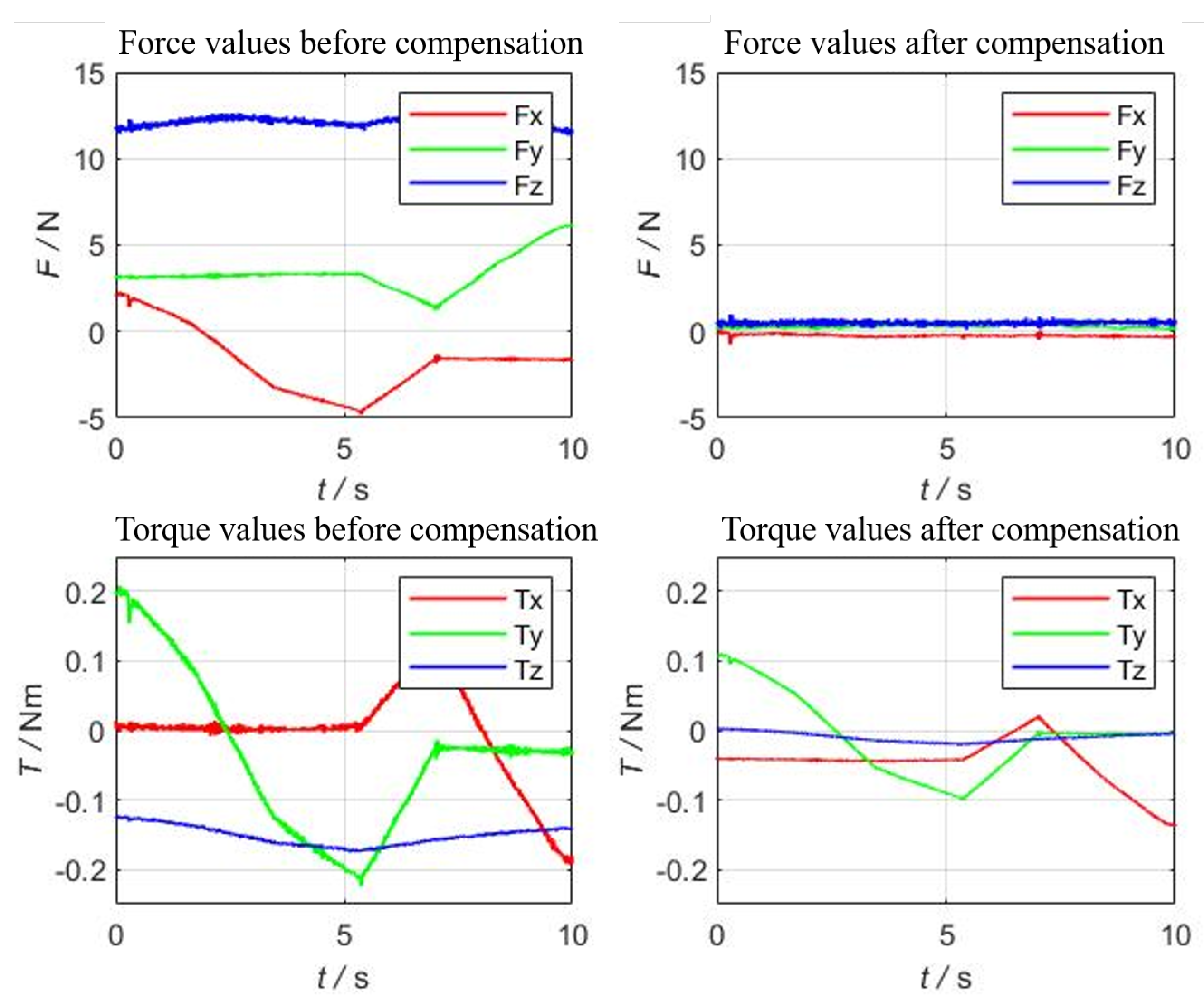
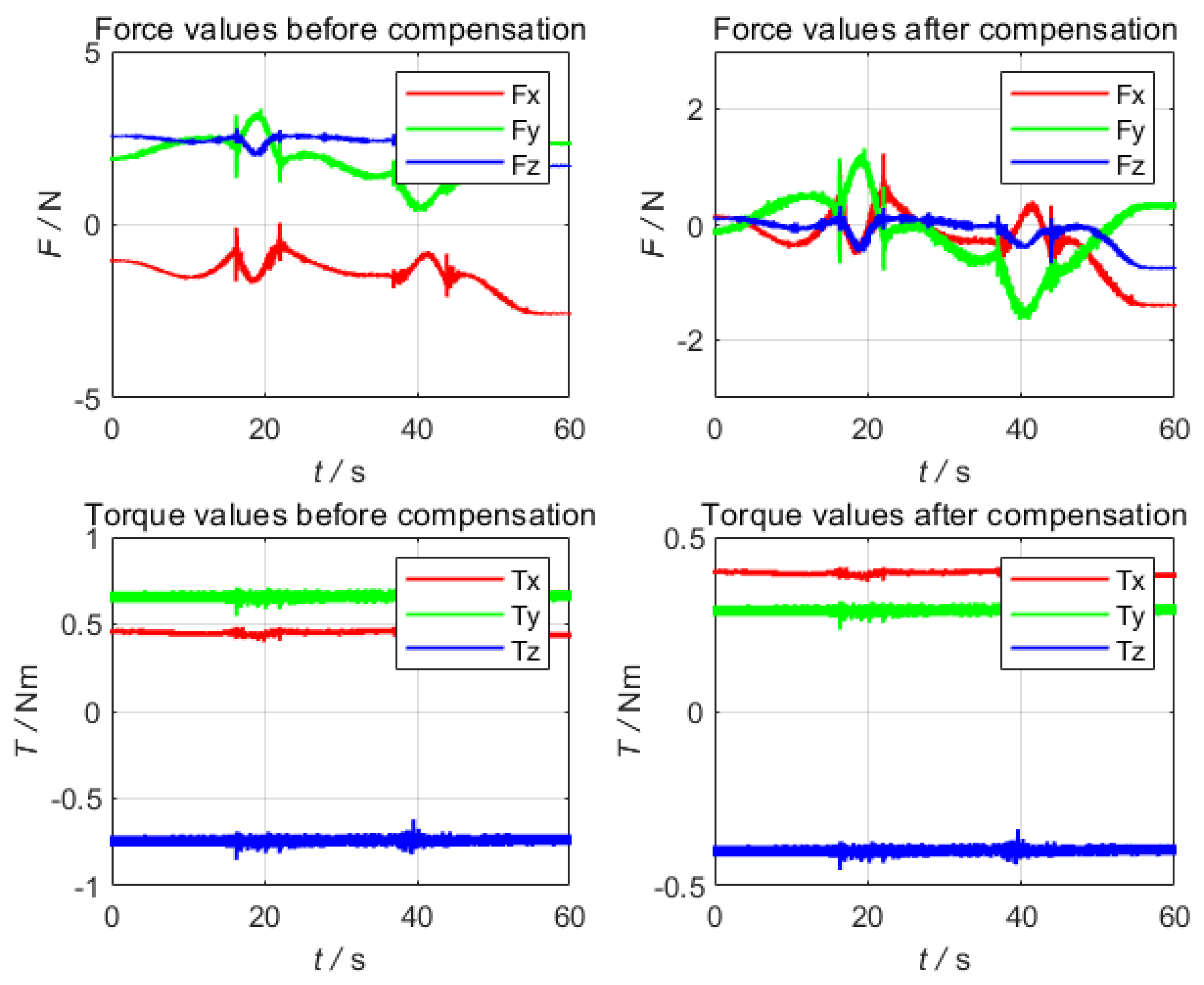
5.2. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Trajin, B.; Regnier, J.; Faucher, J. Comparison Between Stator Current and Estimated Mechanical Speed for the Detection of Bearing Wear in Asynchronous Drives. IEEE Trans. Ind. Electron. 2009, 56, 4700–4709. [Google Scholar] [CrossRef]
- Albu-Schäffer, A.; Haddadin, S.; Ott, C.; Stemmer, A.; Wimböck, T.; Hirzinger, G. The DLR lightweight robot: Design and control concepts for robots in human environments. Ind. Robot. 2007, 34, 376–385. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.B.; Seok, D.Y.; Lee, S.Y.; Kim, J.; Kang, G.; Kim, U.; Choi, H.R. 6-Axis Force/Torque Sensor With a Novel Autonomous Weight Compensating Capability for Robotic Applications. IEEE Robot. Autom. Lett. 2020, 5, 6686–6693. [Google Scholar] [CrossRef]
- Kostic, D.; De Jager, B.; Steinbuch, M.; Hensen, R. Modeling and identification for high-performance robot control: An RRR-robotic arm case study. IEEE Trans. Control. Syst. Technol. 2004, 12, 904–919. [Google Scholar] [CrossRef]
- Ludovico, D.; Guardiani, P.; Lasagni, F.; Lee, J.; Cannella, F.; Caldwell, D.G. Design of Non-Circular Pulleys for Torque Generation: A Convex Optimisation Approach. IEEE Robot. Autom. Lett. 2021, 6, 958–965. [Google Scholar] [CrossRef]
- Alamdari, A.; Haghighi, R.; Krovi, V. Gravity-Balancing of Elastic Articulated-Cable Leg-Orthosis Emulator. Mech. Mach. Theory 2018, 131, 351–370. [Google Scholar] [CrossRef]
- Zavala-Rio, A.; Santibanez, V. A Natural Saturating Extension of the PD-With-Desired-Gravity-Compensation Control Law for Robot Manipulators With Bounded Inputs. IEEE Trans. Robot. 2007, 23, 386–391. [Google Scholar] [CrossRef]
- Swevers, J.; Verdonck, W.; Naumer, B.; Pieters, S.; Biber, E. An Experimental Robot Load Identification Method for Industrial Application. Int. J. Robot. Res. 2002, 21, 701–712. [Google Scholar] [CrossRef]
- Kelly, R.; Santibaez, V.; Reyes, F. On saturated-proportional derivative feedback with adaptive gravity compensation of robot manipulators. Int. J. Adapt. Control. Signal Process. 2015, 10, 465–479. [Google Scholar] [CrossRef]
- Lin, H.; Hui, C.W.V.; Wang, Y.; Deguet, A.; Kazanzides, P.; Au, K.S. A Reliable Gravity Compensation Control Strategy for dVRK Robotic Arms With Nonlinear Disturbance Forces. IEEE Robot. Autom. Lett. 2019, 4, 3892–3899. [Google Scholar] [CrossRef] [Green Version]
- Zhijun, W.; Lu, L.; Zhanxian, L.; Liwen, C. Research on dynamic force compensation for robots based on six-dimensional force sensors. Mech. Des. 2020, 37, 72–77. [Google Scholar]
- Lingtao, H.; Lin, W.; Shui, N.; Jingsong, Y.; Tao, N. Research on robot flexibility control based on force sensor gravity compensation. J. Agric. Mach. 2020, 51, 386–393. [Google Scholar]
- Ni, Z.; Zhang, Y.; Shen, X.; Wu, S.; Wu, Z. Payload parameter identification method of flexible space manipulator. Aircr. Eng. Aerosp. Technol. 2020, 92, 925–938. [Google Scholar] [CrossRef]
- Gen, L.; Pengcheng, L.; Chao, W.; Ye, S. Research on the optimization algorithm of robot load gravity compensation based on genetic algorithm. Aviat. Manuf. Technol. 2021, 64, 52–59. [Google Scholar]
- Che, H.; Yiwen, Z.; Bi, Z.; Yingli, L.; Xingang, Z. Robotic arm load estimation based on optimal excitation pose sequences. Robot 2020, 42, 503–512. [Google Scholar]
- Tao, W.; Bo, P.; Yili, F.; Shuguo, W. Minimally invasive surgical robot force feedback main hand gravity compensation study. Robot 2020, 42, 525–533. [Google Scholar]
- Montalvo, W.; Escobar-Naranjo, J.; Garcia, C.A.; Garcia, M.V. Low-Cost Automation for Gravity Compensation of Robotic Arm. Appl. Sci. 2020, 10, 3823. [Google Scholar] [CrossRef]
- Razmi, M.; Macnab, C.J.B. Near-optimal neural-network robot control with adaptive gravity compensation. Neurocomputing 2020, 389, 83–92. [Google Scholar] [CrossRef]
- Morooka, Y.; Mizuuchi, I. Gravity Compensation Modular Robot:Proposal and Prototyping. J. Robot. Mechatron. 2019, 31, 697–706. [Google Scholar] [CrossRef]
- Jintian, Y.; Yangyang, L.; Quanli, Y.; Hongqiang, S. Research on Compensation Strategy of Additional Force of Main Manipulator with Force Feedback. China Mech. Eng. 2017, 28, 1156–1162. [Google Scholar]
- Jin, J.; Gans, N. Parameter identification for industrial robots with a fast and robust trajectory design approach. Robot. Comput. Integr. Manuf. 2015, 31, 21–29. [Google Scholar] [CrossRef]
- Song, Y.; Duan, J.; Xiang, L.; Li, C.; Yao, J.; Dai, Z. Design and application of a kind of high-precision, loosely coupled six-axis force (torque) sensor. J. Nanjing Univ. Aeronaut. Astronaut. 2022; in press. [Google Scholar]


| Tpye | GTL96003AXX (Self-Developed) |
|---|---|
| Range | Fx/Fy: 300 N, Fz: 500 N, Tx/Ty/Tz: 25 Nm |
| Weight | 700 g |
| Size | Ø80 mm × 40 mm |
| Protection level | IP65 |
| Overload capacity | 500% FS |
| Resolution | 0.1 N/0.02 Nm |
| Acceleration sensing accuracy | acceleration ≤ 0.01 g, angular velocity ≤ 0.05 deg/s |
| (N) | (N) | (N) | (Nm) | (Nm) | (Nm) |
| −0.6672 | 0.8565 | 0.3538 | 0.0228 | 0.0084 | 0.0080 |
| x (cm) | y (cm) | z (cm) | G (N) | U () | V () |
| 0.5 | 0.2 | 5.1 | 8.862 | −9.8716 | −5.3709 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.; Liu, Z.; Bin, Y.; Cui, K.; Dai, Z. Payload Identification and Gravity/Inertial Compensation for Six-Dimensional Force/Torque Sensor with a Fast and Robust Trajectory Design Approach. Sensors 2022, 22, 439. https://doi.org/10.3390/s22020439
Duan J, Liu Z, Bin Y, Cui K, Dai Z. Payload Identification and Gravity/Inertial Compensation for Six-Dimensional Force/Torque Sensor with a Fast and Robust Trajectory Design Approach. Sensors. 2022; 22(2):439. https://doi.org/10.3390/s22020439
Chicago/Turabian StyleDuan, Jinjun, Zhouchi Liu, Yiming Bin, Kunkun Cui, and Zhendong Dai. 2022. "Payload Identification and Gravity/Inertial Compensation for Six-Dimensional Force/Torque Sensor with a Fast and Robust Trajectory Design Approach" Sensors 22, no. 2: 439. https://doi.org/10.3390/s22020439
APA StyleDuan, J., Liu, Z., Bin, Y., Cui, K., & Dai, Z. (2022). Payload Identification and Gravity/Inertial Compensation for Six-Dimensional Force/Torque Sensor with a Fast and Robust Trajectory Design Approach. Sensors, 22(2), 439. https://doi.org/10.3390/s22020439







