Optimization Design of Surface Wave Electromagnetic Acoustic Transducers Based on Simulation Analysis and Orthogonal Test Method
Abstract
:1. Introduction
2. Transduction Mechanism and Governing Equation of EMATs
3. Surface Wave EMAT Modeling and Simulation Analysis
4. Optimal Design of EMATs
4.1. Orthogonal Test Design
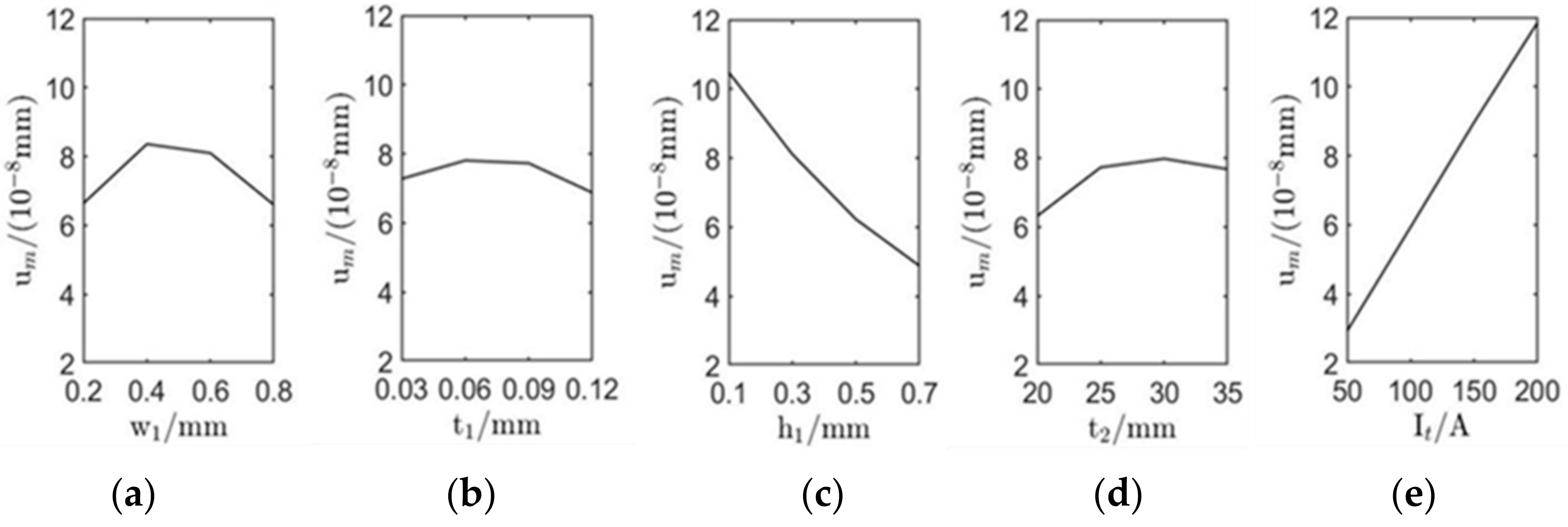
4.2. Analysis of Orthogonal Test Results
4.3. Optimal Design
5. Conclusions
- (1)
- Although the lift-off distance and excitation current play the most significant role in the enhancement of signal amplitude of surface waves, the proper choice of EMAT parameters, such as the thickness of the magnet and coil as well as the width of coil conductors can significantly increase the signal amplitude.
- (2)
- The amplitude of surface wave displacement increases linearly with the increasing excitation current or decreasing lift-off distance, and these two factors have the most significant effect on surface wave displacement. The effect of conductor width and permanent magnet height on surface waves cannot be ignored. Appropriately increasing the wire width and permanent magnet height can also increase the displacement amplitude. The coil thickness has little influence on the displacement, so the conductor thickness should be as small as possible under the condition that the manufacturing process allows.
- (3)
- The lift-off distance and excitation current have similar magnitude effects, and they have a much stronger influence on the signal amplitude of the surface waves excited by the Lorentz forces. This allows the properties of the excited surface waves to be adjusted to meet the requirements of actual applications.
- (4)
- Covering the meander-line-coil with a new material ANSM can dramatically optimize the magnetic circuit, enhance the eddy current density indicated on aluminum plate, improve the Lorentz force density in the X-direction and Y-direction, and also increase the dynamic magnetic induction intensity, thus reinforcing the signal amplitude of ultrasonic surface waves. Simply put, the new material ANSM can improve the overall performance of surface wave EMATs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Maria, K.; Gan, T.H.; Wamadeva, B.; Makis, L.; Vassilios, K.; Istvan, S.; Mohimi, A.; Round, A. High Temperature Shear Horizontal Electromagnetic Acoustic Transducer for Guided Wave Inspection. Sensors 2016, 16, 582. [Google Scholar]
- Huang, S.; Wei, Z.; Zhao, W.; Wang, S. A new omni-directional EMAT for ultrasonic Lamb wave tomography imaging of metallic plate defects. Sensors 2014, 14, 3458–3476. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, X.; Qiu, G. Optimization of a Focusable and Rotatable Shear-Wave Periodic Permanent Magnet Electromagnetic Acoustic Transducers for Plates Inspection. Sensors 2017, 17, 2722. [Google Scholar] [CrossRef] [Green Version]
- Hernandez-Valle, F.; Dixon, S. Initial tests for designing a high temperature EMAT with pulsed electromagnet. NDT E Int. 2010, 43, 171–175. [Google Scholar] [CrossRef]
- Tkocz, J.; Greenshields, D.; Dixon, S. High power phased EMAT arrays for nondestructive testing of as-cast steel. NDT E Int. 2019, 102, 47–55. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Miao, Y.; Yuan, W.; Liu, Z. Study of a spiral-coil EMAT for rail subsurface inspection. Ultrasonics 2020, 108, 106169. [Google Scholar] [CrossRef]
- Wang, S.; Huang, S.; Zhang, Y.; Wei, Z. Multiphysics modeling of a Lorentz force-based meander coil electromagnetic acoustic transducer via steady-state and transient analyses. IEEE Sens. J. 2016, 16, 6641–6651. [Google Scholar] [CrossRef]
- Kang, L.; Wang, S.; Jiang, T.; Zhai, G. Optimal Design of Lamb Wave Electromagnetic Acoustic Transducers for Improving Their Excitation Performance. Jpn. J. Appl. Phys. 2011, 50, 07HD01. [Google Scholar] [CrossRef]
- Wang, S.; Huang, S.; Velichko, A.; Wilcox, P.; Zhao, W. A muilti-objelctive structural optimization of an omnidirectional electromagnetic acoustic transducer. Ultrasonics 2017, 81, 23–31. [Google Scholar] [CrossRef] [Green Version]
- Jia, X.; Ouyang, Q. Optimal Design of Point–Focusing Shear Vertical Wave Electromagnetic Ultrasonic Transducers Based on Orthogonal Test Method. IEEE Sen. J. 2018, 18, 8064–8073. [Google Scholar] [CrossRef]
- Kang, L.; Dixon, S.; Wang, K.; Dai, J. Enhancement of signal amplitude of surface wave EMATs based on 3–D simulation analysis and orthogonal test method. NDT E Int. 2013, 59, 11–17. [Google Scholar] [CrossRef]
- Isla, J.; Cegla, F. Optimization of the Bias Magnetic Field of Shear Wave EMATs. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1148–1160. [Google Scholar] [CrossRef] [Green Version]
- Dhayalan, R.; Murthy, V.; Krishnamurthy, C.V.; Balasubramaniam, K. Improving the signal amplitude of meandering coil EMATs by using ribbon soft magnetic flux concentrators (MFC). Ultrasonics 2011, 51, 675–682. [Google Scholar] [CrossRef]
- Qiu, G.; Song, X.; Zhang, X.; Tu, J.; Chen, T. Pure SH1 Guided-Wave Generation Method with Dual Periodic-Permanent-Magnet Electromagnetic Acoustic Transducers for Plates Inspection. Sensors 2019, 19, 3019. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y. Orthogonal Optimal Design Method for Spiral Coil EMAT Considering Lift-off Effect: A Case Study. IEEE Access 2021, 9, 22062–22070. [Google Scholar] [CrossRef]
- Sun, H.; Wang, S.; Huang, S.; Peng, L.; Zou, J. Point-Focusing Shear-Horizontal Guided Wave EMAT Optimization Method Using Orthogonal Test Theory. IEEE Sen. J. 2020, 20, 6295–6304. [Google Scholar] [CrossRef]
- Thring, C.B.; Fan, Y.; Edwards, R.S. Multi-coil focused EMAT for characterisation of surface-breaking defects of arbitrary orientation. NDT E Int. 2017, 88, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Tkocz, J.; Dixon, S. Electromagnetic acoustic transducer optimisation for surface wave applications. NDT E Int. 2019, 107, 102142. [Google Scholar] [CrossRef]
- Trushkevych, O.; Edwards, R.S. Differential Coil EMAT for Simultaneous Detection of In-Plane and Out-of-Plane Components of Surface Acoustic Waves. IEEE Sen. J. 2020, 20, 11156–11162. [Google Scholar] [CrossRef]
- Sun, H.; Uchimoto, T.; Takagi, T. New combination of magnet and coil of electromagnetic acoustic transducer for generating and detecting Rayleigh wave. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 832–839. [Google Scholar] [CrossRef]
- Kang, L.; Zhang, C.; Dixon, S.; Zhao, H.; Hill, S.; Liu, M. Enhancement of Ultrasonic Signal Using a New Design of Rayleigh–Wave Electromagnetic Acoustic Transducer. NDT E Int. 2017, 86, 36–43. [Google Scholar] [CrossRef]
- Wang, S.; Lei, K.; Li, Z.; Zhai, G.; Long, Z. 3–D modeling and analysis of meander–line–coil surface wave EMATs. Mechatronics 2012, 22, 653–660. [Google Scholar] [CrossRef]
- Jin, L.; Liu, X.; Kou, X.; Yang, Q.; Guo, F. An Activity Determination Method of Crack Defects in Aluminum Plate and Steel Plate Based on EMAT. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
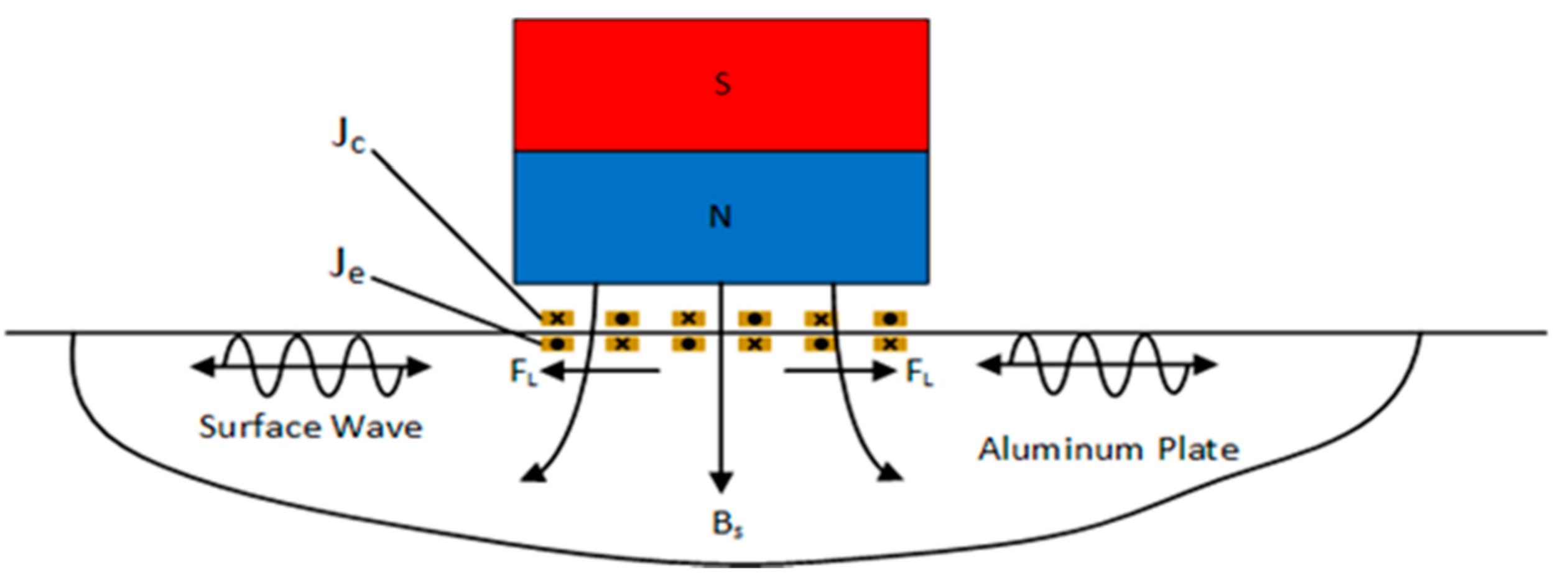
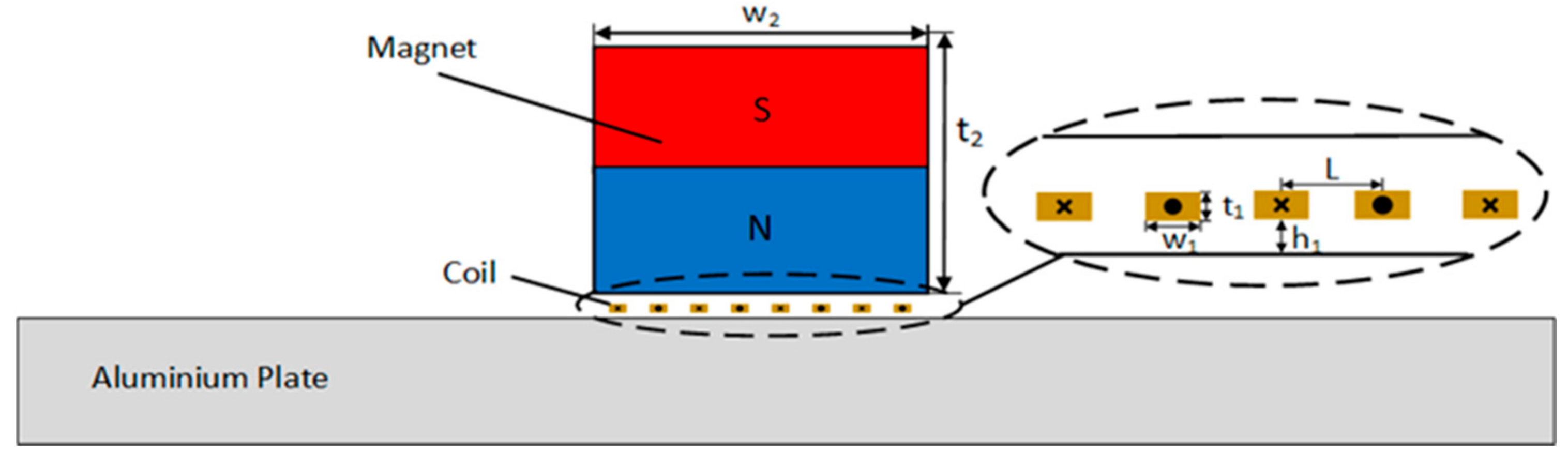











| Object | Parameter | Value |
|---|---|---|
| Coil | Width | 0.1 mm |
| Thickness | 0.05 mm | |
| List-off distance | 0.1 mm | |
| Resistivity | Ωm | |
| Magnet | Width | 22 mm |
| Thickness | 20 mm | |
| Magnetic flux density | 1.35 T | |
| List-off distance | 1.0 mm | |
| Aluminum Plate | Width | 320 mm |
| Thickness | 20 mm | |
| Density | 2700 kg/m3 | |
| Electrical conductivity | S/m | |
| Young’s modulus | Pa | |
| Poisson’s ratio | 0.33 | |
| Excitation Current | Peak value | 50 A |
| Frequency | 500 kHz |
| Levels | |||||
|---|---|---|---|---|---|
| 1 | 0.2 | 0.03 | 0.1 | 20 | 50 |
| 2 | 0.4 | 0.06 | 0.3 | 25 | 100 |
| 3 | 0.6 | 0.09 | 0.5 | 30 | 150 |
| 4 | 0.8 | 0.12 | 0.7 | 35 | 200 |
| Run | |||||||
|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (mm) | (A) | |||
| 1 | 0.2 | 0.03 | 0.1 | 20 | 50 | 3.95 | 1.63 |
| 2 | 0.2 | 0.06 | 0.3 | 25 | 100 | 6.53 | 2.69 |
| 3 | 0.2 | 0.09 | 0.5 | 30 | 150 | 7.85 | 3.23 |
| 4 | 0.2 | 0.12 | 0.7 | 35 | 200 | 8.23 | 3.37 |
| 5 | 0.4 | 0.03 | 0.3 | 30 | 200 | 13.9 | 5.67 |
| 6 | 0.4 | 0.06 | 0.1 | 35 | 150 | 13.6 | 5.60 |
| 7 | 0.4 | 0.09 | 0.7 | 20 | 100 | 3.52 | 1.46 |
| 8 | 0.4 | 0.12 | 0.5 | 25 | 50 | 2.43 | 1.01 |
| 9 | 0.6 | 0.03 | 0.5 | 35 | 100 | 5.53 | 2.28 |
| 10 | 0.6 | 0.06 | 0.7 | 30 | 50 | 2.00 | 0.83 |
| 11 | 0.6 | 0.09 | 0.1 | 25 | 200 | 16.2 | 6.65 |
| 12 | 0.6 | 0.12 | 0.3 | 20 | 150 | 8.68 | 3.56 |
| 13 | 0.8 | 0.03 | 0.7 | 25 | 150 | 5.76 | 2.37 |
| 14 | 0.8 | 0.06 | 0.5 | 20 | 200 | 9.12 | 3.73 |
| 15 | 0.8 | 0.09 | 0.3 | 35 | 50 | 3.35 | 1.39 |
| 16 | 0.8 | 0.12 | 0.1 | 30 | 100 | 8.17 | 3.35 |
| Amplitude | ||||||
|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (mm) | (A) | ||
| k1 | 6.64 | 7.28 | 10.48 | 6.32 | 2.93 | |
| k2 | 8.36 | 7.81 | 8.11 | 7.73 | 5.94 | |
| k3 | 8.10 | 7.73 | 6.23 | 7.98 | 8.97 | |
| mm) | k4 | 6.60 | 6.88 | 4.88 | 7.68 | 11.9 |
| Ru | 1.76 | 0.93 | 5.60 | 1.66 | 8.97 | |
| (0.93) | ||||||
| k1 | 2.73 | 2.98 | 4.31 | 2.59 | 1.21 | |
| k2 | 3.43 | 3.21 | 3.82 | 3.18 | 2.44 | |
| k3 | 3.33 | 3.18 | 2.56 | 3.27 | 3.69 | |
| mm) | k4 | 2.71 | 2.82 | 2.01 | 3.16 | 4.85 |
| Rv | 0.72 | 0.39 | 2.30 | 0.68 | 3.64 | |
| (0.39) | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, J.; Zhang, J.; Jia, X.; Gao, R. Optimization Design of Surface Wave Electromagnetic Acoustic Transducers Based on Simulation Analysis and Orthogonal Test Method. Sensors 2022, 22, 524. https://doi.org/10.3390/s22020524
Lan J, Zhang J, Jia X, Gao R. Optimization Design of Surface Wave Electromagnetic Acoustic Transducers Based on Simulation Analysis and Orthogonal Test Method. Sensors. 2022; 22(2):524. https://doi.org/10.3390/s22020524
Chicago/Turabian StyleLan, Ju, Jingjun Zhang, Xiaojuan Jia, and Ruizhen Gao. 2022. "Optimization Design of Surface Wave Electromagnetic Acoustic Transducers Based on Simulation Analysis and Orthogonal Test Method" Sensors 22, no. 2: 524. https://doi.org/10.3390/s22020524
APA StyleLan, J., Zhang, J., Jia, X., & Gao, R. (2022). Optimization Design of Surface Wave Electromagnetic Acoustic Transducers Based on Simulation Analysis and Orthogonal Test Method. Sensors, 22(2), 524. https://doi.org/10.3390/s22020524





