A Study on the Correlation between Change in the Geometrical Dimension of a Free-Falling Molten Glass Gob and Its Viscosity
Abstract
:1. Introduction
2. Related Work
2.1. Relation between the Surface Tension and the Temperature of Molten Glass
2.2. Relation between the Surface Tension and the Viscosity of Molten Glass
3. Theory
3.1. The Importance of Glass Composition
3.2. Viscosity for Glass Container Manufacturing
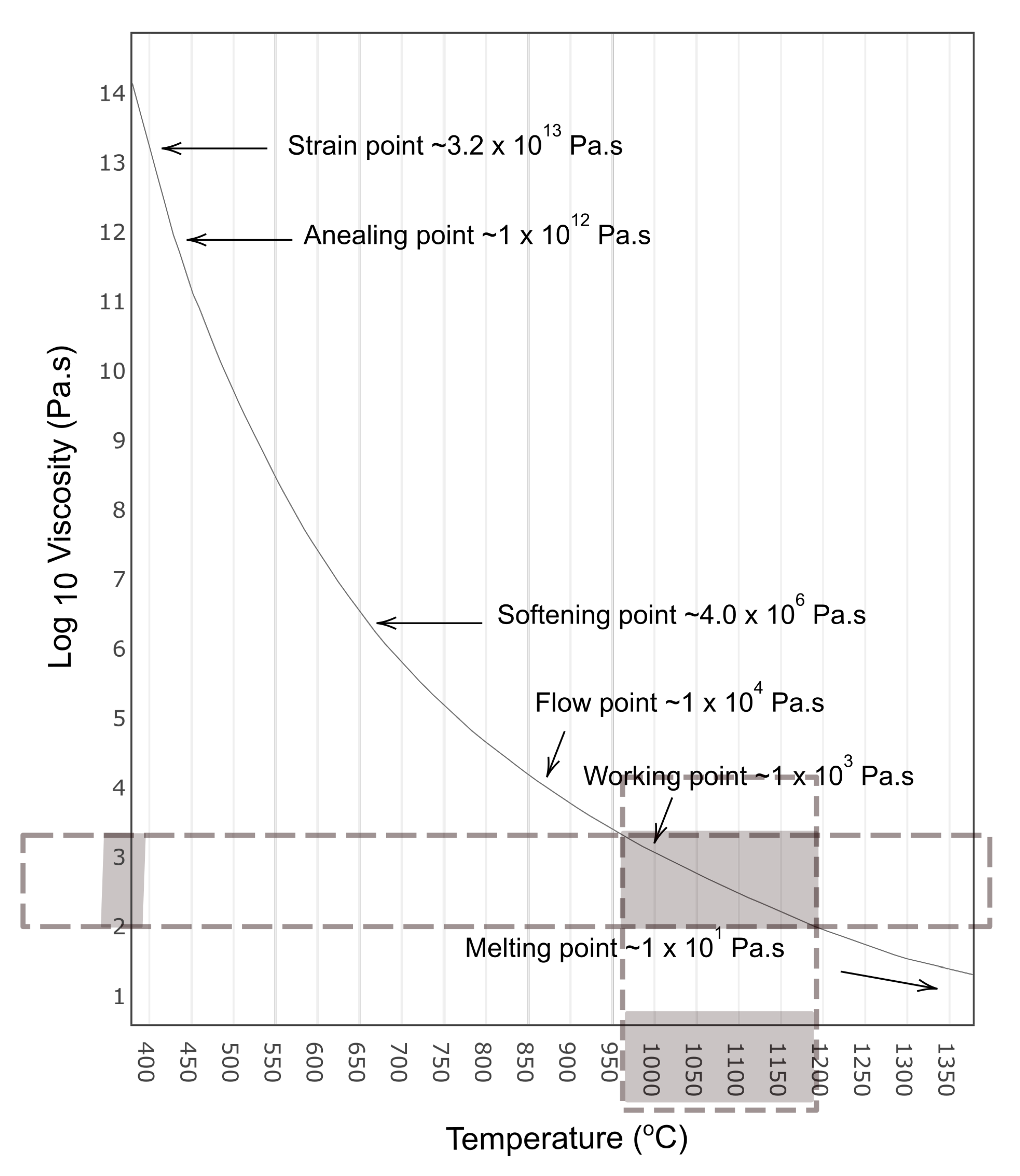
3.3. Relation between the Temperature and the Viscosity of Glass Melt
4. Materials and Methods
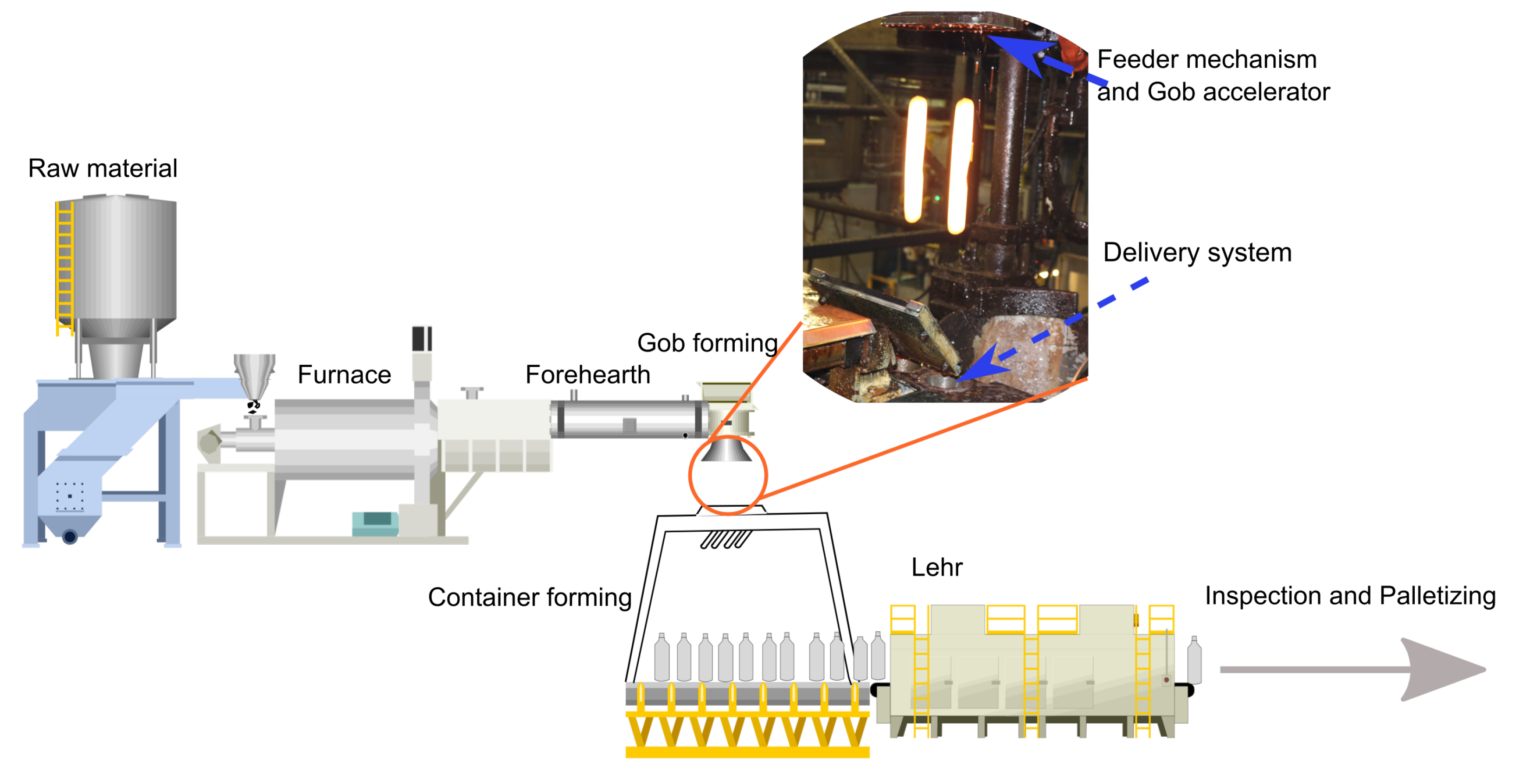
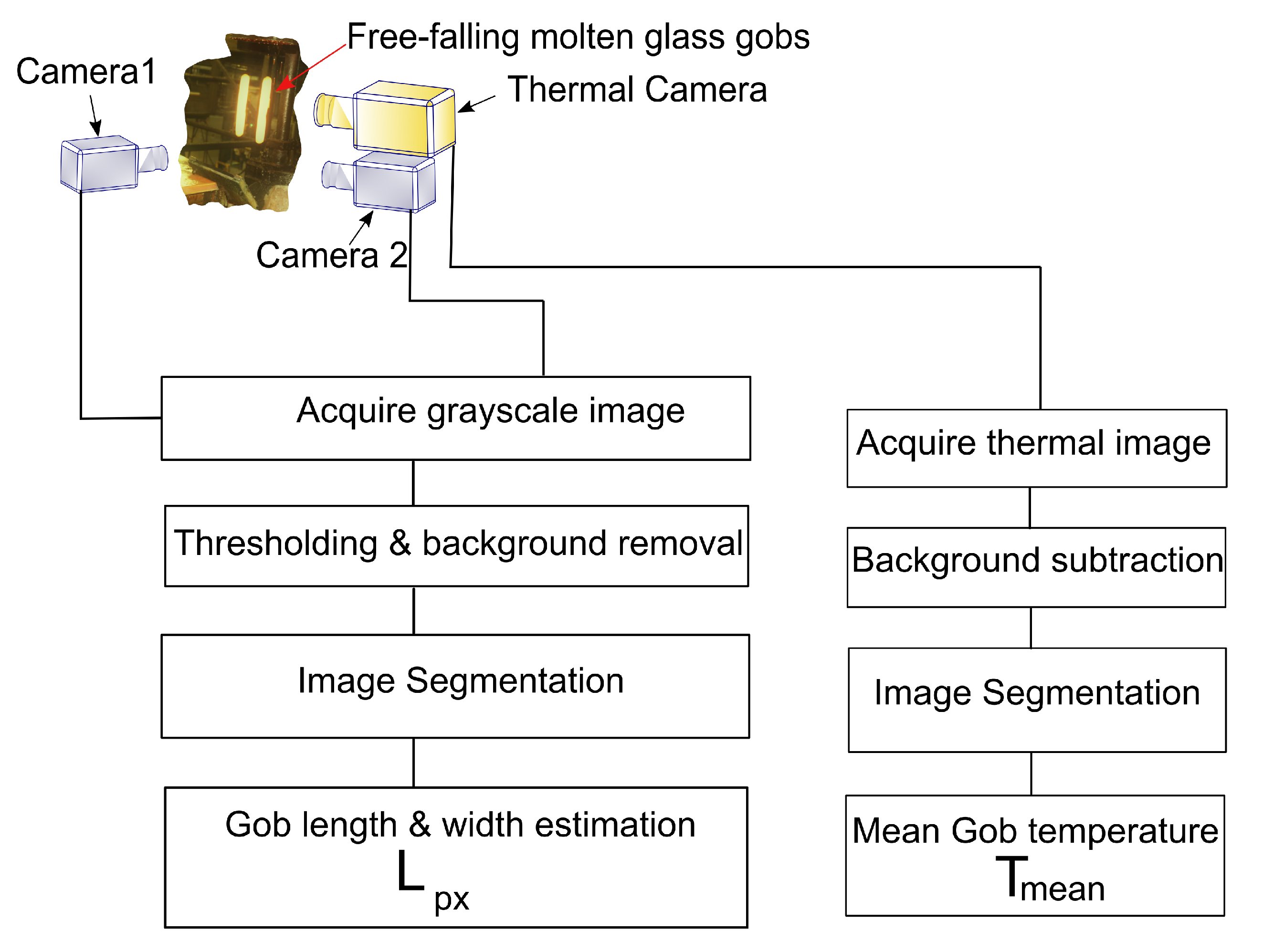
4.1. Experimental Setup
4.2. Methodology to Find the Relation between Gob Shape, Gob Temperature and Gob Viscosity
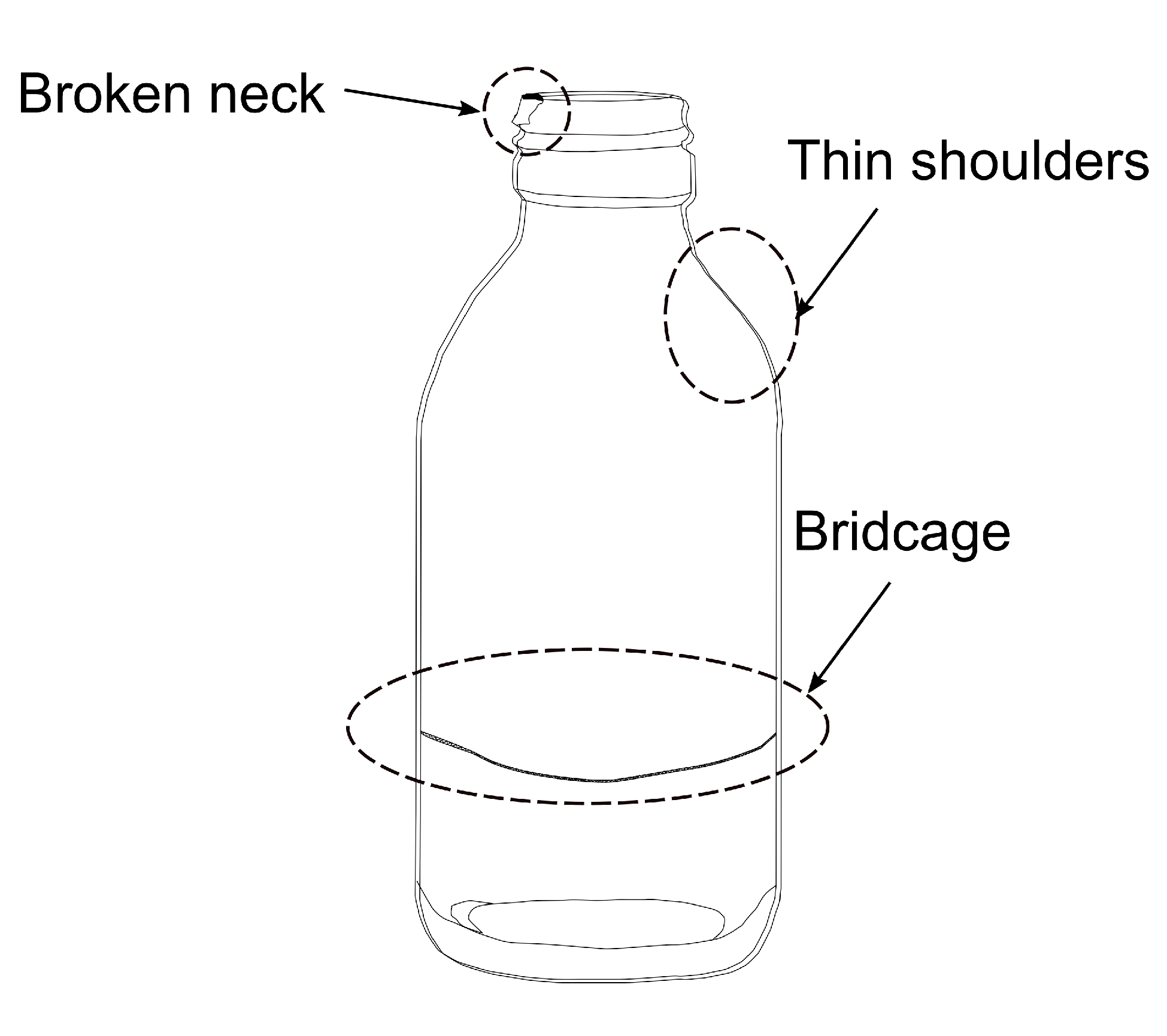
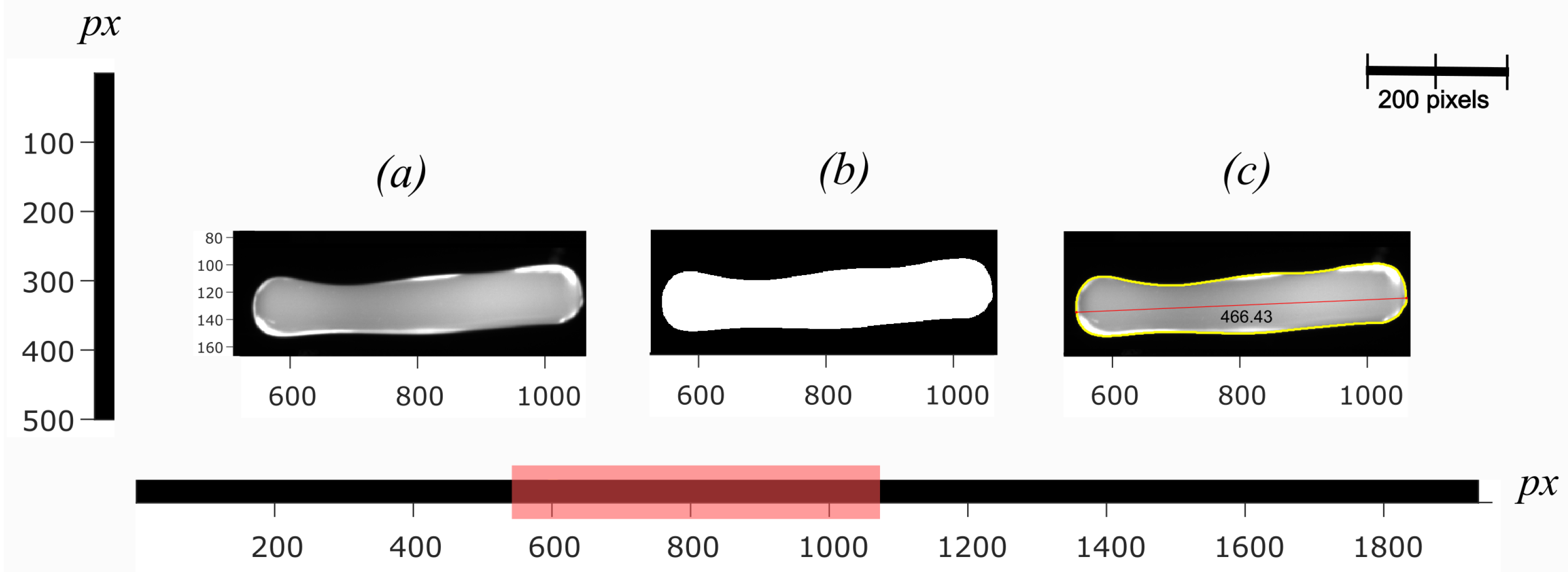
4.2.1. Determination of Geometrical Shape Change Rate,
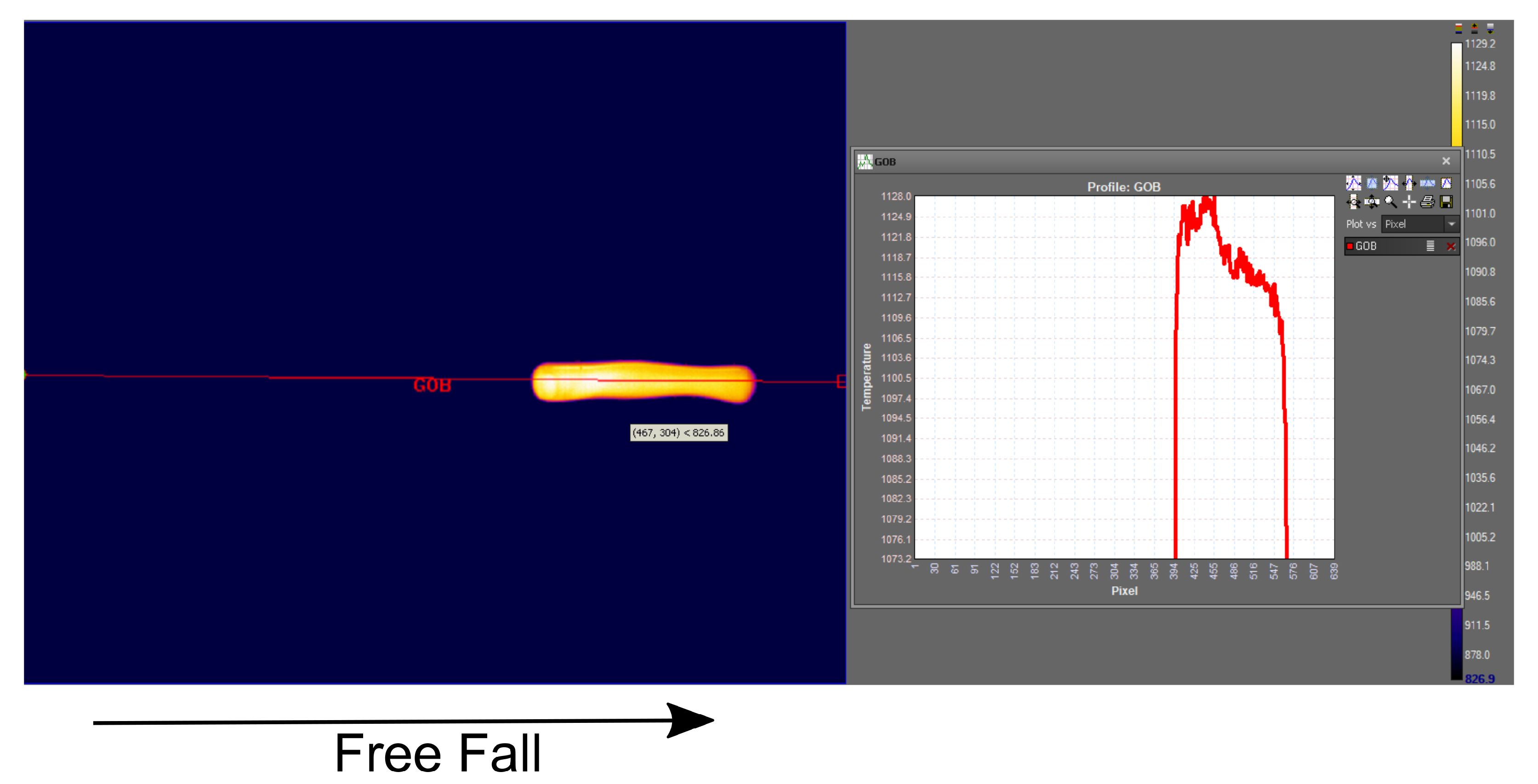
4.2.2. Measurement of the Temperature of the Molten Gob
4.2.3. Model to Correlate Viscosity and Temperature in the Molten Gob with Its
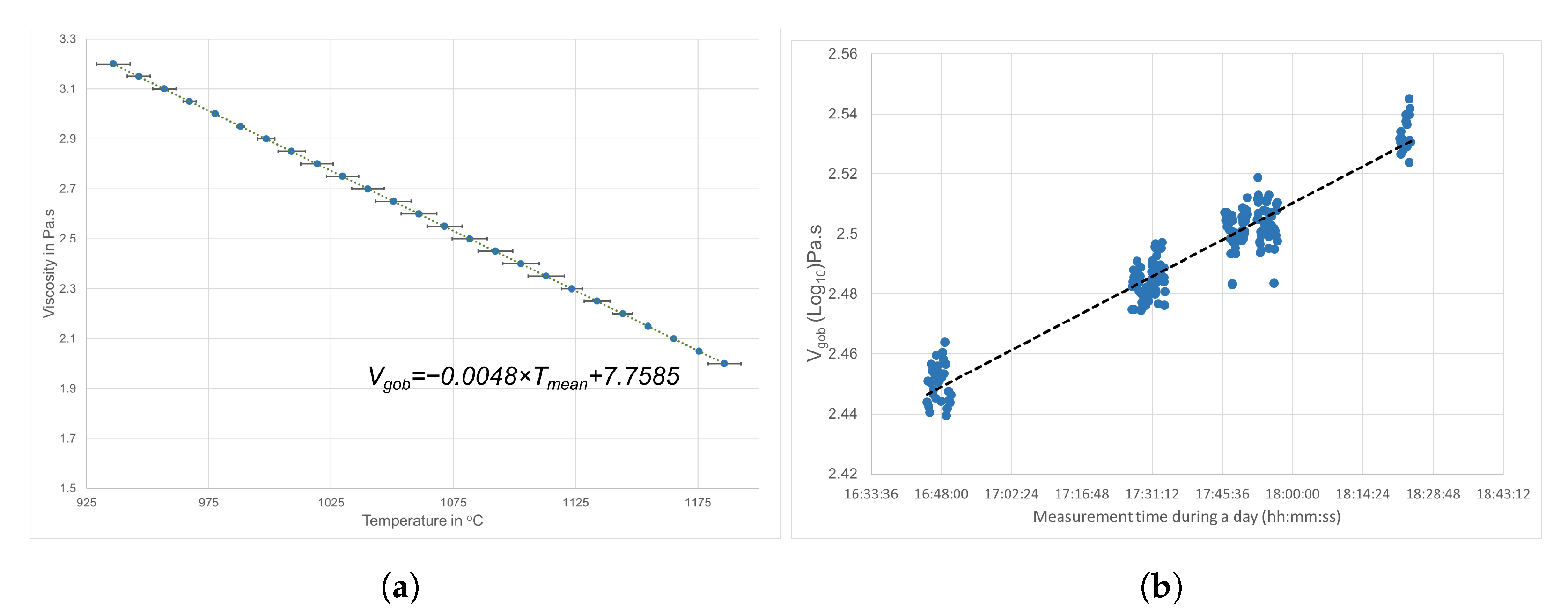
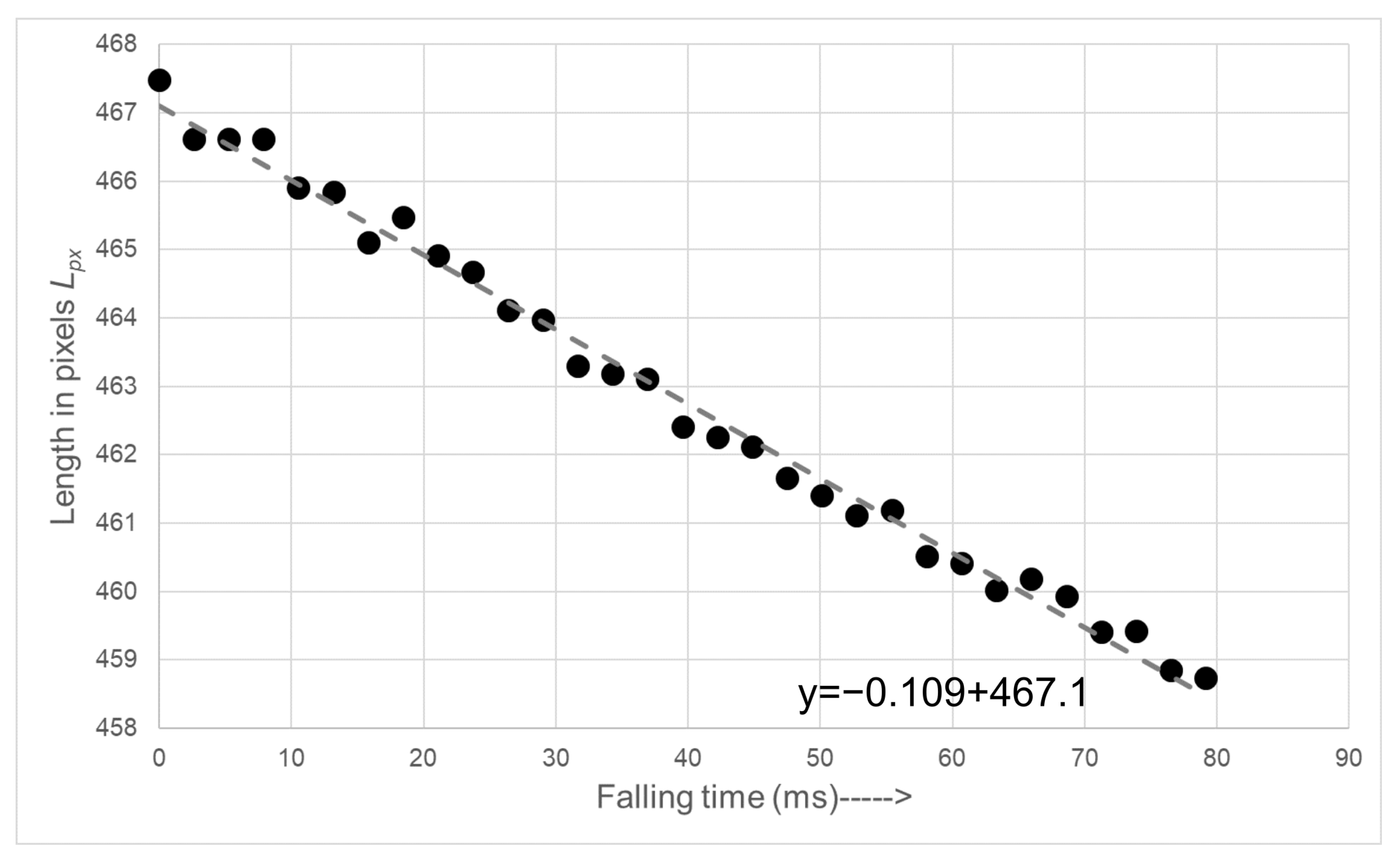
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hyre, M.R.; Paul, K. The Effect of Shear Angle on Gob Formation. In A Collection of Papers Presented at the 60th Conference on Glass Problems: Ceramic Engineering and Science Proceedings; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2000; pp. 87–107. [Google Scholar]
- Gough, B.; Eng, P.; Matovich, D. Predictive-adaptive temperature control of molten glass. In Proceedings of the IEEE Industry Applications Society Dynamic Modeling Control Applications for Industry Workshop, Vancouver, BC, Canada, 26–27 May 1997; pp. 51–55. [Google Scholar] [CrossRef]
- Kai, H.; Tobias, N. Case Study: Gob Loading in a Glass Moulding Machine. Procedia CIRP 2016, 39, 203–208. [Google Scholar] [CrossRef]
- Le Baurhis, E. Glass: Mechanics and Technology, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Butler, D.; Zhang, H. Intelligent software sensors and process prediction for glass container forming processes based on multivariate statistical process control techniques. In Proceedings of the 2012 UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 281–285. [Google Scholar] [CrossRef]
- Laizola, E.; Jimenez, A.R.; Calvache, M.; Seco, F. Computer-vision-based gob inspection system for monitoring and control in the glass industry. In Proceedings of the Electronic Imaging 2003, Santa Clara, CA, USA, 20–24 January 2003; p. 12. [Google Scholar]
- Pye, L.D.; Stevens, H.J.; LaCourse, W.C. (Eds.) Introduction to Glass Science. In Proceedings of the Tutorial Symposium held at the State University of New York, College of Ceramics at Alfred University, Alfred, NY, USA,, 8–19 June 1970; Springer: Boston, MA, USA, 1972. [Google Scholar] [CrossRef]
- Kovačec, M.; Pilipović, A.; Štefanić, N. Improving the quality of glass containers production with plunger process control. CIRP J. Manuf. Sci. Technol. 2010, 3, 304–310. [Google Scholar] [CrossRef] [Green Version]
- Musgraves, J.D.; Hu, J.; Calvez, L. (Eds.) Springer Handbook of Glass; Springer Handbooks; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Bakhtiyarov, S.; Overfelt, R. Measurement of liquid metal viscosity by rotational technique. Acta Mater. 1999, 47, 4311–4319. [Google Scholar] [CrossRef]
- Joshi, D.; Joseph, P.F. Parallel Plate Viscometry for Glass at High Viscosity. J. Am. Ceram. Soc. 2014, 97, 354–357. [Google Scholar] [CrossRef]
- Dorfman, A.; Hess, K.U.; Dingwell, D. Centrifuge-assisted falling-sphere viscometry. Eur. J. Mineral. 1996, 8, 507–514. [Google Scholar] [CrossRef]
- Shartsis, L.; Spinner, S. Viscosity and density of molten optical glasses. J. Res. Natl. Bur. Stand. 1951, 46, 176. [Google Scholar] [CrossRef]
- HAGY, H.E. Experimental Evaluation of Beam-Bending Method of Determining Glass Viscosities in the Range 108 to 1015 Poises. J. Am. Ceram. Soc. 1963, 46, 93–97. [Google Scholar] [CrossRef]
- Xu, D.; Wang, H.; Shi, J.; Xie, D. The design of metallurgical slag and molten metal viscosity test system. In Proceedings of the 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shengyang, China, 20–22 December 2013; pp. 733–737. [Google Scholar] [CrossRef]
- Biosca, A.; Borrós, S.; Clemente, V.P.; Granada, A.A.G. Glass Gob Modeling and Experimental Validation Using a Drop Test. MATEC Web Conf. 2018, 167, 02009. [Google Scholar] [CrossRef] [Green Version]
- Hussain, M.; O’Nils, M.; Lundgren, J. Multi-Camera Based Setup for Geometrical Measurement of Free-Falling Molten Glass Gob. Sensors 2021, 21, 1041. [Google Scholar] [CrossRef]
- Carratu, M.; Liguori, C.; Pietrosanto, A.; O’Nils, M.; Lundgren, J. Data Fusion for Timber Bundle Volume Measurement. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Hans, A. Electromagnetic in-line measurement of viscosity. In Proceedings of the IMTC/2002, 19th IEEE Instrumentation and Measurement Technology Conference (IEEE Cat. No.00CH37276), Anchorage, AK, USA, 21–23 May 2002; Volume 2, pp. 1023–1028. [Google Scholar] [CrossRef]
- Lillie, H.R. Viscosity of glass between the strain point and melting temperature1. J. Am. Ceram. Soc. 1931, 14, 502–512. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Sethuraman, S. Ultrasonic interferometric sensor for rheological changes of fluids. Rev. Sci. Instruments 2006, 77, 084902. [Google Scholar] [CrossRef]
- Moradian, A.; Mostaghimi, J. Measurement of Surface Tension, Viscosity, and Density at High Temperatures by Free-Fall Drop Oscillation. Metall. Mater. Trans. B 2008, 39, 280–290. [Google Scholar] [CrossRef]
- Matsumoto, T.; Fujii, H.; Ueda, T.; Kamai, M.; Nogi, K. Oscillating drop method using a falling droplet. Rev. Sci. Instruments 2004, 75, 1219–1221. [Google Scholar] [CrossRef]
- Griffith. A, A. VI. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1921, 221, 163–198. [Google Scholar] [CrossRef] [Green Version]
- Washburn, E.; Shelton, G.; Libman, E. The Viscosities and Surface Tensions of the Soda-Lime-Silica Glasses at High Temperatures. Univ. Ill. Bull. 1924, 21, 33–48. [Google Scholar]
- Pietenpol, W.B. Surface Tension of Molten Glass. Physics 1936, 7, 26–31. [Google Scholar] [CrossRef]
- Pye, L.D.; Montenero, A.; Joseph, I. (Eds.) Properties of Glass-Forming Melts; Taylor & Francis: Boca Raton, FL, USA, 2005. [Google Scholar]
- Fulcher, G.S. Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 1925, 8, 339–355. [Google Scholar] [CrossRef]
- Infrared Pyrometry in the Glass Industry. Available online: https://www.calex.co.uk/site/wp-content/uploads/2015/07/ir-in-glass-industry.pdf (accessed on 21 April 2021).
- Flir System Inc. Datasheet Flir A6750sc; Datasheet RND_033_US; Flir System Inc.: Wilsonville, OR, USA, 2015. [Google Scholar]
- Lakatos, T. Viscosity-Temperature relations in glass composed of SiO2-Al2O3-Na2O-K2O-Li2O-CaO-MgO-BaO-PbO-B2O3. Glastek. Tidskr. 1976, 31, 51–54. [Google Scholar]
- Davis, J.W.; Sharma, V. Background-Subtraction in Thermal Imagery Using Contour Saliency. Int. J. Comput. Vis. 2007, 71, 161–181. [Google Scholar] [CrossRef]
- Pearson, K. VII. Mathematical contributions to the theory of evolution.—III. Regression, heredity, and panmixia. Trans. R. Soc. London. Ser. A Contain. Pap. Math. Phys. Character 1896, 187, 253–318. [Google Scholar] [CrossRef] [Green Version]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Viskanta, R.; Lim, J. Transient cooling of a cylindrical glass gob. J. Quant. Spectrosc. Radiat. Transf. 2002, 73, 481–490. [Google Scholar] [CrossRef]
- Evans, J.D. Straightforward Statistics for the Behavioral Sciences; Straightforward Statistics for the Behavioral Sciences; Thomson Brooks/Cole Publishing Co.: Belmont, CA, USA, 1996; pp. 256–260. [Google Scholar]





| Viscosity Ranges from some Glass Manufacturing Operations. | |
|---|---|
| Note: viscosity values are converted to log10 Pa.s | |
| Glass melting | 0.5 to 1.5 |
| Sealing glasses to other glasses or to metals | 2.5 to 2.8 |
| Producing gobs for container forming | 2.6 to 3.2 |
| Drawing sheet glass (Fourcault process) | 3.0 to 3.4 |
| Glass pressing | 3.0 to 5.3 |
| Surface of a bottle during blowing | 4.7 to 9.0 |
| Sinter glass powder to a solid body | 5.0 |
| Sinter glass powder to form a porous body | 7.0 to 7.8 |
| Dilatometric softening point | 10.3 to 10.7 |
| Annealing range | 11.0 to 13.0 |
| Stress release occurs in a few seconds | 11.8 |
| Temperature for matching expansion curves for seals | 13.0 to 13.5 |
| Stress release too slow to be useful | above 13.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, M.; O’Nils, M.; Lundgren, J.; Shallari, I. A Study on the Correlation between Change in the Geometrical Dimension of a Free-Falling Molten Glass Gob and Its Viscosity. Sensors 2022, 22, 661. https://doi.org/10.3390/s22020661
Hussain M, O’Nils M, Lundgren J, Shallari I. A Study on the Correlation between Change in the Geometrical Dimension of a Free-Falling Molten Glass Gob and Its Viscosity. Sensors. 2022; 22(2):661. https://doi.org/10.3390/s22020661
Chicago/Turabian StyleHussain, Mazhar, Mattias O’Nils, Jan Lundgren, and Irida Shallari. 2022. "A Study on the Correlation between Change in the Geometrical Dimension of a Free-Falling Molten Glass Gob and Its Viscosity" Sensors 22, no. 2: 661. https://doi.org/10.3390/s22020661
APA StyleHussain, M., O’Nils, M., Lundgren, J., & Shallari, I. (2022). A Study on the Correlation between Change in the Geometrical Dimension of a Free-Falling Molten Glass Gob and Its Viscosity. Sensors, 22(2), 661. https://doi.org/10.3390/s22020661








