Next Article in Journal
Spatio-Temporal Modeling and Simulation of Asian Soybean Rust Based on Fuzzy System
Next Article in Special Issue
Revisiting the Analysis of Radiative Mid-Range Wireless Link for Pacemakers
Previous Article in Journal
Using a Deep Learning Model to Explore the Impact of Clinical Data on COVID-19 Diagnosis Using Chest X-ray
Previous Article in Special Issue
Acoustic Power Measurement and Thermal Bioeffect Evaluation of Therapeutic Langevin Transducers
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sensors
Volume 22
Issue 2
10.3390/s22020670
sensors-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modal Frequencies Associations with Musculoskeletal Components of Human Legs for Extracorporeal Bone Healing Assessment Based on a Vibration Analysis Approach

by
Benjamin Steven Vien
1,*,
Wing Kong Chiu
1,
Matthias Russ
2,3 and
Mark Fitzgerald
2,3
1
Department of Mechanical and Aerospace Engineering, Monash University, Wellington Road, Clayton 3800, Australia
2
The Alfred Hospital, 55 Commercial Road, Melbourne 3004, Australia
3
National Trauma Research Institute, 89 Commercial Road, Melbourne 3004, Australia
*
Author to whom correspondence should be addressed.
Sensors 2022, 22(2), 670; https://doi.org/10.3390/s22020670
Submission received: 13 December 2021 / Revised: 11 January 2022 / Accepted: 14 January 2022 / Published: 16 January 2022
(This article belongs to the Collection Medical Applications of Sensor Systems and Devices)
Browse Figures
Versions Notes

Abstract

Reliable and quantitative assessments of bone quality and fracture healing prompt well-optimised patient healthcare management and earlier surgical intervention prior to complications of nonunion and malunion. This study presents a clinical investigation on modal frequencies associations with musculoskeletal components of human legs by using a prototype device based on a vibration analysis method. The findings indicated that the first out-of-plane and coupled modes in the frequency range from 60 to 110 Hz are associated with the femur length, suggesting these modes are suitable quantitative measures for bone evaluation. Furthermore, higher-order modes are shown to be associated with the muscle and fat mass of the leg. 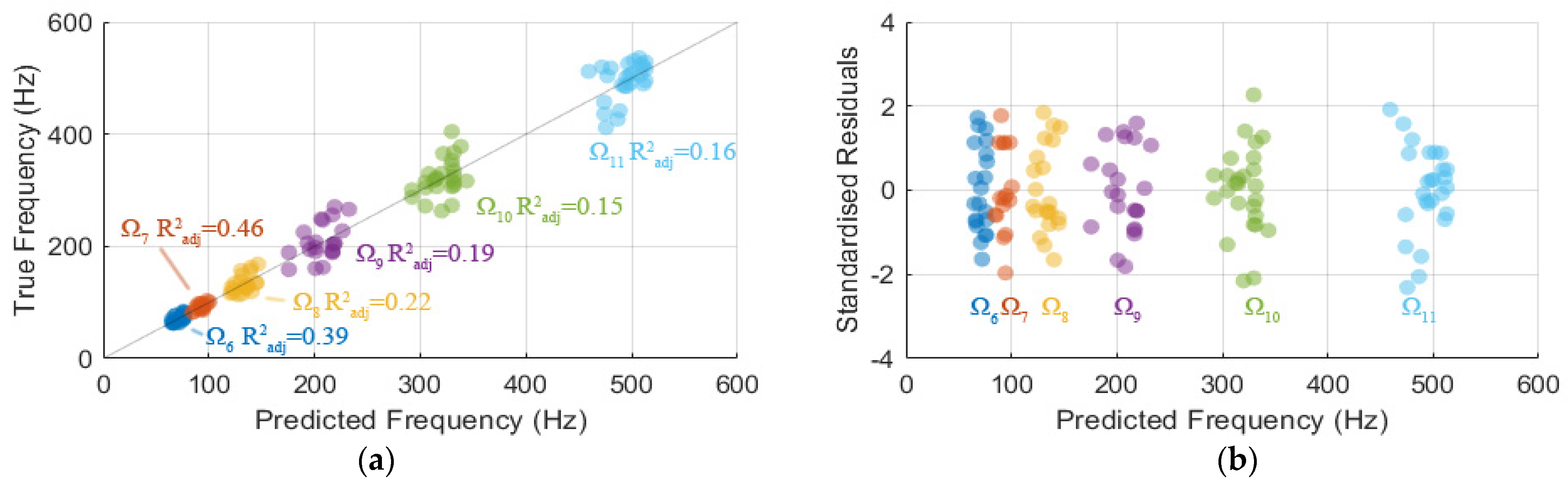In addition, mathematical models are formulated via a stepwise regression approach to determine the modal frequencies using the measured leg components as variables. The optimal models of the first modes consist of only femur length as the independent variable and explain approximately 43% of the variation of the modal frequencies. The subsequent findings provide insights for further development on utilising vibration-based methods for practical bone and fracture healing monitoring.
Keywords: vibration analysis; fracture healing; bone assessment; human health monitoring; biomechanics; medical device; modal frequency vibration analysis; fracture healing; bone assessment; human health monitoring; biomechanics; medical device; modal frequency

Share and Cite

MDPI and ACS Style

Vien, B.S.; Chiu, W.K.; Russ, M.; Fitzgerald, M. Modal Frequencies Associations with Musculoskeletal Components of Human Legs for Extracorporeal Bone Healing Assessment Based on a Vibration Analysis Approach. Sensors 2022, 22, 670. https://doi.org/10.3390/s22020670

AMA Style

Vien BS, Chiu WK, Russ M, Fitzgerald M. Modal Frequencies Associations with Musculoskeletal Components of Human Legs for Extracorporeal Bone Healing Assessment Based on a Vibration Analysis Approach. Sensors. 2022; 22(2):670. https://doi.org/10.3390/s22020670

Chicago/Turabian Style

Vien, Benjamin Steven, Wing Kong Chiu, Matthias Russ, and Mark Fitzgerald. 2022. "Modal Frequencies Associations with Musculoskeletal Components of Human Legs for Extracorporeal Bone Healing Assessment Based on a Vibration Analysis Approach" Sensors 22, no. 2: 670. https://doi.org/10.3390/s22020670

APA Style

Vien, B. S., Chiu, W. K., Russ, M., & Fitzgerald, M. (2022). Modal Frequencies Associations with Musculoskeletal Components of Human Legs for Extracorporeal Bone Healing Assessment Based on a Vibration Analysis Approach. Sensors, 22(2), 670. https://doi.org/10.3390/s22020670

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop