Modeling of Respiratory Motion to Support the Minimally Invasive Destruction of Liver Tumors
Abstract
:1. Introduction
- Breath-holding—this requires the patient to hold their breath during inhalation or expiration. This requires close cooperation between the patient and the doctor, which is not always possible due to the patient’s condition and accompanying stress.
- The tracking of respiratory movements—in this case, the patient can breathe freely.
- Gating—the patient can breathe freely, and procedural activities are performed in a specific phase of the respiratory cycle, selected when planning the procedure. According to reports from the American Society of Medical Physicists, this method is used by many cancer hospitals [7].
2. Materials and Methods
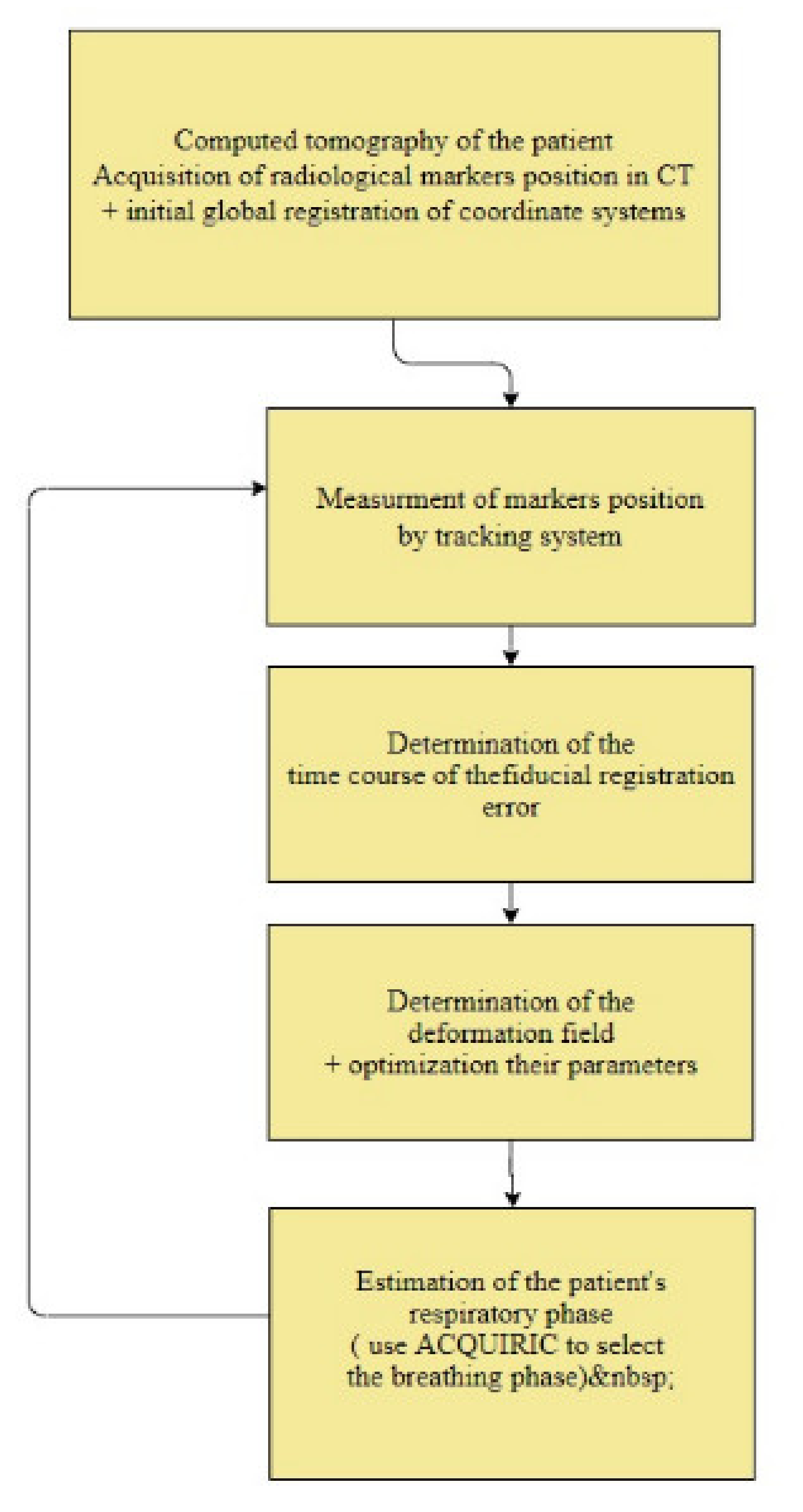
2.1. Modeling of Respiratory Movements as a Problem of Time–Space Adjustment
- Initial global registration of coordinate systems;
- Measurement of the position of markers on the patient’s body;
- Determination of the time course of the marker registration error;
- Determination of the deformation field;
- Optimization of the selection of parameters for determining the deformation field;
- Estimation of the patient’s respiratory phase;
- Adaptation of the AQUIRC approach.
2.1.1. Initial Global Registration of Coordinate Systems
2.1.2. Measuring the Position of Markers on the Patient’s Body
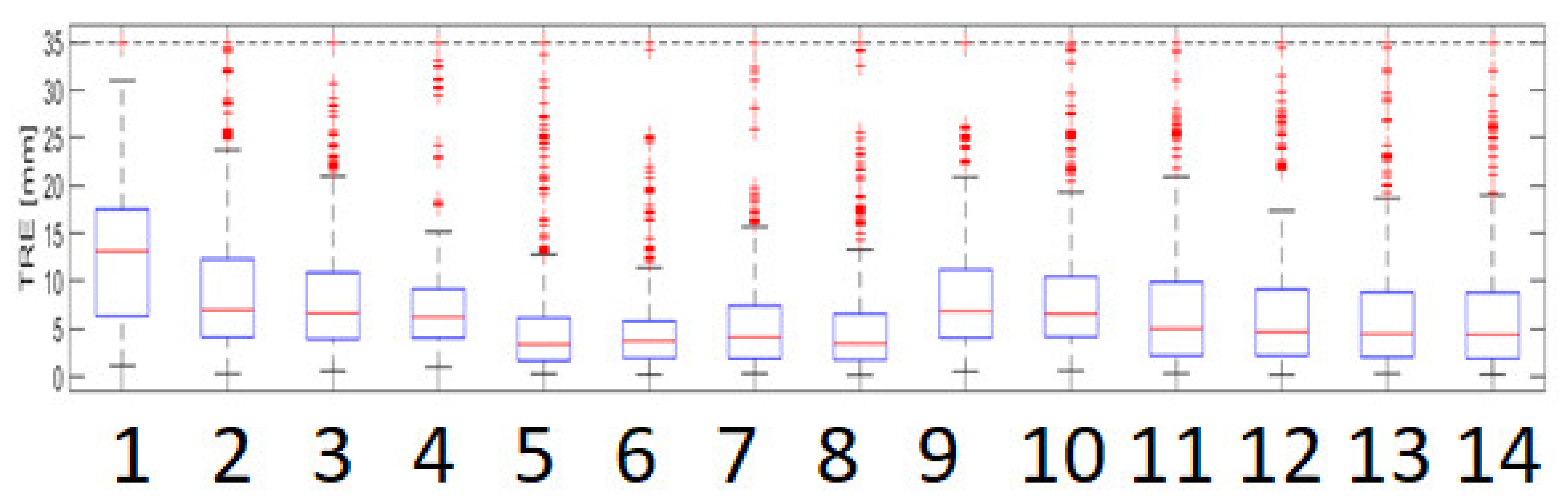
2.1.3. Determination of the Time Course of the Marker Registration Error
- The position of the markers on the patient’s surface during the respiratory cycle is measured.
2.1.4. Determination of the Deformation Field
TPS Spline Curves
EBS Spline Curves—Interpolation Approach
2.1.5. Optimization of the Selection of Parameters for Determining the Deformation Field
PSO Algorithm
Algorithm of Swarm Optimization—Differential Evolution
2.1.6. Estimation of the Patient’s Respiratory Phase
2.1.7. Adaptation of the AQUIRC Approach to the Problem of Reducing the Time–Space Error of the Target Point during Minimally Invasive Abdominal Procedures
2.1.8. Conducted Experiments
2.2. Synchronization of Information from Pre-Operative and Intraoperative Image Sequences
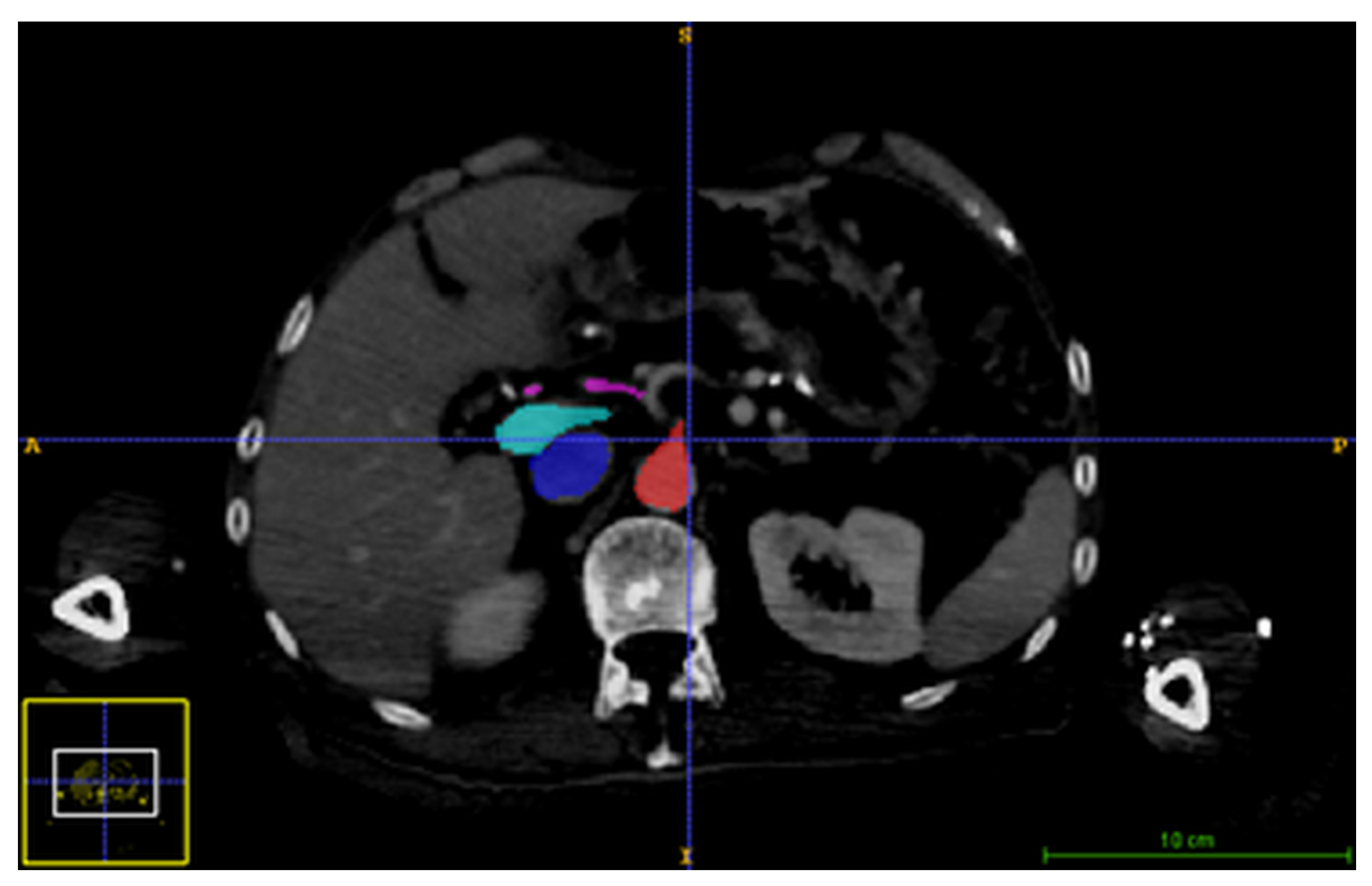
2.2.1. Image Acquisition
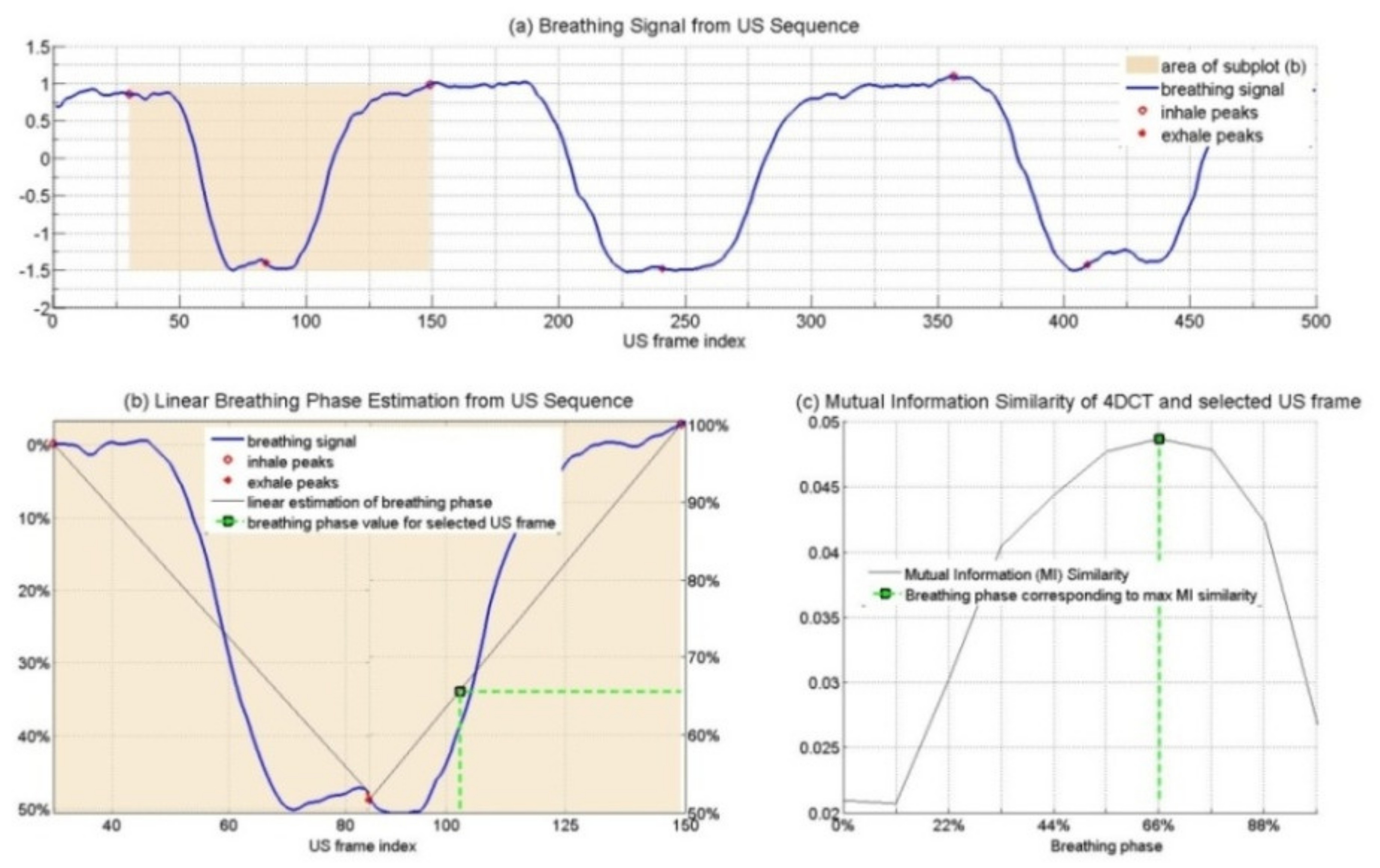
2.2.2. Respiratory Phase Signal Estimation from US Images
2.2.3. Determining the Spatio-Temporal Correspondence between the Intraoperative US Sequence and Pre-Operative the 4D CT Images
- Two-dimensional CT sequences were generated from the four-dimensional CT that corresponded spatially to the US sequence;
- The breathing signal from the 2D CT sequence was estimated (based on the same method as described for US images);
- Hilbert’s transformation angles were calculated to estimate the breathing signal from the corresponding CT sequence, and the phase values were normalized in scope (0–100%);
- For every US frame, the corresponding 4D CT phase was determined by comparing the phase values.
2.2.4. Validation Method
3. Results
3.1. Modeling of Respiratory Movements as a Problem of Time–Space Adjustment
3.2. Synchronization of Information from Pre-Operative and Intraoperative Images
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Abou-Alfa, G.K.; Jarnagin, W.; Lowery, M. Liver and Bile Duct Cancer. In Abeloff’s Clinical Oncology; Elsevier: Amsterdam, The Netherlands, 2014; pp. 1373–1396.e8. [Google Scholar] [CrossRef]
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018, 68, 394–424. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banz, V.M.; Muller, P.C.; Tinguely, P.; Inderbitzin, D.; Ribes, D.; Peterhans, M.; Candinas, D.; Weber, S. Intraoperative image-guided navigation system: Development and applicability in 65 patients under-going liver surgery. Langenbecks. Arch. Surg. 2016, 401, 495–502. [Google Scholar] [CrossRef] [PubMed]
- Karaosmanoglu, A.D.; Onur, M.R.; Ozmen, M.N.; Akata, D.; Karcaaltincaba, M. Magnetic Resonance Imaging of Liver Metastasis. Semin. Ultrasound. CT MR 2016, 37, 533–548. [Google Scholar] [CrossRef] [PubMed]
- Seminars in Ultrasound, CT and MRI|Liver Imaging|ScienceDirect.com by Elsevier. Available online: https://www.sciencedirect.com/journal/seminars-in-ultrasound-ct-and-mri/vol/37/issue/6 (accessed on 12 August 2022).
- Spinczyk, D.; Stronczek, M.; Badura, A.; Sperka, P.; Krywalska, D.; Wolinska, A.; Krason, A.; Fabian, S.; Bas, M.; Woloshuk, A.; et al. Initial clinical evaluation of image fusion based on rigid registration and supporting percutaneous liver tumor ablation. Biocybern. Biomed. Eng. 2020, 40, 1378–1390. [Google Scholar] [CrossRef]
- Keall, J.P.; Mageras, G.S.; Balter, J.M.; Emery, R.S.; Forster, K.M.; Jiang, S.B.; Kapatoes, J.M.; Low, D.A.; Murphy, M.J.; Murray, B.R.; et al. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Med. Phys. 2006, 33, 3874–3900. [Google Scholar] [CrossRef]
- Von Siebenthal, M.; Székely, G.; Lomax, A.J.; Cattin, P.C. Systematic errors in respiratory gating due to intrafraction deformations of the liver. Med. Phys. 2007, 34, 3620–3629. [Google Scholar] [CrossRef]
- Rijkhorst, E.-J.; Heanes, D.; Odille, F.; Hawkes, D.; Barratt, D. Simulating Dynamic Ultrasound Using MR-Derived Motion Models to Assess Respiratory Synchronisation for Image-Guided Liver Interventions; Springer: Berlin/Heidelberg, Germany, 2010; pp. 113–123. [Google Scholar]
- Crum, W.R.; Tanner, C.; Hawkes, D.J. Anisotropic multi-scale fluid registration: Evaluation in magnetic resonance breast imaging. Phys. Med. Biol. 2005, 50, 5153–5174. [Google Scholar] [CrossRef]
- Brock, K.K.; Sharpe, M.B.; Dawson, L.A.; Kim, S.M.; Jaffray, D.A. Accuracy of finite element model-based multi-organ deformable image registration. Med. Phys. 2005, 32, 1647–1659. [Google Scholar] [CrossRef]
- Claron Nav Hx40-Specification, n.d. Available online: https://www.claronav.com/microntracker/microntracker-specifications/ (accessed on 21 July 2022).
- Horn, B.K.P.; Hilden, H.M.; Negahdaripourt, S. Closed-form solution of absolute orientation using orthonormal matrices. J. Opt. Soc. Am. A 1988, 5, 1127–1135. [Google Scholar] [CrossRef]
- Pol, E.J.D.; Viergever, M.H. Medical Image Matching—A Review with Classification. IEEE Eng. Med. Biol. Mag. 1993, 12, 26–39. [Google Scholar] [CrossRef]
- Davis, M.H.; Khotanzad, A.; Flamig, D.P.; Harms, S.E. A physics-Based coordinate transformation for 3-D image matching. IEEE Trans. Med. Imaging 1997, 16, 317–328. [Google Scholar] [CrossRef]
- Harder, R.L.; Desmarais, R.N. Interpolation using surface splines. ARC 2012, 9, 189–191. [Google Scholar] [CrossRef]
- Chou, P. Elasticity; Tensor, Dyadic, and Engineering Approaches; Van Nostrand: Princeton, NJ, USA, 1967. [Google Scholar]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity (1951 Edition)|Open Library. Available online: https://openlibrary.org/books/OL18982406M/Theory_of_elasticity_by_S._Timoshenko_and_J.N._Goodier (accessed on 22 July 2022).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Heppner, F.; Grenander, U. A Stochastic Nonlinear Model for Coordinate Bird Flocks. In The Ubiquity of Chaos; Krasner, S., Ed.; American Association for the Advancement of Science: Washington, DC, USA, 1990. [Google Scholar]
- Hare, E. Sociobiology, the New Synthesis: Edward O. Wilson. Br. J. Psychiatry 1987, 150, 709–711. [Google Scholar] [CrossRef]
- Wahab, M.N.A.; Nefti-Meziani, S.; Atyabi, A. A Comprehensive Review of Swarm Optimization Algorithms. PLoS ONE 2015, 10, e0122827. [Google Scholar] [CrossRef] [Green Version]
- Price, K.V. Differential evolution: A fast and simple numerical optimizer. Bienn. Conf. N. Am. Fuzzy Inf. Process. Soc. NAFIPS 1996, 524–527. [Google Scholar] [CrossRef]
- Storn, R. On the usage of differential evolution for function optimization. Bienn. Conf. N. Am. Fuzzy Inf. Process. Soc. NAFIPS 1996, 519–523. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Fitzpatrick, J.M.; West, J.B. The distribution of target registration error in rigid-body point-based registration. IEEE Trans. Med. Imaging 2001, 20, 917–927. [Google Scholar] [CrossRef]
- Zhang, Q.; Pevsner, A.; Hertanto, A.; Hu, Y.-C.; Rosenzweig, K.E.; Ling, C.C.; Mageras, G.S. A patient-specific respiratory model of anatomical motion for radiation treatment planning. Physics 2007, 34, 4772–4781. [Google Scholar] [CrossRef] [Green Version]
- Barrett, K.E.; Barman, S.M.; Brooks, H.L.; Yuan, J.X.-J. Ganong’s Review of Medical Physiology; McGraw Hill: New York, NY, USA, 2019; p. 750. [Google Scholar]
- Datteri, R.D.; Dawant, B.M. Estimation and Reduction of Target Registration Error. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7512, pp. 139–146. [Google Scholar] [CrossRef] [Green Version]
- Woods, R.P.; Grafton, S.T.; Holmes, C.J.; Cherry, S.R.; Mazziotta, J.C. Automated image registration: I. General methods and intrasubject, intramodality validation. J. Comput. Assist. Tomogr. 1998, 22, 139–152. [Google Scholar] [CrossRef] [Green Version]
- Holden, M.; Hill, D.L.G.; Denton, E.R.E.; Jarosz, J.M.; Cox, T.C.S.; Rohlfing, T.; Goodey, J.; Hawkes, D.J. Voxel similarity measures for 3-D serial MR brain image registration. IEEE Trans. Med. Imaging 2000, 19, 94–102. [Google Scholar] [CrossRef]
- Fitzpatrick, J. Detecting failure, assessing success. Med. Image Regist. 2001, 117–139. [Google Scholar] [CrossRef]
- Spinczyk, D.; Fabian, S. Target Registration Error minimization involving deformable organs using elastic body splines and Particle Swarm Optimization approach. Surg. Oncol. 2017, 26, 489–497. [Google Scholar] [CrossRef]
- Luthi, M.; Blanc, R.; Albrecht, T.; Gass, T.; Goksel, O.; Buchler, P.; Kistler, M.; Bousleiman, H.; Reyes, M.; Cattin, P.; et al. Statismo—A Framework for PCA Based Statistical Models; Kitware: New York, NY, USA, 2012. [Google Scholar]
- Spinczyk, D.; Blanc, R.; Rit, S.; Sarrut, D.; Melodelima, D. Estimation of respiratory breathing signal from 2D US sequences and 4DCT of the liver. IEEE Int. Ultrason. Symp. IUS 2014, 2339–2342. [Google Scholar] [CrossRef]
- Spinczyk, D. Towards the clinical integration of an image-guided navigation system for percutaneous liver tumor ablation using freehand 2D ultrasound images. Comput. Aided Surg. 2015, 20, 61–72. [Google Scholar] [CrossRef]
- Russakoff, D.B.; Tomasi, C.; Rohlfing, T.; Maurer, C.R. Image Similarity Using Mutual Information of Regions. Lect. Notes Comput. Sci. (Including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform.) 2004, 3023, 596–607. [Google Scholar] [CrossRef]
- Maier-Hein, L.; Maleike, D.; Neuhaus, J.; Franz, A.; Wolf, I.; Meinzer, H.-P. Soft tissue navigation using needle-shaped markers: Evaluation of navigation aid tracking accuracy and CT registration. Med. Imaging 2007 Vis. Image-Guided Proced. 2007, 6509, 650926. [Google Scholar] [CrossRef]
- Heiselman, J.S.; Clements, L.W.; Collins, J.A.; Weis, J.A.; Simpson, A.L.; Geevarghese, S.K.; Kingham, T.P.; Jarnagin, W.R.; Miga, M.I. Characterization and correction of intraoperative soft tissue deformation in image-guided laparo-scopic liver surgery. J. Med. Imaging 2018, 5, 1. [Google Scholar] [CrossRef]
- Gee, J.C.; Reivich, M.; Bilaniuk, L.; Hackney, D.; Zimmerman, R.; Kovacic, S.; Bajcsy, R.K. Evaluation of multiresolution elastic matching using MRI data. Proc. SPIE 1991, 1445, 226–234. [Google Scholar] [CrossRef]
- Galmén, K.; Jakobsson, J.G.; Freedman, J.; Harbut, P. High frequency jet ventilation during stereotactic ablation of liver tumours: An observational study on blood gas analysis as a measure of lung function during general anaesthesia [version 1; peer review: 3 approved]. F1000Research 2019, 8, 386. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spinczyk, D.; Fabian, S.; Król, K. Modeling of Respiratory Motion to Support the Minimally Invasive Destruction of Liver Tumors. Sensors 2022, 22, 7740. https://doi.org/10.3390/s22207740
Spinczyk D, Fabian S, Król K. Modeling of Respiratory Motion to Support the Minimally Invasive Destruction of Liver Tumors. Sensors. 2022; 22(20):7740. https://doi.org/10.3390/s22207740
Chicago/Turabian StyleSpinczyk, Dominik, Sylwester Fabian, and Krzysztof Król. 2022. "Modeling of Respiratory Motion to Support the Minimally Invasive Destruction of Liver Tumors" Sensors 22, no. 20: 7740. https://doi.org/10.3390/s22207740
APA StyleSpinczyk, D., Fabian, S., & Król, K. (2022). Modeling of Respiratory Motion to Support the Minimally Invasive Destruction of Liver Tumors. Sensors, 22(20), 7740. https://doi.org/10.3390/s22207740





