Structural Design of Ocean Temperature and Depth Sensor with Quick Response and High Sensitivity
Abstract
1. Introduction
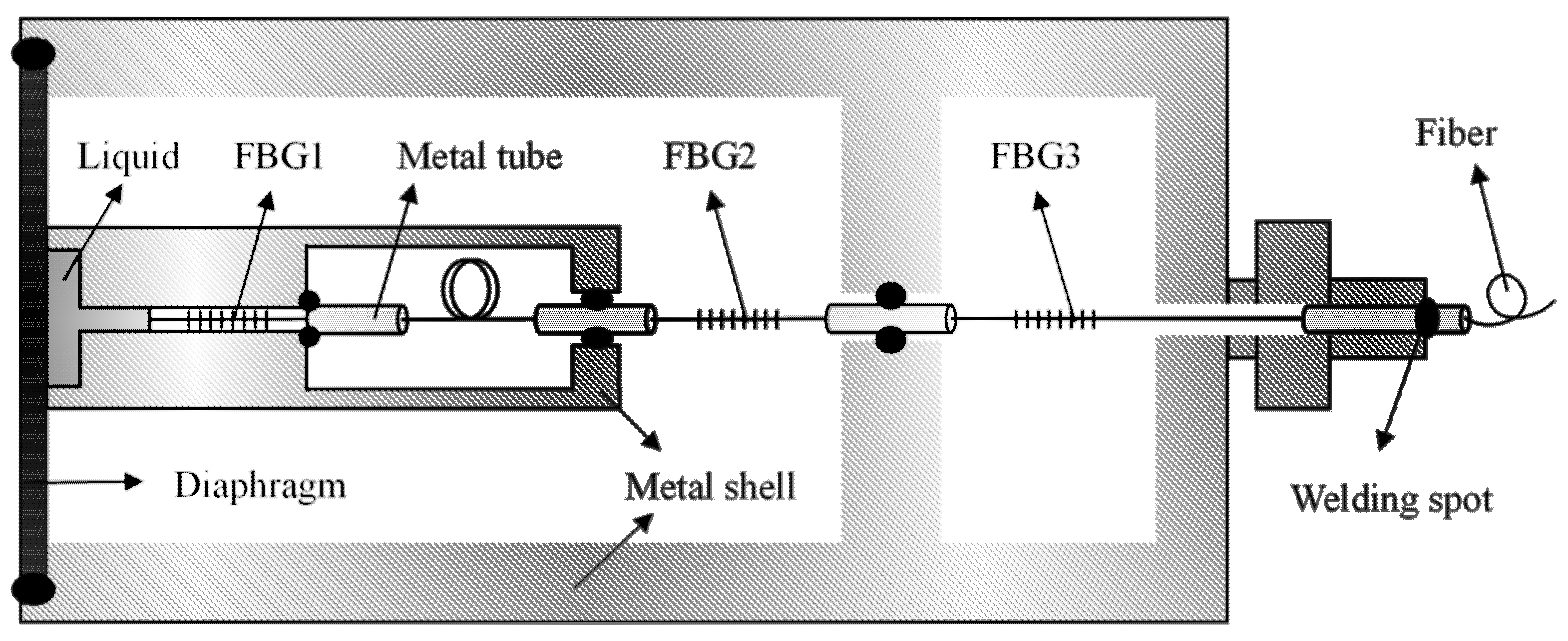
2. Structural Design and Principle
2.1. Principle of Temperature Compensation
2.2. Principle of Temperature Sensing
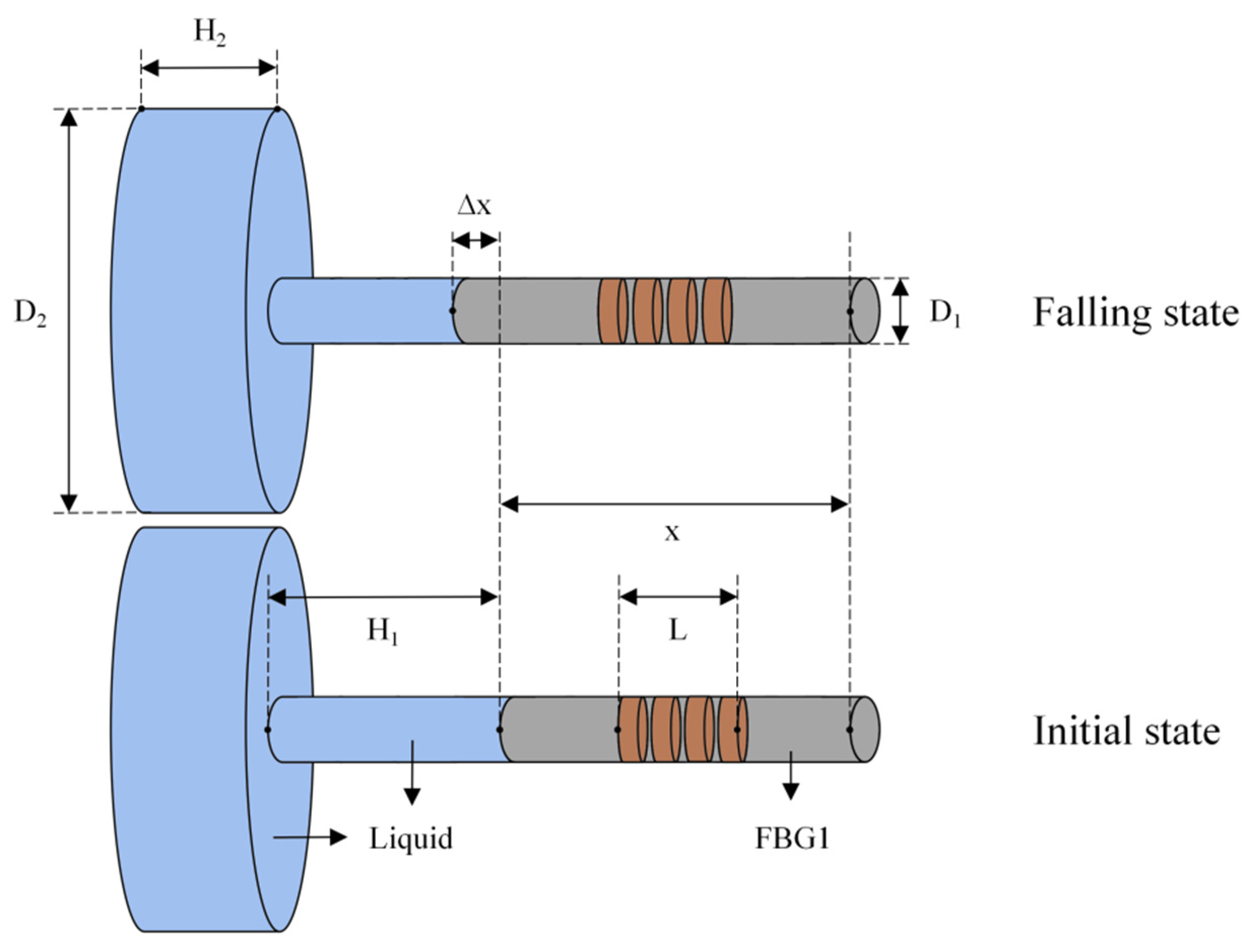
2.3. Principle of Depth Sensing
3. Simulation and Analysis
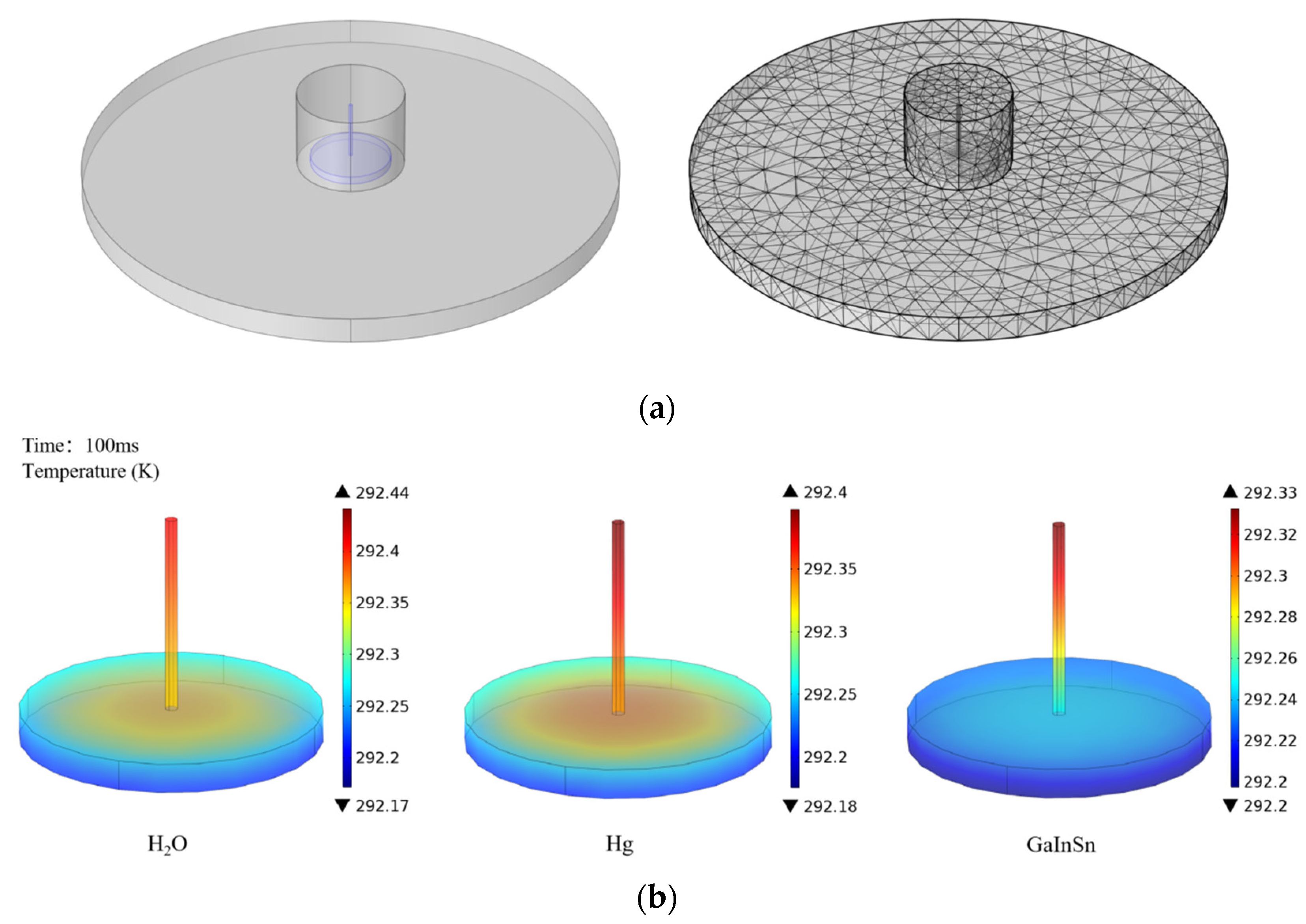
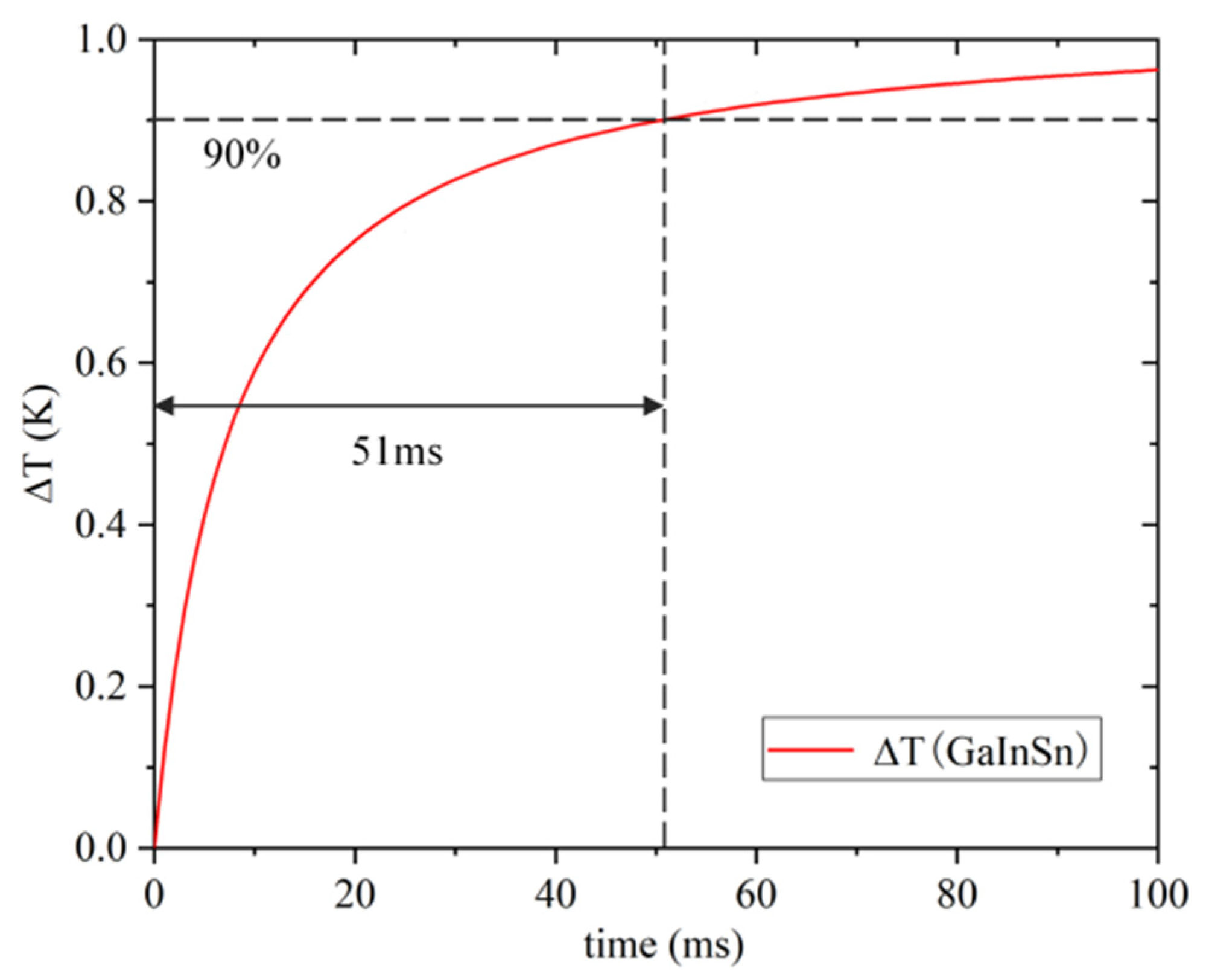
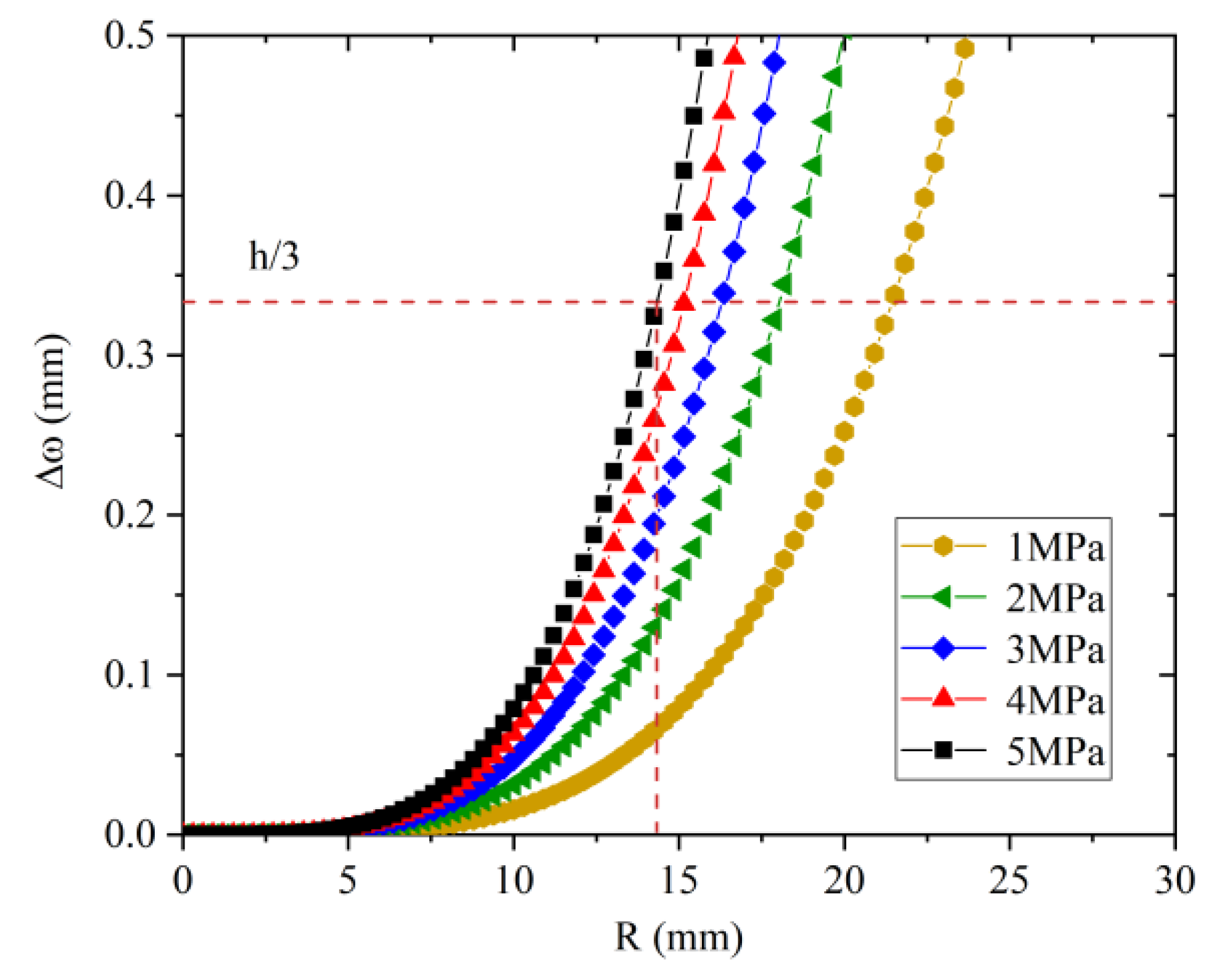
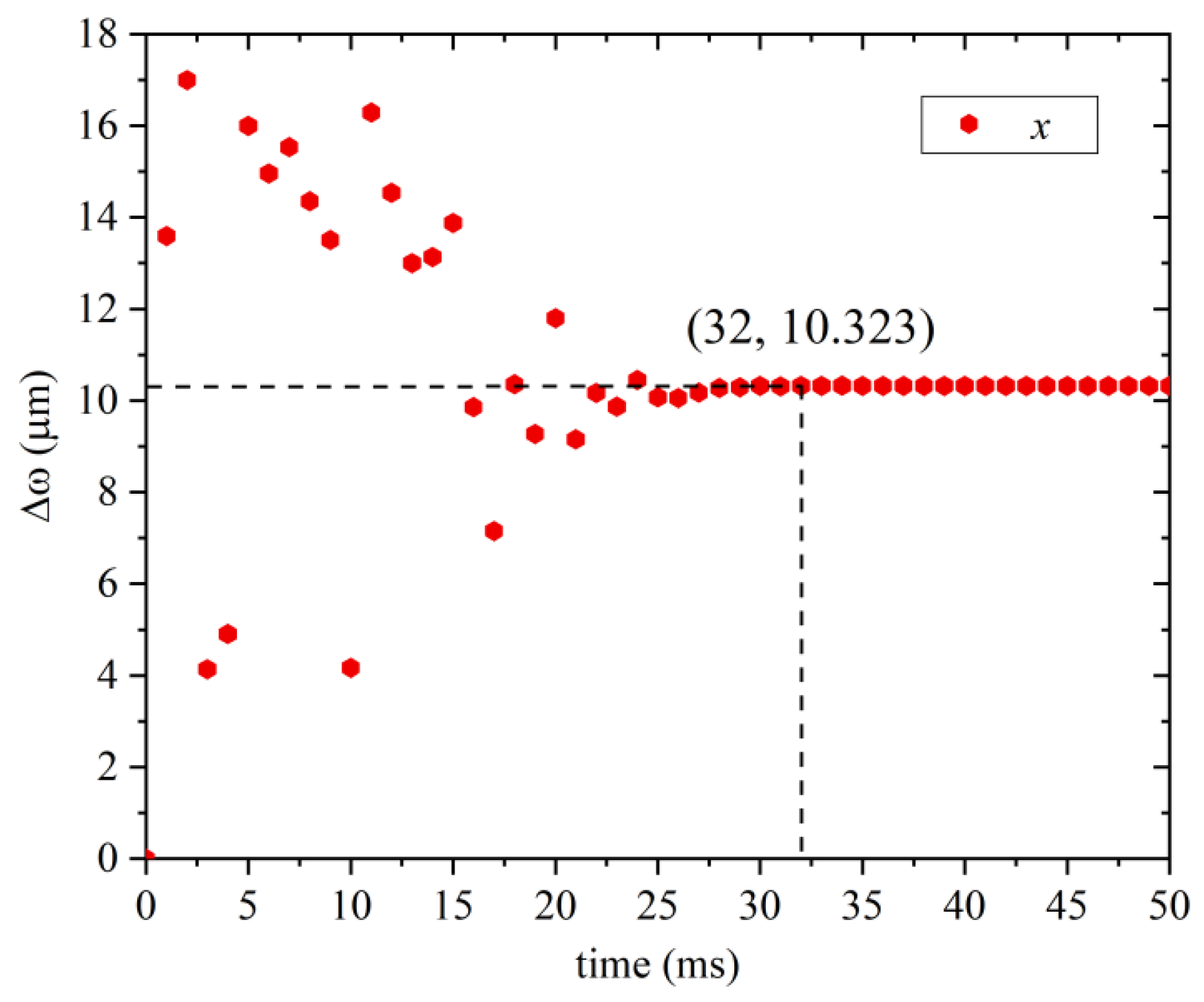
3.1. Response Time Analysis
3.2. Temperature and Depth Sensitivity Analyses
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rutterford, L.A. Future fish distributions constrained by depth in warming seas. Nat. Clim. Chang. 2015, 5, 569. [Google Scholar] [CrossRef]
- Bringas, F.; Goni, G. Early dynamics of Deep Blue XBT probes. J. Atmos. Ocean. Technol. 2015, 32, 2253–2263. [Google Scholar] [CrossRef]
- Goes, M.; Goni, G.; Dong, S. An optimal XBT-based monitoring system for the S outh A tlantic meridional overturning circulation at 34° S. J. Geophys. Res. Ocean. 2015, 120, 161–181. [Google Scholar] [CrossRef]
- Ciuffardi, T.; Napolitano, E.; Iacono, R.; Reseghetti, F.; Raiteri, G.; Bordone, A. Analysis of surface circulation structures along a frequently repeated XBT transect crossing the Ligurian and Tyrrhenian Seas. Ocean Dyn. 2016, 66, 767–783. [Google Scholar] [CrossRef]
- Ridgway, K.R.; Coleman, R.C.; Bailey, R.J.; Sutton, P. Decadal variability of East Australian Current transport inferred from repeated high-density XBT transects, a CTD survey and satellite altimetry. J. Geophys. Res. Ocean. 2008, 113. [Google Scholar] [CrossRef]
- Le Menn, M. State of the Art and Needs in Ocean Temperature Measurements; Euramet Workshop on Sea Water Metrology: Boras, Sweden, 2018. [Google Scholar]
- Stark, J.; Gorman, J.; Hennessey, M.; Reseghetti, F.; Willis, J.; Lyman, J.; Abraham, J.; Borghini, M. A computational method for determining XBT depths. Ocean Sci. 2011, 7, 733–743. [Google Scholar] [CrossRef]
- Hamon, M.; Reverdin, G.; Le Traon, P.Y. Empirical correction of XBT data. J. Atmos. Ocean. Technol. 2012, 29, 960–973. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber grating sensors. J. Light. Technol. 1997, 15, 1442–1463. [Google Scholar]
- Hill, K.O.; Meltz, G. Fiber bragg grating technology fundamentals and overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Duraibabu, D.B.; Leen, G.; Toal, D.; Newe, T.; Lewis, E.; Dooly, G. Underwater depth and temperature sensing based on fiber optic technology for marine and fresh water applications. Sensors 2017, 17, 1228. [Google Scholar] [CrossRef] [PubMed]
- Mishra, V.; Lohar, M.; Amphawan, A. Improvement in temperature sensitivity of FBG by coating of diferent materials. Optik 2016, 127, 825–828. [Google Scholar] [CrossRef]
- Luo, D.; Ma, J.; Ibrahim, Z.; Ismail, Z. Etched FBG coated with polyimide for simultaneous detection the salinity and temperature. Opt. Commun. 2017, 392, 218–222. [Google Scholar] [CrossRef]
- Pospori, A.; Marques, C.A.F.; Sáez-Rodríguez, D.; Nielsen, K.; Bang, O.; Webb, D.J. Thermal and chemical treatment of polymer optical fbre Bragg grating sensors for enhanced mechanical sensitivity. Opt. Fiber Technol. 2017, 36, 68–74. [Google Scholar] [CrossRef]
- Qu, Y.; Wang, W.; Peng, J.; Lv, D.; Dai, J.; Yang, M. Sensitivity-enhanced temperature sensor based on metalized optical fiber grating for marine temperature monitoring. In Proceedings of the International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017. [Google Scholar]
- Zhao, Y.; Wu, Q.; Zhang, Y. Simultaneous measurement of salinity, temperature and pressure in seawater using optical fiber SPR sensor. Measurement 2019, 148, 106792. [Google Scholar] [CrossRef]
- Ameen, O.F.; Younus, M.H.; Aziz, M.S.; Azmi, A.I.; Ibrahim, R.R.; Ghoshal, S.K. Graphene diaphragm integrated FBG sensors for simultaneous measurement of water level and temperature. Sens. Actuators A Phys. 2016, 252, 225–232. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Gao, R.X.; Li, Y.; Zhao, X.L.; Qu, S.L. Ultracompact Fiber Sensor Tip Based on Liquid Polymer-filled Fabry-Perot Cavity with High Temperature Sensitivity. Sens. Actuators B Chem. 2016, 233, 496–501. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, Y.; Xue, R.; Liu, Y.; Cao, K.J.; Qu, S.L. Compact Optical Fiber Temperature Sensor with High Sensitivity Based on Liquid-filled Silica Capillary Tube. Appl. Opt. 2018, 57, 1061–1066. [Google Scholar] [CrossRef] [PubMed]
- Yuan, S.; Tong, Z.; Zhao, J.; Zhang, W.; Cao, Y. High Temperature Fiber Sensor based on Spherical-shape Structures with High Sensitivity. Opt. Commun. 2014, 332, 154–157. [Google Scholar] [CrossRef]
- Yu, Y.; Bian, Q.; Lu, Y.; Zhang, X.; Yang, J.; Liang, L. High sensitivity all optical fiber conductivity-temperature-depth (CTD) sensing based on an optical microfiber coupler (OMC). J. Light. Technol. 2018, 37, 2739–2747. [Google Scholar] [CrossRef]
- Vorathin, E.; Hafizi, Z.M.; Ismail, N.; Loman, M.; Aizzuddin, A.M.; Lim, K.S.; Ahmad, H. FBG water-level transducer based on PVC-cantilever and rubber diaphragm structure. IEEE Sens. J. 2019, 19, 7407–7414. [Google Scholar] [CrossRef]
- Wei, Z.; Song, D.; Zhao, Q.; Cui, H. High pressure sensor based on fbre Bragg grating and carbon fbre laminated composite. IEEE Sens. J. 2008, 8, 1615–1619. [Google Scholar] [CrossRef]
- Duraibabu, D.B.; Poeggel, S.; Omerdic, E.; Capocci, R.; Lewis, E.; Newe, T.; Leen, G.; Toal, D.; Dooly, G. An Optical Fibre Depth (Pressure) Sensor for Remote Operated Vehicles in Underwater Applications. Sensors 2017, 17, 406. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Chen, G.; Xu, C.; Xu, W. Design and experimental study of a sensitization structure with fiber grating sensor for nonintrusive pipeline pressure detection. ISA Trans. 2020, 101, 442–452. [Google Scholar] [CrossRef]
- Vengal Rao, P.; Srimannarayana, K.; Sai Shankar, M.; Kishore, P.; Sengupta, D.; Saidi Reddy, P. A diaphragm based low-cost fiber optic pressure sensor. Microw. Opt. Technol. Lett. 2012, 54, 2229–2231. [Google Scholar] [CrossRef]
- Ch, S.V.; Reddy, P.S.; Vijeesh, V.P.; Afzulpurkar, S.; Prabhudesai, S. A diaphragm based fiber bragg grating (fbg) type pressure sensor for ocean applications. Proc. SPIE 2019, 11088, 77–84. [Google Scholar]
- Zhao, Q.; Wang, Y.; Sun, P.; Du, D.; Yu, L.; Zhang, J.; Ding, B.; Han, G.; Qu, Y. Shipborne expendable all-optical fiber ocean temperature-depth profile sensor. Appl. Opt. 2022, 61, 2089–2095. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.-k.; Zhao, Y.; Zhao, Q.; Lv, R.-Q. High sensitivity optical fiber pressure sensor based on thin-walled oval cylinder. Sens. Actuators A Phys. 2020, 310, 112042. [Google Scholar]
- Liu, T.; Yin, J.; Jiang, J.; Liu, K.; Wang, S.; Zou, S. Differential-pressure-based fiber-optic temperature sensor using Fabry–Perot interferometry. Opt. Lett. 2015, 40, 1049–1052. [Google Scholar] [CrossRef] [PubMed]
- Vaddadi, V.S.C.S.; Parne, S.R.; Afzulpurkar, S.; Desai, S.P.; Parambil, V.V. Design and development of pressure sensor based on Fiber Bragg Grating (FBG) for ocean applications. Eur. Phys. J. Appl. Phys. 2020, 90, 30501. [Google Scholar] [CrossRef]
- Hanawa, K.; Rual, P.; Bailey, R.; Sy, A.; Szabados, M. A new depth-time equation for Sippican or TSK T-7, T-6 and T-4 expendable bathythermographs (XBT). Deep Sea Res. Part I 1995, 42, 1423–1451. [Google Scholar] [CrossRef]
- Kizu, S.; Yoritaka, H.; Hanawa, K. A new fall-rate equation for T-5 expendable bathythermograph (XBT) by TSK. J. Oceanogr. 2005, 61, 115–121. [Google Scholar] [CrossRef]
- Ribeiro, N.; Mata, M.M.; de Azevedo, J.L.L.; Cirano, M. An assessment of the XBT fall-rate equation in the Southern Ocean. J. Atmos. Ocean. Technol. 2018, 35, 911–926. [Google Scholar] [CrossRef]
- Vorathin, E.; Hafizi, Z.; Aizzuddin, A.; Zaini, M.K.A.; Lim, K.S. Temperature-independent chirped FBG pressure transducer with high sensitivity. Opt. Lasers Eng. 2019, 117, 49–56. [Google Scholar] [CrossRef]
- Sheng, H.-J.; Fu, M.-Y.; Chen, T.-C.; Liu, W.-F.; Bor, S.-S. A lateral pressure sensor using a fiber Bragg grating. IEEE Photonics Technol. Lett. 2004, 16, 1146–1148. [Google Scholar] [CrossRef]
- Pachava, V.R.; Kamineni, S.; Madhuvarasu, S.S.; Putha, K.; Mamidi, V.R. FBG based high sensitive pressure sensor and its low-cost interrogation system with enhanced resolution. Photonic Sens. 2015, 5, 321–329. [Google Scholar] [CrossRef]
- Khakpour, R.; Mansouri, S.R.M.; Bahadorimehr, A.R. Analytical comparison for square, rectangular and circular diaphragms in MEMS applications. In Proceedings of the 2010 International Conference on Electronic Devices, Systems and Applications, Kuala Lumpur, Malaysia, 11–14 April 2010; pp. 297–299. [Google Scholar]
- Dickey, M.D.; Chiechi, R.C.; Larsen, R.J.; Weiss, E.A.; Weitz, D.A.; Whitesides, G.M. Eutectic Gallium-Indium (EGaIn): A Liquid Metal Alloy for the Formation of Stable Structures in Microchannels at Room Temperature. Adv. Funct. Mater. 2008, 18, 1097. [Google Scholar] [CrossRef]




| Liquid (20 °C) | H2O | Hg | GaInSn |
|---|---|---|---|
| Thermal conductivity (W/m∙K) | 0.599 | 8.30 | 16.5 |
| Thermal expansion coefficient (1/K) | 2.08 × 10−4 | 6.04 × 10−6 | 2.5 × 10−5 |
| Parameter | P/MPa | E/105 MPa | μ | R/mm | h/mm | λ/nm | x/mm | H2/mm |
|---|---|---|---|---|---|---|---|---|
| Value | 1.0 | 1.06 | 0.33 | 10 | 0.5 | 1550 | 10 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, Y.; Zeng, L.; Li, Z.; Chen, H.; Qiao, Z.; Qu, Y.; Liu, G.; Li, L. Structural Design of Ocean Temperature and Depth Sensor with Quick Response and High Sensitivity. Sensors 2022, 22, 7756. https://doi.org/10.3390/s22207756
Liu Z, Zhang Y, Zeng L, Li Z, Chen H, Qiao Z, Qu Y, Liu G, Li L. Structural Design of Ocean Temperature and Depth Sensor with Quick Response and High Sensitivity. Sensors. 2022; 22(20):7756. https://doi.org/10.3390/s22207756
Chicago/Turabian StyleLiu, Zhaoyue, Yuanchong Zhang, Lina Zeng, Zaijin Li, Hao Chen, Zhongliang Qiao, Yi Qu, Guojun Liu, and Lin Li. 2022. "Structural Design of Ocean Temperature and Depth Sensor with Quick Response and High Sensitivity" Sensors 22, no. 20: 7756. https://doi.org/10.3390/s22207756
APA StyleLiu, Z., Zhang, Y., Zeng, L., Li, Z., Chen, H., Qiao, Z., Qu, Y., Liu, G., & Li, L. (2022). Structural Design of Ocean Temperature and Depth Sensor with Quick Response and High Sensitivity. Sensors, 22(20), 7756. https://doi.org/10.3390/s22207756






