2D Temperature Field Reconstruction Using Optical Frequency Domain Reflectometry and Machine-Learning Algorithms
Abstract
:1. Introduction
2. Model of 2D Temperature Sensor
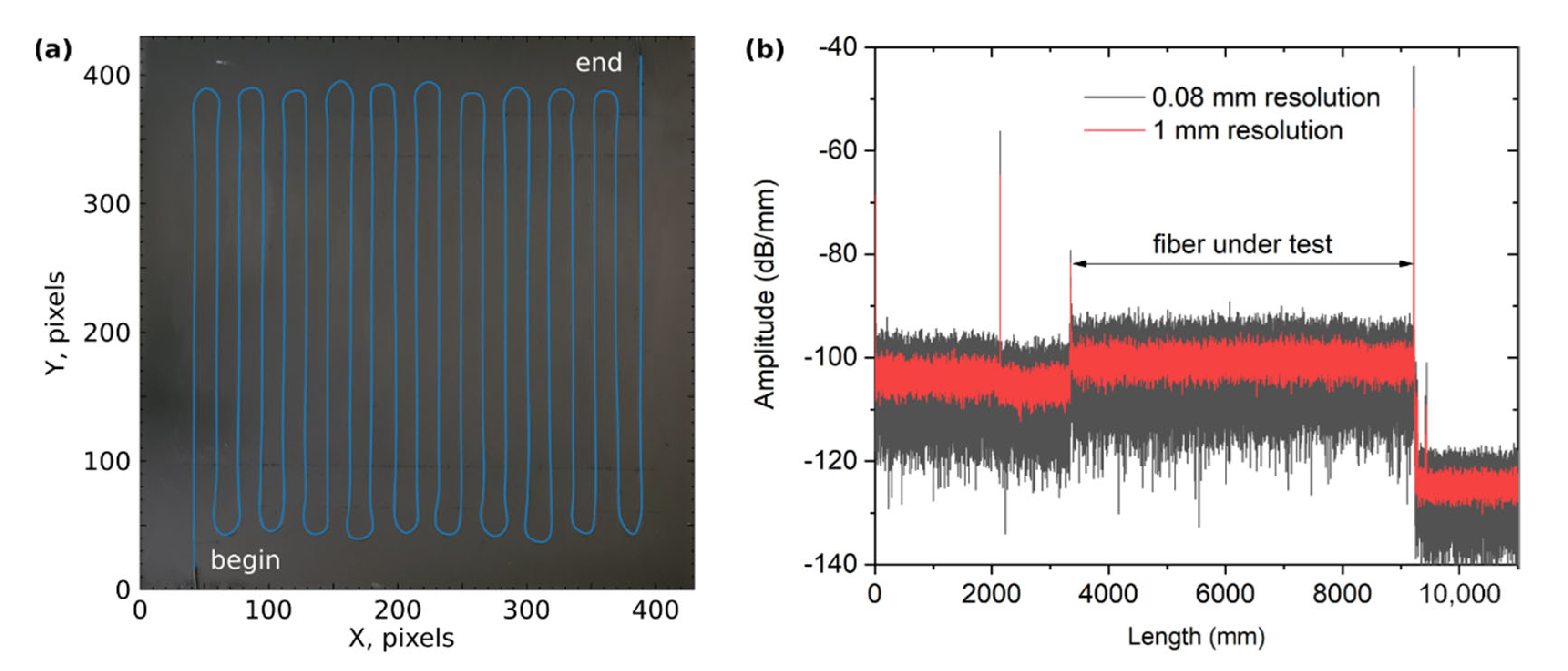
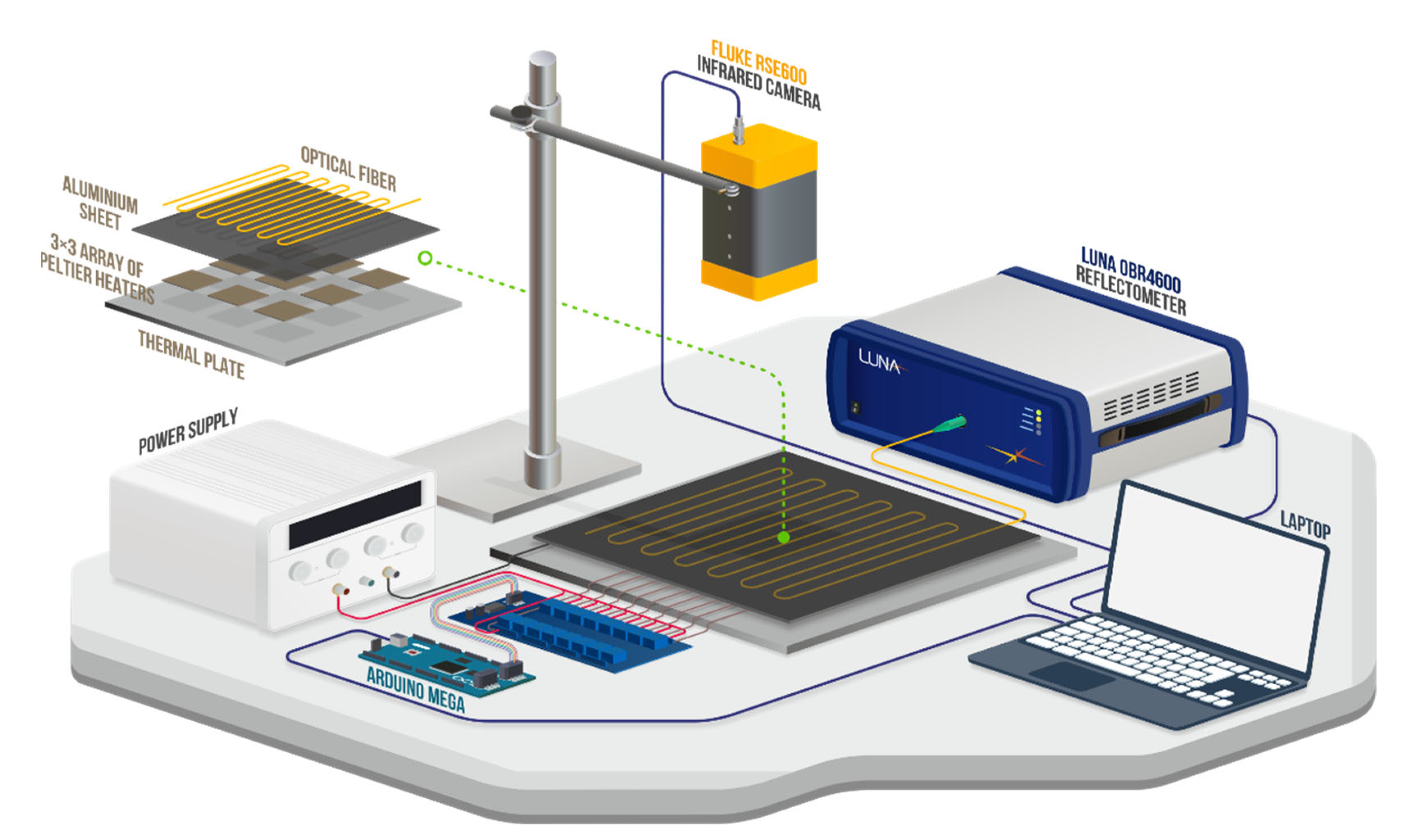
3. Experimental Setup
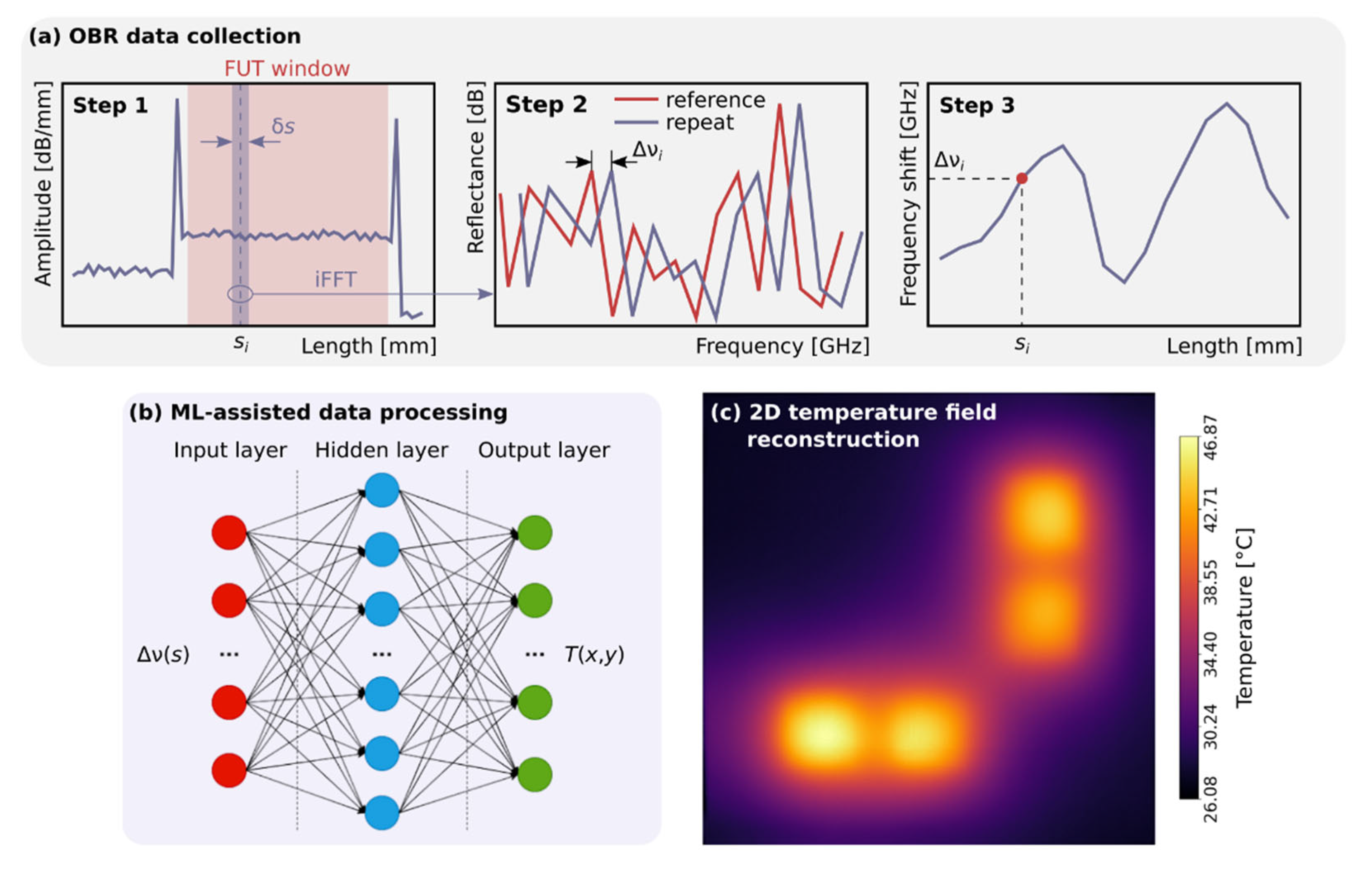
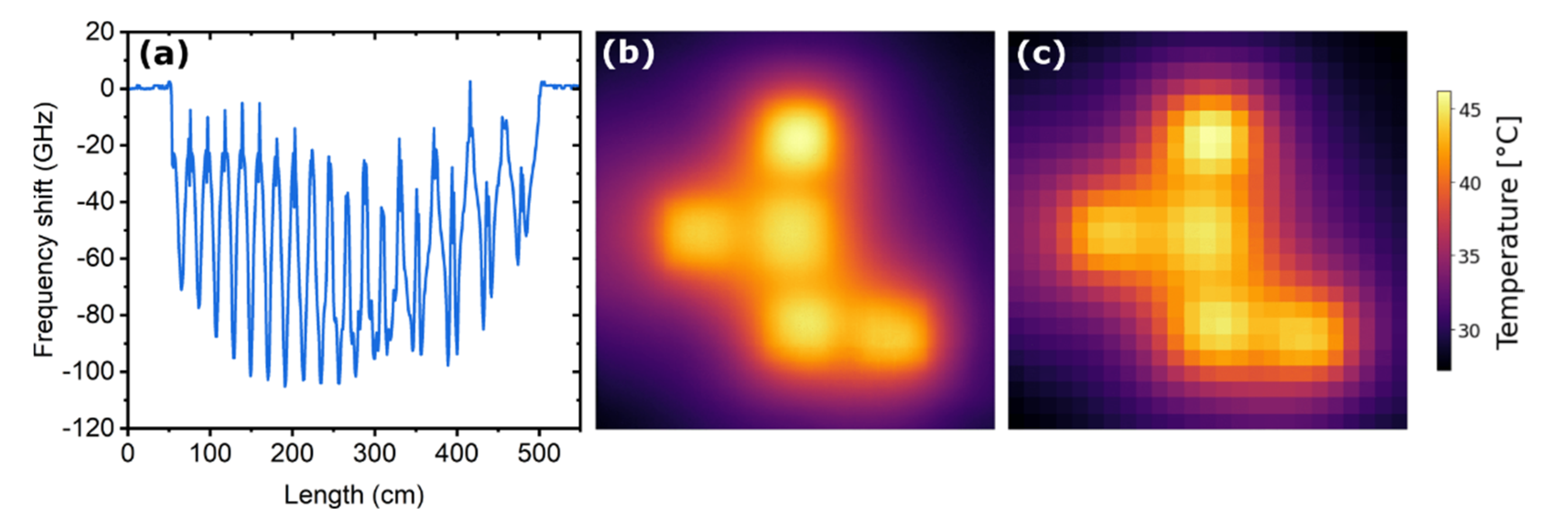
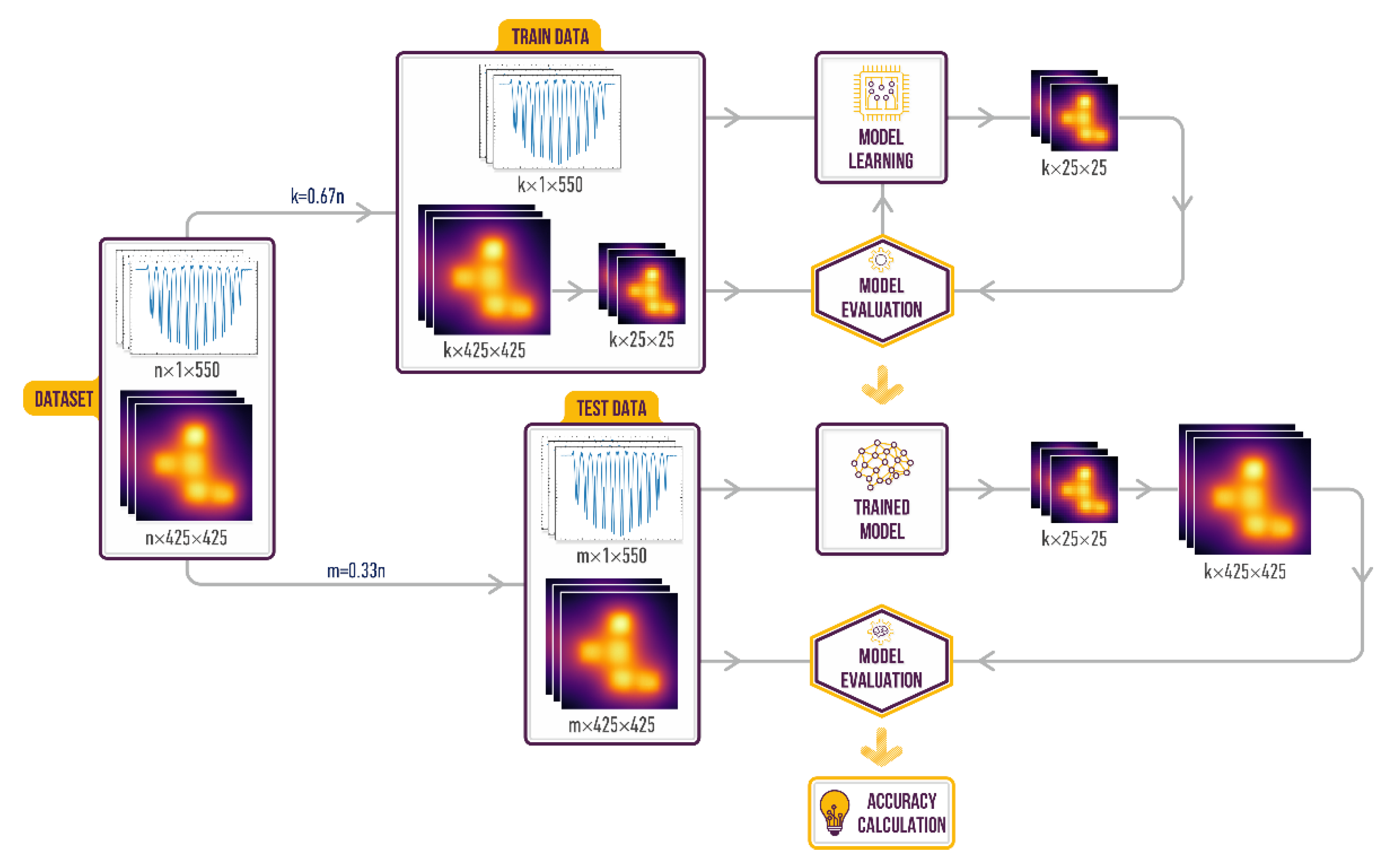
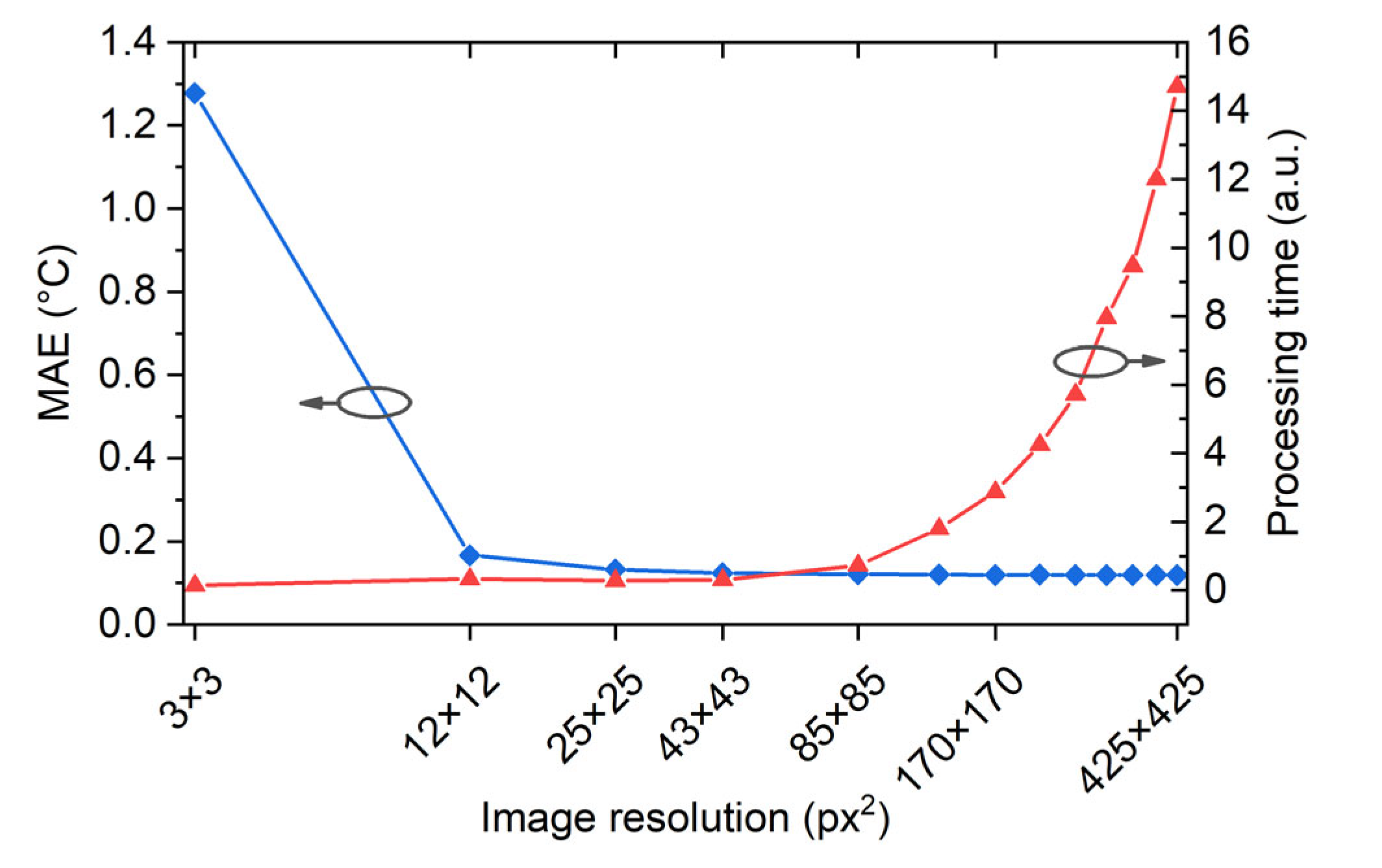
4. Machine Learning Assisted Temperature Field Reconstruction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, P.; Lalam, N.; Badar, M.; Liu, B.; Chorpening, B.T.; Buric, M.P.; Ohodnicki, P.R. Distributed Optical Fiber Sensing: Review and Perspective. Appl. Phys. Rev. 2019, 6, 041302. [Google Scholar] [CrossRef]
- Sahota, J.K.; Gupta, N.; Dhawan, D. Fiber Bragg Grating Sensors for Monitoring of Physical Parameters: A Comprehensive Review. Opt. Eng. 2020, 59, 060901. [Google Scholar] [CrossRef]
- Bao, X.; Wang, Y. Recent Advancements in Rayleigh Scattering-Based Distributed Fiber Sensors. Adv. Devices Instrum. 2021, 2021, 8696571. [Google Scholar] [CrossRef]
- Lun, T.L.T.; Wang, K.; Ho, J.D.L.; Lee, K.H.; Sze, K.Y.; Kwok, K.W. Real-Time Surface Shape Sensing for Soft and Flexible Structures Using Fiber Bragg Gratings. IEEE Robot. Autom. Lett. 2019, 4, 1454–1461. [Google Scholar] [CrossRef]
- Amanzadeh, M.; Aminossadati, S.M.; Kizil, M.S.; Rakić, A.D. Recent Developments in Fibre Optic Shape Sensing. Measurement 2018, 128, 119–137. [Google Scholar] [CrossRef] [Green Version]
- Tan, D.; Wang, Z.; Xu, B.; Qiu, J. Photonic Circuits Written by Femtosecond Laser in Glass: Improved Fabrication and Recent Progress in Photonic Devices. Adv. Photonics 2021, 3, 024002. [Google Scholar] [CrossRef]
- Girard, S.; Morana, A.; Ladaci, A.; Robin, T.; Mescia, L.; Bonnefois, J.-J.; Boutillier, M.; Mekki, J.; Paveau, A.; Cadier, B.; et al. Recent Advances in Radiation-Hardened Fiber-Based Technologies for Space Applications. J. Opt. 2018, 20, 093001. [Google Scholar] [CrossRef] [Green Version]
- Bos, J.; Klein, J.; Froggatt, M.; Sanborn, E.; Gifford, D. Fiber Optic Strain, Temperature and Shape Sensing via OFDR for Ground, Air and Space Applications. In Proceedings of the Nanophotonics and Macrophotonics for Space Environments VII, San Diego, CA, USA, 24 September 2013; Volume 8876, p. 887614. [Google Scholar]
- Guo, Z.; Yan, J.; Han, G.; Greenwood, D.; Marco, J.; Yu, Y. High Sensing Accuracy Realisation with Millimetre/Sub-Millimetre Resolution in Optical Frequency Domain Reflectometer. J. Light. Technol. 2022, 40, 4050–4056. [Google Scholar] [CrossRef]
- LUNA OBR 4600: Optical Backscatter Reflectometer. Available online: https://lunainc.com/product/obr-4600 (accessed on 11 October 2022).
- Soller, B.J.; Gifford, D.K.; Wolfe, M.S.; Froggatt, M.E.; Yu, M.H.; Wysocki, P.F. Measurement of Localized Heating in Fiber Optic Components with Millimeter Spatial Resolution. In Proceedings of the 2006 Optical Fiber Communication Conference and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 5–10 March 2006; p. OFN3. [Google Scholar]
- Sypabekova, M.; Aitkulov, A.; Blanc, W.; Tosi, D. Reflector-Less Nanoparticles Doped Optical Fiber Biosensor for the Detection of Proteins: Case Thrombin. Biosens. Bioelectron. 2020, 165, 112365. [Google Scholar]
- Wu, J.; Wang, M.; Zhao, K.; Huang, S.; Zaghloul, M.; Cao, R.; Carpenter, D.; Zheng, G.; Rountree, S.; Chen, K.P.; et al. Distributed Fiber Sensors with High Spatial Resolution in Extreme Radiation Environments in Nuclear Reactor Cores. J. Light. Technol. 2021, 39, 4873–4883. [Google Scholar] [CrossRef]
- Sang, A.K.; Froggatt, M.E.; Gifford, D.K.; Kreger, S.T.; Dickerson, B.D. One Centimeter Spatial Resolution Temperature Measurements in a Nuclear Reactor Using Rayleigh Scatter in Optical Fiber. IEEE Sens. J. 2008, 8, 1375–1380. [Google Scholar] [CrossRef]
- Duncan, R.G.; Froggatt, M.E.; Kreger, S.T.; Seeley, R.J.; Gifford, D.K.; Sang, A.K.; Wolfe, M.S. High-Accuracy Fiber-Optic Shape Sensing. In Proceedings of the SPIE 6530, Sensor Systems and Networks: Phenomena, Technology, and Applications for NDE and Health Monitoring 2007, San Diego, CA, USA, 6 April 2007; p. 65301S. [Google Scholar]
- Khan, A.; Shin, J.K.; Lim, W.C.; Kim, N.Y.; Kim, H.S. A Deep Learning Framework for Vibration-Based Assessment of Delamination in Smart Composite Laminates. Sensors 2020, 20, 2335. [Google Scholar] [CrossRef] [Green Version]
- Sobczyk, M.; Wiesenhütter, S.; Noennig, J.R.; Wallmersperger, T. Smart Materials in Architecture for Actuator and Sensor Applications: A Review. J. Intell. Mater. Syst. Struct. 2022, 33, 379–399. [Google Scholar] [CrossRef]
- Venketeswaran, A.; Lalam, N.; Wuenschell, J.; Ohodnicki, P.R.; Badar, M.; Chen, K.P.; Lu, P.; Duan, Y.; Chorpening, B.; Buric, M. Recent Advances in Machine Learning for Fiber Optic Sensor Applications. Adv. Intell. Syst. 2021, 4, 2100067. [Google Scholar] [CrossRef]
- Cowie, B.M.; Webb, D.J.; Tam, B.; Slack, P.; Brett, P.N. Fibre Bragg Grating Sensors for Distributive Tactile Sensing. Meas. Sci. Technol. 2007, 18, 138–146. [Google Scholar] [CrossRef]
- Massari, L.; Schena, E.; Massaroni, C.; Saccomandi, P.; Menciassi, A.; Sinibaldi, E.; Oddo, C.M. A Machine-Learning-Based Approach to Solve Both Contact Location and Force in Soft Material Tactile Sensors. Soft Robot. 2020, 7, 409–420. [Google Scholar] [CrossRef]
- Tejedor, J.; Macias-Guarasa, J.; Martins, H.F.; Pastor-Graells, J.; Corredera, P.; Martin-Lopez, S. Machine Learning Methods for Pipeline Surveillance Systems Based on Distributed Acoustic Sensing: A Review. Appl. Sci. 2017, 7, 841. [Google Scholar] [CrossRef] [Green Version]
- Peng, Z.; Jian, J.; Wen, H.; Gribok, A.; Wang, M.; Liu, H.; Huang, S.; Mao, Z.-H.; Chen, K.P. Distributed Fiber Sensor and Machine Learning Data Analytics for Pipeline Protection against Extrinsic Intrusions and Intrinsic Corrosions. Opt. Express 2020, 28, 27277–27292. [Google Scholar] [CrossRef]
- Arief, H.A.; Wiktorski, T.; Thomas, P.J. A Survey on Distributed Fibre Optic Sensor Data Modelling Techniques and Machine Learning Algorithms for Multiphase Fluid Flow Estimation. Sensors 2021, 21, 2801. [Google Scholar] [CrossRef]
- Stork, A.L.; Baird, A.F.; Horne, S.A.; Naldrett, G.; Lapins, S.; Kendall, J.-M.; Wookey, J.; Verdon, J.P.; Clarke, A.; Williams, A. Application of Machine Learning to Microseismic Event Detection in Distributed Acoustic Sensing Data. Geophysics 2020, 85, KS149–KS160. [Google Scholar] [CrossRef]
- Peng, Z.; Wen, H.; Jian, J.; Gribok, A.; Wang, M.; Huang, S.; Liu, H.; Mao, Z.-H.; Chen, K.P. Identifications and Classifications of Human Locomotion Using Rayleigh-Enhanced Distributed Fiber Acoustic Sensors with Deep Neural Networks. Sci. Rep. 2020, 10, 21014. [Google Scholar] [CrossRef] [PubMed]
- Kreger, S.T.; Gifford, D.K.; Froggatt, M.E.; Soller, B.J.; Wolfe, M.S. High Resolution Distributed Strain or Temperature Measurements in Single- and Multi-Mode Fiber Using Swept-Wavelength Interferometry. In Proceedings of the Optical Fiber Sensors, Cancun, Mexico, 23–27 October 2006; p. ThE42. [Google Scholar]
- Gifford, D.K.; Froggatt, M.E.; Kreger, S.T. High Precision, High Sensitivity Distributed Displacement and Temperature Measurements Using OFDR-Based Phase Tracking. In Proceedings of the 21st International Conference on Optical Fiber Sensors, Ottawa, ON, Canada, 15 May 2011; Volume 7753, p. 77533l. [Google Scholar]
- Du, Y.; Liu, T.; Ding, Z.; Han, Q.; Liu, K.; Jiang, J.; Chen, Q.; Feng, B. Cryogenic Temperature Measurement Using Rayleigh Backscattering Spectra Shift by OFDR. IEEE Photonics Technol. Lett. 2014, 26, 1150–1153. [Google Scholar] [CrossRef]
- Sang, A.K.; Froggatt, M.E.; Gifford, D.K.; Dickerson, B.D. One Centimeter Spatial Resolution Temperature Measurements from 25 to 850 °C Using Rayleigh Scatter in Gold Coated Fiber. In Proceedings of the 2007 Quantum Electronics and Laser Science Conference, Baltimore, MD, USA, 6–11 May 2007; pp. 1–2. [Google Scholar]
- Luo, M.; Liu, J.; Tang, C.; Wang, X.; Lan, T.; Kan, B. 0.5 Mm Spatial Resolution Distributed Fiber Temperature and Strain Sensor with Position-Deviation Compensation Based on OFDR. Opt. Express 2019, 27, 35823. [Google Scholar] [CrossRef]
- Soller, B.J.; Gifford, D.K.; Wolfe, M.S.; Froggatt, M.E. High Resolution Optical Frequency Domain Reflectometry for Characterization of Components and Assemblies. Opt. Express 2005, 13, 666–674. [Google Scholar] [CrossRef] [Green Version]
- Froggatt, M.; Moore, J. High-Spatial-Resolution Distributed Strain Measurement in Optical Fiber with Rayleigh Scatter. Appl. Opt. 1998, 37, 1735–1740. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Zhang, Q.; Xu, C.-Y.; Sun, P.; Hu, P. Reconstruction of High Spatial Resolution Surface Air Temperature Data across China: A New Geo-Intelligent Multisource Data-Based Machine Learning Technique. Sci. Total Environ. 2019, 665, 300–313. [Google Scholar] [CrossRef]
- Ma, T.; Liu, Y.; Cao, C. Neural Networks for 3D Temperature Field Reconstruction via Acoustic Signals. Mech. Syst. Signal Process. 2019, 126, 392–406. [Google Scholar] [CrossRef]
- Ren, T.; Li, H.; Modest, M.F.; Zhao, C. Efficient Two-Dimensional Scalar Fields Reconstruction of Laminar Flames from Infrared Hyperspectral Measurements with a Machine Learning Approach. J. Quant. Spectrosc. Radiat. Transf. 2021, 271, 107724. [Google Scholar] [CrossRef]
- Prajapati, A.; Naik, S.; Mehta, S. Evaluation of Different Image Interpolation Algorithms. Int. J. Comput. Appl. 2012, 58, 6–12. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]

| Approach | MAE, °C | RMSE, °C |
|---|---|---|
| FFNN with a thermal image compression to 25 × 25 and the output decompression to 425 × 425 | 0.086 | 0.123 |
| Linear regression with a thermal image compression to 25 × 25 and the output decompression to 425 × 425 | 0.128 | 0.176 |
| Linear regression without thermal image compression/decompression procedure | 0.118 | 0.155 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wolf, A.; Shabalov, N.; Kamynin, V.; Kokhanovskiy, A. 2D Temperature Field Reconstruction Using Optical Frequency Domain Reflectometry and Machine-Learning Algorithms. Sensors 2022, 22, 7810. https://doi.org/10.3390/s22207810
Wolf A, Shabalov N, Kamynin V, Kokhanovskiy A. 2D Temperature Field Reconstruction Using Optical Frequency Domain Reflectometry and Machine-Learning Algorithms. Sensors. 2022; 22(20):7810. https://doi.org/10.3390/s22207810
Chicago/Turabian StyleWolf, Alexey, Nikita Shabalov, Vladimir Kamynin, and Alexey Kokhanovskiy. 2022. "2D Temperature Field Reconstruction Using Optical Frequency Domain Reflectometry and Machine-Learning Algorithms" Sensors 22, no. 20: 7810. https://doi.org/10.3390/s22207810
APA StyleWolf, A., Shabalov, N., Kamynin, V., & Kokhanovskiy, A. (2022). 2D Temperature Field Reconstruction Using Optical Frequency Domain Reflectometry and Machine-Learning Algorithms. Sensors, 22(20), 7810. https://doi.org/10.3390/s22207810






