An Adaptive Prescribed Performance Tracking Motion Control Methodology for Robotic Manipulators with Global Finite-Time Stability
Abstract
1. Introduction
- the proposed PPFs ensure position tracking errors are managed in a pre-designed performance domain. Especially, the Steady-State Error (SSE) boundaries will be symmetrical to zero, so when the transformed error is zero, the tracking error will be as well;
- a fixed-time USOSMO is proposed to directly estimate the lumped uncertainty;
- in addition to determining the highest acceptable range of tracking errors at the steady state, the modified Non-singular Integral Sliding Mode Surface (NISMS) can also eliminate singularities and achieve finite-time convergence;
- the Adaptive Super-twisting Control Law (ASTwCL) is applied to deal with observer output errors and chattering. In this way, the control design clears the upper boundary requirement of all uncertainty.
- the proposed APPTMC ensures the effective reduction of harmful chattering behaviors by active compensations;
- guarantees prescribed performance in the sense of finite-time Lyapunov stability;
- the effectiveness of the APPTMC has been fully confirmed through simulations.
2. Problem Statement
2.1. Dynamic Modeling of Robotic Manipulators
2.2. Related Definitions and Lemmas
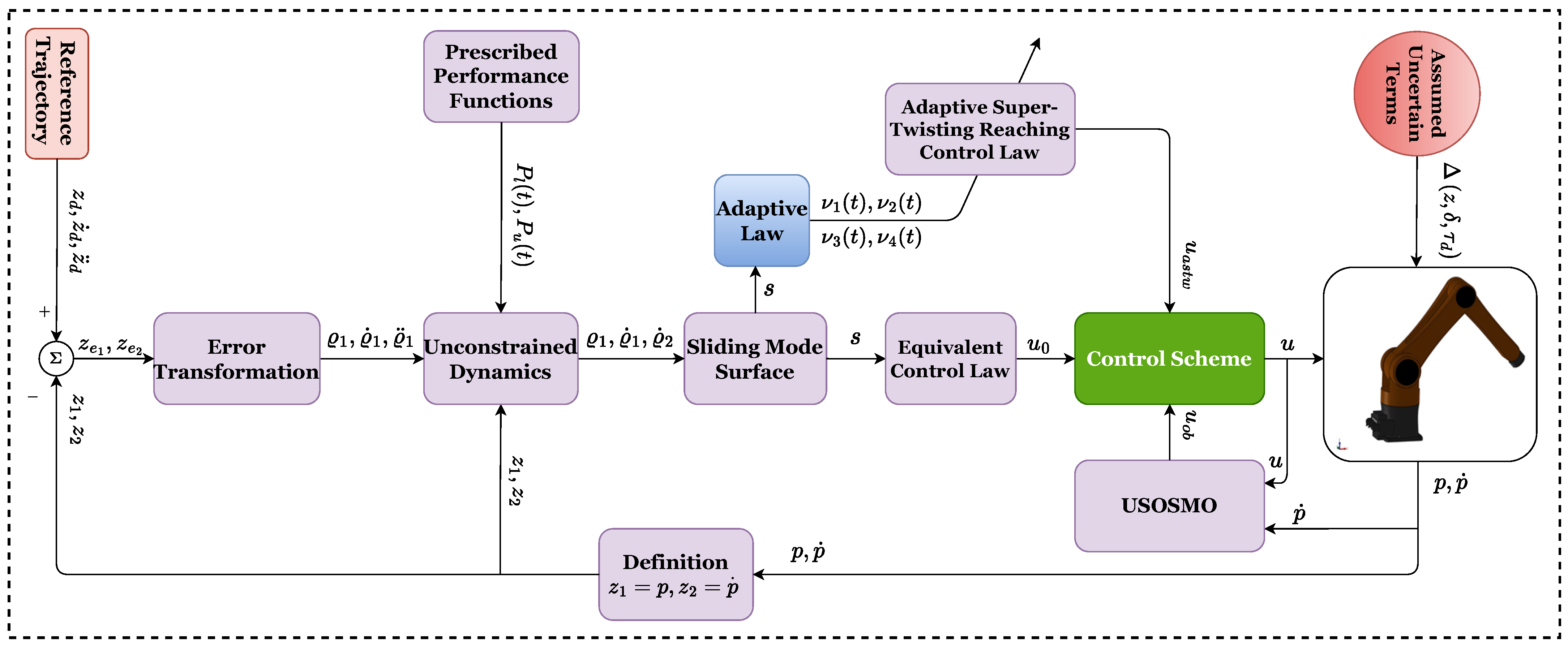
3. Development of the Proposed Strategy
3.1. Design of an USOSMO
3.2. Design of the PPC
- it is a smooth and strictly increasing function;
- ;
- if ;
- .
3.3. Design of NISMS
3.4. Proposed Controller Design
4. Simulations
4.1. Configuration of the Robot System and Control Parameter Selection
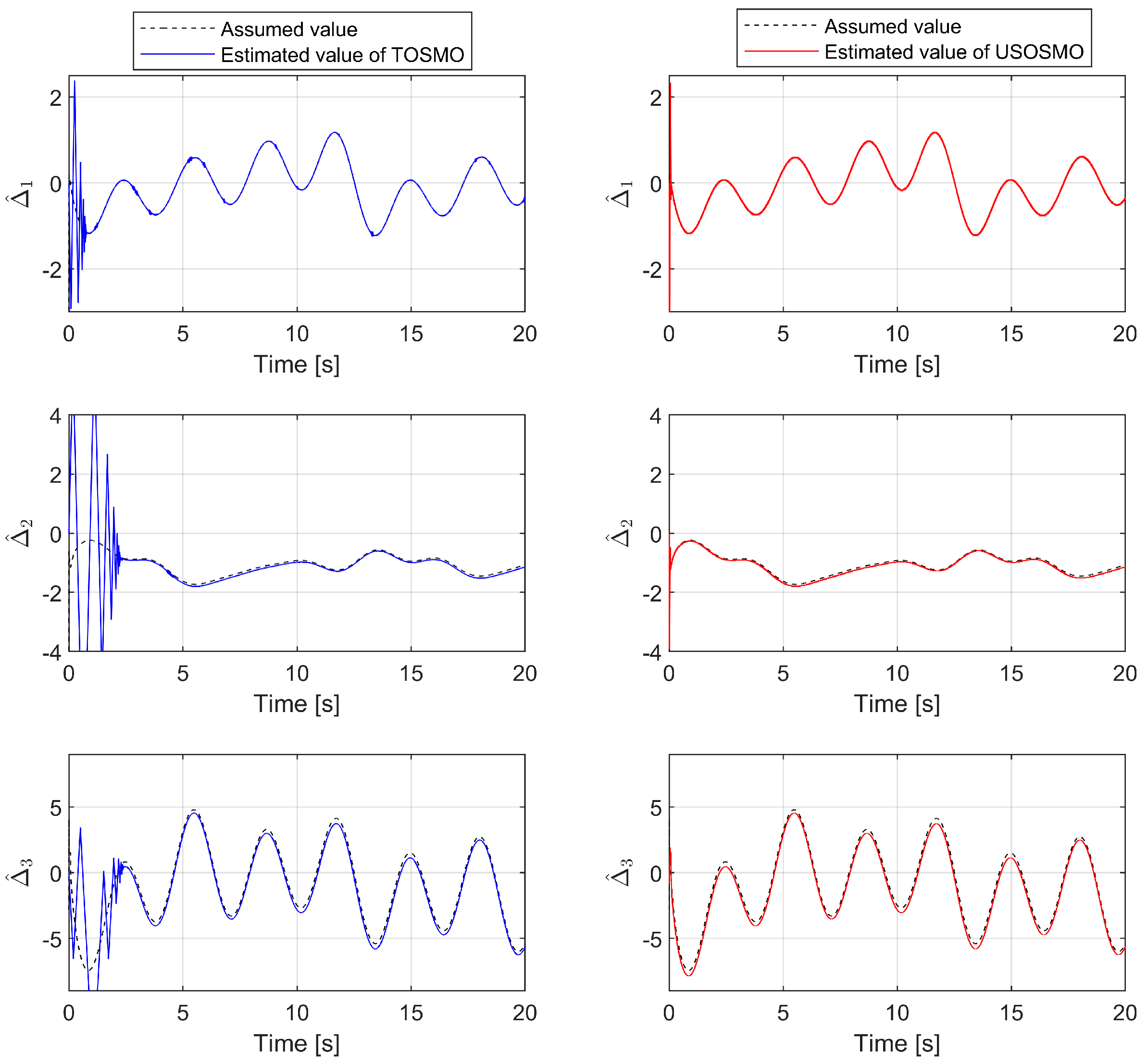
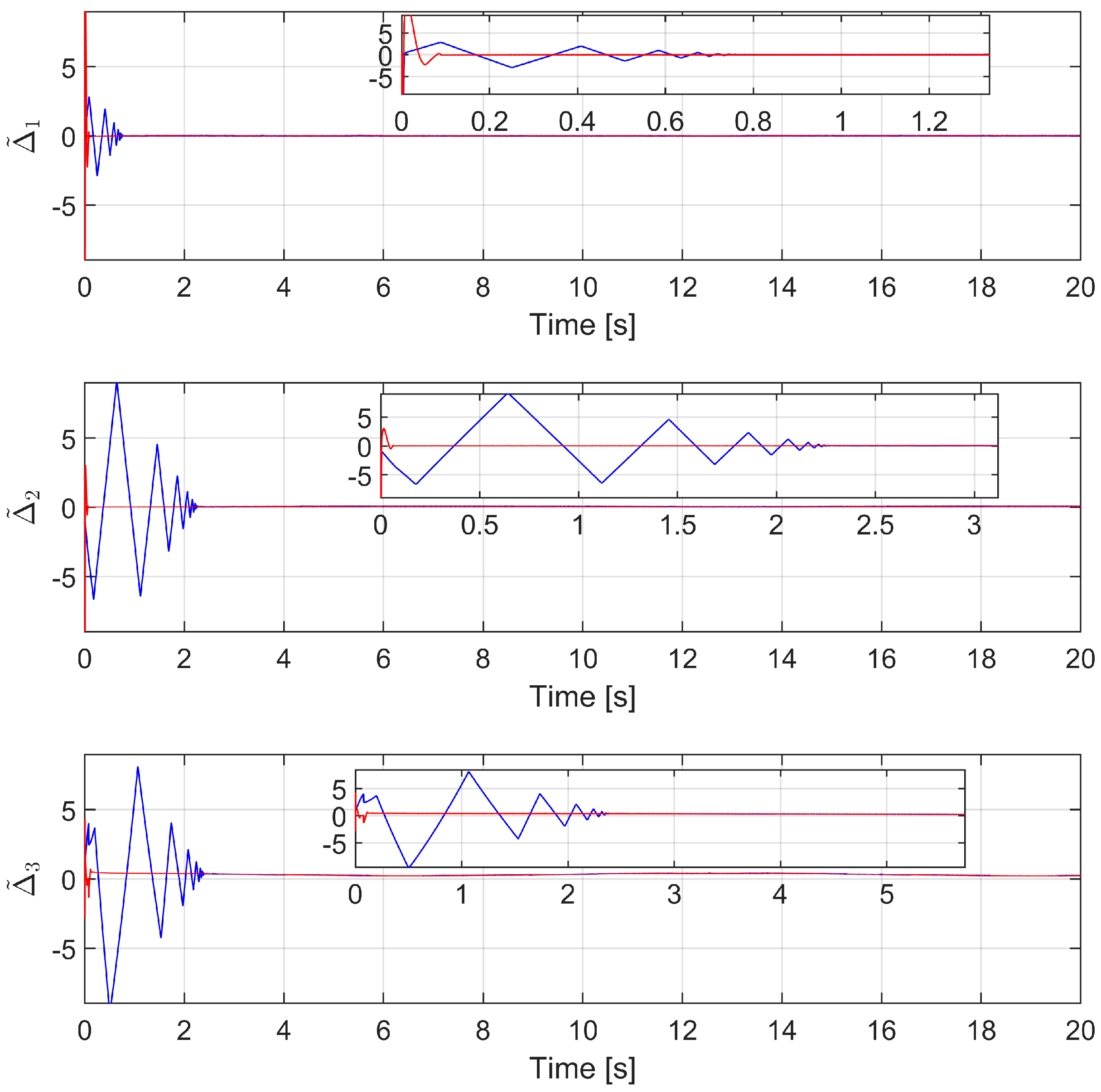
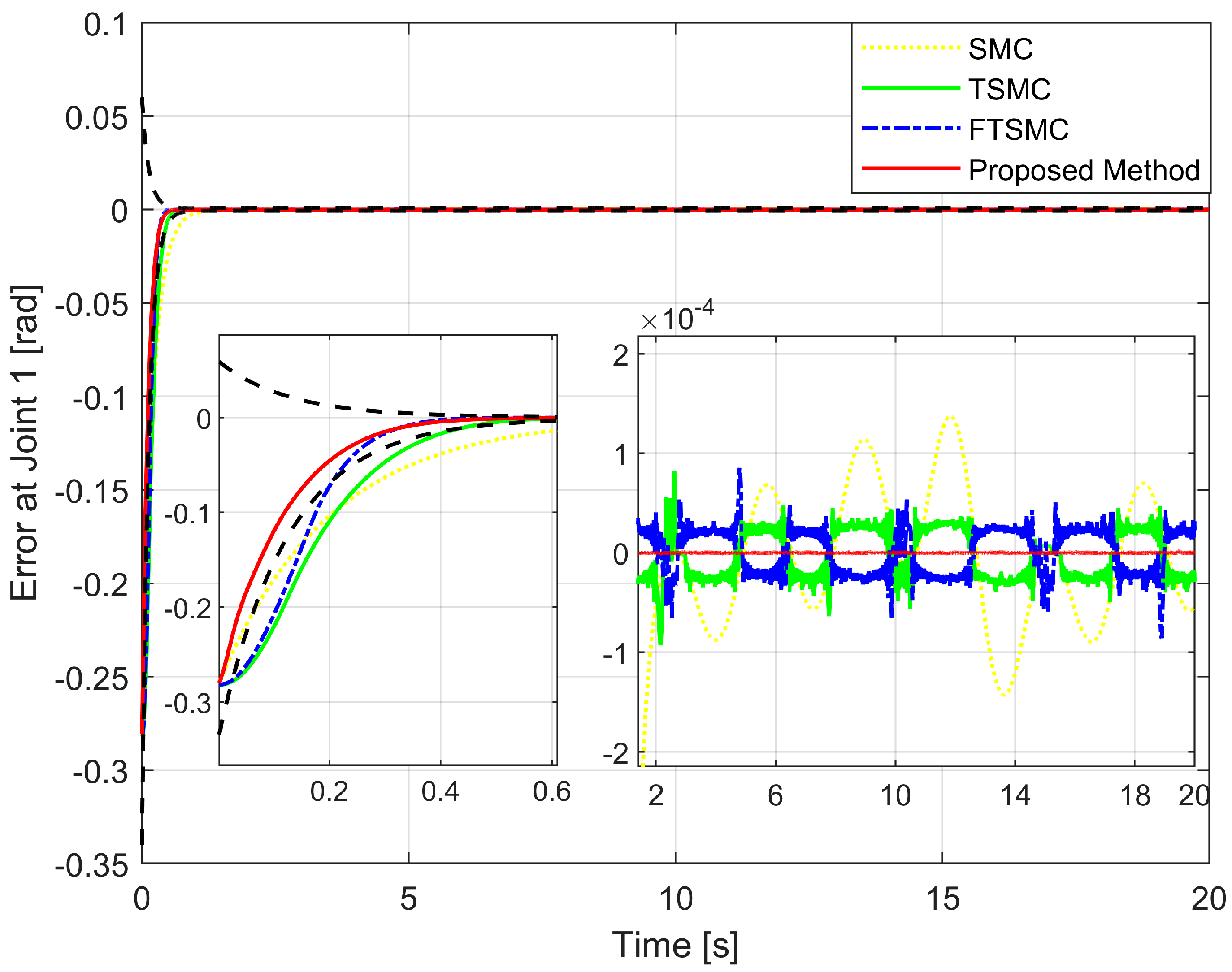
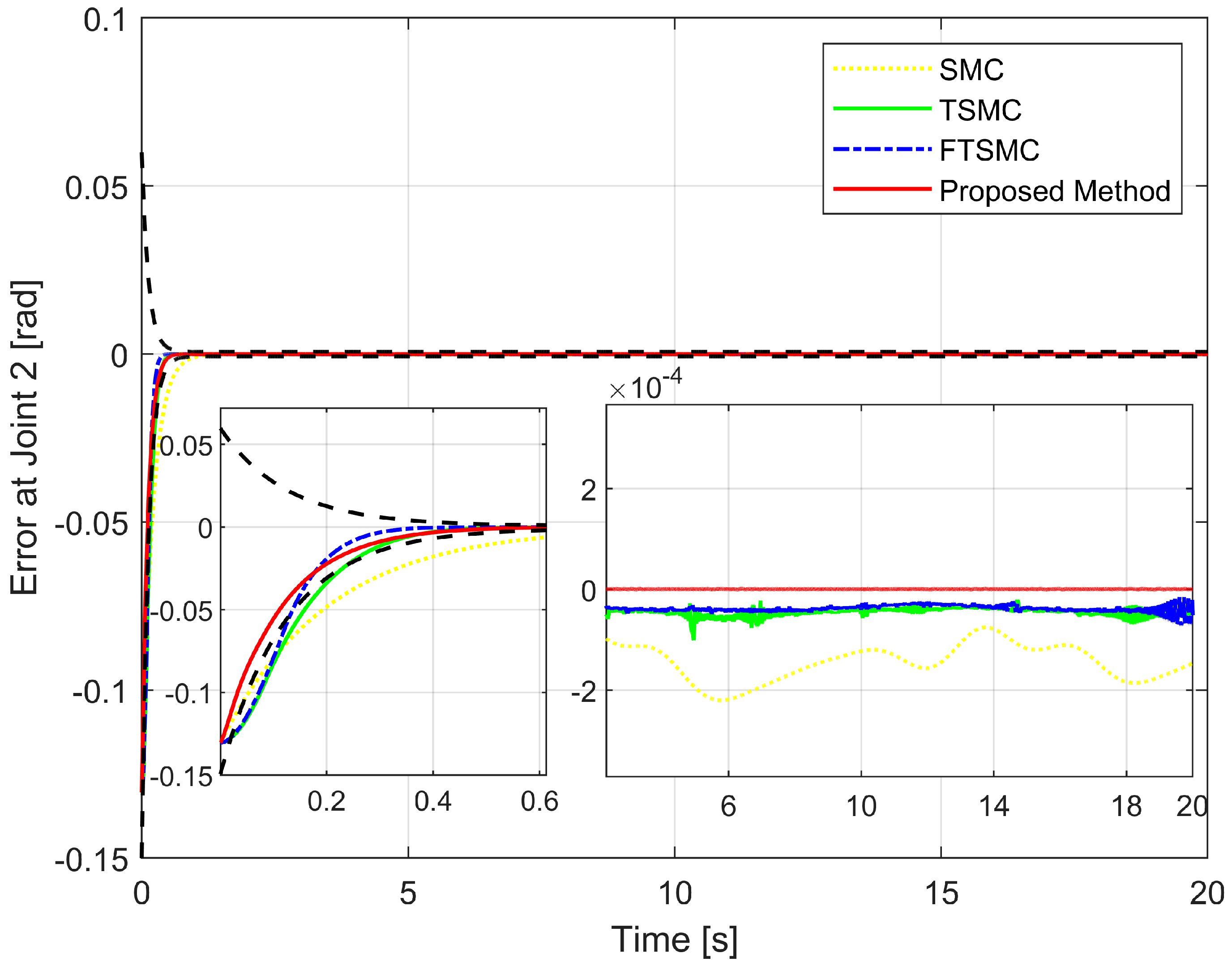
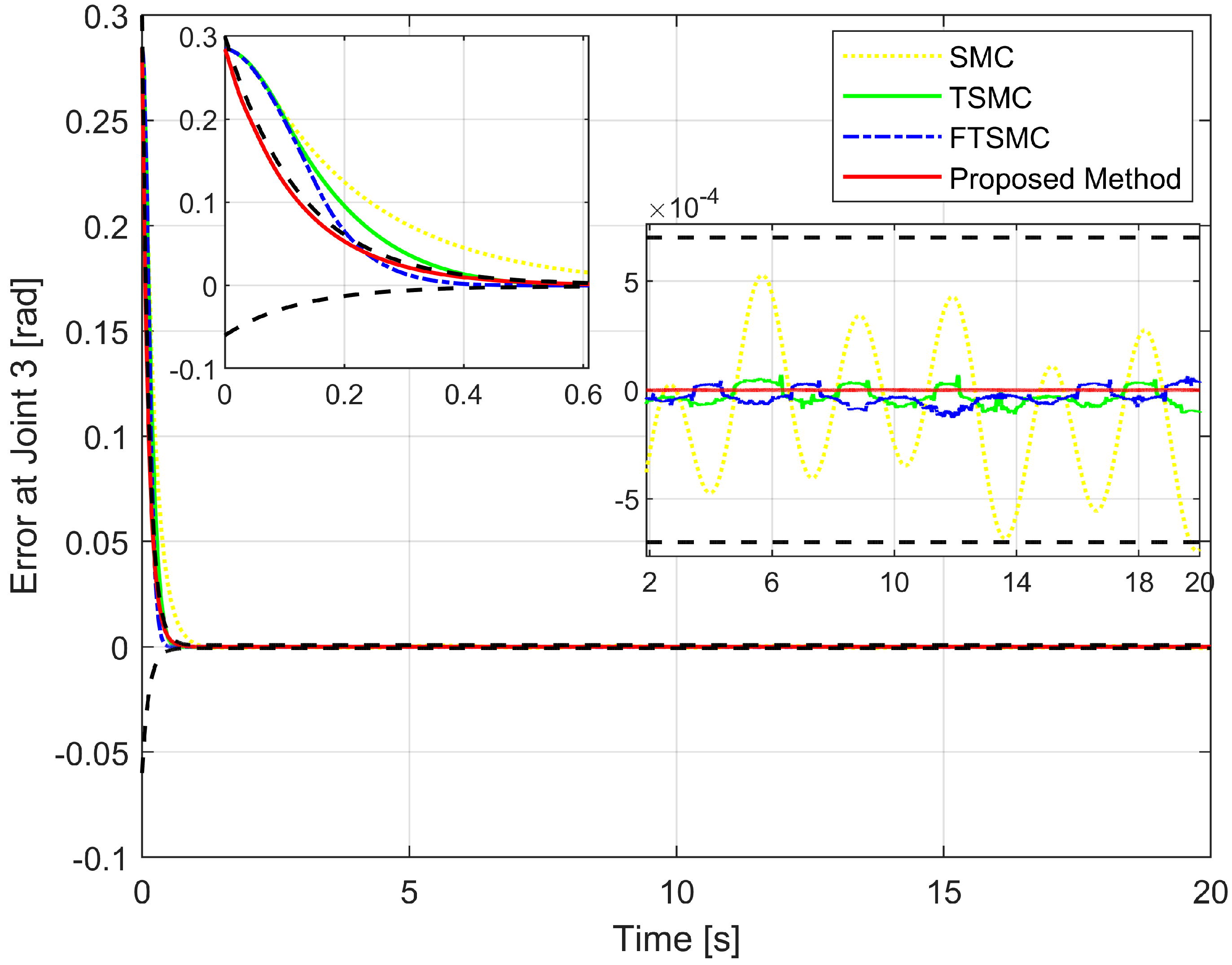
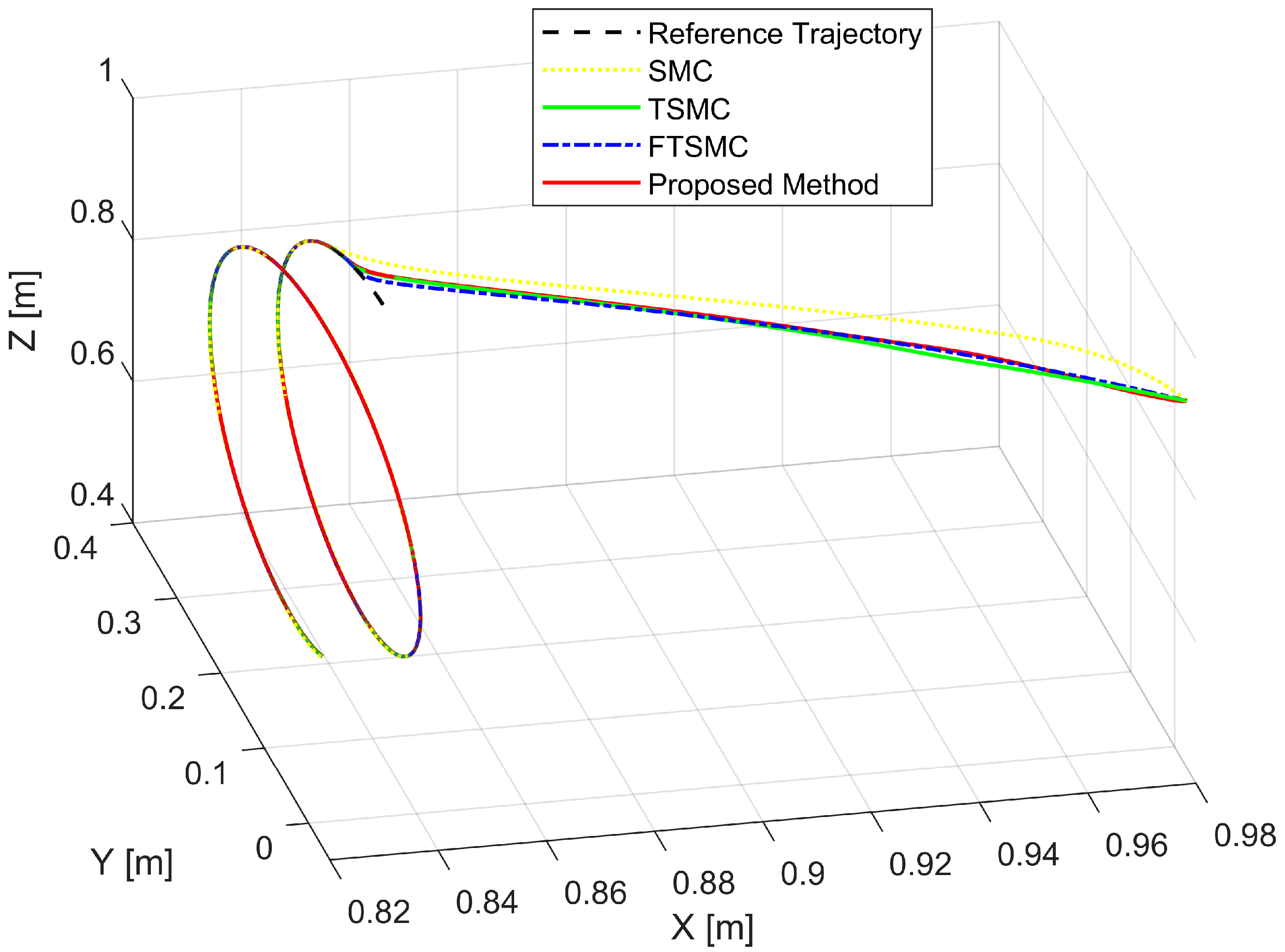
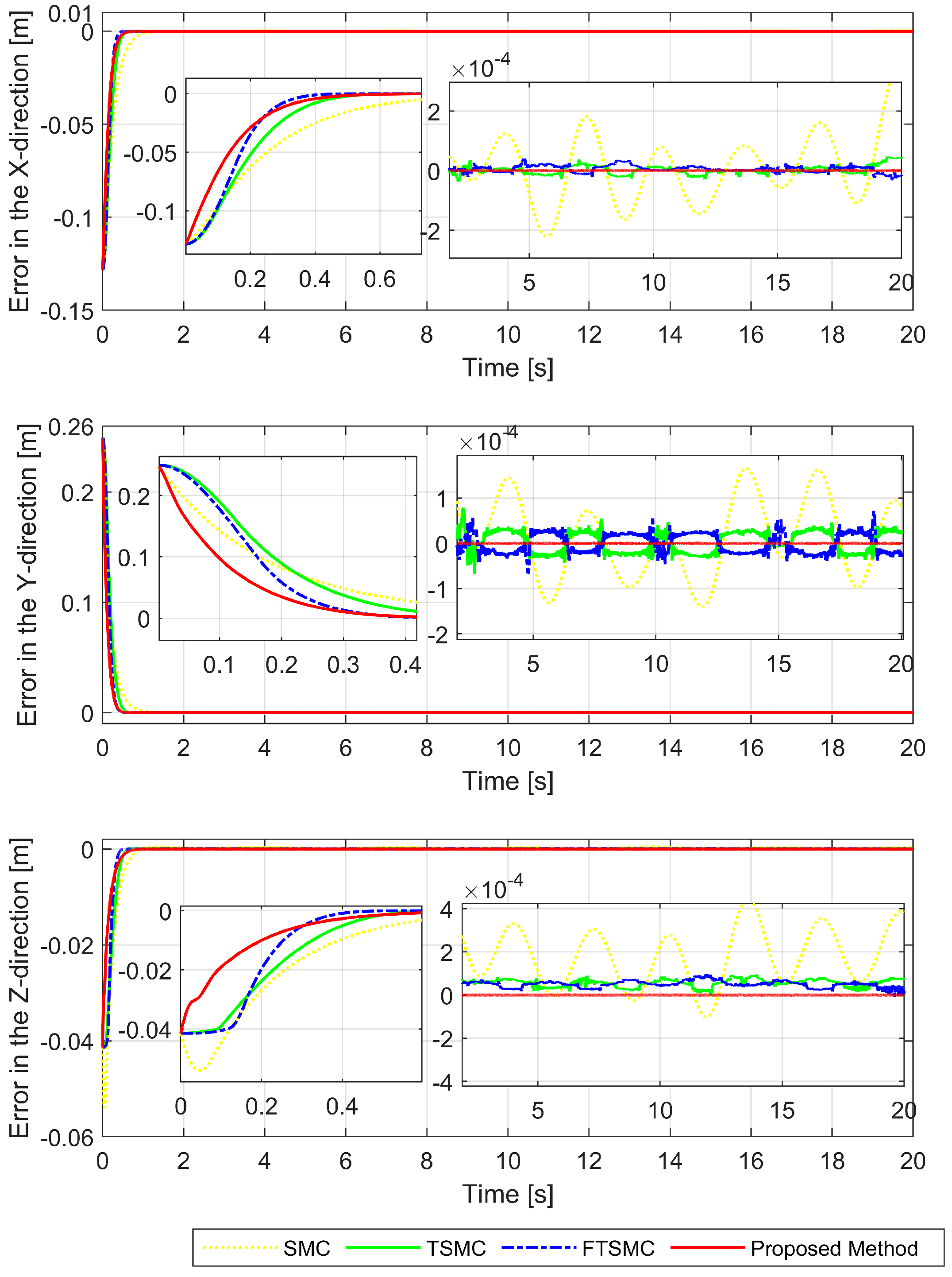
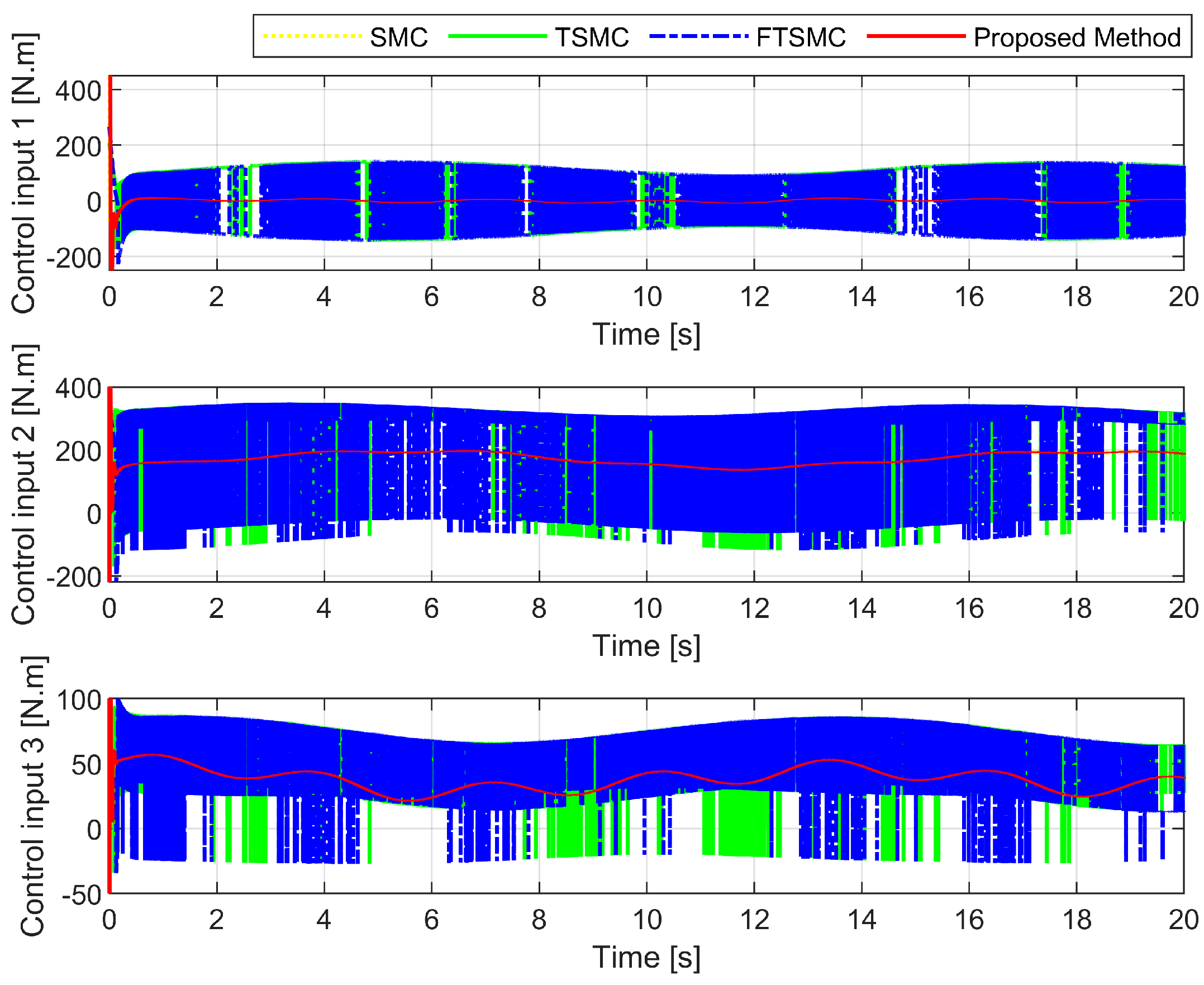
4.2. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CTC | Computed Torque Control |
| ACM | Adaptive Control Method |
| BsCM | Back-stepping Control Method |
| SMC | Sliding Mode Control |
| ISMC | Integral Sliding Mode Control |
| SSE | Steady-State Error |
| SOSMC | Second-Order Sliding Mode Control |
| TSMC | Terminal Sliding Mode Control |
| NTSMC | Non-singular Terminal Sliding Mode Control |
| FTSMC | Fast Terminal Sliding Mode Control |
| FNTSMC | Fast Non-singular Terminal Sliding Mode Control |
| NISMS | Nonsingular Integral Sliding Mode Surfac |
| FnTCM | Finite-Time Control Method |
| FxTCM | Fixed-Time Control Method |
| DO | Disturbance Observer |
| FnTDO | Finite-Time Disturbance Observer |
| FxTDO | Fixed-Time Disturbance Observer |
| SOSMO | Second-Order Sliding Mode Observer |
| USOSMO | Uniform Second-Order Sliding Mode Observer |
| TOSMO | Third-Order Sliding Mode Observer |
| ASTwCL | Adaptive Super-twisting Control Law |
| PPC | Prescribed Performance Control |
| PCP | Prescribed Control Performance |
| PPF | Prescribed Performance Function |
| ETF | Error Transformation Function |
| DOF | Degrees of Freedom |
| RMSM | Roots-Mean-Square Method |
| RMSE | Roots-Mean-Square Error |
| SMO-CM | Sliding Mode Observer-based Control Method |
| TDE-CM | Time-Delay Estimation-based Control Method |
| DO-CM | Disturbance Observer-based Control Method |
| ADRCM | Active Disturbance Rejection Control Method |
| APPTMC | Adaptive Prescribed Performance Tracking Motion Control |
References
- Appleton, E.; Williams, D.J. Industrial Robot Applications; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Craig, J.J. Introduction to Robotics: Mechanics and Control; Pearson Educacion: Madrid, Spain, 2005. [Google Scholar]
- Kelly, R. A tuning procedure for stable PID control of robot manipulators. Robotica 1995, 13, 141–148. [Google Scholar] [CrossRef]
- Pervozvanski, A.A.; Freidovich, L.B. Robust stabilization of robotic manipulators by PID controllers. Dyn. Control 1999, 9, 203–222. [Google Scholar] [CrossRef]
- Cervantes, I.; Alvarez-Ramirez, J. On the PID tracking control of robot manipulators. Syst. Control Lett. 2001, 42, 37–46. [Google Scholar] [CrossRef]
- Parra-Vega, V.; Arimoto, S.; Liu, Y.H.; Hirzinger, G.; Akella, P. Dynamic sliding PID control for tracking of robot manipulators: Theory and experiments. IEEE Trans. Robot. Autom. 2003, 19, 967–976. [Google Scholar] [CrossRef]
- Edwards, C.; Colet, E.F.; Fridman, L.; Colet, E.F.; Fridman, L.M. Advances in Variable Structure and Sliding Mode Control; Springer: Berlin/Heidelberg, Germany, 2006; Volume 334. [Google Scholar]
- Su, C.Y.; Leung, T.P. A sliding mode controller with bound estimation for robot manipulators. IEEE Trans. Robot. Autom. 1993, 9, 208–214. [Google Scholar] [CrossRef]
- Baek, J.; Jin, M.; Han, S. A new adaptive sliding-mode control scheme for application to robot manipulators. IEEE Trans. Ind. Electron. 2016, 63, 3628–3637. [Google Scholar] [CrossRef]
- Shang, W.; Cong, S. Nonlinear computed torque control for a high-speed planar parallel manipulator. Mechatronics 2009, 19, 987–992. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.J. A backstepping global fast terminal sliding mode control for trajectory tracking control of industrial robotic manipulators. IEEE Access 2021, 9, 31921–31931. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Composite adaptive control of robot manipulators. Automatica 1989, 25, 509–519. [Google Scholar] [CrossRef]
- Utkin, V.; Lee, H. Chattering problem in sliding mode control systems. In Proceedings of the International Workshop on Variable Structure Systems, 2006. VSS’06, Alghero, Sardinia, 5–7 June 2006; pp. 346–350. [Google Scholar]
- Nguyen, V.C.; Vo, A.T.; Kang, H.J. A non-singular fast terminal sliding mode control based on third-order sliding mode observer for a class of second-order uncertain nonlinear systems and its application to robot manipulators. IEEE Access 2020, 8, 78109–78120. [Google Scholar] [CrossRef]
- Vo, A.T.; Truong, T.N.; Kang, H.J. A Novel Tracking Control Algorithm With Finite-Time Disturbance Observer for a Class of Second-Order Nonlinear Systems and its Applications. IEEE Access 2021, 9, 31373–31389. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, G.; Ouyang, H.; Mei, L. Novel Fixed-Time Nonsingular Fast Terminal Sliding Mode Control for Second-Order Uncertain Systems Based on Adaptive Disturbance Observer. IEEE Access 2020, 8, 126615–126627. [Google Scholar] [CrossRef]
- Van, M.; Ceglarek, D. Robust fault tolerant control of robot manipulators with global fixed-time convergence. J. Frankl. Inst. 2020, 358, 699–722. [Google Scholar] [CrossRef]
- Rojsiraphisal, T.; Mobayen, S.; Asad, J.H.; Vu, M.T.; Chang, A.; Puangmalai, J. Fast terminal sliding control of underactuated robotic systems based on disturbance observer with experimental validation. Mathematics 2021, 9, 1935. [Google Scholar] [CrossRef]
- Ba, D.X. A Fast Adaptive Time-delay-estimation Sliding Mode Control for Robot Manipulators. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 904–911. [Google Scholar] [CrossRef]
- Vo, A.T.; Kang, H. A Novel Fault-Tolerant Control Method for Robot Manipulators Based on Non-Singular Fast Terminal Sliding Mode Control and Disturbance Observer. IEEE Access 2020, 8, 109388–109400. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, W. Active disturbance rejection control: Methodology and theoretical analysis. ISA Trans. 2014, 53, 963–976. [Google Scholar] [CrossRef]
- Chang, J.L. Dynamic output integral sliding-mode control with disturbance attenuation. IEEE Trans. Autom. Control 2009, 54, 2653–2658. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.J.; Van, M. A Novel Active Fault-Tolerant Tracking Control for Robot Manipulators with Finite-Time Stability. Sensors 2021, 21, 8101. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans. Cybern. 2016, 47, 1681–1693. [Google Scholar] [CrossRef]
- Vo, A.T.; Truong, T.N.; Kang, H.J.; Van, M. A Robust Observer-Based Control Strategy for n-DOF Uncertain Robot Manipulators with Fixed-Time Stability. Sensors 2021, 21, 7084. [Google Scholar] [CrossRef] [PubMed]
- Rubagotti, M.; Estrada, A.; Castaños, F.; Ferrara, A.; Fridman, L. Integral sliding mode control for nonlinear systems with matched and unmatched perturbations. IEEE Trans. Autom. Control 2011, 56, 2699–2704. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, C.; Pan, L.; Yu, H. Integral sliding mode control: Performance, modification, and improvement. IEEE Trans. Ind. Inform. 2017, 14, 3087–3096. [Google Scholar] [CrossRef]
- Mu, C.; He, H. Dynamic behavior of terminal sliding mode control. IEEE Trans. Ind. Electron. 2017, 65, 3480–3490. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Rabiee, H.; Ataei, M.; Ekramian, M. Continuous nonsingular terminal sliding mode control based on adaptive sliding mode disturbance observer for uncertain nonlinear systems. Automatica 2019, 109, 108515. [Google Scholar] [CrossRef]
- Vo, A.T.; Kang, H.J. An Adaptive Terminal Sliding Mode Control for Robot Manipulators With Non-Singular Terminal Sliding Surface Variables. IEEE Access 2019, 7, 8701–8712. [Google Scholar] [CrossRef]
- Doan, Q.V.; Vo, A.T.; Le, T.D.; Kang, H.J.; Nguyen, N.H.A. A novel fast terminal sliding mode tracking control methodology for robot manipulators. Appl. Sci. 2020, 10, 3010. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV. Aerosp. Sci. Technol. 2019, 93, 105306. [Google Scholar] [CrossRef]
- Nojavanzadeh, D.; Badamchizadeh, M. Adaptive fractional-order non-singular fast terminal sliding mode control for robot manipulators. IET Control Theory Appl. 2016, 10, 1565–1572. [Google Scholar] [CrossRef]
- Van, M. An enhanced robust fault tolerant control based on an adaptive fuzzy PID-nonsingular fast terminal sliding mode control for uncertain nonlinear systems. IEEE/ASME Trans. Mechatron. 2018, 23, 1362–1371. [Google Scholar] [CrossRef]
- Van, M.; Do, V.T.; Khyam, M.O.; Do, X.P. Tracking control of uncertain surface vessels with global finite-time convergence. Ocean Eng. 2021, 241, 109974. [Google Scholar] [CrossRef]
- Cruz-Zavala, E.; Moreno, J.A.; Fridman, L.M. Uniform robust exact differentiator. IEEE Trans. Autom. Control 2011, 56, 2727–2733. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, M. Fixed-time Disturbance Observer-based Sliding Mode Control for Mismatched Uncertain Systems. Int. J. Control Autom. Syst. 2022, 20, 2792–2804. [Google Scholar] [CrossRef]
- Nguyen, V.C.; Vo, A.T.; Kang, H.J. A finite-time fault-tolerant control using non-singular fast terminal sliding mode control and third-order sliding mode observer for robotic manipulators. IEEE Access 2021, 9, 31225–31235. [Google Scholar] [CrossRef]
- Van, M.; Franciosa, P.; Ceglarek, D. Fault diagnosis and fault-tolerant control of uncertain robot manipulators using high-order sliding mode. Math. Probl. Eng. 2016, 2016, 7926280. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Tran, X.T.; Oh, H. Prescribed performance adaptive finite-time control for uncertain horizontal platform systems. ISA Trans. 2020, 103, 122–130. [Google Scholar] [CrossRef]
- Huang, H.; He, W.; Li, J.; Xu, B.; Yang, C.; Zhang, W. Disturbance observer-based fault-tolerant control for robotic systems with guaranteed prescribed performance. IEEE Trans. Cybern. 2020, 52, 772–783. [Google Scholar] [CrossRef]
- Yang, P.; Su, Y. Proximate fixed-time prescribed performance tracking control of uncertain robot manipulators. IEEE/ASME Trans. Mechatron. 2021, 27, 3275–3285. [Google Scholar] [CrossRef]
- Wang, S.; Na, J.; Chen, Q. Adaptive predefined performance sliding mode control of motor driving systems with disturbances. IEEE Trans. Energy Convers. 2020, 36, 1931–1939. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y.; Chen, B. Fault-tolerant control of an aerial manipulator with guaranteed tracking performance. Int. J. Robust Nonlinear Control 2022, 32, 960–986. [Google Scholar] [CrossRef]
- Zuo, Z. Non-singular fixed-time terminal sliding mode control of non-linear systems. IET Control Theory Appl. 2015, 9, 545–552. [Google Scholar] [CrossRef]
- Ding, S.; Levant, A.; Li, S. Simple homogeneous sliding-mode controller. Automatica 2016, 67, 22–32. [Google Scholar] [CrossRef]
- Laghrouche, S.; Liu, J.; Ahmed, F.S.; Harmouche, M.; Wack, M. Adaptive second-order sliding mode observer-based fault reconstruction for PEM fuel cell air-feed system. IEEE Trans. Control Syst. Technol. 2014, 23, 1098–1109. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Niku, S.B. Introduction to Robotics: Analysis, Control, Applications; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Levant, A. Chattering analysis. IEEE Trans. Autom. Control 2010, 55, 1380–1389. [Google Scholar] [CrossRef]



| Description | Notation |
|---|---|
| the real n-dimensional space | |
| the set of m by n real matrices | |
| the transpose of | |
| Euclidean norm of | |
| absolute value of | |
| vector of joint angular acceleration | |
| vector of joint angular velocity | |
| vector of joint angular position | |
| vector of system state | |
| vector of tracking error | |
| vector of the desired trajectory | |
| vector of NISMS | |
| the first-order derivative of x | |
| the second-order derivative of x | |
| Euler’s number |
| Description | Link 1 | Link 2 | Link 3 |
|---|---|---|---|
| Link Length (m) | |||
| Link Weight (kg) | |||
| Center of Mass (mm) | |||
| Inertia (kg.m) |
| Type of the Assumed Uncertainty | Functions |
|---|---|
| Calculated-Dynamical Errors | |
| Frictions | |
| Exterior Disturbances | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vo, A.T.; Truong, T.N.; Kang, H.-J. An Adaptive Prescribed Performance Tracking Motion Control Methodology for Robotic Manipulators with Global Finite-Time Stability. Sensors 2022, 22, 7834. https://doi.org/10.3390/s22207834
Vo AT, Truong TN, Kang H-J. An Adaptive Prescribed Performance Tracking Motion Control Methodology for Robotic Manipulators with Global Finite-Time Stability. Sensors. 2022; 22(20):7834. https://doi.org/10.3390/s22207834
Chicago/Turabian StyleVo, Anh Tuan, Thanh Nguyen Truong, and Hee-Jun Kang. 2022. "An Adaptive Prescribed Performance Tracking Motion Control Methodology for Robotic Manipulators with Global Finite-Time Stability" Sensors 22, no. 20: 7834. https://doi.org/10.3390/s22207834
APA StyleVo, A. T., Truong, T. N., & Kang, H.-J. (2022). An Adaptive Prescribed Performance Tracking Motion Control Methodology for Robotic Manipulators with Global Finite-Time Stability. Sensors, 22(20), 7834. https://doi.org/10.3390/s22207834










