Research on the Machinability of Micro-Tapered Hole Group in Piezoelectric Atomizer and the Improvement Method
Abstract
1. Introduction
2. Atomizer Structure and Laser Drilling Principle
2.1. Atomizer Structure
2.2. Laser Drilling Principle
3. Theoretical Analysis
3.1. Establishment of Vibration Model
3.2. Diameter Distribution Model of Tapered Holes on the Metal Sheet
3.3. Laser Drilling Model under Three Working Procedures
4. Measurement of Tapered Hole Diameter on the Metal Sheet
5. Experimental Analysis of Error Interference
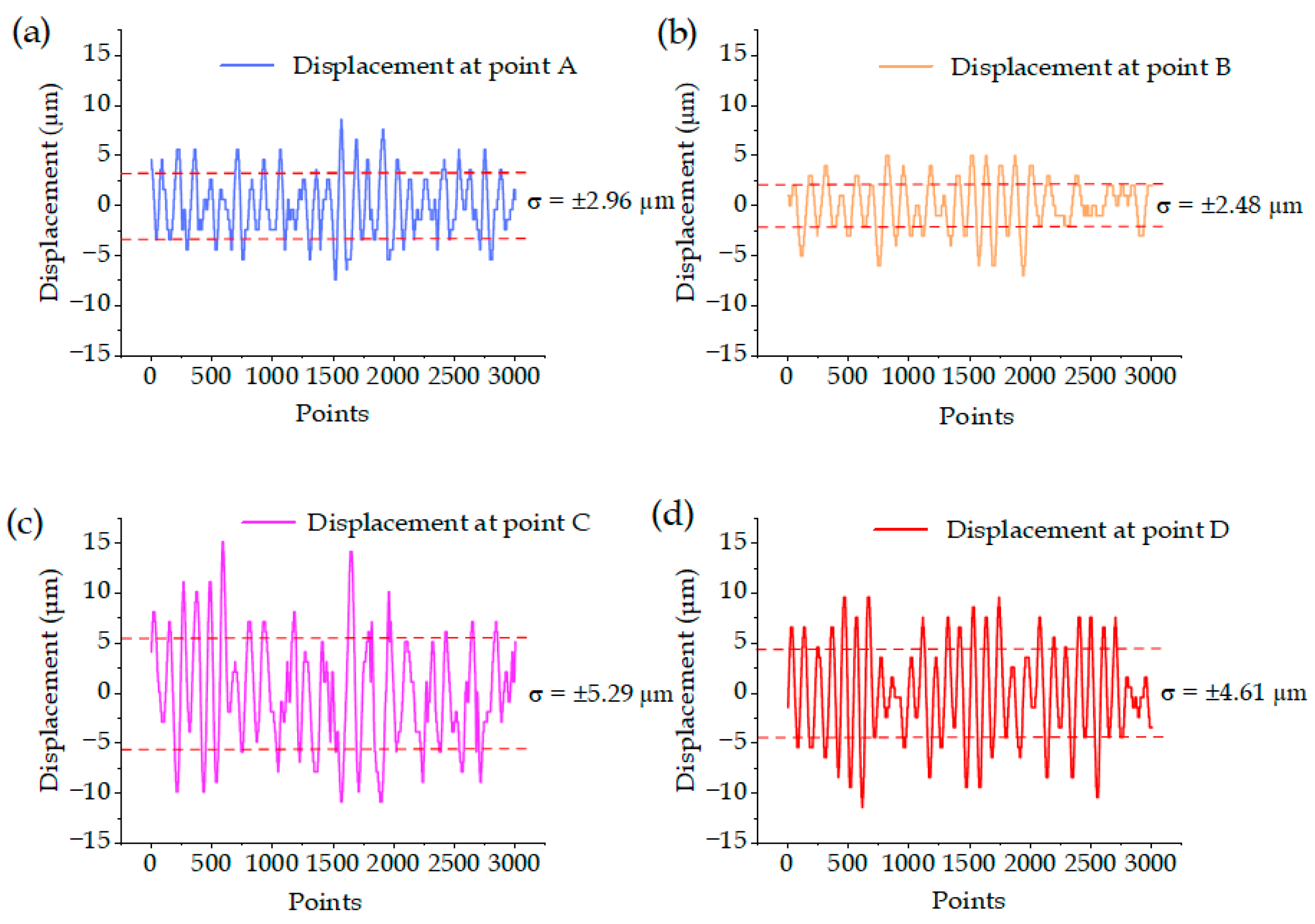
5.1. Experiment on Vibration Interference Errors in the External Environment
5.2. Interference Error Experiment on the Electrical System and Optical Control System Inside the Laser Machine
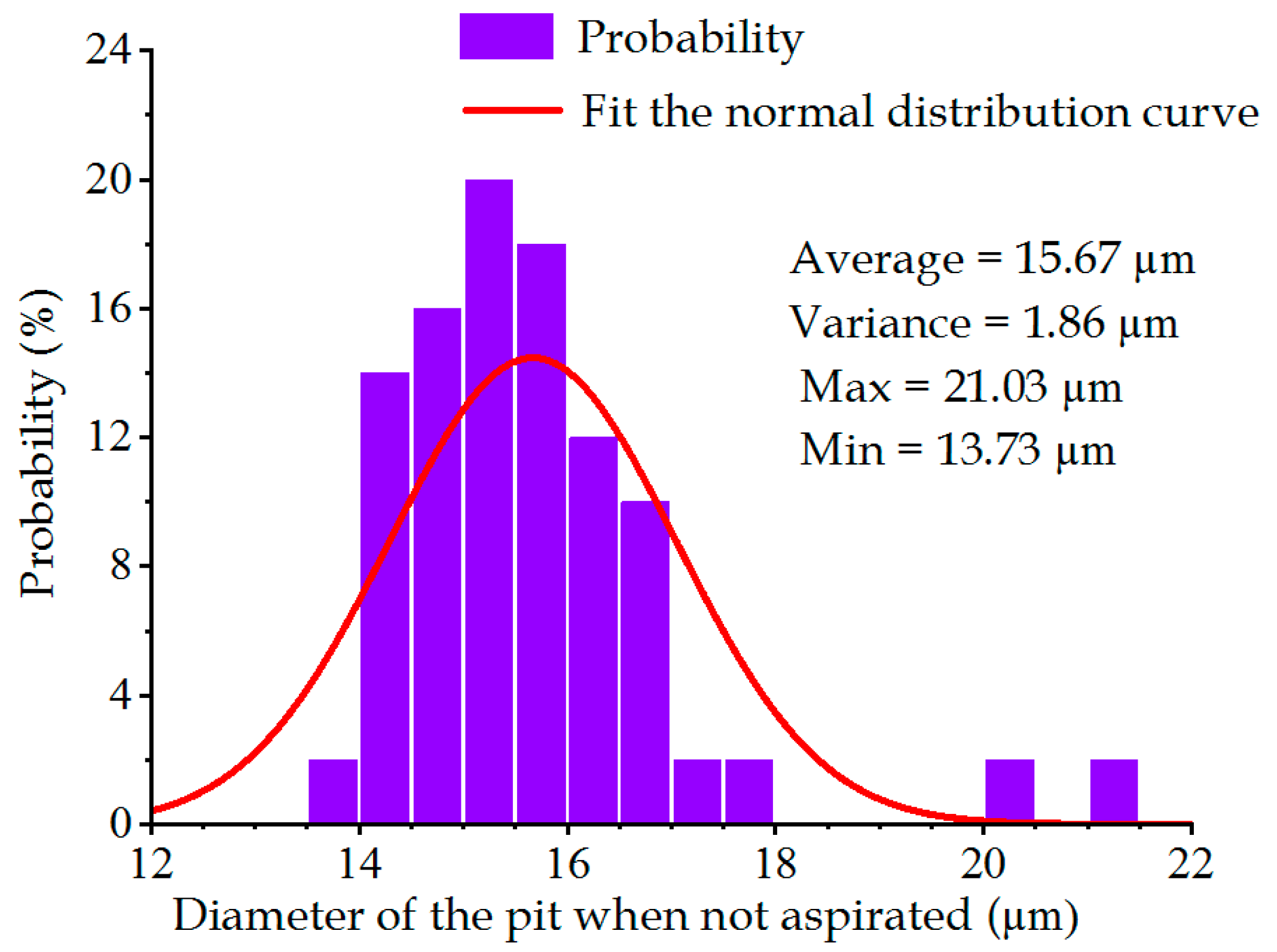
- The pit diameter under the non-aspirated state was analytically calculated. The average value of the pit diameter was known as 15.67 μm. According to Equations (27)–(30), the depth of the first working procedure was 18 μm. Given the identical volume of the metal sheet molten by laser energy each time, the depth after the second working procedure was about 17 μm, the pit diameter was about 18.87 μm, the depth after the third working procedure was 15 μm, and the pit diameter was about 22.07 μm. Since the preset value of the large diameter was 20 μm, the hole diameter of the metal sheet increased by 2.07 μm, owing the error in the processing algorithm. Therefore, the initial laser spot diameter was set to be too large due to the machining algorithm.
- The laser machine consists of five major parts: a solid-state laser, electrical system, optical system, and a three-coordinate moving table. In the laser machine, the optical system and control system influence the laser beam to accurately focus on the machined part of the work piece, including the laser focusing device and the observation and aiming device. Laser focusing deviations led to the enlargement of hole diameter, due to the internal error of the device, the vibration of the metal sheet and its uneven surface. The laser beam energy supplied by the electrical system to the laser was inconsistent; thus, so was the laser energy between pits, accompanied by the unconcentrated diameter distribution.
5.3. Error Analysis
- The average value of downward vibration displacement of the laser machine was 9.15 μm; namely, the distance from the laser machine to the metal sheet was shortened to 9.15 μm. As a result, the large diameter increased by 0.61 μm, which accounted for 20.00% of the error as seen in Equation (17).
- The tapered holes of the metal sheet were subjected to outward excessive melting in the machining process due to the initial spot diameter that was set too large. Through the processing algorithm Equation (30), the large diameter after the three working procedures was calculated to be 22.07 μm; thus, the large diameter increased by 2.07 μm, accounting for 67.87% of the error.
- Due to the optical system and the control system of the laser machine, the laser could not be accurately focused on the work piece, thus leading to positional deviation and error in the laser energy supplied by the electrical system to the laser; moreover, the metal sheet was uneven as a result of the suction device. All of these factors led to the inconsistent laser energy between holes, and this deviation accounted for 12.13% of the error.
6. Error Correction
6.1. Correction of Interference Error Induced by External Environmental Vibration
6.2. Error Correction between Electrical System and Optical Control System Inside the Laser Machine
- Since the machined diameter exceeded the standard value due to the inappropriate setting of the initial diameter of the laser spot, according to Equation (30), it could be inferred that should be 14.72 μm when is 20 μm. Diameter was changed by reducing the laser energy to 1.75 J.
- The error induced by the optical system and the electrical system in the laser machine could be corrected as follows: firstly, for the focusing deviation, the offset compensation could be set to ensure machining positional accuracy; thus, it was necessary to regularly check the offset compensation. Secondly, the focusing accuracy was also influenced by the roughness of the machined object. The focusing accuracy could be improved by ensuring the smoothness of the machined object surface; thus, the stainless steel material could be polished before machining to reduce surface roughness.
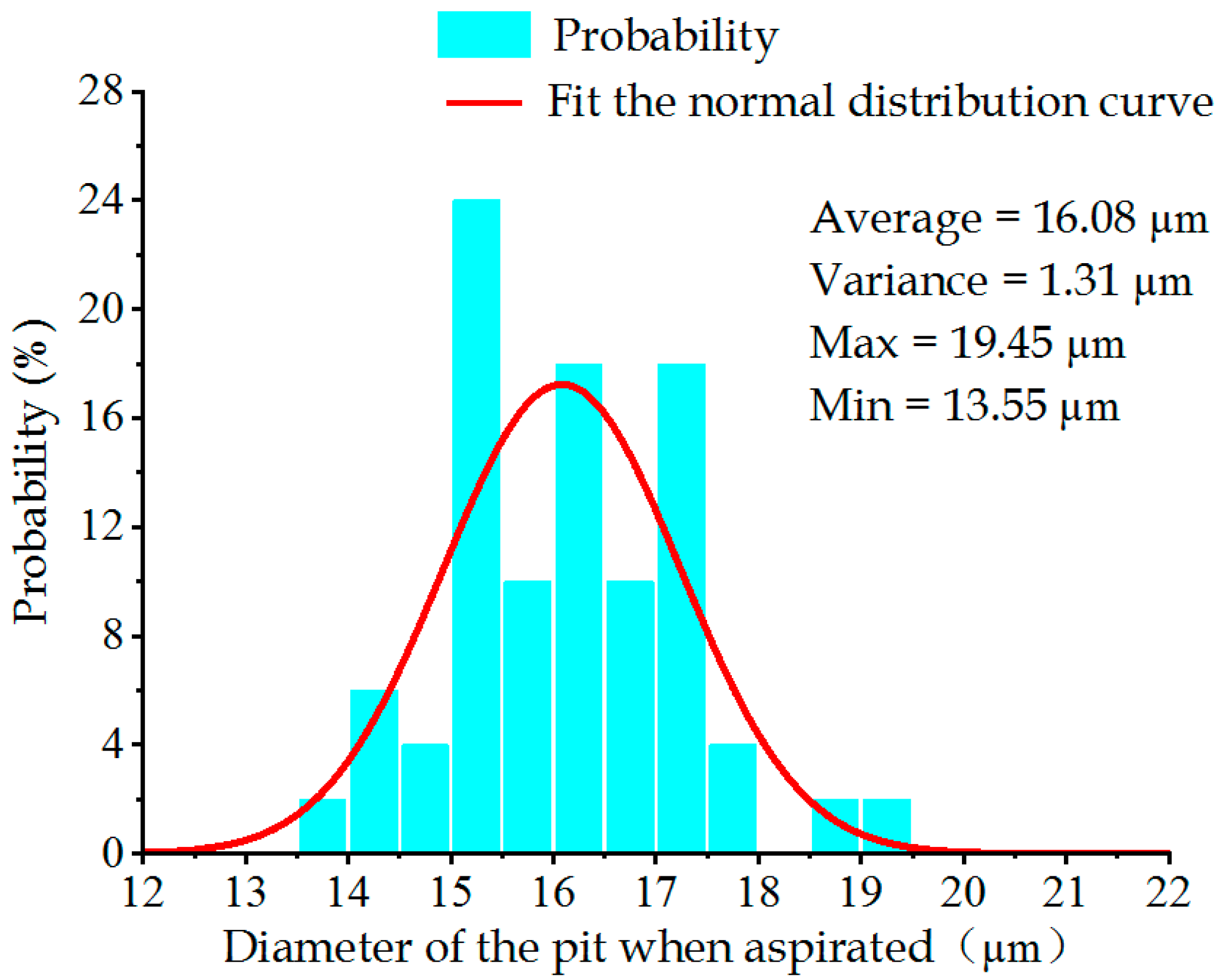
6.3. Comparative Experiment on the Diameter Measurement of Tapered Holes on the Metal Sheet
7. Conclusions
- Two main factors, external vibration disturbance and internal system errors inside the laser processor, were explored; consequently, the vibration model of the machining device and the laser machining model of three procedures were established, respectively.
- Based on the models and the experimental results, it was found that the errors in diameter caused by these two factors accounted for 20% and 67.87% of the total deviation, respectively.
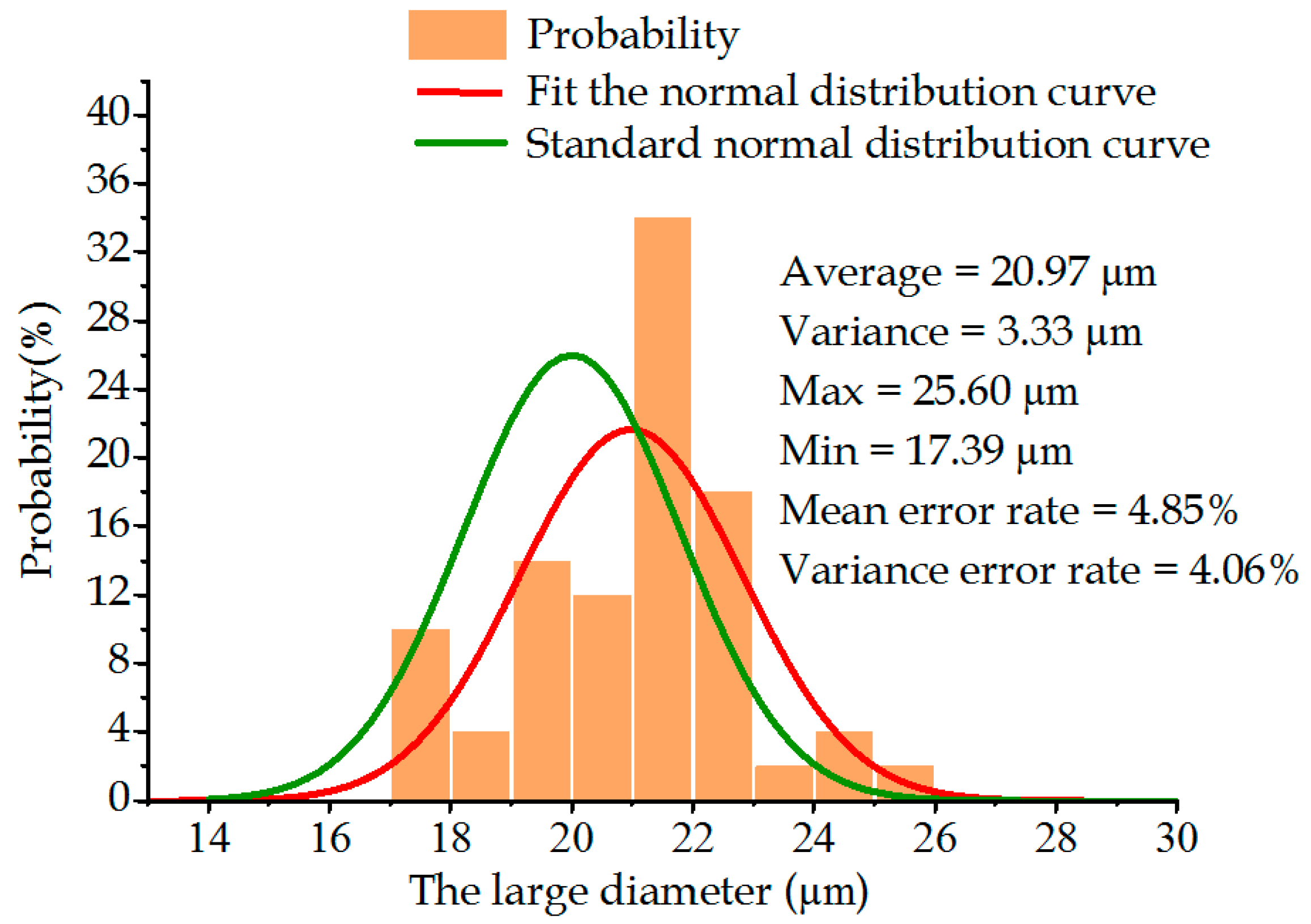
- An optimization method was proposed, whereby a damping system was added to the machining device, and the diameter of the initial laser spot was corrected. The experimental results showed that the deviation of the average value of the large diameter declined from 15.25% to 4.85%, and the deviation of the small diameter declined from 15.83% to 4.83%.
- The proposed model of laser drilling was established for the machining situation with three processes. The cone angle of tapered holes, the thickness of the metal sheet and the melting point of different materials determined the volume of metal to be machined away, which in turn, determined the number of processes. For other applications, the model of the laser machining must be modified by increasing or decreasing the number of procedures. From the modified model, the diameter of laser spot can be obtained, through which the same error reduction results can be obtained.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Sieber, I.; Zeltner, D.; Ungerer, M. Design and experimental setup of a new concept of an aerosol-on-demand print head. Aerosl. Sci. Technol. 2022, 56, 355–366. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, W.; Peng, Y. Experimental study on optimal spray parameters of piezoelectric atomizer based spray cooling. Int. J. Heat Mass Transf. 2016, 103, 57–65. [Google Scholar] [CrossRef]
- He, W.; Luo, Z.B.; Deng, X.; Xia, Z. A novel spray cooling device based on a dual synthetic jet actuator integrated with a piezoelectric atomizer. Heat Mass Transf. 2020, 56, 1551–1563. [Google Scholar] [CrossRef]
- Law, J.; Kong, K.W.; Chan, H.Y. Atomization of High-Viscosity Fluids for Aromatherapy Using Micro-heaters for Heterogeneous Bubble Nucleation. Sci. Rep. 2017, 7, 40289. [Google Scholar] [CrossRef]
- Waghule, T.; Singhvig, G.; Dubey, S.K.; Pandey, M.M.; Gupta, G.; Singh, M.; Dua, K. Microneedles: A smart approach and increasing potential for transdermal drug delivery system. Biomed Pharm. 2019, 109, 1249–1258. [Google Scholar] [CrossRef]
- Hsieh, S.S.; Huang, C.F.; Lu, Y.M. Water spray heat transfer through a piezoelectric atomizer with a single-hole micronozzle. J. Mech. Sci. Technol. 2020, 34, 3427–3436. [Google Scholar]
- Ahmed, T.; Kourmatzis, A.; Masri, A.R. Atomization behaviour of a hybrid air-blast-electrostatic atomizer for spray combustion. Fuel 2021, 288, 119716. [Google Scholar] [CrossRef]
- Meahara, N.; Ueha, S.; Mori, E. Influence of the vibrating system of a multipinhole-plate ultrasonic nebulizer on its performance. Rev. Sci. Instrum. 1986, 57, 2870–2876. [Google Scholar]
- Maehara, N.; Ueha, S.; Mori, E. Optimum Design Procedure for Multi-Pinhole-Plate Ultrasonic Atomizer. Jpn. J. Appl. Phys. 1987, 26, 215–217. [Google Scholar] [CrossRef]
- De Heij, B.; van der Schoot, B.; Bo, H.U. Characterisation of a fL droplet generator for inhalation drug therpy. Sens. Actuators A Phys. 2000, 85, 430–434. [Google Scholar] [CrossRef]
- Toda, K. Ultrasonic Vibrating Device. U.S. Patent 5,297,734, 29 March 1994. [Google Scholar]
- Toda, K.; Akimura, Y. An ultrasonic atomizing device using coupled-mode vibration. Rev. Sci. Instrum. 1994, 65, 3276–3278. [Google Scholar] [CrossRef]
- Toda, K.; Ishii, J. Operation Performance of Self-Oscillation Ultrasonic Vibrating Device for Liquid Atomization. Jpn. J. Appl. Phys. 1995, 34, 5332–5334. [Google Scholar] [CrossRef]
- Stemme, E.; Larsson, S.G. The piezoelectric capillary injector-a new hydrodynamic method for dot pattern generation. IEEE Trans. Electron Devices 1973, 20, 14–19. [Google Scholar] [CrossRef]
- Kyser, E.L.; Sears, S.B. Method and Apparatus for Recording with Writing Fluids and Drop Projection Means Therefor. U.S. Patent 3,946,398, 23 March 1976. [Google Scholar]
- Mikalesen, A. Apparatus and Method Employing Phase Change Ink. U.S. Patent 4 742 364A, 3 May 1988. [Google Scholar]
- Lynn, C. A Xaar perspective on ‘The Inkjet DRUPA’. Soc. Imaging Sci. Technol. 2009, 2009, 437–439. [Google Scholar]
- Roche, P.E.; Hansson, A.; Khuri-Yakub, B.T. Control of a drop-ejector used as photo-resist dispenser. Math. Control. Smart Struct. 1998, 3323, 446–454. [Google Scholar]
- Brunahl, J.; Grishin, A.M. Piezoelectric shear mode drop-on-demand inkjet actuator. Sens. Actuators A Phys. 2002, 101, 371–382. [Google Scholar] [CrossRef]
- Meacham, J.M.; Ejimofor, C.; Kumar, S. Micromachined ultrasonic droplet generator based on a liquid horn structure. Rev. Sci. Instrum. 2004, 75, 1347–1352. [Google Scholar] [CrossRef]
- Meacham, J.M.; Varady, M.J.; Degertekin, F.L. Droplet formation and ejection from a micromachined ultrasonic droplet generator: Visualization and scaling. Phys. Fluids 2005, 17, 100605. [Google Scholar] [CrossRef]
- Meacham, J.M.; Varady, M.J.; Fedorov, A.G. A Micromachined ultrsonic atomizer based on a liquid horn structure. In Proceedings of the IEEE International Ultrasonics Symposium Conference, Rotterdam, The Netherlands, 18–21 September 2005; pp. 1155–1159. [Google Scholar]
- Zarnitsyn, V.G.; Meacham, J.M.; Varady, M.J. Electrosonic ejector microarray for drug and gene delivery. Biomed. Microdevices 2008, 10, 299–308. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Liu, Y. Development of a resonant piezoelectric micro-jet for high-viscosity liquid using a longitudinal transducer. Mech. Syst. Signal Process. 2021, 146, 107012. [Google Scholar] [CrossRef]
- Harada, T.; Ishikawa, N.; Kanda, T. Droplet generation using a torsional Langevin-type transducer and a micropore plate. Sens. Actuators A Phys. 2009, 155, 168–174. [Google Scholar] [CrossRef]
- Omori, K.; Fujimoto, N.; Kanda, T. Core-shell droplet generation device using a flexural bolt-clamped langevin-type ultrasonic transducer. Actuators 2021, 10, 55. [Google Scholar] [CrossRef]
- Lu, C.F.; Liu, W.C.; Chen, C.J. Anti-wetting trench of nozzle plate for piezoelectric actuating dispenser. In Proceedings of the 2009 4th International Microsystems, Packaging, Assembly and Circuits Technology Conference, Taipei, Taiwan, 21–23 October 2009; pp. 674–677. [Google Scholar]
- McCarthy, S.D.; Gonzalez, H.E.; Higgins, B.D. Future trends in nebulized therapies for pulmonary disease. J. Pers. Med. 2020, 10, 37. [Google Scholar] [CrossRef]
- Zhang, G.P.; Li, Y.F.; Chen, T.F. Comparative study of the efficacy and Dham lacokinetics of reduning injection and atomization inhalation. Biomed. Pharm. Ther. 2019, 118, 109226. [Google Scholar] [CrossRef]
- Moody, G.B.; Luckett, P.M.; Shockley, C.M. Clinical efficacy of vibrating mesh and jet nebulizers with different interfaces in pediatric subjects with asthma. Respir. Care 2020, 65, 1451–1463. [Google Scholar] [CrossRef]
- Yan, Q.; Sun, W.; Zhang, L. Effects of vibration characteristics on the atomization performance in the medical piezoelectric atomization device induced by intra-hole fluctuation. Chin. J. Mech. Eng. 2021, 34, 123. [Google Scholar] [CrossRef]
- FDAU. Reviewer Guidance for Nebulizers, Metered Dose Inhalers. Spacers and Actuators. 2014. Available online: http://www.fda.gov/medicaldevices/deviceregulationandguidance/guidancedocuments/ucm081282.htm (accessed on 2 September 2022).
- Wang, G.; Zhou, Z.; Yuan, S. Experimental Research and Development on Piezoelectrically Actuated Microjet for IDT. Instrum. Tech. Sens. 2002, 37–39. [Google Scholar] [CrossRef]
- Wang, G. Theoretical and Experimental Analysis of Droplet Characteristics in Piezoelectrically Actuated Microjet. Chin. J. Sci. Instrum. 2002, 23, 6–8. [Google Scholar]
- Feng, Y.; Zhou, Z.; Ye, X. Characterization of the pressure wave in piezoelectrically actuated micro jet. Micronanoelectronic Technol. 2003, 1, 506–511. (In Chinese) [Google Scholar]
- Yan, Q.; Zhang, J.; Huang, J. Effect of vibration characteristics on the atomization rate in a micro-tapered aperture atomizer. Sensors 2018, 18, 934. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, Q.; Huang, J. Experimental V erification of the Pumping Effect Caused by the Micro-Tapered Hole in a Piezoelectric Atomizer. Sensors 2018, 18, 2311. [Google Scholar] [CrossRef]
- Yan, Q.; Wu, C.; Zhang, J. Effect of the dynamic cone angle on the atomization performance of a piezoceramic vibrating mesh atomizer. Appl. Sci. 2019, 9, 1836. [Google Scholar] [CrossRef]
- Yan, Q.; Sun, W.; Zhang, J. Study on the influencing factors of the atomization rate in a piezoceramic vibrating mesh atomizer. Appl. Sci. 2020, 10, 2422. [Google Scholar] [CrossRef]
- Shen, S.C.; Wang, Y.J.; Chen, Y.Y. Design and fabrication of medical micro-nebulizer. Sens. Actuators A Phys. 2008, 144, 135–143. [Google Scholar] [CrossRef]
- Shen, S.C. A new cymbal-shaped high power microactuator for nebulizer application. Microelectron. Eng. 2010, 87, 89–97. [Google Scholar] [CrossRef]
- Shen, S.C.; Wang, Y.J. A Novel Handhold High Power MEMS Atomizer Using Micro Cymbal Shape Nozzle Plate for Inhalation Therapy. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009; Volume 49033, pp. 375–382. [Google Scholar]
- Zhang, J.; Hu, F.J.; Ji, J. Piezoelectric Ceramic Ultrasonic Atomizing Sheet. China Invention Patent 201110413234.5, 13 December 2011. (In Chinese). [Google Scholar]
- Lin, C.Y.; Meng, H.C.; Fu, C. An ultrasonic aersol therapy nebulizer using electroformed palladium-nickel alloy nozzle plates. Sens. Actuators A Phys. 2011, 169, 187–193. [Google Scholar] [CrossRef]
- Guerra-Bravo, E.; Lee, H.J.; Baltazar, A. Vibration analysis of a piezoelectric ultrasonic atomizer to control atomization rate. Appl. Sci. 2021, 11, 8350. [Google Scholar] [CrossRef]
- Zhang, L.; Tong, H.; Li, Y. Precision machining of micro tool electrodes in micro EDM for drilling array micro holes. Precis. Eng. 2015, 39, 100–106. [Google Scholar] [CrossRef]
- Li, Z.; Bai, J.; Cao, Y. Fabrication of microelectrode with large aspect ratio and precision machining of micro-hole array by micro-EDM. J. Mater. Process. Technol. 2019, 268, 70–79. [Google Scholar] [CrossRef]
- Zhu, D.; Qu, N.S.; Li, H.S. Electrochemical micromachining of microstructures of micro hole and dimple array. CIRP Ann. 2009, 58, 177–180. [Google Scholar]
- Egashira, K.; Hayashi, A.; Hirai, Y. Drilling of microholes using electrochemical machining. Precis. Eng. 2018, 54, 338–343. [Google Scholar] [CrossRef]
- He, J.F.; Guo, Z.N.; Lian, H.S. Experiments and simulations of micro-hole manufacturing by electrophoresis-assisted micro-ultrasonic machining. J. Mater. Process. Technol. 2019, 264, 10–20. [Google Scholar] [CrossRef]
- Meng, L.N.; Wang, A.H.; Wu, Y. Blind micro-hole array Ti6Al4V templates for carrying biomaterials fabricated by fiber laser drilling. J. Mater. Process. Technol. 2015, 222, 335–343. [Google Scholar] [CrossRef]
- Li, C.; Zhang, B.; Li, Y. Self-adjusting EDM/ECM high speed drilling of film cooling holes. J. Mater. Process. Technol. 2018, 262, 95–103. [Google Scholar] [CrossRef]
- Al-Ahmari, A.M.A.; Rasheed, M.S.; Mohammed, M.K. A hybrid machining process combining micro-EDM and laser beam machining of nickel–titanium-based shape memory alloy. Mater. Manuf. Process. 2016, 31, 447–455. [Google Scholar] [CrossRef]
- Yilba, B.S.; Ahin, A.Z. Laser heating mechanism including evaporation process initiating laser drilling. Int. J. Mach. Tools Manuf. 1994, 35, 509–518. [Google Scholar] [CrossRef]
- Jun, Y.U. Research on Advantages of UV Laser in Fine Processing Technology. Infrared 2008, 40, 9–13. [Google Scholar]
- Jackson, M.J.; O’neill, W. Laser micro-drilling of tool steel using Nd: YAG lasers. J. Mater. Process. Technol. 2003, 142, 517–525. [Google Scholar] [CrossRef]
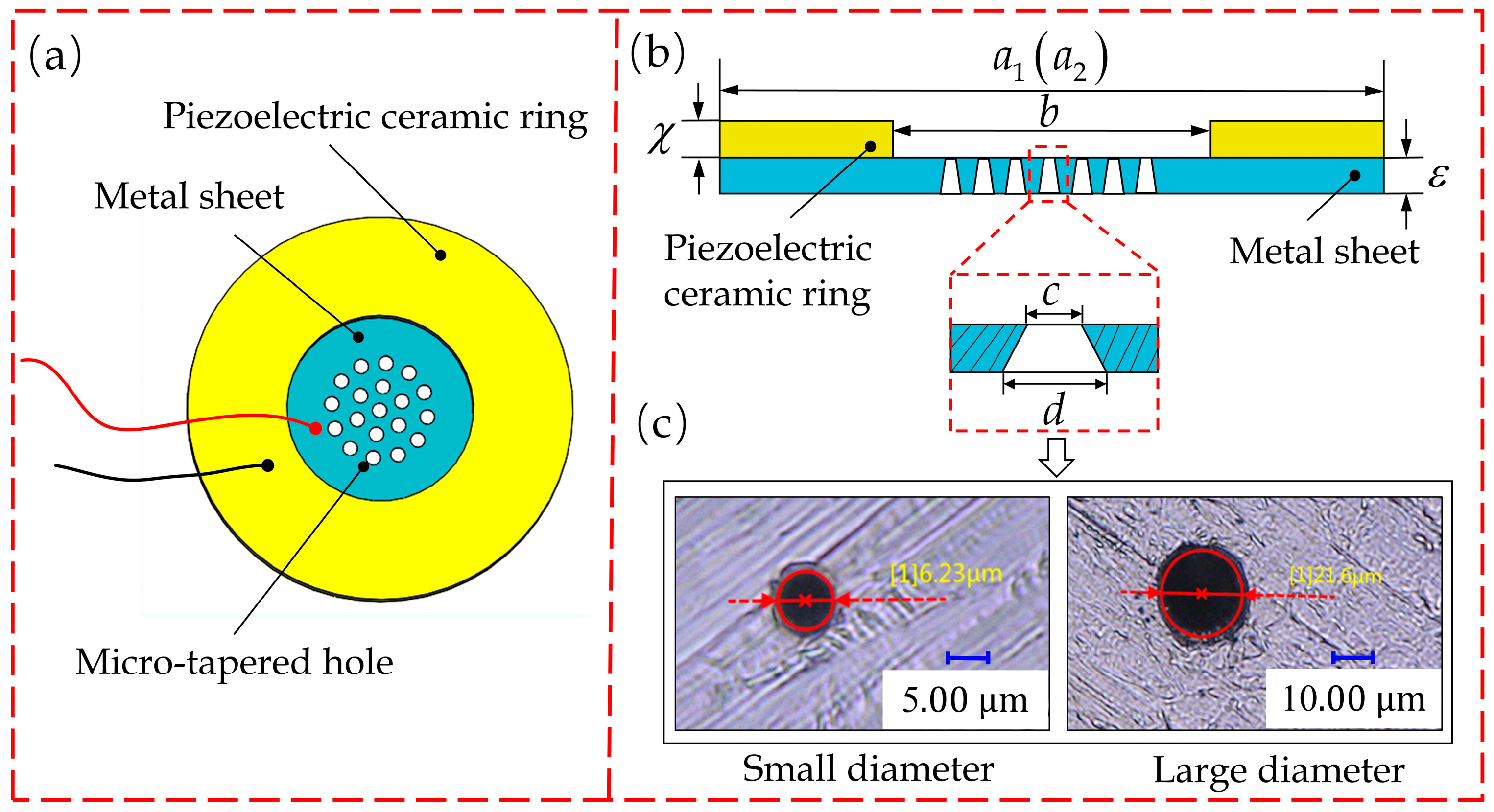












| Parameter | Thickness(mm) | Outer Diameter(mm) | Inner Diameter(mm) | ||
| Piezoelectric ceramics | 0.69 | 16 | 7.75 | ||
| Parameter | Thickness(mm) | Diameter (mm) | Tapered hole number | Small diameter(μm) | Large diameter(μm) |
| Metal sheet | 0.05 | 16 | 300 | 6.00 | 20.00 |
| Parameter (Unit) | Symbol | Value |
|---|---|---|
| Large diameter (μm) | * | |
| Small diameter (μm) | ** | |
| Pulse energy () | ||
| Thickness (μm) | 50 | |
| Density () | 8000 | |
| Melting temperature (°C) | t | 1450 |
| Specific heat capacity (J/(kg·°C)) | C | 0.45 × |
| Latent heat of melting (J/kg) | 2.47 × | |
| Latent heat of vaporization (J/kg) | 6.34 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Huang, X.; Chen, B.; Huo, Y.; Liu, Z.; Zhang, W.; Ma, M.; Zhou, X.; Liang, Z.; Gui, Z.; et al. Research on the Machinability of Micro-Tapered Hole Group in Piezoelectric Atomizer and the Improvement Method. Sensors 2022, 22, 7891. https://doi.org/10.3390/s22207891
Zhang F, Huang X, Chen B, Huo Y, Liu Z, Zhang W, Ma M, Zhou X, Liang Z, Gui Z, et al. Research on the Machinability of Micro-Tapered Hole Group in Piezoelectric Atomizer and the Improvement Method. Sensors. 2022; 22(20):7891. https://doi.org/10.3390/s22207891
Chicago/Turabian StyleZhang, Fan, Xi Huang, Bochuan Chen, Yuxuan Huo, Zheng Liu, Weirong Zhang, Mingdong Ma, Xiaosi Zhou, Zhongwei Liang, Zhenzhen Gui, and et al. 2022. "Research on the Machinability of Micro-Tapered Hole Group in Piezoelectric Atomizer and the Improvement Method" Sensors 22, no. 20: 7891. https://doi.org/10.3390/s22207891
APA StyleZhang, F., Huang, X., Chen, B., Huo, Y., Liu, Z., Zhang, W., Ma, M., Zhou, X., Liang, Z., Gui, Z., & Zhang, J. (2022). Research on the Machinability of Micro-Tapered Hole Group in Piezoelectric Atomizer and the Improvement Method. Sensors, 22(20), 7891. https://doi.org/10.3390/s22207891







