Soil Moisture Sensor Information Enhanced by Statistical Methods in a Reclaimed Water Irrigation Framework
Abstract
1. Introduction
2. Materials and Methods
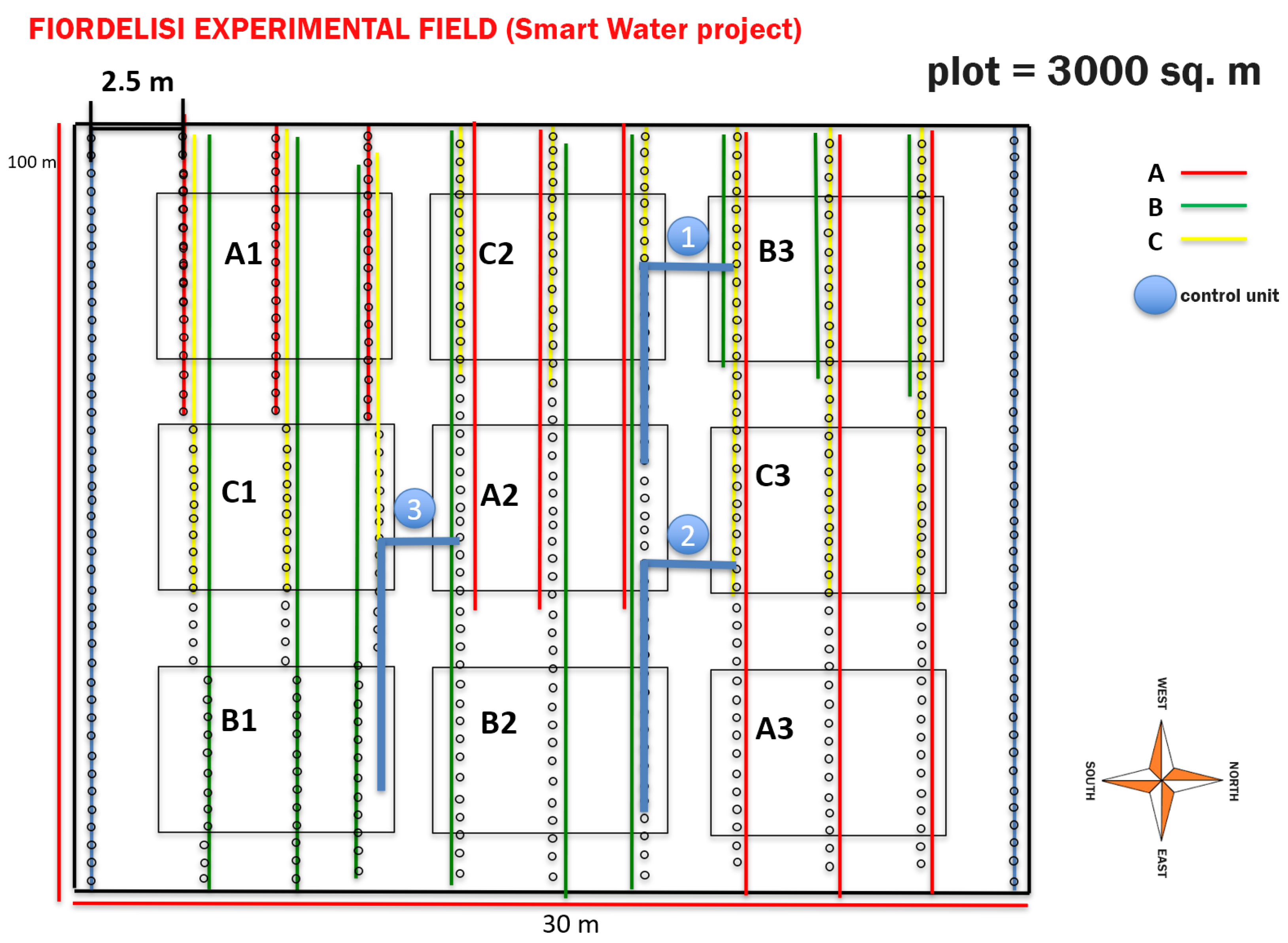
2.1. Study Site and Data Source
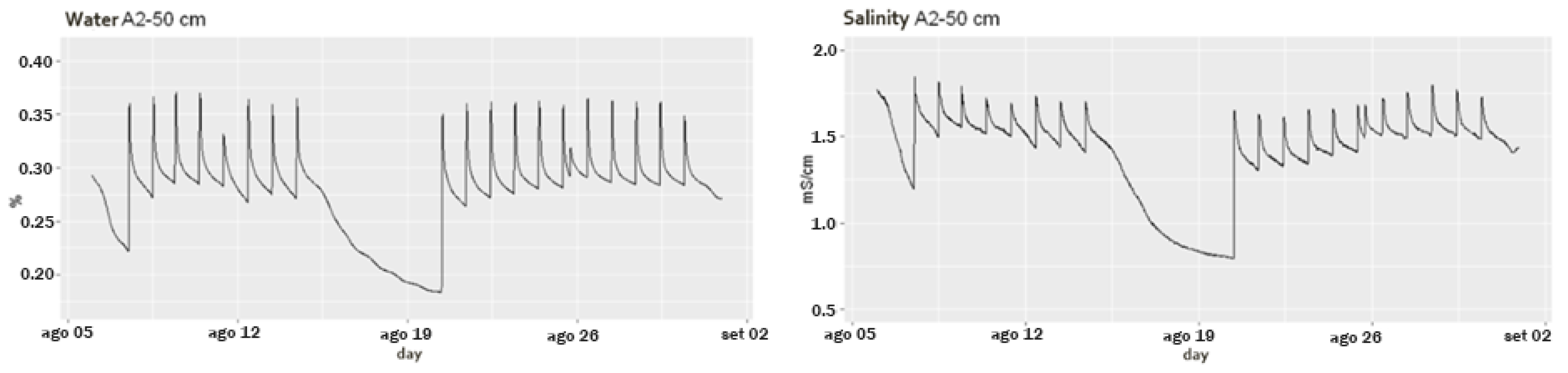
- soil data, i.e., soil water content (%), soil temperature (°C) and soil salinity (mS/cm) at depths of 30 and that were measured continuously by two probes with a 15 min frequency;
- irrigation data, i.e., the daily volume () of water employed to irrigate the tomatoes plants in each treatment block;
- atmospheric data, i.e., the values of rainfall (mm), temperature (°C), humidity (%), radiation and evapotranspiration (mm) that were recorded by a weather station (Stornara) near to the experimental area.
2.2. Datasets
- A:
- fresh water (FW) + conventional fertigation;
- B:
- agro-industrial wastewater (AIW) + conventional fertigation;
- C:
- AIW + smart water fertigation.
- soil data, i.e., the soil water content (%), salinity (mS/cm) and temperature values (°C) at and depths in the A2, B3 and C2 blocks (Figure 2) that were collected continuously every 15 min (for a total of 73 out of 96 daily surveys) over the time period of 5 August 2019 11:15:00–18 December 2019 9:30:00;
- irrigation data, i.e., the water volume () used for irrigation in each treatment block that were recorded daily over the time period of 1 June 2019–31 August 2019 and organized in an Excel file;
- climate data, i.e., data collected by the Stornara weather station, located near the farm, over the time period of 1 January 2019 00:00:00–3 June 2020 23:00:00. These data referred to hourly surveys of the quantities of:
- -
- precipitation (mm);
- -
- temperature (°C);
- -
- humidity (%);
- -
- radiation (Mj/mq);
- -
- wind (speed, gust (m/s) and direction);
- -
- upper and lower leaf wetness;
- -
- atmospheric pressure (hPA);
- -
- dew point (°C);
- -
- Etp (mm).
2.3. Data Pre-Processing and Analysis
2.4. Pre-Processing, Uploading and Visualization of Data in R
2.4.1. Soil Data
2.4.2. Climate Data
2.4.3. Irrigation Data
2.5. Preparing Data in R
- Training Set:
- 6 August 2019 00:00:00–28 August 2019 23:00:00 (23 days; 552 observations);
- Testing Set:
- 29 September 2019 00:00:00–30 September 2019 23:00:00 (2 days; 48 observations).
- Root mean square error
- computed as
- Mean absolute error
- computed as
- Mean absolute percentage error
- computed as
2.6. Formalization of Statistical Methods
3. Results
3.1. Decomposition Methods
- The additive model with the moving average method
- The components of a time series are generally the trend, seasonality and residual. R allows us to determine and estimate these three components using different methods, including decomposed.
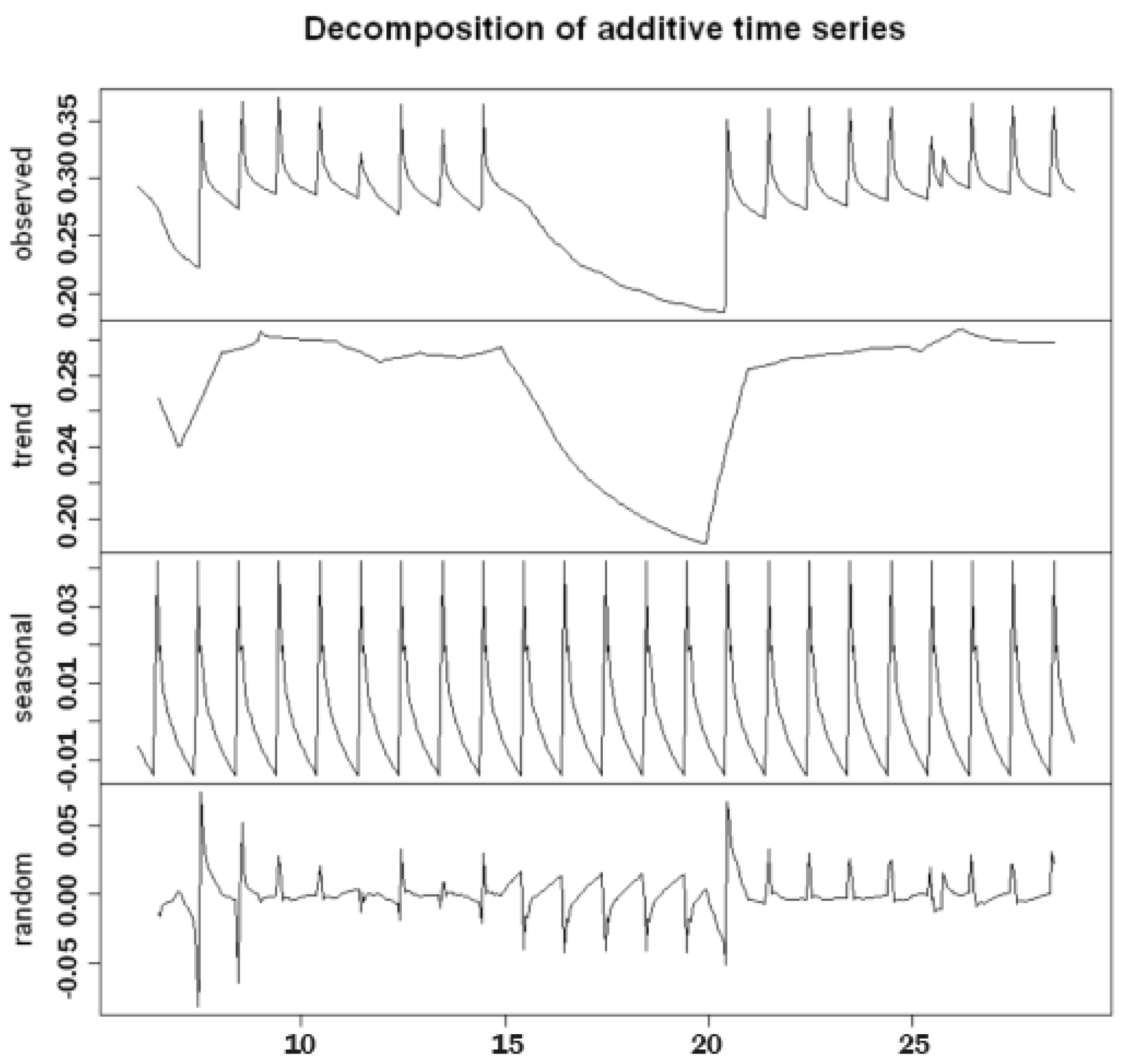
- Excluding the seasonal and residual components, the trend component appeared to be almost stationary on days when irrigation took place and decreased on days when irrigation did not take place. Thus, in order to obtain a constant average, the series needed to be differentiated;
- The seasonal component, due to irrigation, was scanned at intervals of 24 h (daily) and had a constant variance over time, which confirmed that we needed an additive rather than a multiplicative model;
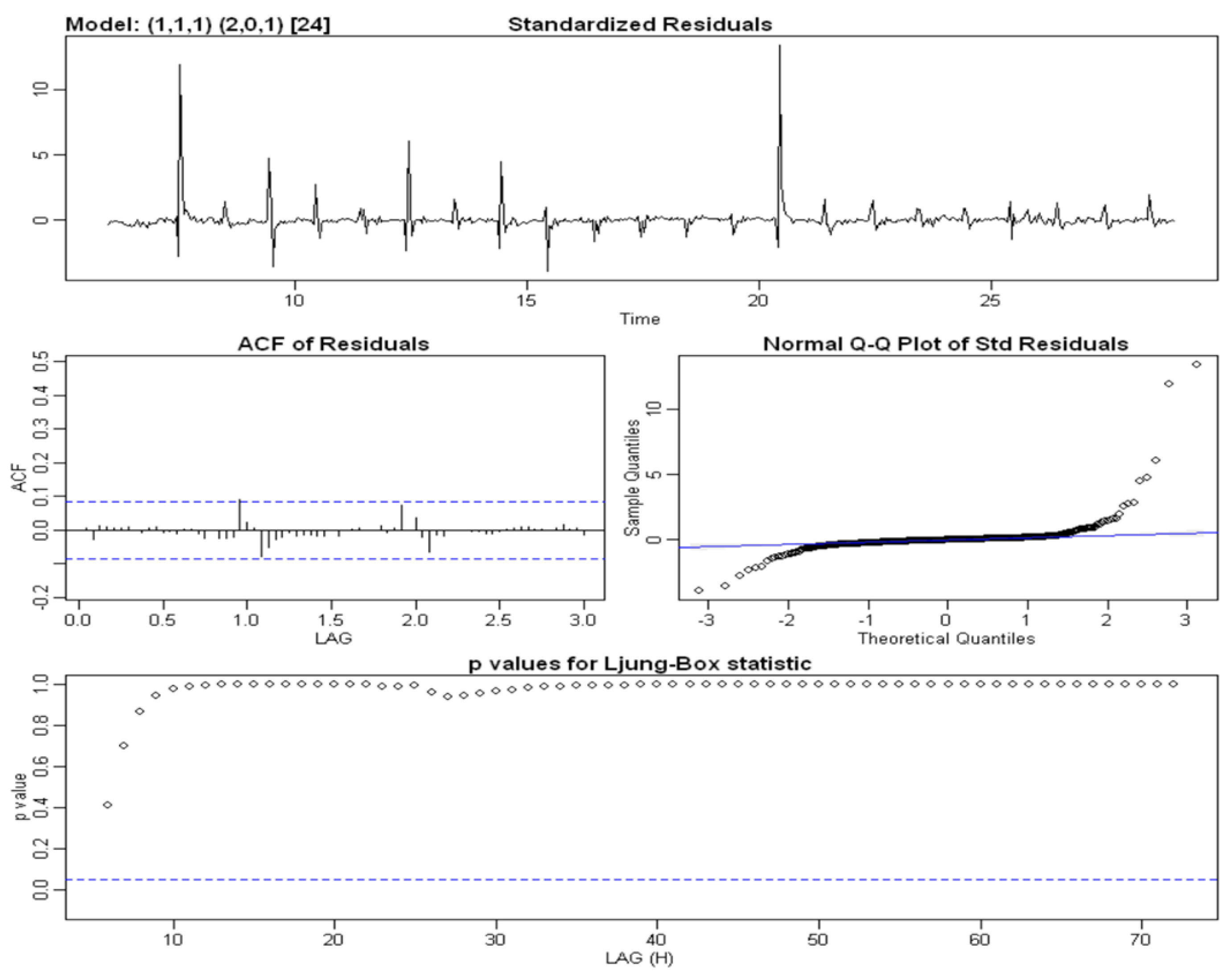
- The residual component, which should exhibit a similar behavior to white noise, instead exhibited a heteroscedastic behavior, with a variance that was not constant over time and peaked about every 24 h. Further confirmation can be obtained by looking at the plot of the distribution diagram and the Q–Q plot of the standardized residual components in Figure 6. Furthermore, the presence of correlation between the residual components is evident in the correlogram in the same figure, in which numerous significant lags can be observed. A verification of this was obtained using the Ljung–Box test: when the null hypothesis was true (i.e., the absence of autocorrelation), the LB statistic behaved asymptotically as a variable random chi-square statistic with k degrees of freedom, where k represents the number of considered lags.
- Holt–Winters exponential smoothing
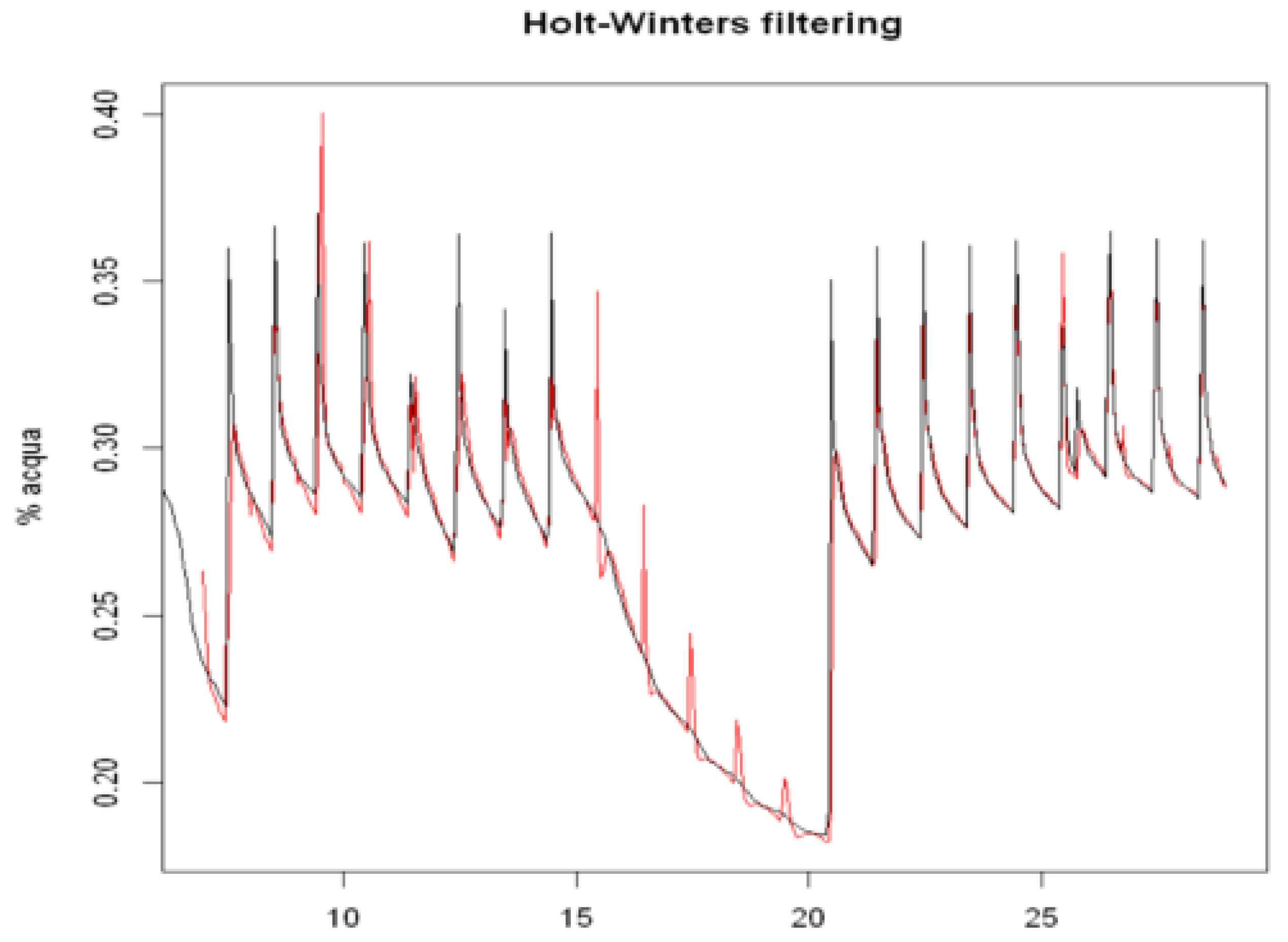
- Exponential smoothing using the Holt–Winters method can be considered as a more sophisticated version of simple additive decomposition using the symmetric (or moving) average method, as seen in the previous section. The idea is to transform a moving average into an exponential average with one or more smoothing parameters. The R stats package provides the HoltWinters() function for the implementation of this method. Using this function with the added seasonality of 24-h periods, we obtained the following table:
| Holt–Winters Method | |
| Soil Water Content at a Depth of 50 cm | |
| alpha | 0.480902 |
| beta | 0 |
| gamma | 0.698756 |
| SSE on the training set | 0.088168 |
| Performance Holt-Winters Method | |
| Soil Water Content at 50 cm, 48 h Forecast | |
| media test | 0.295670 |
| RMSE | 0.009268 |
| MAE | 0.007000 |
| MAPE | 2.371098 |
3.2. Stochastic Methods
- SARIMA model
- This is a seasonal autoregressive moving average model used to better describe the generating function of time series. This model allows us to predict observed values with a reduced number of input variables, following the principle of parameter parsimony. It also provides the ability to extend forecasts over long time horizons. In order to identify the model, we followed the Box–Jenkins procedure.
- Stationarity of time series. The first step was to check the stationarity of time series by analyzing correlograms and performing some statistical tests. When a time series was not stationary, it needed to be transformed into a stationary time series. The graph of the autocorrelation function for SWC suggested the presence of a linear trend and had high correlations among seasonal delays since a decreasing trend occurred during drying periods and peaks occurred after irrigation events: peaks repeated at intervals of about a regular amplitude equal to s = 24 and its multiples, which are called lag or seasonal delays, indicated the presence of the seasonal component of the series and contributed to the time series being non-stationarity on average. To make the time series stationary on average, we applied appropriate transformations. In particular, to remove the linear trend, the regular difference operator of order was applied to the series.
- Identifying the SARIMA model The next step was to analyze the graphs of the global and partial autocorrelation functions of the series, as shown in Figure 10, in order to identify significant delays in identifying hyperparameters. We noticed that the first order differentiation performed on the series eliminated the problem of the series being non-stationarity on average. From an analysis of the graph of the global autocorrelation function, we observed that the second delay was significantly different from the zero peak with regard to the regular part and was in correspondence with the second seasonal delay with regard to the seasonal part. Therefore, we could assume that the model that generated the series under analysis had a regular moving average component q between 0 and 2 and a seasonal moving average component Q between 0 and 2. The graph of the partial autocorrelation function shows a trend similar to that of the global autocorrelation function. Therefore, the series generator model had a regular autoregressive component p and seasonal P between 0 and 2. Using the auto.arima() method, we performed a grid search on the possible hyperparameters identified by the model and selected the best results based on statistic criteria, such as AIC and BIC. The optimal stochastic model for this series, as identified by this method, was a SARIMA process .Figure 10. The correlograms of the autocorrelation function and partial autocorrelation function of the time series data for SWC in the A2 block at a depth of 50 cm following differentiation, which were obtained through the following functions of R:
- > train.diff = diff(train)
- > par(mfrow = c(2,1))
- > acf(train.diff,50, main = ’acf diff(train)’)
- > pacf(train.diff,50, main = ’pacf diff(train)’)
- An augmented Dickey–Fuller test confirmed the alternative stationarity hypothesis:
- > adf.test(train.diff, k = 24)
- Dickey-Fuller = −4.0635, Lag order = 26, p-value = 0.01.
Figure 10. The correlograms of the autocorrelation function and partial autocorrelation function of the time series data for SWC in the A2 block at a depth of 50 cm following differentiation, which were obtained through the following functions of R:- > train.diff = diff(train)
- > par(mfrow = c(2,1))
- > acf(train.diff,50, main = ’acf diff(train)’)
- > pacf(train.diff,50, main = ’pacf diff(train)’)
- An augmented Dickey–Fuller test confirmed the alternative stationarity hypothesis:
- > adf.test(train.diff, k = 24)
- Dickey-Fuller = −4.0635, Lag order = 26, p-value = 0.01.
- Parameter estimation After identifying the possible hyperparameters of the series, we proceeded with the estimation of the model parameters. By applying a procedure based on the iterative method of maximum likelihood (command Arima()), a model was estimated using the parameters reported in the following table:
SARIMA(0, 1, 2, 2, 0, 1, 24) Water Content at a Depth of 50 cm Parameters Coefficient Estimation s.e. t-Value p-Value ma1 −0.1979 0.0416 −4.7612 0 ma2 −0.2173 0.0423 −5.1317 0 sar1 1.2963 0.0623 20.8190 0 sar2 −0.3074 0.0568 −5.4151 0 sma1 −0.8990 0.0477 −18.8336 0 Statistics Estimated 0.000132 Log Likelihood 1670.18 AIC −3328.36 AICc −3328.21 BIC −3302.49 Performance on the Training Set RMSE 0.011426 MAE 0.003525 MAPE 1.169268 - Model verification After estimating a specific model, we checked its goodness and adequacy with respect to the observed data. We analyzed whether the parameter estimates were statistically significant, whether the residual components reflected the assumptions of the stochastic models and whether the parsimony principle was verified by the model, i.e., whether the number of parameters used was as low as possible. The first step was to estimate the coefficients of the model through the verification of the null hypothesis, i.e., . The sarima() method provides the Student’s t-test and the respective p-value for each parameter. Null p-values in the outputs, which are reported in the table, led to the rejection of the null hypothesis for all parameters. A further check to be carried out concerned an analysis of the residual components of the estimated SARIMA model. Firstly, we analyzed the residual plots and correlograms to evaluate their stationary behavior and determine whether they were unrelated, respectively. These diagnostic plots were produced by the same SARIMA procedure and are presented in Figure 11. We observed that the residual time series plot fluctuated around a constant value equal to zero, resulting in the series being stationary on average. The model residual components showed numerous peaks when irrigation occurred; however, these results were slightly lower compared to those obtained by the decomposition models. The plot of the autocorrelation function shows that few delays were significantly correlated, while the Q–Q plot shows a non-normal distribution of residual components due to the presence of outliers and diverging tails at the extremes. Finally, the last graph represents the value of the p-value associated with the Ljung–Box test statistic over time k, which always has a higher level of significance . Consequently, the null hypothesis of non-correlation could be considered to be true.Figure 11. The diagnostic plots of the standardized residue components of the SARIMA model of the time series data for SWC in the A2 block at a depth of 50 cm, which were obtained using the following procedure in R:> model1 <- sarima(train,0,1,2,2,0,1,24, no.constant = TRUE).Figure 11. The diagnostic plots of the standardized residue components of the SARIMA model of the time series data for SWC in the A2 block at a depth of 50 cm, which were obtained using the following procedure in R:> model1 <- sarima(train,0,1,2,2,0,1,24, no.constant = TRUE).
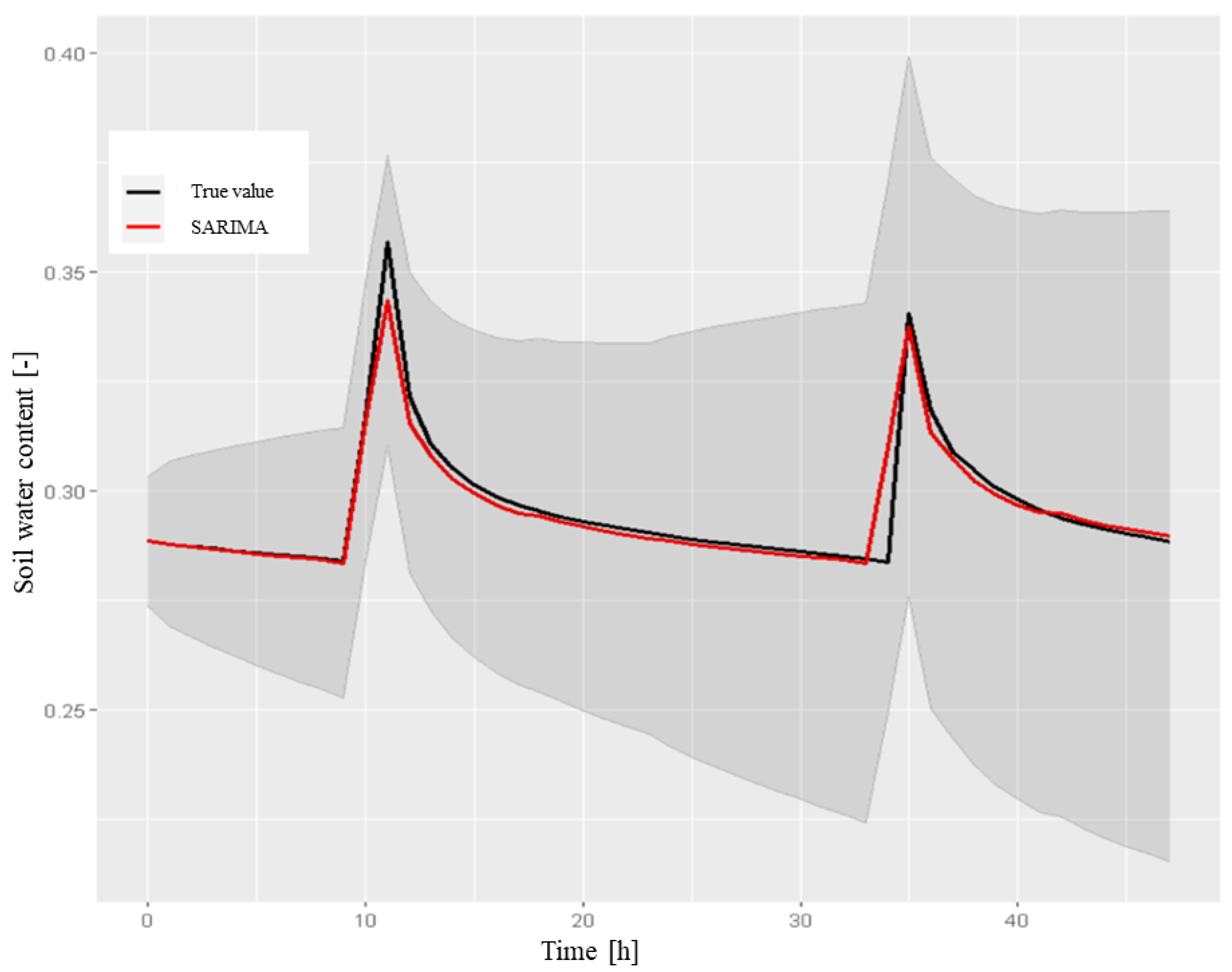
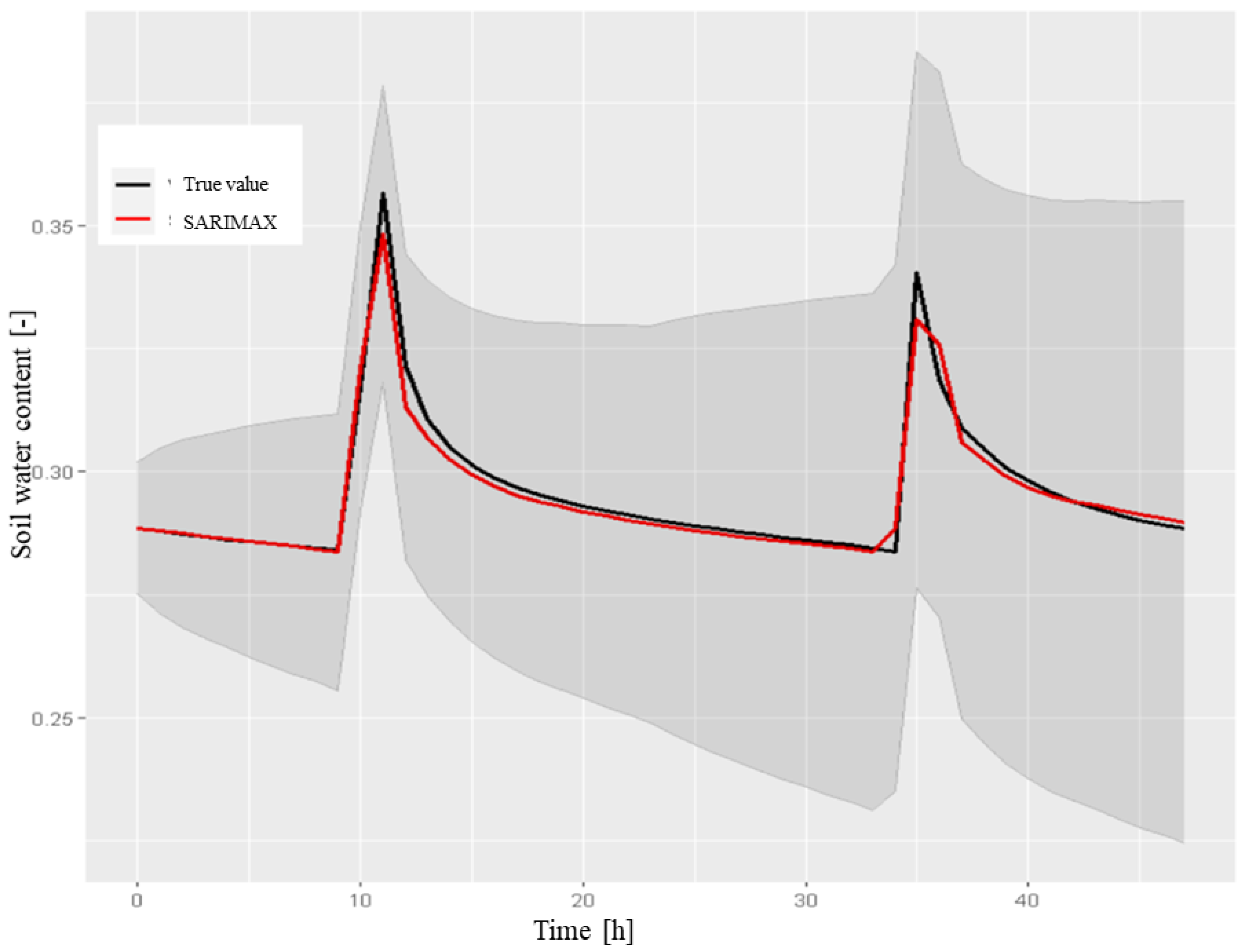
- Evaluation of the predictive capabilities of the model After verifying the model suitability, we tested its predictive capabilities by comparing the results obtained on the testing set and calculating the appropriate metrics. A 48-hour forecast was calculated using the forecast procedure.Figure 12 reports the results of the forecast with the respective 80% confidence interval and the comparison with the testing set. The metric values are shown in Table 1.Table 1. The performance metrics for the SARIMA model (0,1,2,2,0,1,24) for SWC at a depth of 50 cm (48-h forecast).Table 1. The performance metrics for the SARIMA model (0,1,2,2,0,1,24) for SWC at a depth of 50 cm (48-h forecast).
Mean Test 0.295670 RMSE 0.004557 MAE 0.002045 MAPE 0.675001
- SARIMAX model
- The previous tests and graphs highlighted some drawbacks of the SARIMA model, as follows:
- As shown in Figure 12, the model was not able to predict the exact time at which irrigation was performed and the relative SWC peak, assuming that it always occurred at 10:00 am. As previously observed in the testing set, irrigation was also performed at later times (generally 11:00 or 12:00). It was then considered necessary to add this information to the model using the dataset of the volume of water () used for irrigation.Figure 12. The 48-h forecast of SWC in the A2 block at a depth of 50 cm, which was obtained by the SARIMA model on the testing set, with a confidence interval of 80%. We used the following instructions:> sarima.forecast <- forecast(model1, h = 48).Figure 12. The 48-h forecast of SWC in the A2 block at a depth of 50 cm, which was obtained by the SARIMA model on the testing set, with a confidence interval of 80%. We used the following instructions:> sarima.forecast <- forecast(model1, h = 48).
- The model did not consider any influences from external factors. As shown graphically, on 25 August, the rain had an impact on the SWC. This required a study of the significance of the atmospheric variables for the model.
4. Discussions and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coppola, A.; Abdallah, M.; Dragonetti, G.; Zdruli, P.; Lamaddalena, N. Monitoring and modelling the hydrological behaviour of a reclaimed wadi basin in Egypt. Ecohydrology 2019, 12, e2084. [Google Scholar] [CrossRef]
- Moretti, M.; Van Passel, S.; Camposeo, S.; Pedrero, F.; Dogot, T.; Lebailly, P.; Vivaldi, G. Modelling environmental impacts of treated municipal wastewater reuse for tree crops irrigation in the Mediterranean coastal region. Sci. Total Environ. 2019, 660, 1513–1521. [Google Scholar] [CrossRef] [PubMed]
- Passarella, G.; Barca, E.; Sollitto, D.; Masciale, R.; Bruno, D. Cross-Calibration of Two Independent Groundwater Balance Models and Evaluation of Unknown Terms: The Case of the Shallow Aquifer of “Tavoliere di Puglia” (South Italy). Water Resour. Manag. 2017, 31, 327–340. [Google Scholar] [CrossRef]
- Zaccaria, D.; Lamaddalena, N.; Neale, C.; Merkley, G.; Palmisano, N.; Passarella, G. Simulation of peak-demand hydrographs in pressurized irrigation delivery systems using a deterministic–stochastic combined model. Part I: Model development. Irrig. Sci. 2013, 31, 209–224. [Google Scholar] [CrossRef]
- Berardi, M.; D’Abbicco, M.; Girardi, G.; Vurro, M. Optimizing water consumption in Richards’ equation framework with step-wise root water uptake: A simplified model. Transp. Porous Media 2022, 142, 469–498. [Google Scholar] [CrossRef]
- Mao, Y.; Liu, S.; Nahar, J.; Liu, J.; Ding, F. Soil moisture regulation of agro-hydrological systems using zone model predictive control. Comput. Electron. Agric. 2018, 154, 239–247. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.V. Strong solutions for Richards’ equation with Cauchy conditions and constant pressure gradient. Environ. Fluid Mech. 2020, 20, 165–174. [Google Scholar] [CrossRef]
- Broadbridge, P.; Daly, E.; Goard, J. Exact Solutions of the Richards Equation With Nonlinear Plant-Root Extraction. Water Resour. Res. 2017, 53, 9679–9691. [Google Scholar] [CrossRef]
- De Luca, D.L.; Cepeda, J.M. Procedure to Obtain Analytical Solutions of One-Dimensional Richards’ Equation for Infiltration in Two-Layered Soils. J. Hydrol. Eng. 2016, 21, 04016018. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.; Vurro, M.; Lopez, L. The 1D Richards’ equation in two layered soils: A Filippov approach to treat discontinuities. Adv. Water Resour. 2018, 115, 264–272. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.V.; Lopez, L. A mixed MoL-TMoL for the numerical solution of the 2D Richards’ equation in layered soils. Comput. Math. Appl. 2020, 79, 1990–2001. [Google Scholar] [CrossRef]
- Romano, N.; Brunone, B.; Santini, A. Numerical analysis of one-dimensional unsaturated flow in layered soils. Adv. Water Resour. 1998, 21, 315–324. [Google Scholar] [CrossRef]
- Seus, D.; Mitra, K.; Pop, I.S.; Radu, F.A.; Rohde, C. A linear domain decomposition method for partially saturated flow in porous media. Comput. Methods Appl. Mech. Eng. 2018, 333, 331–355. [Google Scholar] [CrossRef]
- Casulli, V.; Zanolli, P. A Nested Newton-Type Algorithm for Finite Volume Methods Solving Richards’ Equation in Mixed Form. SIAM J. Sci. Comput. 2010, 32, 2255–2273. [Google Scholar] [CrossRef]
- Albuja, G.; Ávila, A.I. A family of new globally convergent linearization schemes for solving Richards’ equation. Appl. Numer. Math. 2021, 159, 281–296. [Google Scholar] [CrossRef]
- Bergamaschi, L.; Putti, M. Mixed finite elements and Newton-type linearizations for the solution of Richards’equation. Int. J. Numer. Methods Eng. 1999, 45, 1025–1046. [Google Scholar] [CrossRef]
- Miller, C.T.; Abhishek, C.; Farthing, M.W. A spatially and temporally adaptive solution of Richards’ equation. Adv. Water Resour. 2006, 29, 525–545. [Google Scholar] [CrossRef]
- Li, H.; Farthing, M.; Miller, C. Adaptive local discontinuous Galerkin approximation to Richards’ equation. Adv. Water Resour. 2007, 30, 1883–1901. [Google Scholar] [CrossRef]
- Tubini, N.; Rigon, R. Implementing the Water, HEat and Transport model in GEOframe (WHETGEO-1D v.1.0): Algorithms, informatics, design patterns, open science features, and 1D deployment. Geosci. Model Dev. 2022, 15, 75–104. [Google Scholar] [CrossRef]
- Coppola, A.; Smettem, K.; Ajeel, A.; Saeed, A.; Dragonetti, G.; Comegna, A.; Lamaddalena, N.; Vacca, A. Calibration of an electromagnetic induction sensor with time-domain reflectometry data to monitor rootzone electrical conductivity under saline water irrigation. Eur. J. Soil Sci. 2016, 67, 737–748. [Google Scholar] [CrossRef]
- Basile, A.; Ciollaro, G.; Coppola, A. Hysteresis in soil water characteristics as a key to interpreting comparisons of laboratory and field measured hydraulic properties. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Helmecke, M.; Fries, E.; Schulte, C. Regulating water reuse for agricultural irrigation: Risks related to organic micro-contaminants. Environ. Sci. Eur. 2020, 32, 1153–1160. [Google Scholar] [CrossRef]
- Ramirez, C.; Almulla, Y.; Nerini, F.F. Reusing wastewater for agricultural irrigation: A water-energy-food Nexus assessment in the North Western Sahara Aquifer System. Environ. Res. Lett. 2021, 16, 044052. [Google Scholar] [CrossRef]
- Vergine, P.; Salerno, C.; Berardi, G.; Pappagallo, G.; Pollice, A. The Self-Forming Dynamic Membrane BioReactor (SFD MBR) as a suitable technology for agro-industrial wastewater treatment. New Biotechnol. 2020, 56, 87–95. [Google Scholar] [CrossRef]
- Foster, T.; Mieno, T.; Brozović, N. Satellite-Based Monitoring of Irrigation Water Use: Assessing Measurement Errors and Their Implications for Agricultural Water Management Policy. Water Resour. Res. 2020, 56, e2020WR028378. [Google Scholar] [CrossRef]
- Brook, A.; Polinova, M.; Housh, M. An integrated modeling framework for real-time irrigation scheduling: The benefit of spectroscopy and weather forecasts. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 17–22 April 2016; p. EPSC2016-327. [Google Scholar]
- Selicato, L.; Esposito, F.; Gargano, G.; Vegliante, M.C.; Opinto, G.; Zaccaria, G.; Ciavarella, S.; Guarini, A.; Del Buono, N. A New Ensemble Method for Detecting Anomalies in Gene Expression Matrices. Mathematics 2021, 9, 882. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.; Notarnicola, F.; Vurro, M. A transversal method of lines for the numerical modeling of vertical infiltration into the vadose zone. Appl. Numer. Math. 2019, 135, 264–275. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.V. A quadrature-based scheme for numerical solutions to Kirchhoff transformed Richards’ equation. J. Comput. Dyn. 2022, 9, 69–84. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G.; Reinsel, G.; Ljung, G. Time Series Analysis: Forecasting and Control; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer: Berlin/Heidelberg, Germany, 2000; Volume 3. [Google Scholar]
- Filipović, N.; Brdar, S.; Mimić, G.; Marko, O.; Crnojević, V. Regional soil moisture prediction system based on Long Short-Term Memory network. Biosyst. Eng. 2022, 213, 30–38. [Google Scholar] [CrossRef]
- Leij, F.J.; Dane, J.H.; Sciortino, A. Hierarchical prediction of soil water content time series. CATENA 2022, 209, 105841. [Google Scholar] [CrossRef]
- Berardi, M.; Andrisani, A.; Lopez, L.; Vurro, M. A new data assimilation technique based on ensemble Kalman filter and Brownian bridges: An application to Richards’ equation. Comput. Phys. Commun. 2016, 208, 43–53. [Google Scholar] [CrossRef]
- Berardi, M.; Vurro, M. The numerical solution of Richards’ equation by means of method of lines and ensemble Kalman filter. Math. Comput. Simul. 2016, 125, 38–47. [Google Scholar] [CrossRef]
- Camporese, M.; Paniconi, C.; Putti, M.; Salandin, P. Comparison of data assimilation techniques for a coupled model of surface and subsurface flow. Vadose Zone J. 2009, 4, 837–845. [Google Scholar] [CrossRef]
- Moreira, P.H.S.; van Genuchten, M.T.; Orlande, H.R.B.; Cotta, R.M. Bayesian estimation of the hydraulic and solute transport properties of a small-scale unsaturated soil column. J. Hydrol. Hydromech. 2016, 64, 30–44. [Google Scholar] [CrossRef]
- Del Buono, N.; Esposito, F.; Selicato, L. Methods for Hyperparameters Optimization in Learning Approaches: An Overview. In Proceedings of the Machine Learning, Optimization, and Data Science, Siena, Italy, 19–23 July 2020; Nicosia, G., Ojha, V., La Malfa, E., Jansen, G., Sciacca, V., Pardalos, P., Giuffrida, G., Umeton, R., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 100–112. [Google Scholar] [CrossRef]
- Jabakhanji, R.; Mohtar, R.H. A peridynamic model of flow in porous media. Adv. Water Resour. 2015, 78, 22–35. [Google Scholar] [CrossRef]
- Lopez, L.; Pellegrino, S.F. A nonperiodic Chebyshev spectral method avoiding penalization techniques for a class of nonlinear peridynamic models. Int. J. Numer. Methods Eng. 2022, 123, 4859–4876. [Google Scholar] [CrossRef]
- Lopez, L.; Pellegrino, S.F. Computation of Eigenvalues for Nonlocal Models by Spectral Methods. J. Peridynamics Nonlocal Model. 2021, 1–22. [Google Scholar] [CrossRef]

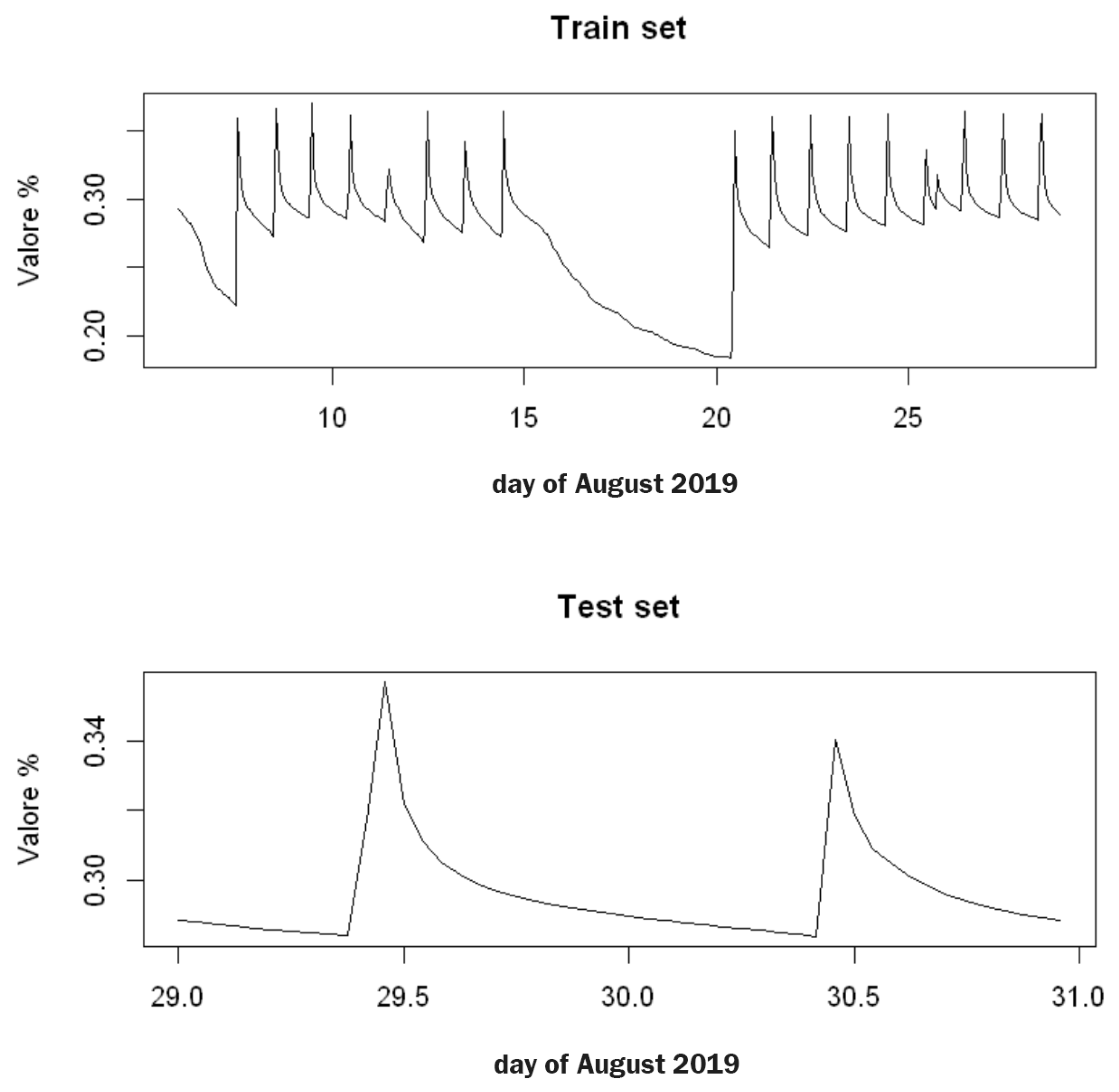
- > df.ts.suolo <- ts(df.suolo.agosto.ora[,2], start = c(6,1), end = c(30,24), frequency = 24)
- > class(df.ts.suolo)
- ’ts’
- > train <- window(df.ts.suolo, start = c(6,1), end = c(28,24))
- > test <- window(df.ts.suolo, start = c(29,1), end = c(30,24))
- > length(train)
- 552
- > length(test)
- 48.
- > df.ts.suolo <- ts(df.suolo.agosto.ora[,2], start = c(6,1), end = c(30,24), frequency = 24)
- > class(df.ts.suolo)
- ’ts’
- > train <- window(df.ts.suolo, start = c(6,1), end = c(28,24))
- > test <- window(df.ts.suolo, start = c(29,1), end = c(30,24))
- > length(train)
- 552
- > length(test)
- 48.
- > dec <- decompose(train, type = ’additive’)
- > plot(dec)
- This shows the behavior of the time series and its trend, seasonal and random components.
- > dec <- decompose(train, type = ’additive’)
- > plot(dec)
- This shows the behavior of the time series and its trend, seasonal and random components.

- > model.train.hw <- HoltWinters(train)
- > plot(model.train.hw).
- > model.train.hw <- HoltWinters(train)
- > plot(model.train.hw).


- > xreg <- cbind(irrigazione, meteo[,2])
- > xreg.ts <- ts(xreg, start = c(6,1), frequency = 24)
- > xreg.train <- window(xreg, start = c(6,1), end = c(28,24))
- > xreg.test <- window(xreg, start = c(29,1), end = c(30,24))
- > model2 <- sarima(train,1,1,1,2,0,1,24, xreg = xreg.train, no.constant = TRUE).
- > xreg <- cbind(irrigazione, meteo[,2])
- > xreg.ts <- ts(xreg, start = c(6,1), frequency = 24)
- > xreg.train <- window(xreg, start = c(6,1), end = c(28,24))
- > xreg.test <- window(xreg, start = c(29,1), end = c(30,24))
- > model2 <- sarima(train,1,1,1,2,0,1,24, xreg = xreg.train, no.constant = TRUE).
| Parameters | ||||
|---|---|---|---|---|
| Coefficient | Estimate | s.e. | t-Value | p-Value |
| ar1 | 0.3933 | 0.1275 | 3.0843 | 0.0021 |
| ma1 | −0.6386 | 0.1043 | −6.1219 | 0.0000 |
| sar1 | 1.2698 | 0.0655 | 19.3838 | 0.0000 |
| sar2 | −0.2767 | 0.0554 | −4.9995 | 0.0000 |
| sma1 | −0.9355 | 0.0764 | −12.2456 | 0.0000 |
| irrigazione | 0.0071 | 0.0007 | 10.8599 | 0.0000 |
| meteo.pioggia | 0.0050 | 0.0022 | 2.2613 | 0.0241 |
| meteo.temperatura | 0.0008 | 0.0007 | 1.0528 | 0.2929 |
| meteo.umidita | 0.0003 | 0.0002 | 1.7974 | 0.0728 |
| meteo.radiazione | 0.0034 | 0.0027 | 1.2462 | 0.2132 |
| meteo.vento.velocita | −0.0004 | 0.0016 | −0.2547 | 0.7991 |
| meteo.vento.raffica | 0.0004 | 0.0008 | 0.4811 | 0.6306 |
| meteo.vento.direzione | 0.0000 | 0.0000 | −1.5981 | 0.1106 |
| meteo.bagnatura.fogliare.sup | 0.0001 | 0.0001 | 1.2025 | 0.2297 |
| meteo.bagnatura.fogliare.inf | −0.0002 | 0.0001 | −1.5021 | 0.1337 |
| meteo.pressione.atmosferica | 0.0036 | 0.0001 | 24.8314 | 0.0000 |
| meteo.punto.di.rugiada | −0.0006 | 0.0007 | −0.9643 | 0.3353 |
| meteo.Etp | −0.0191 | 0.0130 | −1.4719 | 0.1416 |
| Parameters | ||||
|---|---|---|---|---|
| Coefficient | Estimate | s.e. | t-Value | p-Value |
| ar1 | 0.4934 | 0.1143 | 4.3151 | 0 |
| ma1 | −0.6923 | 0.0943 | −7.3425 | 0 |
| sar1 | 1.2766 | 0.0559 | 22.8501 | 0 |
| sar2 | −0.2808 | 0.0511 | −5.4956 | 0 |
| sma1 | −0.9471 | 0.0578 | −16.3963 | 0 |
| irrigazione | 0.0089 | 0.0006 | 14.9233 | 0 |
| meteo.pioggia | 0.0045 | 0.0018 | 2.5251 | 0.0118 |
| Statistics | ||||
| Estimate | 0.000094 | |||
| Log Likelihood | 1762.72 | |||
| AIC | −3509.44 | |||
| AICc | −3509.17 | |||
| BIC | −3474.94 | |||
| Performance on the Training Set | ||||
| RMSE | 0.009627 | |||
| MAE | 0.002935 | |||
| MAPE | 0.989883 | |||
| Mean Test | 0.295670 |
| RMSE | 0.003042 |
| MAE | 0.001951 |
| MAPE | 0.631653 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giorgio, A.; Del Buono, N.; Berardi, M.; Vurro, M.; Vivaldi, G.A. Soil Moisture Sensor Information Enhanced by Statistical Methods in a Reclaimed Water Irrigation Framework. Sensors 2022, 22, 8062. https://doi.org/10.3390/s22208062
Giorgio A, Del Buono N, Berardi M, Vurro M, Vivaldi GA. Soil Moisture Sensor Information Enhanced by Statistical Methods in a Reclaimed Water Irrigation Framework. Sensors. 2022; 22(20):8062. https://doi.org/10.3390/s22208062
Chicago/Turabian StyleGiorgio, Anthony, Nicoletta Del Buono, Marco Berardi, Michele Vurro, and Gaetano Alessandro Vivaldi. 2022. "Soil Moisture Sensor Information Enhanced by Statistical Methods in a Reclaimed Water Irrigation Framework" Sensors 22, no. 20: 8062. https://doi.org/10.3390/s22208062
APA StyleGiorgio, A., Del Buono, N., Berardi, M., Vurro, M., & Vivaldi, G. A. (2022). Soil Moisture Sensor Information Enhanced by Statistical Methods in a Reclaimed Water Irrigation Framework. Sensors, 22(20), 8062. https://doi.org/10.3390/s22208062