A 24 GHz CMOS Direct-Conversion RF Receiver with I/Q Mismatch Calibration for Radar Sensor Applications
Abstract
:1. Introduction
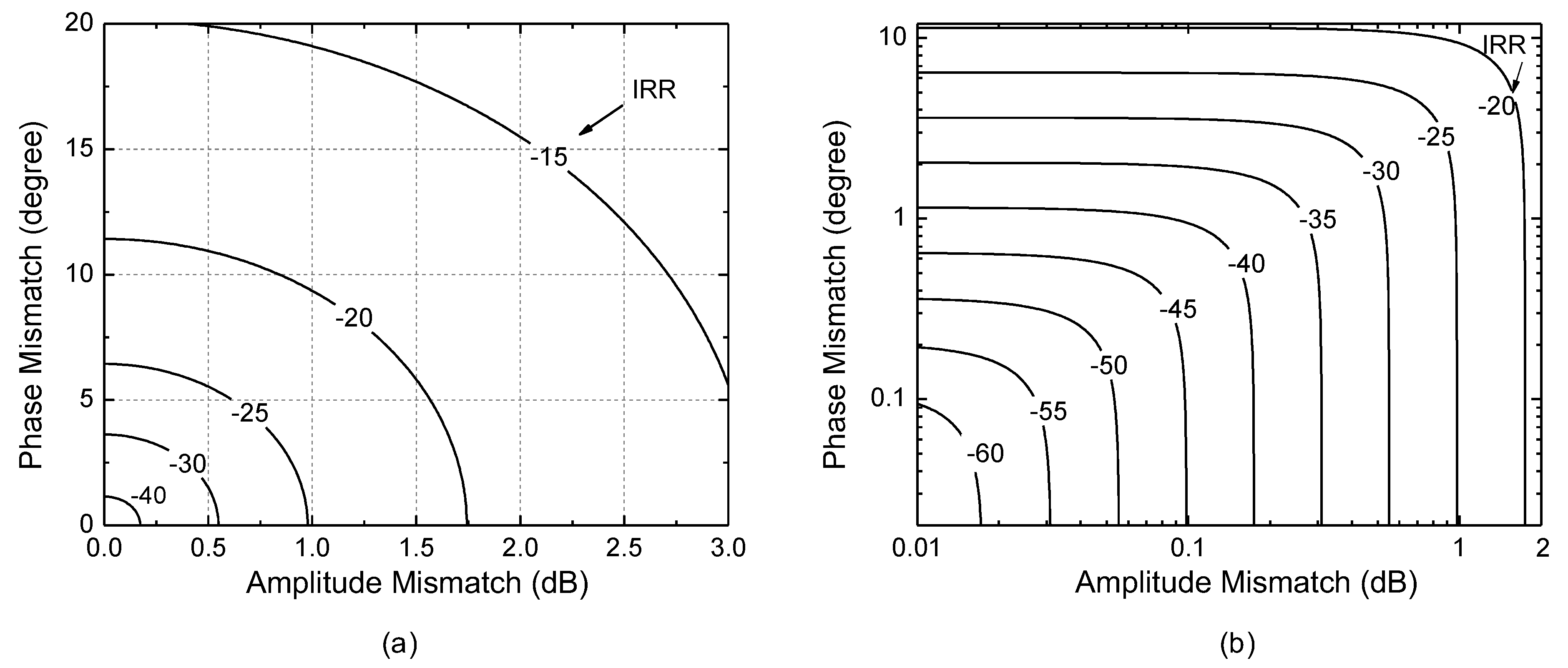
2. Analysis of Image-Rejection Ratio (IRR) with Respect to I/Q Mismatch
3. Circuit Design
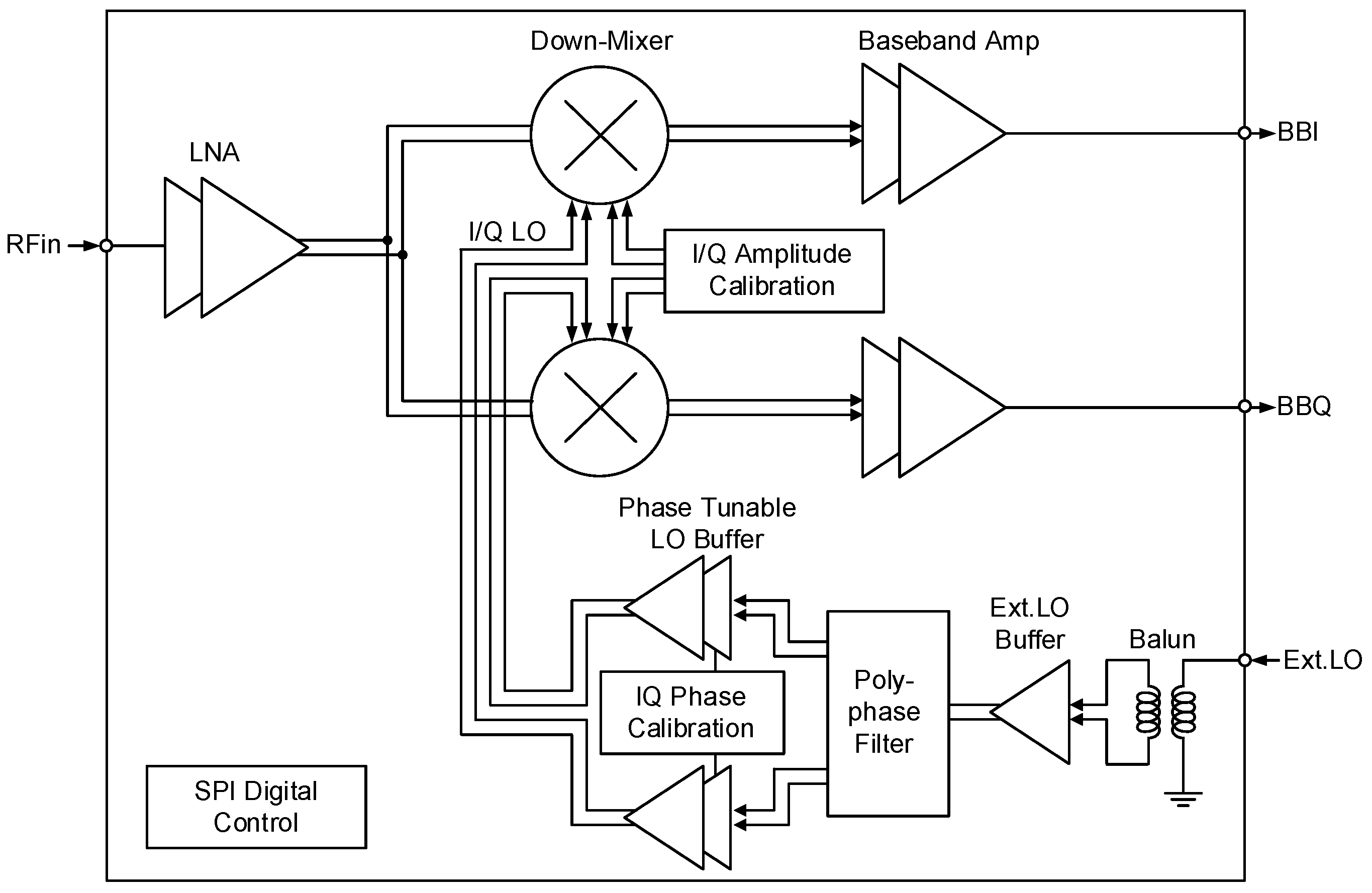
3.1. Architecture
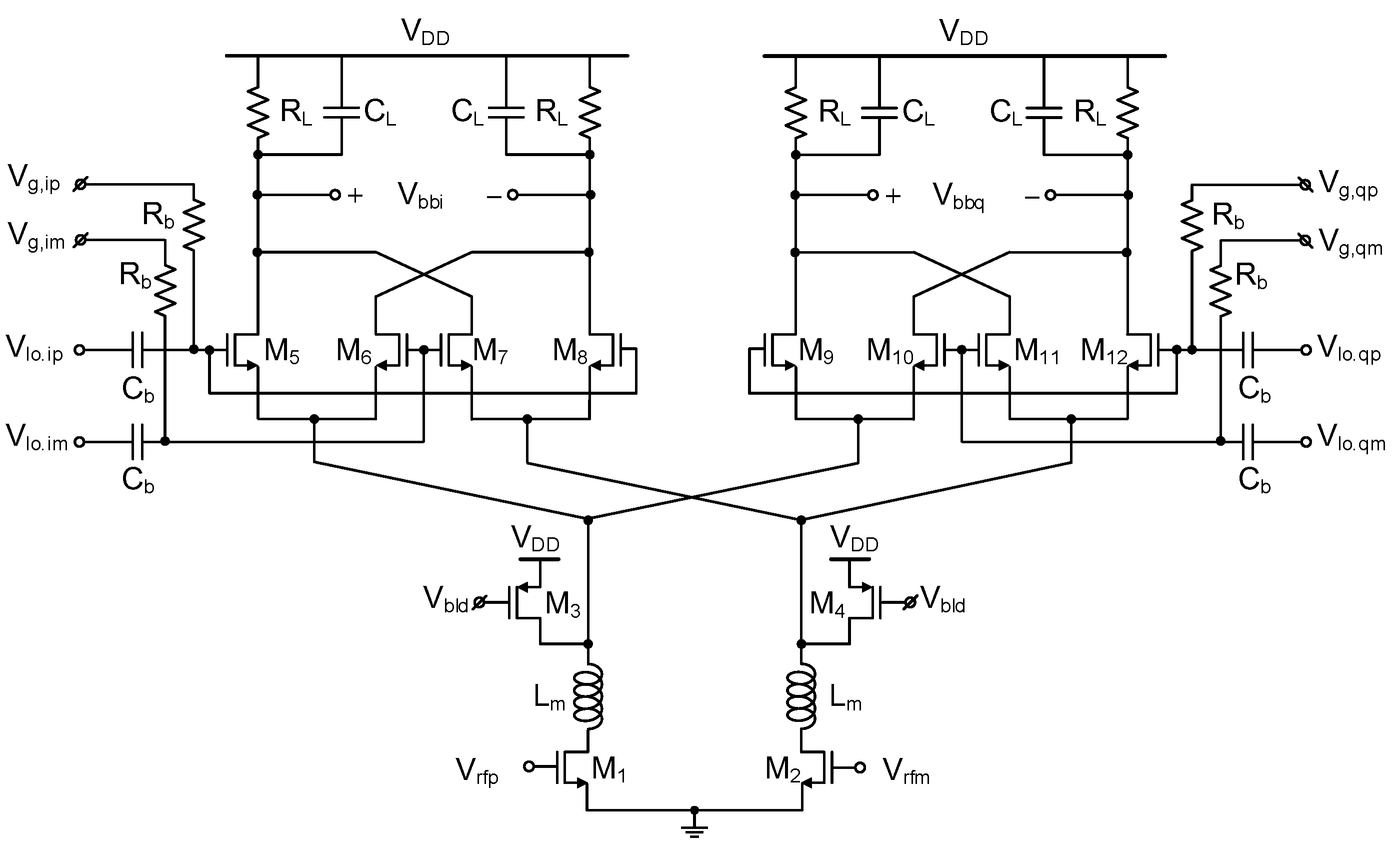
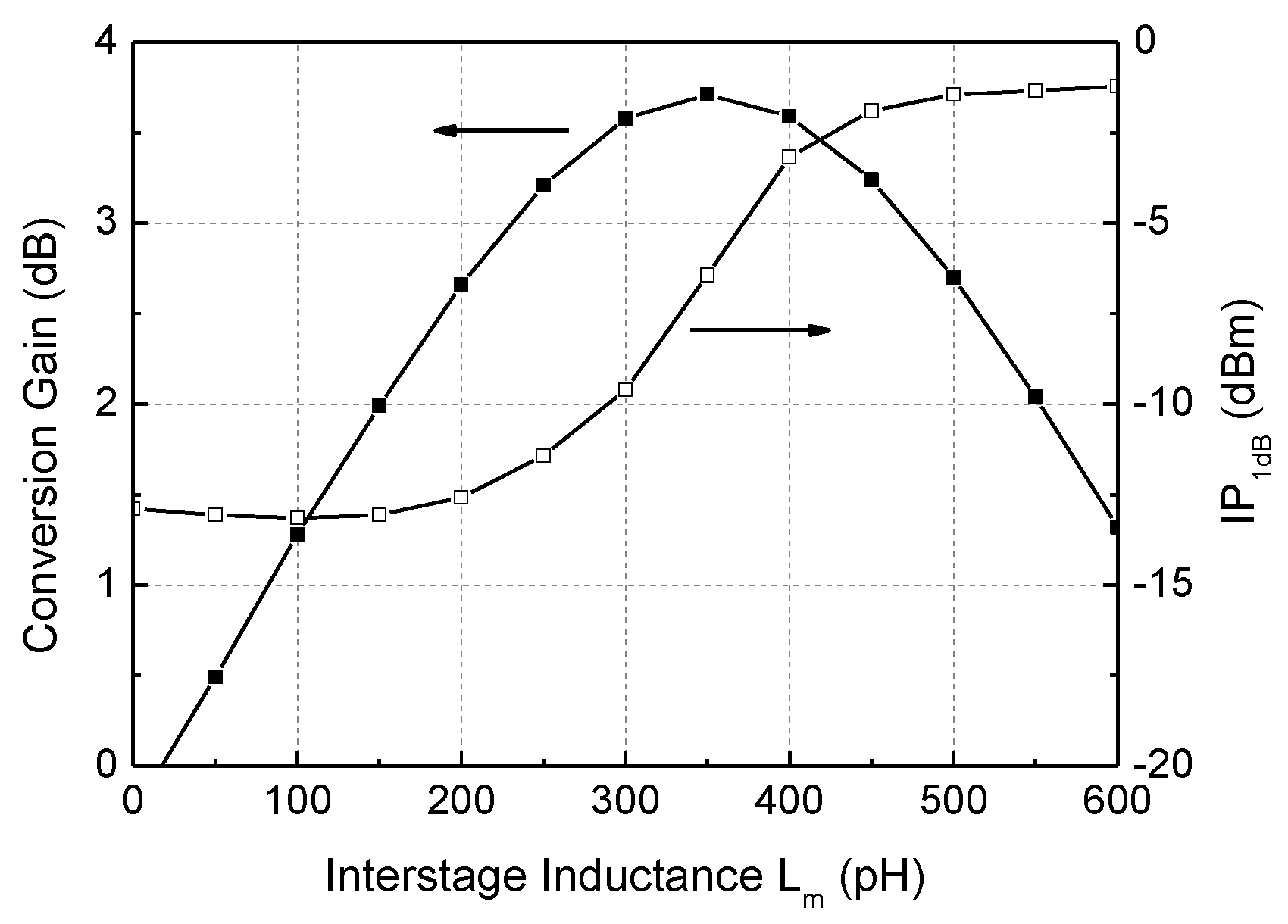
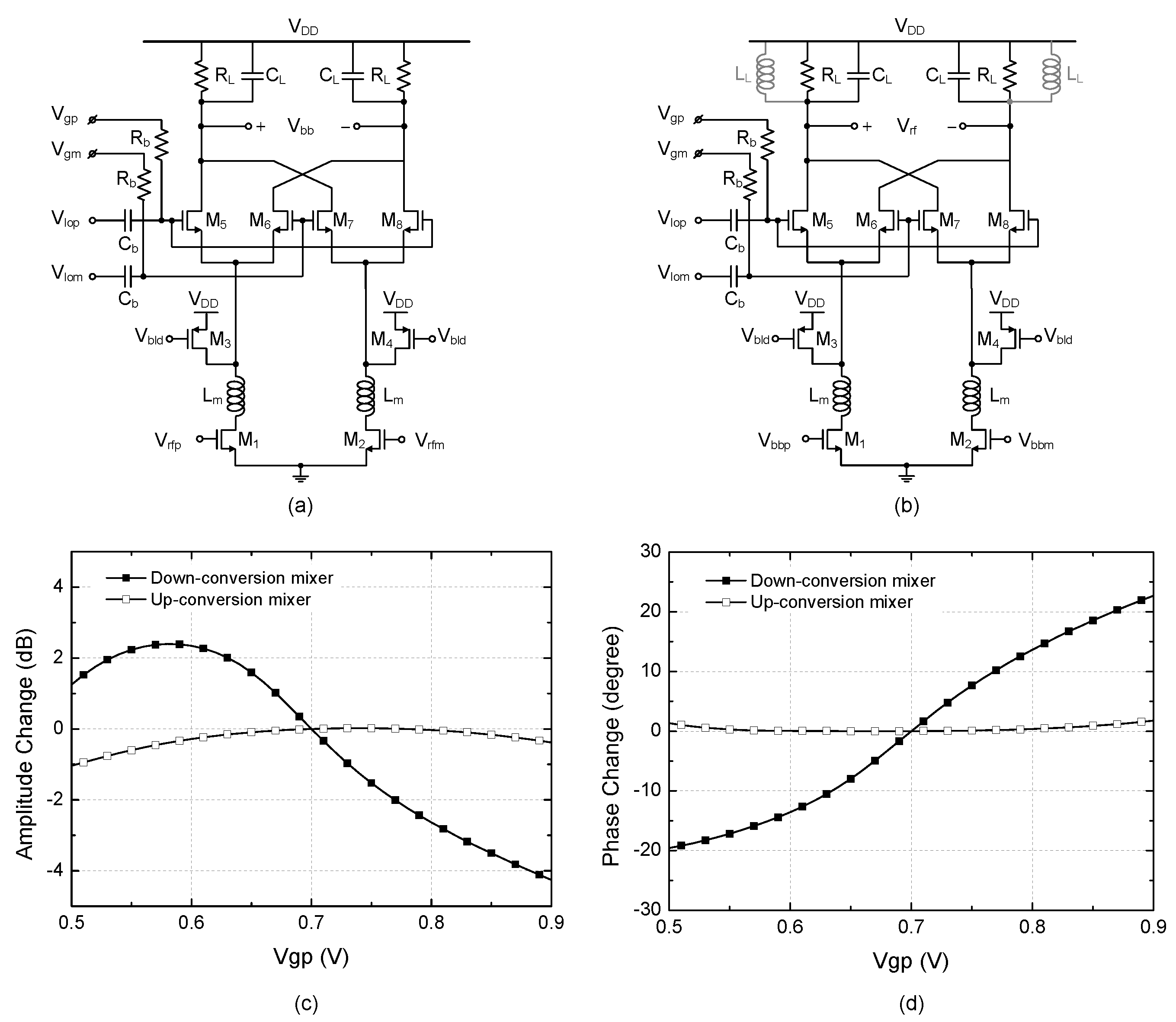
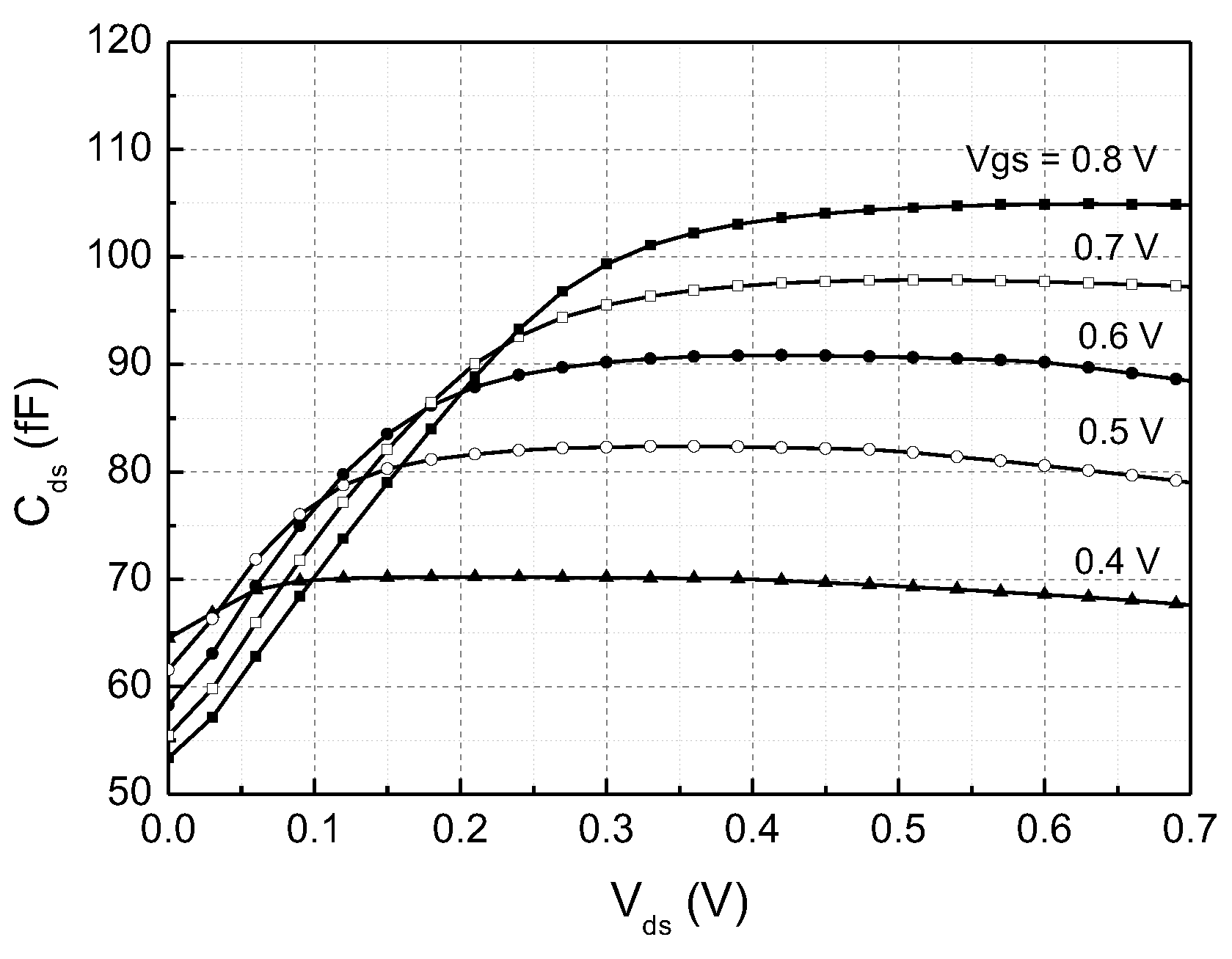
3.2. Down-Conversion Mixer and I/Q Calibration Circuit Design
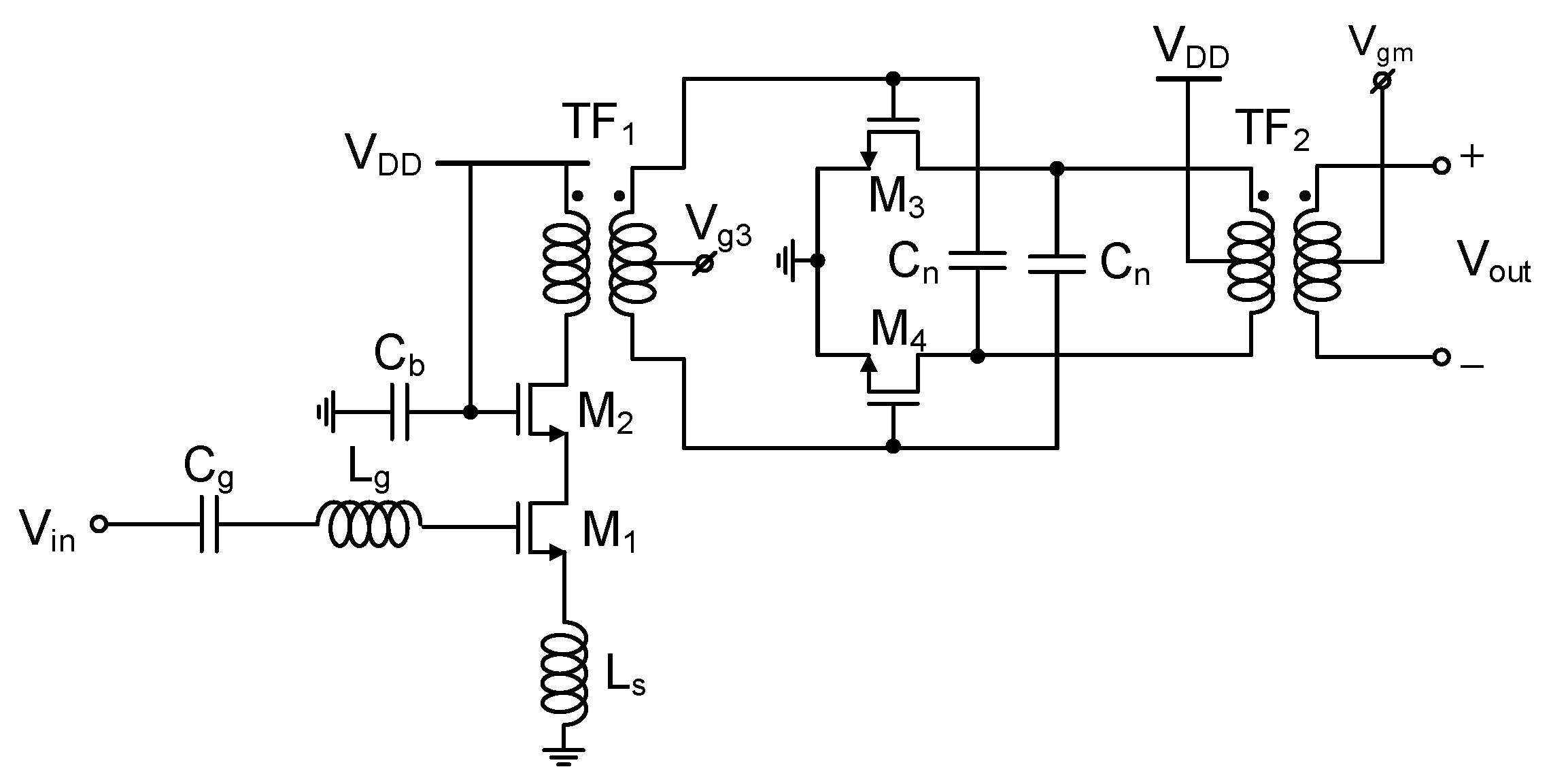
3.3. LNA and Output Buffer
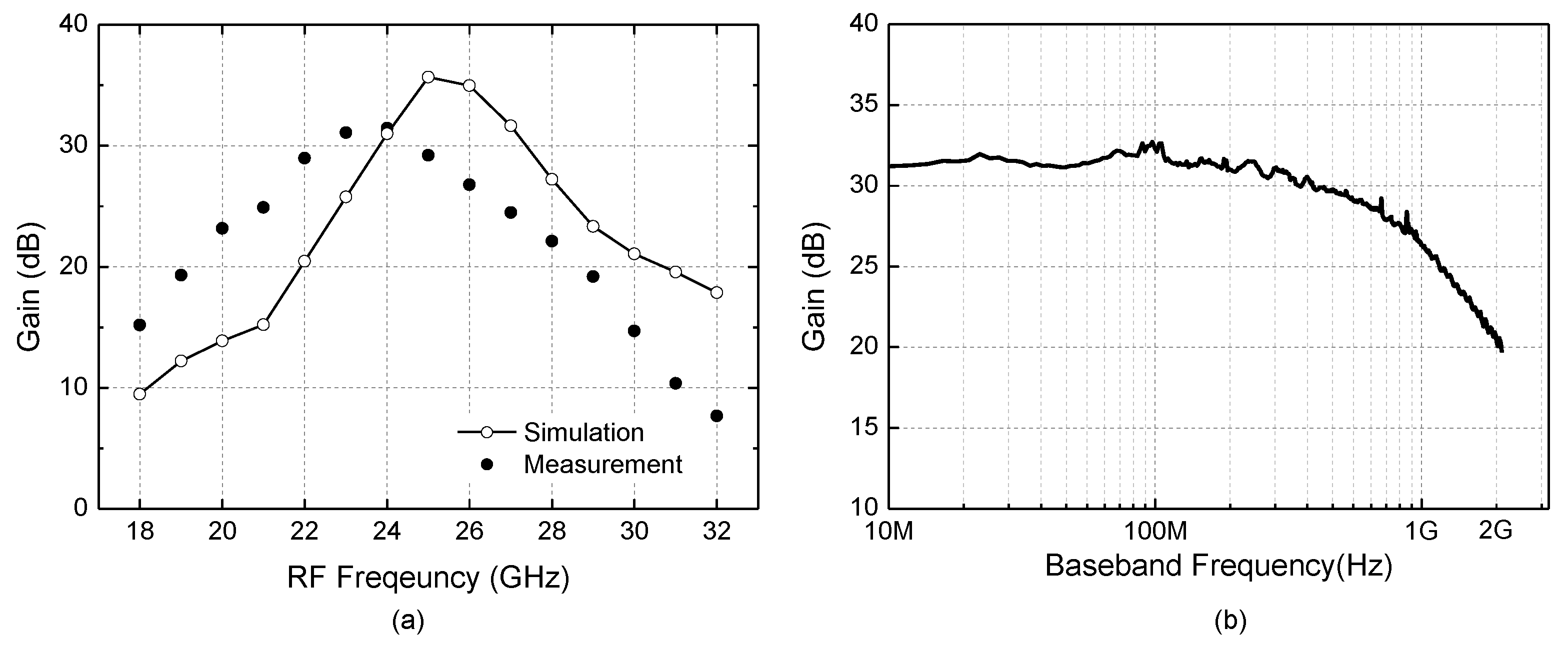
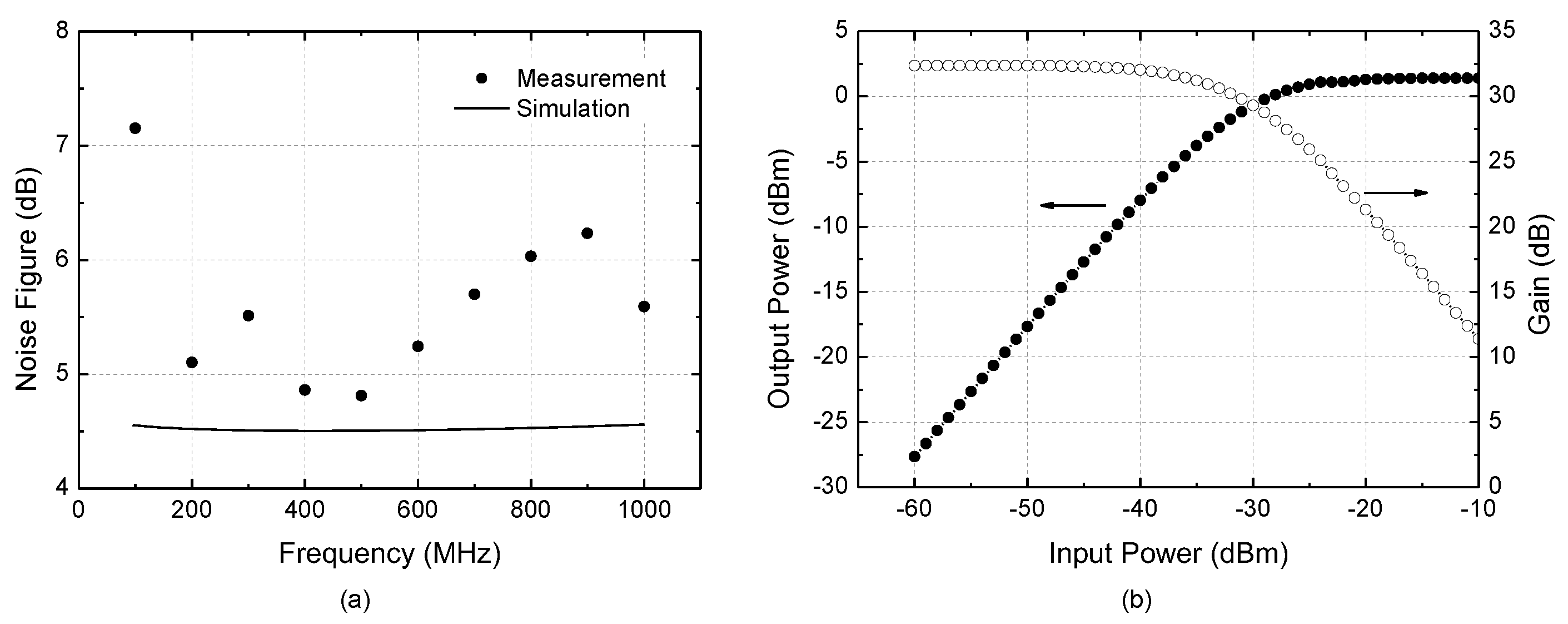
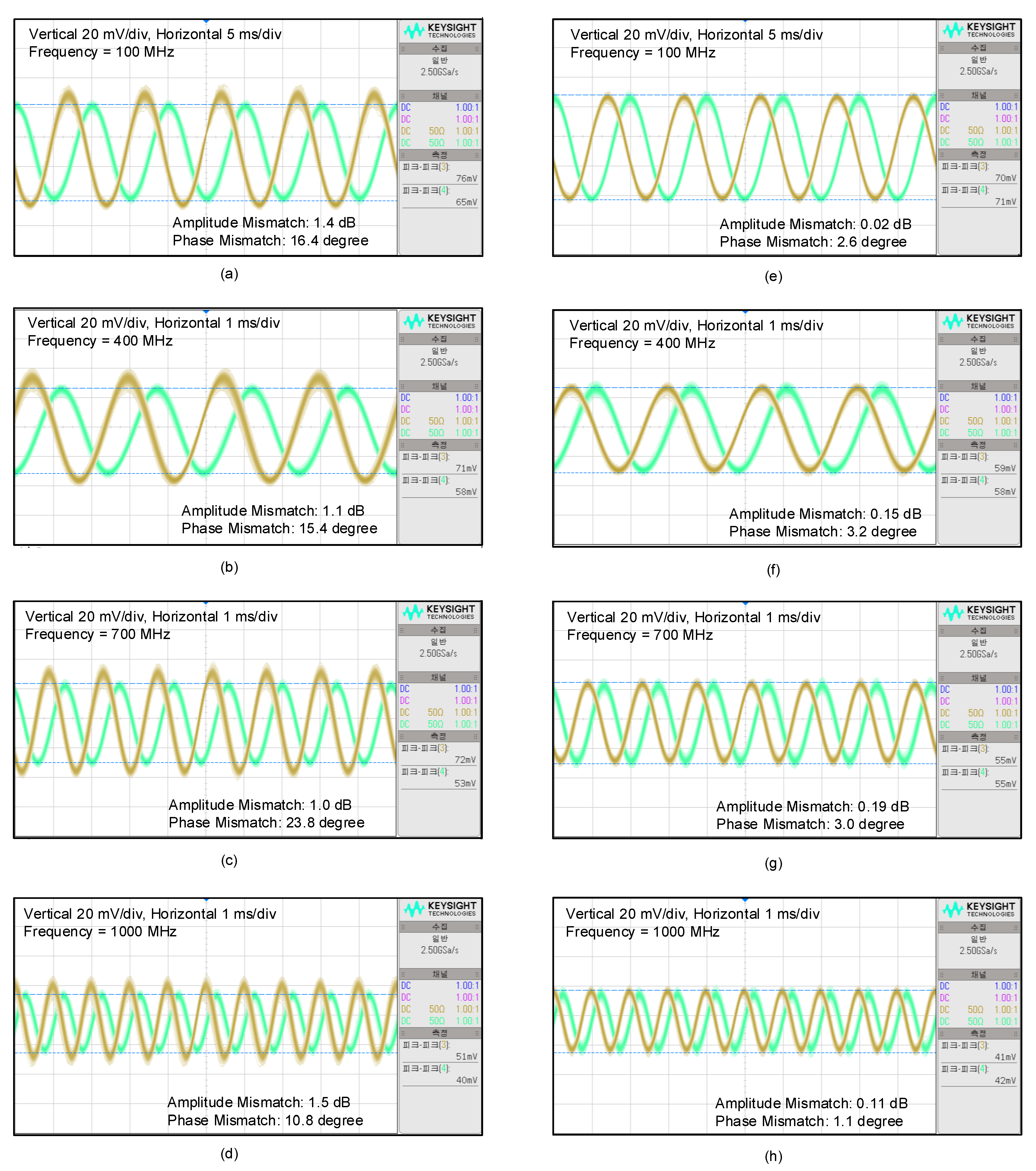
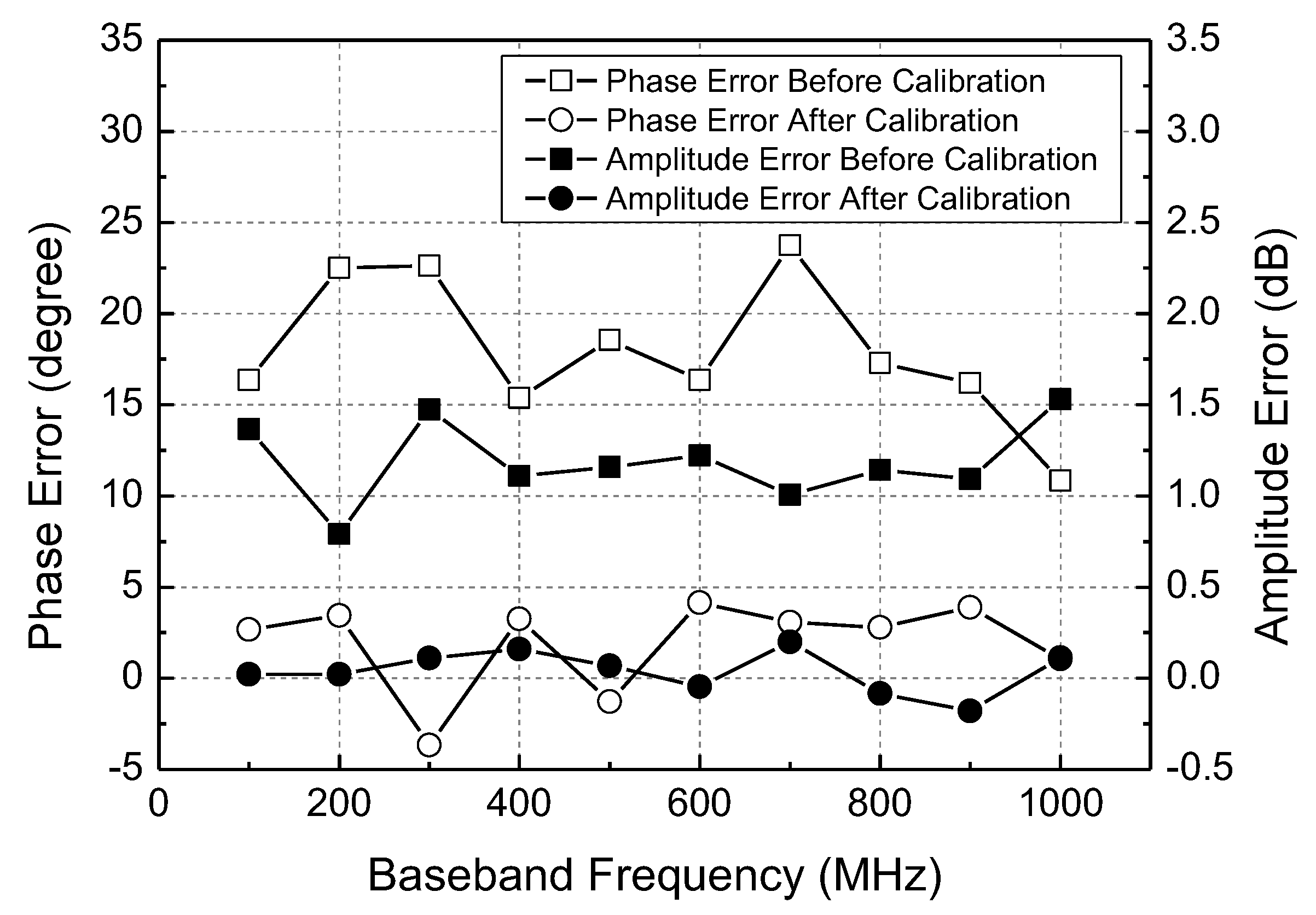
4. Implementation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lazaro, A.; Lazaro, M.; Villarino, R.; Girbau, D.; Paco, P. Car2Car Communication Using a Modulated Backscatter and Automotive FMCW Radar. Sensors 2021, 21, 3656. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Kim, B.; Shin, H. 28-GHz CMOS Direct-Conversion RF Transmitter with Precise and Wide-Range Mismatch Calibration Techniques. Electronics 2022, 11, 840. [Google Scholar] [CrossRef]
- Delwar, T.S.; Siddique, A.; Ryu, J.-Y. A 65 nm Duplex Transconductance Path Up-Conversion Mixer for 24 GHz Automotive Short-Range Radar Sensor Applications. Sensors 2022, 22, 594. [Google Scholar] [CrossRef]
- Gao, L.; Ma, Q.; Rebeiz, G.M. A 20–44-GHz Image-Rejection Receiver with >75-dB Image-Rejection Ratio in 22-nm CMOS FD-SOI for 5G Applications. IEEE Trans. Microw. Theory Techn. 2020, 68, 2823–2832. [Google Scholar] [CrossRef]
- Oh, K.-I.; Ko, G.-H.; Kim, J.-G.; Baek, D. An 18.8–33.9 GHz, 2.26 mW Current-Reuse Injection-Locked Frequency Divider for Radar Sensor Applications. Sensors 2021, 21, 2551. [Google Scholar] [CrossRef]
- Ragonese, E.; Scuderi, A.; Giammello, V.; Messina, E.; Palmisano, G. A Fully Integrated 24GHz UWB Radar Sensor for Automotive Applications. In Proceedings of the International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 8–12 February 2009; pp. 306–307. [Google Scholar]
- Jain, V.; Sundararaman, S.; Heydari, P. A 22–29-GHz UWB Pulse-Radar Receiver Front-End in 0.18-μm CMOS. IEEE Trans. Microw. Theory Techn. 2009, 57, 1903–1914. [Google Scholar] [CrossRef]
- Mazzanti, A.; Sosio, M.; Repossi, M.; Svelto, F. A 24 GHz Subharmonic Direct Conversion Receiver in 65 nm CMOS. IEEE Trans. Circuits Syst. I Reg. Pap. 2011, 58, 88–97. [Google Scholar] [CrossRef]
- Pyo, G.; Yang, J.; Kim, C.-Y.; Hong, S. K-Band Dual-Mode Receiver CMOS IC for FMCW/UWB Radar. IEEE Trans. Circuits Syst. II Exp. Briefs. 2014, 61, 393–397. [Google Scholar] [CrossRef]
- Ding, B.; Yan, S.; Zhao, C.; Tao, L.; Tian, T. A Ka Band FMCW Transceiver Front-End with 2-GHz Bandwidth in 65-nm CMOS. IEEE Trans. Circuits Syst. II Exp. Briefs. 2019, 66, 212–216. [Google Scholar] [CrossRef]
- Kim, H.-T.; Park, B.-S.; Song, S.-S.; Moon, T.-S.; Kim, S.-H.; Kim, J.-M.; Chang, J.-Y.; Ho, Y.-C. A 28-GHz CMOS Direct Conversion Transceiver with Packaged 2 × 4 Antenna Array for 5G Cellular System. IEEE J. Solid State Circuits 2018, 53, 1245–1259. [Google Scholar] [CrossRef]
- Chai, Y.; Niu, X.; He, L.; Li, L.; Cui, T.J. A 60-GHz CMOS Broadband Receiver with Digital Calibration, 20-to-75-dB Gain, and 5-dB Noise Figure. IEEE Trans. Microw. Theory Techn. 2017, 65, 3989–4001. [Google Scholar]
- Wu, R.; Minami, R.; Tsukui, Y.; Kawai, S.; Seo, Y.; Sato, S.; Kimura, K.; Kondo, S.; Ueno, T.; Fajri, N.; et al. 64-QAM 60-GHz CMOS Transceivers for IEEE 802.11ad/ay. IEEE J. Solid State Circuits 2017, 52, 2871–2891. [Google Scholar]
- Lee, S.; Lee, Y.; Shin, H. A 28-GHz Switched-Beam Antenna with Integrated Butler Matrix and Switch for 5G Applications. Sensors 2021, 21, 5128. [Google Scholar] [CrossRef]
- Aoki, Y.; Dao, M.T.; Min, K.; Hwang, Y.; Kim, Y.; Yang, S.-G. 1.4-GHz Bandwidth Frequency-Dependent I/Q Imbalance Calibration for 5G mmWave Communications. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS), Boston, MA, USA, 2–7 June 2009; pp. 626–629. [Google Scholar]
- Kim, J.; Lee, Y.; Chang, S.; Shin, H. Low-Power CMOS Complex Bandpass Filter with Passband Flatness Tunability. Electronics 2020, 9, 494. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Kim, B.; Lee, Y.; Kim, S.; Shin, H. A 28GHz Direct Conversion Receiver in 65nm CMOS for 5G mmWave Radio. In Proceedings of the International System-on-Chip Design Conference (ISOCC), Jeju, Korea, 6–9 October 2019; pp. 29–30. [Google Scholar]
- Huang, B.-J.; Lin, K.-Y.; Wang, H. Millimeter-Wave Low Power Miniature CMOS Multicascode Low-Noise Amplifiers with Noise Reduction Topology. IEEE Trans. Microw. Theory Techn. 2009, 57, 3049–3059. [Google Scholar]
- Shahani, A.R.; Shaeffer, D.K.; Lee, T.H. A 12-mW Wide Dynamic Range CMOS Front-End for a Portable GPS Receiver. IEEE J. Solid State Circuits 1997, 32, 2061–2070. [Google Scholar] [CrossRef]
- Zhao, D.; Reynaert, P. A 40 nm CMOS E-Band Transmitter with Compact and Symmetric Layout Floor-Plans. IEEE J. Solid State Circuits 2015, 50, 2560–2571. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, Z.; Chen, Z.; Zhang, L.; Liu, H.; Wu, Y.; Zhao, C.; Kang, K. A 24 GHz CMOS Mixer Using Symmetrical Design Methodology with I/Q Imbalance Calibration. In Proceedings of the Asia-Pacific Microwave Conference (APMC), Kuala Lumpur, Malaysia, 13–16 November 2017; pp. 903–905. [Google Scholar]
- Mondal, S.; Singh, R.; Hussein, A.I.; Paramesh, J. A 25–30 GHz Fully-Connected Hybrid Beamforming Receiver for MIMO Communication. IEEE J. Solid State Circuits 2018, 53, 1275–1287. [Google Scholar] [CrossRef]
- Elkholy, M.; Shakib, S.; Dunworth, J.; Aparin, V.; Entesari, K. A Wideband Variable Gain LNA with High OIP3 for 5G Using 40-nm Bulk CMOS. IEEE Microw. Wireless Compn. Lett. 2018, 28, 64–66. [Google Scholar] [CrossRef]
- Chan, W.L.; Long, J.R. A 58–65 GHz Neutralized CMOS Power Amplifier with PAE Above 10% at 1-V Supply. IEEE J. Solid State Circuits 2010, 45, 554–564. [Google Scholar] [CrossRef]
- Choi, C.; Son, J.H.; Lee, O.; Nam, I. A +12-dBm OIP3 60-GHz RF Downconversion Mixer with an Output-Matching, Noise- and Distortion-Canceling Active Balun for 5G Applications. IEEE Microw. Wireless Compn. Lett. 2017, 27, 284–286. [Google Scholar] [CrossRef]
- Kaczaman, D.; Shah, M.; Alam, M.; Rachendine, M.; Cashen, D.; Han, L.; Raghavan, A. A Single-Chip 10-Band WCDMA/HSDPA 4-Band GSM/EDGE SAW-less CMOS Receiver with DigRF 3G Interface and +90 dBm IIP2. IEEE J. Solid-State Circuits 2009, 44, 718–739. [Google Scholar] [CrossRef]
- Chang, S.; Shin, H. 2.4-GHz CMOS Bluetooth RF Receiver with Improved IM2 Distortion Tolerance. IEEE Tran. Microw. Theory Tech. 2020, 68, 4589–4598. [Google Scholar] [CrossRef]
- Lee, Y.; Chang, S.; Kim, J.; Shin, H. A CMOS RF Receiver with Improved Resilience to OFDM-Induced Second-Order Intermodulation Distortion for MedRadio Biomedical Devices and Sensors. Sensors 2021, 21, 5303. [Google Scholar] [CrossRef] [PubMed]



| This Work | [10] | [9] | [8] | [21] | [11] | |
|---|---|---|---|---|---|---|
| RF Receiver Architecture | Direct Conversion | Direct Conversion | Direct Conversion | Direct Conversion | Direct Conversion | Direct Conversion |
| RF Frequency (GHz) | 24 | 35 | 24 | 24 | 24 | 28 |
| I/Q Amplitude Mismatch Calibration | Mixer Gate Bias Control | none | none | none | none | BBA Gain Control |
| I/Q Phase Mismatch Calibration | LO Buffer Cap Control | none | none | none | LO Buffer Cap Control | QVCO Tank Cap Control |
| Gain (dB) | 31.5 | 33 | 36.7 | 31.5 | 24 | 69 |
| IP1dB (dBm) | −35.2 | −23 | −29.7 | −24 | −20 | −68.9 |
| Noise Figure (dB) | 4.8 | 5.9–7.5 | 6.1 | 6.7 | 7.8 | 6.7 |
| CMOS Process | 65 nm | 65 nm | 130 nm | 65 nm | 180 nm | 28 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Kim, S.; Shin, H. A 24 GHz CMOS Direct-Conversion RF Receiver with I/Q Mismatch Calibration for Radar Sensor Applications. Sensors 2022, 22, 8246. https://doi.org/10.3390/s22218246
Lee Y, Kim S, Shin H. A 24 GHz CMOS Direct-Conversion RF Receiver with I/Q Mismatch Calibration for Radar Sensor Applications. Sensors. 2022; 22(21):8246. https://doi.org/10.3390/s22218246
Chicago/Turabian StyleLee, Yongho, Soyeon Kim, and Hyunchol Shin. 2022. "A 24 GHz CMOS Direct-Conversion RF Receiver with I/Q Mismatch Calibration for Radar Sensor Applications" Sensors 22, no. 21: 8246. https://doi.org/10.3390/s22218246
APA StyleLee, Y., Kim, S., & Shin, H. (2022). A 24 GHz CMOS Direct-Conversion RF Receiver with I/Q Mismatch Calibration for Radar Sensor Applications. Sensors, 22(21), 8246. https://doi.org/10.3390/s22218246








