4.1. Data Pre-processing Phase
The data pre-processing phase is to describe how to obtain S, which is a set of training samples of radar images, by acquiring FMCW radar data and processing the digital signal converted by a hardware signal processor, as an input of our algorithm, , where can be a sample of a 2D radar feature or a 3D radar feature. If , each contains the i-th training sample of the Doppler signature, angle signature, and range signature. If , each contains i-th training sample of the range-Doppler signature and the range-angle signature.
In the following, we will describe how to obtain or . The continuous T FMCW signal samples can be expressed as, , for , where is represented as the t-th continuous FMCW radar signals, where m is the sampling chirp number, n is the received antenna number, and T is the chirp number times the chirp duration time. If , consists of multi-features, including a T number of range-Doppler signatures, denoted as , T number of range-Doppler signatures, denoted as , and T number of range-elevation signatures, denoted as , which are extracted from continuous T FMCW signal samples , for , we let . If , consists of multi-features, including a T number of Doppler signatures, denoted as , T number of range signatures, denoted as , T number of azimuth signatures, denoted as , and T number of elevation signatures, denoted as , which are also extracted from the continuous T FMCW signal samples , for , we let = . Consequently, the output of the data pre-processing phase is to extract or from the continuous T FMCW signal samples, , for , as follows.
To obtain a wider range of field-of-view data, a Binary Phase Modulation (BPM) [
27], or called as BPM-MIMO scheme, is firstly executed by utilizing the FMCW MIMO, by applying the BPM function [
27] to yield
, as
, for
, under
, for
, is the continuous
T FMCW signal samples, where
, where
, each is represented as the
3-dimensional data matrix, where
m is the sampling chirp number,
n is the received antenna number, and
c is the chirp number utilized after performing the BPM algorithm.
To eliminate the radar signal noise, a Moving Target Indication (MTI) filtering algorithm [
16] is then utilized, the MTI noise filtering function is performed on
to obtain
, where
, such that
, where
is represented as an
three-dimensional data matrix after performing the MTI noise filtering function to eliminate the radar signal noise, where
. To avoid the different background issue, we adopt the MTI (Moving Target Indication) filter algorithm in our paper. The signal of the non-moving object (no phase difference) will be removed to ensure that the detected object is only detected in a moving condition, such that the movement, or called as phase difference, can be directly retained. We may also call this the static removal operation.
To extract the distance frequency and the Doppler frequency information of the detected objects, a Fast Fourier Transform (FFT) algorithm [
4] is applied to the
data matrix to obtain
data matrix, such that
, where
, by performing the FFT procedure on each column of
, where
. Then, a Fast Fourier Transform (FFT) [
4] algorithm is performed on
to obtain the
data matrix, such that
, where
, by performing the FFT procedure on each row of
, where
.
To reduce the noise frequency generated by the Doppler effects, a Constant False Alarm Rate (CFAR) filtering algorithm [
17] is also utilized for the FFT data matrix
to acquire a new data matrix
, such that
, where
.
The purpose of the background denoising algorithm is to extract the phase frequency between the signals. In our work, we only take the data frames with the largest signals after the Fourier transformation, and then concatenate these data frames together. The intuition is a continuous echo map of the torso. If one or two noises are larger than the torso reflections, or there is a small noise in the process of denoising, it does not matter for the misguided training, since one or two noises of the tens to hundreds of data frames will be moderately retained and will not be particularly problematic.
In the following, we describe how to obtain
from the
, where
. We show how to generate
,
, from
, as follows. We let
be an
two-dimensional data matrix using
, so the range-Doppler signature
, where
, is finally obtained. Based on the beamforming [
28] processing principle, we may obtain the range-azimuth signature,
, where
, and range-elevation signature,
, where
. A beamforming function
B, Reference [
28] is applied to extract the angle frequency information from the received antennas;
and
are obtained, where
and
, where the first to
j-th azimuth antenna data are
of
, and
-th to
n-th elevation antenna data are
of
, where
. Finally,
and
are obtained, where
.
Figure 7 shows an example for our range-Doppler signature
, range-azimuth signature
, and range-elevation signature
.
In the following, we describe how to obtain = from . First, we show how to obtain the Doppler signature ,where . Given , where , we let , by performing the Short-Time Fourier Transform (STFT) operation on , where . Next, the range signature is constructed using , where is the one-dimensional range data of m sampling chirp numbers within t sampling time, under , where . The azimuth signature is then constructed, such that , where is the one-dimensional azimuth data of m sampling chirp numbers within t sampling time, under a range-azimuth signature , where . Finally, the elevation signature is formed by , where is the one-dimensional elevation data of m sampling chirp numbers within t sampling time, under the range-elevation signature , where .
An example is shown in
Figure 8, with the generation of 2D feature signatures of the Doppler signature
, range signature
, azimuth signature
, and elevation signature
. An example of CHM is given in
Figure 9a for the human motions of wave, jumping forward, and the vertical-motion group (including falling and lying down).
Figure 9b provides the human motions of the walking group (including walking forward, walking backward, walking left, and walking right).
Figure 9c displays the human motions of the running group (including running forward, running backward, running left, and running right).
Figure 10a give an examples of continuous human motions with 2D feature signatures under four motions in 12 s, and
Figure 10b shows another example of two motions in 12 s.
4.2. Multi-Feature Embedding Phase
The task of the multi-feature embedding phase is to embed 2D features , and , where , , , and , where , through a CNN embedding module into our designed network.
In the following, we describe how to perform the 2D feature data embedding. Let a CNN embedding module be represented as
, and each 2D feature from
is independently embedded by a different
. In this work,
consists of a first convolution layer of
, with stride of
, batch norm., ReLU, a max pooling layer with a kernel size of
, batch norm., ReLU, a second convolution layer by
with stride of
, batch norm., ReLU, max pooling layer with a kernel size of
, batch norm., ReLU, a third convolution layer by
with stride of
, batch norm., ReLU, and an average pooling is finally used to extract all features. Note that the 2D feature data embedding
aim to embed the spatial information from 2D features
. an example of
can be seen in
Figure 11.
The 2D feature data embedding operations performed through the CNN embedding module
are given as follows.
where
are the embedded features for the 2D original features
, where the data size of each embedded feature is
.
Figure 11a gives an example of
, and
, which are embedded features for the 2D features
, and
.
Another task of the multi-feature embedding phase is to embed the 3D features
, and
, where
,
, and
, where
, through the CNN network into our designed network. In the following, we describe how to perform the 3D feature data embedding. Let a CNN embedding module be represented as
, and each 3D feature from
is independently embedded by a different
. In this work,
consists of a first convolution layer by
with stride of
, batch norm., ReLU, max pooling layer with kernel size of
with stride of
, batch norm., ReLU, a second convolution layer by
with a stride of
, batch norm., ReLU, max pooling layer with kernel size of
with stride of
; and then an average pooling is used to extract all the features. Finally, a Multilayer Perceptron (MLP) is additionally used to embed the features into the temporal space. Note that the purpose of the 3D feature data embedding
aims to first embed the 3D features into the spatial space, and MLP is then used to embed the 3D features into the spatial space. An example of
can be seen in
Figure 12.
The 3D feature data embedding operations performed through the CNN embedding module
is given as follows:
where
, and
are the embedded features for the 3D original features
, and
, where the data size of each embedded feature is
.
Figure 12a gives an example of
, and
, embedded features for the 3D features
, and
.
4.3. Transformer-Based Encoding Phase
In the multi-feature embedding phase, the 2D embedded features , or the 3D embedded features , and are embedded into our Transformer-based network, then we describe how to perform our Transformer-based encoding procedure. This phase is divided into the positional embedding operation, Transformer-encoder operation, and feature fusion operation, which are described as follows. It is observed that we let each different 2D embedded feature or different 3D embedded feature be embedded into the disjoint Transformer encoder, and all of the different embedding features among the different disjoint Transformer encoders will be merged together in the feature fusion operation.
In the following, we describe the positional embedding operation, based on our 2D/3D embedded features. Let
be the position embedding function [
13] for the 2D embedded features
and
.
where
and
are position embedding after performing the
function to the 2D embedded features
, and
, respectively. We denote the 2D position embedding feature as
.
Let
be the position embedding function for the 3D embedded features
,
, and
, as follows.
where
,
, and
are position embedded after performing the
function to the 3D embedded features
, and
, respectively. We denote the 3D position embedding feature,
. The
function follows the existing position embedding function from [
13], such that
Next, we describe the Transformer-encoder operation by applying our 2D/3D embedded features. Let the 2D position embedding feature be
, and the 3D position embedding feature be
. We then utilize a Transformer encoder,
, for the 2D position embedding feature,
.
where
is the 2D embedding feature after performing the Transformer encoder for
. Similarly, we then also utilize a Transformer encoder,
, for the 3D position embedding feature,
, as follows.
where
is the 3D embedding feature after performing the Transformer encoder for
. The Transformer encoder
follows the existing result from [
13], which is to calculate the linear transformation of the self-attention weight matrices, the key and value of
(or
). Let
Q,
K, and
V be the calculation matrices of
(or
), and let
,
, and
be the linear transformation matrices, while the self-attention operation matrices with
,
, and
corresponding to
(or
), are obtained through the linear mapping, normalized by the softmax function. The multi-head features
are obtained using multi-head self-attention features; the self-attention-based encoder, denoted as
, from [
13], is expressed as follows.
where
is the feature signature from the linear transformation matrices
,
, and
,where
and
h is the weight between the features, after the dot product operation of the number of layers
Q and
K in the multi-head operation, and is divided by the variance value
to obtain the weight matrix between 0 and 1; the weight is extracted through the normalization of the softmax function. Finally, the
i-th self-attention
is obtained through multiplication by
V, and the multiple self-attention
are concatenated to produce the final self-attention output features.
In the following, we describe how to perform the feature fusion operation. After the Transformer-encoder operation, 2D position embedding feature, and the 3D position embedding feature are obtained from different Transformer encoders. All of these disjoint embedded features should be merged together before our proposed Transformer-based decoder. Let be denoted as the merged 2D embedded features for all 2D position embedding features; we have . Let denoted as the merged 3D embedded features for all 3D position embedding feature, we have . Finally, we further utilize the multi-layer perceptron , and the average pooling layer , for the feature training and feature extraction, as follows. , . Note that or are simplified as for the following explanations, where and .
Examples of the position embedding of the 2D signature,
, and the 3D signature,
, are given in
Figure 11b and
Figure 12b. The Transformer-encoder operations are performed to have
and
, as shown in
Figure 11b and
Figure 12b. The fusion features
and
are obtained in
Figure 11c and
Figure 12c.
4.4. Transformer-Sequential-Decoding Phase
For the fused feature , where or after performing the Transformer-based encoder phase, the proposed Transformer-sequential-decoding phase is then performed. The proposed Transfer-sequential-decoding phase consists of the CTC-decoder, Transformer-sequential-decoder, and Transformer-importance-decoder; each decoder produces a set of predicted label sequences, where , , and are sets of predicted label sequences of CTC-decoder, Transformer-sequential-decoder, and Transformer-importance-decoder, under the ground-true label sequence for all for and . We will describe how to generate these predicted label sequences from the CTC-decoder, Transformer-sequential-decoder, and Transformer-importance-decoder. Finally, a joint-decoding operation is proposed to jointly combine these predicted label sequences to provide a best predicted label sequence, which is nearer to an optimal solution. First, the CTC decoder is described.
CTC decoder: The fused feature
, where
or
, occurs after performing the Transformer-based encoder phase; the proposed Transfer-sequential-decoding phase is then performed. As mentioned in
Section 3.2, the connectionist temporal classification (CTC) [
14] technique is utilized to overcome the blank segment and meaningless feature sequence for the long-time series motion recognition; the CTC technique is integrated into our scheme as the first one feature decoder. Let a set of predicted label sequences
, for all
for
, where the fused feature of
is
or
. As shown in
Figure 13c, the task of the CTC decoder is performed using the fusion feature FF to obtain
, and the loss
can be calculated via Equation (
1) under the predicted label sequence
and the ground-true label sequence
Y.
Transformer-sequential-decoder: To allow the continuous human motion to more effectively learn its temporal correlation, a second decoder, the Transformer-sequential-decoder, is built in our trained model. The output of the Transformer-sequential-decoder is for and , where the fused feature of is simplified as . The basic idea of the Transformer-sequential-decoder is to sequentially decode the Doppler, angle, and range embedded features, and these embedded features are extracted from Transformer-encoder.
The sequential operation of Transformer-sequential-decoder is represented by
where
,
, and
if 2D features are used;
and
, if 3D features are utilized. The additional weight,
E, is the Doppler feature enhancement matrix, which is obtained by
, where
is the transformation weight matrix [
22] and
M is the label feature matrix, which is obtained by
, by performing the mask self-attention operation on the input label
Y and mask matrix
[
22] to prevent the mechanism of observing a subsequent time scale problem.
The sequential operation is stated below. The first function
is initially performed, where
is same as
in Equation (
11), if
or
. The output of
is used again for the second function
,
if
or
with the additional weight,
E. Finally, the output of
is used again for the third function
, where
, and
. We finally apply the Multilayer Perceptron (MLP) to decode
, where
. The loss function
is calculated by Equation (
2). The detailed procedures of the Transformer-sequential-decoder module are proposed in Algorithm 1.
Our multi-head attention function,
, modified from [
14], is as follows.
Note that the key difference is that the weight calculation for self-attention is modified as , where is the weight parameter set for the linear mapping, and E is the output feature of the decoder.
Our CHMR-HS architecture with the Transformer-sequential-decoder module, Transformer-importance-decoder module, CTC decoder, and Joint decoding module are illustrated in
Figure 13a–d.
Figure 14 displays the detailed operation of the Transformer-sequential-decoder for sequentially decoding the Doppler, Doppler-angle, and Doppler-angle-range features.
| Algorithm 1: Transformer-sequential-decoder processing. |
![Sensors 22 08409 i001]() |
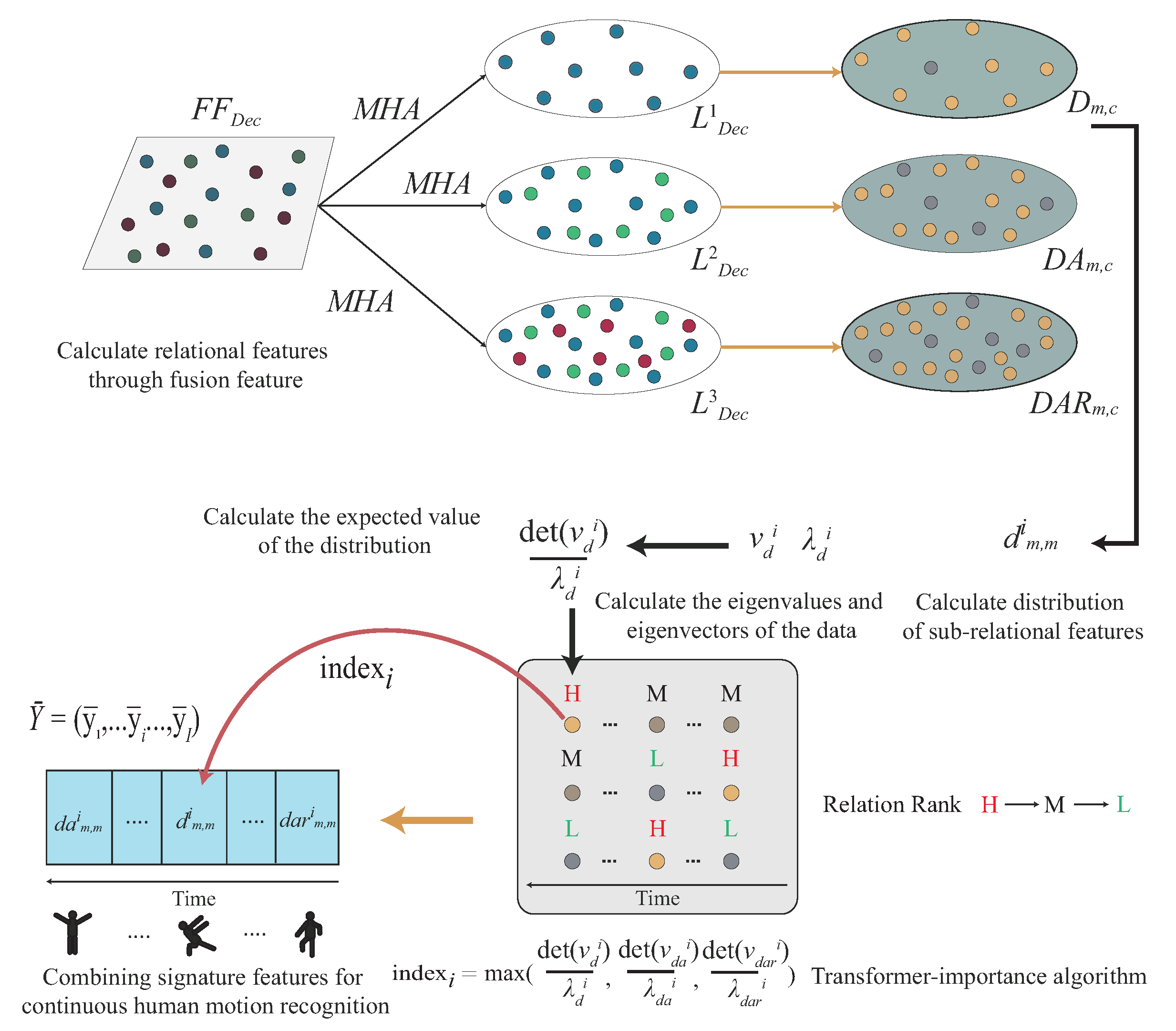
Transformer-importance-decoder: In the Transformer-sequential-decoder, the first output is to only decode the Doppler feature; the second output is to sequentially decode the Doppler and angle features. Finally, the third output is to sequentially decode the Doppler, angle and range features, where , and . In the following, we further design a third decoder, called the Transformer-sequential-decoder, to learn the selection from , or , or among the fixed number of segments, where the fixed number of segment is . Note that the fused feature , is divided into segments; each segment is an matrix, and . Each segment of these segments should learn its importance to smartly select or as one of inputs to perform the MHA function, where the multi-head self-attention (MHA) function is simplified as the MHA function, based on the expected value of distribution of the Doppler, angle, and range features.
First, we let to perform the multi-head self-attention (MHA) function to the fused feature and the label feature matrix M, where or , M is the label feature matrix, and . To estimate the expected value of the distribution of Doppler, angle, and range features, we also calculate , , and , where , , are performed MHA functions to and with , respectively. We also have the results of , because , and .
If , we further divide each of into segments, as , and , , where the sub-relational features , where .
To calculate the expected value of the distribution of the sub-relational features
and
, where
, the eigenvectors
, and
, where
are used to perform the determinant operation to obtain the directed area scalar of the eigenvector. In addition, the eigenvalue
, and
, where
, are used to perform the operation of the expected value of the distribution. Therefore, we have
Finally, let be denoted as the index of the maximum expected value of the i-th segment, where ; the sub-relational features of each segment may be , and , based on their maximum expected value of the distribution, where . Consequently, we have , where , by calculating the expected value of the distribution of , and . If is equal to , then i-segment is adopted by only considering the Doppler feature, where . If is equal to , then i-segment adopts the by considering both the Doppler and angle features, where . If is equal to , then i-segment is adopted the by considering the Doppler, angle, and range features, where . This work will be performed thorough the importance feature combination (IFC) operation, as defined below.
Then, the output of the Transformer-importance-decoder,
, can be represented, as given below.
, where
is a parameter concatenation function to concatenate the training parameters by order through the features generated by iterative training, and updates the parameters obtained by the
t-th decoding parameters from the previous
-th decoding parameters, where
. In addition, the importance feature combination (IFC) function, defined as the sub-relation features
, or
, is selected based on the value of
, where
.
Figure 15 shows the example of the feature selection of the Transformer-importance-decoder. The loss function
is calculated using Equation (
3).
Joint-decoding: The CTC-decoder, Transformer-sequential-decoder, and Transformer-importance-decoder decode the predicted sequence-to-sequence results of
, and
, while
Y is the ground-truth value of the sequence-to-sequence task. The best prediction sequence-to-sequence results of the CTC-decoder, Transformer-sequential-decoder, and Transformer-importance-decoder are
by iteratively searching for minimum values of
, and
, for
R times, where
, and
are the loss functions for
i-th training for the CTC decoder, Transformer-sequential-decoder, and Transformer-importance-decoder, where
, and
R is the training number.
where
,
, and
are the final loss values of the CTC-decoder, Transformer-sequential-decoder, and Transformer-importance-decoder. After the obtaining the best sequence-to-sequence results of
,
,
of the CTC-decoder, Transformer-sequential-decoder, and Transformer-importance-decoder, the next purpose of the join-decoding operation is to search for the best training parameters
, and
, as follows, to satisfy Equation (
4).