Intelligent Control of Groundwater in Slopes with Deep Reinforcement Learning †
Abstract
:1. Introduction
2. Deep Reinforcement Learning for Geosystems
2.1. Basics of Reinforcement Learning for Geosystems
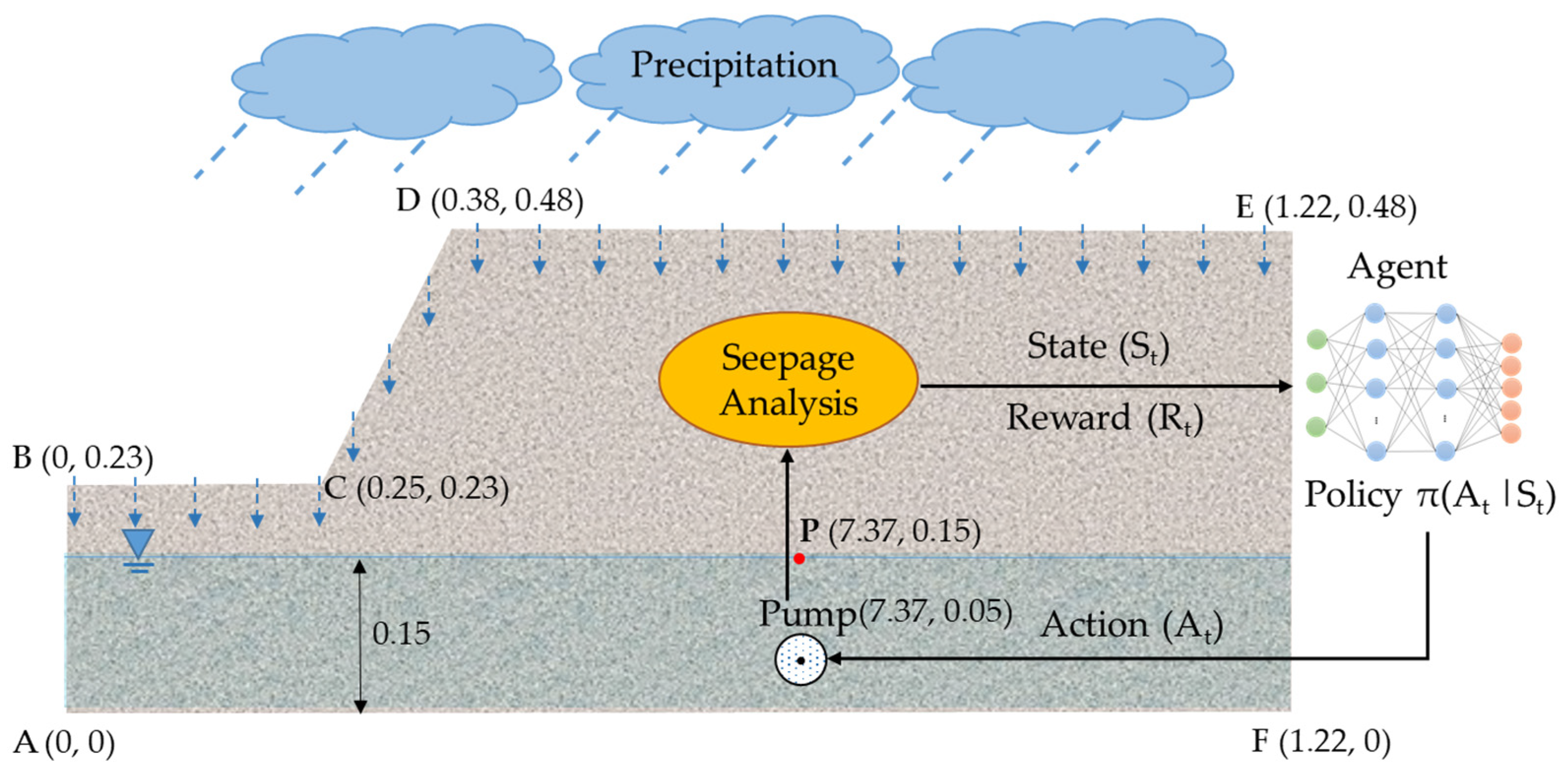
- Environment: In this study, the RL environment is the lab-scale geosystem simulated with a numerical model for seepage. The seepage model informs the agent on the geosystem’s condition and specifies what state it can be in after performing an action. In future real-world applications, this environment can be the geosystem and its surrounding environment in the field. Simulation of the geosystem using a seepage model is thoroughly discussed in Section 2.2.
- Agent: The RL agent works as a pump operator in the RL framework. More specifically, it embodies the neural network algorithm that controls the water table by observing the current state of the geosystem and taking actions to regulate the pump’s flow rate. In this study, a Deep Q-Network (DQN) was adopted as the learning agent, which is covered in depth in Section 2.3.
- State (): The state describes the current condition of the environment (i.e., the geosystem). In this study, the RL agent receives three observations from the environment before taking an action. The observations are (1) the water head at point “P” in Figure 1 representing the distance from the target level, (2) the rain intensity at the current time step, and (3) the rain intensity at the next time step. A transient seepage analysis was performed at each time step to determine the water head at point “P”.
- Action (): An action is an operation taken by the agent in the current state. For this geosystem, an action was considered to control the pump’s flow rate for each time step. The action space contains all the possible actions that the agent can take. To enable intermittent control of the geosystem, five discrete actions were defined, , representing 0%, 25%, 50%, 75%, and 100% of the pumping capacity, respectively.
- Reward (): The reward is the evaluation score or feedback assigned to the agent for its action. At any given time , the agent observes the state of the geosystem, and then, based on this, takes an action to regulate the pump’s flow rate for controlling the water level. Subsequently, the agent receives a reward to assess the action choice. The reward function is defined to designate the desired and undesired actions in the current state. The agent will receive a positive reward if the action can keep the groundwater close to the target level. If the groundwater moves away (up or down) from the target level, the agent will receive a negative reward related to the distance of the water table from the target level.
2.2. Environment Simulation: Seepage Model
2.3. Agent: Deep Q-Network
2.4. Reward Function
3. Performance Evaluation
3.1. PID Controlled Groundwater
3.2. Factor of Safety
4. Network Training and Results
5. Discussion
5.1. Influence of State Space Size
5.2. Effectiveness of Transfer Learning
5.3. Influence of Action Space Size
5.4. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schuster, R.L. The 25 most catastrophic landslides of the 20th century. In Proceedings of the 8th International Conference and Field Trip on Landslides, Granada, Spain, 27–28 September 1996. [Google Scholar]
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Kaleel, M.; Reeza, M. The impact of landslide on environment and socio-economy: GIS based study on Badulla district in Sri Lanka. World Sci. News 2017, 88, 69–84. [Google Scholar]
- Chen, W.; Chen, X.; Peng, J.; Panahi, M.; Lee, S. Landslide susceptibility modeling based on ANFIS with teaching-learning-based optimization and Satin bowerbird optimizer. Geosci. Front. 2021, 12, 93–107. [Google Scholar] [CrossRef]
- Sepúlveda, S.A.; Petley, D.N. Regional trends and controlling factors of fatal landslides in Latin America and the Caribbean. Nat. Hazards Earth Syst. Sci. 2015, 15, 1821–1833. [Google Scholar] [CrossRef] [Green Version]
- Alsubal, S.; Sapari, N.; Harahap, S. The Rise of groundwater due to rainfall and the control of landslide by zero-energy groundwater withdrawal system. Int. J. Eng. Technol. 2018, 7, 921–926. [Google Scholar] [CrossRef] [Green Version]
- Jiji, L.M.; Ganatos, P. Approximate analytical solution for one-dimensional tissue freezing around cylindrical cryoprobes. Int. J. Therm. Sci. 2009, 48, 547–553. [Google Scholar] [CrossRef]
- Cho, S.E. Stability analysis of unsaturated soil slopes considering water-air flow caused by rainfall infiltration. Eng. Geol. 2016, 211, 184–197. [Google Scholar] [CrossRef]
- Sun, D.-M.; Zang, Y.-G.; Semprich, S. Effects of airflow induced by rainfall infiltration on unsaturated soil slope stability. Transp. Porous Media 2015, 107, 821–841. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Kapnick, S.; Stanley, T.; Pascale, S. Changes in extreme precipitation and landslides over High Mountain Asia. Geophys. Res. Lett. 2020, 47, e2019GL085347. [Google Scholar] [CrossRef]
- Kristo, C.; Rahardjo, H.; Satyanaga, A. Effect of variations in rainfall intensity on slope stability in Singapore. Int. Soil Water Conserv. Res. 2017, 5, 258–264. [Google Scholar] [CrossRef]
- Cotterill, D.; Stott, P.; Kendon, E. Increase in the frequency of heavy rainfall events over the UK in the light of climate change. In Proceedings of the EGU General Assembly Conference Abstracts, Online, 4–8 May 2020; p. 11025. [Google Scholar]
- Nicholson, P.G. Soil Improvement and Ground Modification Methods; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Turner, A.K.; Schuster, R.L. Landslides: Investigation and Mitigation; National Academy Press: Washington, DC, USA, 1996. [Google Scholar]
- Yan, L.; Xu, W.; Wang, H.; Wang, R.; Meng, Q.; Yu, J.; Xie, W.-C. Drainage controls on the Donglingxing landslide (China) induced by rainfall and fluctuation in reservoir water levels. Landslides 2019, 16, 1583–1593. [Google Scholar] [CrossRef]
- Holtz, R.D.; Schuster, R.L. Landslides: Investigation and Mitigation. Transp. Res. Board Spec. Rep. 1996, 247, 439–473. [Google Scholar]
- Curden, D.; Varnes, D. Landslides: Investigation and Mitigation; Transportation Research Board: Washington, DC, USA, 1992. [Google Scholar]
- Cashman, P.M.; Preene, M. Groundwater Lowering in Construction: A Practical Guide; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Wang, H.; Zhang, L.; Yin, K.; Luo, H.; Li, J. Landslide identification using machine learning. Geosci. Front. 2021, 12, 351–364. [Google Scholar] [CrossRef]
- Azmoon, B.; Biniyaz, A.; Liu, Z.; Sun, Y. Image-Data-Driven Slope Stability Analysis for Preventing Landslides Using Deep Learning. IEEE Access 2021, 9, 150623–150636. [Google Scholar] [CrossRef]
- Azarafza, M.; Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep learning-based landslide susceptibility mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef]
- Bui, D.T.; Tsangaratos, P.; Nguyen, V.-T.; Van Liem, N.; Trinh, P.T. Comparing the prediction performance of a Deep Learning Neural Network model with conventional machine learning models in landslide susceptibility assessment. Catena 2020, 188, 104426. [Google Scholar] [CrossRef]
- Chen, J.; Yang, T.; Zhang, D.; Huang, H.; Tian, Y. Deep learning based classification of rock structure of tunnel face. Geosci. Front. 2021, 12, 395–404. [Google Scholar] [CrossRef]
- Srivastava, P.; Shukla, A.; Bansal, A. A comprehensive review on soil classification using deep learning and computer vision techniques. Multimed. Tools Appl. 2021, 80, 14887–14914. [Google Scholar] [CrossRef]
- Song, Q.; Wu, Y.; Xin, X.; Yang, L.; Yang, M.; Chen, H.; Liu, C.; Hu, M.; Chai, X.; Li, J. Real-time tunnel crack analysis system via deep learning. IEEE Access 2019, 7, 64186–64197. [Google Scholar] [CrossRef]
- Xue, Y.; Li, Y. A fast detection method via region-based fully convolutional neural networks for shield tunnel lining defects. Comput. -Aided Civ. Infrastruct. Eng. 2018, 33, 638–654. [Google Scholar] [CrossRef]
- Kumar, D.; Roshni, T.; Singh, A.; Jha, M.K.; Samui, P. Predicting groundwater depth fluctuations using deep learning, extreme learning machine and Gaussian process: A comparative study. Earth Sci. Inform. 2020, 13, 1237–1250. [Google Scholar] [CrossRef]
- Shin, M.-J.; Moon, S.-H.; Kang, K.G.; Moon, D.-C.; Koh, H.-J. Analysis of groundwater level variations caused by the changes in groundwater withdrawals using long short-term memory network. Hydrology 2020, 7, 64. [Google Scholar] [CrossRef]
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study among machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 3904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Zhang, P.; Li, H.; Ha, Q.; Yin, Z.-Y.; Chen, R.-P. Reinforcement learning based optimizer for improvement of predicting tunneling-induced ground responses. Adv. Eng. Inform. 2020, 45, 101097. [Google Scholar] [CrossRef]
- Soranzo, E.; Guardiani, C.; Wu, W. The application of reinforcement learning to NATM tunnel design. Undergr. Space 2022, 7, 990–1002. [Google Scholar] [CrossRef]
- Erharter, G.H.; Hansen, T.F.; Liu, Z.; Marcher, T. Reinforcement learning based process optimization and strategy development in conventional tunneling. Autom. Constr. 2021, 127, 103701. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Mysore, S.; Mabsout, B.; Mancuso, R.; Saenko, K. Regularizing action policies for smooth control with reinforcement learning. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 1810–1816. [Google Scholar]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An introduction to deep reinforcement learning. arXiv 2018, arXiv:1811.12560. [Google Scholar]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T. Mastering chess and shogi by self-play with a general reinforcement learning algorithm. arXiv 2017, arXiv:1712.01815. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, N.; Sandholm, T. Superhuman AI for heads-up no-limit poker: Libratus beats top professionals. Science 2018, 359, 418–424. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. Deep reinforcement learning framework for autonomous driving. Electron. Imaging 2017, 2017, 70–76. [Google Scholar] [CrossRef] [Green Version]
- Mullapudi, A.; Lewis, M.J.; Gruden, C.L.; Kerkez, B. Deep reinforcement learning for the real time control of stormwater systems. Adv. Water Resour. 2020, 140, 103600. [Google Scholar] [CrossRef]
- Sun, A.Y. Optimal carbon storage reservoir management through deep reinforcement learning. Appl. Energy 2020, 278, 115660. [Google Scholar] [CrossRef]
- Biniyaz, A.; Azmoon, B.; Liu, Z. Deep Reinforcement Learning for Controlling the Groundwater in Slopes. In Proceedings of the Geo-Congress 2022, Charlotte, NC, USA, 20–23 March 2022; pp. 648–657. [Google Scholar]
- Bhattacharya, B.; Lobbrecht, A.H.; Solomatine, D.P. Neural networks and reinforcement learning in control of water systems. J. Water Resour. Plan. Manag. 2003, 129, 458–465. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning; MIT Press Cambridge: Cambridge, MA, USA, 1998; Volume 135. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef] [Green Version]
- Logg, A.; Wells, G.N. DOLFIN: Automated finite element computing. ACM Trans. Math. Softw. (TOMS) 2010, 37, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Alnæs, M.; Blechta, J.; Hake, J.; Johansson, A.; Kehlet, B.; Logg, A.; Richardson, C.; Ring, J.; Rognes, M.E.; Wells, G.N. The FEniCS project version 1.5. Arch. Numer. Softw. 2015, 3, 100. [Google Scholar] [CrossRef]
- Biniyaz, A.; Azmoon, B.; Liu, Z. Coupled transient saturated–unsaturated seepage and limit equilibrium analysis for slopes: Influence of rapid water level changes. Acta Geotech. 2021, 17, 2139–2156. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Wartalska, K.; Kaźmierczak, B.; Nowakowska, M.; Kotowski, A. Analysis of hyetographs for drainage system modeling. Water 2020, 12, 149. [Google Scholar] [CrossRef] [Green Version]
- Carta, S.; Ferreira, A.; Podda, A.S.; Recupero, D.R.; Sanna, A. Multi-DQN: An ensemble of Deep Q-learning agents for stock market forecasting. Expert Syst. Appl. 2021, 164, 113820. [Google Scholar] [CrossRef]
- Mohamed Shakeel, P.; Baskar, S.; Sarma Dhulipala, V.; Mishra, S.; Jaber, M.M. Maintaining security and privacy in health care system using learning based deep-Q-networks. J. Med. Syst. 2018, 42, 186. [Google Scholar] [CrossRef]
- Zhou, N. Intelligent control of agricultural irrigation based on reinforcement learning. In Proceedings of the Journal of Physics: Conference Series, Xi’an, China, 18–19 October 2020; p. 052031. [Google Scholar]
- Elavarasan, D.; Vincent, P.D. Crop yield prediction using deep reinforcement learning model for sustainable agrarian applications. IEEE Access 2020, 8, 86886–86901. [Google Scholar] [CrossRef]
- Li, W.; Wang, X.; Zhang, R.; Cui, Y.; Mao, J.; Jin, R. Exploitation and exploration in a performance based contextual advertising system. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–28 July 2010; pp. 27–36. [Google Scholar]
- Cohen, J.D.; McClure, S.M.; Yu, A.J. Should I stay or should I go? How the human brain manages the trade-off between exploitation and exploration. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 933–942. [Google Scholar] [CrossRef] [Green Version]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Paz, R.A. The design of the PID controller. Klipsch Sch. Electr. Comput. Eng. 2001, 8, 1–23. [Google Scholar]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control. Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Kasilingam, G.; Pasupuleti, J. Coordination of PSS and PID controller for power system stability enhancement–overview. Indian J. Sci. Technol. 2015, 8, 142–151. [Google Scholar] [CrossRef]
- Bishop, A.W. The use of the slip circle in the stability analysis of slopes. Geotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Vanapalli, S.; Fredlund, D.; Pufahl, D.; Clifton, A. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]













| Definition | Soil |
|---|---|
| [m/s] | 6 × 10–4 |
| [1/m] | 1 × 10–4 |
| Porosity, [–] | 0.32 |
| [Pa] | 1200 |
| Empirical parameter, [–] | 0.6 |
| Parameter | (m3/s) | (m) | |||||
|---|---|---|---|---|---|---|---|
| Value | 0.0002 | 0.02 | 0 | 0.25 | 0.5 | 0.75 | 1 |
| Parameter | |||
|---|---|---|---|
| Value | 0.0088 | 0.0001 | 0.0251 |
| Definition | Soil |
|---|---|
| [kN/m3] | 16.40 |
| [kN/m3] | 19.54 |
| Friction angle, [°] | 34° |
| Cohesion, [kN/m2] | 0 |
| Pore air pressure, [kN/m2] | 0 |
| [–] | 35 |
| [–] | 10 |
| Parameter | Value |
|---|---|
| Number of hidden layers | 2 |
| Number of neurons in each hidden layer | 25, 25 |
| Number of episodes for training | 10,000 |
| Batch size | 60 |
| Learning rate, | 10−3 |
| Gamma, | 0.9 |
| Initial epsilon | 1 |
| Final epsilon | 0.01 |
| Epsilon decay | 0.995 |
| Target network update frequency, N | Every 60 iterations |
| Replay memory size | 5000 |
| Control Method | RMSE | |||
|---|---|---|---|---|
| 15 min-constant | 15 min-normal | 20 min-descending | 25 min-ascending | |
| Uncontrolled | 0.093 | 0.145 | 0.197 | 0.115 |
| PID-controlled | 0.022 | 0.034 | 0.028 | 0.022 |
| DRL-controlled | 0.020 | 0.034 | 0.025 | 0.016 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biniyaz, A.; Azmoon, B.; Liu, Z. Intelligent Control of Groundwater in Slopes with Deep Reinforcement Learning. Sensors 2022, 22, 8503. https://doi.org/10.3390/s22218503
Biniyaz A, Azmoon B, Liu Z. Intelligent Control of Groundwater in Slopes with Deep Reinforcement Learning. Sensors. 2022; 22(21):8503. https://doi.org/10.3390/s22218503
Chicago/Turabian StyleBiniyaz, Aynaz, Behnam Azmoon, and Zhen Liu. 2022. "Intelligent Control of Groundwater in Slopes with Deep Reinforcement Learning" Sensors 22, no. 21: 8503. https://doi.org/10.3390/s22218503
APA StyleBiniyaz, A., Azmoon, B., & Liu, Z. (2022). Intelligent Control of Groundwater in Slopes with Deep Reinforcement Learning. Sensors, 22(21), 8503. https://doi.org/10.3390/s22218503






