Analysis and Correction of Polarization Response Calibration Error of Limb Atmosphere Ultraviolet Hyperspectral Detector
Abstract
:1. Introduction
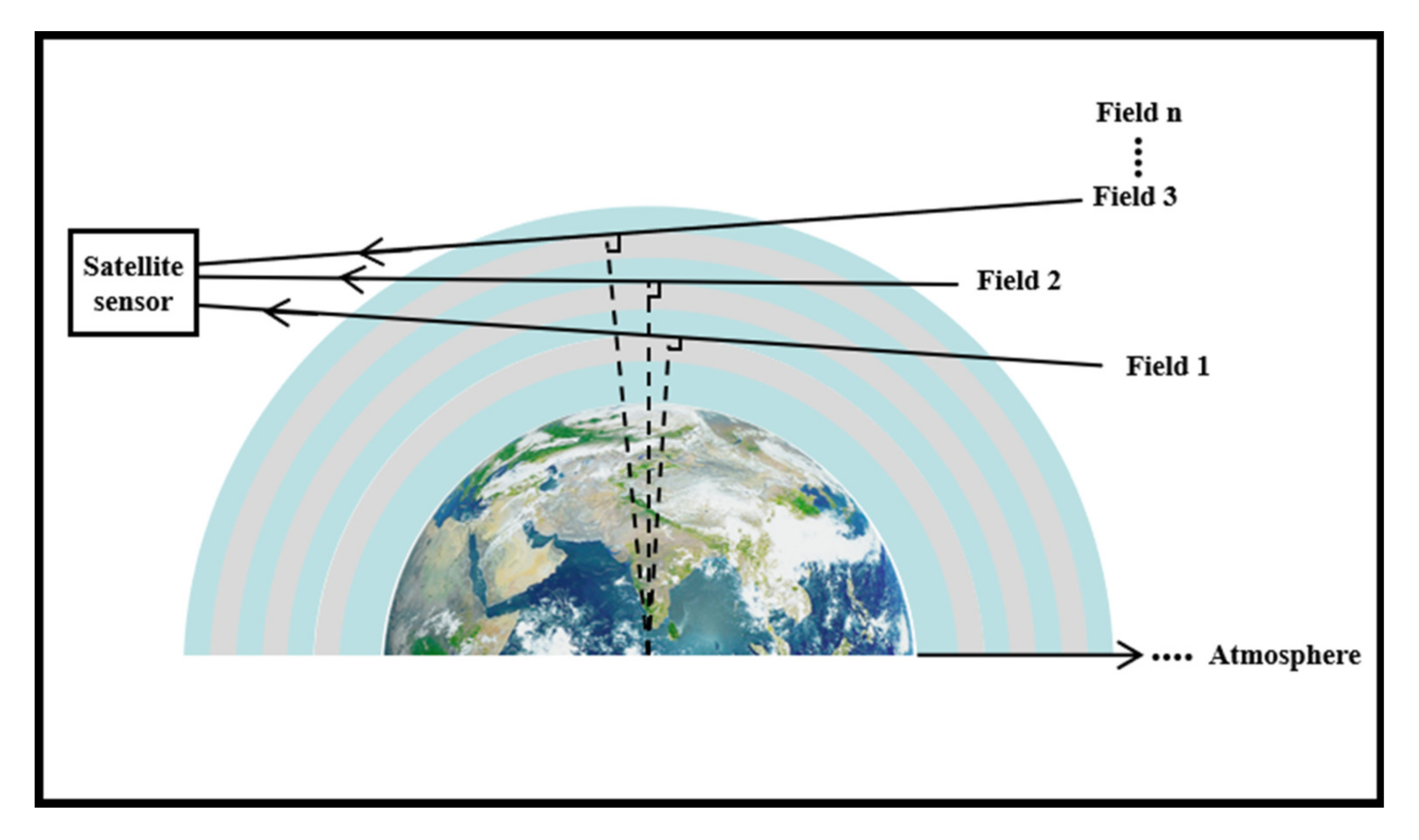
2. On-Orbit Polarization Correction Method for Ultraviolet Hyperspectral Detector
3. Ground Calibration of the Polarization Spectrum Responsivity of the UV Hyperspectral Instrument
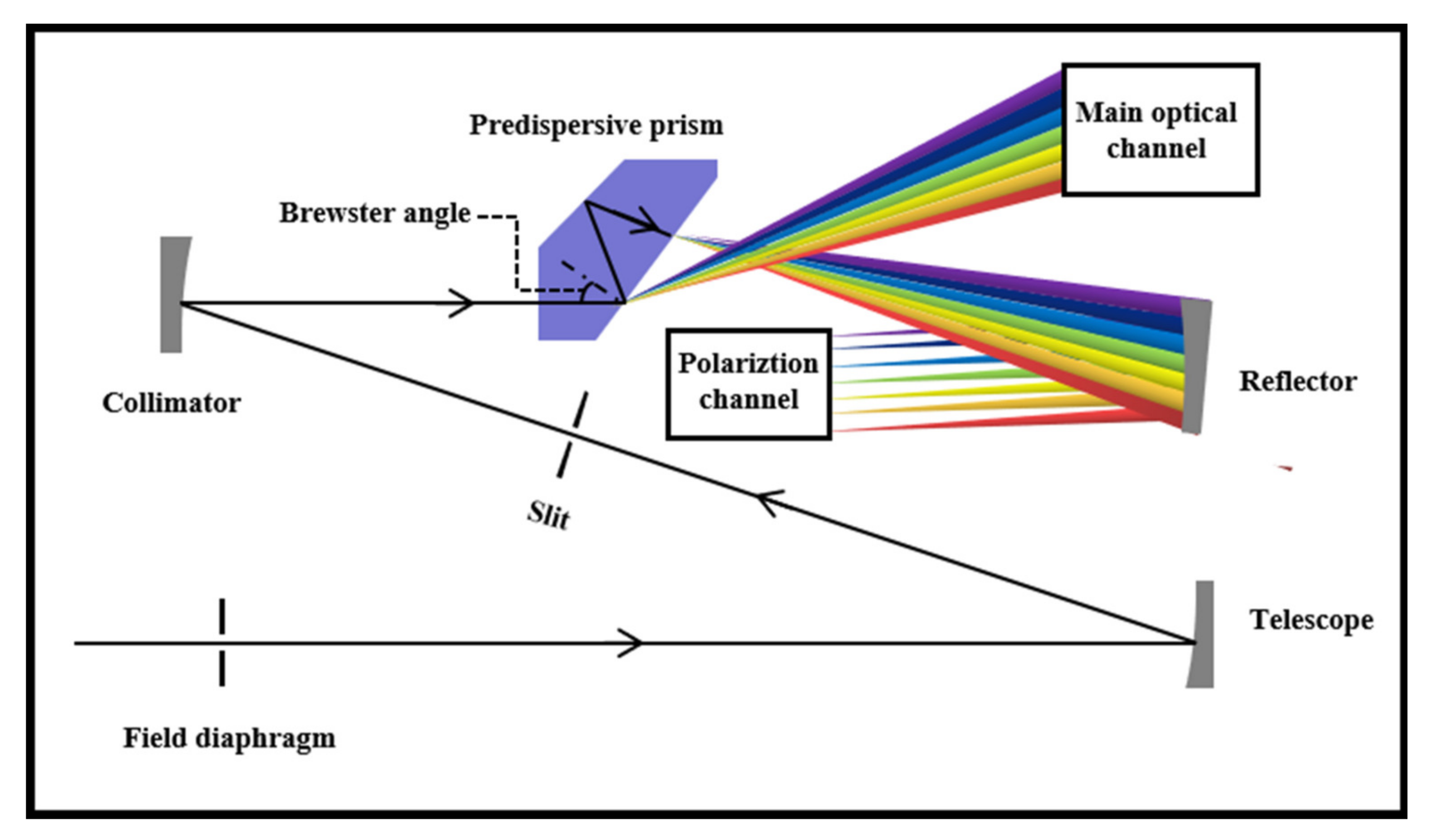
3.1. Instrument Description
3.2. Calibration Method
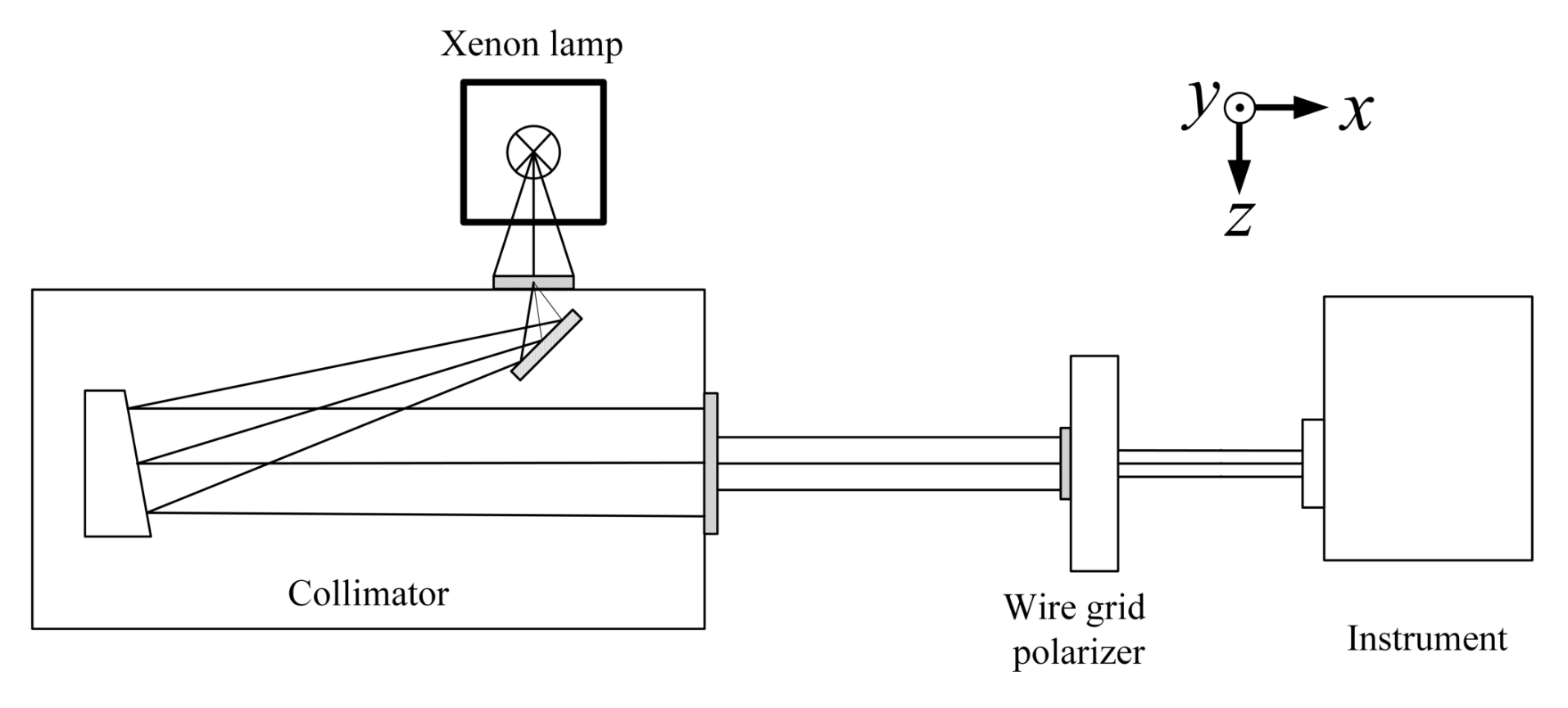
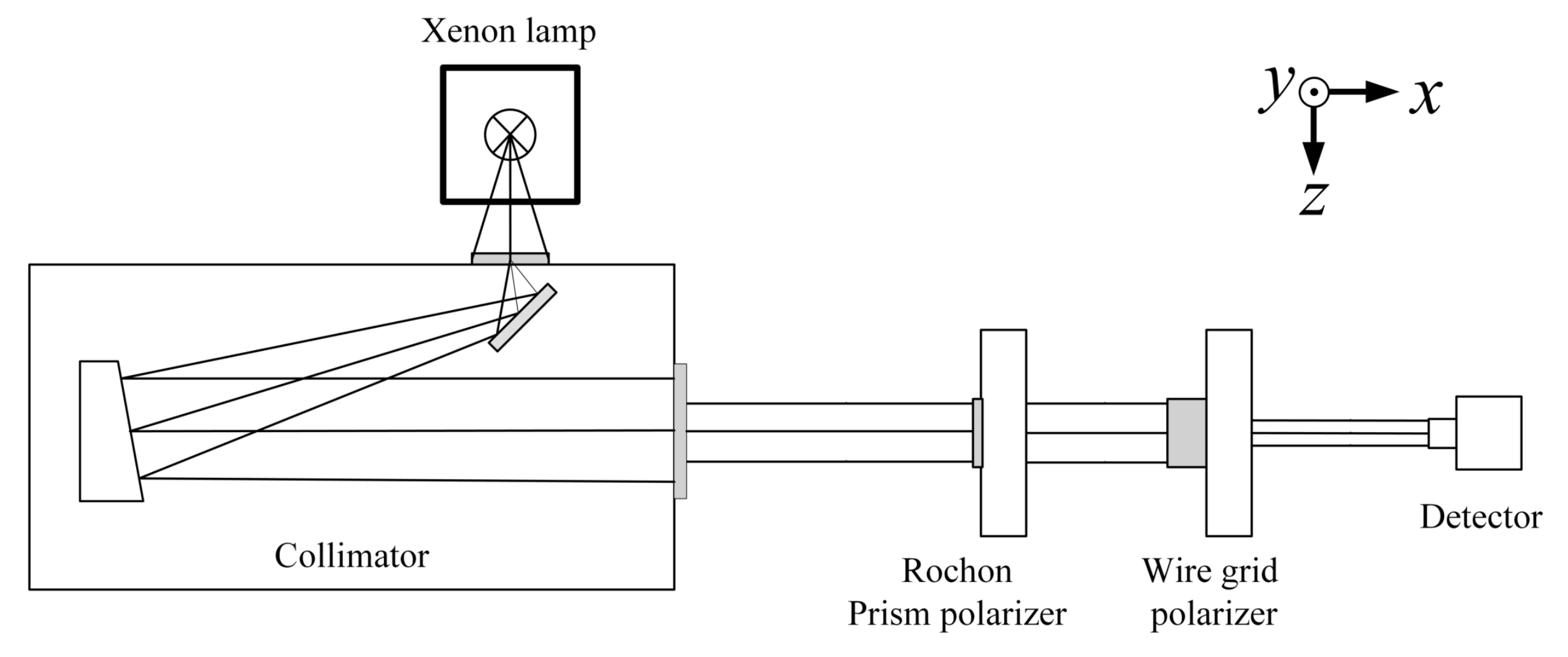
3.3. Experimental Setup
4. Error Source Analysis of Laboratory Calibration of the Polarization Properties
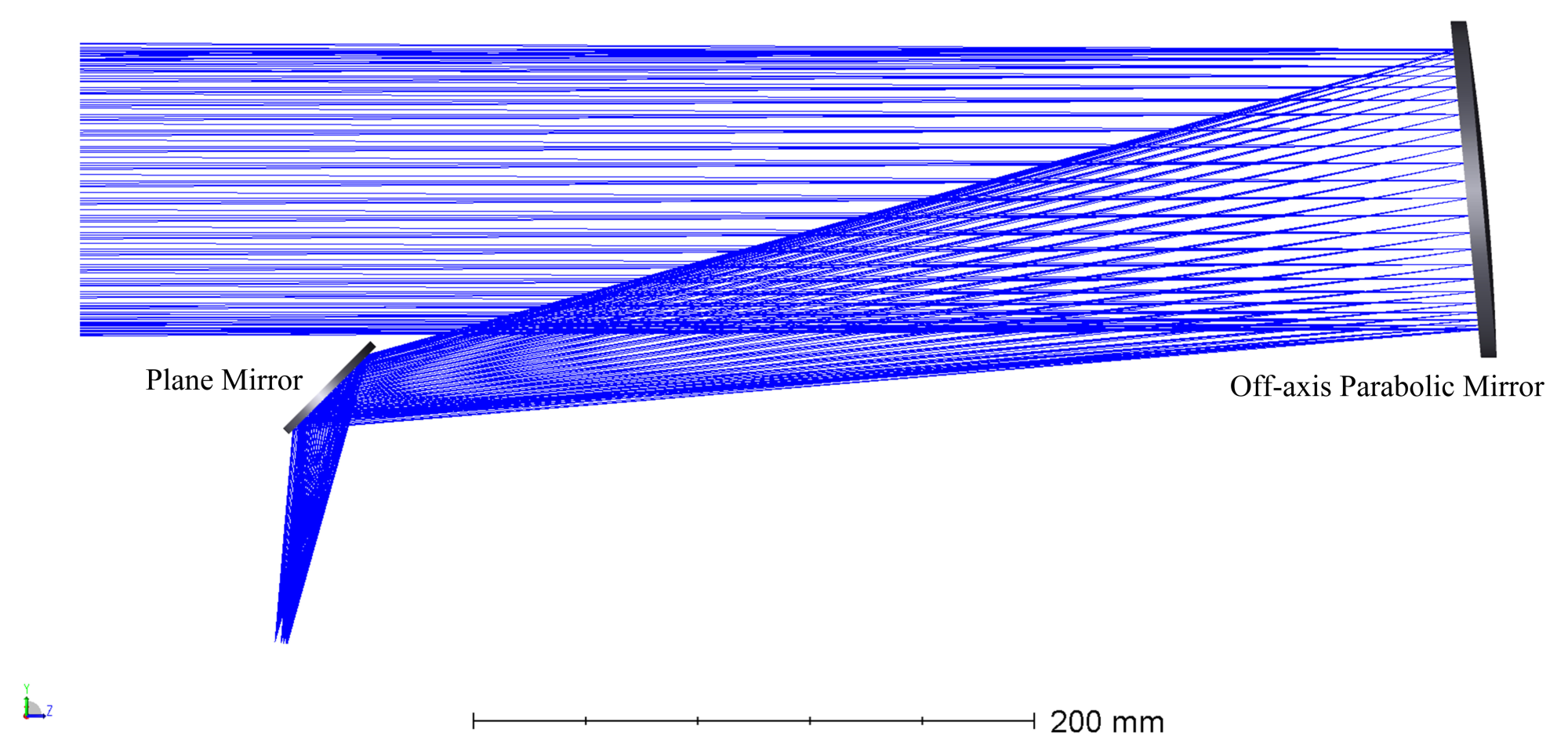
4.1. Effect of UV Collimator on the Uniformity of Output Light Intensity
4.2. Effect of Wire Grid Polarizer on the Polarization Response of Light
5. Detection and Correction of Polarization Measurement System
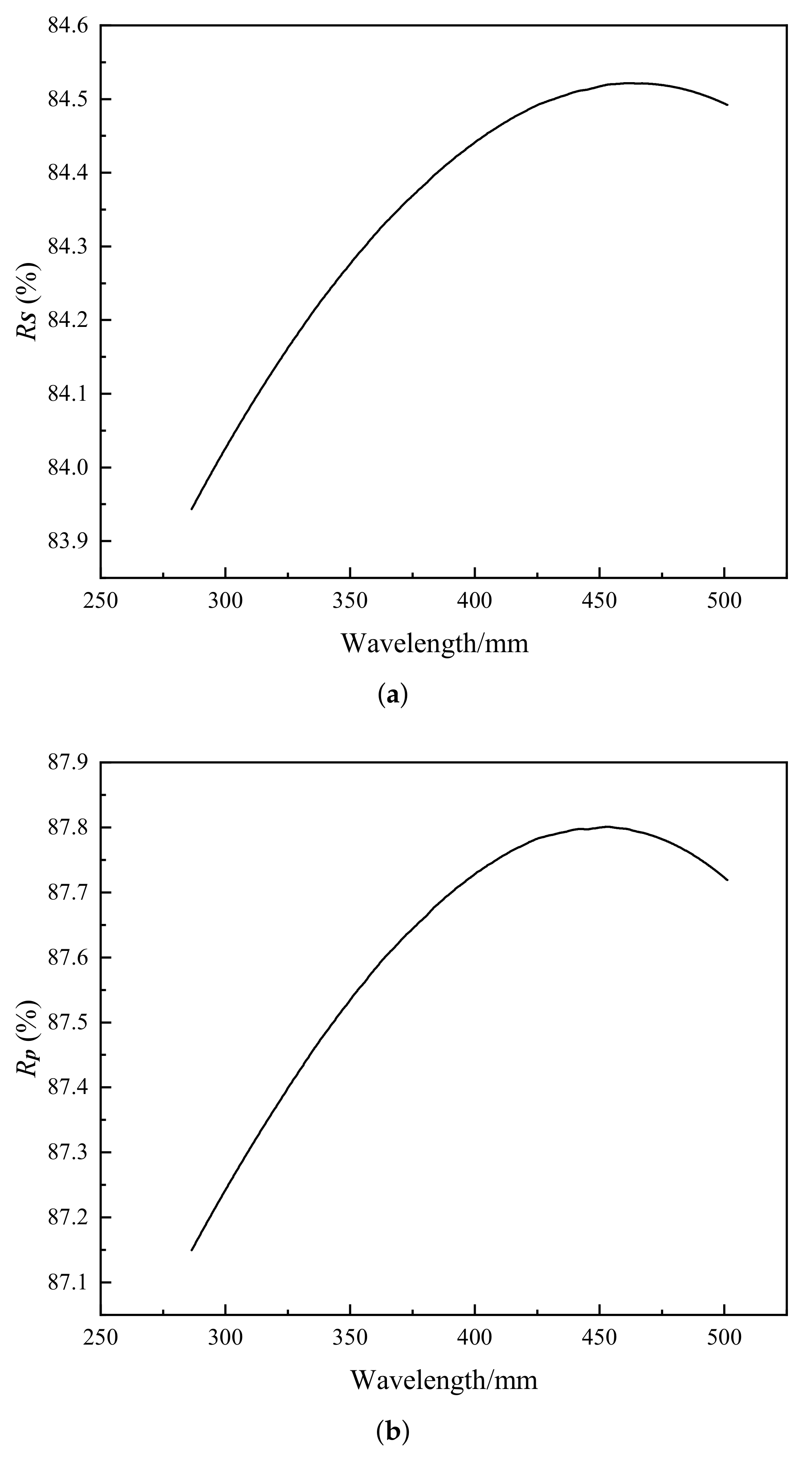
5.1. Muller Matrix of the UV Collimator Correction
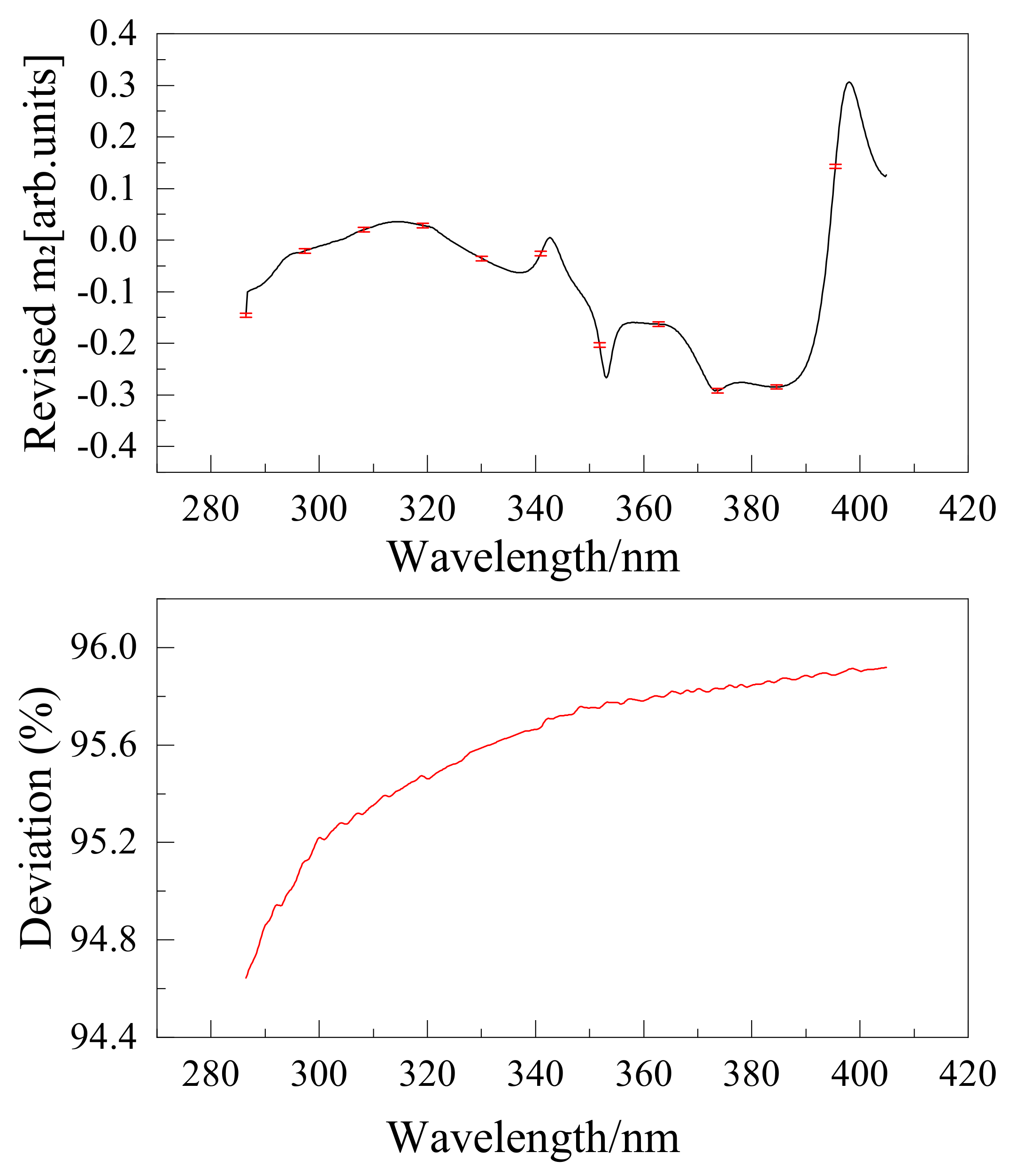
5.2. Detection and Correction of Polarization Attenuation of the Wire Grid Polarizer
5.3. Uncertainty Analysis and Discussion
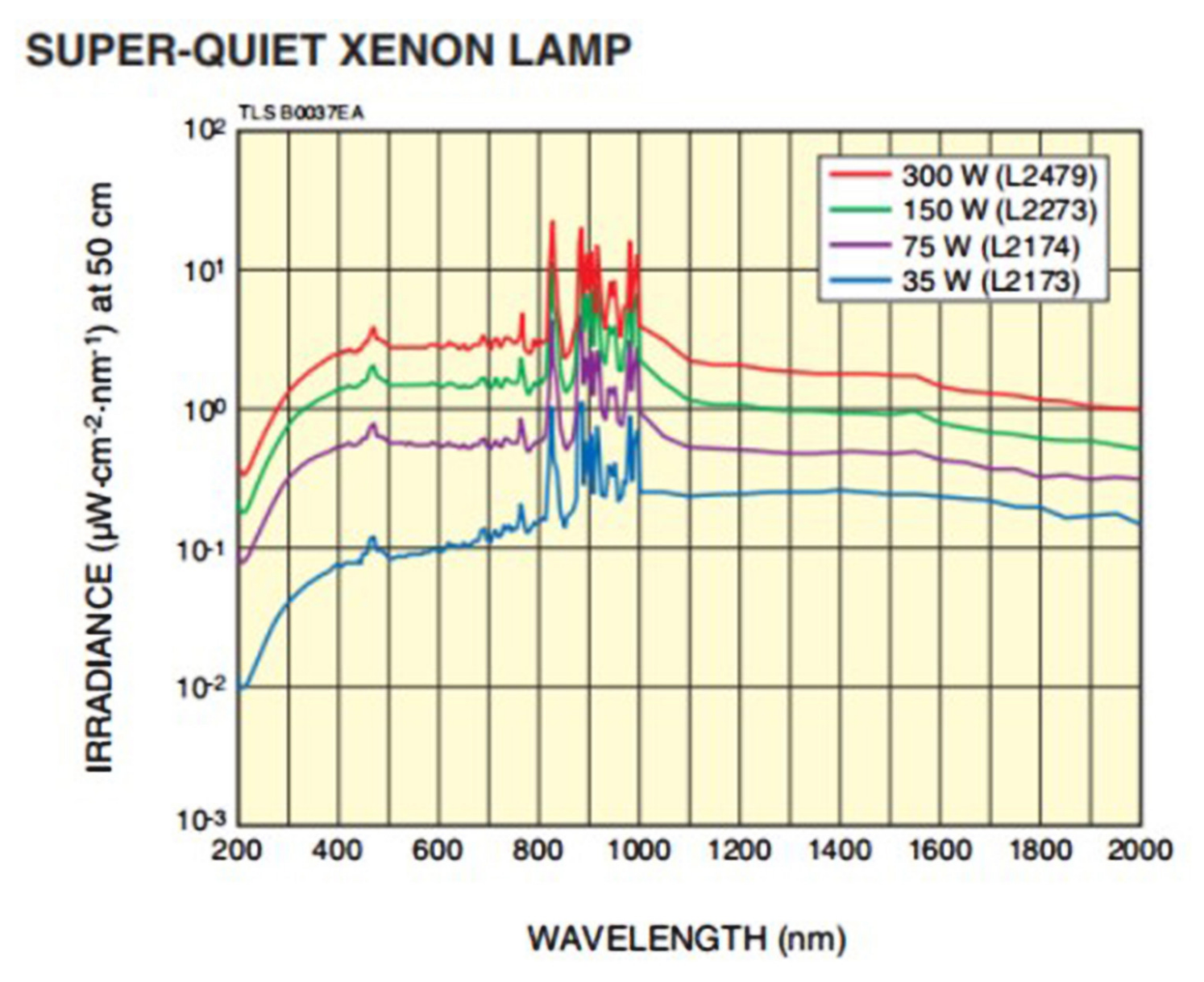
- Stability of polarized light source: The stability of the polarized light source is determined by the stability of the Hamamatsu L2479 xenon lamp. From Section 3.3, the output stability of this xenon lamp is 0.2%, so the uncertainty introduced by the stability of polarized light source is 0.2%;
- Turntable angle accuracy: The turntable angle error causes the polarization angle deviation, which in turn affects the polarization calibration uncertainty of the instrument. From Section 3.3, it can be seen that the turntable angle accuracy is better than 0.01°. By introducing a deviation of ±0.01° to the polarization angle of the incident spectrum, it is calculated that the deviation of the Mueller matrix element value of the instrument is less than 0.1%, so the uncertainty introduced by the turntable rotation angle accuracy is 0.1%;
- The uniformity of the output light intensity of the UV collimator: For the influence of the uniformity of the output light intensity of the UV collimator, please refer to the analysis in Section 4.1. When the output light of the UV collimator has a polarization degree of P, the error introduced to the measurement of the polarization characteristics of the instrument is P. Calculated from Section 5.1, the polarization response due to the UV collimator mirror is approximately 2%. Theoretically, this source of uncertainty can be completely eliminated by calibration. However, due to the influence of the collimator’s field of view of 2° (the incident on the mirror is not an ideal 0-degree parallel light) and coating defects, the residual influence after correction in Section 5.1 is estimated to be 0.8%;
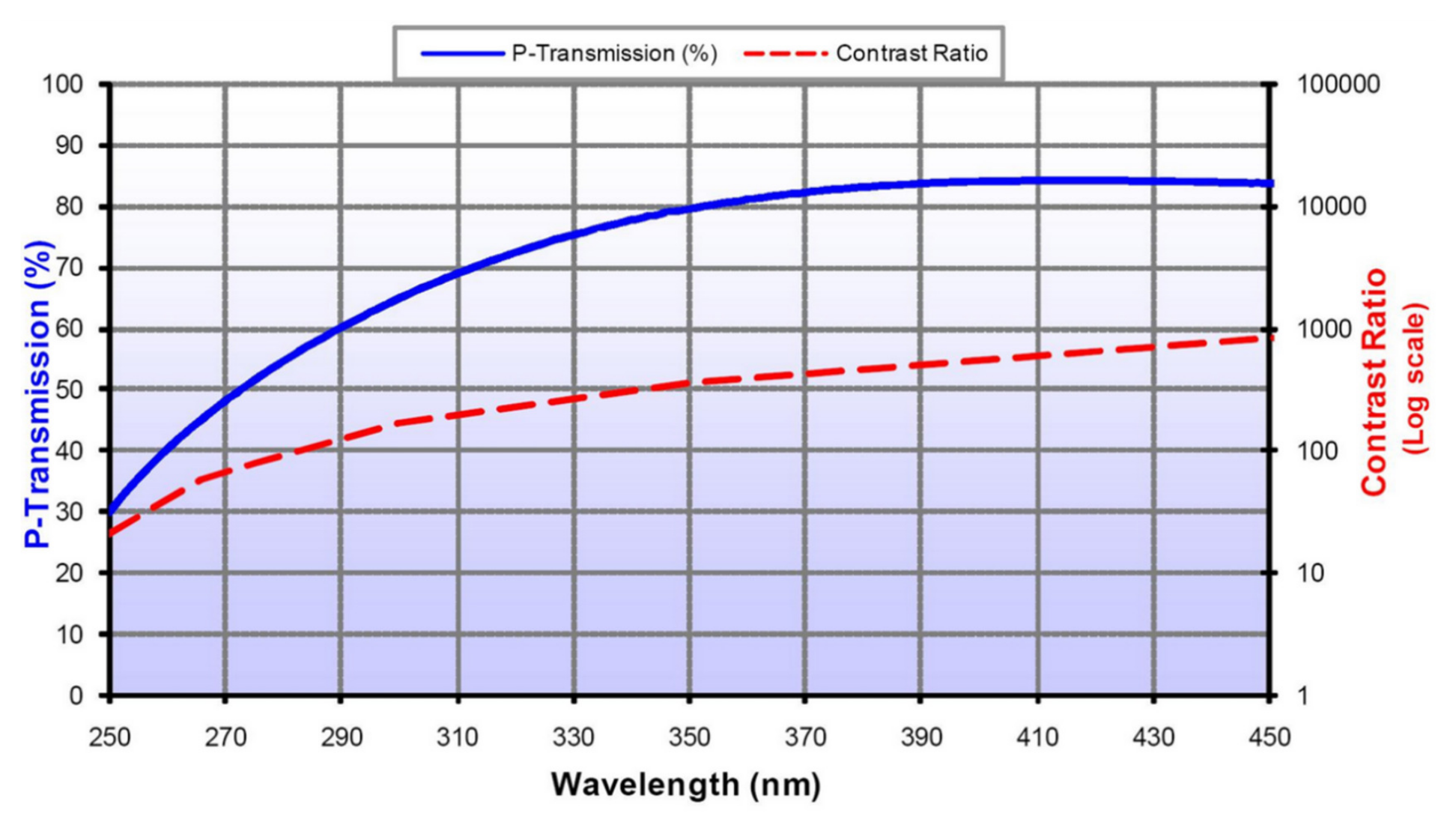
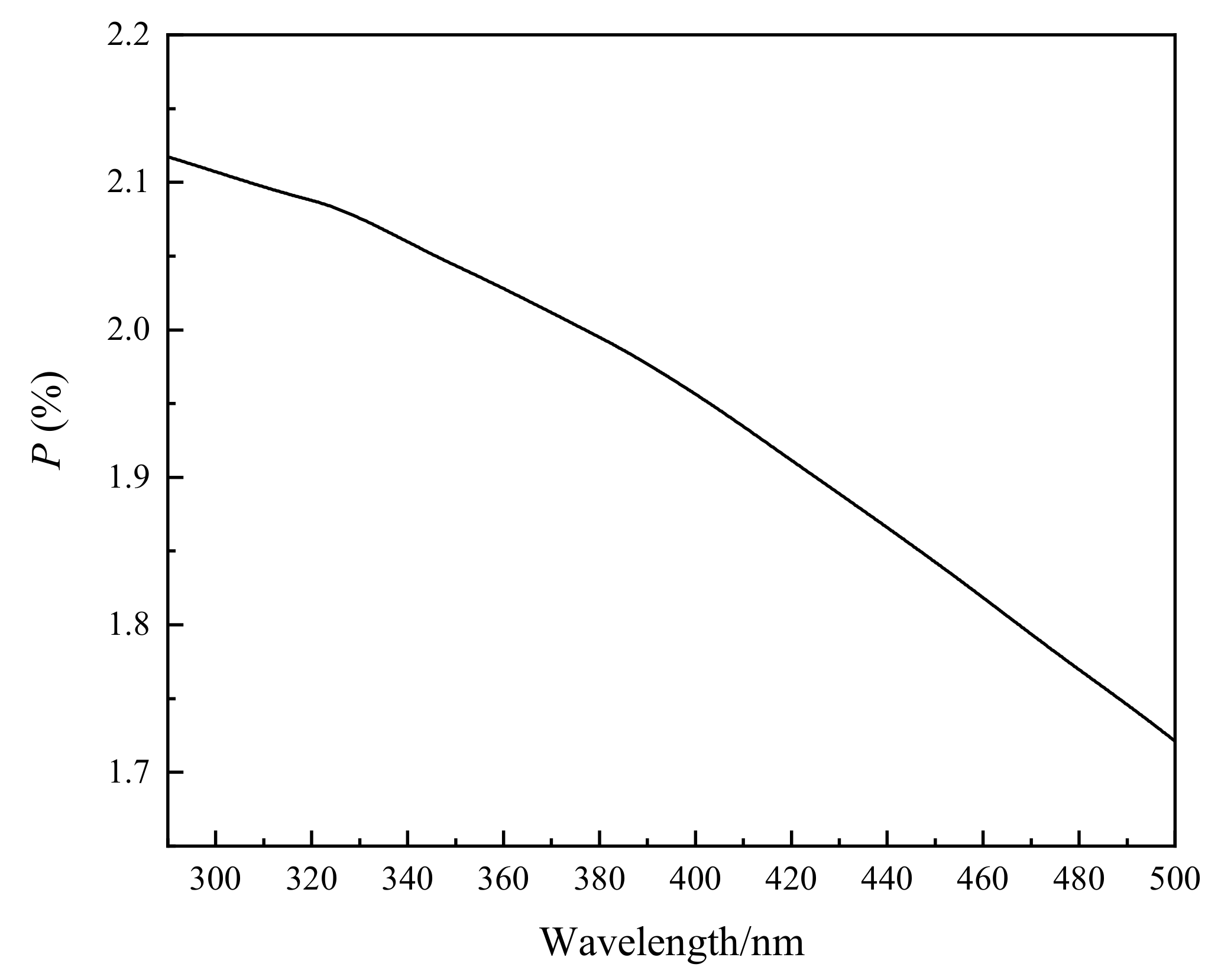
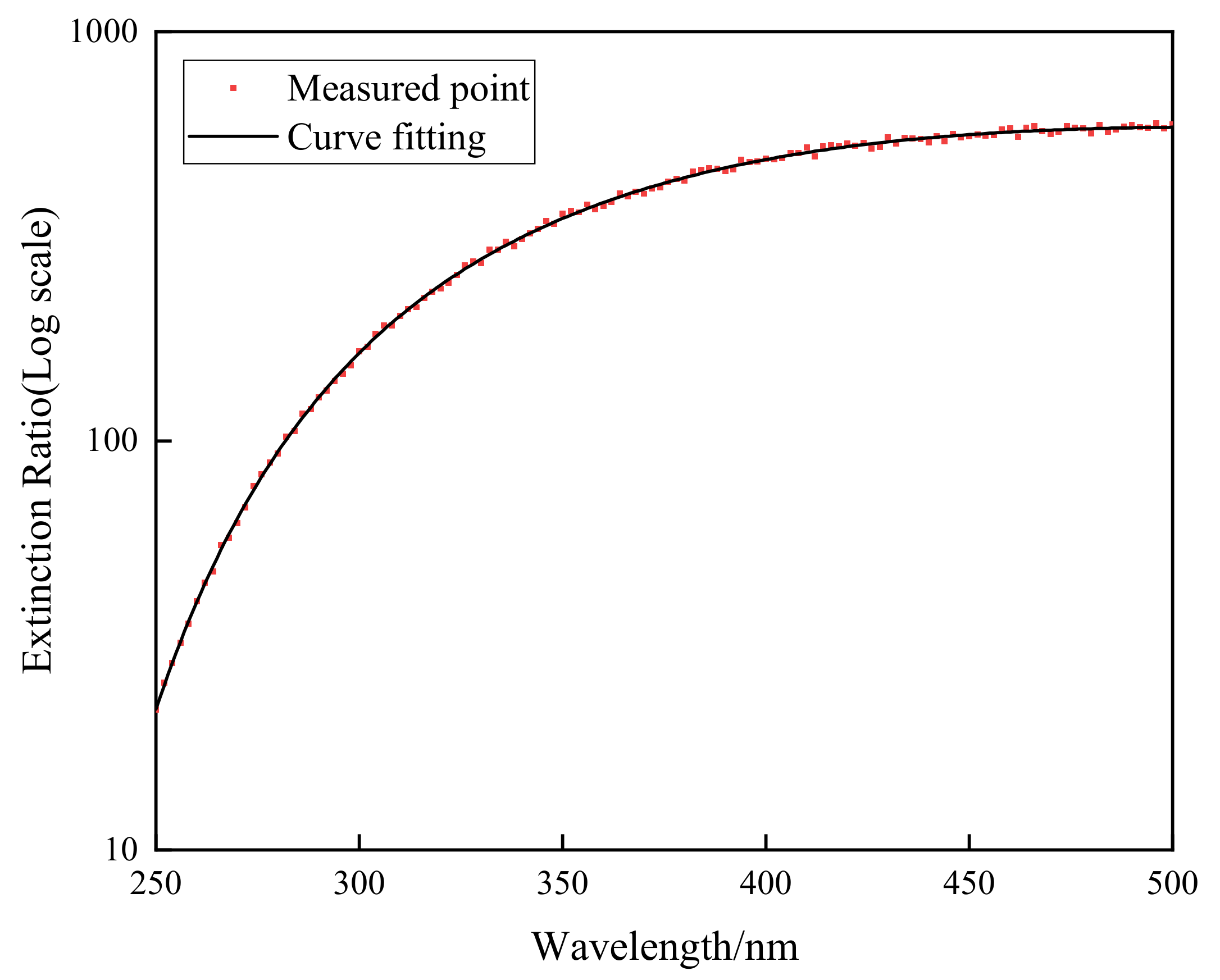
- Wire grid polarizer degree of polarization: The manufacturer gives the typical polarization degree of a wire grid polarizer in the 290–500 nm band as better than 99%, as shown in Figure 6. In the actual test, the polarization degree of the wire grid polarizer at 290 nm measured by the device in Section 5.2 is 98.53%, and the polarization degree after 300 nm is greater than 99%. Therefore, the value of 1.5% is taken when evaluating the uncertainty introduced by the degree of polarization of the wire grid. The uncertainty source is corrected, and the residual uncertainty is estimated to be 0.5%, which is mainly caused by the uncertainty in the measurement process of the polarization degree of the wire grid polarizer;
- Ultraviolet Hyperspectral Detector measurement repeatability: The output signal of the instrument during polarization calibration is analyzed, and it is determined that the repeatability of the output signal of different wavelengths is about 1%;
- Stray light of Ultraviolet Hyperspectral Detector: The influence of stray light during polarization calibration is about 0.2% on the spectral distribution of the signal during polarization calibration and the stray light performance analysis of the instrument itself.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Jun, H.E.; Dai, H.; Hong, J.; Sun, B. Development Status and Trends for Space-Borne Polarization Remote Sensing Atmospheric Aerosols and Particulate Matters. Aerosp. Shanghai 2019, 36, 137–146. [Google Scholar]
- Gao, S.; Maqsood, M.; Bandari, B.; Unwin, M. Development of dual-band circularly polarized antennas and arrays for space-borne satellite remote sensing. In Proceedings of the European Space Agency Antenna Workshop for Space Applications, Noordwijk, The Nethelrands, 1–5 October 2010. [Google Scholar]
- Van Harten, G.; Diner, D.J.; Daugherty, B.J.; Rheingans, B.E.; Bull, M.A.; Seidel, F.C.; Chipman, R.A.; Cairns, B.; Wasilewski, A.P.; Knobelspiesse, K.D. Calibration and validation of airborne multiangle spectropolarimetric imager (AirMSPI) polarization measurements. Appl. Opt. 2018, 57, 4499–4513. [Google Scholar] [CrossRef] [PubMed]
- Qie, L.; Li, Z.; Zhu, S.; Xu, H.; Xie, Y.; Qiao, R.; Hong, J.; Tu, B. In-flight radiometric and polarimetric calibration of the Directional Polarimetric Camera onboard the GaoFen-5 satellite over the ocean. Appl. Opt. 2021, 60, 7186–7199. [Google Scholar] [CrossRef] [PubMed]
- Heath, D.; Krueger, A.J.; Roeder, H.; Henderson, B. The solar backscatter ultraviolet and total ozone mapping spectrometer (SBUV/TOMS) for Nimbus G. Opt. Eng. 1975, 14, 323–331. [Google Scholar] [CrossRef]
- Weiss, H.; Cebula, R.P.; Laamann, K.; Hudson, R.D. Evaluation of the NOAA-11 solar backscatter ultraviolet radiometer, Mod 2 (SBUV/2): Inflight calibration. In Proceedings of the Calibration of Passive Remote Observing Optical and Microwave Instrumentation, Orlando, FL, USA, 3–5 April 1991; Volume 1493, pp. 80–90. [Google Scholar]
- Dittman, M.G.; Leitch, J.W.; Chrisp, M.; Rodriguez, J.V.; Sparks, A.L.; McComas, B.K.; Zaun, N.H.; Frazier, D.; Dixon, T.; Philbrick, R.H.; et al. Limb broadband imaging spectrometer for the NPOESS Ozone Mapping and Profiler Suite (OMPS). In Proceedings of the Earth Observing Systems VII, Seattle, WA, USA, 7–10 July 2002; Volume 4814, pp. 120–130. [Google Scholar]
- De Vries, J.; Voors, R.; Dirksen, R.; Dobber, M. In-orbit performance of the Ozone Monitoring Instrument. In Proceedings of the Sensors, Systems, and Next-Generation Satellites IX, Bruges, Belgium, 19–22 September 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5978, pp. 234–245. [Google Scholar]
- Mariani, A.; Corpaccioli, E.; Fibbi, M.; Veratti, R.; Hahne, A.R.; Callies, J.; Lefebvre, A. Spectrometer for ozone monitoring from space. In Proceedings of the Space Optics 1994: Earth Observation and Astronomy, Garmisch, Germany, 17–22 April 1994; SPIE: Bellingham, WA, USA, 1994; Volume 2209, pp. 57–67. [Google Scholar]
- Krijger, J.; Stammes, P. Current status of SCIAMACHY polarisation measurements. In ESA Special Publication; ESA: Noordwijk, The Netherlands, 2003; Volume 531. [Google Scholar]
- Liebing, P.; Krijger, M.; Snel, R.; Bramstedt, K.; Noël, S.; Bovensmann, H.; Burrows, J.P. In-flight calibration of SCIAMACHY’s polarization sensitivity. Atmos. Meas. Tech. 2018, 11, 265–289. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Ghatak, A.K. Polarization of Light with Applications in Optical Fibers; SPIE Press: Bellingham, WA, USA, 2011; Volume 246. [Google Scholar]
- Liu, M.; Xu, N.; Wang, B.; Qian, W.; Xuan, B.; Cao, J. Polarization independent and broadband achromatic metalens in ultraviolet spectrum. Opt. Commun. 2021, 497, 127182. [Google Scholar] [CrossRef]
- Chipman, R.A.; Lam, W.S.T.; Young, G. Polarized Light and Optical Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Zhou, G.; Li, Y.; Liu, K. Efficient calibration method of total polarimetric errors in a channeled spectropolarimeter. Appl. Opt. 2021, 60, 3623–3628. [Google Scholar] [CrossRef]
- Zhou, G.; Li, Y.; Liu, K. Reconstruction and calibration methods for a Mueller channeled spectropolarimeter. Opt. Express 2022, 30, 2018–2032. [Google Scholar] [CrossRef]
- Song, C.; Zhao, Y. Development Status and Direction of Spaceborne Lidar and Radar for Cloud and Aerosol Remote Sensing. J. Telem. Command. 2017, 38, 10–16. [Google Scholar]
- Djelloul, D.; Abdanour, I.; Philippe, K.; Mohamed, Z.; Mustapha, M. Investigation of Atmospheric Turbidity at Ghardaïa (Algeria) Using Both Ground Solar Irradiance Measurements and Space Data. Atmos. Clim. Sci. 2019, 9, 114. [Google Scholar]
- Cui, C.; Lin, X.; Liu, H.; Li, L.; Zhang, C. Measurement and analysis of polarization quantitative error for grating spectrometer. In Proceedings of the 8th Symposium on Novel Photoelectronic Detection Technology and Applications, Kunming, China, 9–11 November 2021; SPIE: Bellingham, WA, USA, 2022; Volume 12169, pp. 2671–2679. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics; Press Syndicated: Cambridge, UK, 1999. [Google Scholar]
- Zhao, M.; Jiang, Y.; Yang, S.; Li, W. Geometric Aberration Theory of Offner Imaging Spectrometers. Sensors 2019, 19, 4046. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Liu, C.; Liu, S.; Fan, X. Optical Design of Imaging Spectrometer Based on Linear Variable Filter for Nighttime Light Remote Sensing. Sensors 2021, 21, 4313. [Google Scholar] [CrossRef] [PubMed]
- Xing, W.; Ju, X.; Bo, J.; Yan, C.; Yang, B.; Xu, S.; Zhang, J. Polarization Radiometric Calibration in Laboratory for a Channeled Spectropolarimeter. Appl. Sci. 2020, 10, 8295. [Google Scholar] [CrossRef]
- Ghatak, A. Optics; Tata McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Liao, Y. Polarization Optics; Science Press: Beijing, China, 2003; Volume 52. [Google Scholar]
- Yan, J.; Wei, G. Matrix Optics; Ordnance Industry Press: Beijing, China, 1995. [Google Scholar]
- Schutgens, N.; Stammes, P. Parameterization of Earth’s polarization spectrum in the ultra-violet. J. Quant. Spectrosc. Radiat. Transfer 2002, 75, 239–255. [Google Scholar] [CrossRef]
- Welford, W.T. Aberrations of Optical Systems; Routledge: Oxfordshire, UK, 2017. [Google Scholar]
- Shi, L.; Yang, H.; Bai, B.; Liu, W.; Yao, B.; Liu, Y.; Li, X. Transmission channel characteristics of relay dual-polarization MIMO system for hypersonic vehicles under plasma sheath. IEEE Trans. Plasma Sci. 2018, 46, 917–927. [Google Scholar] [CrossRef]
- Kobayashi, K.; West, E.; Noble, M. Polarization measurements in the Vacuum Ultraviolet. In Proceedings of the Polarization Science and Remote Sensing II, San Diego, CA, USA, 31 July–4 August 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5888, pp. 128–139. [Google Scholar]
- Tang, Q.; He, J.; Cao, Z.; Li, F.; Xiao, J.; Chen, L. Polarization-time-block-code in IM/DD PolMux-OFDM transmission system. Opt. Commun. 2014, 315, 295–302. [Google Scholar] [CrossRef]
- Khaliq, A.; Ashraf, S.; Gul, B.; Ahmad, I. Comparative study of 3 × 3 Mueller matrix transformation and polar decomposition. Opt. Commun. 2021, 485, 126756. [Google Scholar] [CrossRef]
- Thompson, B.J.; Goldstein, D.; Goldstein, D.H. Polarized Light, Revised and Expanded; Taylor & Francis: Abingdon, UK, 2003. [Google Scholar]
- Cheng, F.; Su, P.H.; Choi, J.; Gwo, S.; Li, X.; Shih, C.K. Epitaxial growth of atomically smooth aluminum on silicon and its intrinsic optical properties. ACS Nano 2016, 10, 9852–9860. [Google Scholar] [CrossRef]
- Fernández-Perea, M.; Larruquert, J.I.; Aznárez, J.A.; Pons, A.; Méndez, J.A. Vacuum ultraviolet coatings of Al protected with MgF 2 prepared both by ion-beam sputtering and by evaporation. Appl. Opt. 2007, 46, 4871–4878. [Google Scholar] [CrossRef] [PubMed]
- Zhupanov, V.; Vlasenko, O.; Sachkov, M.; Fedoseev, V. New facilities for Al+ MgF2 coating for 2-m class mirrors for UV. In Proceedings of the Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray, Montréal, QC, Canada, 22–27 June 2014; SPIE: Bellingham, WA, USA, 2014; Volume 9144, pp. 979–986. [Google Scholar]
- Shen, J.; Deng, D.; Kong, W.; Liu, S.; Shen, Z.; Wei, C.; He, H.; Shao, J.; Fan, Z. Extended bidirectional reflectance distribution function for polarized light scattering from subsurface defects under a smooth surface. J. Opt. Soc. Am. A 2006, 23, 2810–2816. [Google Scholar] [CrossRef]
- Rodríguez-de Marcos, L.V.; Larruquert, J.I.; Méndez, J.A.; Aznárez, J.A. Self-consistent optical constants of MgF 2, LaF 3, and CeF 3 films. Opt. Mater. Express 2017, 7, 989–1006. [Google Scholar] [CrossRef] [Green Version]
- Qing, K.; Yinlin, Y.; Jianwen, W.; Lei, D.; Jianjun, L.; Haoyu, W.; Jin, H.; Xiaobing, Z. System-level polarized calibration methods in laboratory of directional polarization camera. J. Atmos. Environ. Opt. 2019, 14, 36. [Google Scholar]
- Wu, P.; Min, C.; Zhang, C.; Dai, Y.; Song, W.; Zhang, Y.; Wang, X.; Yuan, X. Tight focusing induced non-uniform polarization change in reflection for arbitrarily polarized incident light. Opt. Commun. 2019, 443, 26–33. [Google Scholar] [CrossRef]
- Zama, T.; Saito, I. Evaluation of polarization dependence of a spectral radiance calibration system in UV and VUV regions. In Proceedings of the AIP Conference, Daegu, Korea, 28 May–2 June 2006; American Institute of Physics: College Park, MA, USA, 2007; Volume 879, pp. 714–717. [Google Scholar]





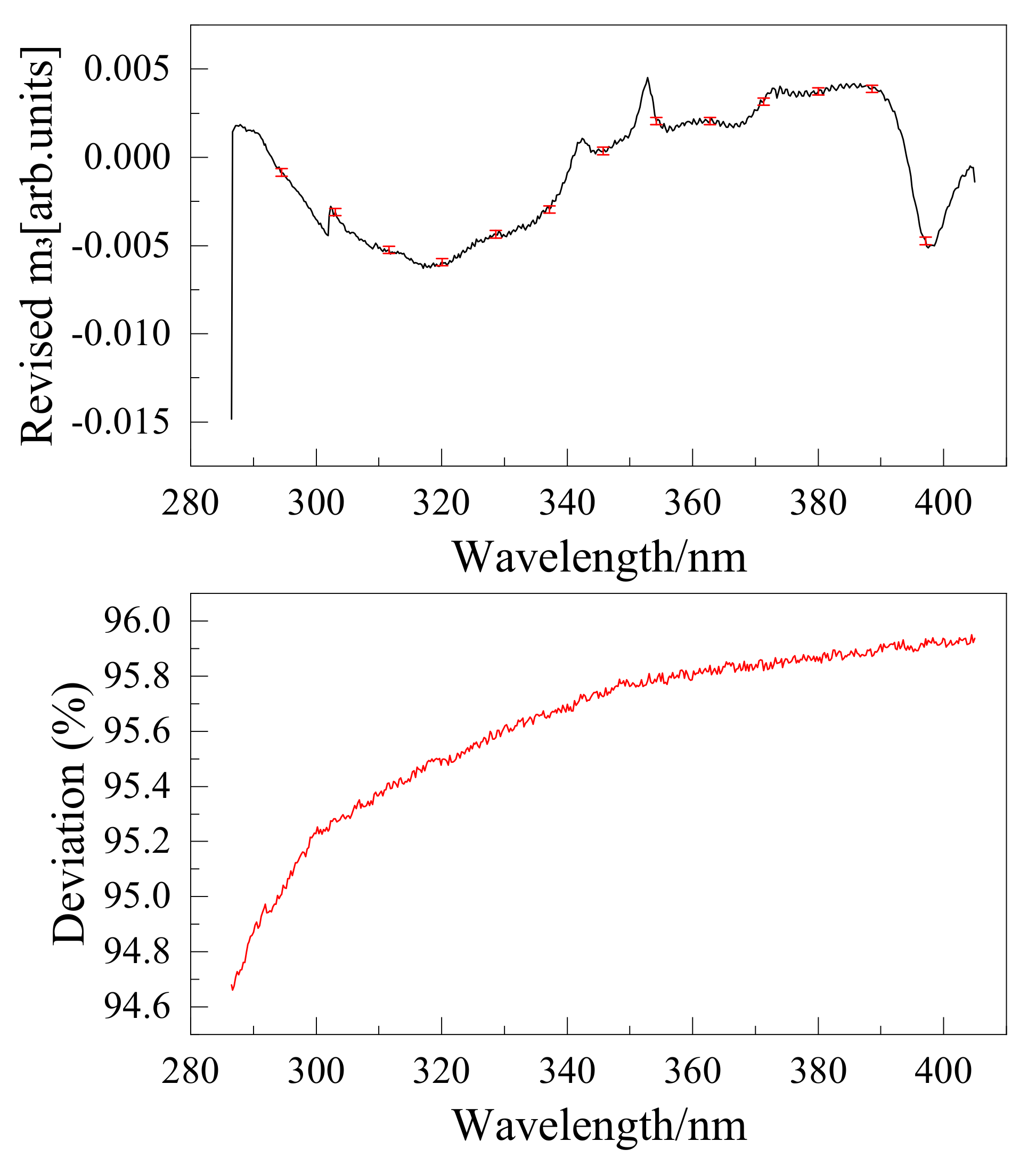
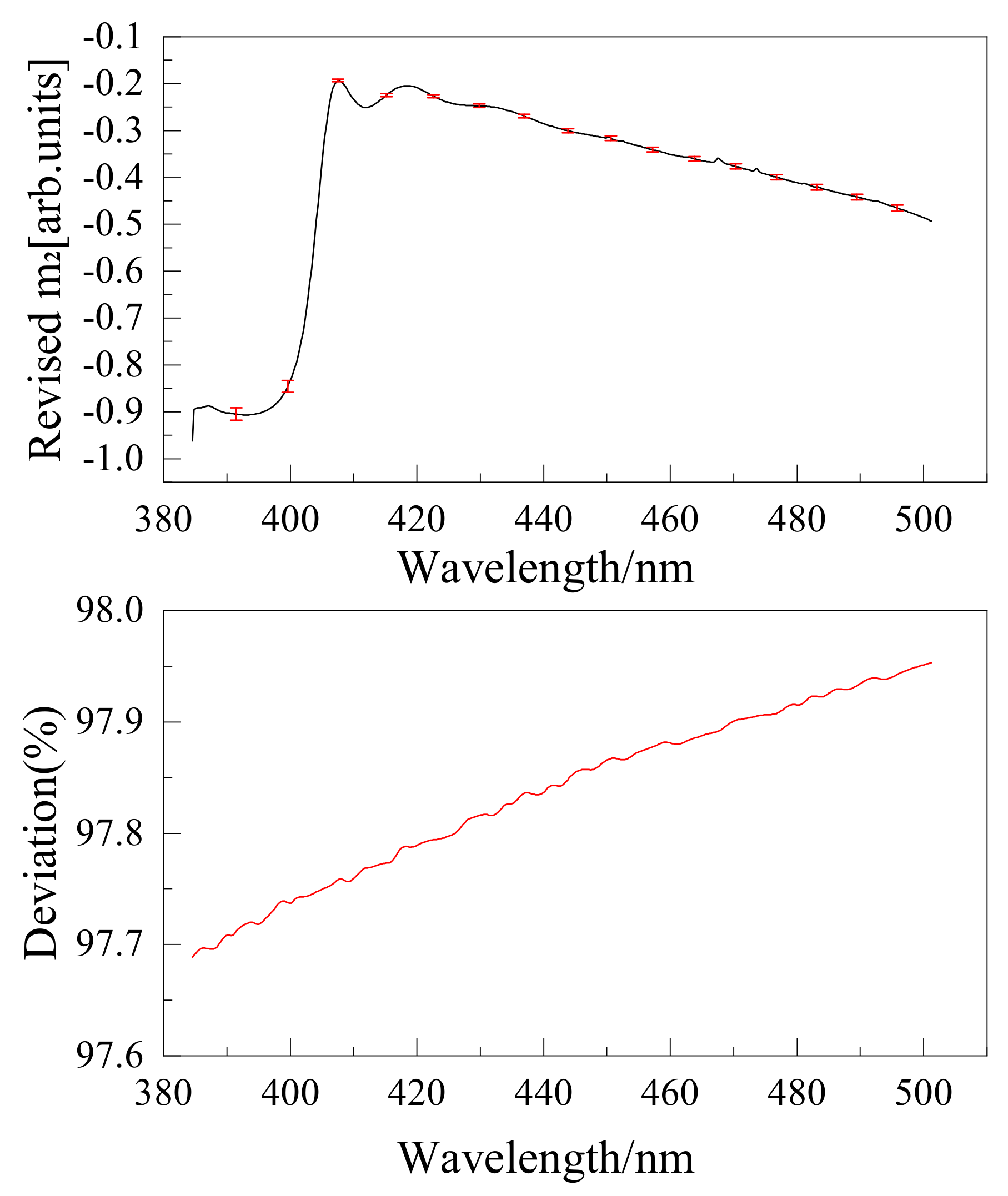
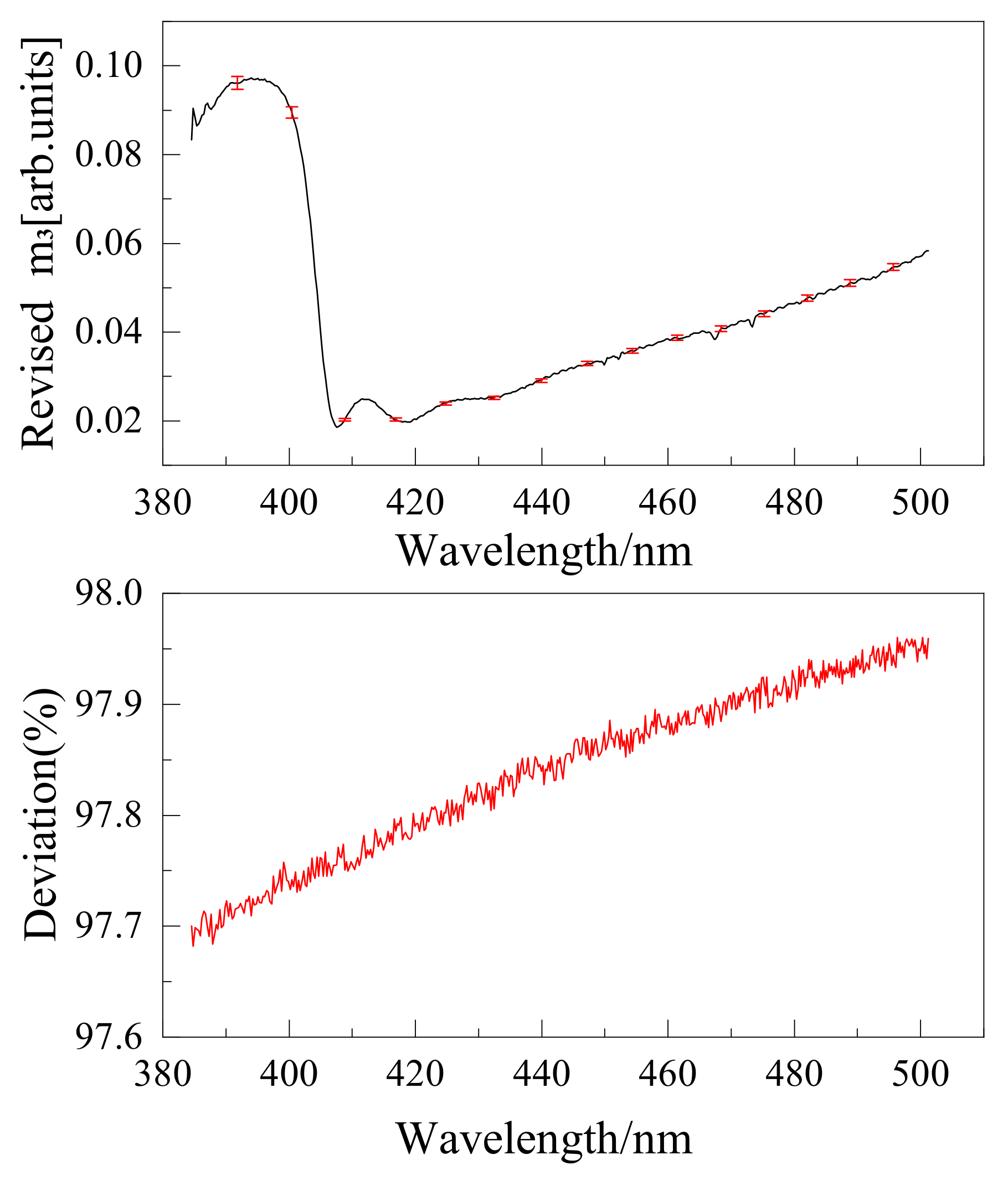
| Instruments | Wavelength (nm) | Resolution (nm) | Dispersion Elements | Detector Type | Polarization Correction Scheme |
|---|---|---|---|---|---|
| TOMS | 308.6–360 | 1.2 | Grating | PMT | Depolarizer |
| SBUV | 160–400 | 1.1 | Grating | PMT | Depolarizer |
| OMPS | 300–1000 | 1.8–40 | Prism | CCD | Polarization compensator |
| OMI | 252–740 | 0.4–0.6 | Grating | CCD | Depolarizer |
| GOME | 240–790 | 0.2–0.4 | Grating | Linear array | PMD |
| SCIAMACHY | 240–2400 | 0.2–0.5 | Grating | Linear array | PMD |
| Parameter Name | Indicator Requirements |
|---|---|
| Spectral range | 290–500 nm |
| Spectral resolution | <0.6 nm |
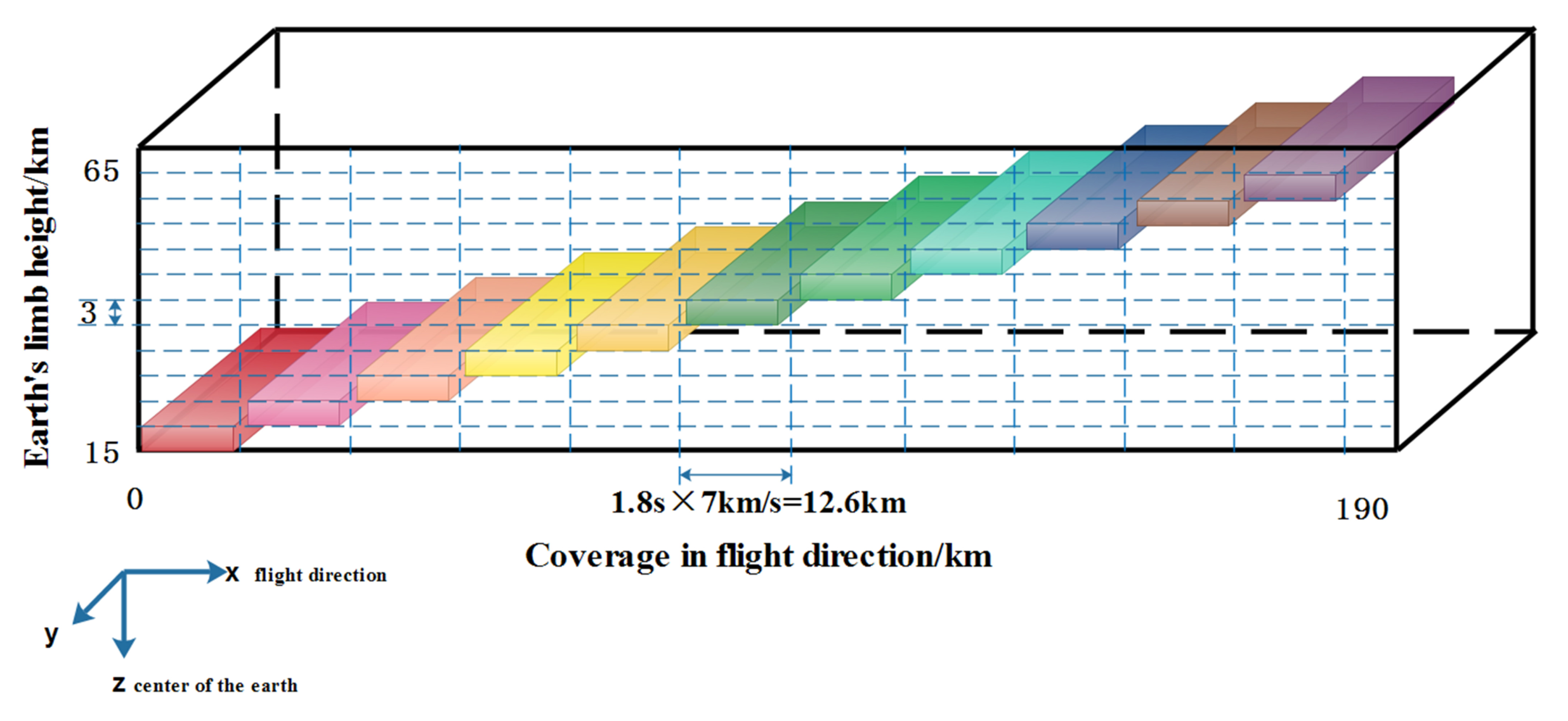
| Limb scan height | 15–60 km |
| Spatial resolution | 3 km (the height direction of the Earth’s limb) |
| Instantaneous field of view | 1.8° * 0.045° |
| Radiometric accuracy | 3% |
| Straylight |
| Sources of Uncertainty | Uncertainty before Calibration | Uncertainty after Calibration | |||
|---|---|---|---|---|---|
| Polarization test system | Stability of the polarized light source | 0.2% | 2.5% | 0.2% | 1.0% |
| Turntable corner accuracy | 0.1% | 0.1% | |||
| The uniformity of the output light intensity of the UV collimator | 2.0% | 0.8% | |||
| Residual error of the wire grid polarizer | 1.5% | 0.5% | |||
| UV hyperspectral | Measurement repeatability | 1.0% | 1.0% | 1.0% | 1.0% |
| Stray light | 0.2% | 0.2% | |||
| Overall uncertainty | 2.7% | 1.4% | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Li, Z.; Huang, Y.; Lin, G.; Zeng, J.; Li, H.; Wang, S.; Han, W. Analysis and Correction of Polarization Response Calibration Error of Limb Atmosphere Ultraviolet Hyperspectral Detector. Sensors 2022, 22, 8542. https://doi.org/10.3390/s22218542
Li H, Li Z, Huang Y, Lin G, Zeng J, Li H, Wang S, Han W. Analysis and Correction of Polarization Response Calibration Error of Limb Atmosphere Ultraviolet Hyperspectral Detector. Sensors. 2022; 22(21):8542. https://doi.org/10.3390/s22218542
Chicago/Turabian StyleLi, Haochen, Zhanfeng Li, Yu Huang, Guanyu Lin, Jiexiong Zeng, Hanshuang Li, Shurong Wang, and Wenyao Han. 2022. "Analysis and Correction of Polarization Response Calibration Error of Limb Atmosphere Ultraviolet Hyperspectral Detector" Sensors 22, no. 21: 8542. https://doi.org/10.3390/s22218542
APA StyleLi, H., Li, Z., Huang, Y., Lin, G., Zeng, J., Li, H., Wang, S., & Han, W. (2022). Analysis and Correction of Polarization Response Calibration Error of Limb Atmosphere Ultraviolet Hyperspectral Detector. Sensors, 22(21), 8542. https://doi.org/10.3390/s22218542






