Quantitative Investigation of Acoustic Emission Waveform Parameters from Crack Opening in a Rail Section Using Clustering Algorithms and Advanced Signal Processing
Abstract
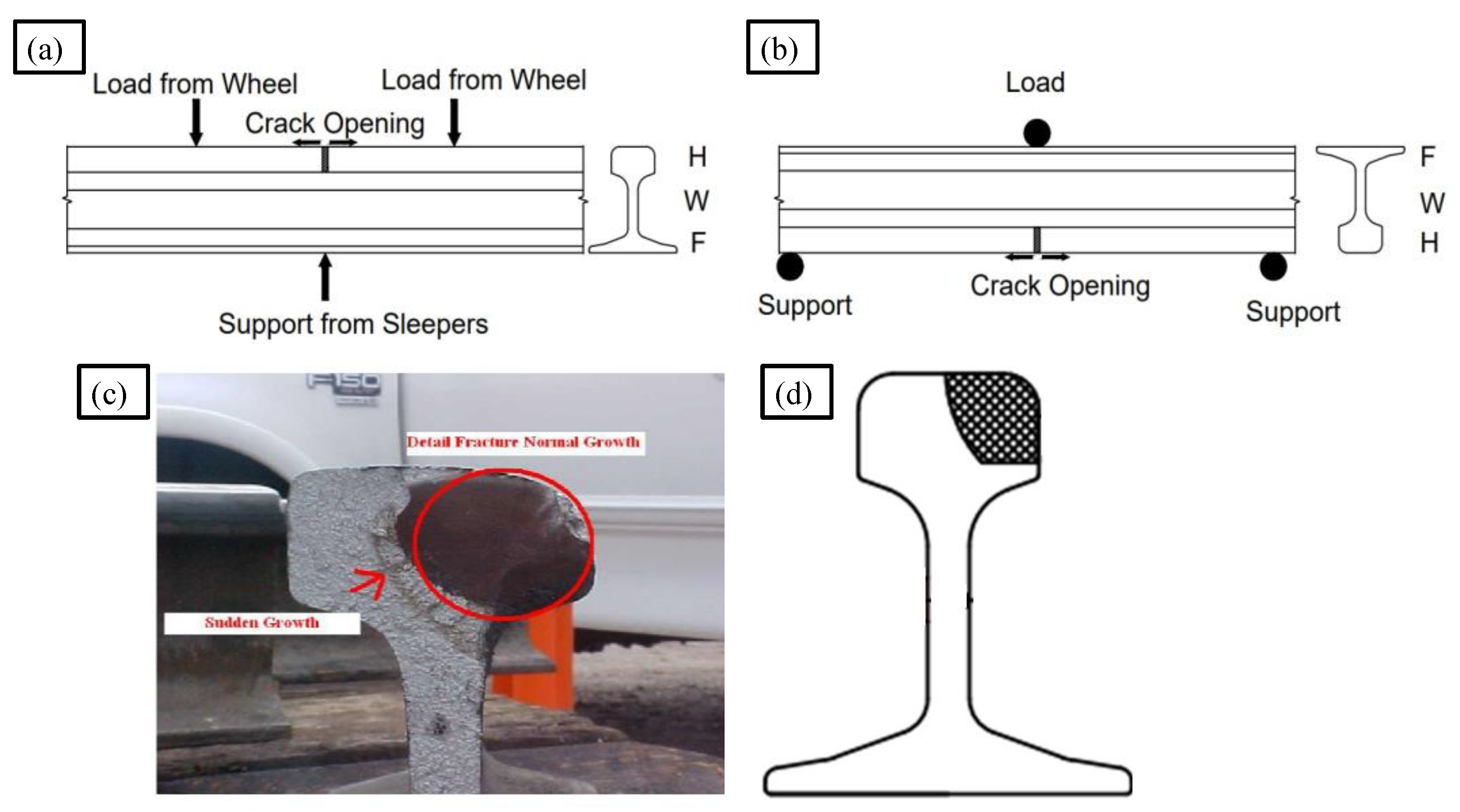
:1. Introduction
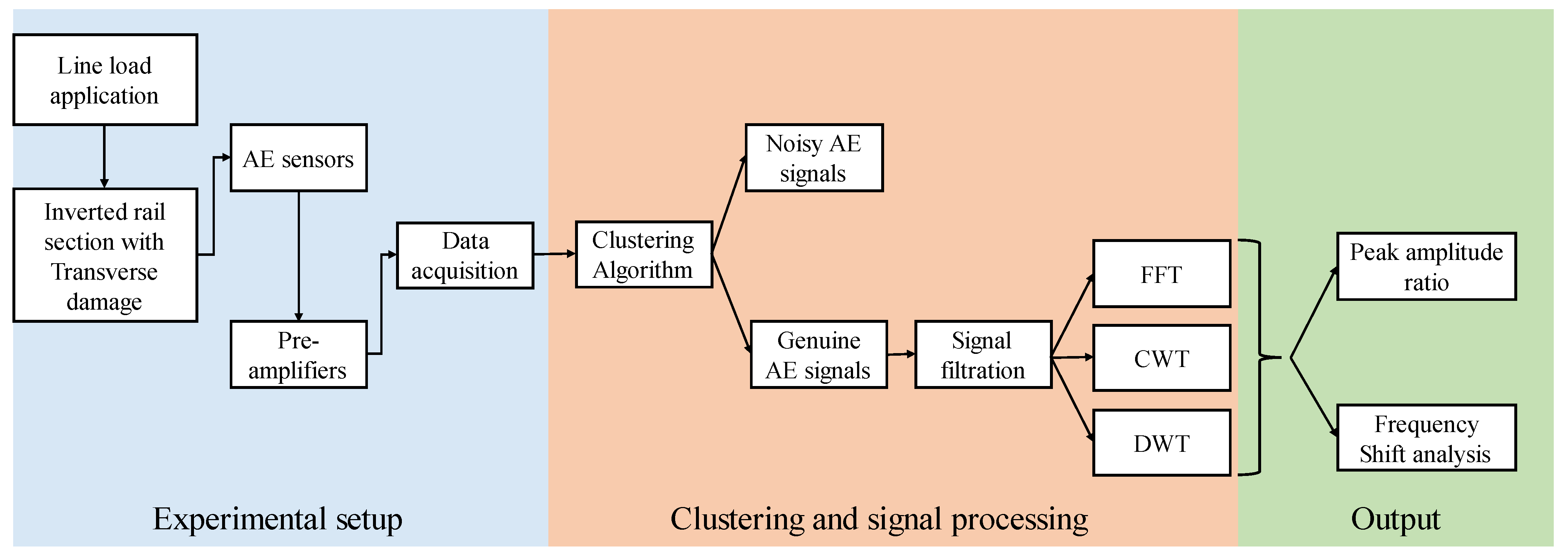
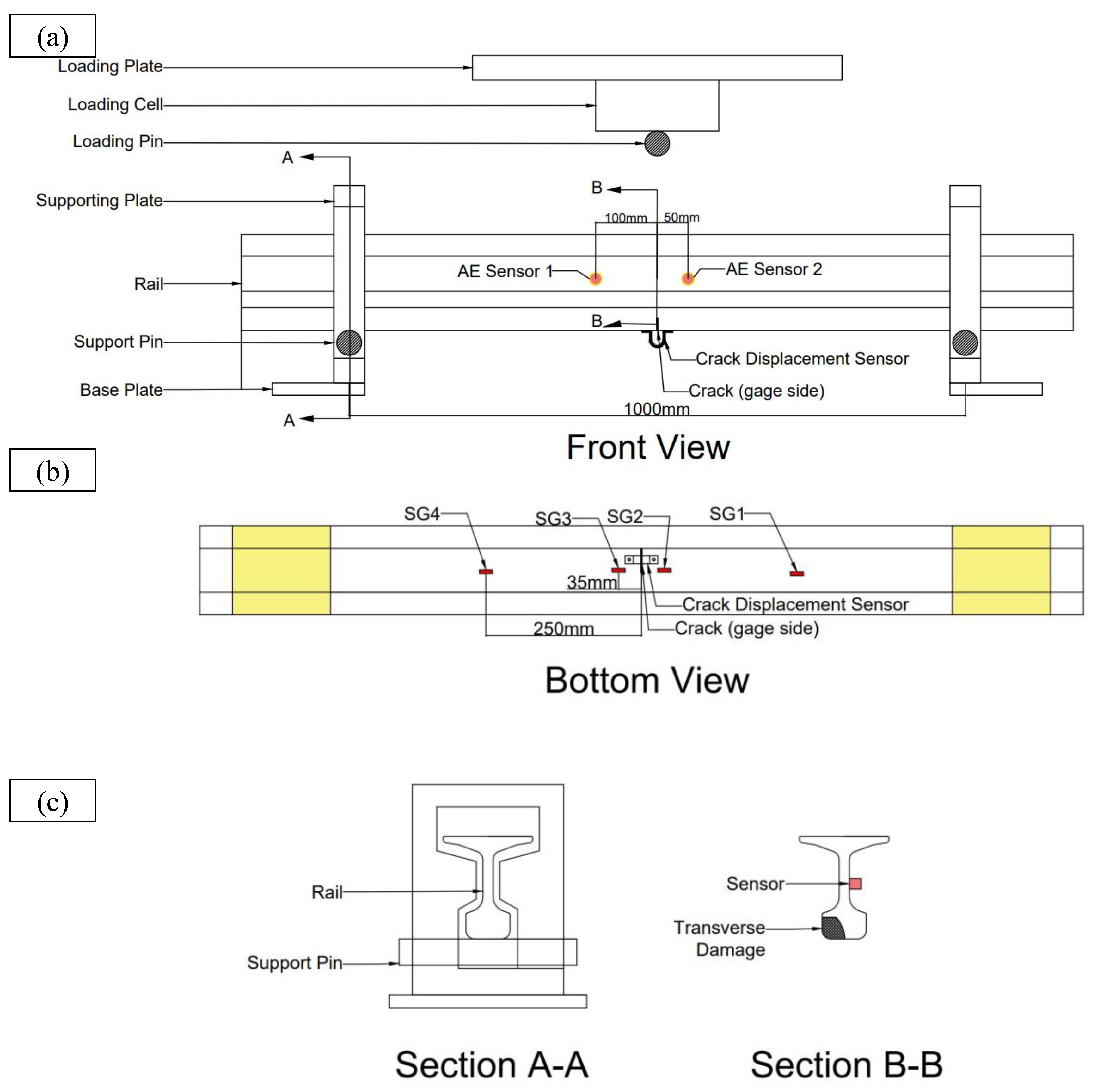
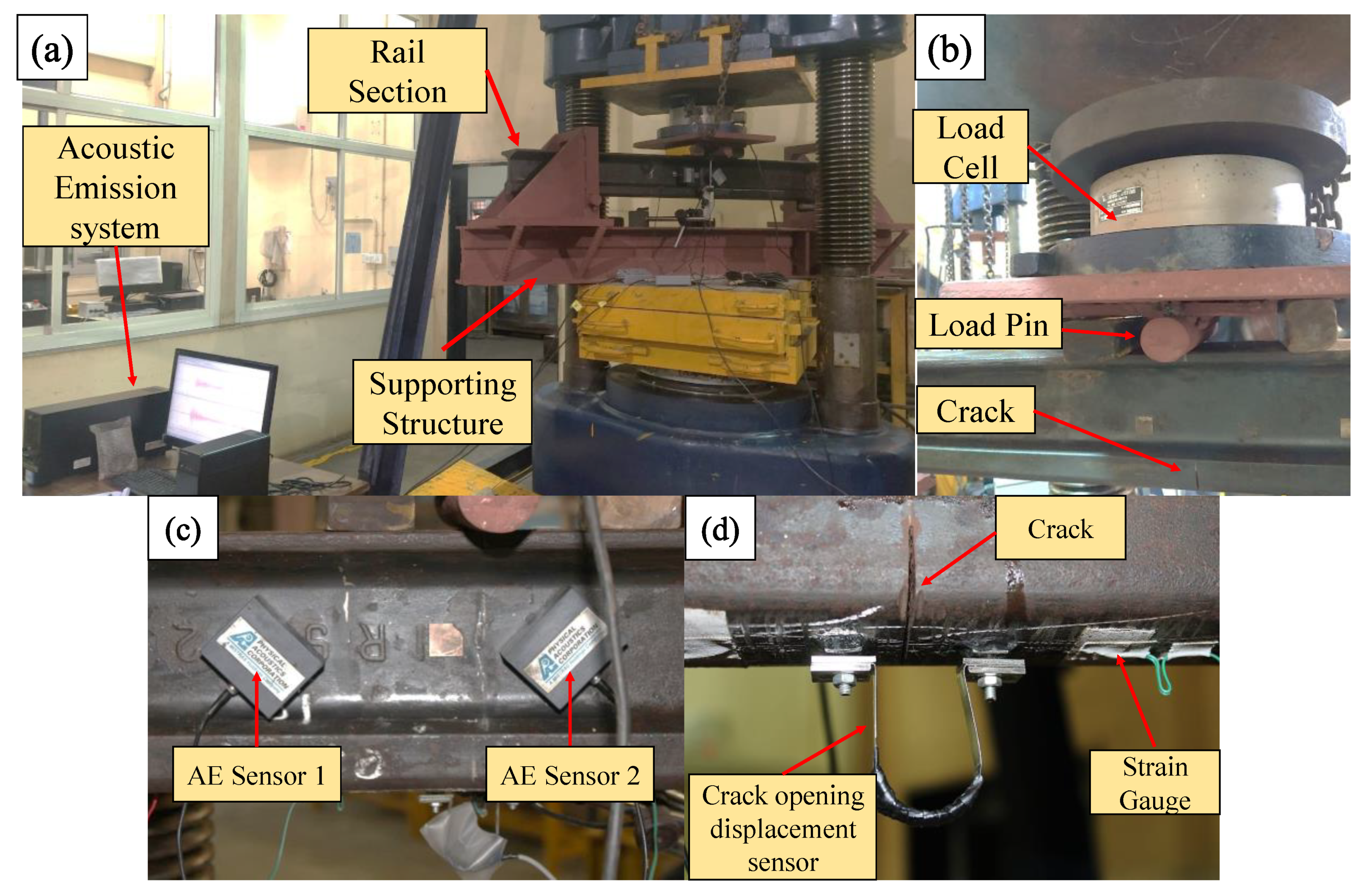
2. Experimental Setup
3. Clustering Algorithm and Signal Processing
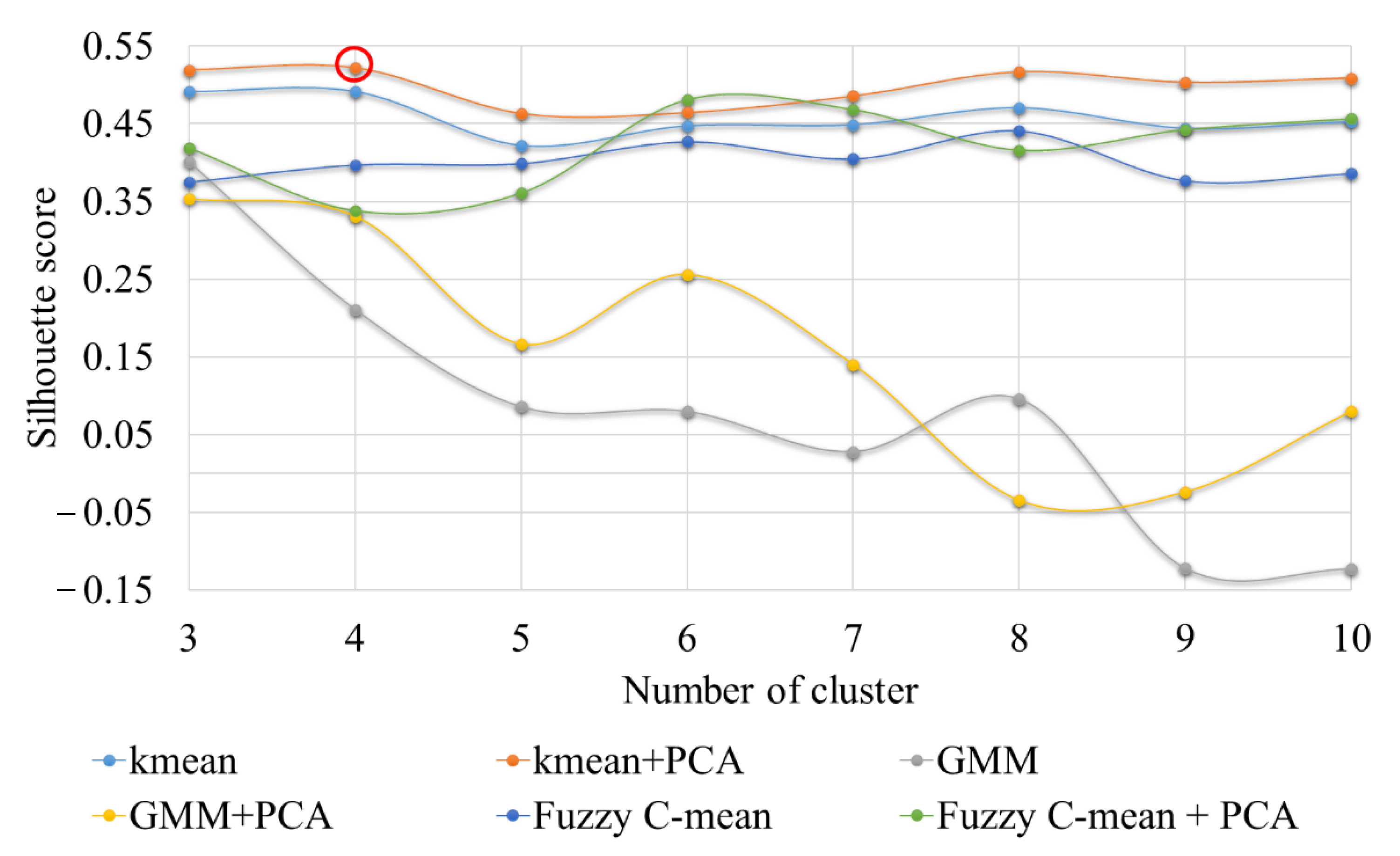
3.1. Clustering Algorithm
| Algorithm 1: K-mean clustering | ||
| Input | X = {x1, x2, …………………, n1} // set of n data items K // number of desired clusters | |
| Output | A set of K clusters | |
| Steps | 1. | Initialize cluster centroids µ1, µ2, ……… µk randomly |
| 2. | Repeat until convergence: {For every i, set For every k, set } | |
| Algorithm 2: Fuzzy C-mean clustering | ||
| Input | X = {x1, x2, …………………, xn} // set of n data items c = number of desired clusters vj = Centre of Cluster m = degree of fuzziness T = Maximum number of iterations uij = Membership degree of the ith datum in the jth cluster i = 1,2,…..,n j = 1,2,……,c U = Fuzzy c-classified matrix of finite set V = Collection of X cluster centres | |
| Output | A set of K clusters | |
| Steps | 1. | Initialization of the c m, T and random initialisation of uij |
| 2. | Determine cluster centre vj | |
| 3. | Determine the change in the membership function matrix where, | |
| 4. | Calculate J(U,V) Membership and cluster centers are updated after each iteration by repeating steps 2 and 3 until the minimum ‘J’ value is achieved or . where β is the termination criterion between [0,1] J is the objective function | |
| Algorithm 3: Gaussian mixture modelling EM algorithm | ||
| Input | X= [x1, x2, …………………, xn] K= number of cluster | |
| Output | p(zk =1|xn), values of for which objective log likelihood is minimum | |
| Steps | 1. | Initialisation with and evaluate log likelihood |
| 2. | E-step | |
| 3. | M-step where, | |
| 4. | Calculate log likelihood with new set of data | |
| 5. | Repeat step 2 to 4 until converged | |
3.2. Signal Processing
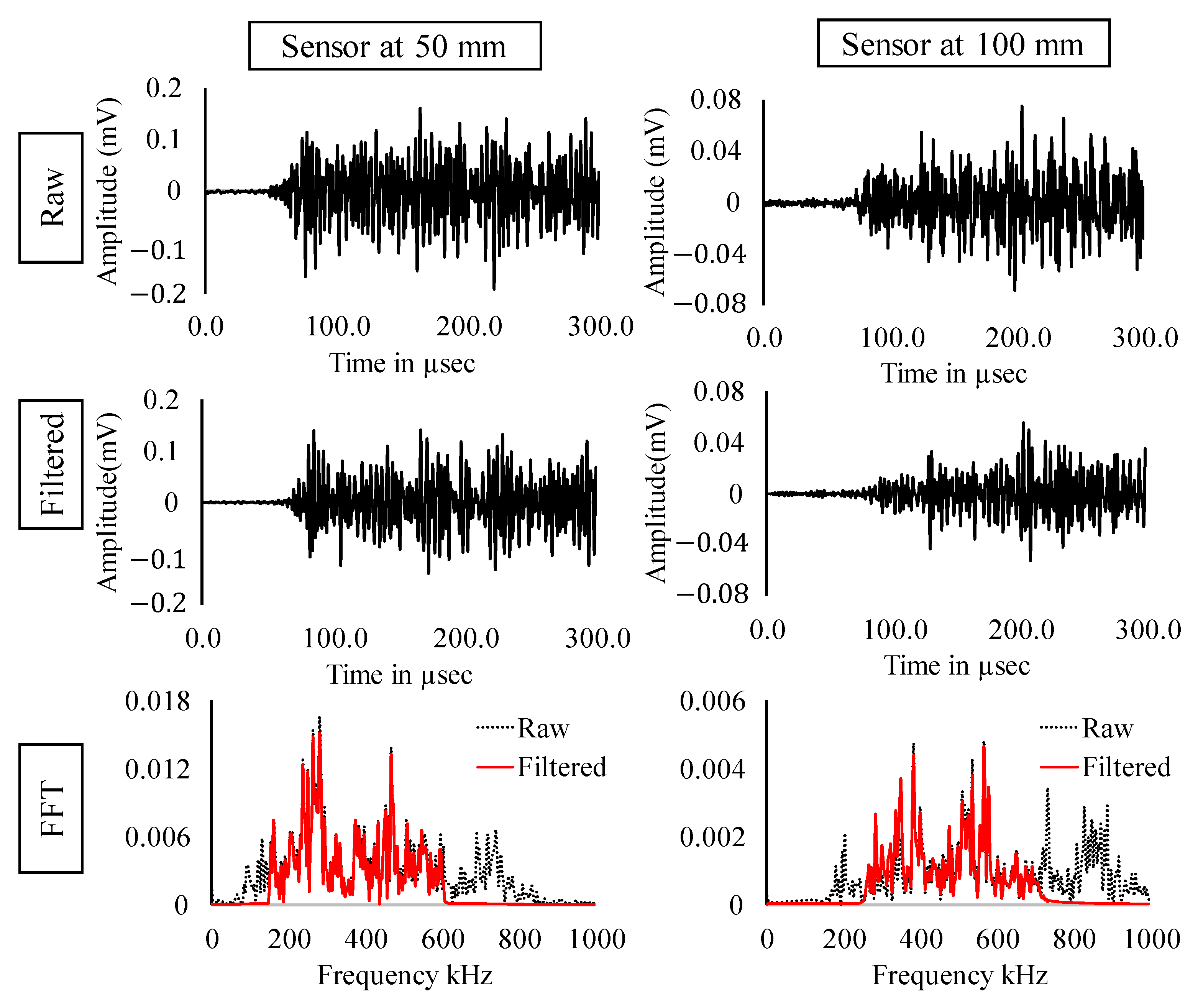
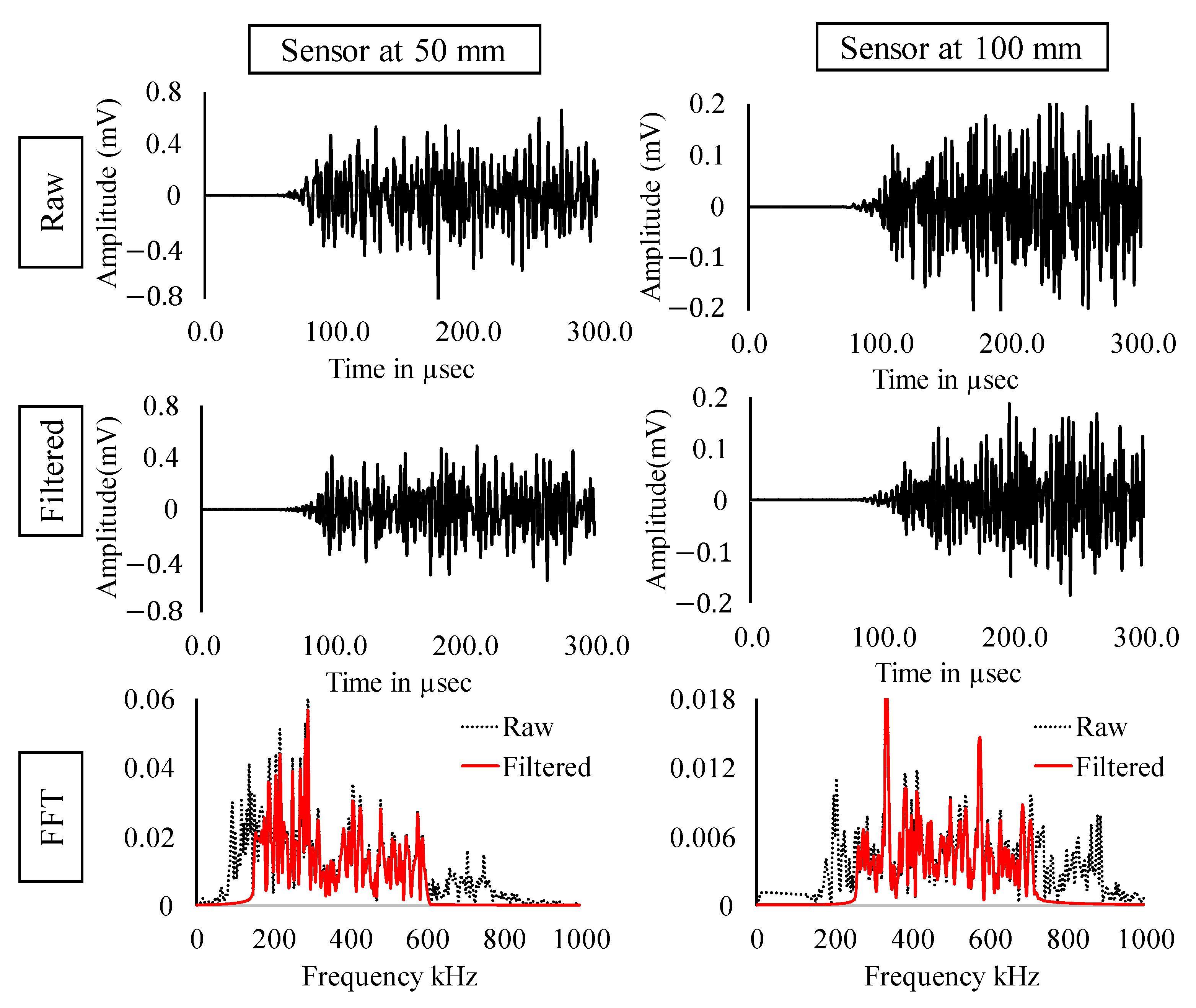
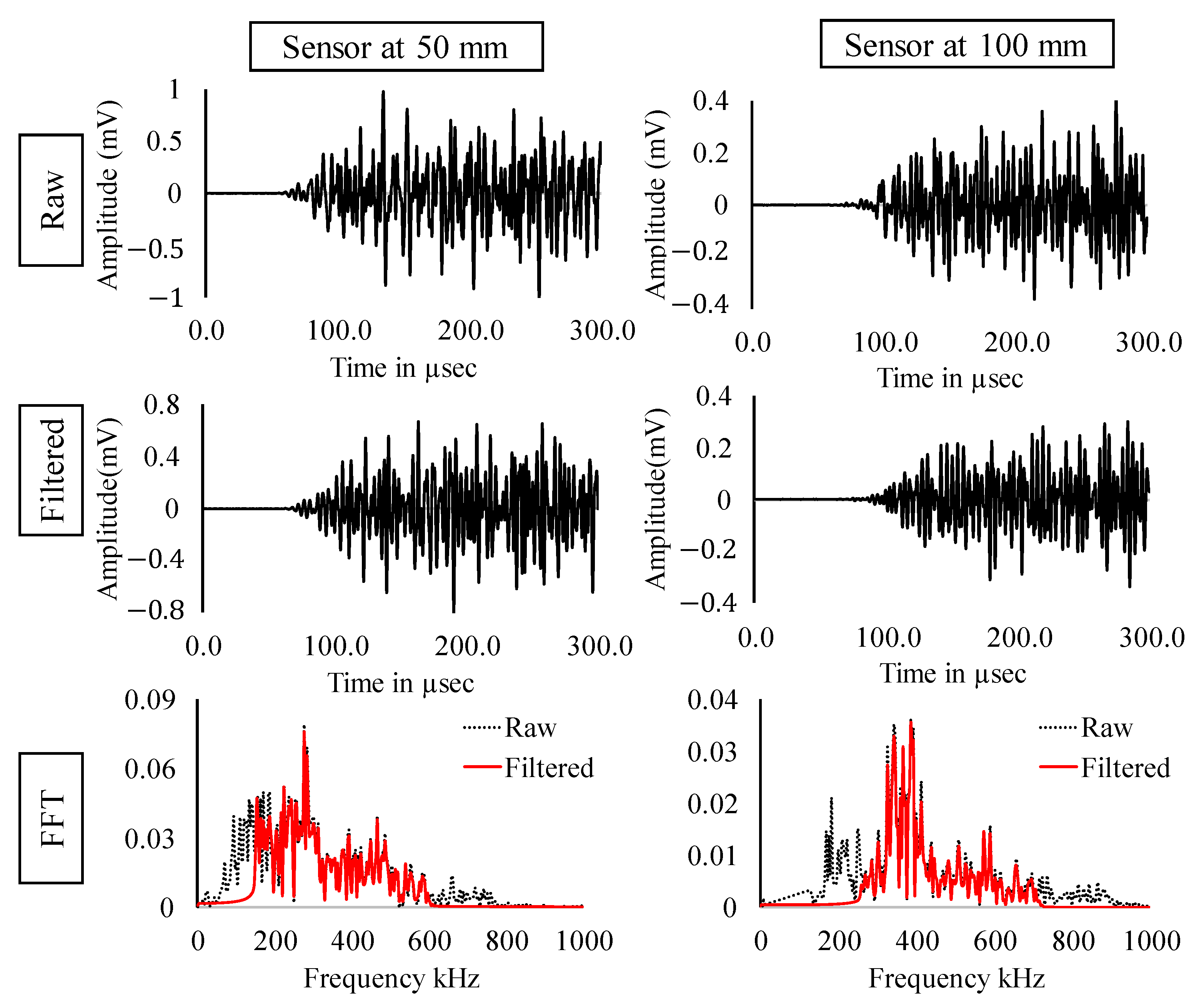
3.2.1. Signal Filtering
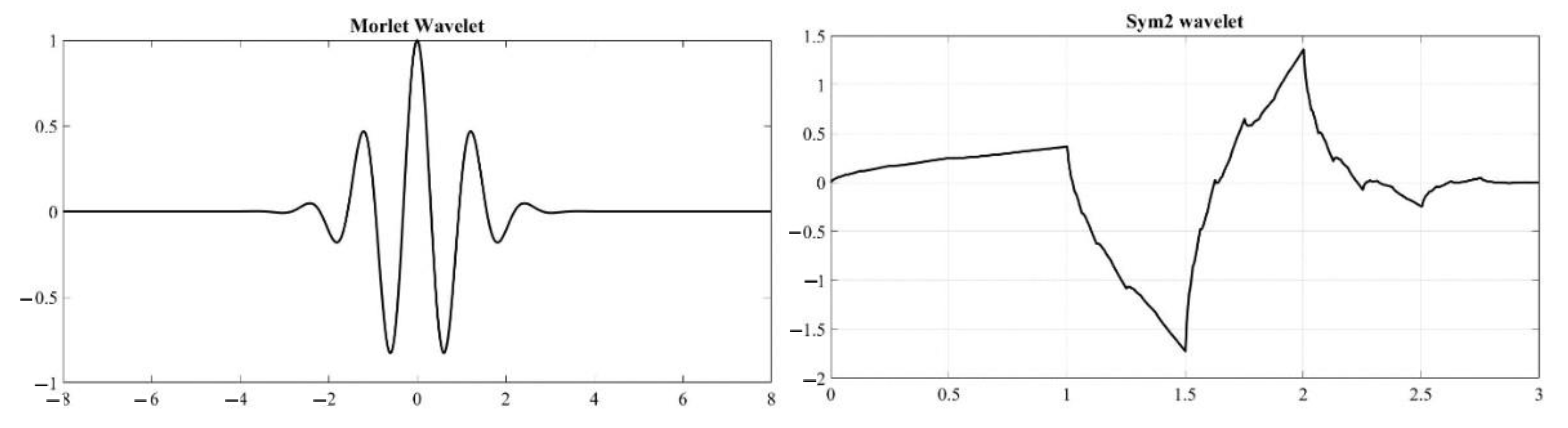
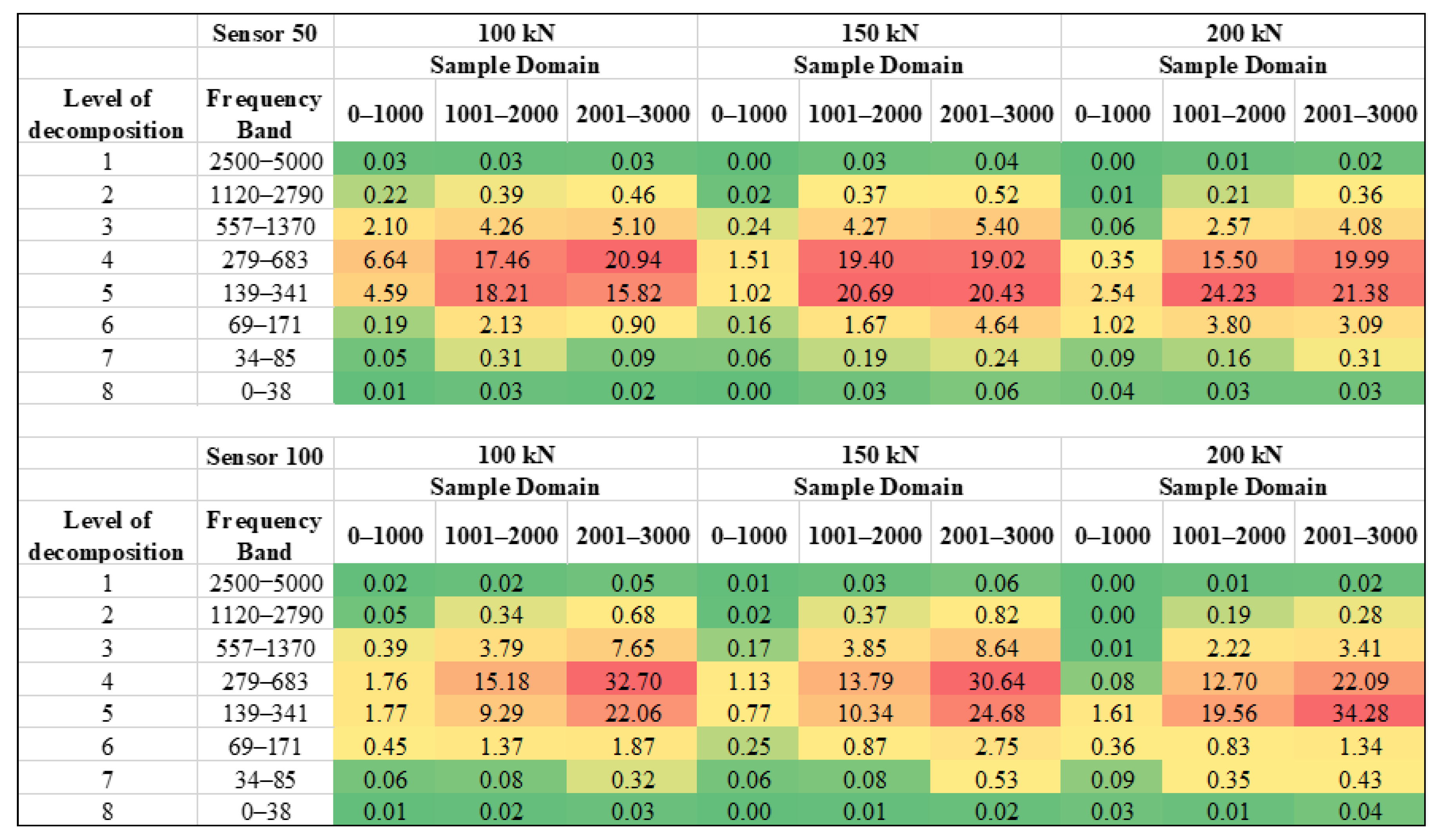
3.2.2. Wavelet Transform
4. Results
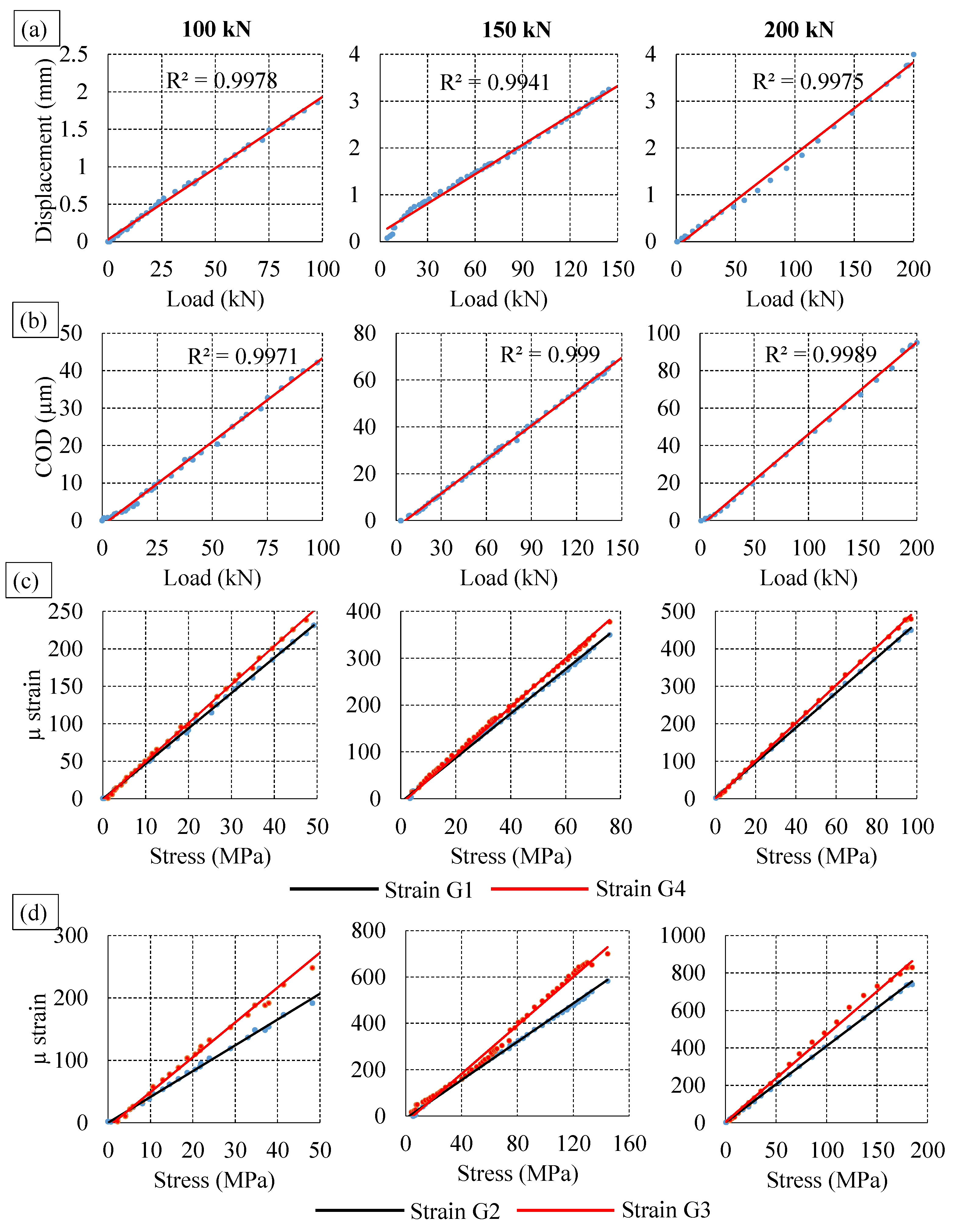
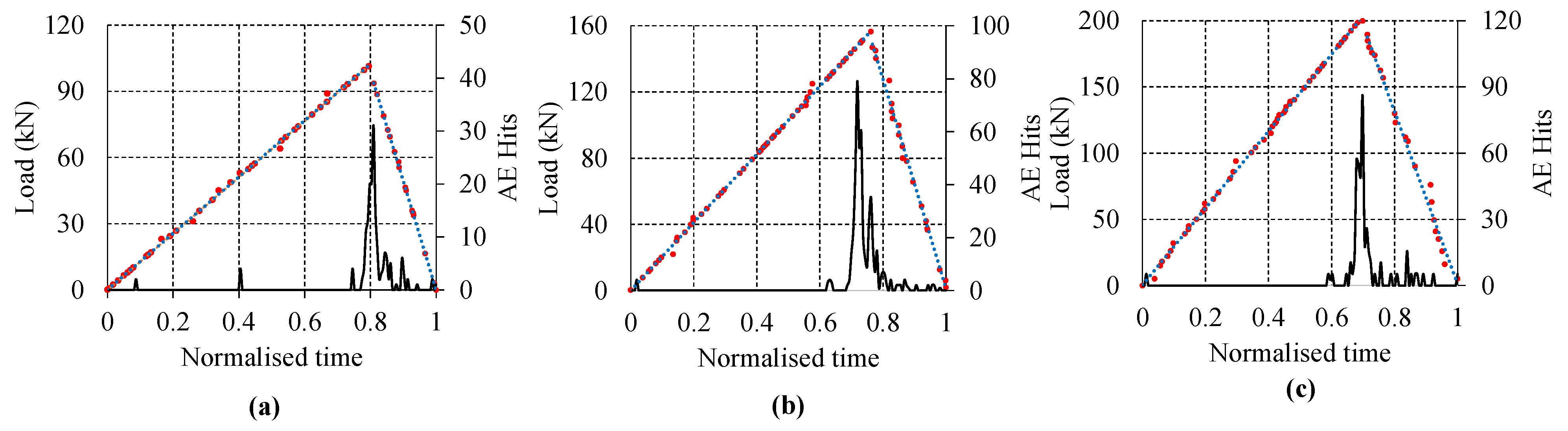
4.1. Experimental Results of the Bending Test of Rail
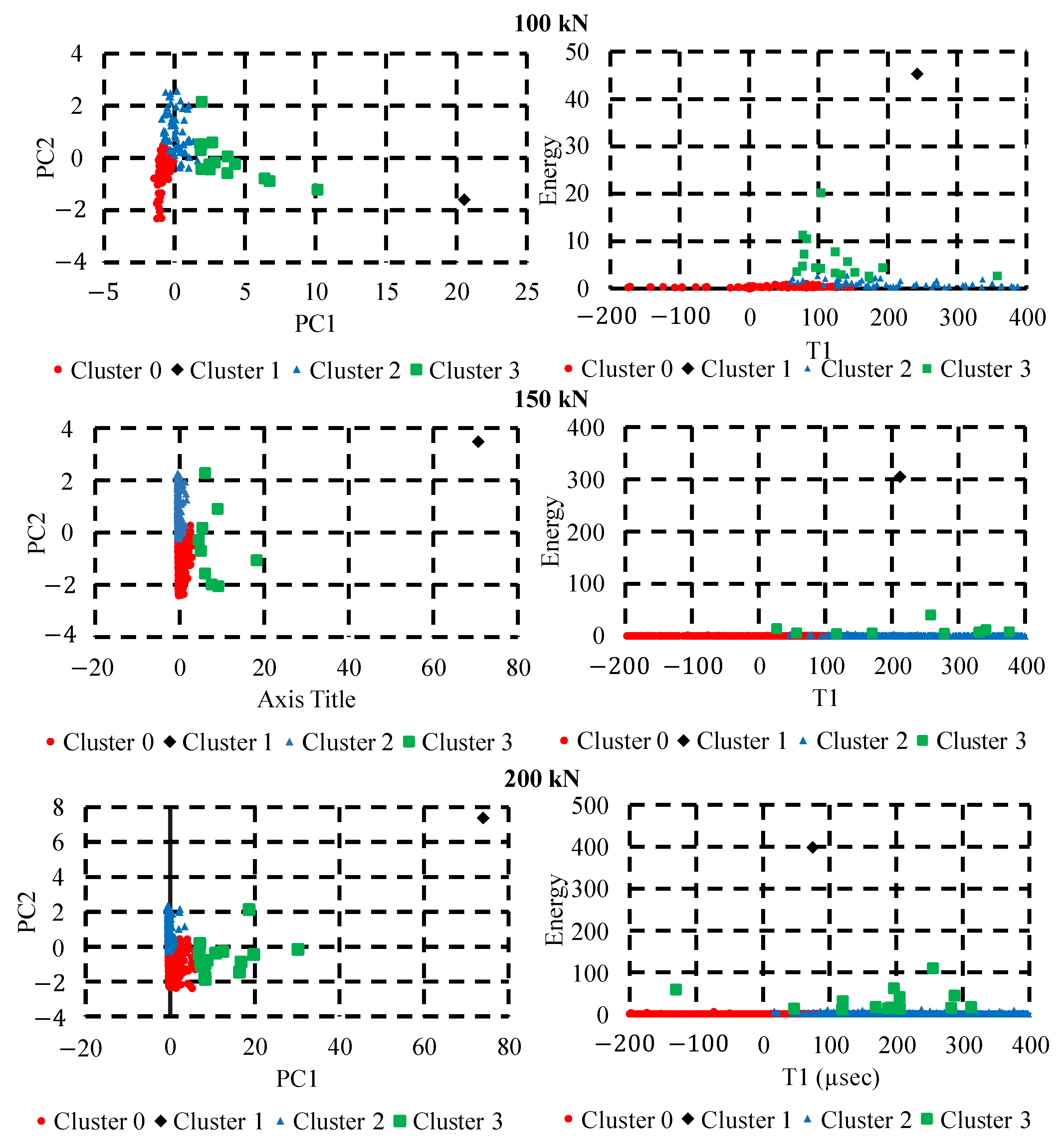
4.2. Clustering of AE Signals Generated during the Experiment
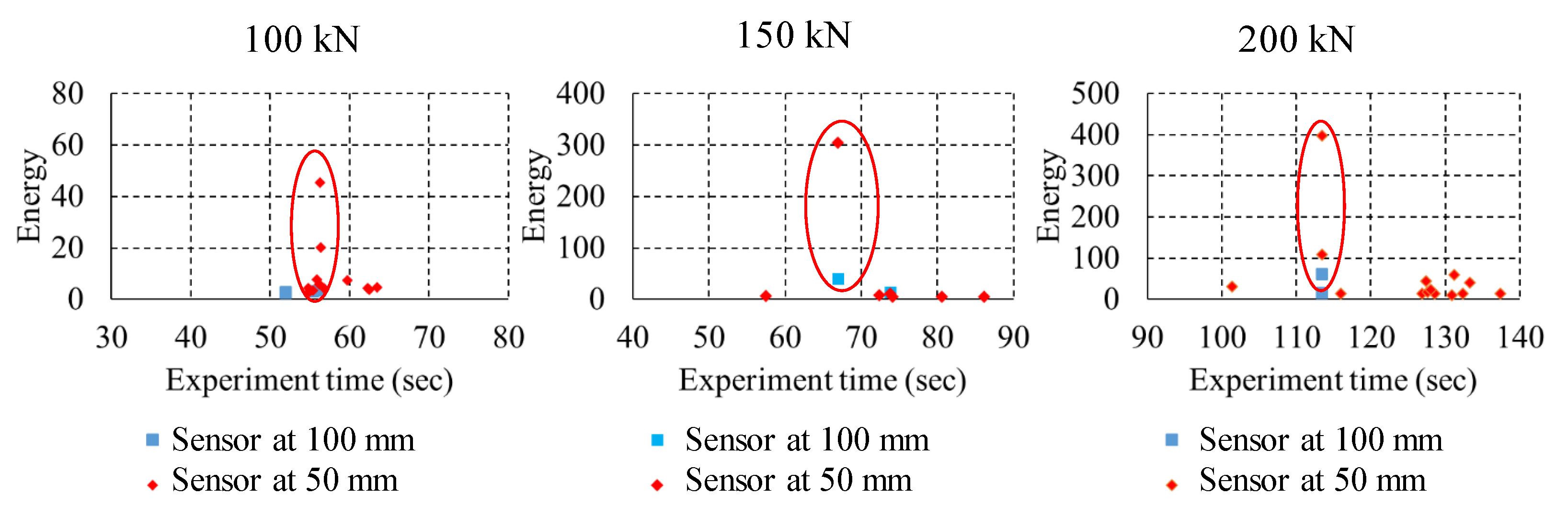
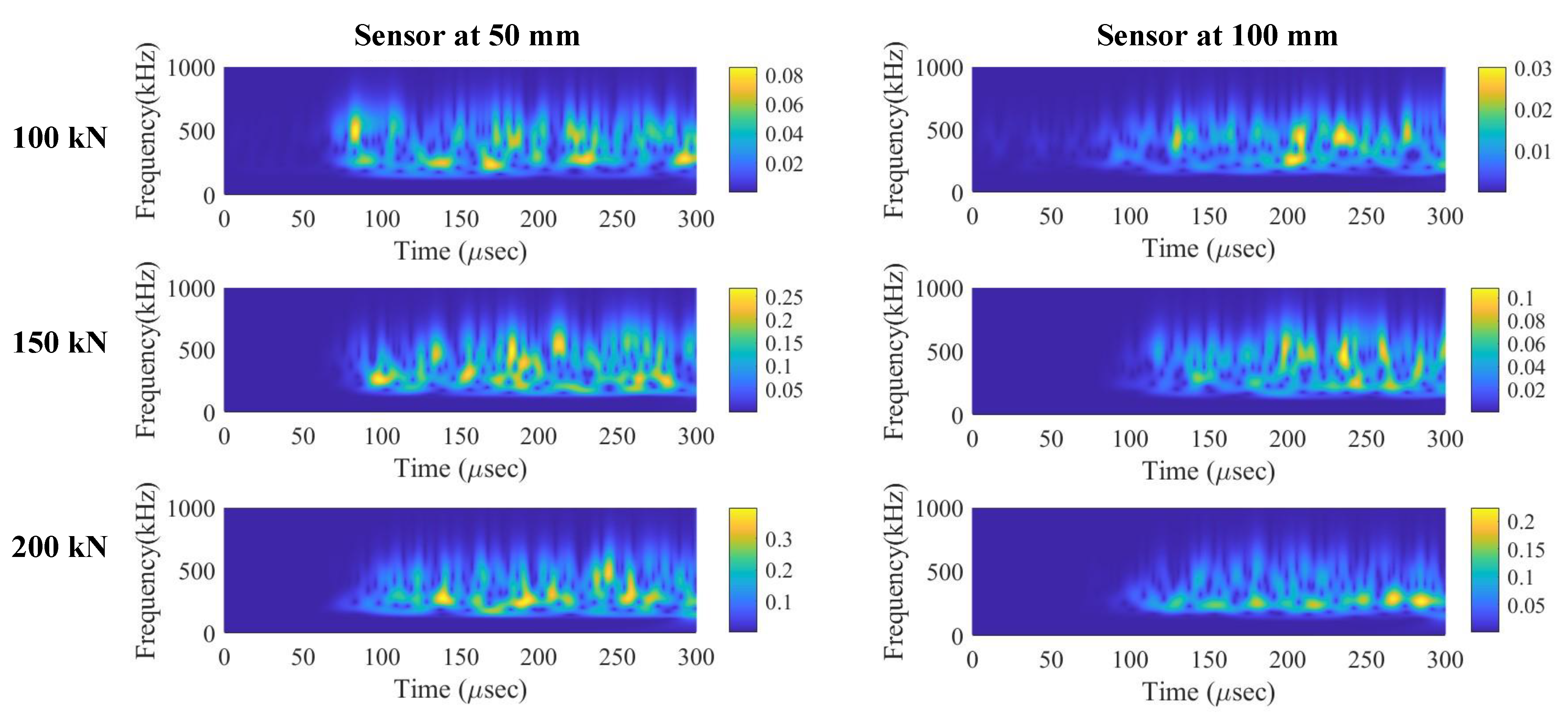
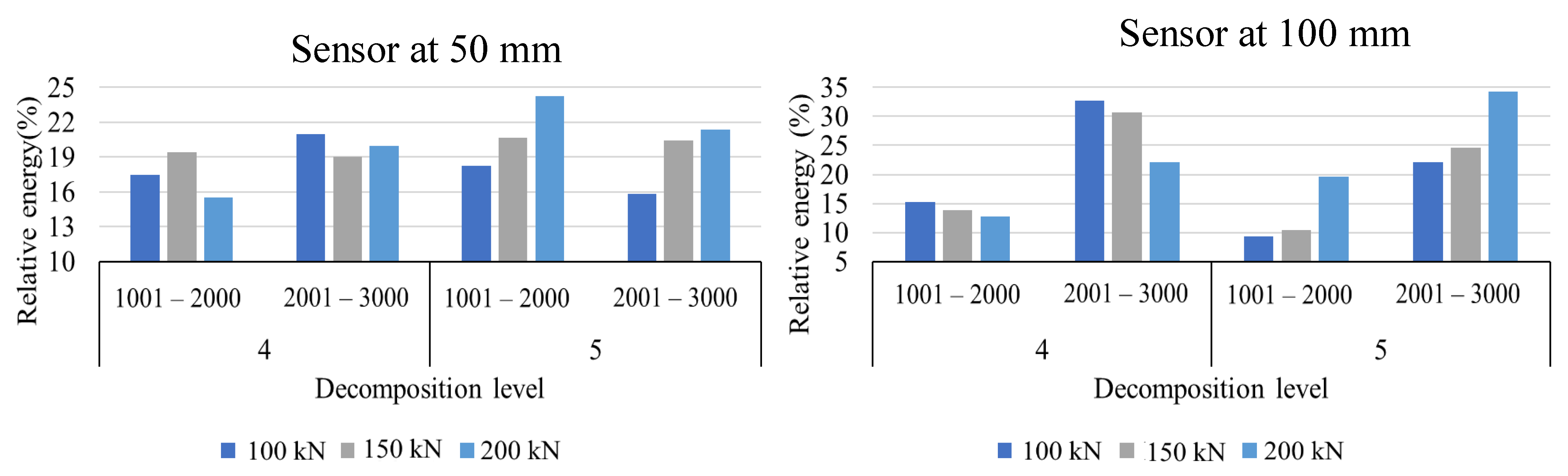
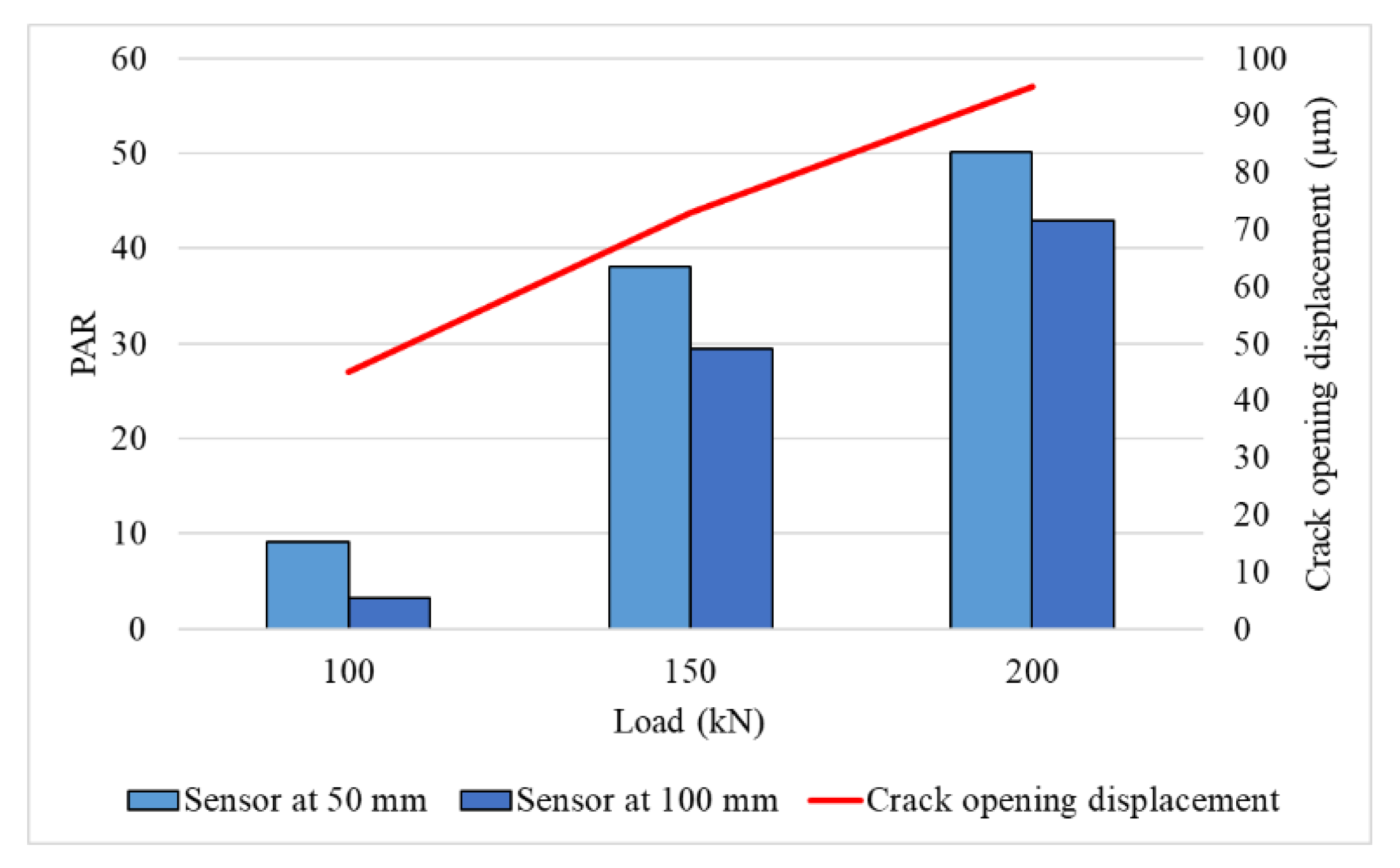
4.3. Analysis of Peak Energy Acoustic Signals
5. Conclusions
- Using a wave-based feature in the clustering method, four distinct clusters were produced from which low-energy clusters could be removed. This method accelerates the separation of required AE signals and results in a reduction of manual labour required.
- From analysis of the AE signal, it was discovered that the signals created by the fracture had a specific frequency content ranging between 140 kHz and 400 kHz.
- The discrete wavelet transforms of AE signals indicated an energy shift in each frequency band and sample region. With increasing load, a considerable shift in the energy distribution in the frequency bands 139–341 kHz and 279–683 kHz was detected.
- Additionally, the peak amplitude ratio was observed to be linearly related to the loads and crack opening displacement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bruzelius, K.; Mba, D. An Initial Investigation on the Potential Applicability of Acoustic Emission to Rail Track Fault Detection. Ndt E Int. 2004, 37, 507–516. [Google Scholar] [CrossRef] [Green Version]
- Bollas, K.; Papasalouros, D.; Kourousis, D.; Anastasopoulos, A. Acoustic Emission Inspection of Rail Wheels. J. Acoust. Emiss. 2010, 28, 215. [Google Scholar]
- Hao, Q.; Wang, Y.; Shen, Y.; Zhang, X. De-Noising of Rail Crack AE Signal Based on Wavelet Modulus Maxima. In Proceedings of the 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Pisa, Italy, 11–14 May 2015; pp. 675–680. [Google Scholar]
- Liang, B.; Iwnicki, S.; Ball, A.E.; Young, A. Adaptive noise cancelling and time–frequency techniques for rail surface defect detection. Mech. Syst. Signal Process. 2015, 54, 41–51. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Kuang, K.S.C.; Koh, C.G. Fatigue crack sizing in rail steel using crack closure-induced acoustic emission waves. Meas. Sci. Technol. 2017, 28, 65601. [Google Scholar] [CrossRef]
- Pomponi, E.; Vinogradov, A. A real-time approach to acoustic emission clustering. Mech. Syst. Signal Process. 2013, 40, 791–804. [Google Scholar] [CrossRef]
- Das, A.K.; Suthar, D.; Leung, C.K. Machine learning based crack mode classification from unlabeled acoustic emission waveform features. Cem. Concr. Res. 2019, 121, 42–57. [Google Scholar] [CrossRef]
- Tang, J.; Soua, S.; Mares, C.; Gan, T.-H. A Pattern Recognition Approach to Acoustic Emission Data Originating from Fatigue of Wind Turbine Blades. Sensors 2017, 17, 2507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pashmforoush, F.; Khamedi, R.; Fotouhi, M.; Hajikhani, M.; Ahmadi, M. Damage Classification of Sandwich Composites Using Acoustic Emission Technique and k-means Genetic Algorithm. J. Nondestruct. Eval. 2014, 33, 481–492. [Google Scholar] [CrossRef]
- Satour, A.; Montrésor, S.; Bentahar, M.; Boubenider, F. Wavelet Based Clustering of Acoustic Emission Hits to Characterize Damage Mechanisms in Composites. J. Nondestruct. Eval. 2020, 39, 37. [Google Scholar] [CrossRef]
- Van Steen, C.; Verstrynge, E. Signal-Based Acoustic Emission Clustering for Differentiation of Damage Sources in Corroding Reinforced Concrete Beams. Appl. Sci. 2022, 12, 2154. [Google Scholar] [CrossRef]
- Li, D.; Wang, Y.; Yan, W.-J.; Ren, W.-X. Acoustic emission wave classification for rail crack monitoring based on synchrosqueezed wavelet transform and multi-branch convolutional neural network. Struct. Health Monit. 2021, 20, 1563–1582. [Google Scholar] [CrossRef]
- Mahajan, H.; Banerjee, S. A machine learning framework for guided wave-based damage detection of rail head using surface-bonded piezo-electric wafer transducers. Mach. Learn. Appl. 2022, 7, 100216. [Google Scholar] [CrossRef]
- Noseda, F.; Marnet, L.R.; Carlim, C.; Costa, L.R.; Junior, N.d.M.; Calôba, L.P.; Soares, S.D.; Clarke, T.; Jacques, R.C. A Neural Network System for Fault Prediction in Pipelines by Acoustic Emission Techniques. Res. Nondestruct. Eval. 2021, 32, 132–146. [Google Scholar] [CrossRef]
- Garrett, J.C.; Mei, H.; Giurgiutiu, V. An Artificial Intelligence Approach to Fatigue Crack Length Estimation from Acoustic Emission Waves in Thin Metallic Plates. Appl. Sci. 2022, 12, 1372. [Google Scholar] [CrossRef]
- Suwansin, W.; Phasukkit, P. Deep Learning-Based Acoustic Emission Scheme for Nondestructive Localization of Cracks in Train Rails under a Load. Sensors 2021, 21, 272. [Google Scholar] [CrossRef] [PubMed]
- Palmer, I.G.; Brindley, B.J.; Harrison, R.P. The relationship between acoustic emission and crack opening displacement measurements. Mater. Sci. Eng. 1974, 14, 3–6. [Google Scholar] [CrossRef]
- CSN EN 14730-1; Railway Applications-Track-Aluminothermic Welding of Rail-Part 1: Approval of Welding Processes. European Committee for Standardization: Brussels, Belgium, 2006.
- Li, G.; Zhao, Z.; Li, Y.; Li, C.-Y.; Lee, C.-C. Preprocessing Acoustic Emission Signal of Broken Wires in Bridge Cables. Appl. Sci. 2022, 12, 6727. [Google Scholar] [CrossRef]
- MISTRAS Group, Inc. Express-8 AE System User’s Manual; MISTRAS Group, Inc.: Princeton Junction, NJ, USA, 2014. [Google Scholar]
- Al-Jumaili, S.K.; Holford, K.; Eaton, M.; McCrory, J.; Pearson, M.; Pullin, R. Classification of acoustic emission data from buckling test of carbon fibre panel using unsupervised clustering techniques. Struct. Health Monit. 2015, 14, 241–251. [Google Scholar] [CrossRef]
- Farhidzadeh, A.; Dehghan-Niri, E.; Salamone, S. Gaussian Mixture Modeling of Acoustic Emissions for Structural Health Monitoring of Reinforced Concrete Structures. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 25–29 August 2013; Volume 8692. [Google Scholar]
- Saldarriaga-Zuluaga, S.D.; López-Lezama, J.M.; Muñoz-Galeano, N. Optimal Coordination of Over-Current Relays in Microgrids Using Principal Component Analysis and K-Means. Appl. Sci. 2021, 11, 7963. [Google Scholar] [CrossRef]
- Abraham, D.A. Chapter 11—Signal Processing. In Applied Underwater Acoustics; Neighbors; Thomas, H., Bradley, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 743–807. ISBN 978-0-12-811240-3. [Google Scholar]
- Ciampa, F.; Meo, M. Acoustic emission source localization and velocity determination of the fundamental mode A0 using wavelet analysis and a Newton-based optimization technique. Smart Mater. Struct. 2010, 19, 45027. [Google Scholar] [CrossRef]
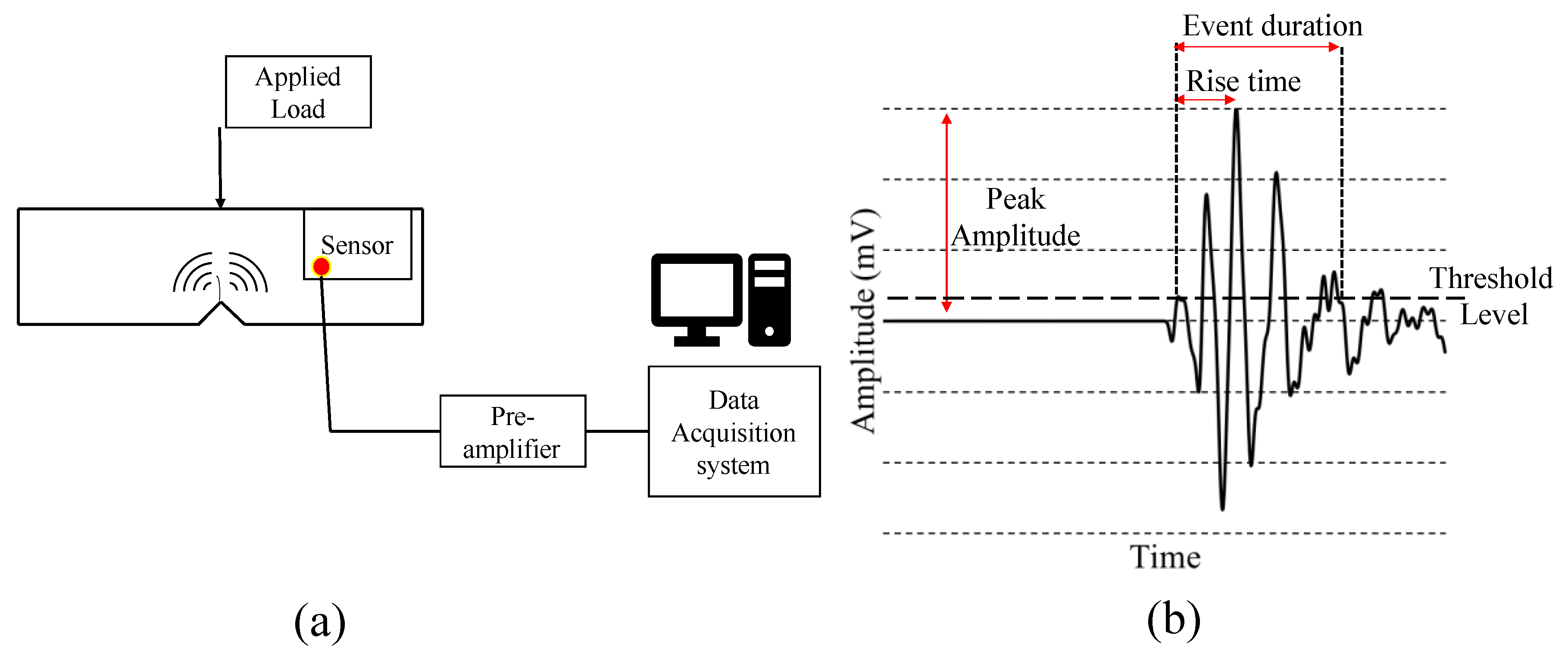

| S. No. | AE Waveform Feature | Expression |
|---|---|---|
| 1. | Energy | |
| 2. | Root mean square of signal | |
| 3. | Fast Fourier Transform Peak amplitude | |
| 4 | Area under FFT | |
| 5. | Peak frequency | |
| 6. | Rise time | T1 = Time in microsecond to peak amplitude |
| 7. | Skewness | |
| 8. | Kurtosis |
| Parameter | Value |
|---|---|
| Response Type | IIR |
| Design Method | Elliptic |
| Exactly match | Passband |
| Filter order | 4 |
| Sampling frequency | 10,000 kHz |
| First stopband frequency | 125 kHz |
| First passband frequency | 150 kHz |
| Second passband frequency | 600 kHz |
| Second stopband frequency | 650 kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahajan, H.; Banerjee, S. Quantitative Investigation of Acoustic Emission Waveform Parameters from Crack Opening in a Rail Section Using Clustering Algorithms and Advanced Signal Processing. Sensors 2022, 22, 8643. https://doi.org/10.3390/s22228643
Mahajan H, Banerjee S. Quantitative Investigation of Acoustic Emission Waveform Parameters from Crack Opening in a Rail Section Using Clustering Algorithms and Advanced Signal Processing. Sensors. 2022; 22(22):8643. https://doi.org/10.3390/s22228643
Chicago/Turabian StyleMahajan, Harsh, and Sauvik Banerjee. 2022. "Quantitative Investigation of Acoustic Emission Waveform Parameters from Crack Opening in a Rail Section Using Clustering Algorithms and Advanced Signal Processing" Sensors 22, no. 22: 8643. https://doi.org/10.3390/s22228643
APA StyleMahajan, H., & Banerjee, S. (2022). Quantitative Investigation of Acoustic Emission Waveform Parameters from Crack Opening in a Rail Section Using Clustering Algorithms and Advanced Signal Processing. Sensors, 22(22), 8643. https://doi.org/10.3390/s22228643







