Equivalent Circuit to Analyze the Transmitting Characteristics of a Cymbal Array
Abstract
1. Introduction
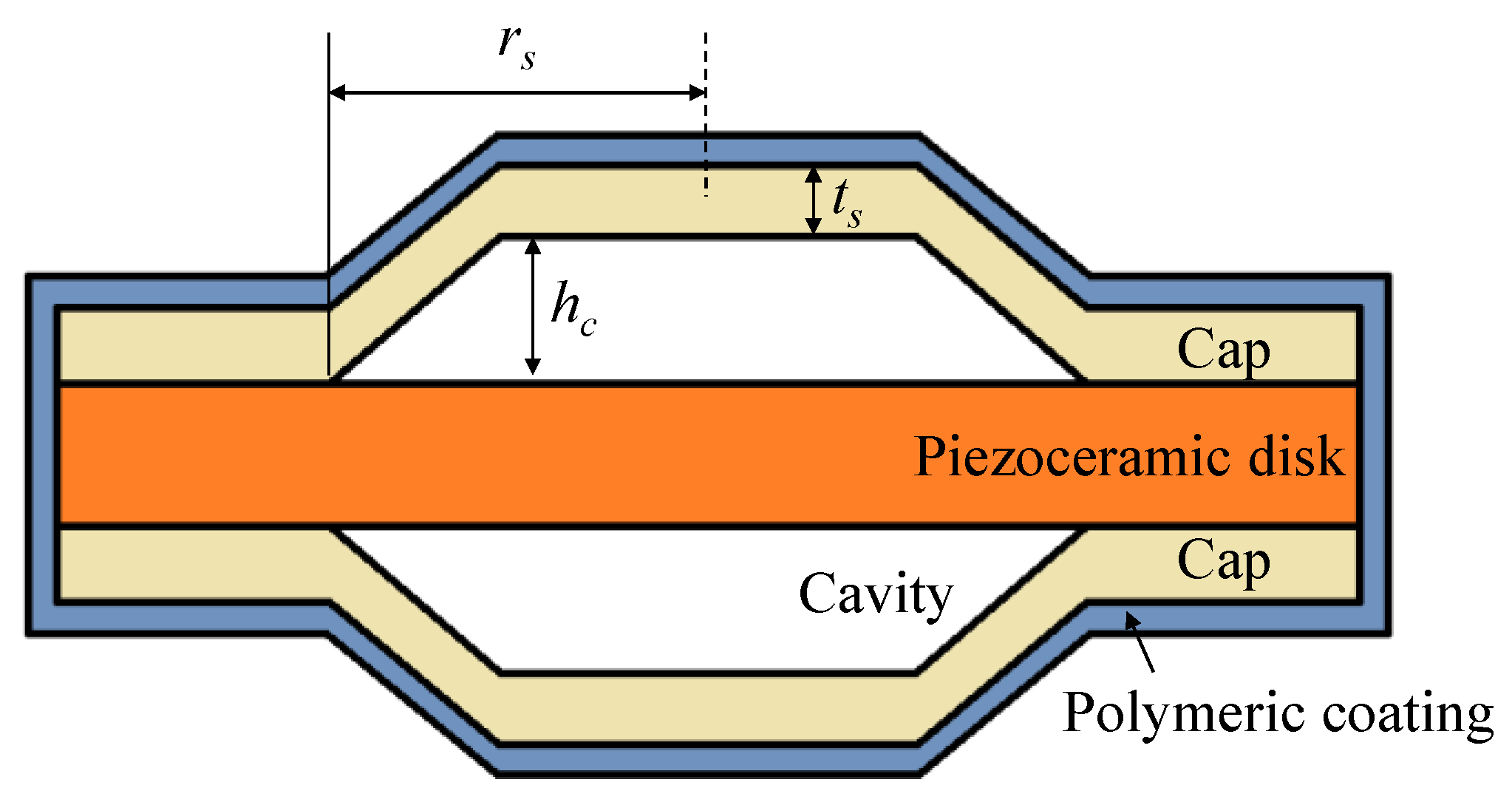
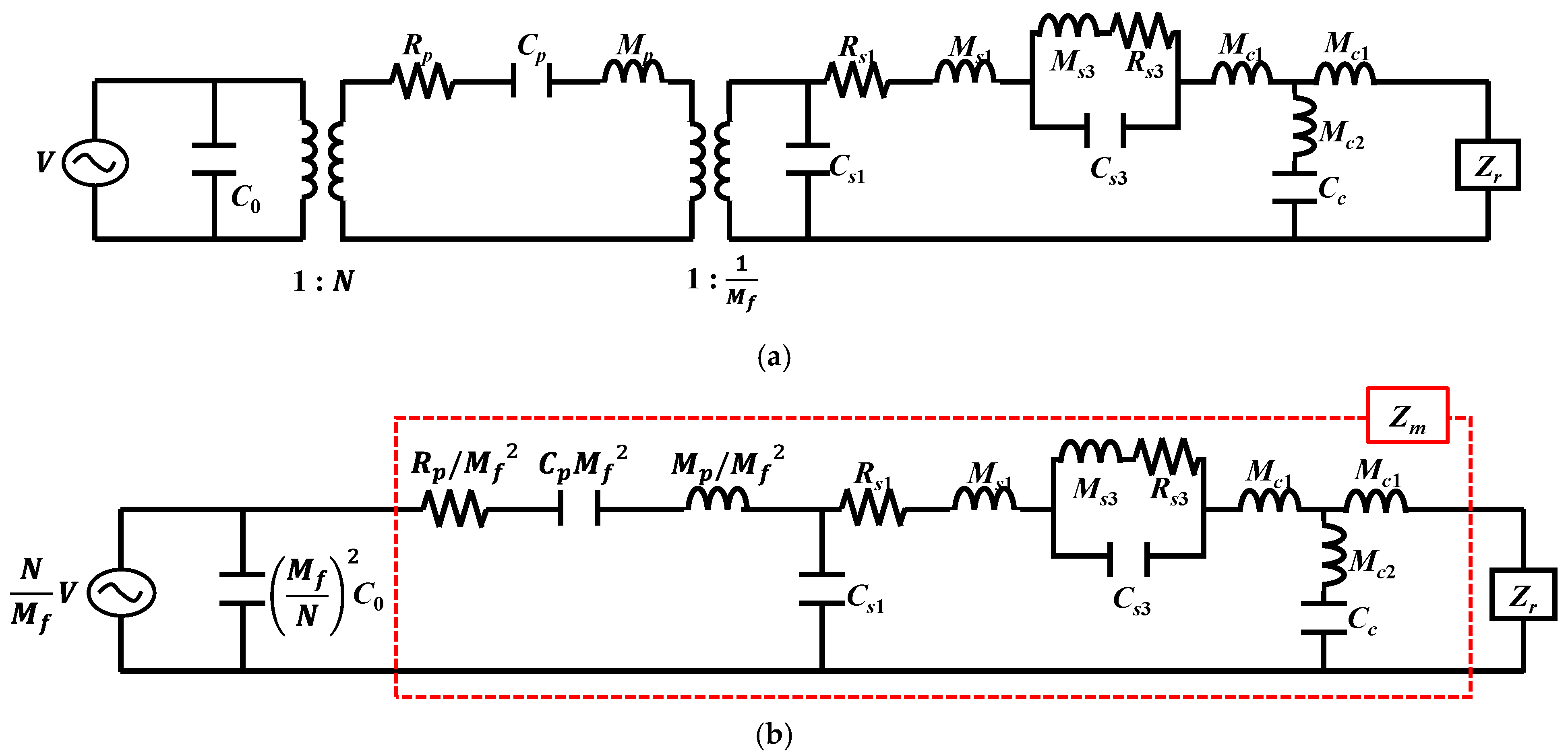
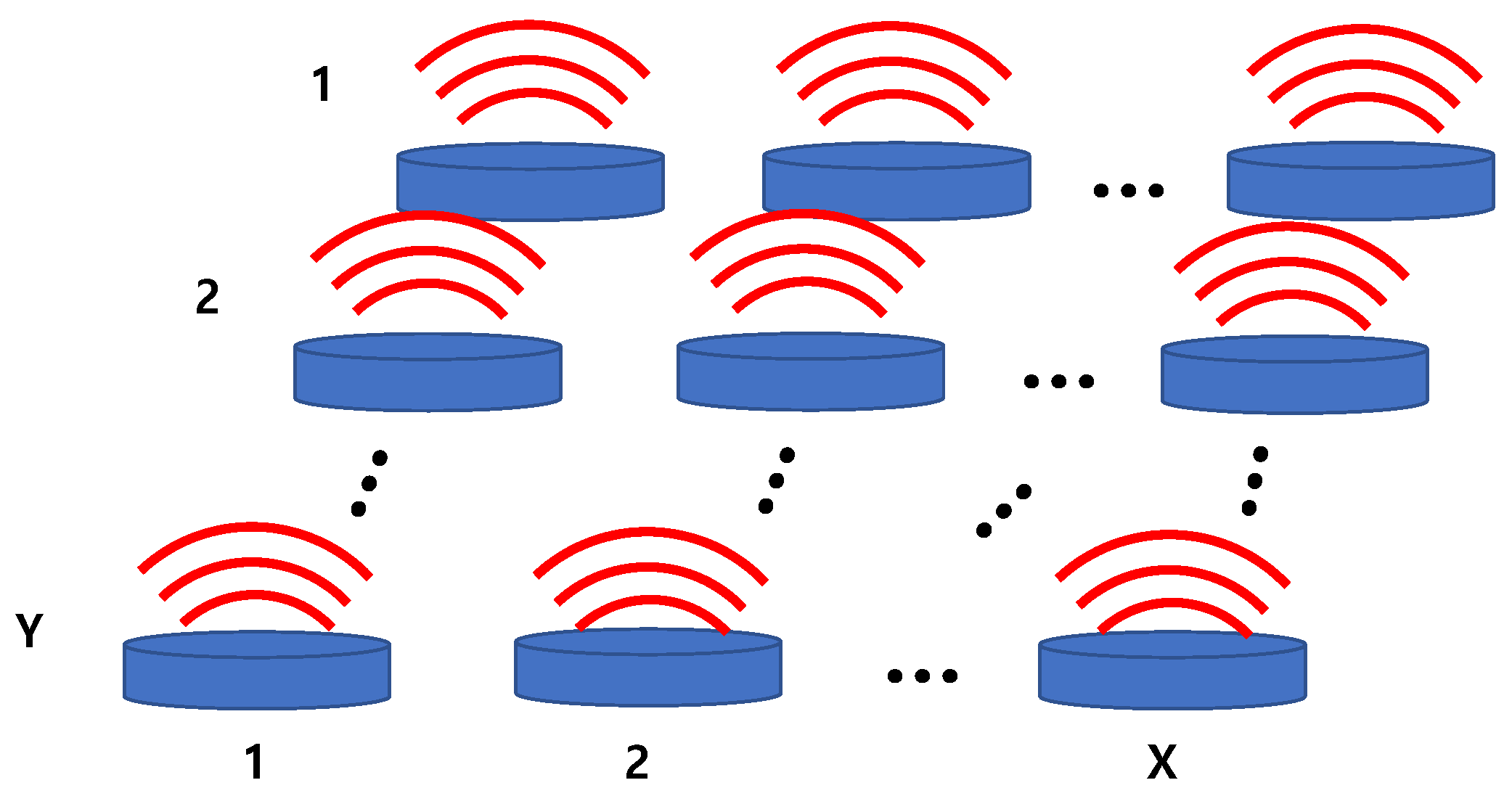
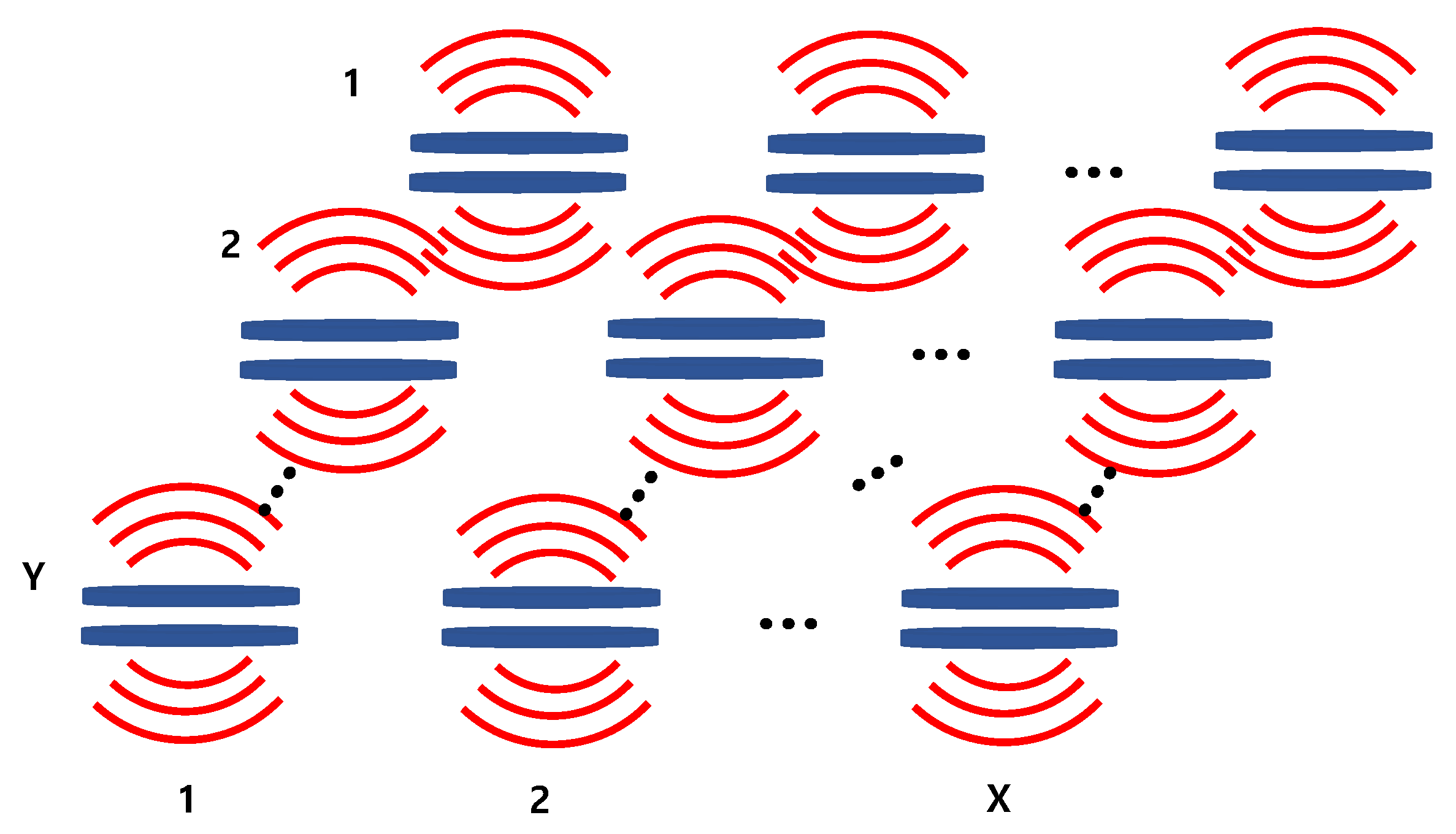
2. Equivalent Circuit of a Cymbal Array
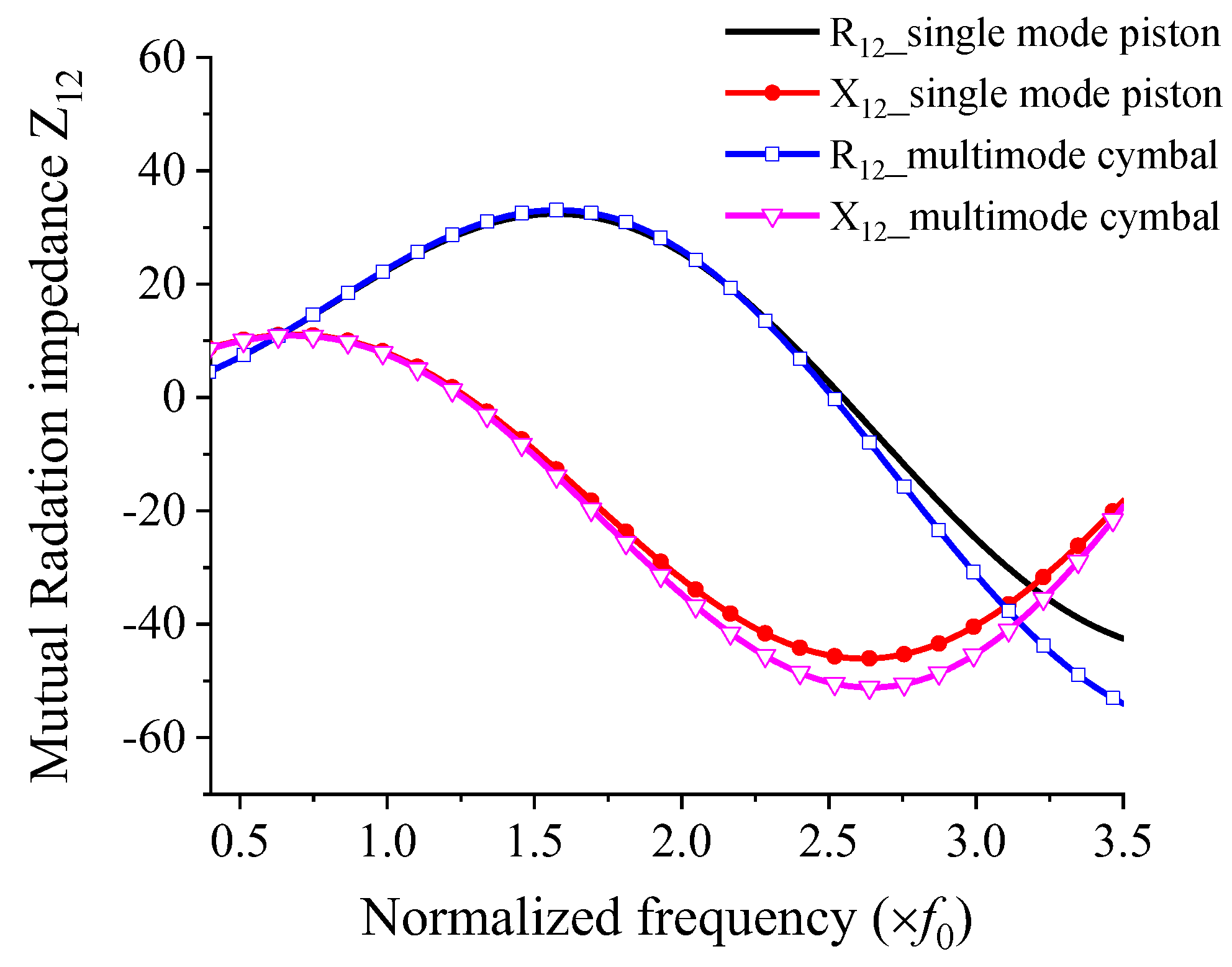
2.1. Mutual Radiation Impedance
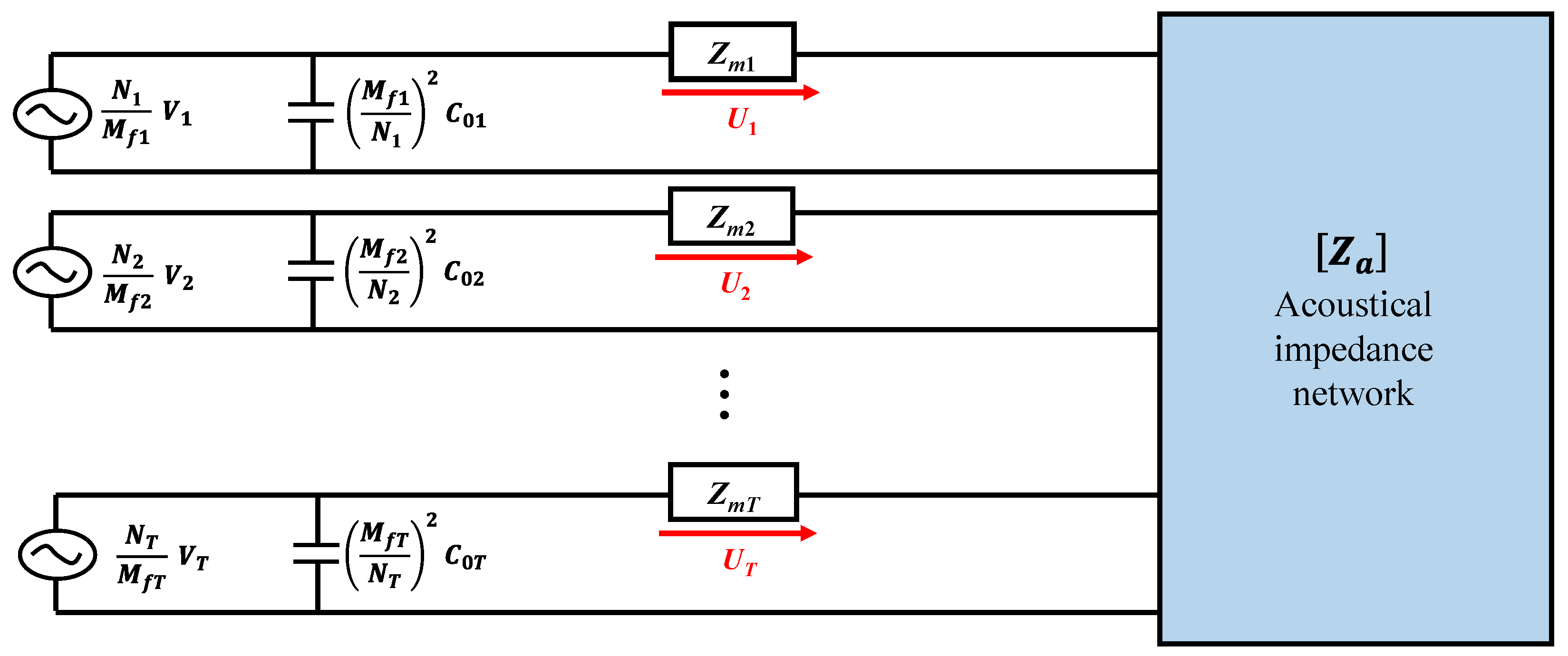
2.2. Acoustic Impedance Network
2.3. Sound Pressure from the Array
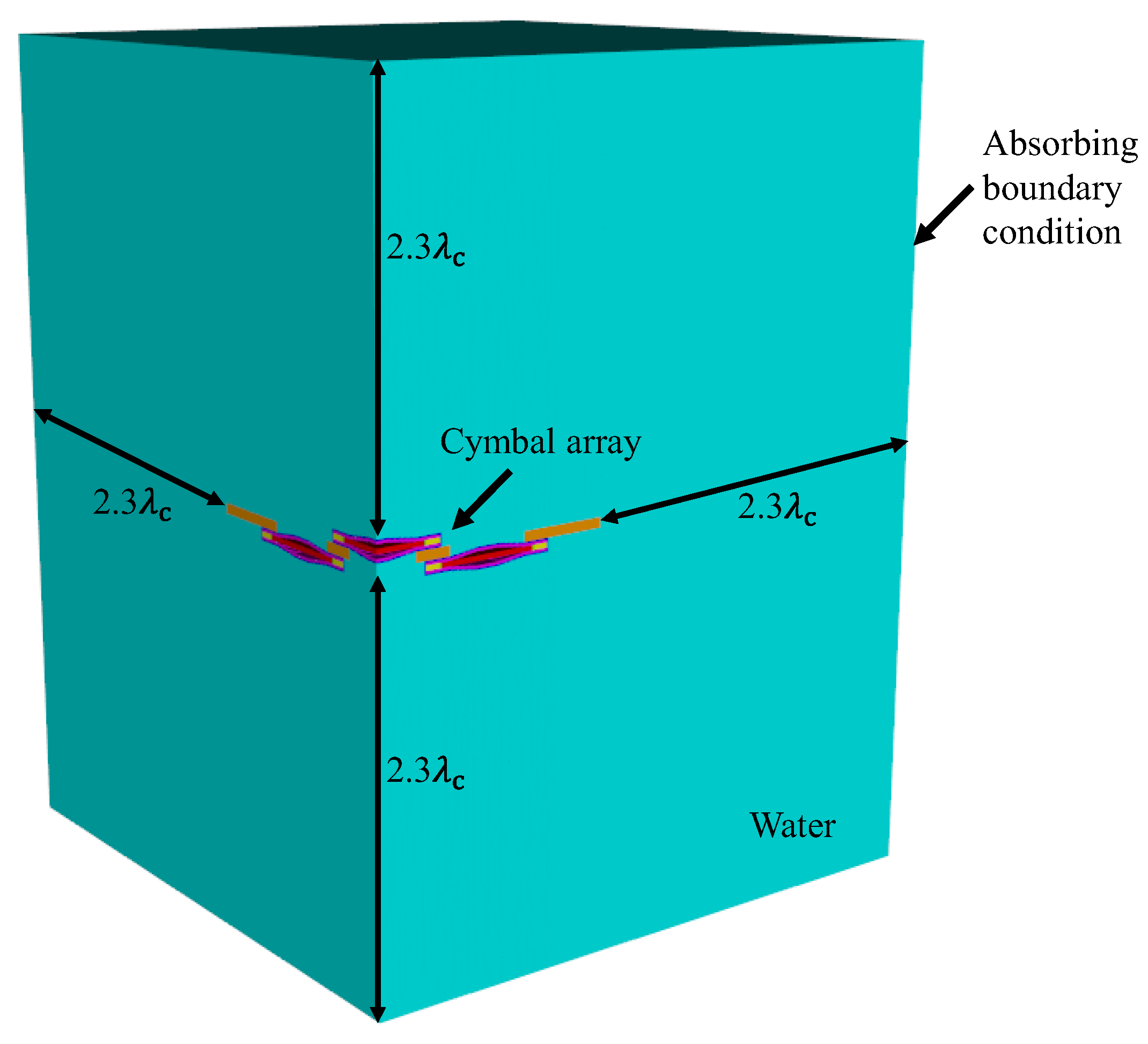
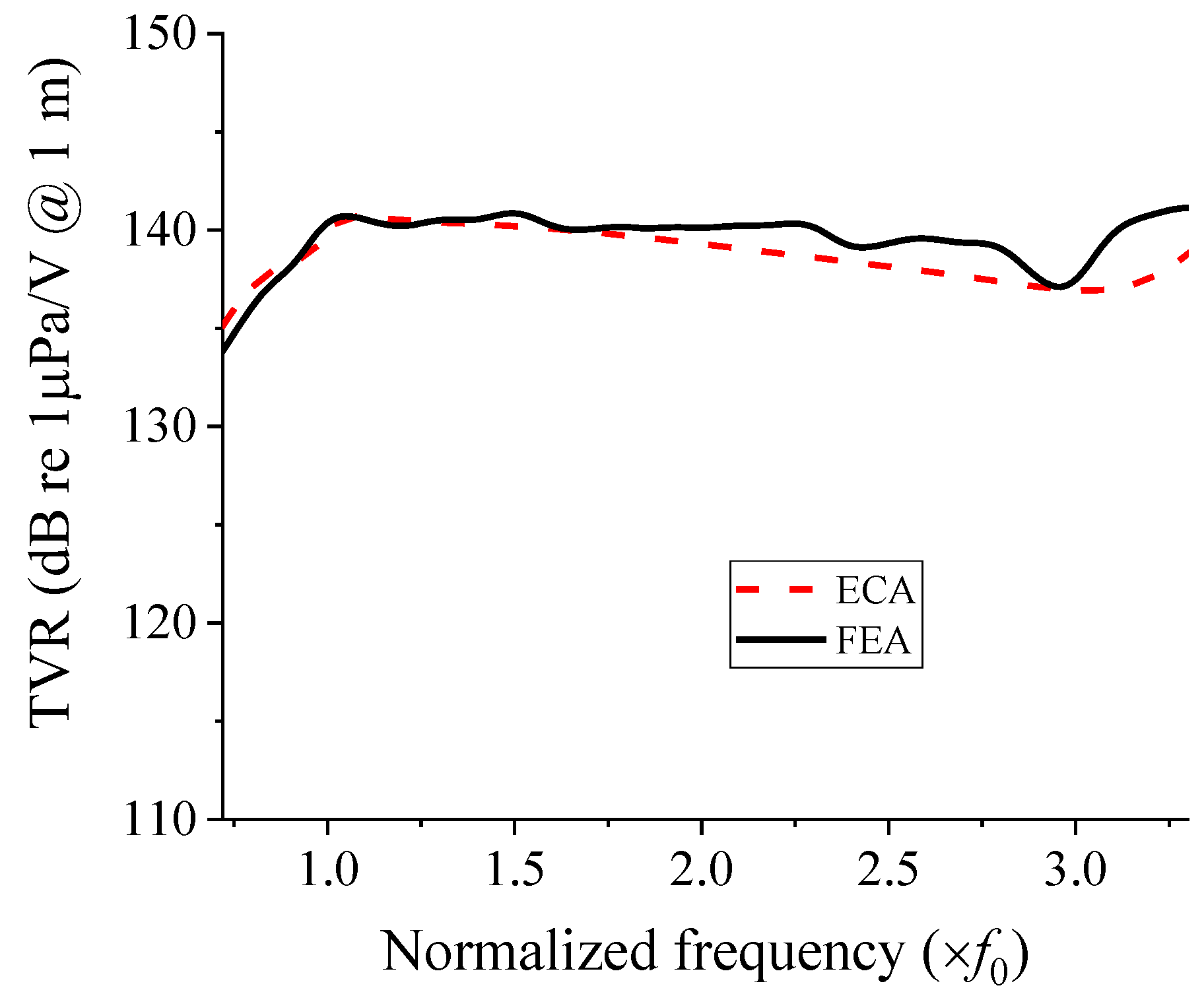
3. Validation of the Equivalent Circuit Analysis
4. Efficiency of the Equivalent Circuit Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dogan, A.; Fernandez, J.F.; Uchino, K.; Newnham, R.E. The “Cymbal” Electromechanical Actuator. In Proceedings of the 10th IEEE International Symposium on Applications of Ferroelectrics, East Brunswick, NJ, USA, 18–21 August 1996. [Google Scholar]
- Zhang, J.; Hughes, W.J.; Bouchilloux, P.; Meyer, R.J., Jr.; Uchino, K.; Newnham, R.E. A class V flextensional transducer: The cymbal. Ultrasonics 1999, 37, 387–393. [Google Scholar] [CrossRef]
- Tressler, J.F.; Cao, W.; Uchino, K.; Newnham, R.E. Ceramic-Metal Composite Transducers for Underwater Acoustic Applications. In Proceedings of the 10th IEEE International Symposium on Applications of Ferroelectrics, East Brunswick, NJ, USA, 18–21 August 1996. [Google Scholar]
- Dogan, A.; Uzgur, E. Size and material effects on cymbal transducer for actuator applications. Ferroelectrics 2006, 331, 53–63. [Google Scholar] [CrossRef]
- Zhang, J.; Hughes, W.J.; Hladky-Hennion, A.C.; Newnham, R.E. Concave cymbal transducers. Mater. Res. Innov. 1999, 2, 252–255. [Google Scholar] [CrossRef]
- Bejarano, F.; Feeney, A.; Lucas, M. A cymbal transducer for power ultrasonics applications. Sens. Actuator A Phys. 2014, 210, 182–189. [Google Scholar] [CrossRef]
- Choi, Y.; Shim, H.; Roh, Y. Comparative analysis of the acoustic characteristics of different types of cymbal transducers. J. Acoust. Soc. Korea 2019, 38, 256–265. [Google Scholar]
- Shim, H.; Roh, Y. Design and fabrication of a wideband cymbal transducer for underwater sensor networks. Sensors 2019, 19, 4659. [Google Scholar] [CrossRef]
- Shim, H.; Roh, Y. Development of an equivalent circuit of a cymbal transducer. IEEE Sens. J. 2021, 21, 13146–13155. [Google Scholar] [CrossRef]
- Shim, H.; Kim, K.; Seo, H.; Roh, Y. New equivalent circuit of a cymbal transducer incorporating the third harmonic mode of vibration. IEEE Sens. J. 2022, 22, 15750–15758. [Google Scholar] [CrossRef]
- Tressler, J.F.; Newnham, R.E.; Hughes, W.J. Capped ceramic underwater sound projector: The “cymbal” transducer. J. Acoust. Soc. Am. 1999, 105, 591–600. [Google Scholar] [CrossRef]
- Zhang, J.; Hladky-Hennion, A.C.; Hughes, W.J.; Newnham, R.E. Modeling and underwater characterization of cymbal transducers and arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 560–568. [Google Scholar] [CrossRef]
- Rajapan, D.; Rajeshwari, P.M.; Sankar, M.; Trinath, K.; Prasad, N.S. Miniaturized Underwater Sensors for the Realization of Conformal Arrays. In Proceedings of the Oceans 2006 Asian Pacific, Singapore, 16–19 May 2006. [Google Scholar]
- Du, Y.Q.; Dai, R.; Pang, D.P. Research on fabrication techniques and performance analysis for 3 × 3 cymbal transducer array. Adv. Mat. Res. 2011, 199–200, 1088–1093. [Google Scholar] [CrossRef]
- Kim, D.; Shim, H.; Oh, C.; Kim, K.; Seo, H.; Roh, Y. Design of a broadband array pattern of underwater cymbal transducers. Sensors 2021, 21, 6119. [Google Scholar] [CrossRef] [PubMed]
- Pyo, S.; Roh, Y. Structural design of an acoustic planar array transducer by using the equivalent circuit method. Ultrasonics 2020, 108, 106219. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Hughes, W.J.; Meyer, R.J., Jr.; Uchino, K.; Newnham, R.E. Cymbal array: A broad band sound projector. Ultrasonics 2000, 37, 523–529. [Google Scholar] [CrossRef]
- Lee, H.; Tak, J.; Moon, W.; Lim, G. Effects of mutual impedance on the radiation characteristics of transducer arrays. J. Acoust. Soc. Am. 2004, 115, 666–679. [Google Scholar] [CrossRef]
- Köymen, H.; Atalar, A.; Taşdelen, A.S. Bilateral CMUT cells and arrays: Equivalent circuits, diffraction constants, and substrate impedance. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 414–423. [Google Scholar] [CrossRef]
- Xu, T.; Zhao, L.; Jiang, Z.; Guo, S.; Li, Z.; Yang, P.; Luo, G.; Sun, L.; Zhang, L. Equivalent circuit models of cell and array for resonant cavity-based piezoelectric micromachined ultrasonic transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 2103–2118. [Google Scholar] [CrossRef]
- Pyo, S.; Lim, Y.; Roh, Y. Analysis of the transmitting characteristics of an acoustic conformal array of multimode tonpilz transducers by the equivalent circuit method. Sens. Actuator A Phys. 2021, 318, 112507. [Google Scholar] [CrossRef]
- Oguz, H.K.; Atalar, A.; Köymen, H. Equivalent circuit-based analysis of CMUT cell dynamics in arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1016–1024. [Google Scholar] [CrossRef]
- Akhbari, S.; Sammoura, F.; Lin, L. Equivalent circuit models for large arrays of curved and flat piezoelectric micromachined ultrasonic transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 432–447. [Google Scholar] [CrossRef]
- Sim, M.J.; Jeong, W.B.; Hong, C. An equivalent circuit based electro-vibro-acoustic model of a cylindrical transducer array. J. Acoust. Soc. Am. 2021, 149, 3228–3240. [Google Scholar] [CrossRef] [PubMed]
- Butler, J.L.; Sherman, C.H. Transducers and Arrays for Underwater Sound, 2nd ed.; Springer: Cham, Switzerland, 2016; pp. 376–384. [Google Scholar]
- Xu, T.; Zhao, L.; Jiang, Z.; Guo, S.; Li, Z.; Yang, P.; Luo, G.; Sun, L.; Zhang, L. Equivalent circuit model for a large array of coupled piezoelectric micromachined ultrasonic transducers with high emission performance. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 718–733. [Google Scholar] [CrossRef] [PubMed]
- Mudiyala, J.; Shim, H.; Kim, D.; Roh, Y. Development of a dual-layer structure for cymbal transducer arrays to achieve a wider bandwidth. Sensors 2022, 22, 6614. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.; Jia, Y.; Huang, Y.; Khoso, N.A.; Deb, H.; Fan, Q.; Shao, J. Preparation of PVDF-TrFE based electrospun nanofibers decorated with PEDOT-CNT/rGO composites for piezo-electric pressure sensor. J. Mater. Sci. Mater. Electron. 2019, 30, 14007–14021. [Google Scholar] [CrossRef]
- Zhang, S.; Li, F.; Luo, J.; Sahul, R.; Shrout, T.R. Relaxor-PbTiO3 Single Crystals for Various Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1572–1580. [Google Scholar] [CrossRef]






| Method | Peak TVR Frequency () | −3 dB Fractional Bandwidth (%) |
|---|---|---|
| Measurement | 1.02 | 102.4 |
| ECA with the new acoustic impedance network | 1.06 | 104.8 |
| ECA with the dual-source network | 1.05 | 76.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shim, H.; Kim, K.; Seo, H.; Roh, Y. Equivalent Circuit to Analyze the Transmitting Characteristics of a Cymbal Array. Sensors 2022, 22, 8743. https://doi.org/10.3390/s22228743
Shim H, Kim K, Seo H, Roh Y. Equivalent Circuit to Analyze the Transmitting Characteristics of a Cymbal Array. Sensors. 2022; 22(22):8743. https://doi.org/10.3390/s22228743
Chicago/Turabian StyleShim, Hayeong, Kyungseop Kim, Heeseon Seo, and Yongrae Roh. 2022. "Equivalent Circuit to Analyze the Transmitting Characteristics of a Cymbal Array" Sensors 22, no. 22: 8743. https://doi.org/10.3390/s22228743
APA StyleShim, H., Kim, K., Seo, H., & Roh, Y. (2022). Equivalent Circuit to Analyze the Transmitting Characteristics of a Cymbal Array. Sensors, 22(22), 8743. https://doi.org/10.3390/s22228743







