A Simple Model for Assessing Millimeter-Wave Attenuation in Brownout Conditions
Abstract
:1. Introduction
1.1. Background
1.2. Objectives of the Current Work and Problem Statement
2. Materials and Methods
2.1. Attenuation Properties of Brownout at MMW
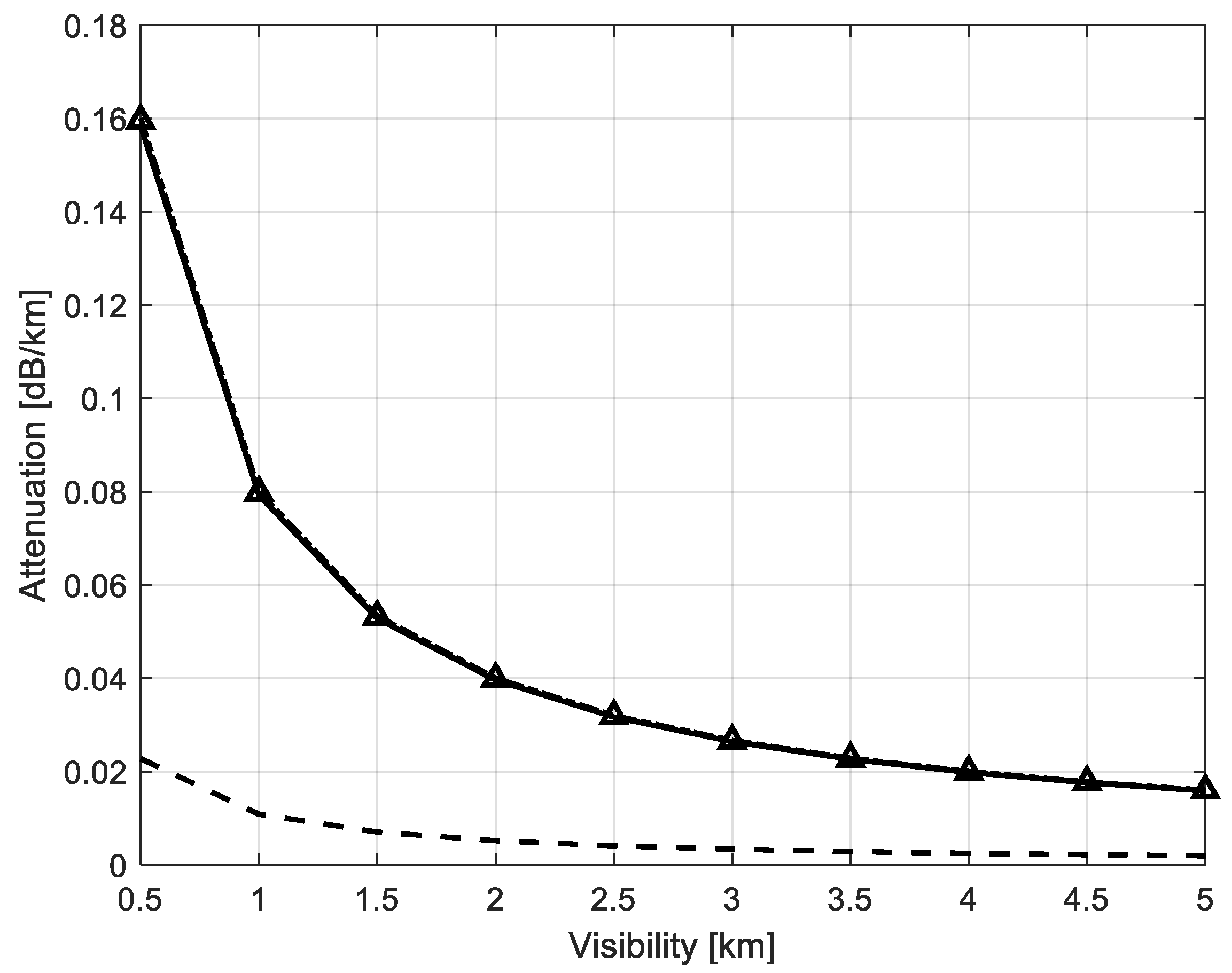
2.1.1. Attenuation Coefficient Estimation
2.1.2. Visibility and Total Particle Density
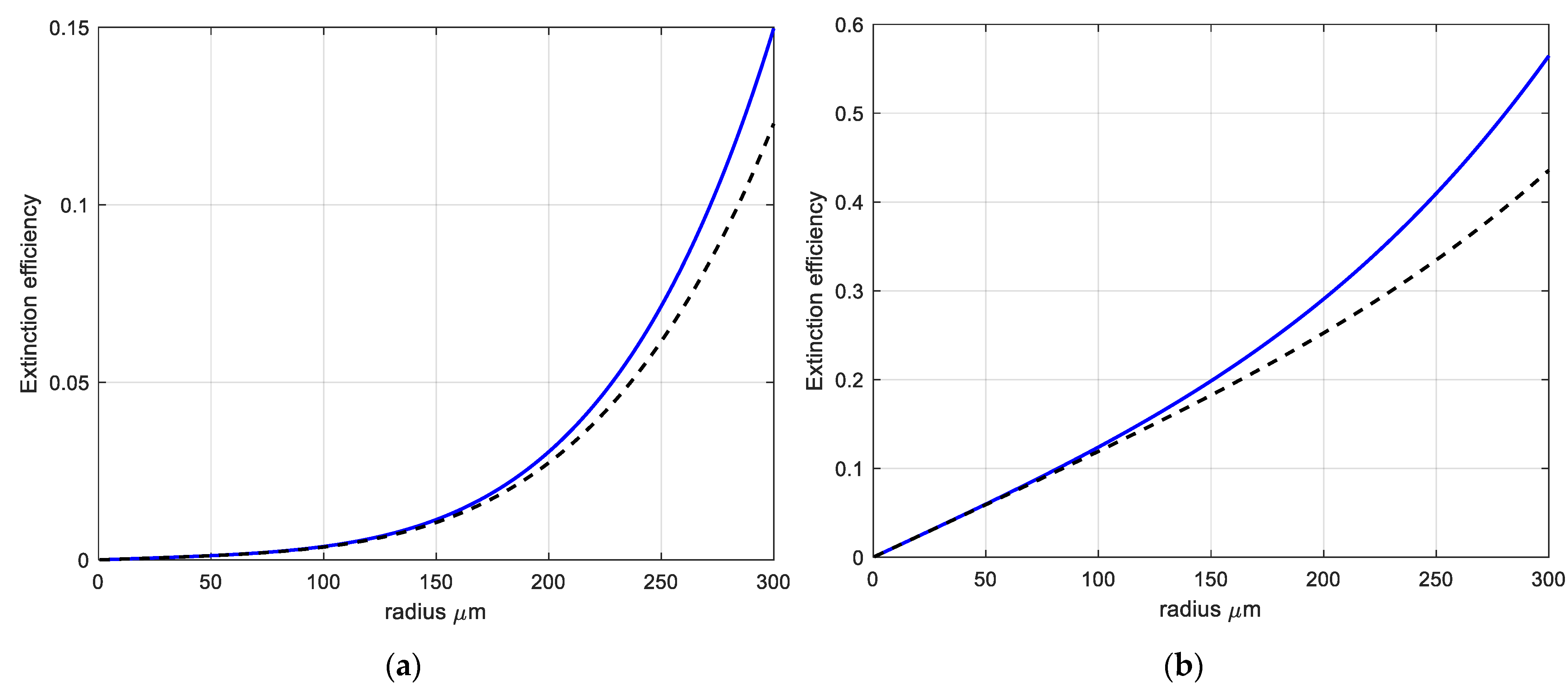
2.1.3. Attenuation Cross-Section Model
2.1.4. Phase Function Model
2.2. Power Transfer in Brownout
2.2.1. Signal Backscattered by the Scene
2.2.2. Noise Backscattered by the Brownout
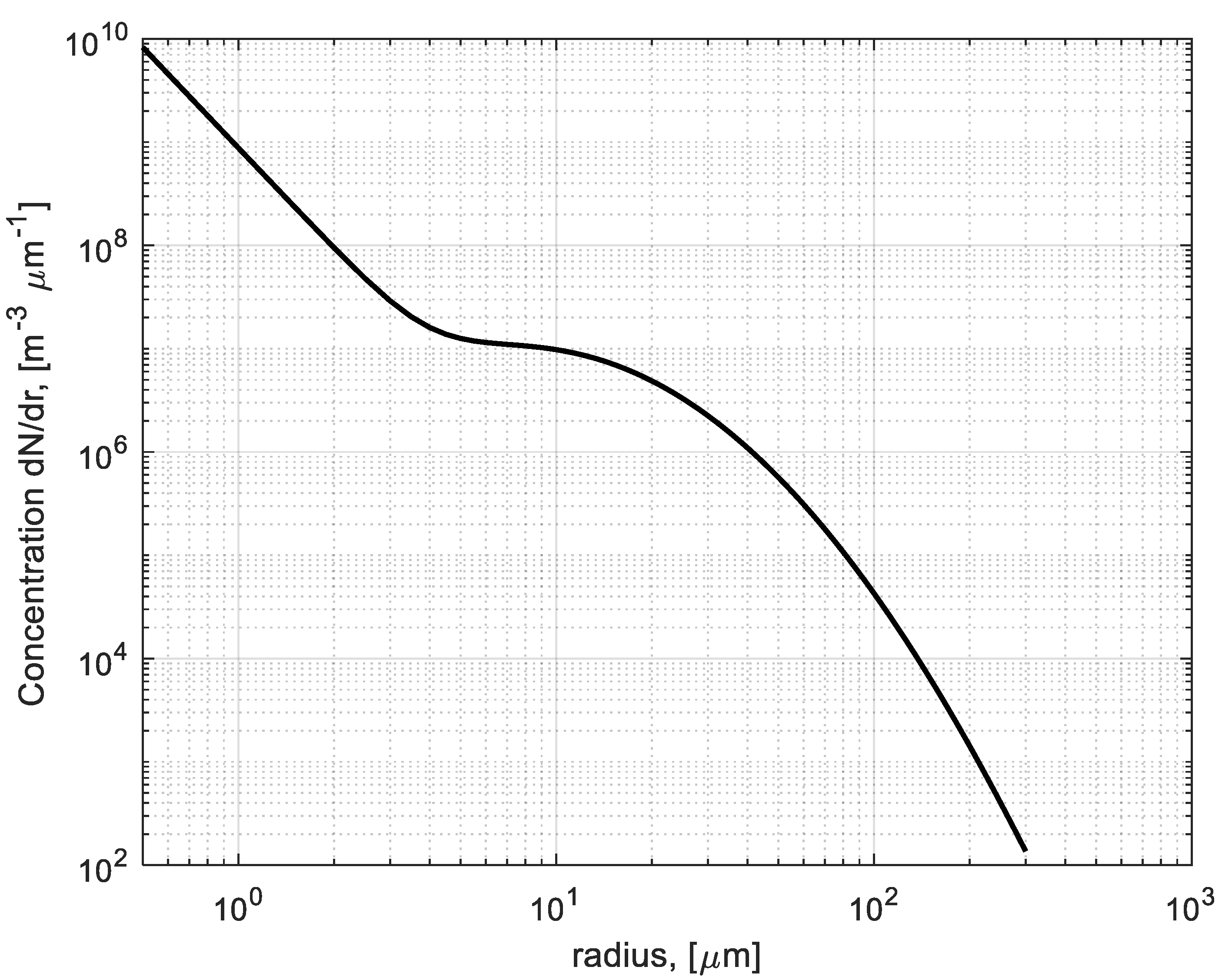
2.2.3. Brownout Particle Size Distribution Model
3. Results
3.1. Comparison with Models and Measured Data
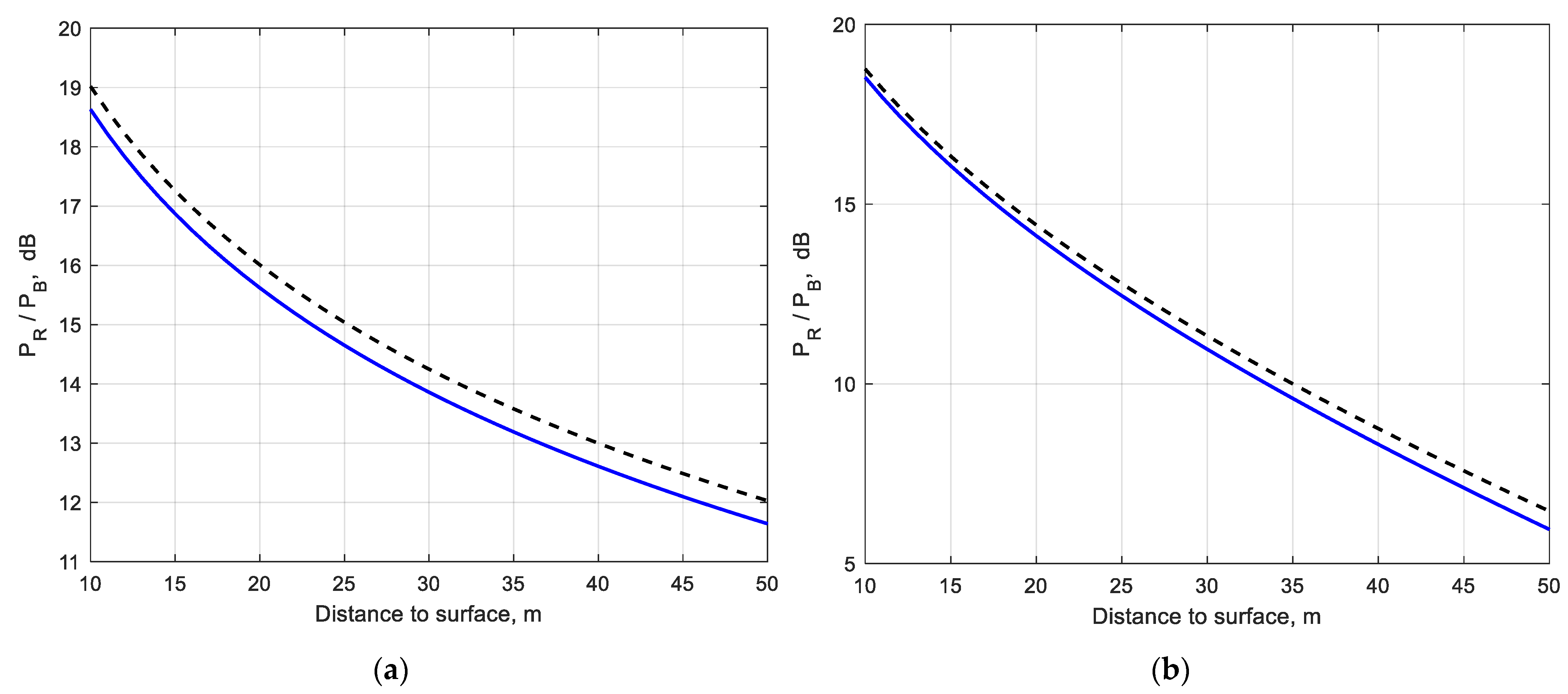
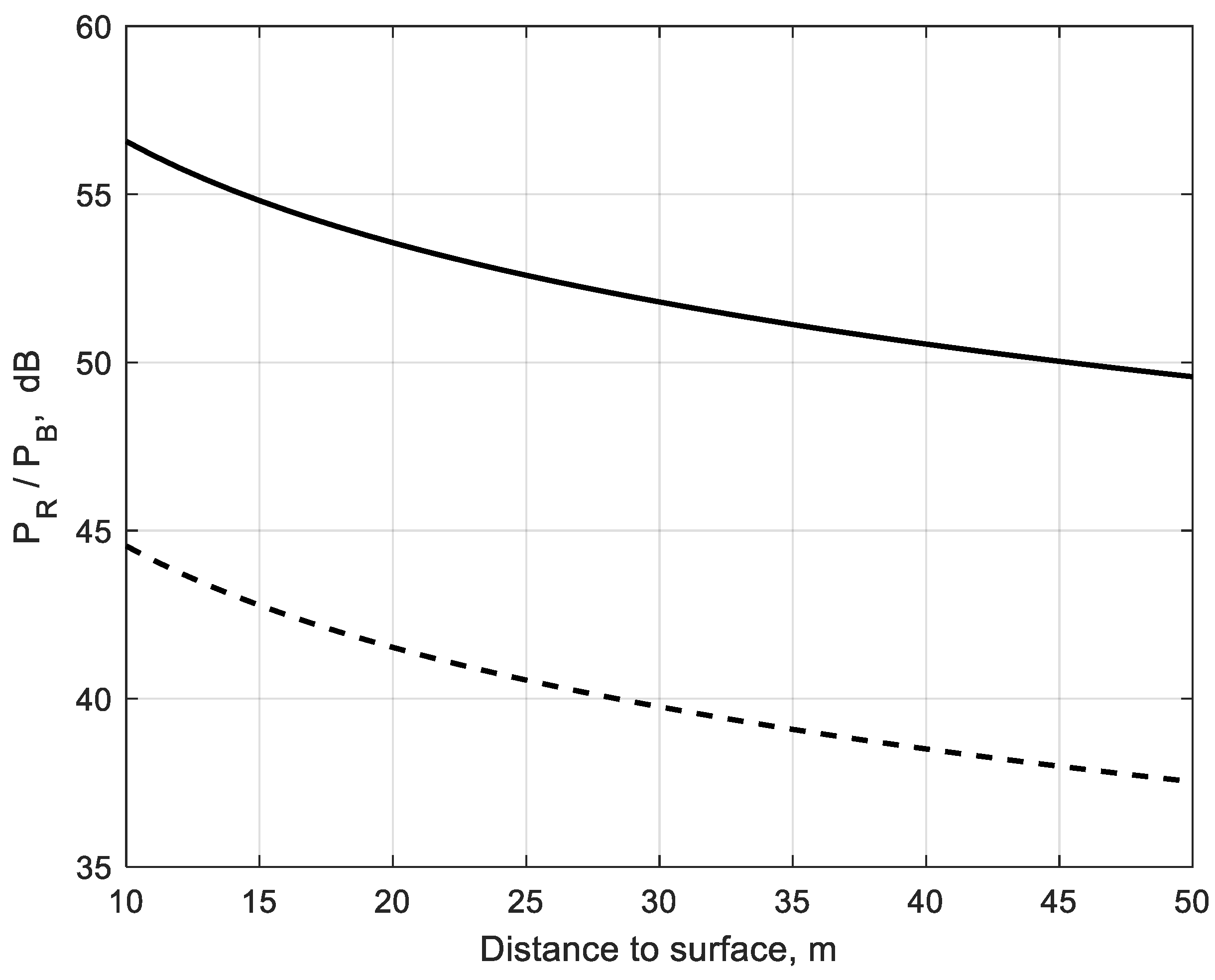
3.2. Power Transfer Estimation in Brownout
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Task Group. Rotary-Wing Brownout Mitigation: Technologies and Training; NATO Science and Technology Organization: Brussels, Belgium, 2012. [Google Scholar]
- Cross, J.; Schneider, J.; Cariani, P. MMW radar enhanced vision systems: The Helicopter Autonomous Landing System (HALS) and Radar-Enhanced Vision System (REVS) are rotary and fixed wing enhanced flight vision systems that enable safe flight operations in degraded visual environments. Degrad. Vis. Environ. Enhanc. Synth. Extern. Vis. Solut. 2013, 8737, 87370G. [Google Scholar]
- Savage, J.; Goodrich, S.; Ott, C.; Szoboszlay, Z.; Perez, A.; Soukup, J.; Burns, H.N. Three-dimensional landing zone joint capability technology demonstration. Degrad. Vis. Environ. Enhanc. Synth. Extern. Vis. Solut. 2014, 9087, 908707. [Google Scholar]
- Phillips, C. Computational Study of Rotorcraft Aerodynamics in Ground Effect and Brownout. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2010. [Google Scholar]
- Ansari, A.J.; Evans, B.G. Microwave propagation in sand and dust storms. IEEE Proc. F Commun. Radar Signal Process. 1982, 129, 315–322. [Google Scholar] [CrossRef]
- Bashir, S.O.; McEwan, N.J. Microwave propagation in dust storms: A review. IEEE Proc. H Microw. Antennas Propag. 1986, 133, 241–247. [Google Scholar] [CrossRef]
- Dong, Q.-F.; Guo, L.-X.; Li, Y.; Zhang, H.; Wang, M.-J. Weathering Sand and Dust Storms: Particle shapes, storm height, and elevation angle sensitivity for microwave propagation in earth-satellite links. IEEE Ant. Propag. Mag. 2017, 59, 58–65. [Google Scholar] [CrossRef]
- Ghobrial, S.I.; Sharif, S.M. Microwave attenuation and cross polarization in dust storms. IEEE Trans. Antennas. Propag. 1987, 35, 418–425. [Google Scholar] [CrossRef]
- Goldhirsh, J. A parameter review and assessment of attenuation and backscatter properties associated with dust storms over desert regions in the frequency range of 1 to 10 GHz. IEEE Trans. Antennas Propag. 1982, 30, 1121–1127. [Google Scholar] [CrossRef]
- Goldhirsh, J. Attenuation and backscatter from derived two-dimensional duststorm model. IEEE Trans. Antennas Propag. 2001, 49, 1703–1711. [Google Scholar] [CrossRef]
- Ali, A.A.; Alhaider, M.A. Millimeter Wave Propagation in Arid Land—A Field Study in Riyadh. IEEE Trans. Antennas Propag. 1992, 40, 492–499. [Google Scholar] [CrossRef]
- Ahmed, A.S.; Ali, A.A.; Alhaider, M.A. Airborne wave into dust storms. IEEE Trans. Geosci. Remote Sens. 1987, 25, 593–595. [Google Scholar] [CrossRef]
- Elabdin, Z.; Islam, M.R.; Khalifa, O.O.; Raouf, H.E.A. Mathematical model for the prediction of microwave signal attenuation due to duststorm. Prog. Electromagn. Res. M 2009, 6, 139–153. [Google Scholar]
- Islam, M.R.; Elshaikh, Z.E.; Elshaikh, O.; Khalifa, O.O.; Zahirul, A.H.M.; Khan, A.S.; Naji, A.W. Prediction of signal attenuation due to duststorms using Mie scattering. IIUM Eng. J. 2010, 11, 71–87. [Google Scholar] [CrossRef]
- Rangwala, M.; Wang, F.; Sarabandi, K. Study of Millimeter-Wave Radar for Helicopter Assisted -Landing System. IEEE Trans. Antennas Propag. 2008, 50, 13–25. [Google Scholar] [CrossRef]
- Prophète, C.; Pierrat, R.; Sik, H.; Kling, E.; Carminati, R.; de Rosny, J. Modeling of an active terahertz imaging system in brownout conditions. Appl. Opt. 2018, 57, 6017–6026. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Islam, M.R.; Elshaikh, Z.E.; Khalifa, O.; Zahirul, A.H.M.; Khan, A.S. Fade margin analysis due to duststorm based on visibility data measured in a desert. Am. J. Appl. Sci. 2010, 7, 551–555. [Google Scholar] [CrossRef] [Green Version]
- Middleton, W.E.K. Vision through the Atmosphere; University of Toronto Press: Toronto, ON, Canada, 1952. [Google Scholar]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; University of Washington: Seattle, DC, USA; Academic Press: Cambridge, MA, USA, 1978; Volume 1. [Google Scholar]
- Alameen, B.; Alfitouri, S.A.; Ahmed, A.A. Effect of dust storms on (GSM) signal north region of Libya. WJARR 2022, 14, 504–519. [Google Scholar]
- Marek, S.L. A Computational Tool for Evaluating THz Imaging Performance in Brownout Conditions at Land Sites throughout the World. Master’s Thesis, Air Force Institute of Technology, WPAFB, OH, USA, 2009. Available online: https://apps.dtic.mil/sti/citations/ADA494962 (accessed on 26 March 2009).
- Fiorino, S.T.; Bartell, R.J.; Krizo, M.G.; Marek, S.L.; Bohn, M.J.; Randall, R.M.; Cusumano, S.J. A computational tool for evaluating THz imaging performance in brownout or whiteout conditions at land sites throughout the world. In Proceedings of the SPIE Defense, Security, and Sensing, Atmospheric Propagation VI, Orlando, FL, USA, 6 May 2009; Volume 7324, p. 732410. [Google Scholar]
- Cowherd, C. Sandblaster 2 Support of See-Through Technologies for Particulate Brownout. Task 5 Final Technical Report, 2007, MRI Project No. 110565.1.001.
- Cornette, W.M.; Shanks, J.G. Physically reasonable analytic expression for the single-scattering phase function. Appl. Opt. 1992, 31, 3152–3160. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.K.; Roy, A.K.; Somerford, D.J. New approximate phase functions for scattering of unpolarized light by dielectric particles. J. Quant. Spectrosc. Radiat. Transf. 1998, 60, 1001–1010. [Google Scholar] [CrossRef]
- Horvath, H. Basic optics, aerosol optics, and the role of scattering for sky radiance. J. Quant. Spectrosc. Radiat. Transf. 2014, 139, 3–12. [Google Scholar] [CrossRef]
- Dillon, T.E.; Schuetz, C.A.; Martin, R.D.; Mackrides, D.G.; Shi, S.; Yao, P.; Shreve, K.; Harrity, C.; Prather, D.W. Passive, real-time millimeter wave imaging for degraded visual environment mitigation. Degrad. Vis. Environ. Enhanc. Synth. Extern. Vis. Solut. 2015, 9471, 947103-1–947103-9. [Google Scholar]



| Particulate Type | Dielectric Constant ε = ε′ − jε″ | Refractive Index m = √ε |
|---|---|---|
| Brownout Desert [21,22,23] | 5.5 − j5.15 × 10−2 | 2.34 − j0.011 |
| Brownout Mid-Latitude [21,22,23] | 3.5 − j4.83 × 10−2 | 1.86 − j0.013 |
| Sand & dust-storm [13] | 3.5 − j1.64 | 1.92 − j0.43 |
| Sand & Dust [15] | 3.0 − j0.6 | 1.74 − j0.17 |
| Sand (Libya) [20] | 4.96 − j0.135 | 2.23 − j0.303 |
| Constant | Real (ε) ≥ 4.5 | 2.0 < Real (ε) < 4.5 |
|---|---|---|
| b1 | 0.9996 | 0.9996 |
| b2 | 1.82 × 10−2 | 1.465 × 10−2 |
| b3 | −1.54 | −1.174 |
| b4 | 0.7161 | 0.4865 |
| Ni | rm (μm) | σ | Type |
|---|---|---|---|
| 0.96 | -- | -- | Linear |
| 0.04 | 14.6 | 0.33 | Log-normal |
| Visibility, km | Dielectric Constant | Ref. [13] | Ref. [10] | Attenuation Ref. [11] | dB/km Proposed Solution * | Measured Ref. [14] |
|---|---|---|---|---|---|---|
| 0.626 | ε = 4 − j1.325 | 0.132 | 0.018 | 0.133 | 0.133 | 0.14 |
| Complex Permittivity ε = ε′ − jε″ | Ref. [13] | Equation (9) | Attenuation in Equation (10) | dB/km Equation (12) | re = 58 μm * | PSD Equation (30) ** |
|---|---|---|---|---|---|---|
| 3.5 − j1.65 | 131.4 | 13.3 | 130.5 | 130.5 | 128 | 132.8 |
| 4.96 − j0.135 | 7.38 | 0.742 | 7.25 | 7.25 | 7.37 | 10.5 |
| 5.5 − j5.15 × 10−2 | 2.5 | 0.25 | 2.4 | 2.4 | 2.66 | 5.9 |
| MMW Link/Transceiver | Parameters |
|---|---|
| Distance to surface | L = 10 ÷ 50 m |
| Surface reflectance | ρ = 0.15 |
| Receiver aperture diameter | DR = 0.5 m |
| Transmitter power | I0 = 1 W |
| Frequency | f = 94 GHz |
| Brownout Desert model | ε = 5.5 − j5.15 × 10−2 |
| Sand & dust-storm | ε = 3.5 − j1.65 |
| Visibility [brownout PSD (30)] | V = 0.004 km |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zilberman, A.; Kopeika, N. A Simple Model for Assessing Millimeter-Wave Attenuation in Brownout Conditions. Sensors 2022, 22, 8889. https://doi.org/10.3390/s22228889
Zilberman A, Kopeika N. A Simple Model for Assessing Millimeter-Wave Attenuation in Brownout Conditions. Sensors. 2022; 22(22):8889. https://doi.org/10.3390/s22228889
Chicago/Turabian StyleZilberman, Arkadi, and Natan Kopeika. 2022. "A Simple Model for Assessing Millimeter-Wave Attenuation in Brownout Conditions" Sensors 22, no. 22: 8889. https://doi.org/10.3390/s22228889





