A Software and Hardware Cooperation Method for Full Nyquist Rate Transmission Symbol Synchronization at E-Band Wireless Communication
Abstract
:1. Introduction
- Large data throughput makes the system not allow too many serial operations;
- The Symbol rate is equal to the sampling rate, which means that there is only one datum in a symbol period;
- No interpolation, no decimation, and no digital pre-shaping, the transmission pulse is ultimately shaped by the channel. So the arrival signal will be uncertain;
- Limited digital hardware resources, all kinds of processes need to be simplified;
- With high carrier frequency, it is difficult to obtain information related to phase discrimination on hardware.
- Propose a method of quickly acquiring the initial phase before communication by using the characteristics of Chirp signal and maximum output energy (MOE) criterion. This method ensures that the system obtains the optimal phase immediately and rapidly after starting.
- Aiming at the fast change of the waveform caused by the channel, a decision method based on the frequency domain characteristics of the sampled signal is proposed. This decision ensures fast phase tracking of the system.
- A method of establishing a gradient table is proposed to solve the problem of slow phase offset. This process provides a long-term guarantee for sampling data accuracy.
- From the perspective of sampling and channel shaping, the difference between full Nyquist rate systems and conventional systems are analyzed.
- Numerical and hardware verifications show that the sampling phase is kept near the optimal phase, which ensures the stable output of effective data and thus improves the bit error rate (BER) performance of the system.
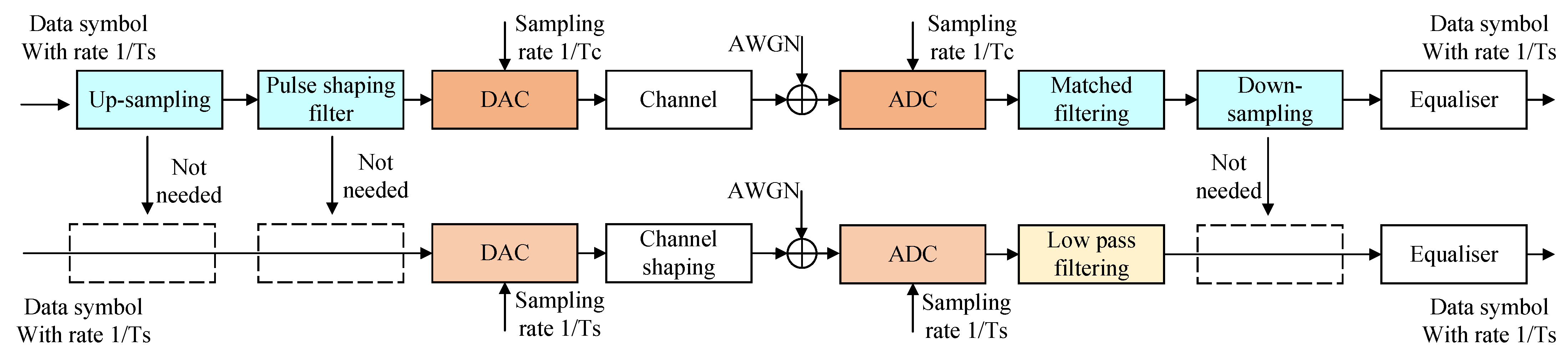
2. Nyquist Transmission Model
2.1. System Model
2.2. Nyquist Rate Sampling
- Spectral null data may exist in the sampling output;
- The data will not only have amplitude changes, but also show frequency selection characteristics.
2.3. Channel Shaping
- In E-band wireless communication, full Nyquist rate transmission architecture is used to meet the requirements without ISI;
- Shaped by an analog channel, unknown changes such as amplitude and phase may occur.
3. Methods
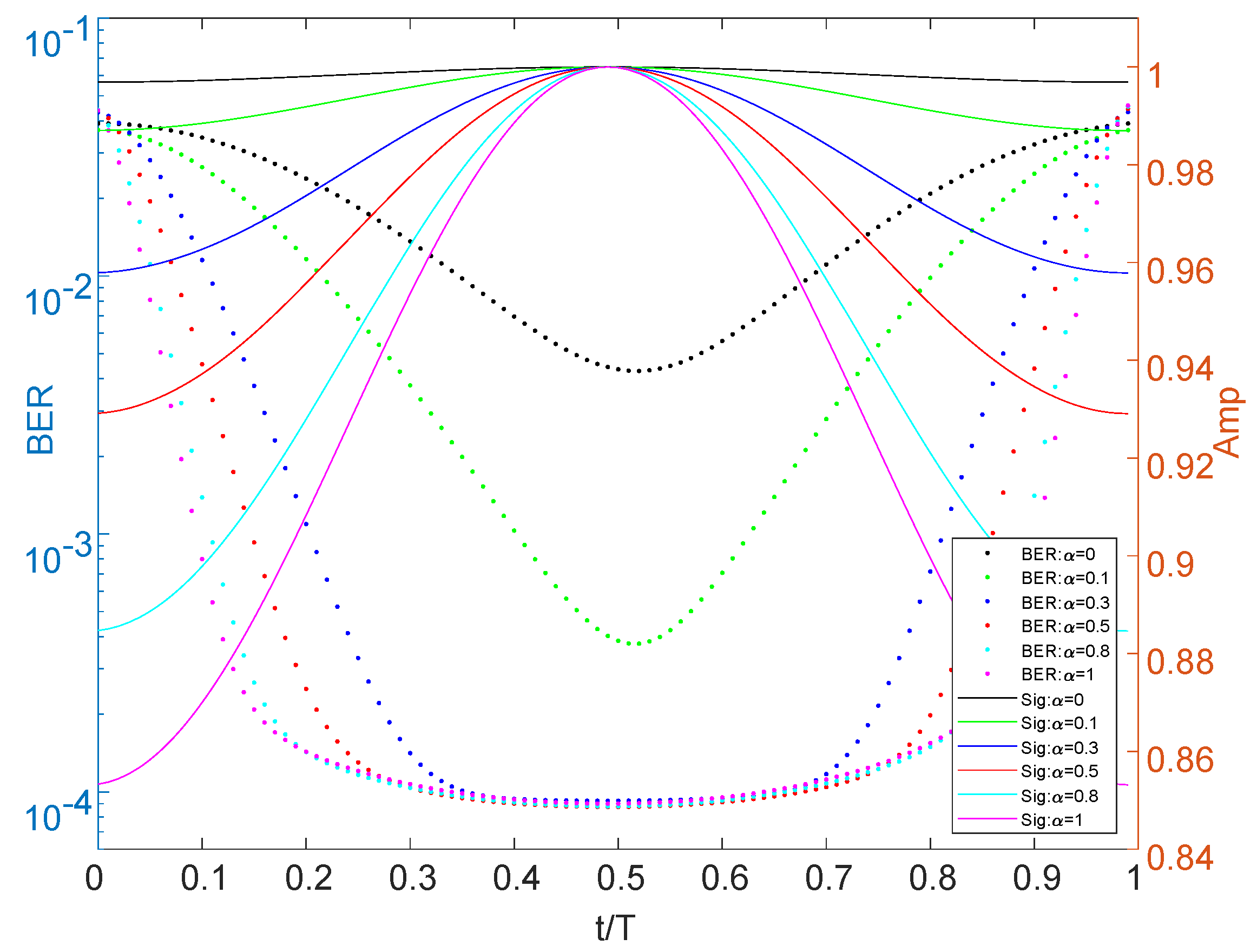
3.1. Maximum Output Energy (MOE) Criterion
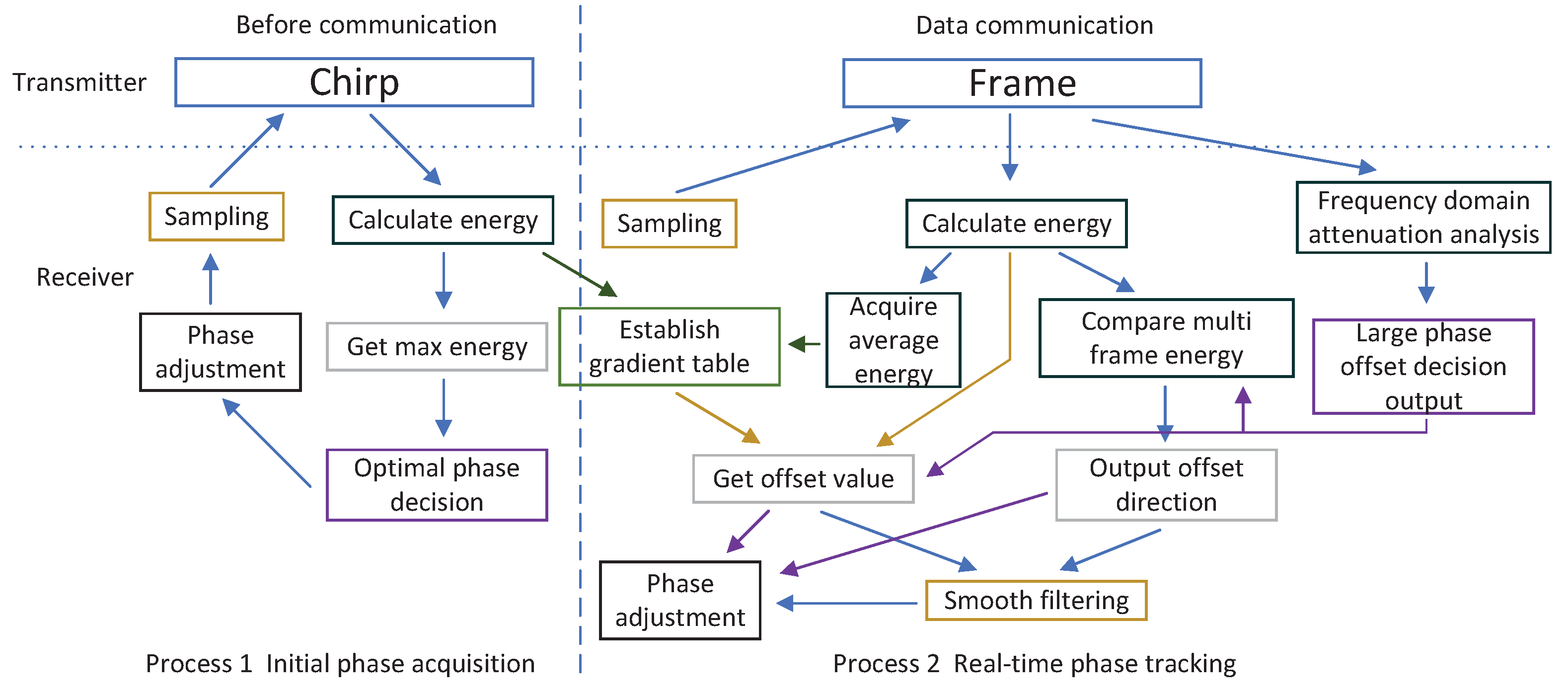
3.2. Initial Phase Acquisition
- The average power change of the received signal is maintained in a constant range in a short time;
- The sampling clock frequency offset of hardware changes very slowly relative to the symbol rate;
- The channel needs to remain fixed during this process.
3.3. Real-Time Phase Tracking
- Different frequencies have different attenuation amplitudes;
- Some high frequencies reflect slow attenuation, but the highest frequency is sensitive to phase change;
- The attenuation curve does not have linearization;
- The attenuation variation is slight around a small phase change interval;
- Before communication, the optimal phase is obtained through Chirp, and the basic data of the table is provided for the follow-up steps;
- In the communication process, frame sequence is used to complete time domain energy calculation and frequency domain phase determination;
- The average energy will be obtained to improve the gradient table;
- Multi-frame energy is used to calculate offset direction;
- Slow offset needs to be filtered smoothly, while fast channel transformation will be sent to adjust directly.
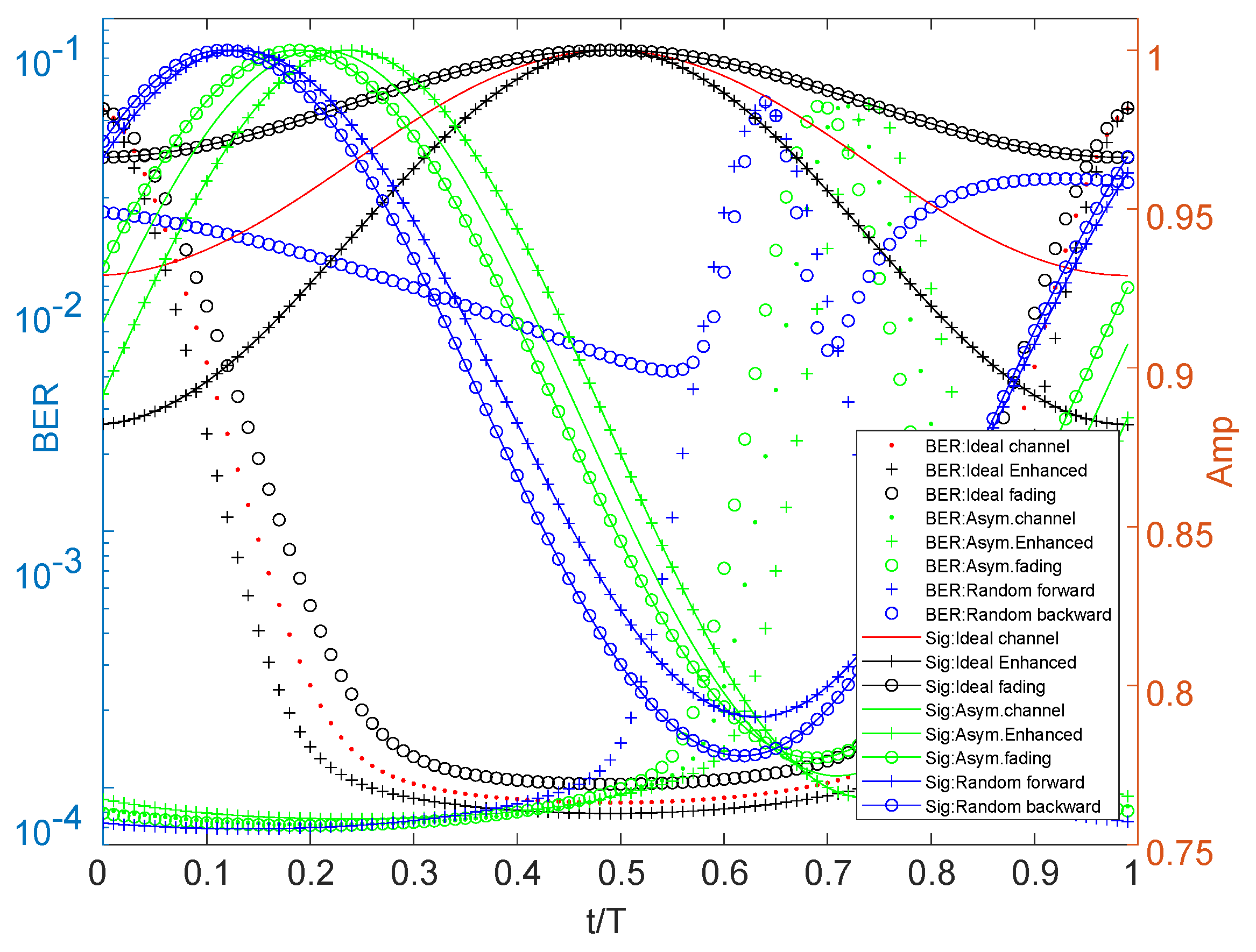
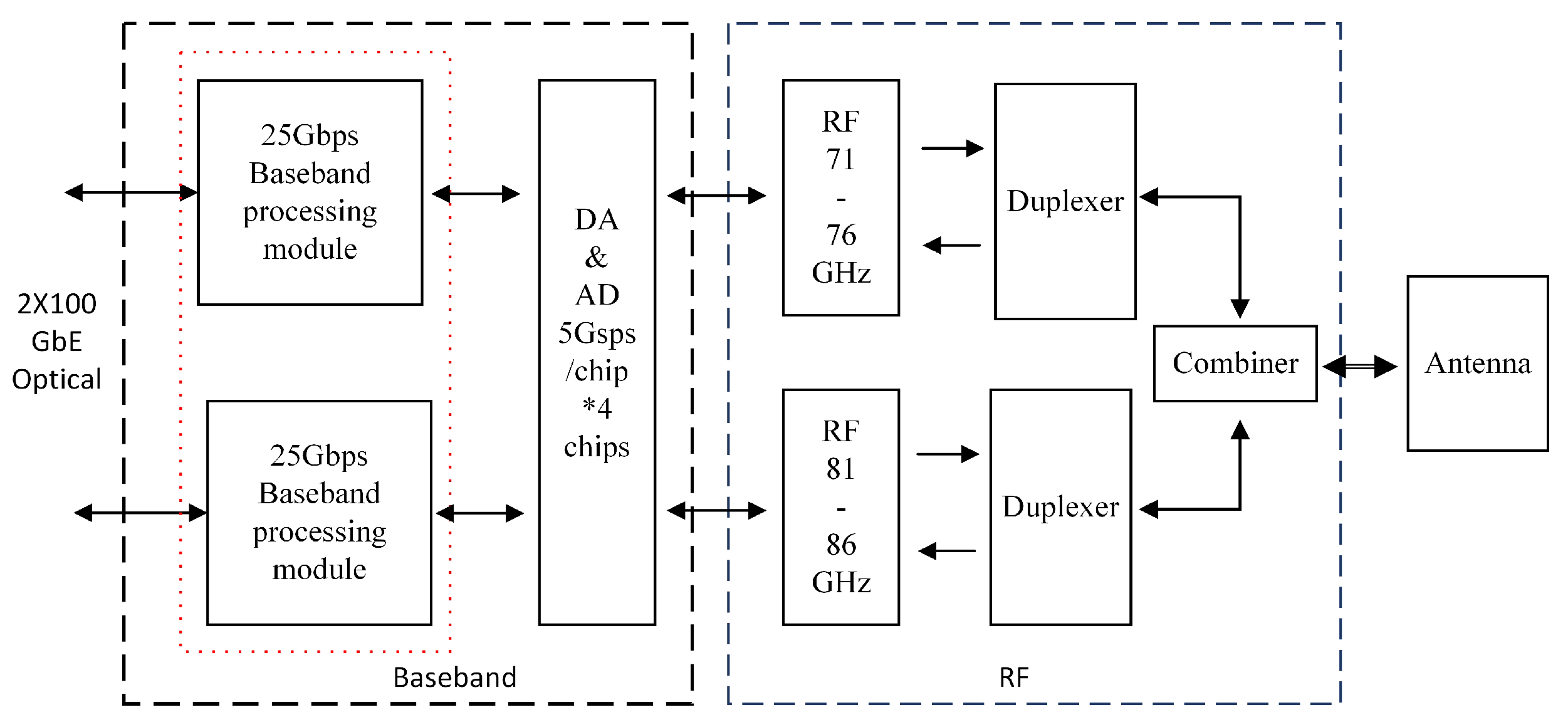
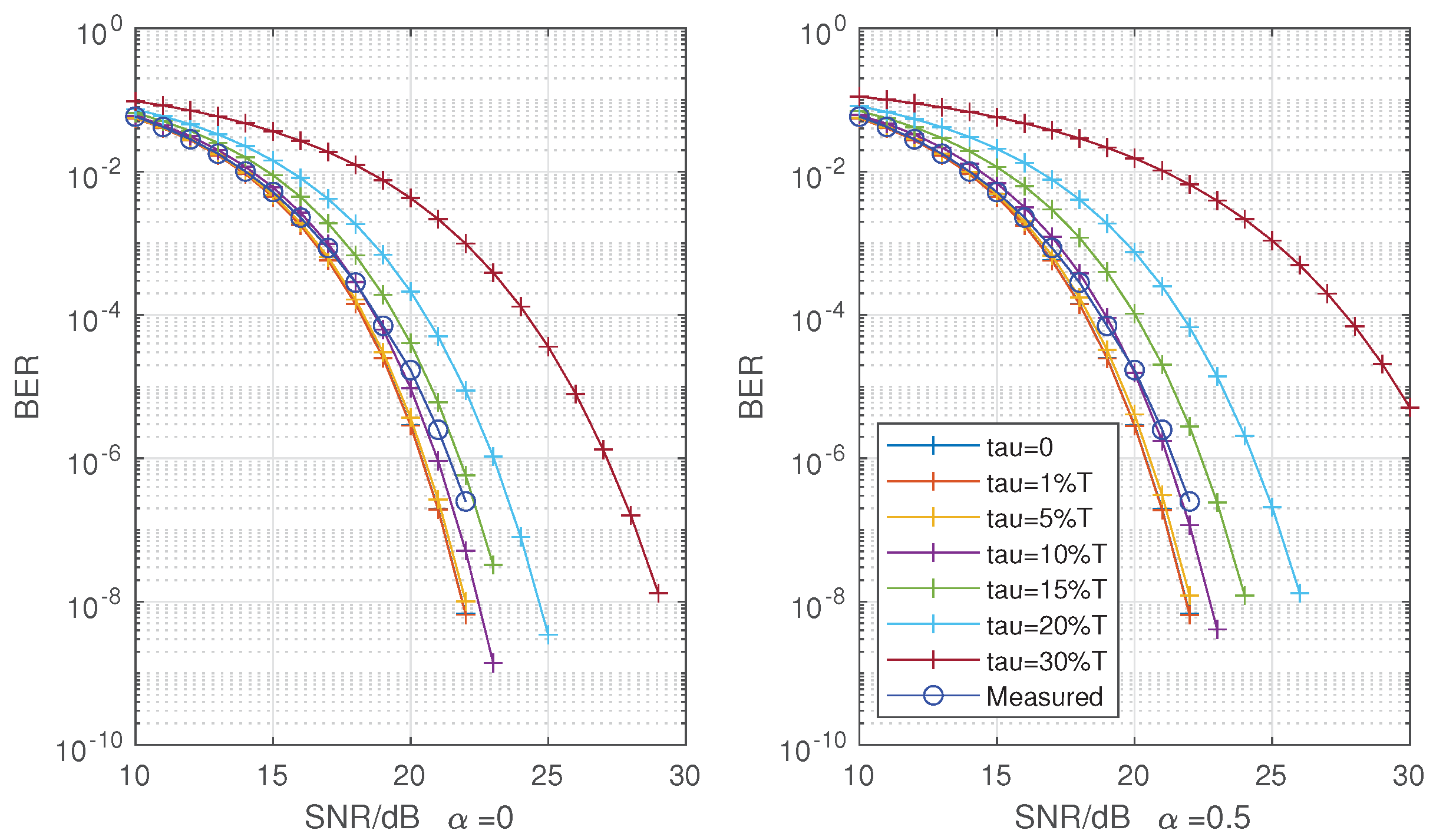
4. Hardware Verifications and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AWGN | Additive White Gaussian Noise |
| ADC | Analog to Digital Converter |
| QAM | Quadrature amplitude modulation |
| DAC | Digital to Analog Converter |
| ISI | Inter symbol interference |
| RC | Root raised cosines |
| MMSE | Minimum mean squared error |
| BER | Bit error rate |
| MOE | Maximum output energy |
| PWM | Pulse width modulation |
| PLL | Phase-locked loop |
| FTN | Faster than Nyquist |
| MIMO | Multiple-in multiple-out |
| THz | Tera-Hertz |
References
- Nie, S.; MacCartney, G.; Sun, S.; Rappaport, T. 28 GHz and 73 GHz signal outage study for millimeter wave cellular and backhaul communications. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 4856–4861. [Google Scholar]
- Hamza, A.; Deogun, J.; Alexander, D. Classification Framework for Free Space Optical Communication Links and Systems. IEEE Commun. Surv. Tutor. 2019, 21, 1346–1382. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, J.; Liu, R.; Guo, Y.; Hanzo, L. Airplane-Aided Integrated Networking for 6G Wireless: Will It Work? IEEE Veh. Technol. Mag. 2019, 14, 84–91. [Google Scholar] [CrossRef]
- Czegledi, C. Demonstrating 139 Gbps and 55.6 bps/Hz Spectrum Efficiency Using 8 × 8 MIMO over a 1.5-km Link at 73.5 GHz. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium, Los Angeles, CA, USA, 4–6 August 2020; pp. 539–542. [Google Scholar]
- Zhang, T.; Zhang, H.; Huang, X.; Suzuki, H.; Pathikulangara, J.; Smart, K.; Du, J.; Guo, J. A 245 GHz Real-Time Wideband Wireless Communication Link with 30 Gbps Data Rate. Photonics 2022, 9, 683. [Google Scholar] [CrossRef]
- Yousefi, M.; Yangzhang, X. Linear and Nonlinear Frequency-Division Multiplexing. IEEE Trans. Inf. Theory 2020, 66, 478–495. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Lv, S.; Wang, X. Adaptive Sub-Nyquist Spectrum Sensing for Ultra-Wideband Communication Systems. Symmetry 2019, 11, 342. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Huang, X.; Zhang, J.; Guo, Y. Dual pulse shaping transmission with sinc function based complementary Nyquist pulses. IET Commun. 2022, 16, 2091–2104. [Google Scholar] [CrossRef]
- Li, S.; Yuan, W.; Yuan, J.; Bai, B.; Wing, D.; Hanzo, L. Time-Domain vs. Frequency-Domain Equalization for FTN Signaling. IEEE Trans. Veh. Technol. 2020, 69, 9174–9179. [Google Scholar] [CrossRef]
- Clark, K.; Liu, Z. Modeling the Performance of the Clock Phase Caching Approach to Clock and Data Recovery. J. Light. Technol. 2022, 40, 1681–1689. [Google Scholar] [CrossRef]
- Lu, C.; Zhigang, C.; Zhi, J. Maximization-Based Simultaneous Localization and Mapping for Millimeter-Wave Communication Systems. Sensors 2022, 22, 6941. [Google Scholar]
- Liu, B.; Guo, X.; Kong, W.; Liu, T.; Dong, R.; Zhang, S. Stabilized Time Transfer via a 1000-km Optical Fiber Link Using High-Precision Delay Compensation System. Photonics 2022, 9, 522. [Google Scholar] [CrossRef]
- Yang, C.; Liu, X.; Jin, J.; Guo, Y.; Zhou, J. A Fast-Settling Phase-Locked Loop Utilizing Cycle-Slipping-Elimination PFDCP. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3998–4002. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Y.; Hong, Z.; Lin, M. A Novel Timing Synchronization Method for DCO-OFDM-Based VLC Systems. IEEE Photonics J. 2021, 13, 1–9. [Google Scholar] [CrossRef]
- Li, S.; Wang, S.; Zhao, C.; Cui, X.; Liu, J. A Non-Data-Aided Feedforward Timing Estimator Based on Multiple Cyclic Correlations for Short-Term Burst Signals. IEEE Commun. Lett. 2022, 26, 2166–2169. [Google Scholar] [CrossRef]
- Hao, X.; Lin, C.; Wu, Q. A Parallel Timing Synchronization Structure in Real-Time High Transmission Capacity Wireless Communication Systems. Electronics 2020, 9, 652. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Cui, S.; Ke, C.; Zhou, K.; Liu, D. All-Digital Timing Recovery for Free Space Optical Communication Signals with a Large Dynamic Range and Low OSNR. IEEE Photonics J. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Pan, P.; Wang, H.; Shen, L.; Lu, C. Equivalence of Joint ML-Decoding and Separate MMSE-ML Decoding for Training-Based MIMO Systems. IEEE Access 2019, 7, 178862–178869. [Google Scholar] [CrossRef]
- Hu, W.; Wang, Z.; Mei, R.; Lin, M. An Efficient Carrier Synchronization Scheme for Demodulation Systems. Electronics 2021, 10, 2942. [Google Scholar] [CrossRef]
- Shen, Y.; Shi, X.; Zhao, S.; Wang, Y. An Improved Phase Deviation Discriminator for Carrier Synchronization of APSK Signal in Satellite-to-Ground Communication Systems. Electronics 2022, 11, 1472. [Google Scholar] [CrossRef]
- Yadav, K.; Hsieh, P.; Carusone, A. Loop Dynamics Analysis of PAM-4 Mueller–Muller Clock and Data Recovery System. IEEE Open J. Circuits Syst. 2022, 3, 216–227. [Google Scholar] [CrossRef]
- Yuan, Y.; Luo, Y.; Zhang, Q.; Zhang, C. TFR Recovery From Incomplete Micro-Doppler Signal via AL-ADMM-Net. IEEE Access 2022, 10, 107395–107401. [Google Scholar] [CrossRef]
- Abdallah, S.; Salameh, A.; Saad, M. Joint Channel, Carrier Frequency Offset and I/Q Imbalance Estimation in Ambient Backscatter Communication Systems. IEEE Commun. Lett. 2021, 25, 2250–2254. [Google Scholar] [CrossRef]
- Lu, L.; Ma, X.; Liang, Y.; Liu, Z.; Fan, X.; Li, L. A 60-GHz Hybrid FMCW-Doppler Radar for Vibration Detection With a Robust I/Q Calibration Method. IEEE Sens. J. 2022, 22, 20464–20474. [Google Scholar] [CrossRef]
- Yang, G.; Zhou, F.; Qiao, G.; Zhao, Y.; Liu, Y.; Lu, Y.; He, Y. Optimized Doppler Estimation and Symbol Synchronization for Mobile M-ary Spread Spectrum Underwater Acoustic Communication. J. Mar. Sci. Eng. 2021, 9, 1001. [Google Scholar] [CrossRef]
- Wang, D.; Guo, R.; Liu, L.; Yuan, H.; Li, X.; Pan, J.; Tang, C. A Method of Whole-Network Adjustment for Clock Offset Based on Satellite-Ground and Inter-Satellite Link Observations. Remote Sens. 2022, 14, 5073. [Google Scholar] [CrossRef]
- Berggren, F.; Popović, B. Joint Radar and Communications With Multicarrier Chirp-Based Waveform. IEEE Open J. Commun. Soc. 2022, 3, 1702–1718. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Cheng, Z.; Li, H.; Zhu, D. A Software and Hardware Cooperation Method for Full Nyquist Rate Transmission Symbol Synchronization at E-Band Wireless Communication. Sensors 2022, 22, 8924. https://doi.org/10.3390/s22228924
Wang F, Cheng Z, Li H, Zhu D. A Software and Hardware Cooperation Method for Full Nyquist Rate Transmission Symbol Synchronization at E-Band Wireless Communication. Sensors. 2022; 22(22):8924. https://doi.org/10.3390/s22228924
Chicago/Turabian StyleWang, Fei, Zhiqun Cheng, Hang Li, and Dan Zhu. 2022. "A Software and Hardware Cooperation Method for Full Nyquist Rate Transmission Symbol Synchronization at E-Band Wireless Communication" Sensors 22, no. 22: 8924. https://doi.org/10.3390/s22228924
APA StyleWang, F., Cheng, Z., Li, H., & Zhu, D. (2022). A Software and Hardware Cooperation Method for Full Nyquist Rate Transmission Symbol Synchronization at E-Band Wireless Communication. Sensors, 22(22), 8924. https://doi.org/10.3390/s22228924






