Unstable Object Points during Measurements—Deformation Analysis Based on Pseudo Epoch Approach
Abstract
:1. Introduction
2. Models, Foundations, and Algorithms of Methods Applied
3. Empirical Tests
3.1. Simulated Leveling Network
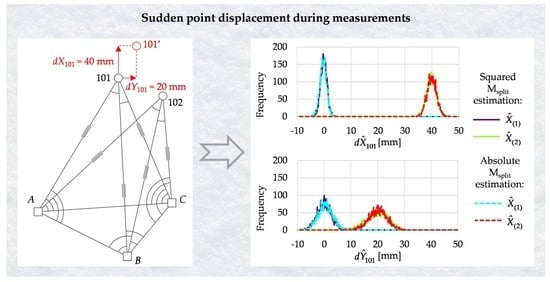
3.2. Simulated Horizontal Network
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Marković, M.Z.; Bajić, J.S.; Batilović, M.; Sušić, Z.; Joža, A.; Stojanović, G.M. Comparative Analysis of Deformation Determination by Applying Fiber-Optic 2D Deflection Sensors and Geodetic Measurements. Sensors 2019, 19, 844. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amiri-Simkooei, A.R.; Alaei-Tabatabaei, S.M.; Zangeneh-Nejad, F.; Voosoghi, B. Stability Analysis of Deformation-Monitoring Network Points Using Simultaneous Observation Adjustment of Two Epochs. J. Surv. Eng. 2017, 143, 04016020. [Google Scholar] [CrossRef] [Green Version]
- Caspary, W.F. Concepts of Network and Deformation Analysis; School of Surveying, University of New South Wales: Sydney, Australia, 1987; ISBN 978-0-85839-044-7. [Google Scholar]
- Chen, Y. Analysis of Deformation Surveys—A Generalized Method; University of New Brunswick: Fredericton, NB, Canada, 1983. [Google Scholar]
- Choudhury, M.M.; Rizos, C.; Harvey, B. A Survey of Techniques and Algorithms in Deformation Monitoring Applications and the Use of the Locata Technology for Such Applications. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 668–678. [Google Scholar]
- Susić, Z.; Batilović, M.; Ninkov, T.; Bulatović, V.; Aleksić, I.R.; Nikolić, G. Geometric Deformation Analysis in Free Geodetic Networks: Case Study for Fruska Gora in Serbia. Acta Geodyn. Geomater. 2017, 14, 341–355. [Google Scholar] [CrossRef] [Green Version]
- Gökalp, E.; Taşçı, L. Deformation Monitoring by GPS at Embankment Dams and Deformation Analysis. Surv. Rev. 2009, 41, 86–102. [Google Scholar] [CrossRef]
- Li, W.; Wang, C. GPS in the Tailings Dam Deformation Monitoring. Procedia Eng. 2011, 26, 1648–1657. [Google Scholar] [CrossRef] [Green Version]
- Wiśniewski, Z.; Duchnowski, R.; Dumalski, A. Efficacy of Msplit Estimation in Displacement Analysis. Sensors 2019, 19, 5047. [Google Scholar] [CrossRef] [Green Version]
- Duchnowski, R. Hodges-Lehmann Estimates in Deformation Analyses. J. Geod. 2013, 87, 873–884. [Google Scholar] [CrossRef] [Green Version]
- Duchnowski, R. Robustness of Strategy for Testing Levelling Mark Stability Based on Rank Tests. Surv. Rev. 2011, 43, 687–699. [Google Scholar] [CrossRef]
- Erdogan, B.; Hekimoglu, S. Effect of Subnetwork Configuration Design on Deformation Analysis. Surv. Rev. 2014, 46, 142–148. [Google Scholar] [CrossRef]
- Shaorong, Z. On Separability for Deformations and Gross Errors. Bull. Geodesique 1990, 64, 383–396. [Google Scholar] [CrossRef]
- Caspary, W.F.; Haen, W.; Borutta, H. Deformation Analysis by Statistical Methods. Technometrics 1990, 32, 49–57. [Google Scholar] [CrossRef]
- Gasinec, J.; Gasincova, S. Landslide Deformation Analysis Based on Robust M-Estimations. Inżynieria Miner. 2016, 17, 171–176. [Google Scholar]
- Ge, Y.; Yuan, Y.; Jia, N. More Efficient Methods among Commonly Used Robust Estimation Methods for GPS Coordinate Transformation. Surv. Rev. 2013, 45, 229–234. [Google Scholar] [CrossRef]
- Gui, Q.; Zhang, J. Robust Biased Estimation and Its Applications in Geodetic Adjustments. J. Geod. 1998, 72, 430–435. [Google Scholar] [CrossRef]
- Hekimoğlu, Ş. Robustifying Conventional Outlier Detection Procedures. J. Surv. Eng. 1999, 125, 69–86. [Google Scholar] [CrossRef]
- Labant, S.; Weiss, G.; Kukučka, P. Robust Adjustment of a Geodetic Network Measured by Satellite Technology in the Dargovských Hrdinov Suburb. Acta Montan. Slovaca 2014, 16, 229–237. [Google Scholar]
- Nowel, K. Robust M-Estimation in Analysis of Control Network Deformations: Classical and New Method. J. Surv. Eng. 2015, 141, 04015002. [Google Scholar] [CrossRef]
- Xu, P. Sign-Constrained Robust Least Squares, Subjective Breakdown Point and the Effect of Weights of Observations on Robustness. J. Geod. 2005, 79, 146–159. [Google Scholar] [CrossRef] [Green Version]
- Hodges, J.L.; Lehmann, E.L. Estimates of Location Based on Rank Tests. Ann. Math. Stat. 1963, 34, 598–611. [Google Scholar] [CrossRef]
- Wiśniewski, Z. Estimation of Parameters in a Split Functional Model of Geodetic Observations (Msplit Estimation). J. Geod. 2009, 83, 105–120. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Iterative Process of Msplit(q) Estimation. J. Surv. Eng. 2020, 146, 06020002. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Msplit Estimation Based on L1 Norm Condition. J. Surv. Eng. 2019, 145, 04019006. [Google Scholar] [CrossRef]
- Duchnowski, R.; Wiśniewski, Z. Shift-Msplit Estimation. Geod. Cartogr. 2011, 60, 79–97. [Google Scholar] [CrossRef]
- Wiśniewski, Z.; Zienkiewicz, M.H. Shift-M*split Estimation in Deformation Analyses. J. Surv. Eng. 2016, 142, 04016015. [Google Scholar] [CrossRef]
- Wyszkowska, P.; Duchnowski, R. Processing TLS Heterogeneous Data by Applying Robust Msplit Estimation. Measurement 2022, 197, 111298. [Google Scholar] [CrossRef]
- Zienkiewicz, M.H. Application of Msplit Estimation to Determine Control Points Displacements in Networks with Unstable Reference System. Surv. Rev. 2015, 47, 174–180. [Google Scholar] [CrossRef]
- Zienkiewicz, M.H.; Baryła, R. Determination of Vertical Indicators of Ground Deformation in the Old and Main City of Gdansk Area by Applying Unconventional Method of Robust Estimation. Acta Geodyn. Geomater. 2015, 12, 249–257. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Li, Z.; He, H.; Zhang, G.; Feng, Q.; Yang, H. A Squared Msplit Similarity Transformation Method for Stable Points Selection of Deformation Monitoring Network. Acta Geod. Cartogr. Sin. 2020, 49, 1419–1429. [Google Scholar] [CrossRef]
- Janicka, J.; Rapiński, J.; Błaszczak-Bąk, W.; Suchocki, C. Application of the Msplit Estimation Method in the Detection and Dimensioning of the Displacement of Adjacent Planes. Remote Sens. 2020, 12, 3203. [Google Scholar] [CrossRef]
- Wiśniewski, Z. Msplit(q) Estimation: Estimation of Parameters in a Multi Split Functional Model of Geodetic Observations. J. Geod. 2010, 84, 355–372. [Google Scholar] [CrossRef]
- Zienkiewicz, M.H.; Hejbudzka, K.; Dumalski, A. Multi Split Functional Model of Geodetic Observations in Deformation Analyses of the Olsztyn Castle. Acta Geodyn. Geomater. 2017, 14, 195–204. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y. Robust Estimation for Dependent Observations. Manuscr. Geod. 1994, 19, 10–17. [Google Scholar]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Statist. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, P. Comparing the Estimates of the Variance of Unit Weight in Multiplicative Error Models. Acta Geod. Geophys. 2015, 50, 353–363. [Google Scholar] [CrossRef] [Green Version]
- Suraci, S.S.; de Oliveira, L.C.; Klein, I.; Rofatto, V.F.; Matsuoka, M.T.; Baselga, S. Monte Carlo-Based Covariance Matrix of Residuals and Critical Values in Minimum L1-Norm. Math. Probl. Eng. 2021, 2021, e8123493. [Google Scholar] [CrossRef]
- Rofatto, V.F.; Matsuoka, M.T.; Klein, I.; Veronez, M.R.; Bonimani, M.L.; Lehmann, R. A Half-Century of Baarda’s Concept of Reliability: A Review, New Perspectives, and Applications. Surv. Rev. 2020, 52, 261–277. [Google Scholar] [CrossRef]
- Spaete, L.P.; Glenn, N.F.; Derryberry, D.R.; Sankey, T.T.; Mitchell, J.J.; Hardegree, S.P. Vegetation and Slope Effects on Accuracy of a LiDAR-Derived DEM in the Sagebrush Steppe. Remote Sens. Lett. 2011, 2, 317–326. [Google Scholar] [CrossRef]
- Baarda, W. A Testing Procedure for Use in Geodetic Networks; Publications on Geodesy 9; Nethelands Geodetic Commision: Delft, The Netherlands, 1968; Volume 2, ISBN 978 90 6132 209. [Google Scholar]
- Pope, A.J. The Statistics of Residuals and the Detection of Outliers; NOAA Technical Report; U.S. Department of Commerce, National Oceanic and Atmospheric Administration, National Ocean Survey, National Geodetic Survey, Geodetic Research and Development Laboratory: Rockville, MD, USA, 1976; Volume NGS 1.
- Baselga, S. Nonexistence of Rigorous Tests for Multiple Outlier Detection in Least-Squares Adjustment. J. Surv. Eng. 2011, 137, 109–112. [Google Scholar] [CrossRef]
- Aydin, C. Power of Global Test in Deformation Analysis. J. Surv. Eng. 2012, 138, 51–56. [Google Scholar] [CrossRef]
- Nowel, K. Application of Monte Carlo Method to Statistical Testing in Deformation Analysis Based on Robust M-Estimation. Surv. Rev. 2016, 48, 212–223. [Google Scholar] [CrossRef]
- Nowel, K. Specification of Deformation Congruence Models Using Combinatorial Iterative DIA Testing Procedure. J. Geod. 2020, 94, 118. [Google Scholar] [CrossRef]
- DeLoach, S.R. Continuous Deformation Monitoring with GPS. J. Surv. Eng. 1989, 115, 93–110. [Google Scholar] [CrossRef]
- Xu, P. Nonlinear Filtering of Continuous Systems: Foundational Problems and New Results. J. Geod. 2003, 77, 247–256. [Google Scholar] [CrossRef]
- Qin, J.; Gao, Z.; Wang, X.; Yang, S. Three-Dimensional Continuous Displacement Measurement with Temporal Speckle Pattern Interferometry. Sensors 2016, 16, 2020. [Google Scholar] [CrossRef] [PubMed]








| Variant | Point | LS | Huber | HLW | ||||
|---|---|---|---|---|---|---|---|---|
| Variant I | 101 | 2.0 | 0.0 | 4.1 | −0.1 | 10.1 | −0.1 | 10.0 |
| 102 | 4.1 | 0.1 | 0.9 | −0.1 | 19.9 | 0.0 | 20.2 | |
| 104 | 1.3 | 0.0 | 0.2 | 0.0 | 3.0 | −0.1 | 1.0 | |
| Variant II | 101 | 6.8 | 6.8 | 9.1 | 0.9 | 10.1 | 0.4 | 10.1 |
| 102 | 11.4 | 11.6 | 10.6 | 0.9 | 20.0 | 0.3 | 20.0 | |
| 104 | 1.8 | 1.8 | 0.2 | 0.9 | 0.0 | 0.3 | 0.0 | |
| Variant III | 101 | 0.8 | 0.6 | 1.0 | 0.9 | 1.6 | 0.4 | 1.9 |
| 102 | 0.3 | 0.3 | 0.4 | −0.1 | 1.5 | −0.1 | 1.4 | |
| 104 | 0.2 | 0.1 | 0.1 | −0.2 | 0.8 | −0.1 | 0.7 | |
| Variant IV | 101 | 1.6 | 1.6 | 1.8 | 0.8 | 2.5 | 1.0 | 2.4 |
| 102 | 1.1 | 1.1 | 1.4 | 0.3 | 2.1 | 0.4 | 2.1 | |
| 104 | 0.3 | 0.3 | 0.1 | 0.2 | 0.2 | 0.2 | 0.1 |
| Variant | Point | LS | Huber | HLW | ||||
|---|---|---|---|---|---|---|---|---|
| Variant I | 101 | 2.1 | 0.6 | 4.1 | 1.2 | 1.4 | 1.2 | 1.9 |
| 102 | 4.1 | 0.5 | 1.0 | 0.9 | 1.0 | 0.9 | 1.0 | |
| 104 | 1.4 | 0.4 | 0.4 | 1.0 | 5.1 | 1.0 | 4.7 | |
| Variant II | 101 | 6.9 | 6.8 | 9.1 | 3.9 | 1.2 | 2.7 | 1.7 |
| 102 | 11.4 | 12.2 | 10.7 | 3.9 | 0.7 | 3.1 | 0.7 | |
| 104 | 1.9 | 1.8 | 0.4 | 3.9 | 1.4 | 2.1 | 2.7 | |
| Variant III | 101 | 1.0 | 0.9 | 1.1 | 1.7 | 2.1 | 1.6 | 2.1 |
| 102 | 0.5 | 0.5 | 0.6 | 0.8 | 1.6 | 0.8 | 1.6 | |
| 104 | 0.4 | 0.4 | 0.4 | 0.9 | 1.3 | 0.8 | 1.2 | |
| Variant IV | 101 | 1.7 | 1.7 | 1.9 | 1.7 | 1.6 | 1.8 | 1.6 |
| 102 | 1.2 | 1.2 | 1.5 | 1.0 | 1.0 | 0.9 | 1.0 | |
| 104 | 0.4 | 0.4 | 0.4 | 1.0 | 1.2 | 1.0 | 1.1 |
| Variant | Estimator | LS | Huber | HLW | ||||
|---|---|---|---|---|---|---|---|---|
| Variant I | −4.4 | 0.6 | 18.8 | −0.1 | 39.8 | −0.2 | 39.9 | |
| 0.0 | 1.6 | 6.6 | 0.0 | 19.2 | 0.2 | 19.4 | ||
| Variant II | 13.2 | 1.2 | 38.2 | −0.1 | 40.0 | −0.3 | 40.0 | |
| 0.6 | 7.5 | 12.6 | 0.1 | 20.1 | 0.5 | 20.2 |
| Variant | Estimator | LS | Huber | HLW | ||||
|---|---|---|---|---|---|---|---|---|
| Variant I | 12.8 | 1.3 | 18.8 | 1.3 | 2.0 | 1.3 | 2.0 | |
| 4.7 | 2.5 | 7.1 | 2.6 | 5.3 | 2.5 | 5.4 | ||
| Variant II | 13.2 | 1.7 | 38.2 | 1.2 | 1.8 | 1.3 | 1.8 | |
| 1.7 | 7.8 | 12.8 | 2.7 | 4.1 | 2.8 | 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duchnowski, R.; Wyszkowska, P. Unstable Object Points during Measurements—Deformation Analysis Based on Pseudo Epoch Approach. Sensors 2022, 22, 9030. https://doi.org/10.3390/s22239030
Duchnowski R, Wyszkowska P. Unstable Object Points during Measurements—Deformation Analysis Based on Pseudo Epoch Approach. Sensors. 2022; 22(23):9030. https://doi.org/10.3390/s22239030
Chicago/Turabian StyleDuchnowski, Robert, and Patrycja Wyszkowska. 2022. "Unstable Object Points during Measurements—Deformation Analysis Based on Pseudo Epoch Approach" Sensors 22, no. 23: 9030. https://doi.org/10.3390/s22239030