Crystalline Hydrate Dehydration Sensing Based on Integrated Terahertz Whispering Gallery Mode Resonators
Abstract
:1. Introduction
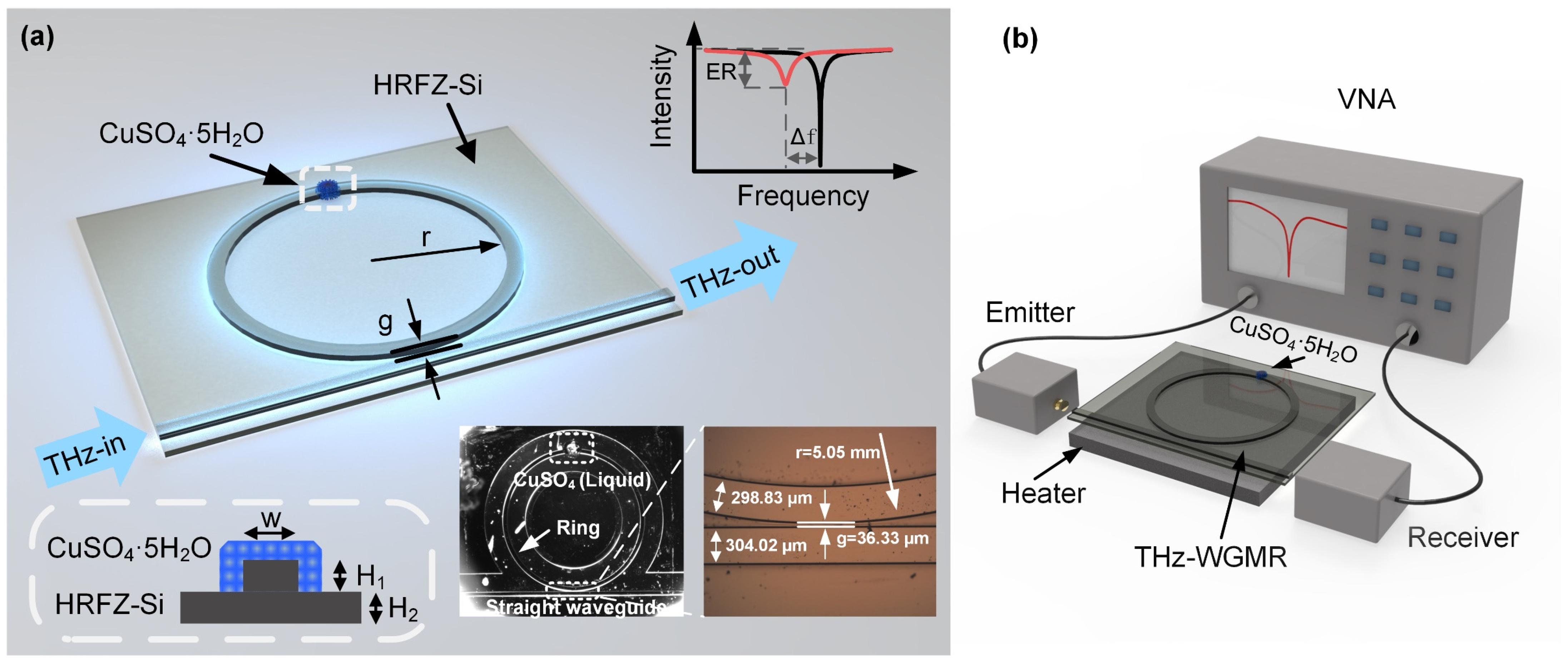
2. Design of Devices and Experiments
3. Results and Discussion
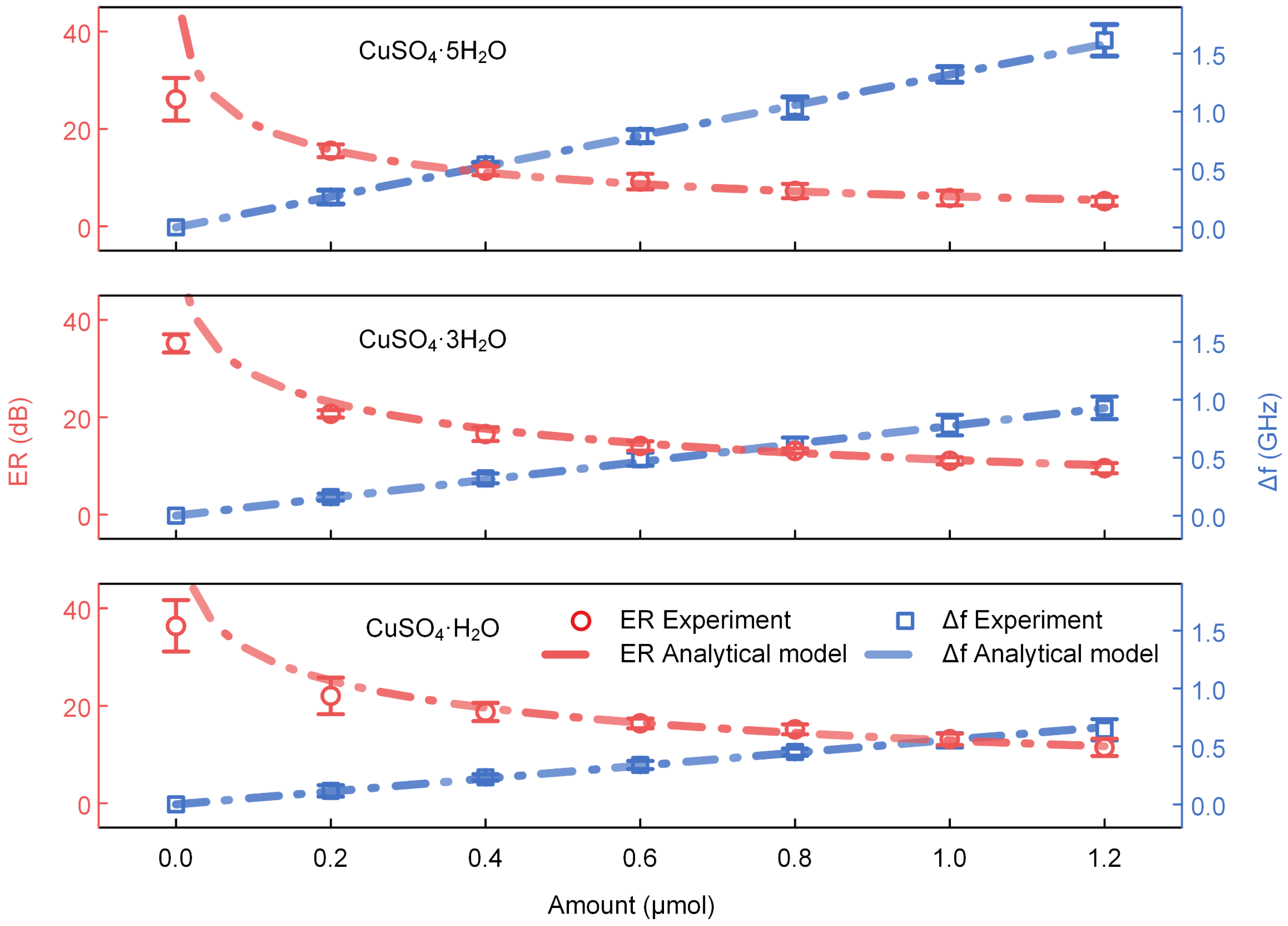
3.1. Water Content Identification of CuSO4·xH2O (x = 5, 3, 1)
3.2. Sensitivity Characterization
3.3. Monitoring of Dynamic Dehydration from CuSO4·5H2O to CuSO4·3H2O at Different Temperatures
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soda, G.; Chiba, T. Deuteron Magnetic Resonance Study of Cupric Sulfate Pentahydrate. J. Chem. Phys. 1969, 50, 439–455. [Google Scholar] [CrossRef]
- Zhang, Y.; Hsung, R.P.; Tracey, M.R.; Kurtz, K.C.M.; Vera, E.L. Copper Sulfate-Pentahydrate-1,10-Phenanthroline Catalyzed Amidations of Alkynyl Bromides. Synthesis of Heteroaromatic Amine Substituted Ynamides. Org. Lett. 2004, 6, 1151–1154. [Google Scholar] [CrossRef] [PubMed]
- Bonfoh, B.; Zinsstag, J.; Farah, Z.; Simbé, C.F.; Alfaroukh, I.O.; Aebi, R.; Badertscher, R.; Collomb, M.; Meyer, J.; Rehberger, B. Raw milk composition of Malian Zebu cows (Bos indicus) raised under traditional system. J. Food Compos. Anal. 2005, 18, 29–38. [Google Scholar] [CrossRef]
- Sharma, S.K.; Jotshi, C.K.; Kumar, S. Thermal stability of sodium salt hydrates for solar energy storage applications. Sol. Energy 1990, 45, 177–181. [Google Scholar] [CrossRef]
- Hadjieva, M.; Stoykov, R.; Filipova, T. Composite salt-hydrate concrete system for building energy storage. Renew. Energy 2000, 19, 111–115. [Google Scholar] [CrossRef]
- Kiatsiriroat, T.; Tiansuwan, J.; Suparos, T.; Na Thalang, K. Performance analysis of a direct-contact thermal energy storage-solidification. Renew. Energy 2000, 20, 195–206. [Google Scholar] [CrossRef]
- Reynard, B.; Bass, J.D. Elasticity of lawsonite and seismological signature of metamorphism and water cycling in the subducting oceanic crust. J. Metamorph. Geol. 2014, 32, 479–487. [Google Scholar] [CrossRef]
- Bezacier, L.; Reynard, B.; Bass, J.D.; Sanchez-Valle, C.; Van de Moortèle, B. Elasticity of antigorite, seismic detection of serpentinites, and anisotropy in subduction zones. Earth Planet. Sci. Lett. 2010, 289, 198–208. [Google Scholar] [CrossRef]
- Chantel, J.; Mookherjee, M.; Frost, D.J. The elasticity of lawsonite at high pressure and the origin of low velocity layers in subduction zones. Earth Planet. Sci. Lett. 2012, 349–350, 116–125. [Google Scholar] [CrossRef]
- Kameda, J.; Hirauchi, K.-i. Rheological properties of composite serpentine-brucite suspensions: Implications for mudflow behavior on forearc seamounts. Mar. Geol. 2018, 403, 191–196. [Google Scholar] [CrossRef]
- Wendlandt, W.W. A new look at the thermal properties of copper sulfate 5-hydrate. Thermochim. Acta 1970, 1, 419–427. [Google Scholar] [CrossRef]
- Charbonnier, F. Thermal behaviour of two new salts of malonic acid: Cu(C3H2O4)·4H2O and Cu(NH4)2(C3H2O4)2. Thermochim. Acta 1974, 10, 285–298. [Google Scholar] [CrossRef]
- Yang, D.; Xie, L.; Bobicki, E.; Xu, Z.; Liu, Q.; Zeng, H. Probing Anisotropic Surface Properties and Interaction Forces of Chrysotile Rods by Atomic Force Microscopy and Rheology. Langmuir 2014, 30, 10809–10817. [Google Scholar] [CrossRef]
- Pignon, F.; Magnin, A.; Piau, J.M. Thixotropic colloidal suspensions and flow curves with minimum: Identification of flow regimes and rheometric consequences. J. Rheol. 1996, 40, 573–587. [Google Scholar] [CrossRef]
- Ndlovu, B.; Forbes, E.; Farrokhpay, S.; Becker, M.; Bradshaw, D.; Deglon, D. A preliminary rheological classification of phyllosilicate group minerals. Miner. Eng. 2014, 55, 190–200. [Google Scholar] [CrossRef]
- Karato, S.-I. Mapping Water Content in the Upper Mantle. Geophys. Monogr. Ser. 2004, 138, 135–152. [Google Scholar] [CrossRef]
- de Castelnuovo, S.; Harness, J.B.; McColm, I.J. The Role of Liquid Water in Crystalline Hydrate Dehydration: Copper sulphate pentahydrate. J. Therm. Anal. Calorim. 2001, 63, 233–247. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, D.; Tkachev, S.N.; Dera, P.K. Partnership for eXtreme Xtallography (PX2)—A state-of-the-art experimental facility for extreme-conditions crystallography: A case study of pressure-induced phase transition in natural ilvaite. Matter Radiat. Extremes 2022, 7, 028401. [Google Scholar] [CrossRef]
- Dong, Z.; Young, V.G.; Sheth, A.; Munson, E.J.; Schroeder, S.A.; Prakash, I.; Grant, D.J.W. Crystal Structure of Neotame Anhydrate Polymorph G. Pharm. Res. 2002, 19, 1549–1553. [Google Scholar] [CrossRef]
- Peets, P.; Kaupmees, K.; Vahur, S.; Leito, I. Reflectance FT-IR spectroscopy as a viable option for textile fiber identification. Heritage Sci. 2019, 7, 93. [Google Scholar] [CrossRef]
- White, R.L. Variable temperature infrared study of copper sulfate pentahydrate dehydration. Thermochim. Acta 2012, 528, 58–62. [Google Scholar] [CrossRef]
- Taylor, E.A.; Mileti, C.J.; Ganesan, S.; Kim, J.H.; Donnelly, E. Measures of Bone Mineral Carbonate Content and Mineral Maturity/Crystallinity for FT-IR and Raman Spectroscopic Imaging Differentially Relate to Physical–Chemical Properties of Carbonate-Substituted Hydroxyapatite. Calcif. Tissue Int. 2021, 109, 77–91. [Google Scholar] [CrossRef]
- Chang, H.; Huang, P.J. Dehydration of CuSO4 5H2O Studied by Thermo-Raman Spectroscopy. J. Chin. Chem. Soc. 1998, 45, 59–66. [Google Scholar] [CrossRef]
- Jurczak, E.; Mazurek, A.H.; Szeleszczuk, Ł.; Pisklak, D.M.; Zielińska-Pisklak, M. Pharmaceutical Hydrates Analysis—Overview of Methods and Recent Advances. Pharmaceutics 2020, 12, 959. [Google Scholar] [CrossRef] [PubMed]
- Sensogut, C.; Yildirim, O.S.; Cinar, I.; Ozdeniz, A.H. A Statistical Study on Thermogravimetry of Some Coals in Turkey. Energy Sources Part A 2007, 30, 334–338. [Google Scholar] [CrossRef]
- Sava, I.; Burescu, A.; Lisa, G. Study of thermal behavior of polyimides containing pendent-substituted azobenzene units. Polym. Bull. 2014, 71, 1359–1373. [Google Scholar] [CrossRef]
- Ng, W.-L.; Ho, C.-C.; Ng, S.-K. Isothermal dehydration of copper sulfate pentahydrate and trihydrate. J. Inorg. Nucl. Chem. 1978, 40, 459–462. [Google Scholar] [CrossRef]
- El-Houte, S.; El-Sayed Ali, M.; Sørensen, O.T. Dehydration of CuSO4·5H2O studied by conventional and advanced thermal analysis techniques. Thermochim. Acta 1989, 138, 107–114. [Google Scholar] [CrossRef]
- Davies, A.G.; Linfield, E.H.; Pepper, M.; Crowe, T.W.; Globus, T.; Woolard, D.L.; Hesler, J.L. Terahertz sources and detectors and their application to biological sensing. Philos. Trans. R. Soc. London. Ser. A: Math. Phys. Eng. Sci. 2004, 362, 365–377. [Google Scholar] [CrossRef]
- Fu, X.; Yang, G.; Sun, J.; Zhou, J. Vibrational Spectra of Copper Sulfate Hydrates Investigated with Low-Temperature Raman Spectroscopy and Terahertz Time Domain Spectroscopy. J. Phys. Chem. A 2012, 116, 7314–7318. [Google Scholar] [CrossRef]
- Ruggiero, M.T.; Korter, T.M. Uncovering the Terahertz Spectrum of Copper Sulfate Pentahydrate. J. Phys. Chem. A 2016, 120, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Afsah-Hejri, L.; Hajeb, P.; Ara, P.; Ehsani, R.J. A Comprehensive Review on Food Applications of Terahertz Spectroscopy and Imaging. Compr. Rev. Food Sci. Food Saf. 2019, 18, 1563–1621. [Google Scholar] [CrossRef] [PubMed]
- Vogt, D.W.; Jones, A.H.; Haase, T.A.; Leonhardt, R. Subwavelength thick ultrahigh-Q terahertz disc microresonators. Photonics Res. 2020, 8, 1183–1188. [Google Scholar] [CrossRef]
- Vogt, D.W.; Jones, A.H.; Schwefel, H.G.L.; Leonhardt, R. Anomalous blue-shift of terahertz whispering-gallery modes via dielectric and metallic tuning. Opt. Lett. 2019, 44, 1319–1322. [Google Scholar] [CrossRef] [Green Version]
- Vogt, D.W.; Leonhardt, R. Terahertz whispering gallery mode bubble resonator. Optica 2017, 4, 809–812. [Google Scholar] [CrossRef] [Green Version]
- Vogt, D.W.; Leonhardt, R. Ultra-high Q terahertz whispering-gallery modes in a silicon resonator. APL Photonics 2018, 3, 051702. [Google Scholar] [CrossRef] [Green Version]
- Yuan, S.; Chen, L.; Wang, Z.; Wang, R.; Wu, X.; Zhang, X. Tunable high-quality Fano resonance in coupled terahertz whispering-gallery-mode resonators. Appl. Phys. Lett. 2019, 115, 201102. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Xie, L.; Ying, Y. Mechanisms and applications of terahertz metamaterial sensing: A review. Nanoscale 2017, 9, 13864–13878. [Google Scholar] [CrossRef]
- Ako, R.T.; Upadhyay, A.; Withayachumnankul, W.; Bhaskaran, M.; Sriram, S. Dielectrics for Terahertz Metasurfaces: Material Selection and Fabrication Techniques. Adv. Opt. Mater. 2020, 8, 1900750. [Google Scholar] [CrossRef]
- Chen, H.T.; O’Hara, J.F.; Azad, A.K.; Taylor, A.J. Manipulation of terahertz radiation using metamaterials. Laser Photonics Rev. 2011, 5, 513–533. [Google Scholar] [CrossRef]
- Walia, S.; Shah, C.M.; Gutruf, P.; Nili, H.; Chowdhury, D.R.; Withayachumnankul, W.; Bhaskaran, M.; Sriram, S. Flexible metasurfaces and metamaterials: A review of materials and fabrication processes at micro- and nano-scales. Appl. Phys. Rev. 2015, 2, 011303. [Google Scholar] [CrossRef]
- Okamoto, K.; Tsuruda, K.; Diebold, S.; Hisatake, S.; Fujita, M.; Nagatsuma, T. Terahertz Sensor Using Photonic Crystal Cavity and Resonant Tunneling Diodes. J. Infrared Millim. Terahertz Waves 2017, 38, 1085–1097. [Google Scholar] [CrossRef]
- Kurt, H.; Citrin, D.S. Photonic crystals for biochemical sensing in the terahertz region. Appl. Phys. Lett. 2005, 87, 041108. [Google Scholar] [CrossRef]
- Islam, M.S.; Sultana, J.; Ahmed, K.; Islam, M.R.; Dinovitser, A.; Ng, B.W.H.; Abbott, D. A Novel Approach for Spectroscopic Chemical Identification Using Photonic Crystal Fiber in the Terahertz Regime. IEEE Sens. J. 2018, 18, 575–582. [Google Scholar] [CrossRef]
- Vogt, D.W.; Jones, A.H.; Leonhardt, R. Terahertz Gas-Phase Spectroscopy Using a Sub-Wavelength Thick Ultrahigh-Q Microresonator. Sensors 2020, 20, 3005. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yuan, S.; Dong, G.; Wang, R.; Chen, L.; Wu, X.; Zhang, X. On-chip single-mode high-Q terahertz whispering gallery mode resonator. Opt. Lett. 2019, 44, 2835–2838. [Google Scholar] [CrossRef]
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Kumar Selvaraja, S.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Liu, L.; Dong, J.; Gao, D.; Zheng, A.; Zhang, X. On-chip passive three-port circuit of all-optical ordered-route transmission. Sci. Rep. 2015, 5, 10190. [Google Scholar] [CrossRef] [Green Version]
- Yuan, S.; Chen, L.; Wang, Z.; Wang, R.; Wu, X.; Zhang, X. Tunable high-quality Fano resonance in coupled terahertz whispering-gallery-mode resonators. Appl. Phys. Lett. 2019, 115, 201102. [Google Scholar] [CrossRef] [Green Version]
- Vogt, D.W.; Jones, A.H.; Leonhardt, R. Thermal tuning of silicon terahertz whispering-gallery mode resonators. Appl. Phys. Lett. 2018, 113, 011101. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Z.; Yuan, S.; Deng, W.; Cai, J.; Qiu, Y.; Zhao, Y.; Wang, Z.; Chen, L.; Liu, H.; Wu, X.; et al. Crystalline Hydrate Dehydration Sensing Based on Integrated Terahertz Whispering Gallery Mode Resonators. Sensors 2022, 22, 9116. https://doi.org/10.3390/s22239116
Hou Z, Yuan S, Deng W, Cai J, Qiu Y, Zhao Y, Wang Z, Chen L, Liu H, Wu X, et al. Crystalline Hydrate Dehydration Sensing Based on Integrated Terahertz Whispering Gallery Mode Resonators. Sensors. 2022; 22(23):9116. https://doi.org/10.3390/s22239116
Chicago/Turabian StyleHou, Zhibo, Shixing Yuan, Wentao Deng, Jiahua Cai, Yaqin Qiu, Yunong Zhao, Ziwei Wang, Liao Chen, Huan Liu, Xiaojun Wu, and et al. 2022. "Crystalline Hydrate Dehydration Sensing Based on Integrated Terahertz Whispering Gallery Mode Resonators" Sensors 22, no. 23: 9116. https://doi.org/10.3390/s22239116
APA StyleHou, Z., Yuan, S., Deng, W., Cai, J., Qiu, Y., Zhao, Y., Wang, Z., Chen, L., Liu, H., Wu, X., & Zhang, X. (2022). Crystalline Hydrate Dehydration Sensing Based on Integrated Terahertz Whispering Gallery Mode Resonators. Sensors, 22(23), 9116. https://doi.org/10.3390/s22239116






