A New Concept of Contiguous-Swath SAR Imaging with High Resolution: Strip-Spot SAR †
Abstract
1. Introduction
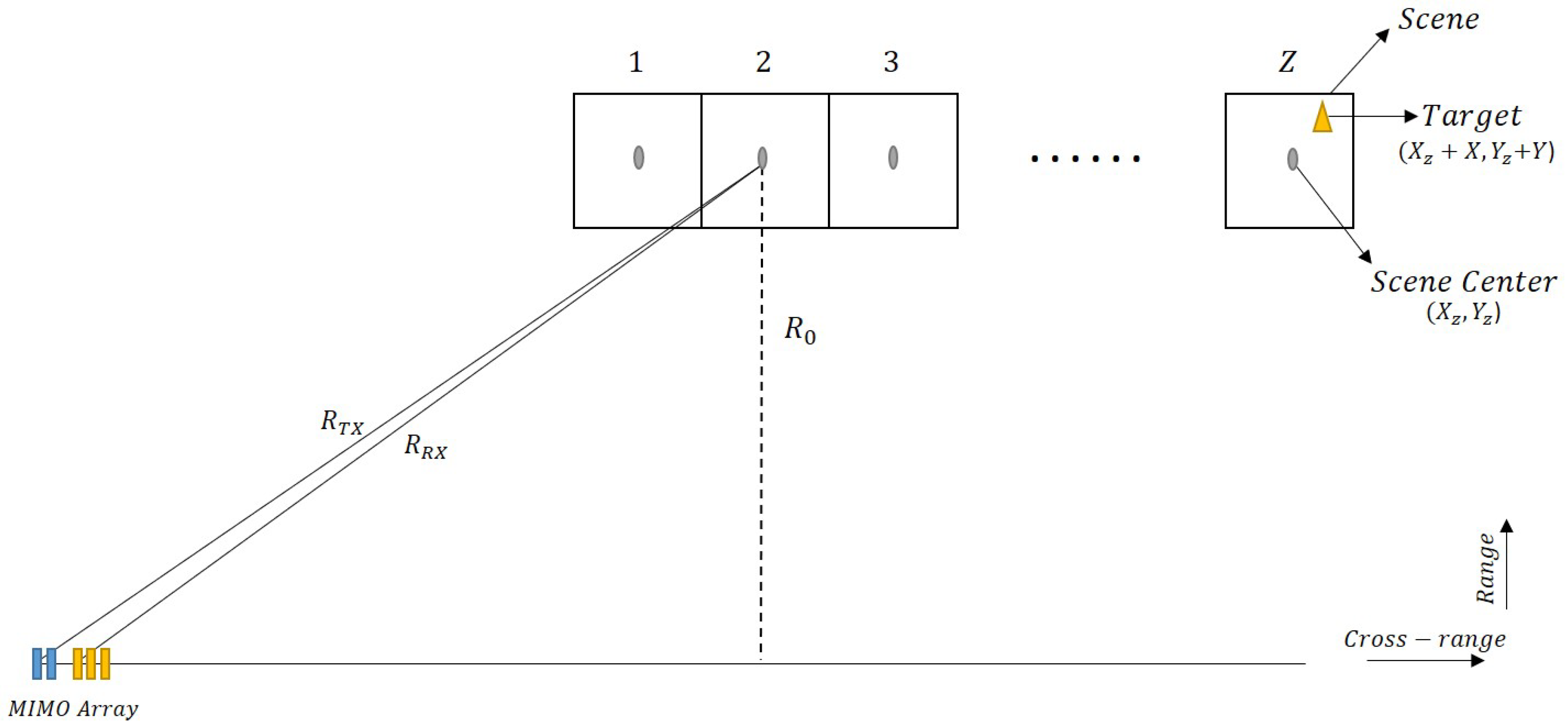
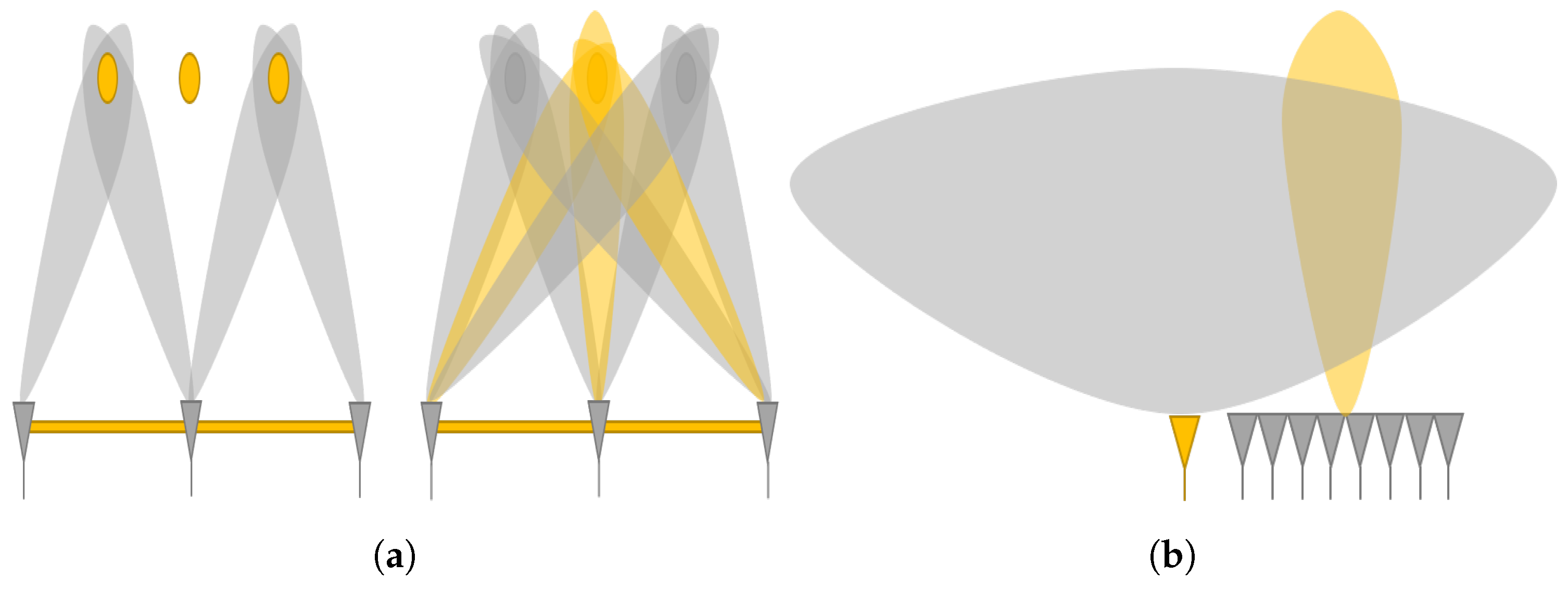
2. Strip-Spot SAR
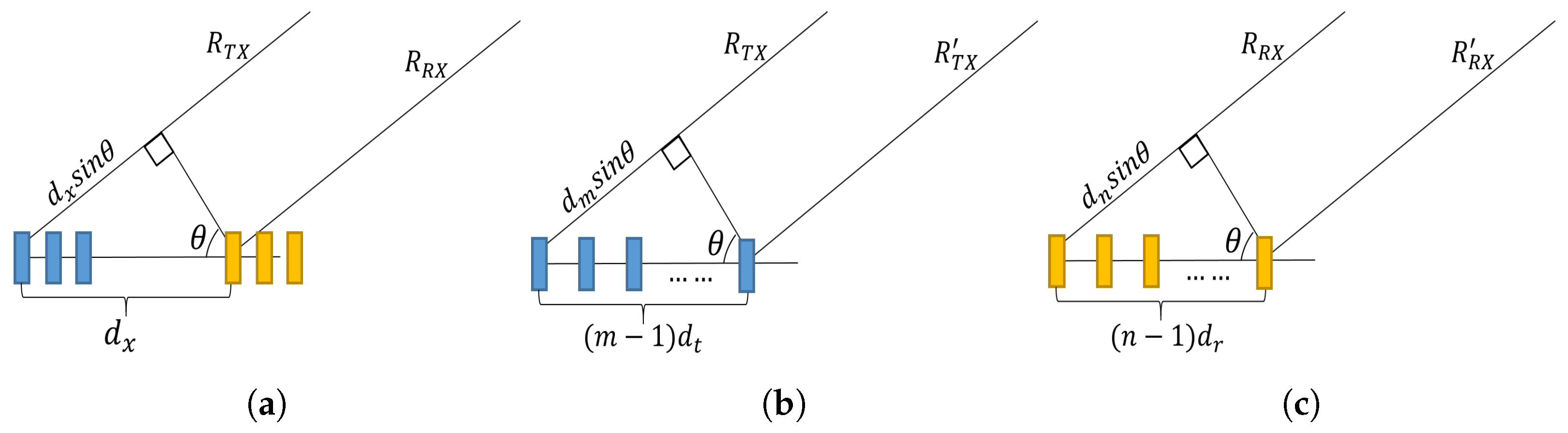
2.1. Signal Model
2.2. Image Formation
3. Experiments
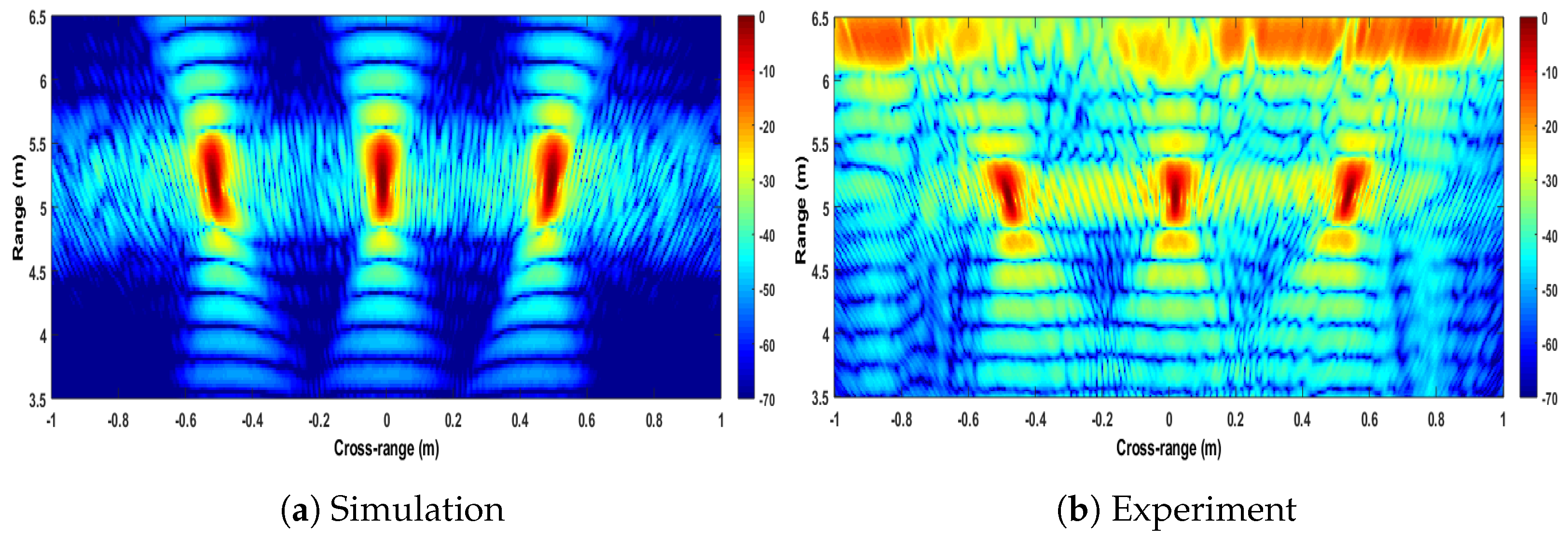
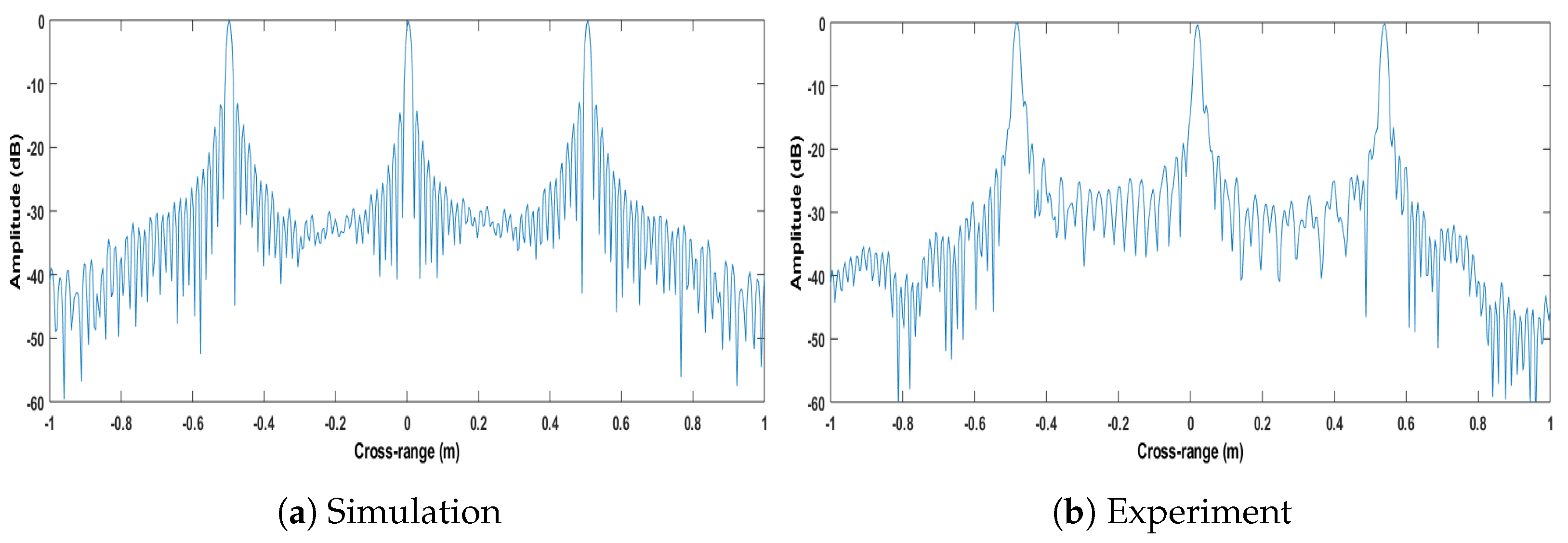
3.1. Experiment at 24 GHz
Results
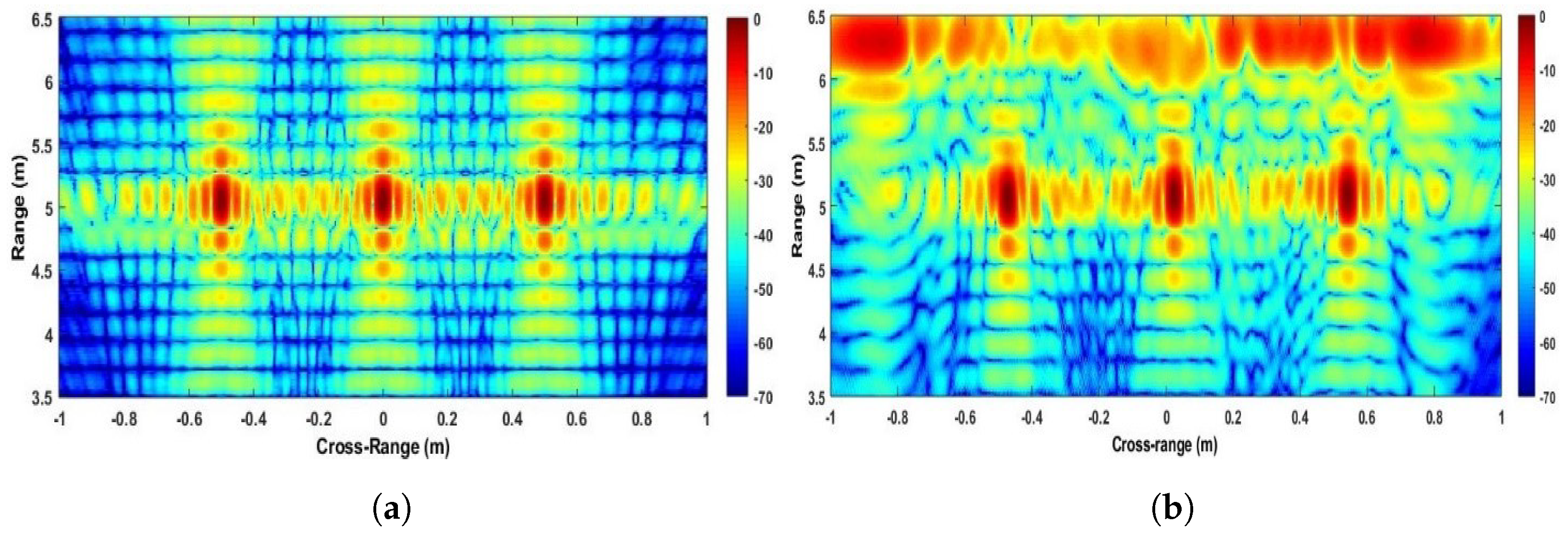
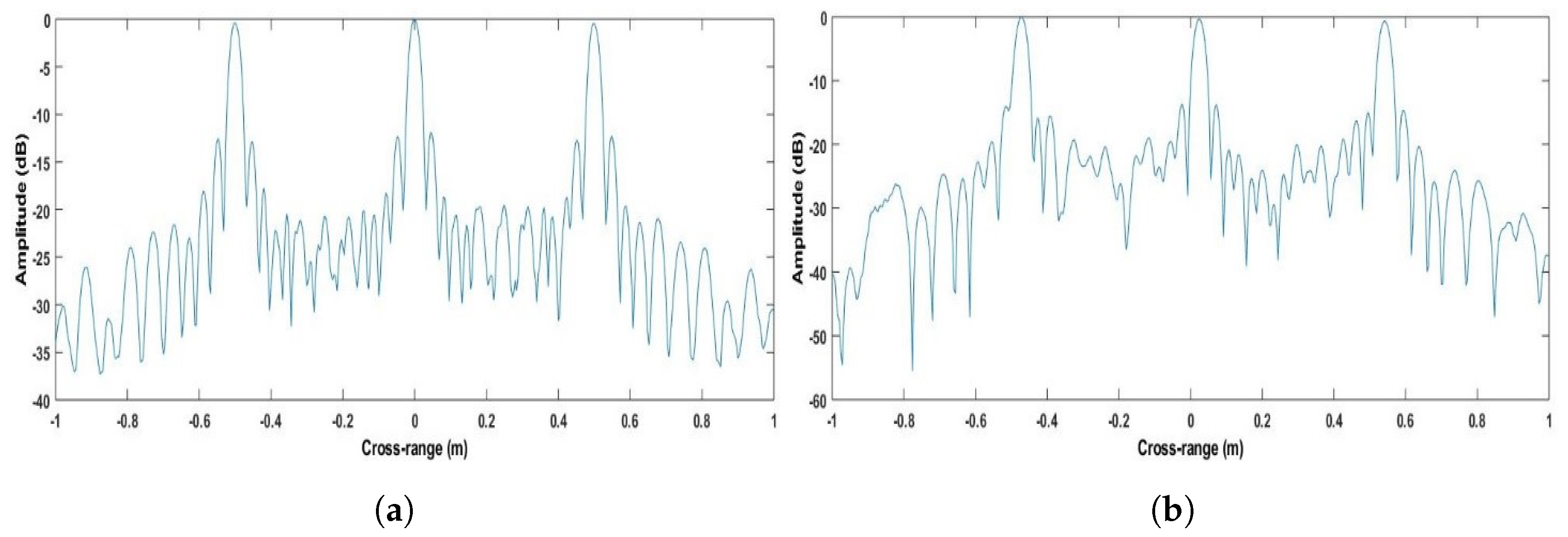
4. Experiments at 77 GHz
4.1. Results
4.2. Discussion
5. Performance Analysis
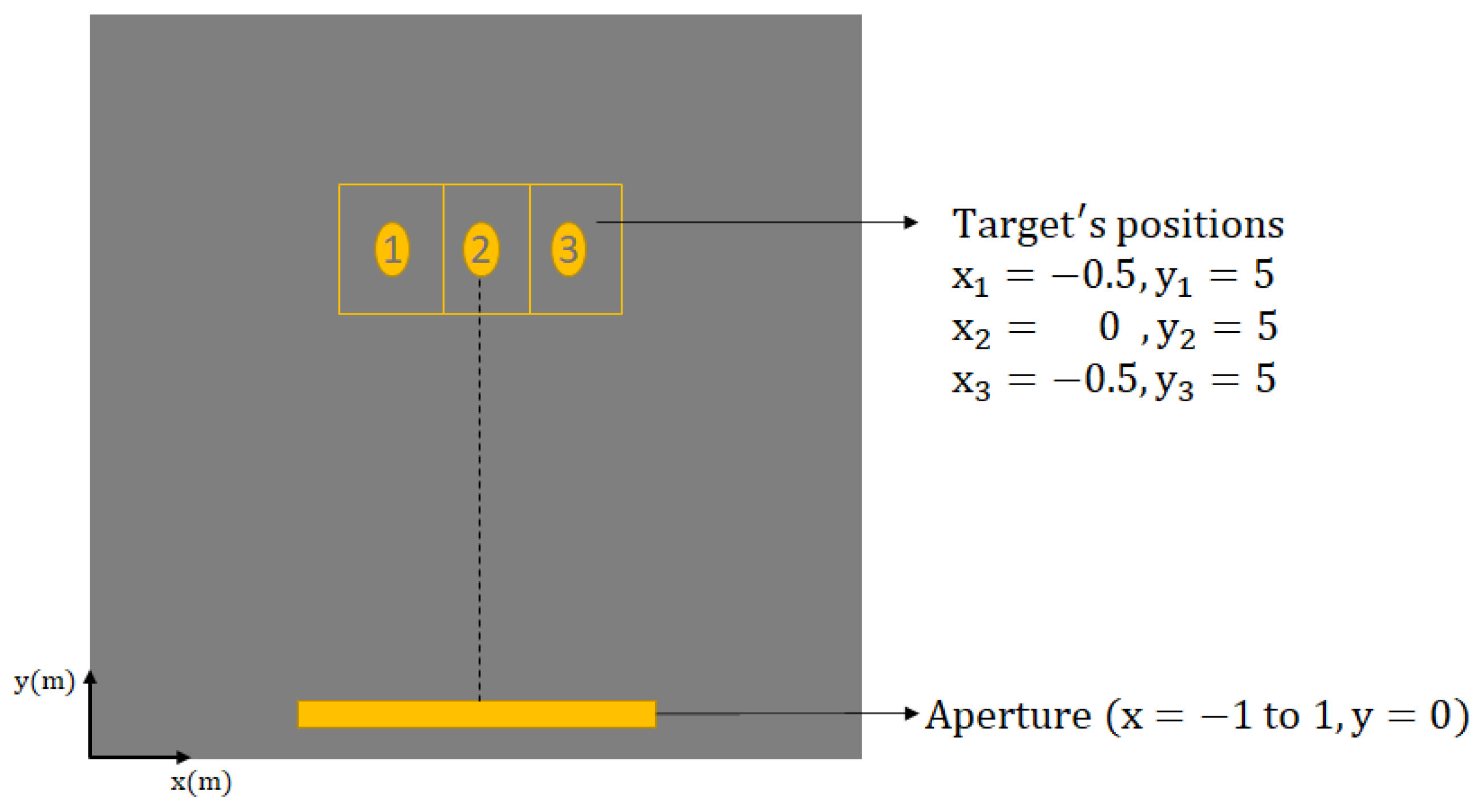
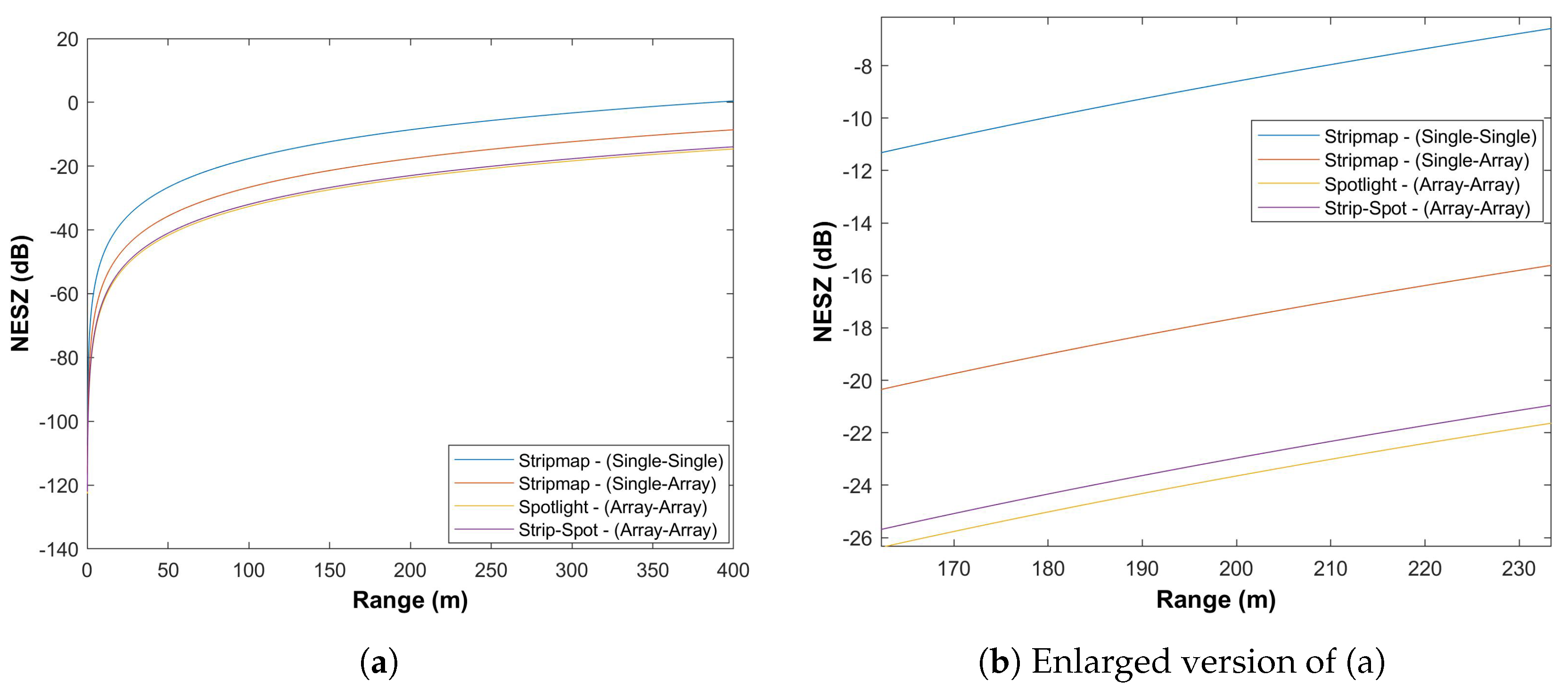
5.1. Sensitivity Analysis
5.1.1. Sensitivity of the Strip-Spot Concept
5.1.2. The Case Study for the Experiment
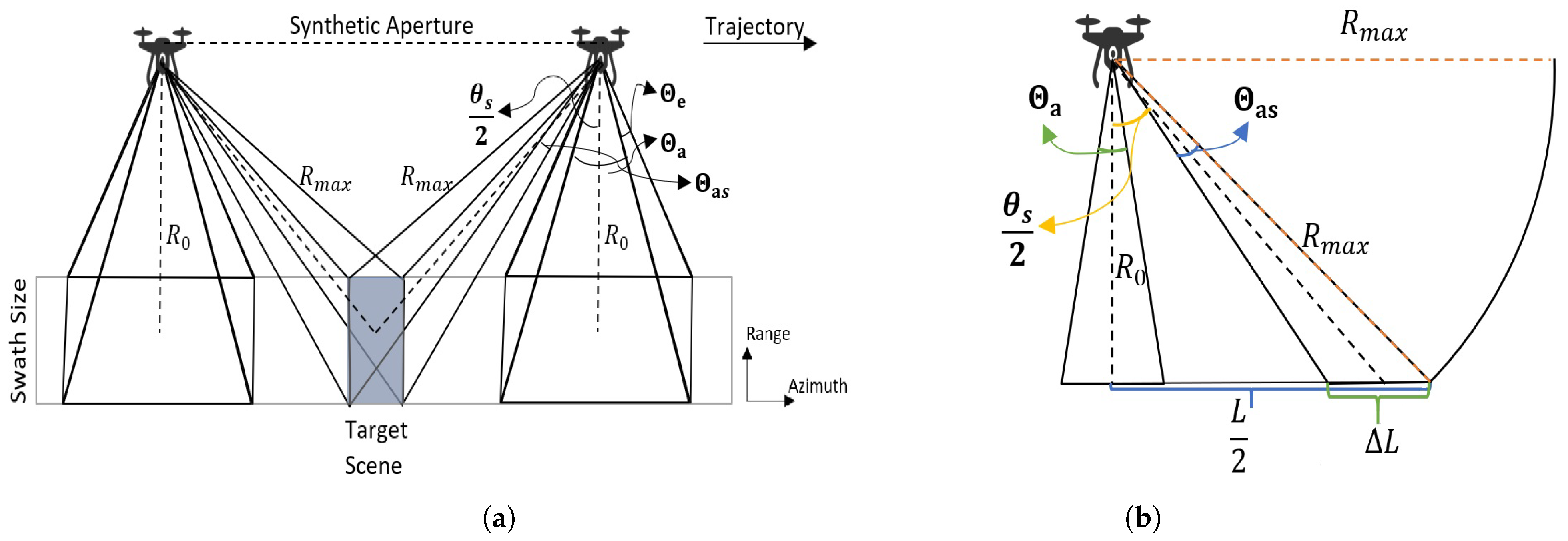
5.2. Scene Size
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar; Wiley: New York, NY, USA, 1991; Volume 11. [Google Scholar]
- Suess, M.; Grafmueller, B.; Zahn, R. A novel high resolution, wide swath SAR system. In Scanning the Present and Resolving the Future, Proceedings of the IGARSS 2001, IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, NSW, Australia, 9–13 July 2001; IEEE: New York, NY, USA, 2001; Volume 3, pp. 1013–1015. [Google Scholar] [CrossRef]
- Heer, C.; Soualle, F.; Zahn, R.; Reber, R. Investigations on a new high resolution wide swath SAR concept. In Proceedings of the IGARSS 2003, 2003 IEEE International Geoscience and Remote Sensing Symposium (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; IEEE: New York, NY, USA, 2001; Volume 1, pp. 521–523. [Google Scholar] [CrossRef]
- Younis, M. Digital Beam-Forming for High Resolution Wide Swath Real and Synthetic Aperture Radar. Ph.D. Thesis, Institute of Radio Frequency Engineering and Electronics (IHE), Karlsruhe, Germany, 2004. [Google Scholar]
- Krieger, G.; Younis, M.; Huber, S.; Bordoni, F.; Patyuchenko, A.; Kim, J.; Laskowski, P.; Villano, M.; Rommel, T.; Lopez-Dekker, P.; et al. Digital beamforming and MIMO SAR: Review and new concepts. In Proceedings of the EUSAR 2012, 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012; pp. 11–14. [Google Scholar]
- Krieger, G. MIMO-SAR: Opportunities and pitfalls. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2628–2645. [Google Scholar] [CrossRef]
- Gebert, N.; Krieger, G.; Moreira, A. Digital beamforming on receive: Techniques and optimization strategies for high-resolution wide-swath SAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 564–592. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Klare, J.; Gierull, C.H. MIMO SAR processing for multichannel high-resolution wide-swath radars. IEEE Trans. Geosci. Remote Sens. 2013, 52, 5034–5055. [Google Scholar] [CrossRef]
- Krieger, G.; Younis, M.; Gebert, N.; Huber, S.; Bordoni, F.; Patyuchenko, A.; Moreira, A. Advanced concepts for high-resolution wide-swath SAR imaging. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 1–4. [Google Scholar]
- Wang, R.; Pei, J.; Zhang, Y.; Li, M.; Huang, Y.; Wu, J. An auxiliary parking method based on automotive millimeter wave SAR. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2503–2506. [Google Scholar]
- Harrer, F.; Pfeiffer, F.; Löffler, A.; Gisder, T.; Buchberger, C.; Biebl, E. Multi channel approaches for an automotive synthetic aperture radar. In Proceedings of the 2018 11th German Microwave Conference (GeMiC), Freiburg, Germany, 12–14 March 2018; pp. 391–394. [Google Scholar]
- Rizzi, M.; Tagliaferri, D.; Tebaldini, S.; Nicoli, M.; Russo, I.; Mazzucco, C.; Monti-Guarnieri, A.V.; Prati, C.M.; Spagnolini, U. Navigation-Aided Automotive SAR Imaging in Urban Environments. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2979–2982. [Google Scholar]
- Fembacher, F.; Khalid, F.B.; Balazs, G.; Nugraha, D.T.; Roger, A. Real-time synthetic aperture radar for automotive embedded systems. In Proceedings of the 2018 15th European Radar Conference (EuRAD), Madrid, Spain, 26–28 September 2018; pp. 517–520. [Google Scholar]
- Clarke, D.; Andre, D.; Zhang, F. Synthetic aperture radar for lane boundary detection in driver assistance systems. In Proceedings of the 2016 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Baden-Baden, Germany, 19–21 September 2016; pp. 238–243. [Google Scholar]
- Kurz, V.; Pfeiffer, F.; Lach, M.; van Driesten, C.; Biebl, E. Radar Backscattering Of Vegetation For The Automotive 77 GHz Band. In Proceedings of the 2021 21st International Radar Symposium (IRS), Berlin, Germany, 21–22 June 2021; pp. 1–7. [Google Scholar]
- Lee, T.Y.; Skvortsov, V.; Kim, M.S.; Han, S.H.; Ka, M.H. Application of W-band FMCW radar for road curvature estimation in poor visibility conditions. IEEE Sens. J. 2018, 18, 5300–5312. [Google Scholar] [CrossRef]
- Yurduseven, O.; Fromenteze, T.; Decroze, C.; Fusco, V.F. Frequency-diverse computational automotive radar technique for debris detection. IEEE Sens. J. 2020, 20, 13167–13177. [Google Scholar] [CrossRef]
- Farhadi, M.; Feger, R.; Fink, J.; Wagner, T.; Stelzer, A. Automotive synthetic aperture radar imaging using tdm-mimo. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–14 May 2021; pp. 1–6. [Google Scholar]
- Gisder, T.; Meinecke, M.M.; Biebl, E. Synthetic aperture radar towards automotive applications. In Proceedings of the 2019 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019; pp. 1–10. [Google Scholar]
- Korkmaz, F.; Antoniou, M. High-Resolution, Contiguous SAR Imaging Using Co-Located MIMO Arrays: Experimental Proof of Concept. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar]
- Ramasubramanian, K.; Ginsburg, B. AWR1243 Sensor: Highly Integrated 76–81-GHz Radar Front-End for Emerging ADAS Applications; Texas Instruments White Paper. 2017. Available online: https://www.ti.com/lit/wp/spyy003/spyy003.pdf (accessed on 22 September 2022).
- Gov, H.D. Proposed Rules Federal Register. Public Law 2015, 114, 11. [Google Scholar]
- Rao, A.P.; Sarma, N. Adaptive beamforming algorithms for smart antenna systems. Methods 2014, 4, 10–11. [Google Scholar]
- Jakowatz, C.V.; Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Thompson, P.A. Spotlight-Mode Synthetic Aperture Radar: A Signal Processing Approach: A Signal Processing Approach; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Soumekh, M. Synthetic Aperture Radar Signal Processing and Imaging Using High Performance Computing; Technical Report; State University of New York at Buffalo Department of Electrical and Computer Engineering: Buffalo, NY, USA, 2000. [Google Scholar]
- Richards, M.A.; Scheer, J.; Holm, W.A.; Melvin, W.L. Principles of Modern Radar; SciTech Pub.: Raleigh, NC, USA, 2010; Volume 1. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]




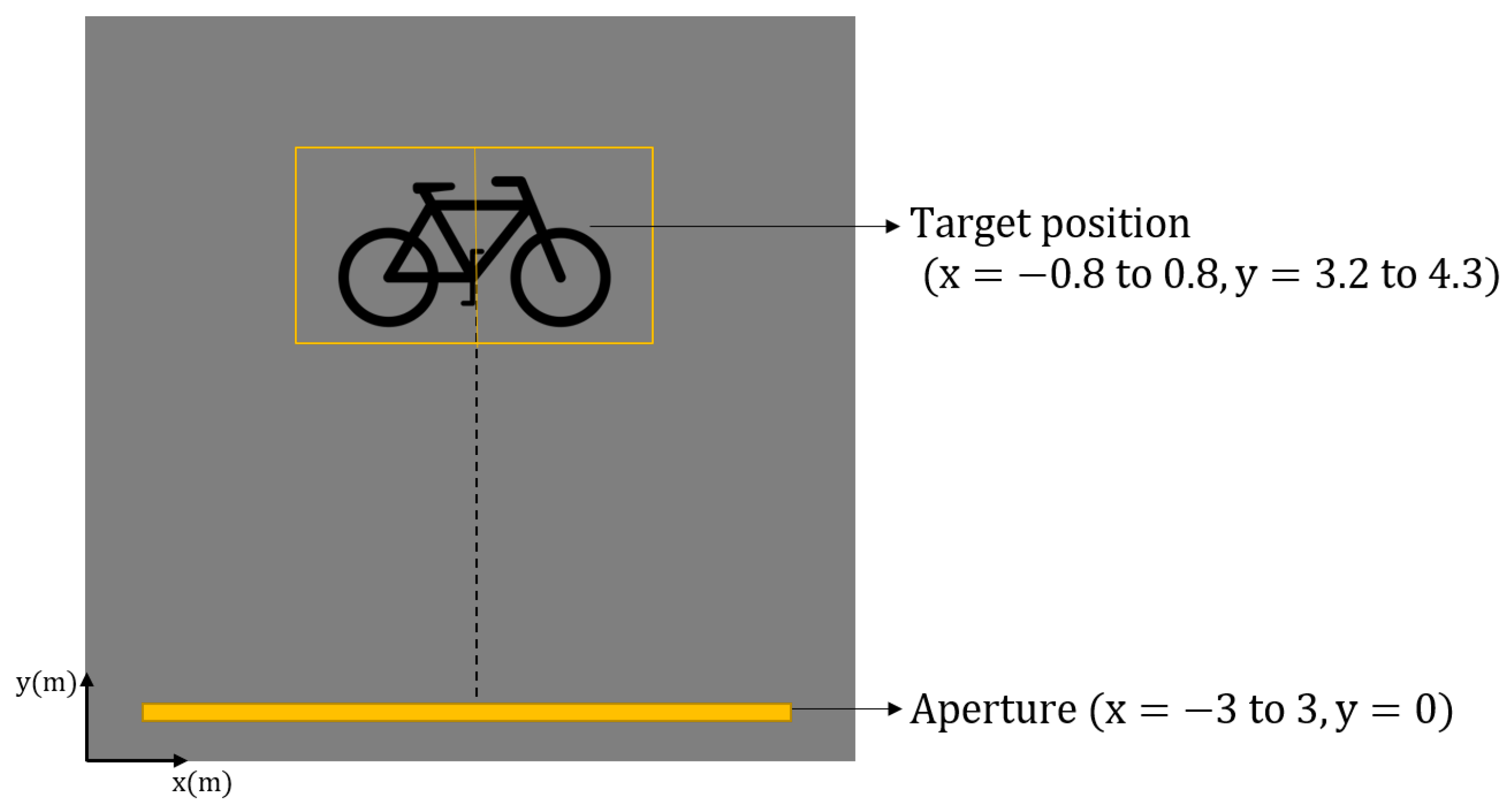


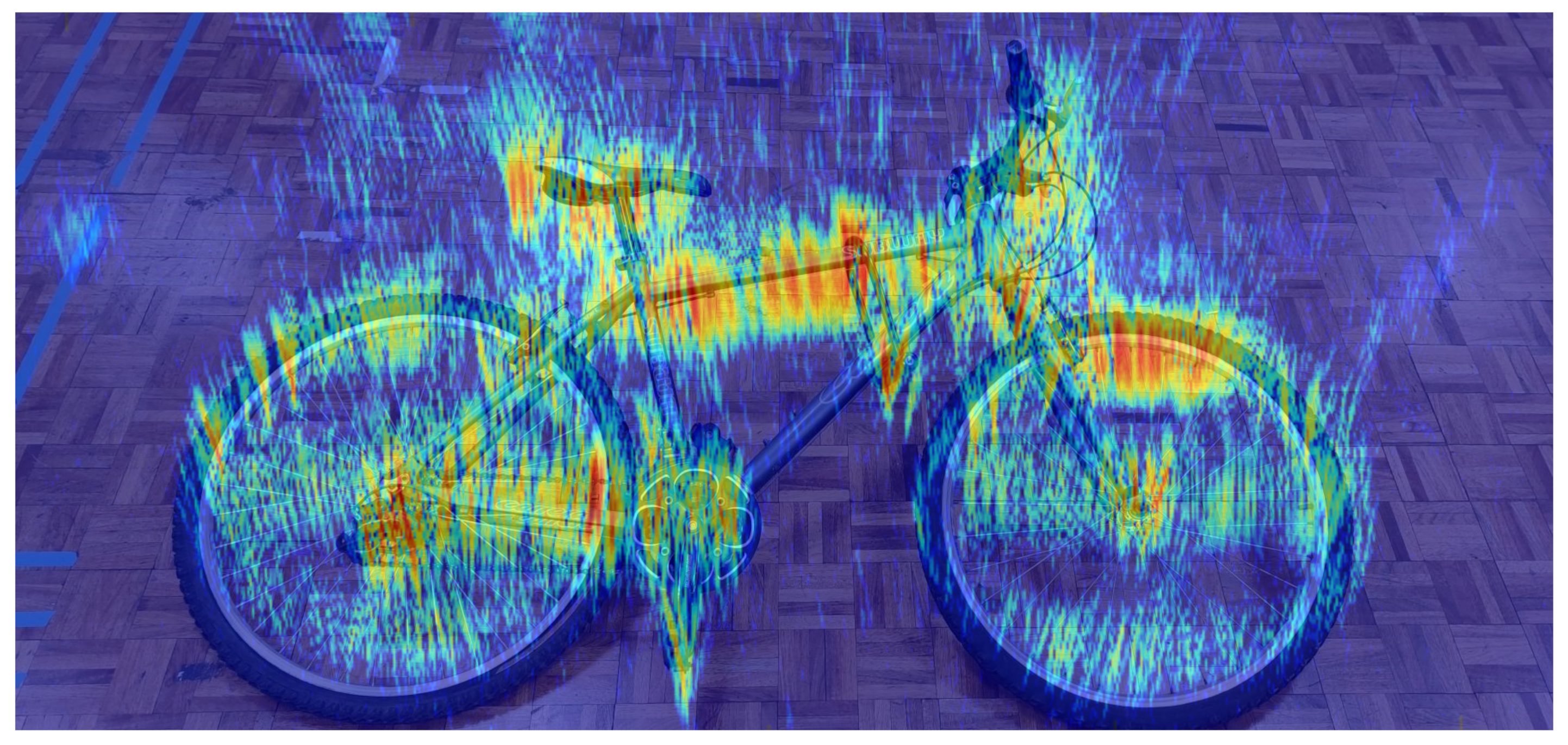


| Parameter | Value | Value | Unit |
|---|---|---|---|
| Type | 24 GHz Front End | 77 GHz Front End | |
| Frequency | 24 | 77 | GHz |
| Beamwidth-V (Tx) | 12.8 | 13.2 | Degree |
| Beamwidth-V (Rx) | 12.8 | 12.8 | Degree |
| Beamwidth-H (Tx) | 76.5 | 51 | Degree |
| Beamwidth-H (Rx) | 76.5 | 76.5 | Degree |
| Amount of Transmitter | 2 | 4 | - |
| Amount of Transmitter | 8 | 8 | - |
| Transmitter Power | 8 | 10 | dBm |
| Antenna Gain (Tx) | 13.2 | 17 | dBi |
| Antenna Gain (Rx) | 13.2 | 15 | dBi |
| Mode | Frequency | Range | Aperture | Cross-Range Resolution |
|---|---|---|---|---|
| (GHz) | (m) | (m) | (mm) | |
| Stripmap | 24 | 5.1 | 2 | 29.0 |
| Strip-Spot | 24 | 5.1 | 2 | 15.8 |
| Stripmap | 77 | 3.2 | 6 | 6.97 |
| Strip-Spot | 77 | 3.2 | 6 | 3.53 |
| Tx | Rx | Mode | Sensitivity |
|---|---|---|---|
| 0.25 cm Single | Single | Stripmap | |
| 0.25 cm Single | Array | Stripmap | |
| 0.25 cm Array | Array | Spotlight | |
| 0.25 cm Array | Array | Strip-Spot |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Transmit Power | 10 | dBm | |
| Transmit Antenna Gain | 17 | dBi | |
| Receiver Antenna Gain | 15 | dBi | |
| Transmit Number | M | 4 | - |
| Receiver Number | N | 8 | - |
| Wavelength | m | ||
| Range resolution | m | ||
| Velocity | V | 10 | m/s |
| Boltzmann Constant | k | 1.38 × | - |
| Temperature | T | 295 | K |
| Noise Figure | F | 10 | dB |
| Signal Loss | 4 | dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korkmaz, F.; Antoniou, M. A New Concept of Contiguous-Swath SAR Imaging with High Resolution: Strip-Spot SAR. Sensors 2022, 22, 9153. https://doi.org/10.3390/s22239153
Korkmaz F, Antoniou M. A New Concept of Contiguous-Swath SAR Imaging with High Resolution: Strip-Spot SAR. Sensors. 2022; 22(23):9153. https://doi.org/10.3390/s22239153
Chicago/Turabian StyleKorkmaz, Furkan, and Michail Antoniou. 2022. "A New Concept of Contiguous-Swath SAR Imaging with High Resolution: Strip-Spot SAR" Sensors 22, no. 23: 9153. https://doi.org/10.3390/s22239153
APA StyleKorkmaz, F., & Antoniou, M. (2022). A New Concept of Contiguous-Swath SAR Imaging with High Resolution: Strip-Spot SAR. Sensors, 22(23), 9153. https://doi.org/10.3390/s22239153






