A Proposed System for Multi-UAVs in Remote Sensing Operations
Abstract
:1. Introduction
2. Materials and Methods
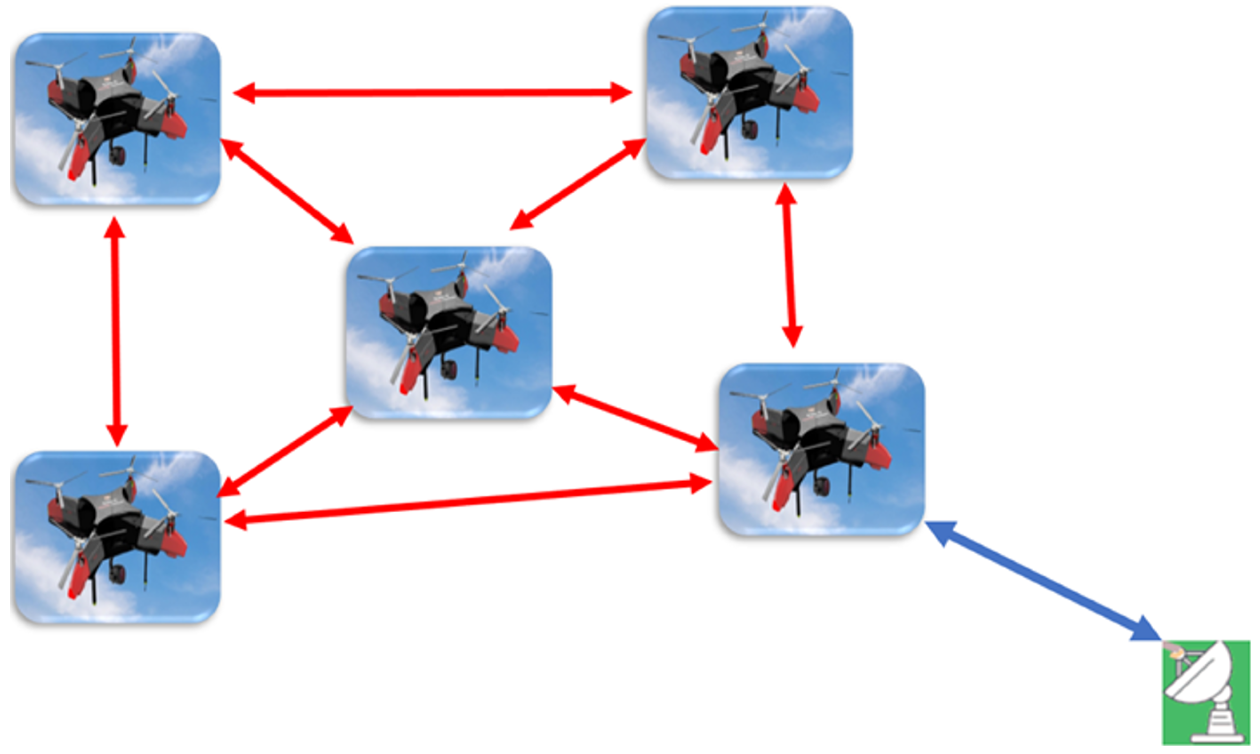
2.1. Control Strategy
2.2. Multi-UAV Mission Management
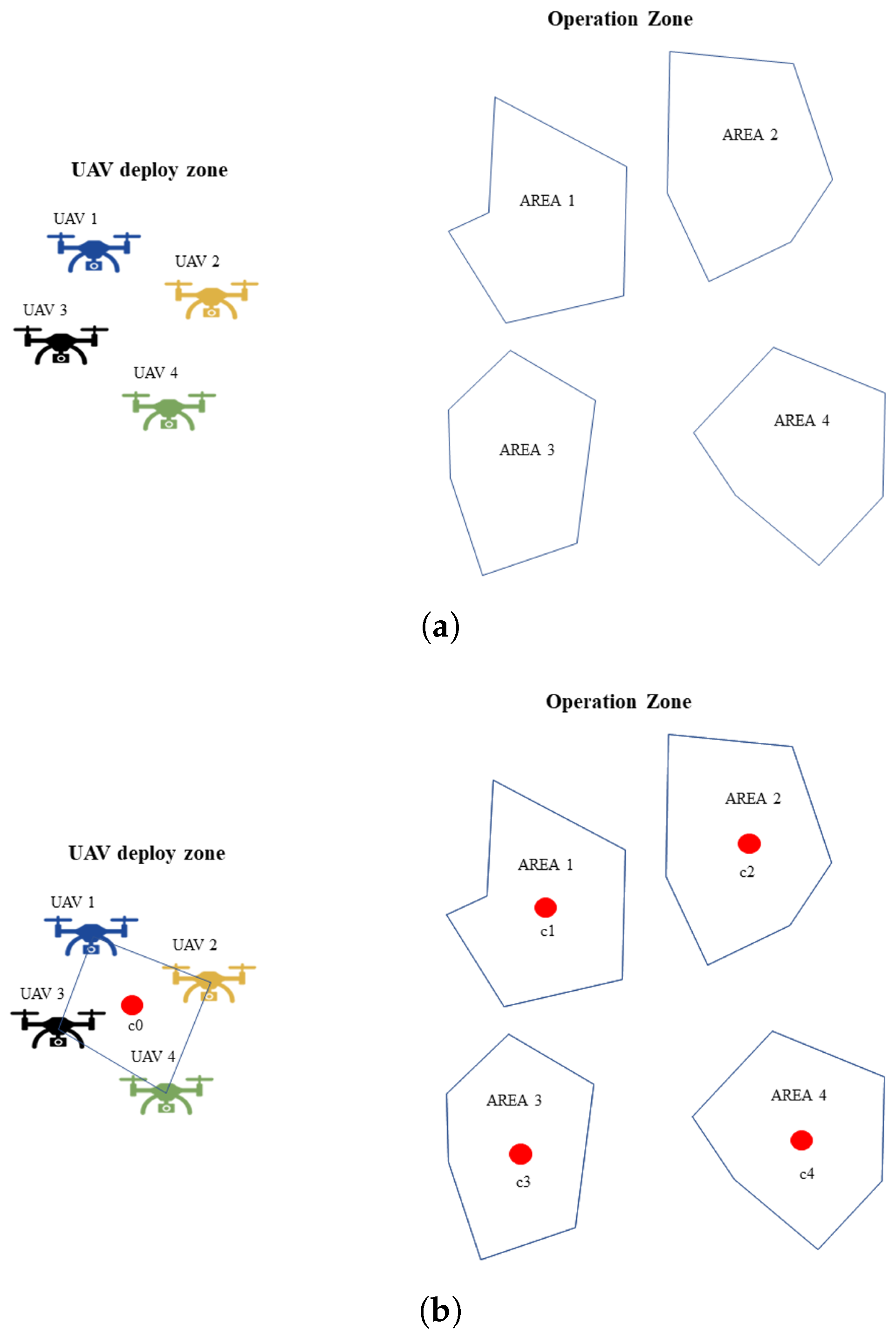
2.2.1. Problem Statement
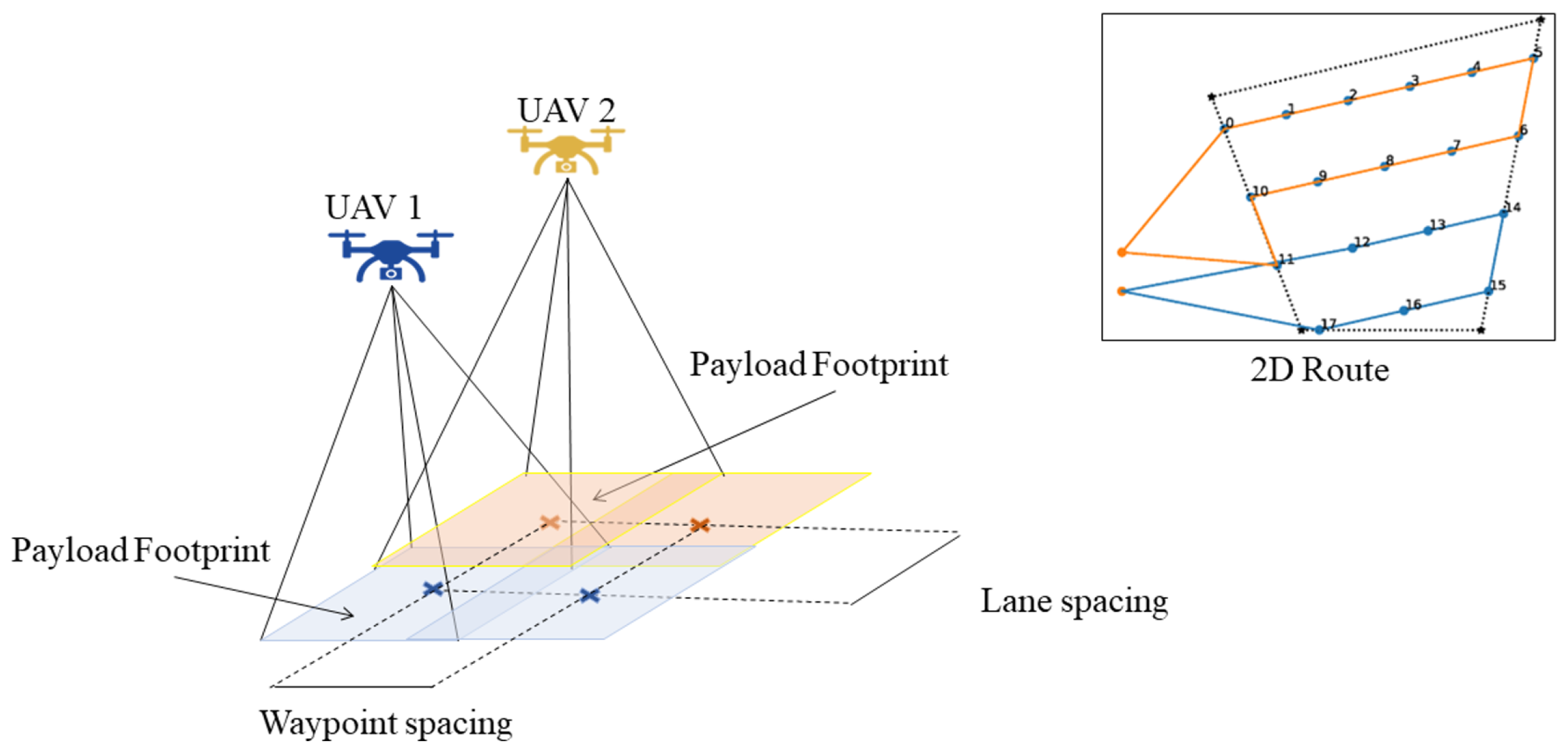
2.2.2. Coverage Path Planning Algorithm
3. Results
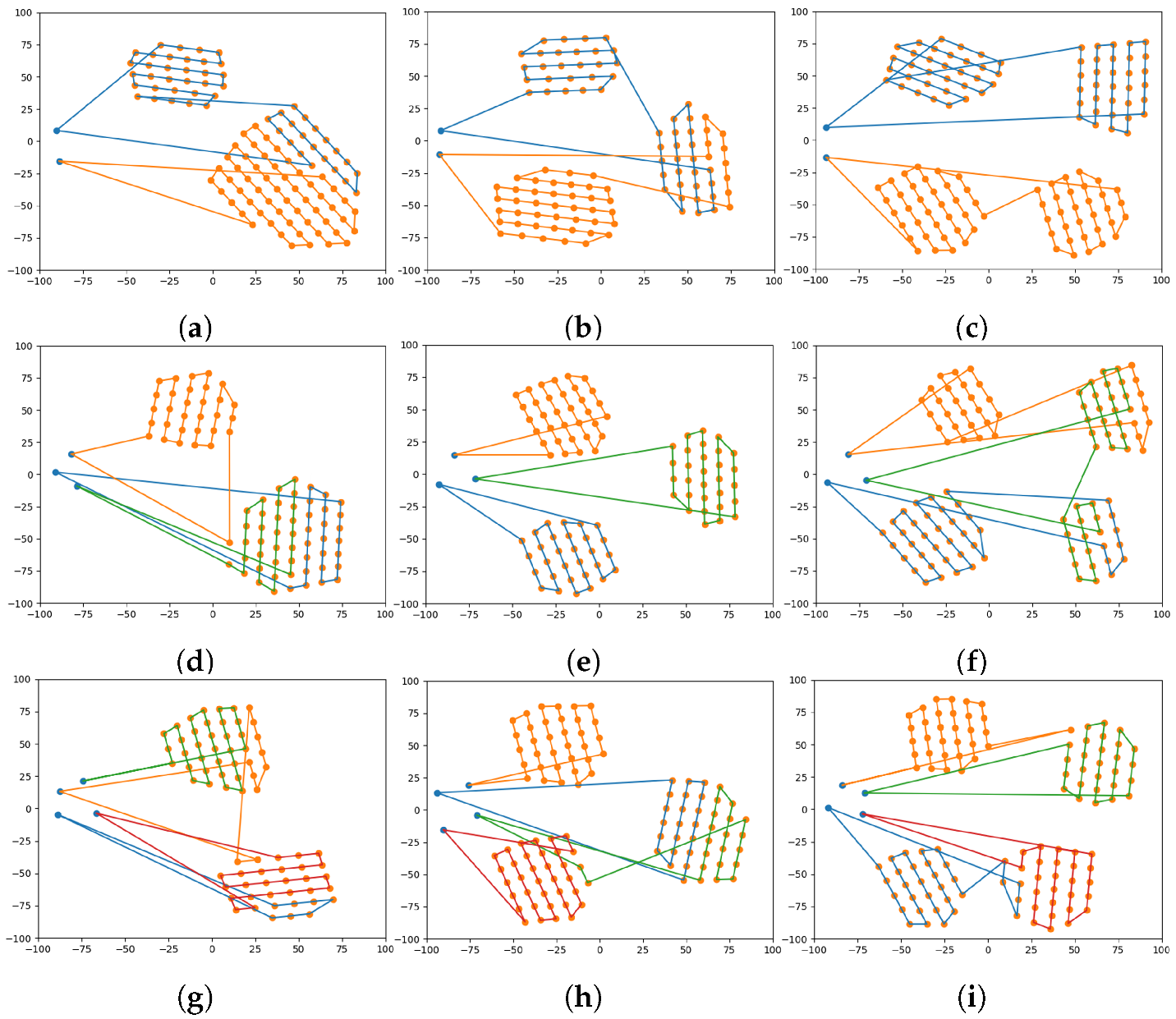
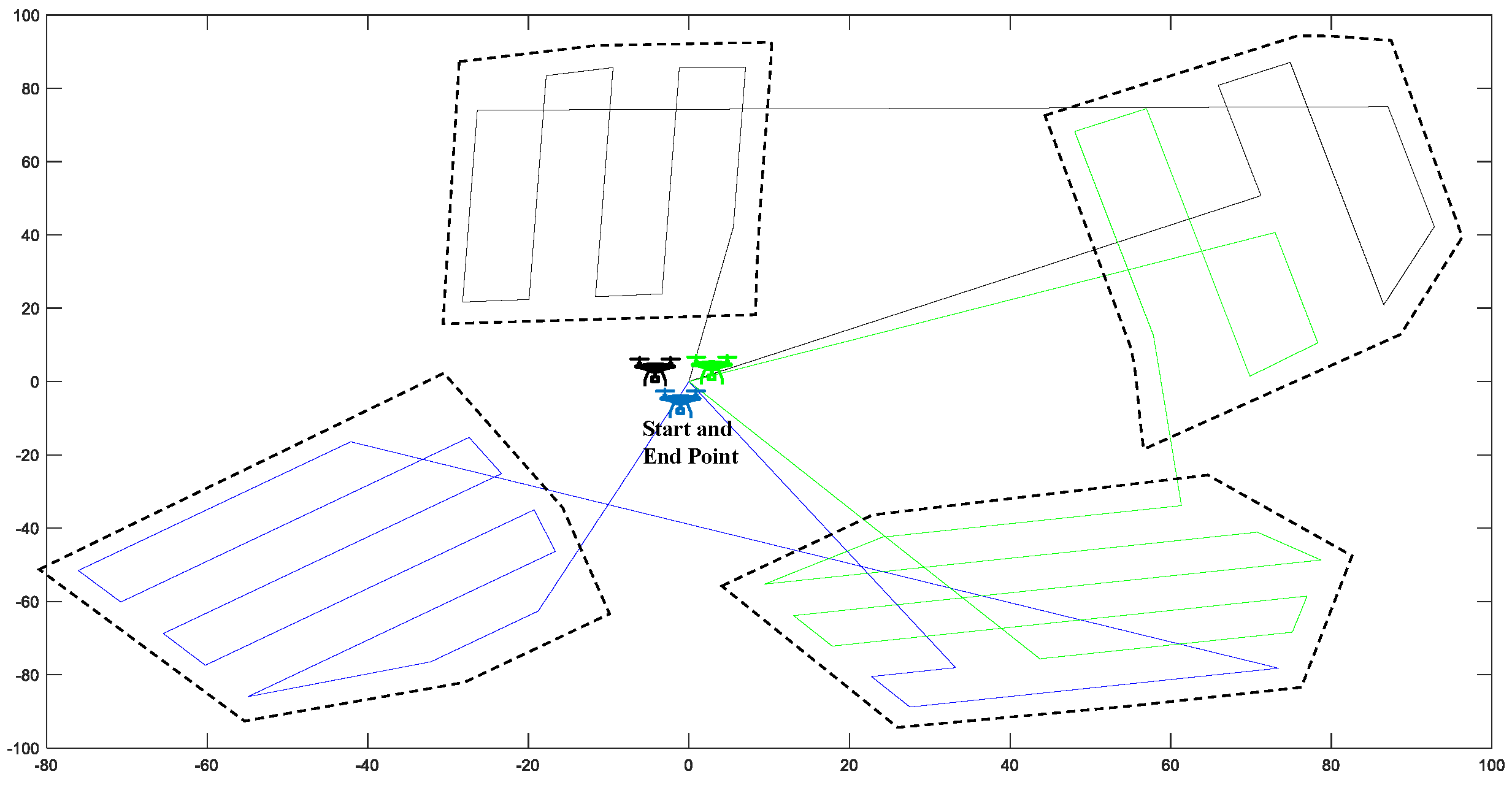
3.1. Numerical Results
3.2. Simulation Results
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| UAS | Unmanned Aerial System |
| H2020 | Horizon 2020 |
| GCS | Ground Control Station |
| MANET | Mobile ad hoc Network |
| VANET | Vehicle ad hoc Network |
| FANET | Flying ad hoc Network |
| UWVANET | Underwater ad hoc Network |
| POWELL-BINPAT | Powell Optimized Bin Packing Trajectory Planner |
| CPP | Coverage Path Planning |
| TSP | Traveling Salesman Problem |
References
- Wang, C.; Su, Y.; Wang, J.; Wang, T.; Gao, Q. UAVSwarm Dataset: An Unmanned Aerial Vehicle Swarm Dataset for Multiple Object Tracking. Remote Sens. 2022, 14, 2601. [Google Scholar] [CrossRef]
- Peña, P.F.; Ragab, A.R.; Luna, M.A.; Isaac, M.S.A.; Campoy, P. WILD HOPPER: A heavy-duty UAV for day and night firefighting operations. Heliyon 2022, 8, e09588. [Google Scholar] [CrossRef] [PubMed]
- Ragab, A.R.; Isaac, M.S.A.; Luna, M.A.; Peña, P.F. Unmanned Aerial Vehicle Swarming. In Proceedings of the 2021 IEEE International Conference on Engineering and Emerging Technologies (ICEET), Istanbul, Turkey, 27–28 October 2021; pp. 1–6. [Google Scholar]
- Ragab, A.R.; Peña, P.F.; Luna, M.A.; Isaac, M.S.A. Systemic Integrated Unmanned Aerial System. Int. J. Online Biomed. Eng. 2022, 18. [Google Scholar] [CrossRef]
- Yao, J.; Ordonez, R.; Gazi, V. Swarm tracking using artificial potentials and sliding mode control. J. Dyn. Sys. Meas. Control. 2007, 129, 749–754. [Google Scholar] [CrossRef]
- Chai, X.; Wang, Q.; Yu, Y.; Sun, C. Robust Time-Varying Output Formation Control for Swarm Systems with Nonlinear Uncertainties. Complexity 2020, 2020, 2069170. [Google Scholar] [CrossRef] [Green Version]
- Cepeda-Gomez, R.; Olgac, N.; Sierra, D.A. Application of sliding mode control to swarms under conflict. IET Control. Theory Appl. 2011, 5, 1167–1175. [Google Scholar] [CrossRef]
- Hu, J.; Yang, J. Application of distributed auction to multi-UAV task assignment in agriculture. Int. J. Precis. Agric. Aviat. 2018, 1, 44–50. [Google Scholar] [CrossRef] [Green Version]
- Luna, M.A.; Ragab, A.R.; Isac, M.S.A.; Peña, P.F.; Cervera, P.C. A New Algorithm Using Hybrid UAV Swarm Control System for Firefighting Dynamical Task Allocation. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; pp. 655–660. [Google Scholar]
- Ramirez-Atencia, C.; Bello-Orgaz, G.; Camacho, D. Solving complex multi-UAV mission planning problems using multi-objective genetic algorithms. Soft Comput. 2017, 21, 4883–4900. [Google Scholar] [CrossRef]
- Zhen, Z.; Xing, D.; Gao, C. Cooperative search-attack mission planning for multi-UAV based on intelligent self-organized algorithm. Aerosp. Sci. Technol. 2018, 76, 402–411. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, C.; Coombes, M. Spraying coverage path planning for agriculture unmanned aerial vehicles. In Proceedings of the 2021 IEEE 26th International Conference on Automation and Computing (ICAC), Portsmouth, UK, 2–4 September 2021; pp. 1–6. [Google Scholar]
- Pham, T.H.; Bestaoui, Y.; Mammar, S. Aerial robot coverage path planning approach with concave obstacles in precision agriculture. In Proceedings of the 2017 IEEE Workshop on Research, Education and Development of Unmanned Aerial Systems (RED-UAS), Linköping, Sweden, 3–5 October 2017; pp. 43–48. [Google Scholar]
- Mansouri, S.S.; Kanellakis, C.; Fresk, E.; Kominiak, D.; Nikolakopoulos, G. Cooperative coverage path planning for visual inspection. Control. Eng. Pract. 2018, 74, 118–131. [Google Scholar] [CrossRef]
- Shang, Z.; Bradley, J.; Shen, Z. A co-optimal coverage path planning method for aerial scanning of complex structures. Expert Syst. Appl. 2020, 158, 113535. [Google Scholar] [CrossRef]
- Hayat, S.; Yanmaz, E.; Bettstetter, C.; Brown, T.X. Multi-objective drone path planning for search and rescue with quality-of-service requirements. Auton. Robot. 2020, 44, 1183–1198. [Google Scholar] [CrossRef]
- Li, B.; Patankar, S.; Moridian, B.; Mahmoudian, N. Planning large-scale search and rescue using team of uavs and charging stations. In Proceedings of the 2018 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Philadelphia, PA, USA, 6–8 August 2018; pp. 1–8. [Google Scholar]
- Savkin, A.V.; Huang, H. Asymptotically Optimal Path Planning for Ground Surveillance by a Team of UAVs. IEEE Syst. J. 2021, 16, 3446–3449. [Google Scholar] [CrossRef]
- Xie, J.; Carrillo, L.R.G.; Jin, L. An integrated traveling salesman and coverage path planning problem for unmanned aircraft systems. IEEE Control. Syst. Lett. 2018, 3, 67–72. [Google Scholar] [CrossRef]
- Vasquez-Gomez, J.I.; Herrera-Lozada, J.C.; Olguin-Carbajal, M. Coverage path planning for surveying disjoint areas. In Proceedings of the 2018 IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 899–904. [Google Scholar]
- Xie, J.; Chen, J. Multiregional Coverage Path Planning for Multiple Energy Constrained UAVs. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17366–17381. [Google Scholar] [CrossRef]
- Ale Isaac, M.S.; Luna, M.A.; Ragab, A.R.; Ale Eshagh Khoeini, M.M.; Kalra, R.; Campoy, P.; Flores Peña, P.; Molina, M. Medium-Scale UAVs: A Practical Control System Considering Aerodynamics Analysis. Drones 2022, 6, 244. [Google Scholar] [CrossRef]
- Isaac, M.A.; Naghash, A.; Mirtajedini, S. Control and guidance of an autonomous quadrotor landing phase on a moving platform. In Proceedings of the IMAV Annual Conference of Autonomous Vehicles, Madrid, Spain, 29 September–4 October 2019. [Google Scholar]
- Isaac, M.S.A.; Ragab, A.R.; Garcés, E.C.; Luna, M.A.; Peña, P.F.; Cervera, P.C. Mathematical Modeling and Designing a Heavy Hybrid-Electric Quadcopter, Controlled by Flaps. Unmanned Syst. 2022, 10, 241–253. [Google Scholar] [CrossRef]
- Huang, W.H. Optimal line-sweep-based decompositions for coverage algorithms. In Proceedings of the IEEE 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), Seoul, Republic of Korea, 21–26 May 2001; 1, pp. 27–32. [Google Scholar]
- Luna, M.A.; Ale Isaac, M.S.; Ragab, A.R.; Campoy, P.; Flores Peña, P.; Molina, M. Fast Multi-UAV Path Planning for Optimal Area Coverage in Aerial Sensing Applications. Sensors 2022, 22, 2297. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Powell, M.J. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput. J. 1964, 7, 155–162. [Google Scholar] [CrossRef]








| No. UAVs | No. Areas | UAV 1 | UAV 2 | UAV 3 | UAV 4 | Av | SD | CV |
|---|---|---|---|---|---|---|---|---|
| 2 | 2 | 702.58 | 707.39 | - | - | 704.98 | 3.40 | 0.48 |
| 3 | 925.25 | 908.20 | - | - | 916.73 | 12.05 | 1.32 | |
| 4 | 886.39 | 952.45 | - | - | 919.42 | 46.70 | 5.08 | |
| 3 | 2 | 557.71 | 496.80 | 529.41 | - | 527.97 | 30.48 | 5.77 |
| 3 | 626.84 | 569.27 | 659.26 | - | 618.46 | 45.58 | 7.37 | |
| 4 | 792.35 | 675.95 | 782.72 | - | 750.34 | 64.60 | 8.61 | |
| 4 | 2 | 472.83 | 395.66 | 416.31 | 490.24 | 443.76 | 44.99 | 10.14 |
| 3 | 430.83 | 494.15 | 489.77 | 513.73 | 482.12 | 35.74 | 7.41 | |
| 4 | 586.58 | 546.09 | 509.70 | 592.72 | 558.77 | 38.71 | 6.93 |
| No. UAVs | UAV id | Total Time (s) | Total Distance (m) |
| 3 | UAV1 | 178.106 | 888.954 |
| No. Areas | UAV2 | 169.203 | 845.994 |
| 4 | UAV3 | 173.627 | 867.694 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flores Peña, P.; Luna, M.A.; Ale Isaac, M.S.; Ragab, A.R.; Elmenshawy, K.; Martín Gómez, D.; Campoy, P.; Molina, M. A Proposed System for Multi-UAVs in Remote Sensing Operations. Sensors 2022, 22, 9180. https://doi.org/10.3390/s22239180
Flores Peña P, Luna MA, Ale Isaac MS, Ragab AR, Elmenshawy K, Martín Gómez D, Campoy P, Molina M. A Proposed System for Multi-UAVs in Remote Sensing Operations. Sensors. 2022; 22(23):9180. https://doi.org/10.3390/s22239180
Chicago/Turabian StyleFlores Peña, Pablo, Marco Andrés Luna, Mohammad Sadeq Ale Isaac, Ahmed Refaat Ragab, Khaled Elmenshawy, David Martín Gómez, Pascual Campoy, and Martin Molina. 2022. "A Proposed System for Multi-UAVs in Remote Sensing Operations" Sensors 22, no. 23: 9180. https://doi.org/10.3390/s22239180
APA StyleFlores Peña, P., Luna, M. A., Ale Isaac, M. S., Ragab, A. R., Elmenshawy, K., Martín Gómez, D., Campoy, P., & Molina, M. (2022). A Proposed System for Multi-UAVs in Remote Sensing Operations. Sensors, 22(23), 9180. https://doi.org/10.3390/s22239180









