Influence of Polymer Processing on the Double Electrical Percolation Threshold in PLA/PCL/GNP Nanocomposites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Samples’ Preparation
2.2.1. Nanocomposite Blends Preparation
2.2.2. Compression Moulding
2.2.3. Filament Preparation
2.2.4. Fused Filament Fabrication
2.3. Characterisation Techniques
2.3.1. Scanning Electron Microscopy (SEM)
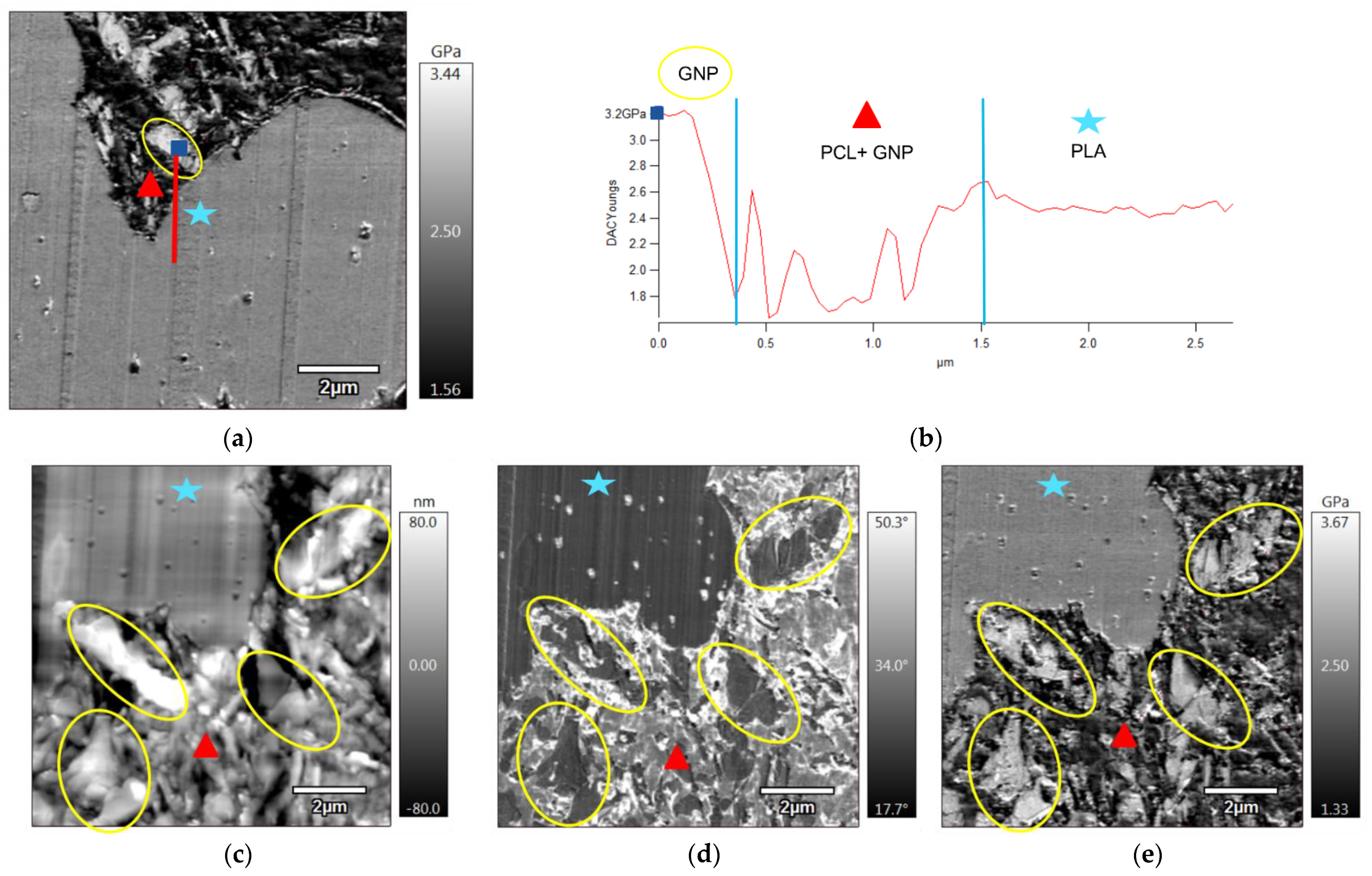
2.3.2. Atomic Force Microscopy (AFM)
2.3.3. Solvent Extraction Method
- The extraction left the sample compact (no fragmentation into small pieces);PLA is 100% continuous and the PCL continuity is quantified by the weight fraction of PCL that is extracted according to Equation (1):where, m1 is the mass of the graphene-filled PCL phase before the solvent dissolution (mg) (;m2 is the mass of graphene-filled PCL phase after the solvent dissolution (mg) (;This is the case of samples containing high PLA percentage;
- The sample fell apart:PCL is 100% continuous and the PLA continuity is represented by the biggest compact PLA piece released at the end of the extraction. The percentage of continuity of PLA in this case is calculated according to Equation (2):where, m’ is the mass of the biggest part of PLA (mg);m″ is the mass of PLA in the sample before the solvent dissolution (mg) (In the case of the co-continuous samples and samples containing dispersed PLA nodules in the PCL phase, the samples exhibit a fully dispersed PLA structure and a complete disintegration after the dissolution of the PCL phase where the mass of the biggest PLA part is too low to yield a negligible percentage of continuity of PLA.
2.3.4. Electrical Resistance Measurements
2.3.5. Rheological Measurements
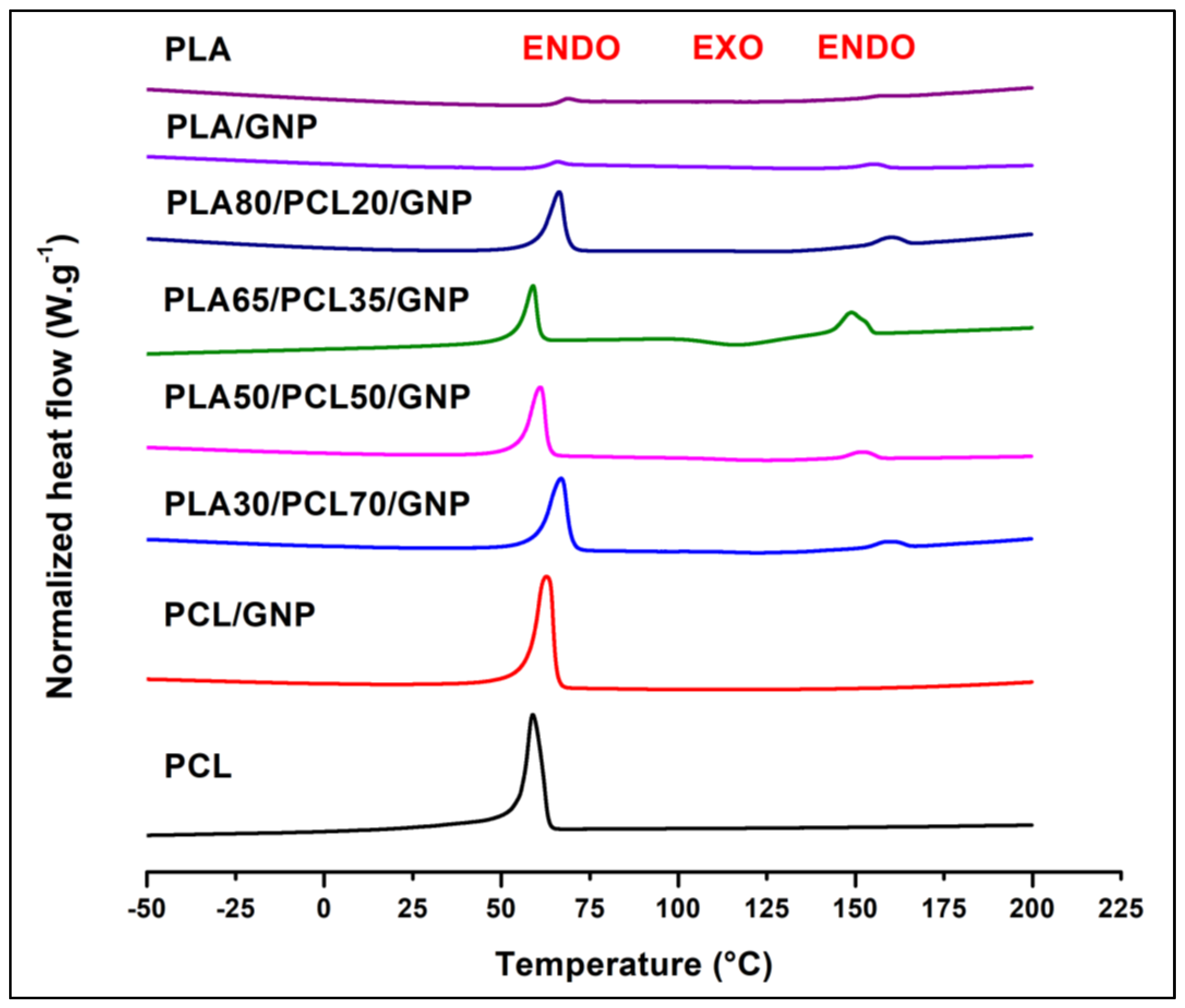
2.3.6. Differential Scanning Calorimetry (DSC)
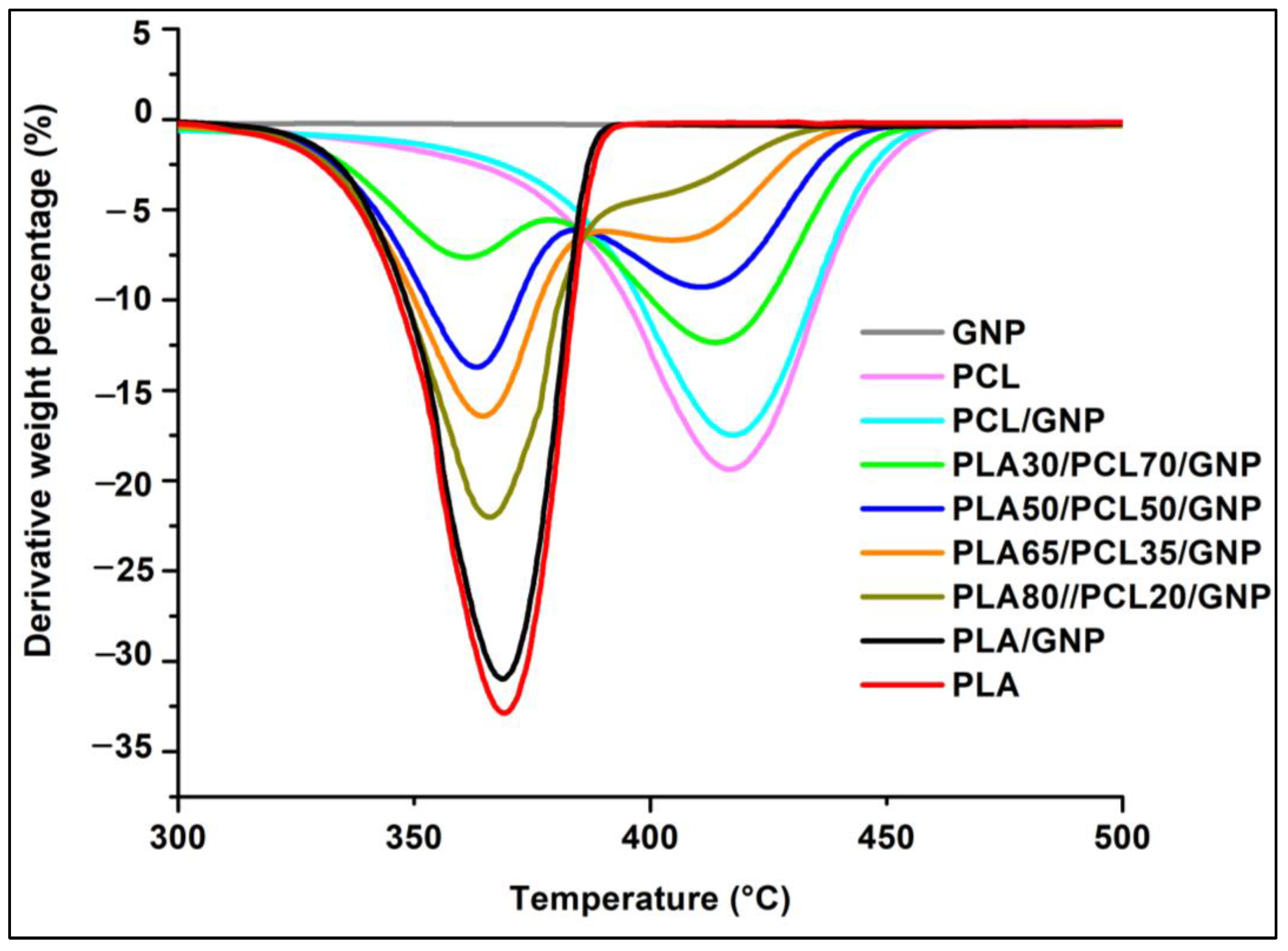
2.3.7. Thermogravimetric Analysis (TGA)
3. Results and Discussion
3.1. Selective Localisation of Graphene in the PCL Phase in Compression-Moulded Samples
3.2. Theoretical Prediction of the Co-Continuity
3.3. Experimental Prediction of the Co-Continuity Range in the Compression-Moulded Samples
3.3.1. SEM Results
3.3.2. Electrical Resistivity and Solvent Extraction Method Results
3.3.3. Melt Shear Rheology Results
3.3.4. DSC Results
3.3.5. TGA Results
- Influence of the annealing time on the co-continuity and therefore on the electrical conductivity;
- Influence of the twin-screw extrusion protocol on the co-continuity and the electrical conductivity;
- Effect of the graphene content on the co-continuity and the electrical conductivity.
3.4. Influence of Annealing Time during Compression Moulding on the Co-Continuity
3.5. Influence of the Extrusion Protocol
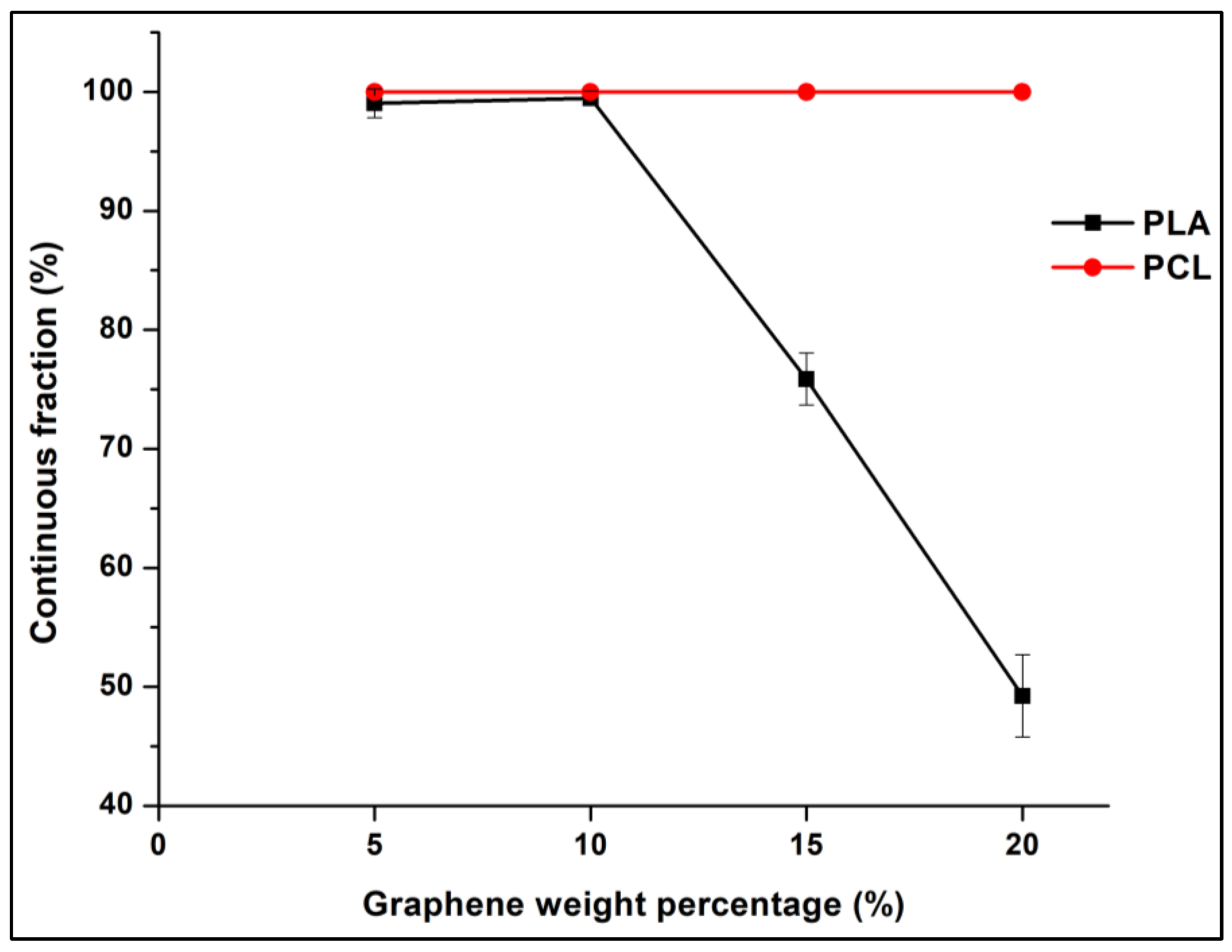
3.6. Influence of GNP Content on the Co-Continuity
3.7. Influence of 3D Printing on the Co-Continuity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kuang, T.; Ju, J.; Chen, F.; Liu, X.; Zhang, S.; Liu, T.; Peng, X. Coupled effect of self-assembled nucleating agent, Ni-CNTs and pressure-driven flow on the electrical, electromagnetic interference shielding and thermal conductive properties of poly (lactic acid) composite foams. Compos. Sci. Technol. 2022, 230, 109736. [Google Scholar] [CrossRef]
- Kuang, T.; Ju, J.; Yang, Z.; Geng, L.; Peng, X. A facile approach towards fabrication of lightweight biodegradable poly (butylene succinate)/carbon fiber composite foams with high electrical conductivity and strength. Compos. Sci. Technol. 2018, 159, 171–179. [Google Scholar] [CrossRef]
- Gao, T.; Li, Y.-Y.; Bao, R.-Y.; Liu, Z.-Y.; Xie, B.-H.; Yang, M.-B.; Yang, W. Tailoring co-continuous like morphology in blends with highly asymmetric composition by MWCNTs: Towards biodegradable high-performance electrical conductive poly(l-lactide)/poly(3-hydroxybutyrate-co-4-hydroxybutyrate) blends. Compos. Sci. Technol. 2017, 152, 111–119. [Google Scholar] [CrossRef]
- Tolvanen, J.; Hannu, J.; Hietala, M.; Kordas, K.; Jantunen, H. Biodegradable multiphase poly(lactic acid)/biochar/graphite composites for electromagnetic interference shielding. Compos. Sci. Technol. 2019, 181, 107704. [Google Scholar] [CrossRef]
- Scaffaro, R.; Maio, A.; Lo Re, G.; Parisi, A.; Busacca, A. Advanced piezoresistive sensor achieved by amphiphilic nanointerfaces of graphene oxide and biodegradable polymer blends. Compos. Sci. Technol. 2018, 156, 166–176. [Google Scholar] [CrossRef]
- Liu, Y.; He, H.; Tian, G.; Wang, Y.; Gao, J.; Wang, C.; Xu, L.; Zhang, H. Morphology evolution to form double percolation polylactide/polycaprolactone/MWCNTs nanocomposites with ultralow percolation threshold and excellent EMI shielding. Compos. Sci. Technol. 2021, 214, 108956. [Google Scholar] [CrossRef]
- Huang, J.; Mao, C.; Zhu, Y.; Jiang, W.; Yang, X. Control of carbon nanotubes at the interface of a co-continuous immiscible polymer blend to fabricate conductive composites with ultralow percolation thresholds. Carbon N. Y. 2014, 73, 267–274. [Google Scholar] [CrossRef]
- Sadeghi, A.; Moeini, R.; Yeganeh, J.K. Highly conductive PP/PET polymer blends with high electromagnetic interference shielding performances in the presence of thermally reduced graphene nanosheets prepared through melt compounding. Polym. Compos. 2019, 40, E1461–E1469. [Google Scholar] [CrossRef]
- Bai, L.; He, S.; Fruehwirth, J.W.; Stein, A.; Macosko, C.W.; Cheng, X. Localizing graphene at the interface of cocontinuous polymer blends: Morphology, rheology, and conductivity of cocontinuous conductive polymer composites. J. Rheol. 2017, 61, 575–587. [Google Scholar] [CrossRef]
- Tu, C.; Nagata, K.; Yan, S. Influence of melt-mixing processing sequence on electrical conductivity of polyethylene/polypropylene blends filled with graphene. Polym. Bull. 2017, 74, 1237–1252. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, T.-T.; Yang, J.-H.; Zhang, N.; Huang, T.; Wang, Y. Selective localization of reduced graphene oxides at the interface of PLA/EVA blend and its resultant electrical resistivity. Polym. Compos. 2017, 38, 1982–1991. [Google Scholar] [CrossRef]
- Feng, J.; Chan, C.; Li, J. A method to control the dispersion of carbon black in an immiscible polymer blend. Polym. Eng. Sci. 2003, 43, 1058–1063. [Google Scholar] [CrossRef]
- Liebscher, M.; Tzounis, L.; Pötschke, P.; Heinrich, G. Influence of the viscosity ratio in PC/SAN blends filled with MWCNTs on the morphological, electrical, and melt rheological properties. Polymer 2013, 54, 6801–6808. [Google Scholar] [CrossRef]
- Göldel, A.; Kasaliwal, G.R.; Pötschke, P.; Heinrich, G. The kinetics of CNT transfer between immiscible blend phases during melt mixing. Polymer 2012, 53, 411–421. [Google Scholar] [CrossRef]
- Taghizadeh, A.; Favis, B.D. Carbon nanotubes in blends of polycaprolactone/thermoplastic starch. Carbohydr. Polym. 2013, 98, 189–198. [Google Scholar] [CrossRef] [PubMed]
- Gubbels, F.; Jerome, R.; Vanlathem, E.; Deltour, R.; Blacher, S.; Brouers, F. Kinetic and Thermodynamic Control of the Selective Localization of Carbon Black at the Interface of Immiscible Polymer Blends. Chem. Mater. 1998, 10, 1227–1235. [Google Scholar] [CrossRef]
- Gubbels, F.; Jerome, R.; Teyssie, P.; Vanlathem, E.; Deltour, R.; Calderone, A.; Parente, V.; Bredas, J.L. Selective Localization of Carbon Black in Immiscible Polymer Blends: A Useful Tool To Design Electrical Conductive Composites. Macromolecules 1994, 27, 1972–1974. [Google Scholar] [CrossRef]
- Cheah, K.; Forsyth, M.; Simon, G.P. Processing and morphological development of carbon black filled conducting blends using a binary host of poly(styrene co-acrylonitrile) and poly(styrene). J. Polym. Sci. Part B Polym. Phys. 2000, 38, 3106–3119. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, J.; Huang, T.; Zhang, N.; Chen, C.; Wang, Y. Selective localization of carbon nanotubes at the interface of Poly(L-lactide)/Ethylene-co-vinyl Acetate resulting in lowered electrical resistivity. Compos. Part B Eng. 2013, 55, 463–469. [Google Scholar] [CrossRef]
- Maiti, S.; Shrivastava, N.K.; Khatua, B.B. Reduction of percolation threshold through double percolation in melt-blended polycarbonate/acrylonitrile butadiene styrene/multiwall carbon nanotubes elastomer nanocomposites. Polym. Compos. 2013, 34, 570–579. [Google Scholar] [CrossRef]
- Bose, S.; Bhattacharyya, A.R.; Bondre, A.P.; Kulkarni, A.R.; Pötschke, P. Rheology, electrical conductivity, and the phase behavior of cocontinuous PA6/ABS blends with MWNT: Correlating the aspect ratio of MWNT with the percolation threshold. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 1619–1631. [Google Scholar] [CrossRef]
- Chen, J.; Cui, X.; Zhu, Y.; Jiang, W.; Sui, K. Design of superior conductive polymer composite with precisely controlling carbon nanotubes at the interface of a co-continuous polymer blend via a balance of π-π interactions and dipole-dipole interactions. Carbon N. Y. 2017, 114, 441–448. [Google Scholar] [CrossRef]
- Strugova, D.; Ferreira Junior, J.C.; David, É.; Demarquette, N.R. Ultra-Low Percolation Threshold Induced by Thermal Treatments in Co-Continuous Blend-Based PP/PS/MWCNTs Nanocomposites. Nanomaterials 2021, 11, 1620. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Cui, X.; Sui, K.; Zhu, Y.; Jiang, W. Balance the electrical properties and mechanical properties of carbon black filled immiscible polymer blends with a double percolation structure. Compos. Sci. Technol. 2017, 140, 99–105. [Google Scholar] [CrossRef]
- Gubbels, F.; Blacher, S.; Vanlathem, E.; Jerome, R.; Deltour, R.; Brouers, F.; Teyssie, P. Design of Electrical Composites: Determining the Role of the Morphology on the Electrical Properties of Carbon Black Filled Polymer Blends. Macromolecules 1995, 28, 1559–1566. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, X.; Hao, X.; Starý, Z.; Schubert, D.W. Enhancing the electrical conductivity of carbon black-filled immiscible polymer blends by tuning the morphology. Eur. Polym. J. 2016, 78, 106–115. [Google Scholar] [CrossRef]
- Luo, Y.; Xiong, S.-Y.; Zhang, F.; He, X.-X.; Lu, X.; Peng, R.-T. Preparation of conductive polylactic acid/high density polyethylene/carbon black composites with low percolation threshold by locating the carbon black at the Interface of co-continuous blends. J. Appl. Polym. Sci. 2021, 138, 50291. [Google Scholar] [CrossRef]
- Lu, X.; Kang, B.; Shi, S. Selective Localization of Carbon Black in Bio-Based Poly (Lactic Acid)/Recycled High-Density Polyethylene Co-Continuous Blends to Design Electrical Conductive Composites with a Low Percolation Threshold. Polymers 2019, 11, 1583. [Google Scholar] [CrossRef] [Green Version]
- Kou, Y.; Cote, A.T.; Liu, J.; Cheng, X.; Macosko, C.W. Robust networks of interfacial localized graphene in cocontinuous polymer blends. J. Rheol. 2021, 65, 1139–1153. [Google Scholar] [CrossRef]
- Bai, L.; Sharma, R.; Cheng, X.; Macosko, C.W. Kinetic Control of Graphene Localization in Co-continuous Polymer Blends via Melt Compounding. Langmuir 2018, 34, 1073–1083. [Google Scholar] [CrossRef]
- Bertolini, M.C.; Dul, S.; Barra, G.M.O.; Pegoretti, A. Poly(vinylidene fluoride)/thermoplastic polyurethane flexible and 3D printable conductive composites. J. Appl. Polym. Sci. 2021, 138, 50305. [Google Scholar] [CrossRef]
- Kocun, M.; Labuda, A.; Meinhold, W.; Revenko, I.; Proksch, R. Fast, High Resolution, and Wide Modulus Range Nanomechanical Mapping with Bimodal Tapping Mode. ACS Nano 2017, 11, 10097–10105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bourry, D.; Favis, B.D. Cocontinuity and phase inversion in HDPE/PS blends: Influence of interfacial modification and elasticity. J. Polym. Sci. Part B Polym. Phys. 1998, 36, 1889–1899. [Google Scholar] [CrossRef]
- Mani, S.; Malone, M.F.; Winter, H.H. Influence of phase separation on the linear viscoelastic behavior of a miscible polymer blend. J. Rheol. 1992, 36, 1625–1649. [Google Scholar] [CrossRef]
- Ajji, A.; Choplin, L.; Prud’Homme, R.E. Rheology of polystyrene/poly(vinyl methyl ether)blends near the phase transition. J. Polym. Sci. Part B Polym. Phys. 1991, 29, 1573–1578. [Google Scholar] [CrossRef]
- Steinmann, S.; Gronski, W.; Friedrich, C. Influence of selective filling on rheological properties and phase inversion of two-phase polymer blends. Polymer 2002, 43, 4467–4477. [Google Scholar] [CrossRef]
- Galloway, J.; Montminy, M.; Macosko, C. Image analysis for interfacial area and cocontinuity detection in polymer blends. Polymer 2002, 43, 4715–4722. [Google Scholar] [CrossRef]
- Steinmann, S.; Gronski, W.; Friedrich, C. Cocontinuous polymer blends: Influence of viscosity and elasticity ratios of the constituent polymers on phase inversion. Polymer 2001, 42, 6619–6629. [Google Scholar] [CrossRef]
- Galloway, J.; Macosko, C. Comparison of methods for the detection of cocontinuity in poly(ethylene oxide)/polystyrene blends. Polym. Eng. Sci. 2004, 44, 714–727. [Google Scholar] [CrossRef]
- Marin, N.; Favis, B. Co-continuous morphology development in partially miscible PMMA/PC blends. Polymer 2002, 43, 4723–4731. [Google Scholar] [CrossRef]
- Willemse, R.; Posthuma de Boer, A.; van Dam, J.; Gotsis, A. Co-continuous morphologies in polymer blends: A new model. Polymer 1998, 39, 5879–5887. [Google Scholar] [CrossRef]
- Willemse, R.C.; Posthuma de Boer, A.; van Dam, J.; Gotsis, A.D. Co-continuous morphologies in polymer blends: The influence of the interfacial tension. Polymer 1999, 40, 827–834. [Google Scholar] [CrossRef]
- Li, J.; Ma, P.L.; Favis, B.D. The Role of the Blend Interface Type on Morphology in Cocontinuous Polymer Blends. Macromolecules 2002, 35, 2005–2016. [Google Scholar] [CrossRef]
- Dedecker, K.; Groeninckx, G. Reactive compatibilisation of A/(B/C) polymer blends. Part 2. Analysis of the phase inversion region and the co-continuous phase morphology. Polymer 1998, 39, 4993–5000. [Google Scholar] [CrossRef]
- Filippone, G.; Dintcheva, N.T.; La Mantia, F.P.; Acierno, D. Using organoclay to promote morphology refinement and co-continuity in high-density polyethylene/polyamide 6 blends-Effect of filler content and polymer matrix composition. Polymer 2010, 51, 3956–3965. [Google Scholar] [CrossRef]
- Omonov, T.; Harrats, C.; Moldenaers, P.; Groeninckx, G. Phase continuity detection and phase inversion phenomena in immiscible polypropylene/polystyrene blends with different viscosity ratios. Polymer 2007, 48, 5917–5927. [Google Scholar] [CrossRef]
- Mirzadeh, A.; Lafleur, P.G.; Kamal, M.R.; Dubois, C. The effect of compatibilizer on the co-continuity and nanoclay dispersion level of tpe nanocomposites based on PP/EPDM. Polym. Eng. Sci. 2010, 50, 2131–2142. [Google Scholar] [CrossRef]
- Chaput, S.; Carrot, C.; Castro, M.; Prochazka, F. Co-continuity interval in immiscible polymer blends by dynamic mechanical spectroscopy in the molten and solid state. Rheol. Acta 2004, 43, 417–426. [Google Scholar] [CrossRef]
- Mekhilef, N.; Favis, B.D.; Carreau, P.J. Morphological stability, interfacial tension, and dual-phase continuity in polystyrene-polyethylene blends. J. Polym. Sci. Part B Polym. Phys. 1997, 35, 293–308. [Google Scholar] [CrossRef]
- Schwach, E.; Avérous, L. Starch-based biodegradable blends: Morphology and interface properties. Polym. Int. 2004, 53, 2115–2124. [Google Scholar] [CrossRef]
- Omonov, T.S.; Harrats, C.; Groeninckx, G.; Moldenaers, P. Anisotropy and instability of the co-continuous phase morphology in uncompatibilized and reactively compatibilized polypropylene/polystyrene blends. Polymer 2007, 48, 5289–5302. [Google Scholar] [CrossRef]
- Yuan, Z.; Favis, B.D. Coarsening of immiscible co-continuous blends during quiescent annealing. AIChE J. 2005, 51, 271–280. [Google Scholar] [CrossRef]
- Hammani, S.; Moulai-Mostefa, N.; Benyahia, L.; Tassin, J.-F. Effects of composition and extrusion parameters on the morphological development and rheological properties of PP/PC blends. Co-continuity investigation. J. Polym. Res. 2012, 19, 9940. [Google Scholar] [CrossRef]
- Calberg, C.; Blacher, S.; Gubbels, F.; Brouers, F.; Deltour, R.; Jérôme, R. Electrical and dielectric properties of carbon black filled co-continuous two-phase polymer blends. J. Phys. D Appl. Phys. 1999, 32, 1517–1525. [Google Scholar] [CrossRef]
- Masarra, N.-A.; Batistella, M.; Quantin, J.-C.; Regazzi, A.; Pucci, M.F.; El Hage, R.; Lopez-Cuesta, J.-M. Fabrication of PLA/PCL/Graphene Nanoplatelet (GNP) Electrically Conductive Circuit Using the Fused Filament Fabrication (FFF) 3D Printing Technique. Materials 2022, 15, 762. [Google Scholar] [CrossRef] [PubMed]
- Patwa, R.; Kumar, A.; Katiyar, V. Crystallization kinetics, morphology, and hydrolytic degradation of novel bio-based poly(lactic acid)/crystalline silk nano-discs nanobiocomposites. J. Appl. Polym. Sci. 2018, 135, 46590. [Google Scholar] [CrossRef]
- Kweon, H.Y.; Yoo, M.K.; Park, I.K.; Kim, T.H.; Lee, H.C.S.H.M.; Lee, H.C.S.H.M.; Oh, J.S.; Akaike, T.; Cho, C.S. A novel degradable polycarbonate networks for tissue engineering. Biomaterials 2003, 24, 801–808. [Google Scholar] [CrossRef] [PubMed]
- Nuzzo, A.; Bilotti, E.; Peijs, T.; Acierno, D.; Filippone, G. Nanoparticle-induced co-continuity in immiscible polymer blends—A comparative study on bio-based PLA-PA11 blends filled with organoclay, sepiolite, and carbon nanotubes. Polymer 2014, 55, 4908–4919. [Google Scholar] [CrossRef]
- Kashfipour, M.A.; Guo, M.; Mu, L.; Mehra, N.; Cheng, Z.; Olivio, J.; Zhu, S.; Maia, J.M.; Zhu, J. Carbon nanofiber reinforced Co-continuous HDPE/PMMA composites: Exploring the role of viscosity ratio on filler distribution and electrical/thermal properties. Compos. Sci. Technol. 2019, 184, 107859. [Google Scholar] [CrossRef]
- Available online: https://www.natureworksllc.com/~/media/Technical_Resources/Technical_Data_Sheets/TechnicalDataSheet_2003D_FFP-FSW_pdf.pdf (accessed on 26 October 2022).
- Jeantet, L.; Regazzi, A.; Taguet, A.; Pucci, M.; Caro, A.-S.; Quantin, J.-C. Biopolymer blends for mechanical property gradient 3D printed parts. Express Polym. Lett. 2021, 15, 137–152. [Google Scholar] [CrossRef]
- Zhong, T.; Li, J.; Zhang, K. A molecular dynamics study of Young’s modulus of multilayer graphene. J. Appl. Phys. 2019, 125, 175110. [Google Scholar] [CrossRef]
- de Aguiar, J.; Decol, M.; Pachekoski, W.M.; Becker, D. Mixing-sequence controlled selective localization of carbon nanoparticles in PLA/PCL blends. Polym. Eng. Sci. 2019, 59, 323–329. [Google Scholar] [CrossRef]
- Botlhoko, O.J.; Ray, S.S.; Ramontja, J. Influence of functionalized exfoliated reduced graphene oxide nanoparticle localization on mechanical, thermal and electronic properties of nanobiocomposites. Eur. Polym. J. 2018, 102, 130–140. [Google Scholar] [CrossRef]
- Miles, I.S.; Zurek, A. Preparation, structure, and properties of two-phase co-continuous polymer blends. Polym. Eng. Sci. 1988, 28, 796–805. [Google Scholar] [CrossRef]
- Paul, D.R.; Barlow, J.W. Polymer Blends. J. Macromol. Sci. Part C 1980, 18, 109–168. [Google Scholar] [CrossRef]
- Ho, R.M.; Wu, C.H.; Su, A.C. Morphology of plastic/rubber blends. Polym. Eng. Sci. 1990, 30, 511–518. [Google Scholar] [CrossRef]
- Kitayama, N.; Keskkula, H.; Paul, D.R. Reactive compatibilization of nylon 6/styrene-acrylonitrile copolymer blends: Part 1. Phase inversion behavior. Polymer 2000, 41, 8041–8052. [Google Scholar] [CrossRef]
- Everaert, V.; Aerts, L.; Groeninckx, G. Phase morphology development in immiscible PP/(PS/PPE) blends influence of the melt-viscosity ratio and blend composition. Polymer 1999, 40, 6627–6644. [Google Scholar] [CrossRef]
- Metelkin, V.I.; Blekht, V.S. Formation of a continuous phase in heterogeneous polymer mixtures. Colloid J. USSR 1984, 46, 425–429. [Google Scholar]
- Utracki, L.A. History of commercial polymer alloys and blends (from a perspective of the patent literature). Polym. Eng. Sci. 1995, 35, 2–17. [Google Scholar] [CrossRef]
- Antunes, C.F.; van Duin, M.; Machado, A.V. Morphology and phase inversion of EPDM/PP blends–Effect of viscosity and elasticity. Polym. Test. 2011, 30, 907–915. [Google Scholar] [CrossRef]
- Mekhilef, N.; Verhoogt, H. Phase inversion and dual-phase continuity in polymer blends: Theoretical predictions and experimental results. Polymer 1996, 37, 4069–4077. [Google Scholar] [CrossRef]
- Pötschke, P.; Paul, D.R. Formation of Co-continuous Structures in Melt-Mixed Immiscible Polymer Blends. J. Macromol. Sci. Part C 2003, 43, 87–141. [Google Scholar] [CrossRef]
- Wang, L.; Shi, C.; Guo, Z.-X.; Yu, J. Tailoring the morphology of polypropylene/polyamide 66 blend at an asymmetric composition by using organoclay and maleic anhydride grafted polypropylene. J. Ind. Eng. Chem. 2014, 20, 259–267. [Google Scholar] [CrossRef]
- Kong, M.; Huang, Y.; Chen, G.; Yang, Q.; Li, G. Retarded relaxation and breakup of deformed PA6 droplets filled with nanosilica in PS matrix during annealing. Polymer 2011, 52, 5231–5236. [Google Scholar] [CrossRef]
- Kontopoulou, M.; Liu, Y.; Austin, J.R.; Parent, J.S. The dynamics of montmorillonite clay dispersion and morphology development in immiscible ethylene–propylene rubber/polypropylene blends. Polymer 2007, 48, 4520–4528. [Google Scholar] [CrossRef]
- Li, Y.; Shimizu, H. Novel morphologies of poly(phenylene oxide) (PPO)/polyamide 6 (PA6) blend nanocomposites. Polymer 2004, 45, 7381–7388. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, Y.; Zhang, Y.; Zhang, X.; Zhou, W. Electrical properties and conductive mechanisms of immiscible polypropylene/Novolac blends filled with carbon black. Eur. Polym. J. 2007, 43, 5097–5106. [Google Scholar] [CrossRef]
- Zhao, J.; Yin, X.; Shi, J.; Zhao, X.; Wang, X.; Chen, M.; Dang, Z.M.; Hu, G.H. Effect of the mixing on the dielectric constant of poly(vinylidene fluoride)/isotactic polypropylene blends. Sci. Adv. Mater. 2013, 5, 505–511. [Google Scholar] [CrossRef]
- Hadaeghnia, M.; Ahmadi, S.; Ghasemi, I.; Wood-Adams, P.M. Manipulating the morphology of PA6/POE blends using graphene to achieve balanced electrical and mechanical properties. Compos. Sci. Technol. 2020, 200, 108412. [Google Scholar] [CrossRef]
- Lyu, Y.; Pang, J.; Gao, Z.; Zhang, Q.; Shi, X. Characterization of the compatibility of PVC/PLA blends by Aid of Rheological Responses. Polymer 2019, 176, 20–29. [Google Scholar] [CrossRef]
- Pötschke, P.; Abdel-Goad, M.; Alig, I.; Dudkin, S.; Lellinger, D. Rheological and dielectrical characterization of melt mixed polycarbonate-multiwalled carbon nanotube composites. Polymer 2004, 45, 8863–8870. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Zhang, M.; Yu, W. Selective Localization of Multiwalled Carbon Nanotubes in Poly(ε-caprolactone)/Polylactide Blend. Biomacromolecules 2009, 10, 417–424. [Google Scholar] [CrossRef] [PubMed]
- Bose, S.; Özdilek, C.; Leys, J.; Seo, J.W.; Wübbenhorst, M.; Vermant, J.; Moldenaers, P. Phase Separation as a Tool to Control Dispersion of Multiwall Carbon Nanotubes in Polymeric Blends. ACS Appl. Mater. Interfaces 2010, 2, 800–807. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Cardinaels, R.; Mewis, J.; Moldenaers, P. Rheological properties of PDMS/clay nanocomposites and their sensitivity to microstructure. Rheol. Acta 2009, 48, 1049. [Google Scholar] [CrossRef] [Green Version]
- Meng, Y.; Sharma, S.; Chung, J.S.; Gan, W.; Hur, S.H.; Choi, W.M. Enhanced Electromagnetic Interference Shielding Properties of Immiscible Polyblends with Selective Localization of Reduced Graphene Oxide Networks. Polymers 2022, 14, 967. [Google Scholar] [CrossRef] [PubMed]
- Sivanjineyulu, V.; Behera, K.; Chang, Y.-H.; Chiu, F.-C. Selective localization of carbon nanotube and organoclay in biodegradable poly(butylene succinate)/polylactide blend-based nanocomposites with enhanced rigidity, toughness and electrical conductivity. Compos. Part A Appl. Sci. Manuf. 2018, 114, 30–39. [Google Scholar] [CrossRef]
- Laske, S.; Ziegler, W.; Kainer, M.; Wuerfel, J.; Holzer, C. Enhancing the temperature stability of PLA by compounding strategies. Polym. Eng. Sci. 2015, 55, 2849–2858. [Google Scholar] [CrossRef]
- Wu, D.; Lin, D.; Zhang, J.; Zhou, W.; Zhang, M.; Zhang, Y.; Wang, D.; Lin, B. Selective Localization of Nanofillers: Effect on Morphology and Crystallization of PLA/PCL Blends. Macromol. Chem. Phys. 2011, 212, 613–626. [Google Scholar] [CrossRef]
- de Paula Cavalcante, M.; de Menezes, L.R.; da Rocha Rodrigues, E.J.; Tavares, M.I.B. Selective localization of nanohydroxyapatite in poly(3-hydroxybutyrate)/polycaprolactone blends composites and its effects on crystallization and molecular dynamics. J. Mater. Sci. 2021, 56, 3692–3712. [Google Scholar] [CrossRef]
- Cayla, A.; Campagne, C.; Rochery, M.; Devaux, E. Melt spun multifilament yarns of carbon nanotubes-based polymeric blends: Electrical, mechanical and thermal properties. Synth. Met. 2012, 162, 759–767. [Google Scholar] [CrossRef]
- Díez-Pascual, A.M.; Díez-Vicente, A.L. Poly (3-hydroxybutyrate)/ZnO bionanocomposites with improved mechanical, barrier and antibacterial properties. Int. J. Mol. Sci. 2014, 15, 10950–10973. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivorra-Martinez, J.; Quiles-Carrillo, L.; Boronat, T.; Torres-Giner, S.; A Covas, J. Assessment of the mechanical and thermal properties of injection-molded poly (3-hydroxybutyrate-co-3-hydroxyhexanoate)/hydroxyapatite nanoparticles parts for use in bone tissue engineering. Polymers 2020, 12, 1389. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.; Zhang, S.; Han, B.; Sun, H.; Wang, G.; Jiang, Z. Multi-walled carbon nanotube induced co-continuity of poly (ether ether ketone)/polyimide blends for high performance conductive materials. Rsc Adv. 2014, 4, 42175–42182. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, Q.; Huang, Y.; Liao, X.; Niu, Y. Influence of phase coarsening and filler agglomeration on electrical and rheological properties of MWNTs-filled PP/PMMA composites under annealing. Polymer 2015, 79, 159–170. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Cui, X.; Hu, Y.; Lei, L.; Zhu, Y.; Jiang, W. Thermal annealing induced enhancement of electrical properties of a co-continuous polymer blend filled with carbon nanotubes. Compos. Sci. Technol. 2018, 167, 522–528. [Google Scholar] [CrossRef]
- Cipriano, B.H.; Kota, A.K.; Gershon, A.L.; Laskowski, C.J.; Kashiwagi, T.; Bruck, H.A.; Raghavan, S.R. Conductivity enhancement of carbon nanotube and nanofiber-based polymer nanocomposites by melt annealing. Polymer 2008, 49, 4846–4851. [Google Scholar] [CrossRef]
- Alig, I.; Skipa, T.; Lellinger, D.; Pötschke, P. Destruction and formation of a carbon nanotube network in polymer melts: Rheology and conductivity spectroscopy. Polymer 2008, 49, 3524–3532. [Google Scholar] [CrossRef]
- Zhang, R.; Dowden, A.; Deng, H.; Baxendale, M.; Peijs, T. Conductive network formation in the melt of carbon nanotube/thermoplastic polyurethane composite. Compos. Sci. Technol. 2009, 69, 1499–1504. [Google Scholar] [CrossRef]
- Pan, Y.; Cheng, H.K.F.; Li, L.; Chan, S.H.; Zhao, J.; Juay, Y.K. Annealing induced electrical conductivity jump of multi-walled carbon nanotube/polypropylene composites and influence of molecular weight of polypropylene. J. Polym. Sci. Part B Polym. Phys. 2010, 48, 2238–2247. [Google Scholar] [CrossRef]
- Cao, Q.; Song, Y.; Tan, Y.; Zheng, Q. Thermal-induced percolation in high-density polyethylene/carbon black composites. Polymer 2009, 50, 6350–6356. [Google Scholar] [CrossRef]
- Skipa, T.; Lellinger, D.; Böhm, W.; Saphiannikova, M.; Alig, I. Influence of shear deformation on carbon nanotube networks in polycarbonate melts: Interplay between build-up and destruction of agglomerates. Polymer 2010, 51, 201–210. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.; Yang, J.; Zhang, J.; Niu, Y.; Wang, Z. Thermal Annealing Induced Enhancements of Electrical Conductivities and Mechanism for Multiwalled Carbon Nanotubes Filled Poly(Ethylene-co-Hexene) Composites. ACS Appl. Mater. Interfaces 2012, 4, 6468–6478. [Google Scholar] [CrossRef]
- Tao, J.-R.; Yang, D.; Yang, Y.; He, Q.-M.; Fei, B.; Wang, M. Migration mechanism of carbon nanotubes and matching viscosity-dependent morphology in Co-continuous Poly(lactic acid)/Poly(ε-caprolactone) blend: Towards electromagnetic shielding enhancement. Polymer 2022, 252, 124963. [Google Scholar] [CrossRef]
- Lyu, Y.; Yin, H.; Chen, Y.; Zhang, Q.; Shi, X. Structure and evolution of multiphase composites for 3D printing. J. Mater. Sci. 2020, 55, 6861–6874. [Google Scholar] [CrossRef]
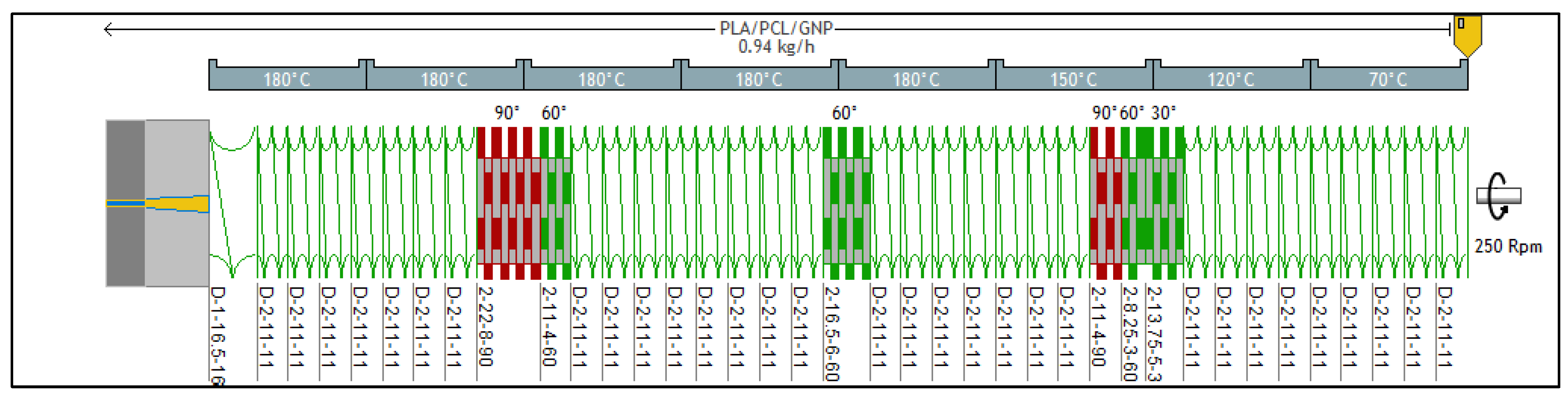











| Extruded Bionanocomposites | Graphene Percentage | PLA and PCL Percentages | Objective |
|---|---|---|---|
| PLAx/PCLy/10 wt.% GNP | 10 wt.% GNP | x and y range between 0 and 100 wt.% (with respect to the total weight fraction of 90 wt.% of polymers), | Exploring the co-continuity range in the compression-moulded samples at 10 wt.% of GNP, |
| PLA65/PCL35/x wt.% GNP | x varies between 5 and 20 wt.% | Fixed at 65 wt.% and 35 wt.% for PLA and PCL, respectively, (with respect to the total weight fraction of 90 wt.% of polymers), | Exploring the influence of the graphene percentage on the co-continuous microstructure in the compression-moulded samples, |
| PLA65/PCL35/10 wt.% GNP (2 extrusion steps) | 10 wt.% | PLA and 10 wt.% of GNP (with respect to the PLA/PCL/GNP composite) were blended and subsequently the resulting composite was melt-blended with PCL (PLA and PCL proportions were 65 and 35 wt.% with respect to the total weight of the 90 wt.% of polymers). | Studying if mixing GNP with the less favourable PLA phase would cause its migration to the more favourable PCL phase and the consequences of this migration on the co-continuous microstructure, |
| Sample Name | Complex Viscosity (Pa·s) (120 Rad·s−1) | Complex Viscosity (Pa·s) (628 Rad·s−1) | Storage Modulus (Pa) (120 Rad·s−1) | Storage Modulus (Pa) (628 Rad·s−1) |
|---|---|---|---|---|
| PLA | 1409 | 545.16 | 117,630 | 287,750 |
| PCL/10% GNP | 197 | 144.07 | 10,168 | 36,269 |
| PCL/15% GNP | 672 | 280.76 | 67,115 | 127,125 |
| PCL/20% GNP | 1971 | 623.83 | 222,643 | 329,913 |
| Authors | Equation | Results (628 Rad·s−1) | Results (120 Rad·s−1) | Reference |
|---|---|---|---|---|
| Paul–Barlow | PLA52/PCL48/10 wt.% GNP | PLA45/PCL55/10 wt.% GNP | [66] | |
| Kitayama et al. | PLA58/PCL42/10 wt.% GNP | PLA55/PCL45/10 wt.% GNP | [68] | |
| Steinmann et al. | PLA52/PCL48/10 wt.% GNP | PLA51/PCL49/10 wt.% GNP | [38] | |
| Ho et al. | PLA49/PCL51/10 wt.% GNP | PLA47/PCL53/10 wt.% GNP | [67] | |
| Everaert et al. | PLA54/PCL46/10 wt.% GNP | PLA53/PCL47/10 wt.% GNP | [69] | |
| Metelkin–Blekht | PLA47/PCL53/10 wt.% GNP | - | [70] | |
| Utracki | [46,72,73] | PLA53/PCL47/10 wt.% GNP | PLA51/PCL49/10 wt.% GNP | [71] |
| Bourry–Favis | PLA60/PCL40/10 wt.% GNP | - | [33] |
| Sample | Electrical Volume Resistivity (Ω·cm) | Electric Current (mA) (5 v) | LED (5 v) |
|---|---|---|---|
| PLA/GNP | 4865.9 ± 65.11 | 10−6 ± 7 × 10−4 | No light |
| PLA80/PCL20/GNP | 4900.43 ± 90.19 | 10−6 ± 4 × 10−3 | No light |
| PLA70/PCL30/GNP | 30.23 ± 1.17 | 9 ± 6 × 10−2 |  |
| PLA65/PCL35/GNP | 25.78 ± 5.11 | 9.24 ± 4 × 10−2 |  |
| PLA60/PCL40/GNP | 53.67 ± 12.24 | 6.13 ± 8 × 10−2 |  |
| PLA55/PCL45/GNP | 66.89 ± 10.26 | 5 ± 9 × 10−2 |  |
| PLA50/PCL50/GNP | 75.67 ± 15.19 | 3.1 ± 5 × 10−2 |  |
| PLA45/PCL55/GNP | 104.25 ± 12.38 | 2.3 ± 10−2 |  |
| PLA40/PCL60/GNP | 125.61 ± 20.81 | 1.4 ± 2 × 10−2 |  |
| PLA30/PCL70/GNP | 237.34 ± 25.33 | 0.9 ± 10−2 |  |
| PCL/GNP | 500 ± 30.33 | 0.01 ± 5 × 10−2 |  |
| Sample Name | Tm (PLA) (°C) | Tm (PCL) (°C) | Tc (PLA) (°C) | Xc (PLA) (%) | Xc (PCL) (%) |
|---|---|---|---|---|---|
| PCL | - | 58 ± 0.17 | - | - | 49.5 ± 0.1 |
| PCL/GNP | - | 62 ± 1.7 | - | - | 52.5 ± 0.2 |
| PLA30/PCL70/GNP | 156 ± 0.1 | 63 ± 1.9 | 124 ± 1.1 | 1.8 ± 0.1 | 49.6 ± 0.1 |
| PLA50/PCL50/GNP | 153 ± 0.14 | 61 ± 1.1 | 124 ± 3.1 | 1.5 ± 0.05 | 50.7 ± 0.1 |
| PLA65/PCL35/GNP | 148 ± 2.1 | 58 ± 2.1 | 115 ± 3.4 | 7.2 ± 0.2 | 58.5 ± 0.4 |
| PLA80/PCL20/GNP | 155 ± 1.19 | 63 ± 1.8 | 132 ± 1.8 | 1.2 ± 0.04 | 50.9 ± 0.4 |
| PLA/GNP | 155 ± 1.12 | - | 133 ± 1.7 | 0.5 ± 0.001 | - |
| PLA | 156 ± 2.3 | - | - | 0.9 ± 0.001 | - |
| Sample Name | Maximal Degradation Temperature (Tmax) of Each Polymer | Total Mass Loss (%) | Experimental Percentage of Char Yield (at 600 °C) | Theoretical Percentage of Char Yield (at 600 °C) | Onset Temperature (Tonset) (°C) | |
|---|---|---|---|---|---|---|
| PLA | PCL | |||||
| PCL | - | 416 ± 1.6 | 100 ± 0 | 0 | - | 383 ± 2.1 |
| PCL/GNP | - | 414 ± 1.7 | 97 ± 0.01 | 7.1 ± 0.1 | 9 ± 0.4 | 383 ± 1.4 |
| PLA30/PCL70/GNP | 361 ± 2 | 413 ± 3.6 | 97 ± 0.04 | 8.1 ± 1.07 | 9 ± 0.4 | 351 ± 0.6 |
| PLA50/PCL50/GNP | 363 ± 2.1 | 413 ± 2.2 | 98 ± 0.02 | 8.2 ± 0.04 | 9 ± 0.4 | 352 ± 0.4 |
| PLA65/PCL35/GNP | 364 ± 4.4 | 412 ± 1.8 | 95 ± 0.1 | 14.5 ± 0.9 | 9 ± 0.4 | 355 ± 1.1 |
| PLA80/PCL20/GNP | 365 ± 1.7 | 410 ± 4.8 | 97 ± 0.1 | 8.1 ± 0.06 | 9 ± 0.4 | 351 ± 2 |
| PLA/GNP | 368 ± 2.4 | - | 100 ± 0 | 4 ± 0.5 | 9 ± 0.4 | 351 ± 0.2 |
| PLA | 366 ± 4.6 | - | 100 ± 0 | 0 | - | 345 ± 0.6 |
| Time (min) | Electrical Volume Resistivity (Ω·cm) | Electric Current (mA) (5 v) | LED (5 v) | Continuous PLA Fraction (%) (Solvent Extraction Method) |
|---|---|---|---|---|
| 10 | 38.25 ± 8.1 | 8.56 ± 8 × 10−2 |  | 85.247 ± 1.681 |
| 20 | 33.98 ± 9.4 | 8.89 ± 2 × 10−2 |  | 90.527 ± 2.485 |
| 35 | 25.78 ± 5.11 | 9.24 ± 4 × 10−2 |  | 99.481 ± 0.607 |
| Number of Twin Screw Extrusion Steps | Electrical Volume Resistivity (Ω·cm) | Electric Current (mA) (5 v) | LED (5 v) | Continuous PLA Fraction (%) (Solvent Extraction Method) |
|---|---|---|---|---|
| One | 25.78 ± 5.11 | 9.24 ± 4 × 10−2 |  | 99.481 ± 0.607 |
| Two | 30.22 ± 2.81 | 9.05 ± 6 × 10−2 |  | 95.843 ± 0.759 |
| Weight Percentage of Graphene (%) | Electrical Volume Resistivity (Ω·cm) | Electric Current (mA) (5 v) | LED (5 v) |
|---|---|---|---|
| 5 | 486.5 ± 10 | 18 × 10−3 ± 5 × 10−3 |  |
| 10 | 25.78 ± 5.11 | 9.24 ± 4 × 10−2 |  |
| 15 | 12 × 10−2 ± 3 × 10−3 | 15.65 ± 1.94 |  |
| 20 | 2 × 10−3 ± 6 × 10−4 | 25.55 ± 6.88 |  |
| Sample | Electrical Volume Resistivity (3D Printed) (Ω·cm) | Electric Current (3D Printed) (mA) (5 v) | LED (3D Printed) (5 v) | Electrical Volume Resistivity (Compression Moulded) (Ω·cm) | Electric Current (Compression Moulded) (mA) (5 v) | LED (Compression Moulded) (5 v) |
|---|---|---|---|---|---|---|
| PLA80/PCL20/GNP | >107 | - | No light | 4900.43 ± 90.19 | 10−6 ± 4 × 10−3 | No light |
| PLA65/PCL35/GNP | 1000.53 ± 30.22 | 10−3 ± 10−2 |  | 25.78 ± 5.11 | 9.24 ± 4 × 10−2 |  |
| PLA50/PCL50/GNP | 3277.83 ± 89.32 | 9 × 10−6 ± 5 × 10−5 | No light | 75.67 ± 15.19 | 3.1 ± 5 × 10−2 |  |
| PLA40/PCL60/GNP | 5371.62 ± 90.44 | 6 × 10−6 ± 7 × 10−5 | No light | 125.61 ± 20.81 | 1.4 ± 2 × 10−2 |  |
| PLA30/PCL70/GNP | 7000 ± 101.34 | 10−7 ± 9 × 10−5 | No light | 237.34 ± 25.33 | 0.9 ± 10−2 |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masarra, N.-A.; Quantin, J.-C.; Batistella, M.; El Hage, R.; Pucci, M.F.; Lopez-Cuesta, J.-M. Influence of Polymer Processing on the Double Electrical Percolation Threshold in PLA/PCL/GNP Nanocomposites. Sensors 2022, 22, 9231. https://doi.org/10.3390/s22239231
Masarra N-A, Quantin J-C, Batistella M, El Hage R, Pucci MF, Lopez-Cuesta J-M. Influence of Polymer Processing on the Double Electrical Percolation Threshold in PLA/PCL/GNP Nanocomposites. Sensors. 2022; 22(23):9231. https://doi.org/10.3390/s22239231
Chicago/Turabian StyleMasarra, Nour-Alhoda, Jean-Christophe Quantin, Marcos Batistella, Roland El Hage, Monica Francesca Pucci, and José-Marie Lopez-Cuesta. 2022. "Influence of Polymer Processing on the Double Electrical Percolation Threshold in PLA/PCL/GNP Nanocomposites" Sensors 22, no. 23: 9231. https://doi.org/10.3390/s22239231
APA StyleMasarra, N. -A., Quantin, J. -C., Batistella, M., El Hage, R., Pucci, M. F., & Lopez-Cuesta, J. -M. (2022). Influence of Polymer Processing on the Double Electrical Percolation Threshold in PLA/PCL/GNP Nanocomposites. Sensors, 22(23), 9231. https://doi.org/10.3390/s22239231









