Vision-Based Structural Modal Identification Using Hybrid Motion Magnification
Abstract
1. Introduction
2. Materials and Methods
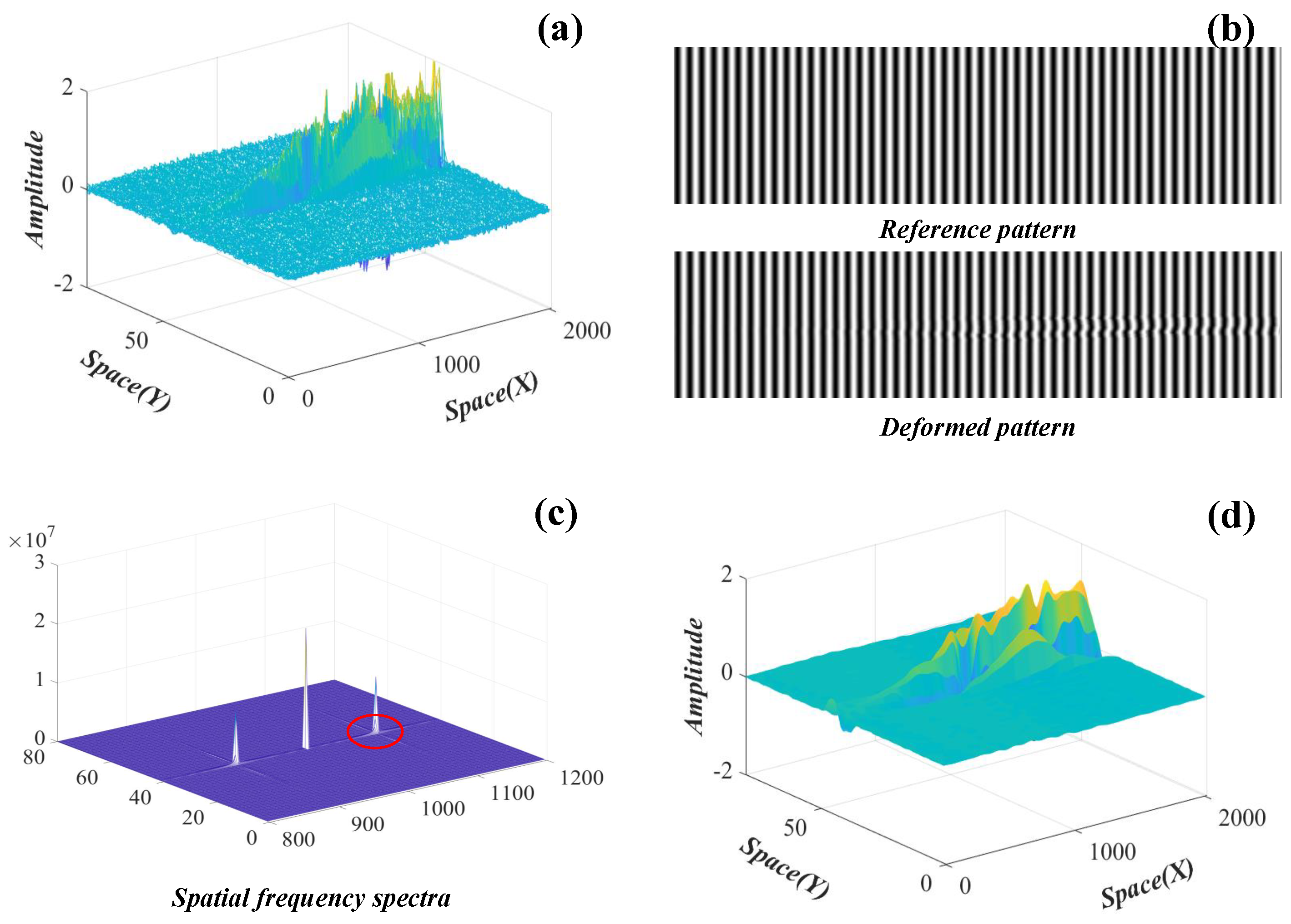
2.1. Structural Vibration and Intensity Variations
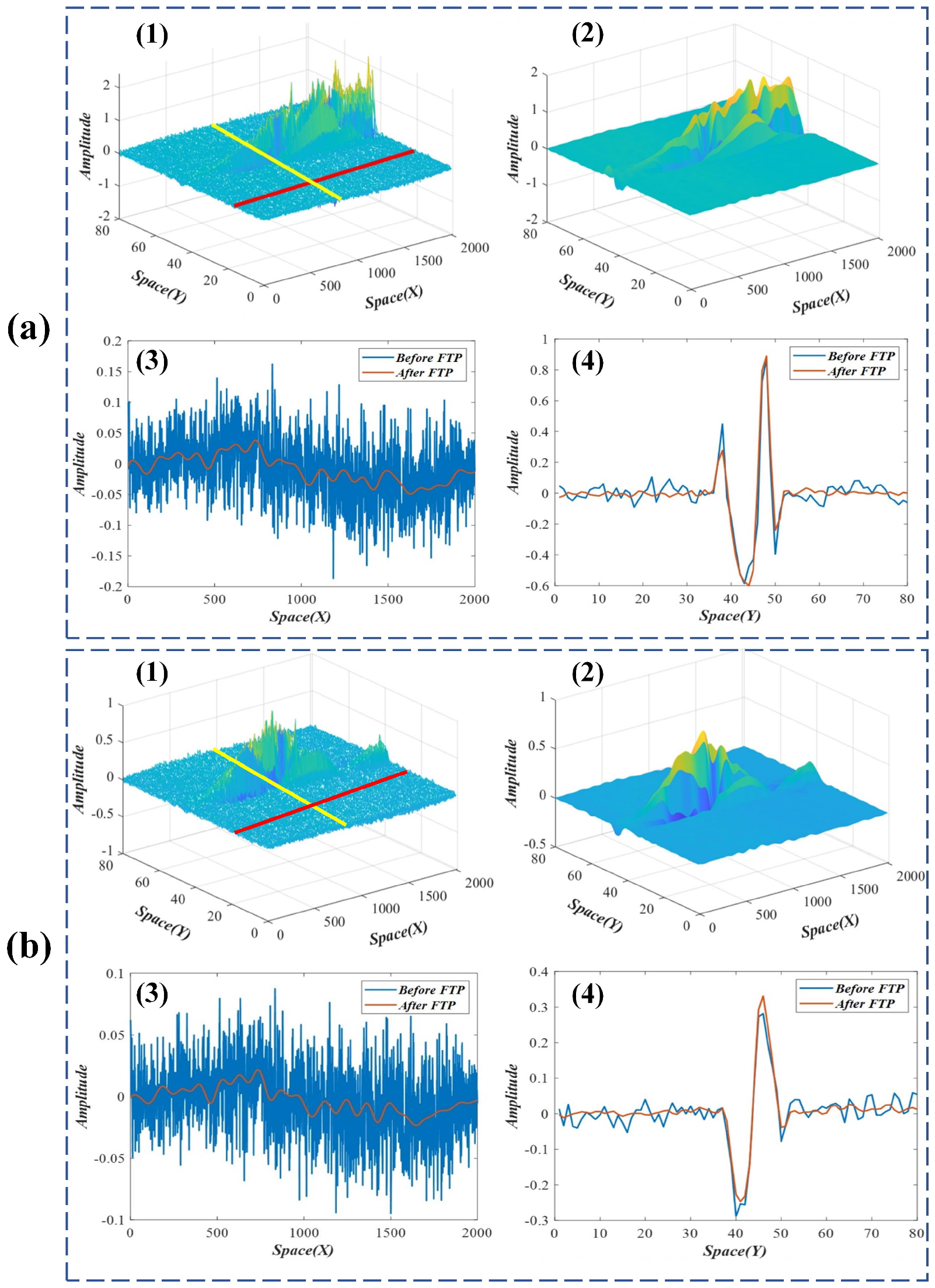
2.2. Linear Motion Processing
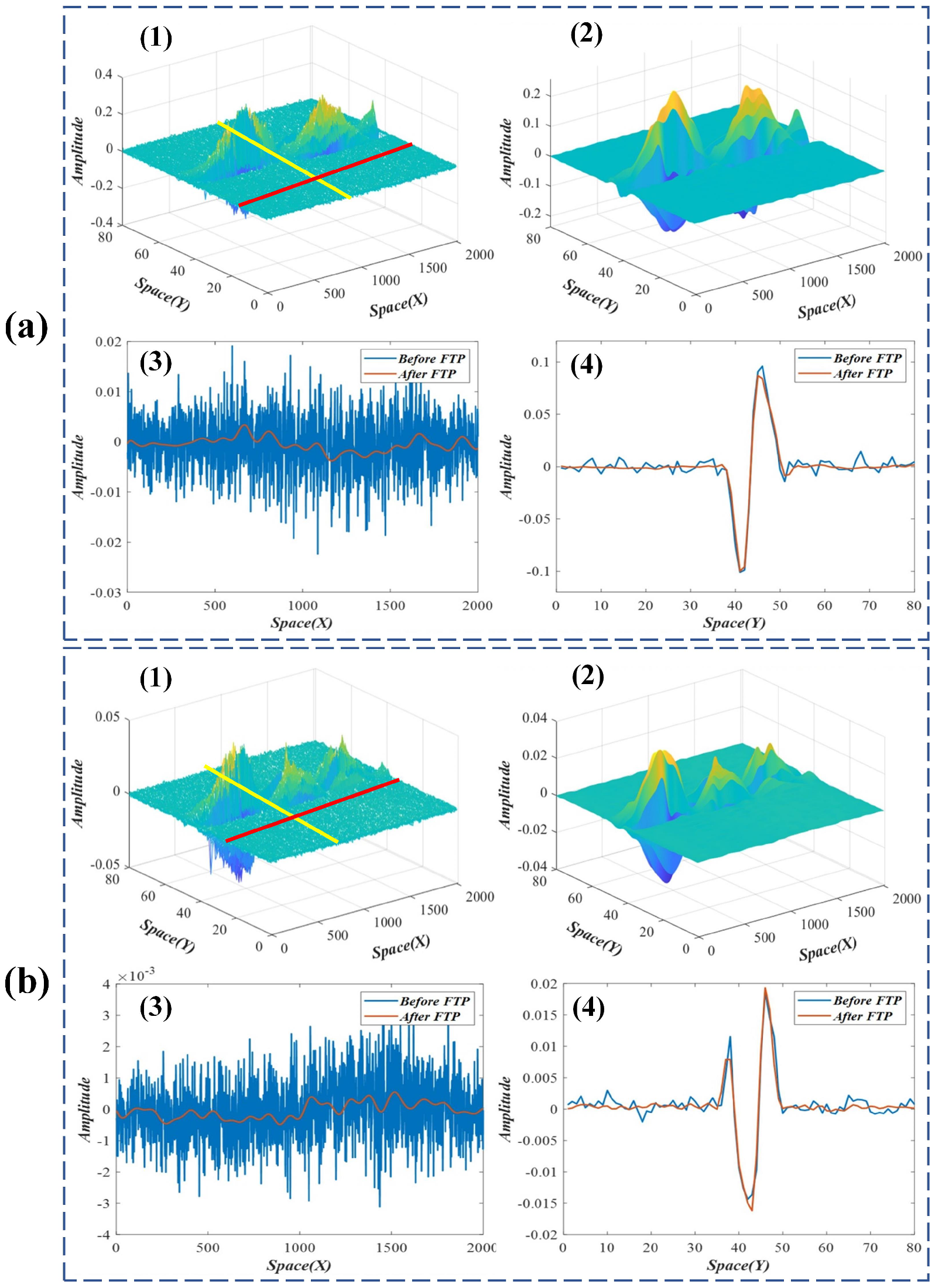
2.3. Weight Enhancement of the FTP
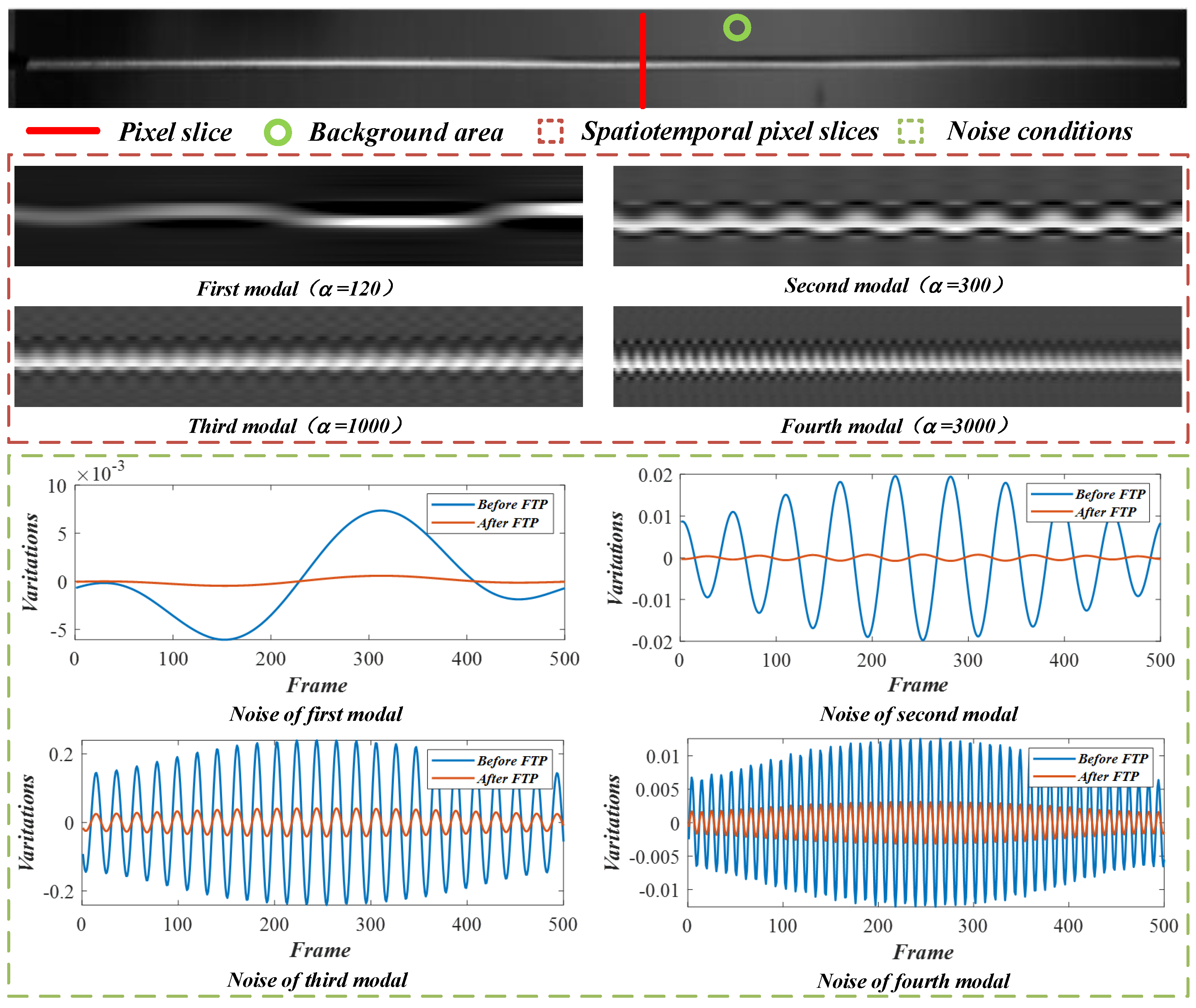
2.4. Phase-Based Motion Processing
3. Results
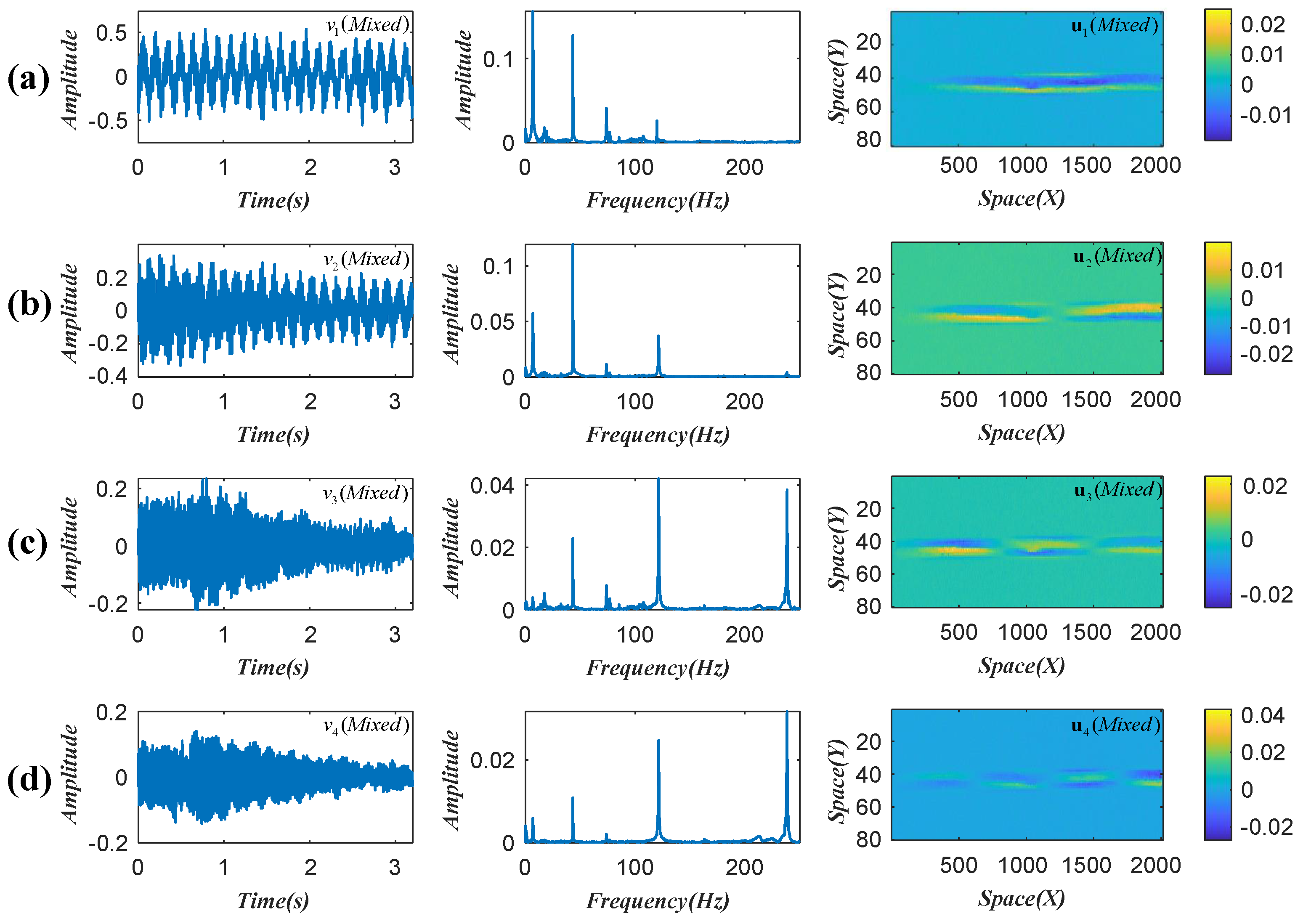
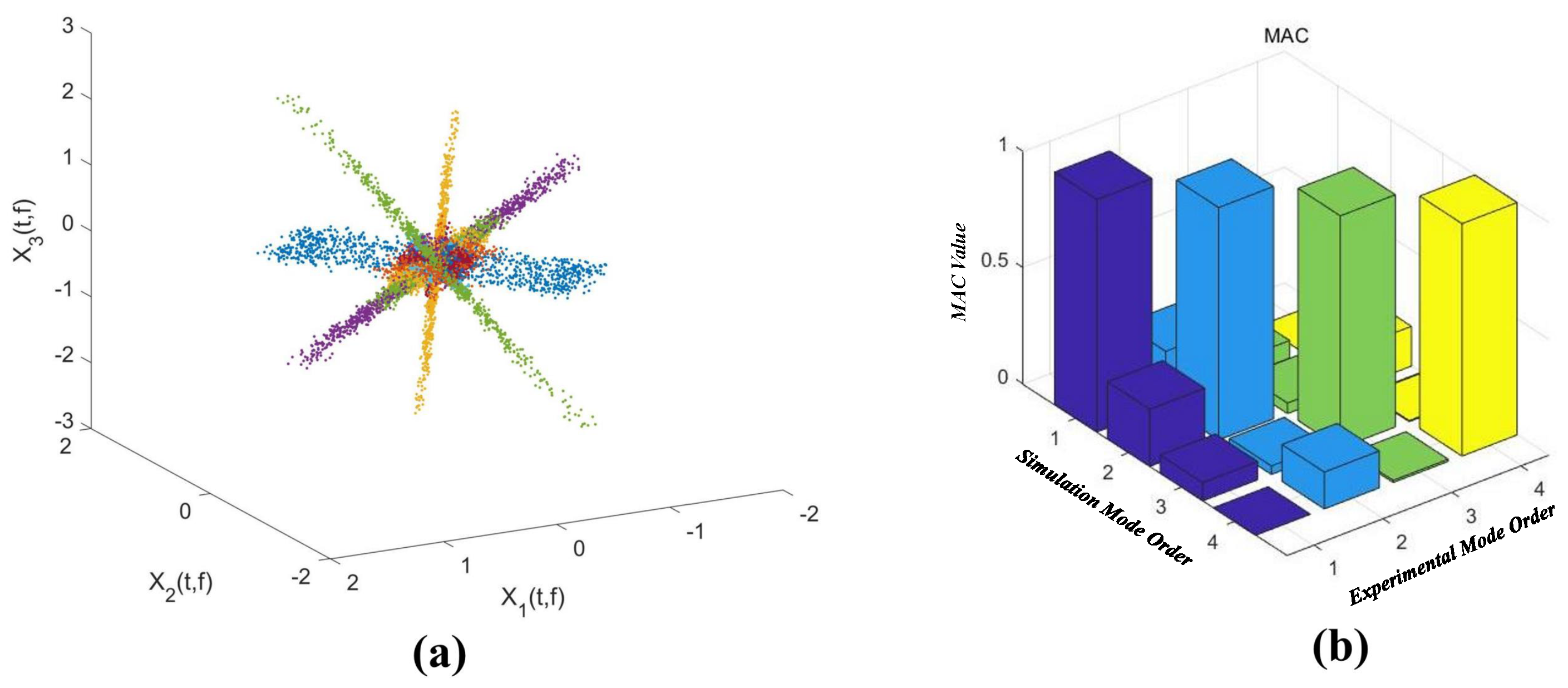
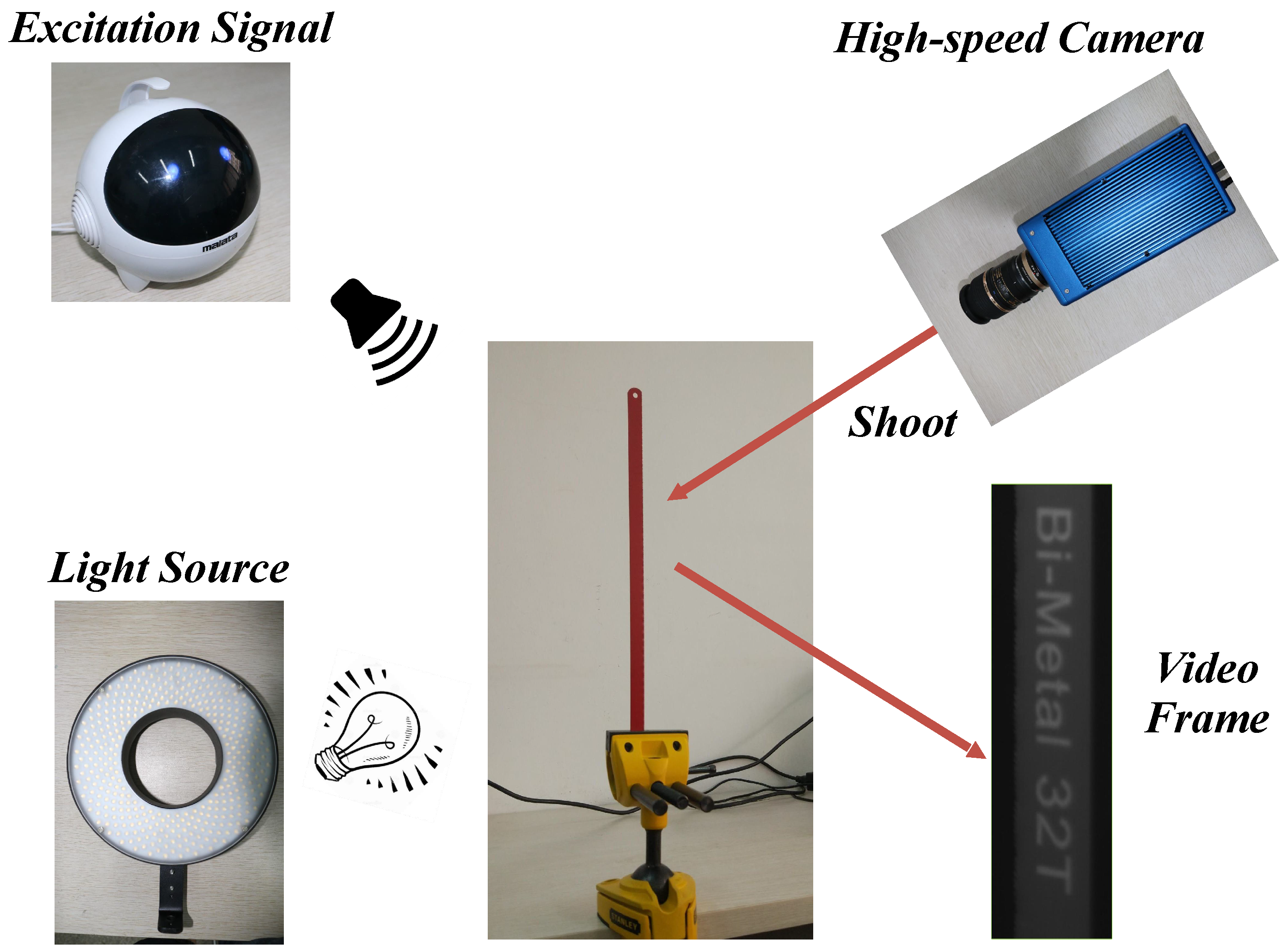
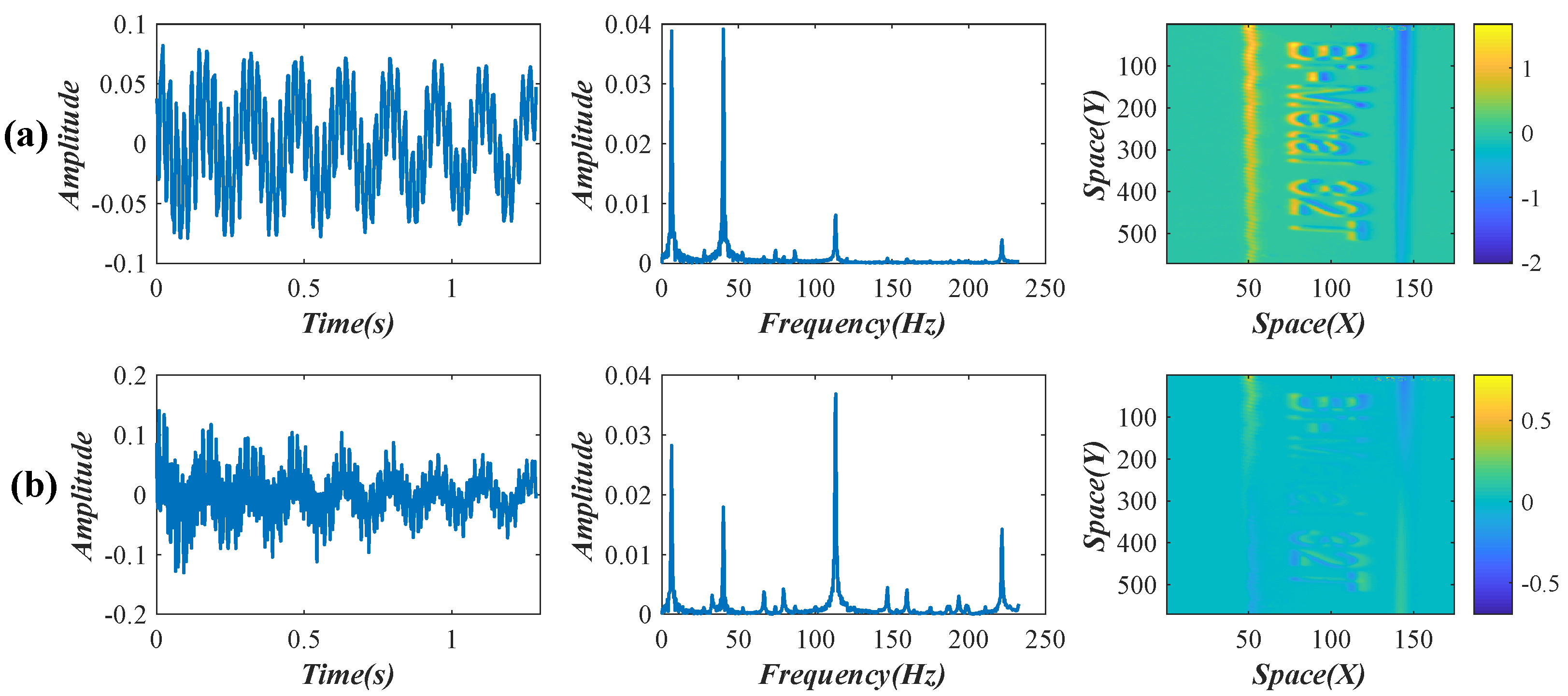
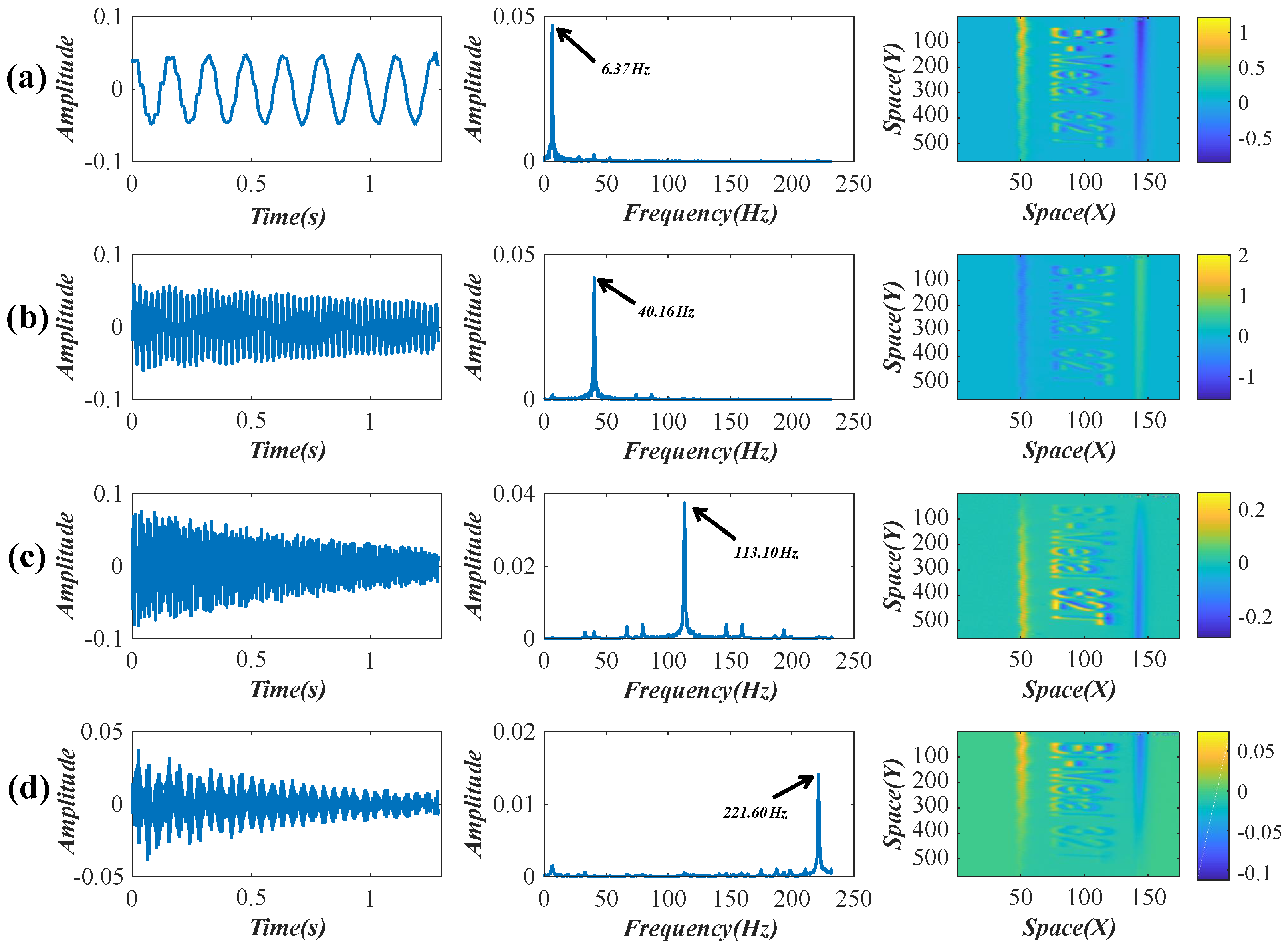
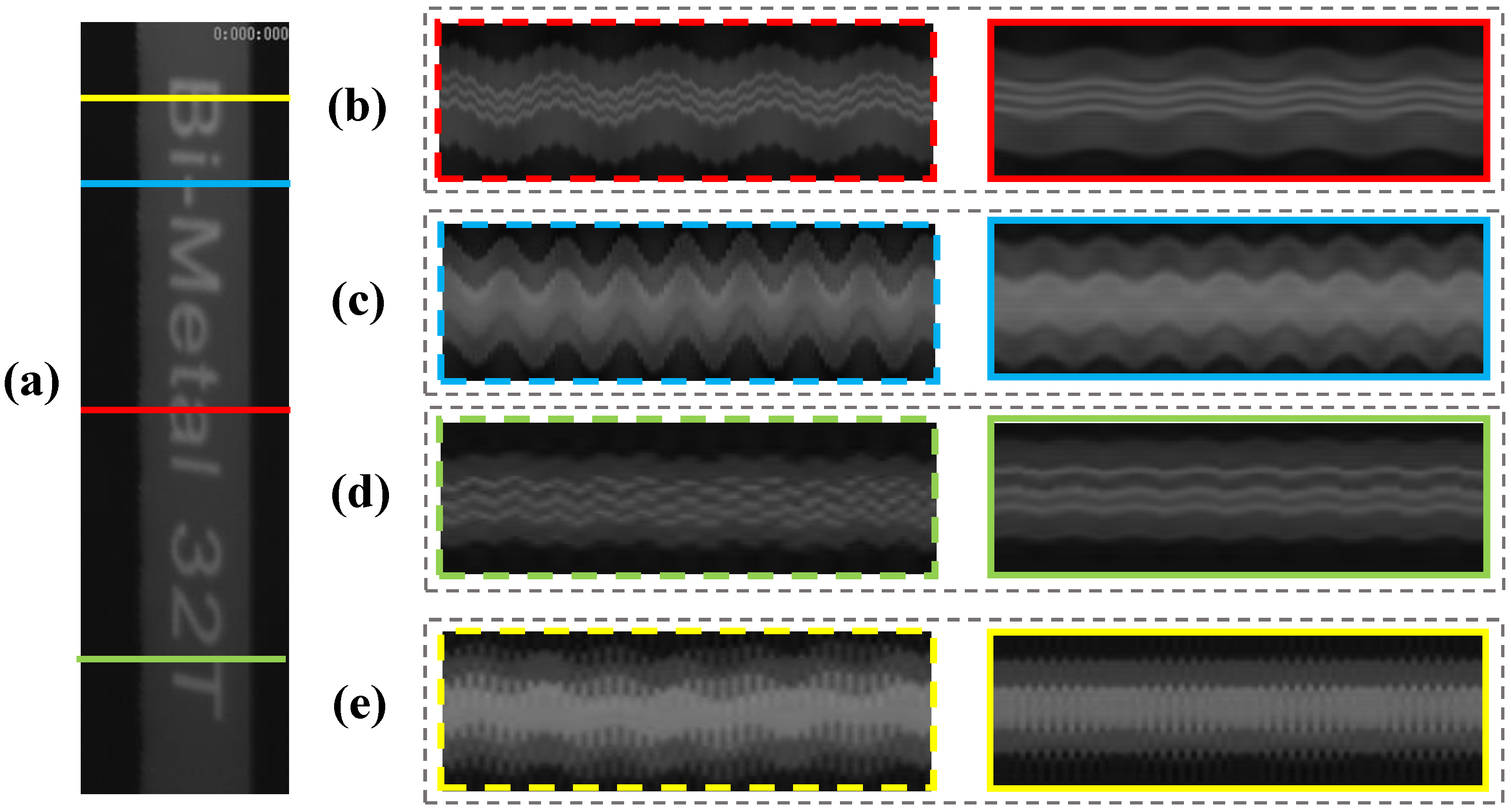
3.1. Vibration Analysis of a Lightweight Beam
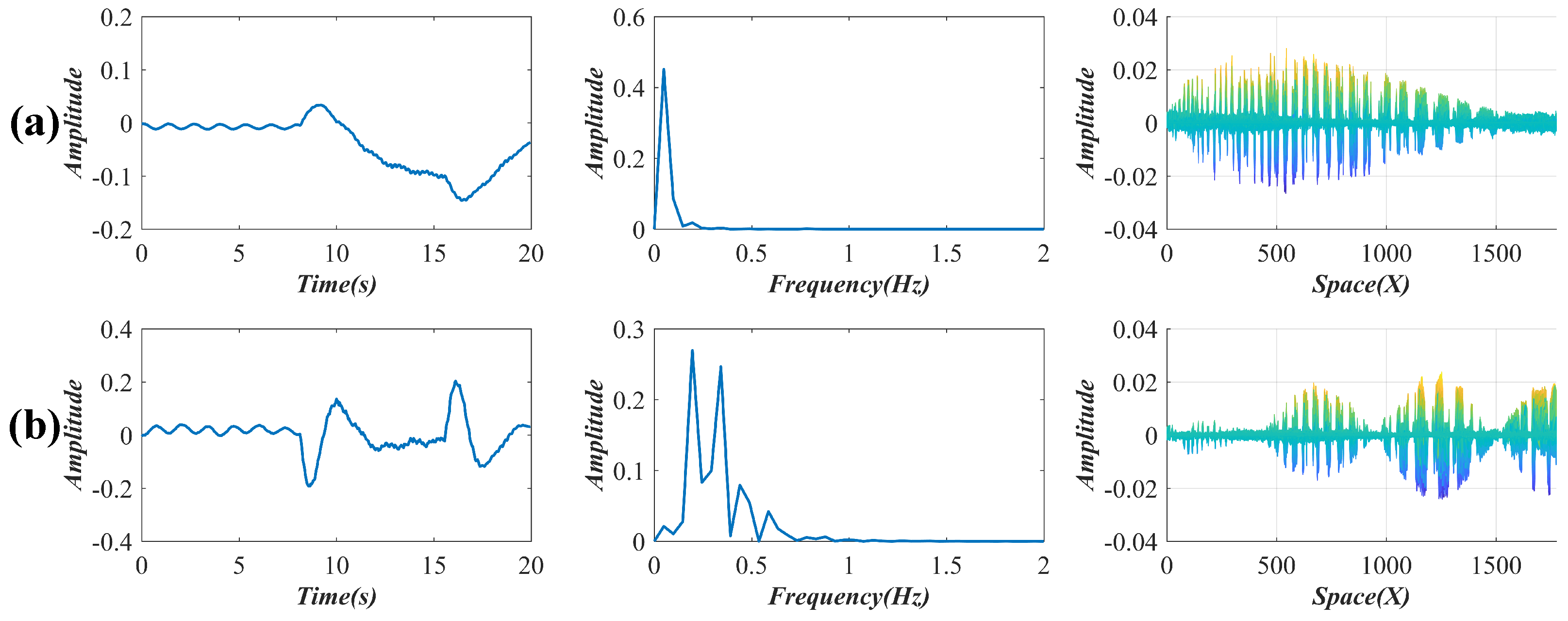
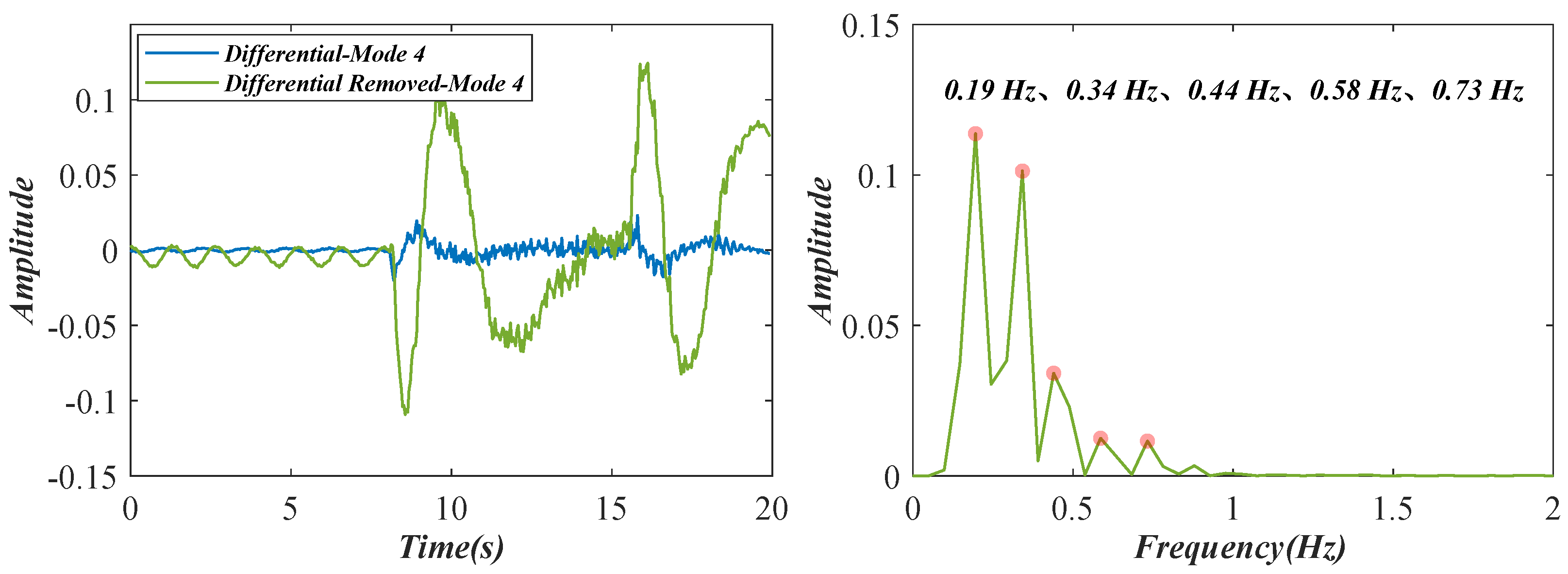
3.2. Vibration Analysis of the Nanfeihe Truss Bridge
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, Z.; Yu, J.; Meng, X. Modal Parameters Identification of Bridge Structures from GNSS Data Using the Improved Empirical Wavelet Transform. Remote Sens. 2021, 13, 3375. [Google Scholar] [CrossRef]
- Cakar, O.; Sanliturk, K.Y. Elimination of transducer mass loading effects from frequency response functions. Mech. Syst. Signal Proc. 2005, 19, 87–104. [Google Scholar] [CrossRef]
- Zuo, D.; Hua, J.; Van Landuyt, D. A model of pedestrian-induced bridge vibration based on full-scale measurement. Eng. Struct. 2012, 45, 117–126. [Google Scholar] [CrossRef]
- Olaszek, P.; Świercz, A.; Boscagli, F. The Integration of Two Interferometric Radars for Measuring Dynamic Displacement of Bridges. Remote Sens. 2021, 13, 3668. [Google Scholar] [CrossRef]
- Khuc, T.; Catbas, F.N. Completely contactless structural health monitoring of real-life structures using cameras and computer vision. Struct. Control. Health Monit. 2017, 24, e1852. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection—A review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Kalybek, M.; Bocian, M.; Pakos, W.; Grosel, J.; Nikitas, N. Performance of Camera-Based Vibration Monitoring Systems in Input-Output Modal Identification Using Shaker Excitation. Remote Sens. 2021, 13, 3471. [Google Scholar] [CrossRef]
- Seo, S.; Ko, Y.; Chung, M. Evaluation of Field Applicability of High-Speed 3D Digital Image Correlation for Shock Vibration Measurement in Underground Mining. Remote Sens. 2022, 14, 3133. [Google Scholar] [CrossRef]
- Frankovský, P.; Delyová, I.; Sivák, P.; Bocko, J.; Živčák, J.; Kicko, M. Modal Analysis Using Digital Image Correlation Technique. Materials 2022, 15, 5658. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Cai, J.; Zhang, D.; Chen, X.; Wang, Y. Nonlinear Correction for Fringe Projection Profilometry with Shifted-Phase Histogram Equalization. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Patil, K.; Srivastava, V.; Baqersad, J. A multi-view optical technique to obtain mode shapes of structures. Measurement 2018, 122, 358–367. [Google Scholar] [CrossRef]
- Zhang, D.; Hou, W.; Guo, J.; Zhang, X. Efficient subpixel image registration algorithm for high precision visual vibrometry. Measurement 2021, 173, 108538. [Google Scholar] [CrossRef]
- Wu, H.Y.; Rubinstein, M.; Shih, E.; Guttag, J.; Durand, F.; Freeman, W.T. Eulerian Video Magnification for Revealing Subtle Changes in the World. ACM Trans. Graph. 2012, 31, 1–8. [Google Scholar] [CrossRef]
- Wadhwa, N.; Rubinstein, M.; Durand, F.; Freeman, W.T. Phase-Based Video Motion Processing. ACM Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Wadhwa, N.; Freeman, W.T.; Durand, F.; Wu, H.Y.; Guttag, J.V. Eulerian video magnification and analysis. Commun. ACM 2016, 60, 87–95. [Google Scholar] [CrossRef]
- Chen, J.G.; Wadhwa, N.; Cha, Y.J.; Durand, F.; Freeman, W.T.; Buyukozturk, O. Modal identification of simple structures with high-speed video using motion magnification. J. Sound Vibr. 2015, 345, 58–71. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Nagarajaiah, S.; Kenyon, G.; Farrar, C.; Mascareñas, D. Blind identification of full-field vibration modes of output-only structures from uniformly-sampled, possibly temporally-aliased (sub-Nyquist), video measurements. J. Sound Vibr. 2017, 390, 232–256. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Mancini, T.; Talken, Z.; Kenyon, G.; Farrar, C.; Mascareñas, D. Blind identification of full-field vibration modes from video measurements with phase-based video motion magnification. Mech. Syst. Signal Proc. 2017, 85, 567–590. [Google Scholar] [CrossRef]
- Davis, A.; Bouman, K.L.; Chen, J.G.; Rubinstein, M.; Büyüköztürk, O.; Durand, F.; Freeman, W.T. Visual Vibrometry: Estimating Material Properties from Small Motions in Video. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 732–745. [Google Scholar] [CrossRef]
- Wadhwa, N.; Chen, J.G.; Sellon, J.B.; Wei, D.; Rubinstein, M.; Ghaffari, R.; Freeman, D.M.; Büyüköztürk, O.; Wang, P.; Sun, S.; et al. Motion microscopy for visualizing and quantifying small motions. Proc. Natl. Acad. Sci. USA 2017, 114, 11639–11644. [Google Scholar] [CrossRef]
- Silva, M.; Martinez, B.; Figueiredo, E.; Costa, J.C.; Yang, Y.; Mascareñas, D. Nonnegative matrix factorization-based blind source separation for full-field and high-resolution modal identification from video. J. Sound Vibr. 2020, 487, 115586. [Google Scholar] [CrossRef]
- Yang, Y.; Dorn, C.; Farrar, C.; Mascareñas, D. Blind, simultaneous identification of full-field vibration modes and large rigid-body motion of output-only structures from digital video measurements. Eng. Struct. 2020, 207, 110183. [Google Scholar] [CrossRef]
- Eitner, M.; Miller, B.; Sirohi, J.; Tinney, C. Effect of broad-band phase-based motion magnification on modal parameter estimation. Mech. Syst. Signal Proc. 2021, 146, 106995. [Google Scholar] [CrossRef]
- Siringoringo, D.M.; Wangchuk, S.; Fujino, Y. Noncontact operational modal analysis of light poles by vision-based motion-magnification method. Eng. Struct. 2021, 244, 112728. [Google Scholar] [CrossRef]
- Chen, J.G.; Adams, T.M.; Sun, H.; Bell, E.S.; Oral, B. Camera-Based Vibration Measurement of the World War I Memorial Bridge in Portsmouth, New Hampshire. J. Struct. Eng. 2018, 144, 04018207. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, J.; Lei, X.; Zhu, C. Note: Sound recovery from video using SVD-based information extraction. Rev. Sci. Instrum. 2016, 87, 198–516. [Google Scholar] [CrossRef] [PubMed]
- Qin, S.; Zhu, C.; Jin, Y. Sparse Component Analysis Based on Hierarchical Hough Transform. Circuits Syst. Signal Process. 2017, 36, 1569–1585. [Google Scholar]
- Xu, Y.; Brownjohn, J.M.; Hester, D. Enhanced sparse component analysis for operational modal identification of real-life bridge structures. Mech. Syst. Signal Proc. 2019, 116, 585–605. [Google Scholar] [CrossRef]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Optics 1983, 22, 3977. [Google Scholar] [CrossRef]
- Berryman, F.; Pynsent, P.; Cubillo, J. A theoretical comparison of three fringe analysis methods for determining the three-dimensional shape of an object in the presence of noise. Opt. Lasers Eng. 2003, 39, 35–50. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-Reference Image Quality Assessment in the Spatial Domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef]
- Feng, M.Q.; Fukuda, Y.; Feng, D.; Mizuta, M. Nontarget Vision Sensor for Remote Measurement of Bridge Dynamic Response. J. Bridge Eng. 2015, 20, 04015023.1–04015023.12. [Google Scholar] [CrossRef]
- Hermanns, L.; Gimenez, J.G.; Alarcon, E. Efficient computation of the pressures developed during high-speed train passing events. Comput. Struct. 2005, 83, 793–803. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Model Updating of Railway Bridge Using In Situ Dynamic Displacement Measurement under Trainloads. J. Bridge Eng. 2015, 20, 04015019. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Y.; Shen, W.; Kong, F. A stochastic analysis method of transient responses using harmonic wavelets, part 1: Time-invariant structural systems. Mech. Syst. Signal Proc. 2021, 160, 107870. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Y.; Shen, W. A stochastic analysis method of transient responses using harmonic wavelets, part 2: Time-dependent vehicle-bridge systems. Mech. Syst. Signal Proc. 2022, 162, 107871. [Google Scholar] [CrossRef]





| Mode | Factor | Factor | Factor | BRISQUE | BRISQUE |
|---|---|---|---|---|---|
| Order | (Original) | () | () | (Original) | (Improved) |
| 1st | 350 | 10 | 40 | 50.94 | 45.48 |
| 2nd | 600 | 30 | 25 | 46.78 | 44.13 |
| 3rd | 1000 | 100 | 15 | 50.20 | 44.30 |
| 4th | 12,000 | 1000 | 20 | 56.00 | 43.69 |
| Dimensions (mm) | Young’s Modulus | Density |
|---|---|---|
| N·m−2 | kg·m−3 |
| Mode Order | Theoretical (Hz) | Experimental (Hz) | Error Rate (%) |
|---|---|---|---|
| 1st | 6.41 | 6.37 | 0.62 |
| 2nd | 40.17 | 40.16 | 0.02 |
| 3rd | 112.43 | 113.10 | 0.59 |
| 4th | 220.31 | 221.60 | 0.08 |
| Mode | Factor | Factor | Factor | BRISQUE | BRISQUE |
|---|---|---|---|---|---|
| Order | (Original) | () | () | (Original) | (Improved) |
| 1st | 10 | 0.15 | 100 | 50.84 | 40.45 |
| 2nd | 15 | 0.2 | 200 | 52.10 | 41.58 |
| 3rd | 60 | 2 | 50 | 48.04 | 41.75 |
| 4th | 100 | 5 | 30 | 49.24 | 40.78 |
| Mode Number | 1 | 2 | 3 | 4 |
| Linear () | 10 | 15 | 25 | 30 |
| Phase-based () | 400 | 400 | 800 | 800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Zhu, A.; Hou, W.; Liu, L.; Wang, Y. Vision-Based Structural Modal Identification Using Hybrid Motion Magnification. Sensors 2022, 22, 9287. https://doi.org/10.3390/s22239287
Zhang D, Zhu A, Hou W, Liu L, Wang Y. Vision-Based Structural Modal Identification Using Hybrid Motion Magnification. Sensors. 2022; 22(23):9287. https://doi.org/10.3390/s22239287
Chicago/Turabian StyleZhang, Dashan, Andong Zhu, Wenhui Hou, Lu Liu, and Yuwei Wang. 2022. "Vision-Based Structural Modal Identification Using Hybrid Motion Magnification" Sensors 22, no. 23: 9287. https://doi.org/10.3390/s22239287
APA StyleZhang, D., Zhu, A., Hou, W., Liu, L., & Wang, Y. (2022). Vision-Based Structural Modal Identification Using Hybrid Motion Magnification. Sensors, 22(23), 9287. https://doi.org/10.3390/s22239287








