Three-Dimensional Localization of Buried Polyethylene Pipes Using Acoustic Method
Abstract
:1. Introduction
2. Modeling with a Single Propagation Medium (M1)
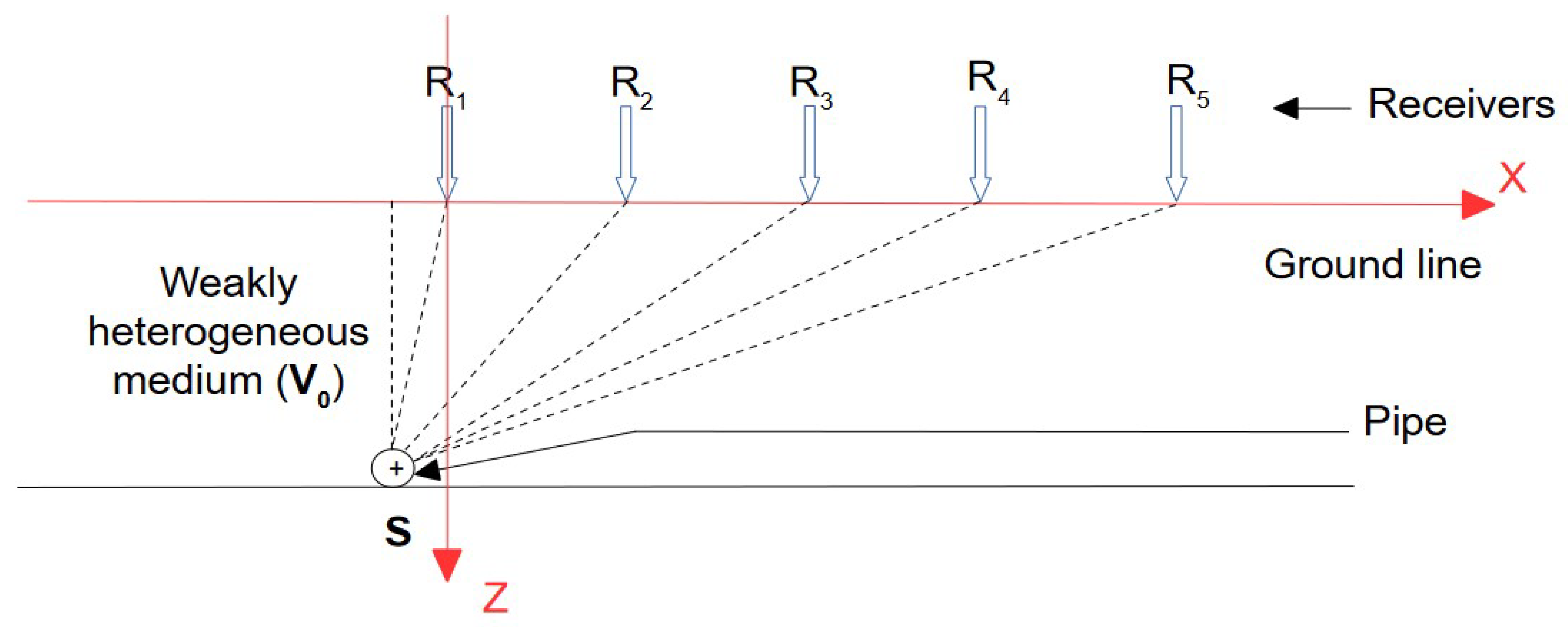
2.1. Propagation Time Modeling M1
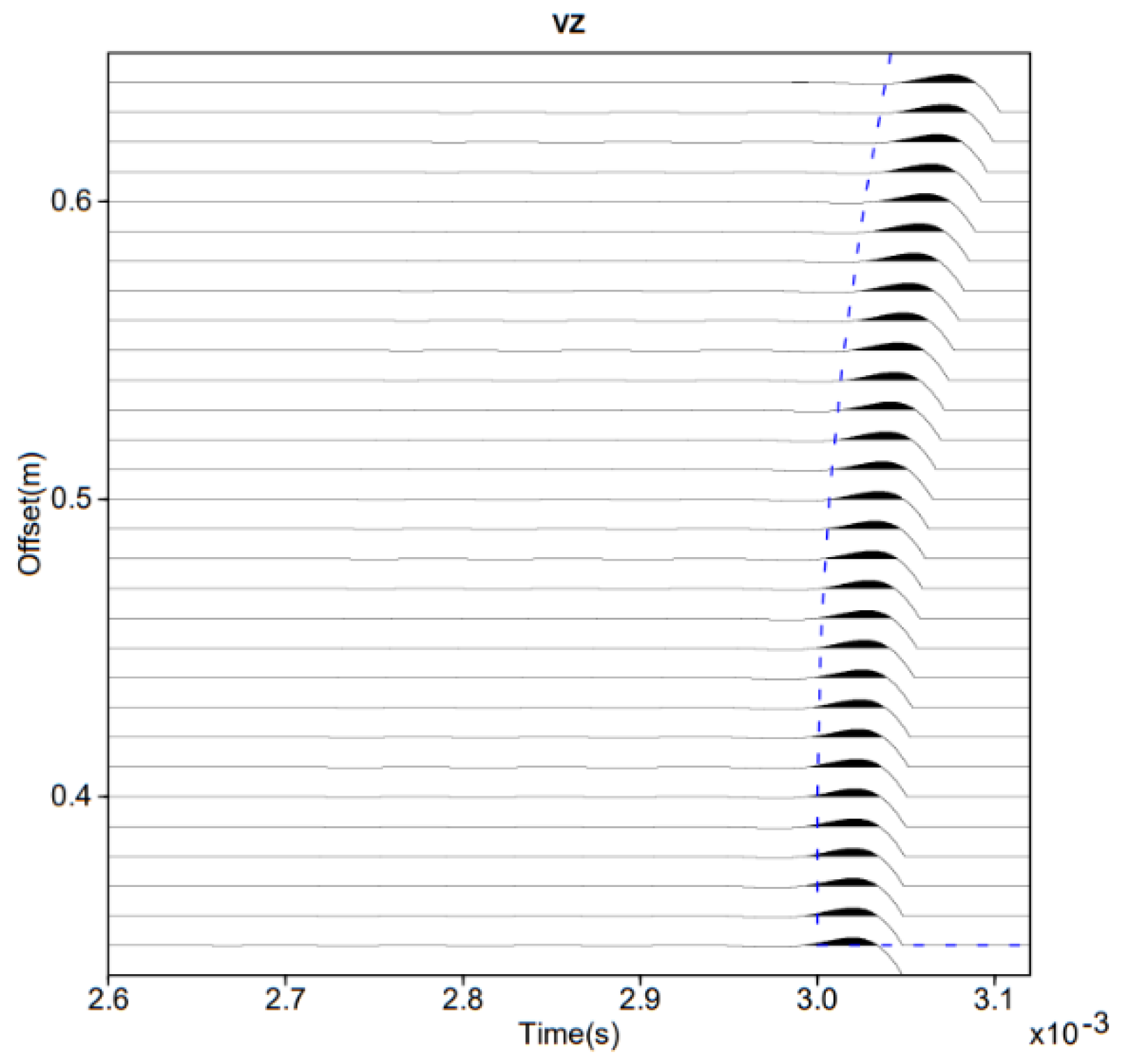
2.2. Validation of Travel Time Estimate of M1 through Comparison with a Finite Difference Modeling of the Full Wavefield
2.3. Cramer–Rao Bound from Model M1
2.3.1. Calculation of the Cramer–Rao Bound from Model M1
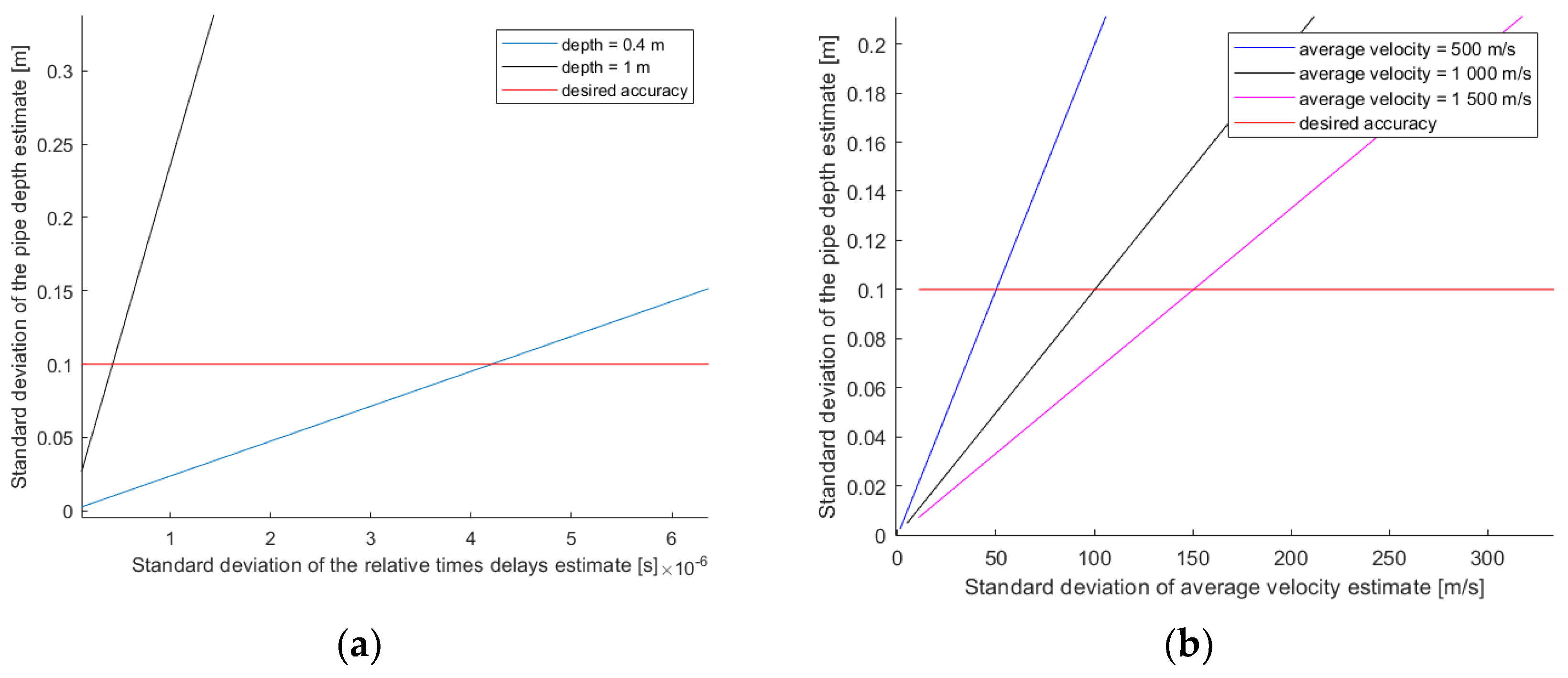
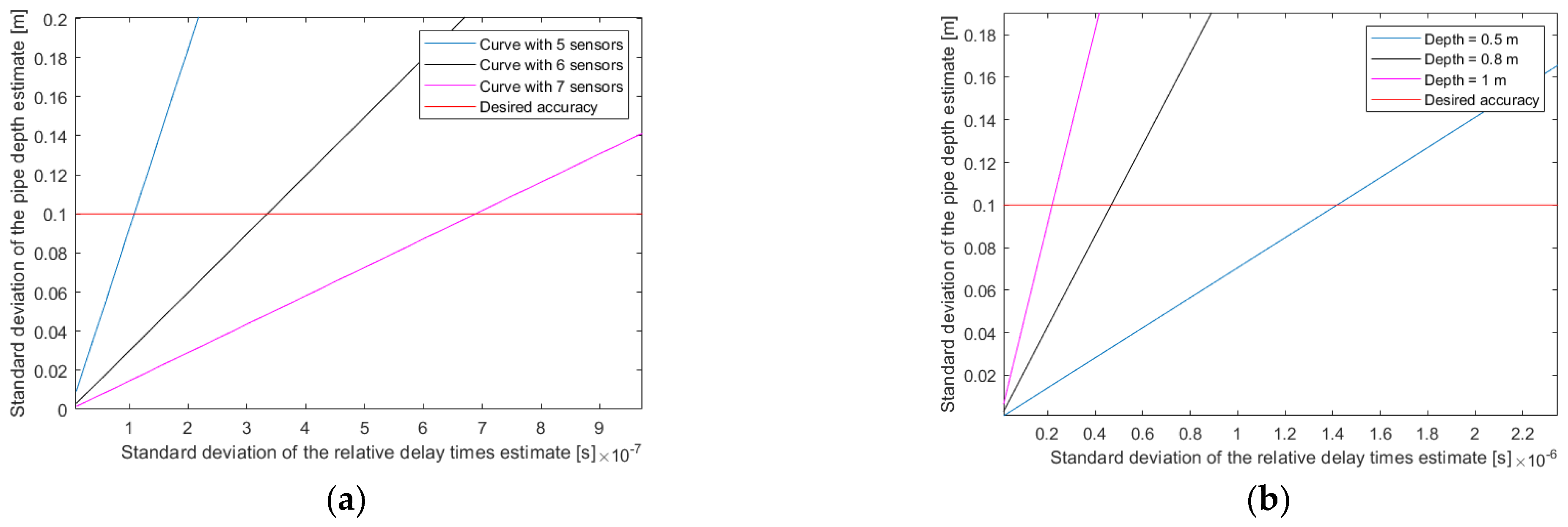
2.3.2. Numerical Simulation Using the Cramer–Rao Bound
2.4. Adaptation of the MUSIC Algorithm for Model M1
2.4.1. Presentation of the MUSIC Algorithm Adapted to Our Problem
- Estimate the variance–covariance matrix of the system from the signals received by sensors.
- Decompose the variance–covariance matrix of the system into eigenvalues and eigenvectors.
- Definition of the noise subspace, denoted by Ub, with the eigenvectors corresponding to the smallest eigenvalues.
- Construction of a family of vectors, denoted by ‘a’, parametrized by the variables we want to estimate, S and V0 (Equation (1)). This family of vectors is constructed from the modeling of relative delay times (Equation (3)).
- 5.
- Knowing that the signal subspace and the noise subspace are orthogonal, the project of a (S,V0) on the noise subspace must be at the minimum for the values of S and V0 corresponding best to the received signal. It is traditional to take the inverse of this projection and to look for the values of S and V0 that maximize this criterion, which is denoted by Cmusic.
2.4.2. Test of Estimator Using Numerical Simulation
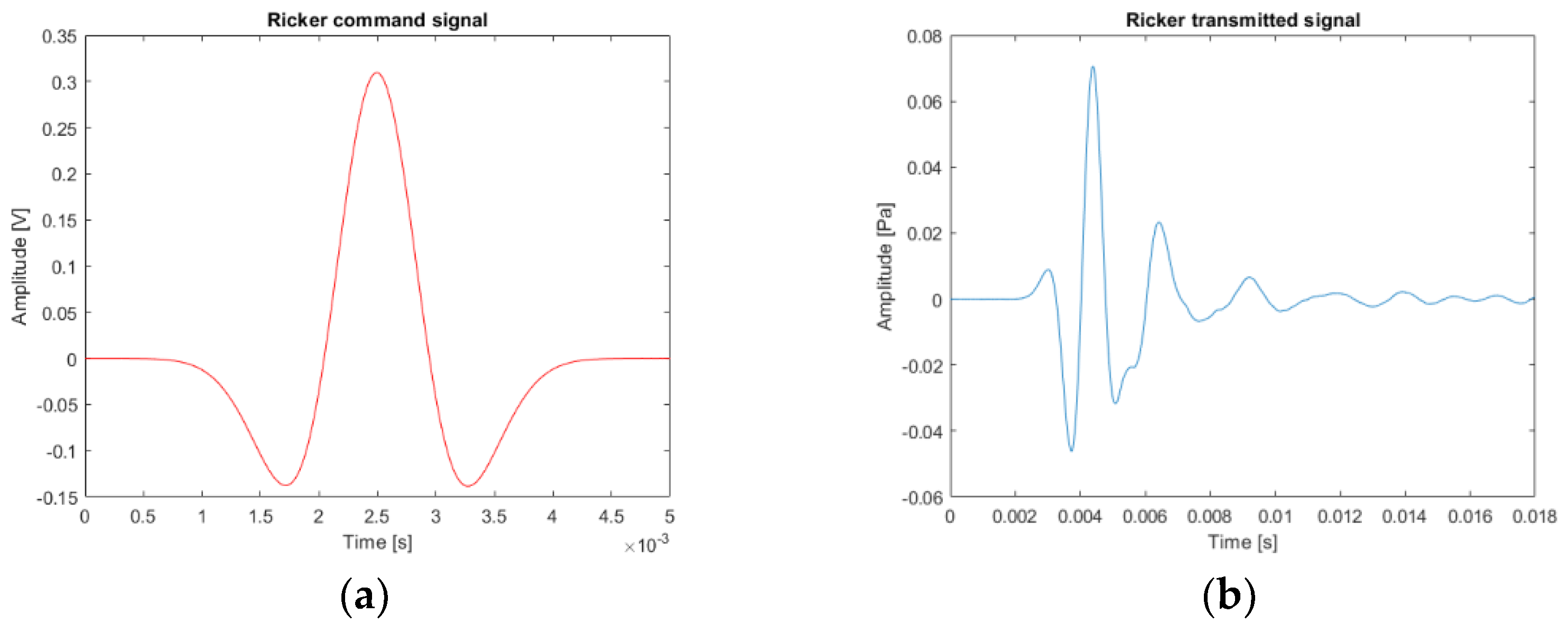
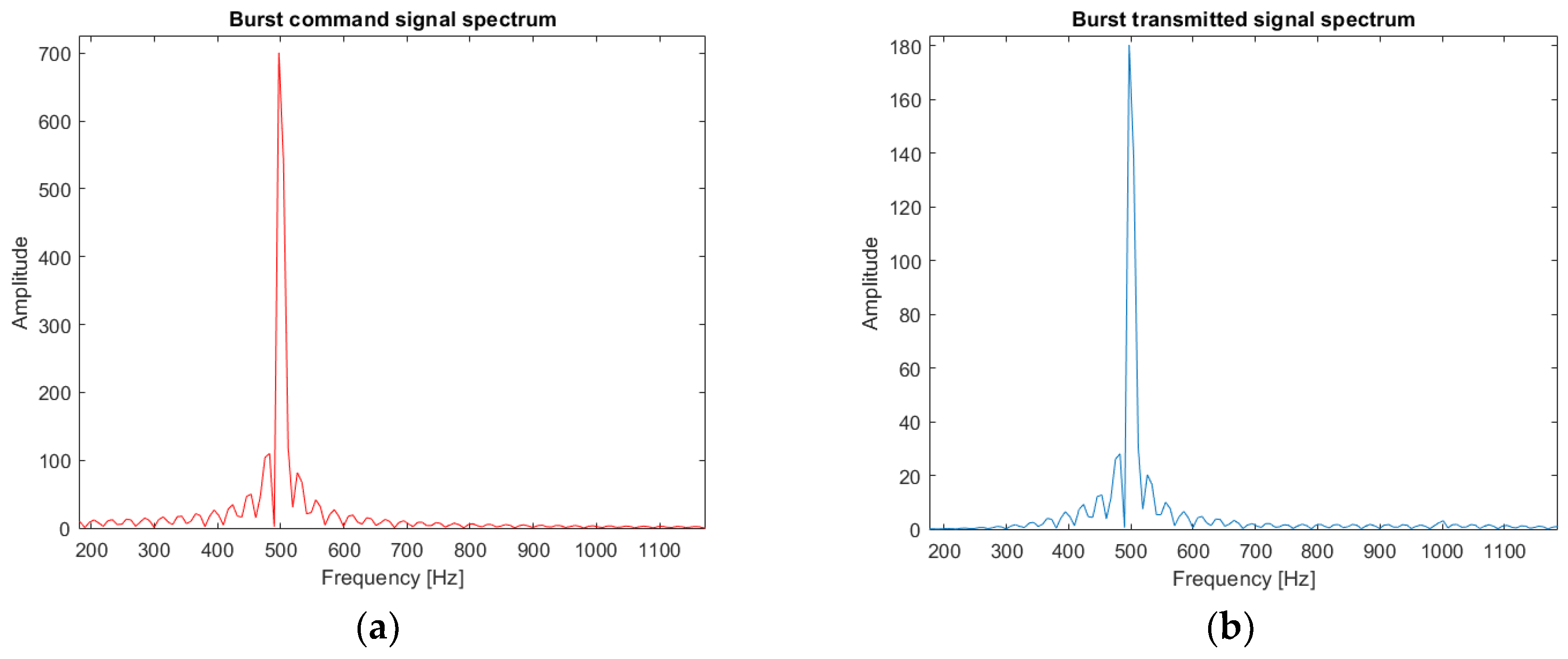
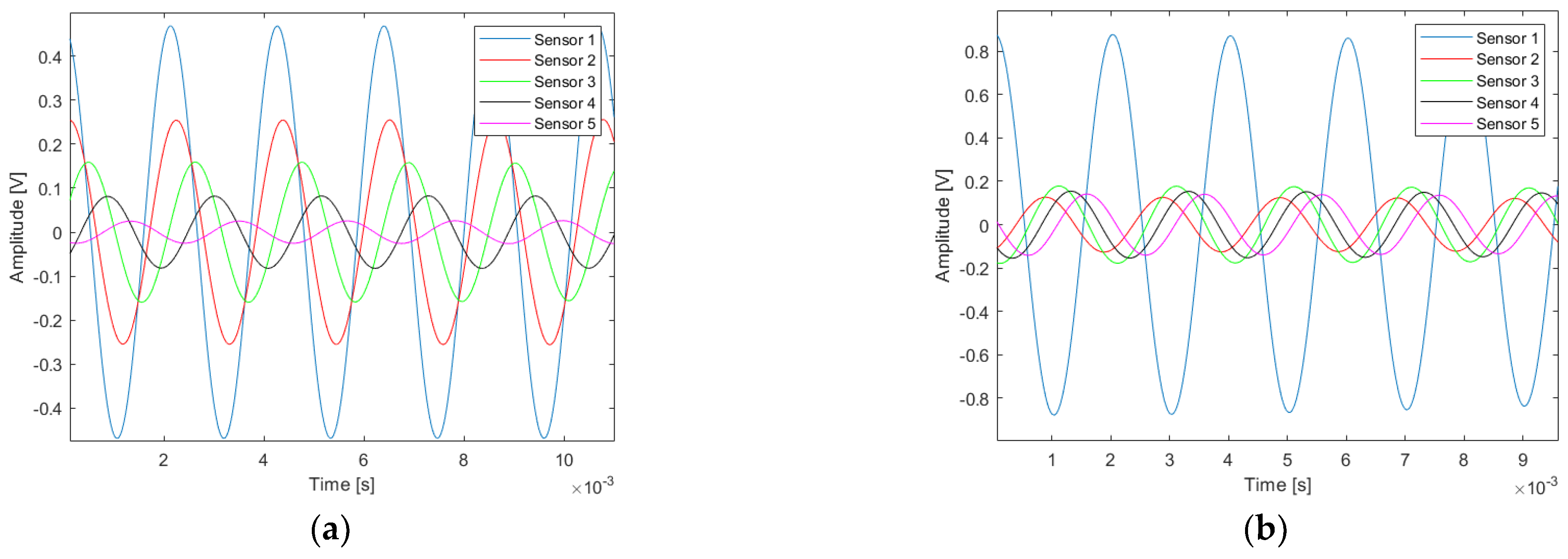
2.5. Experimental Measurements
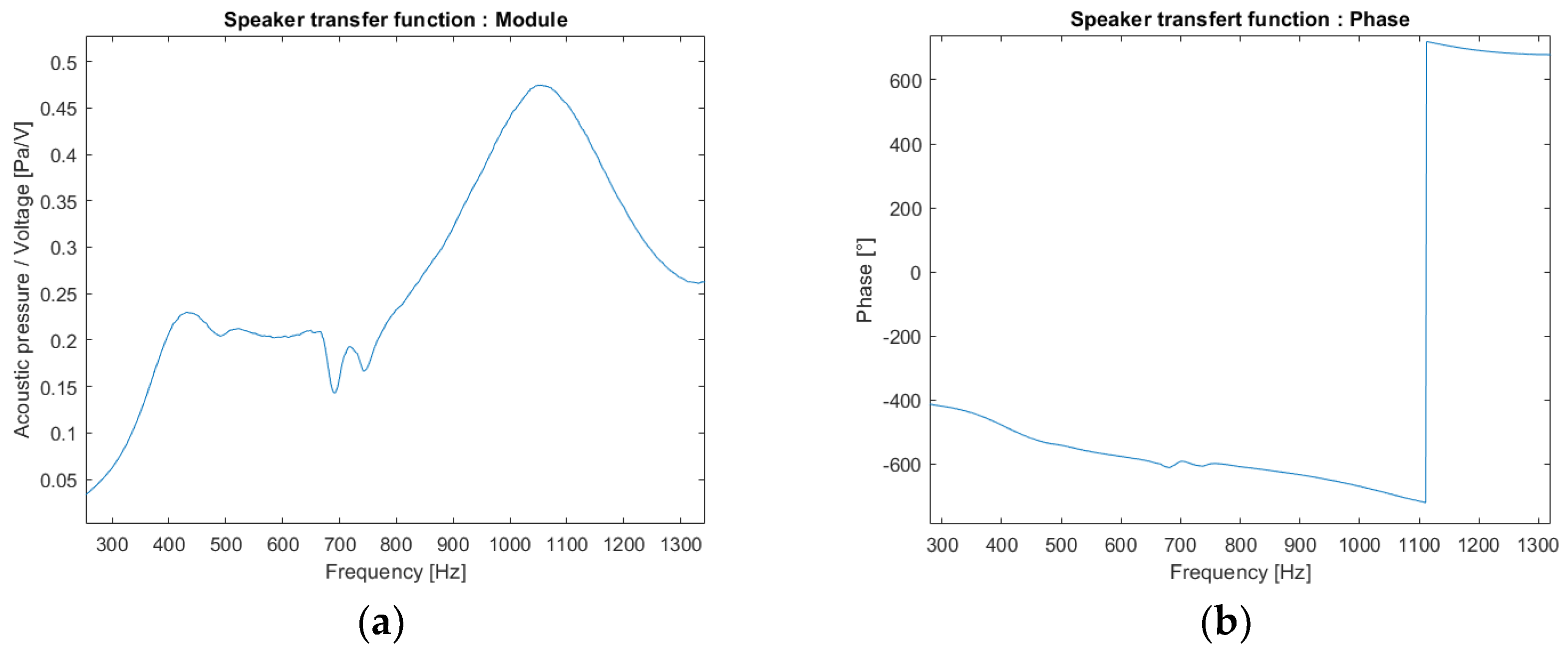
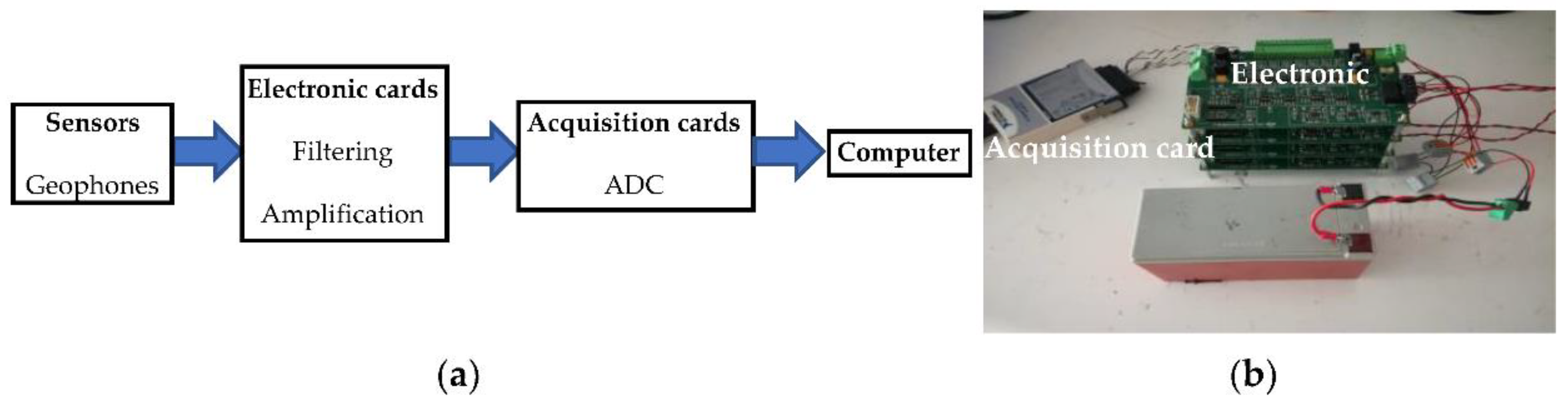
2.5.1. Experimental Set-Up
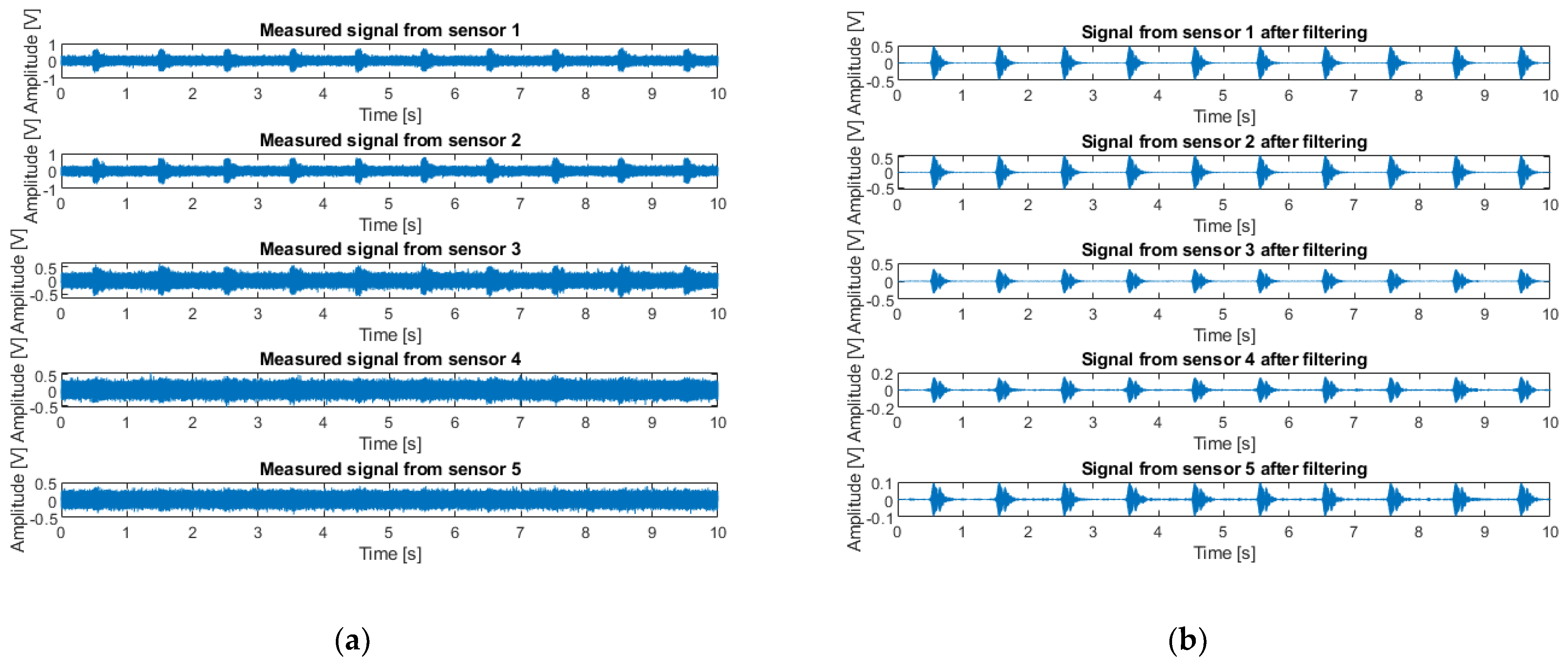
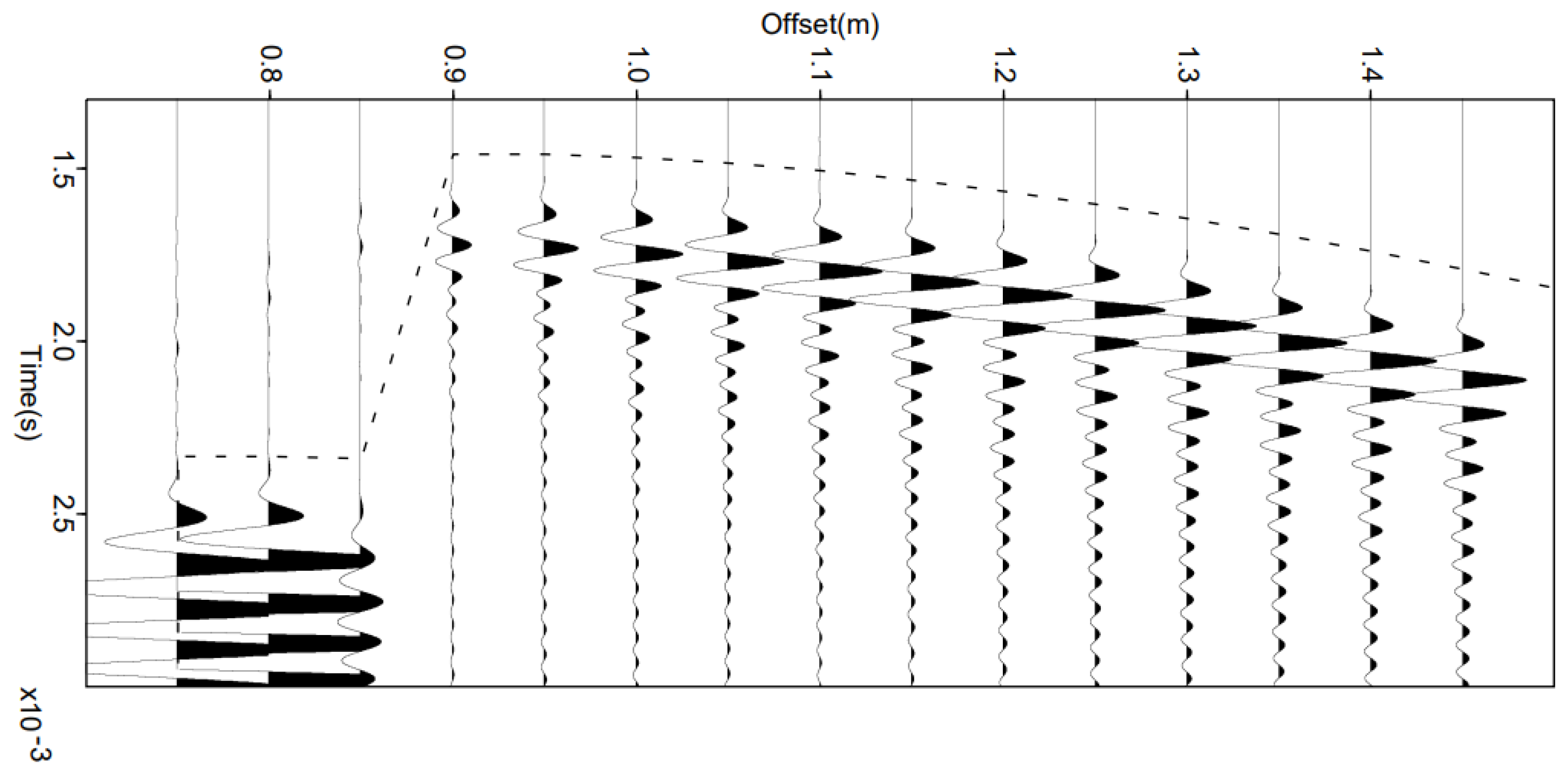
2.5.2. Experimental Results
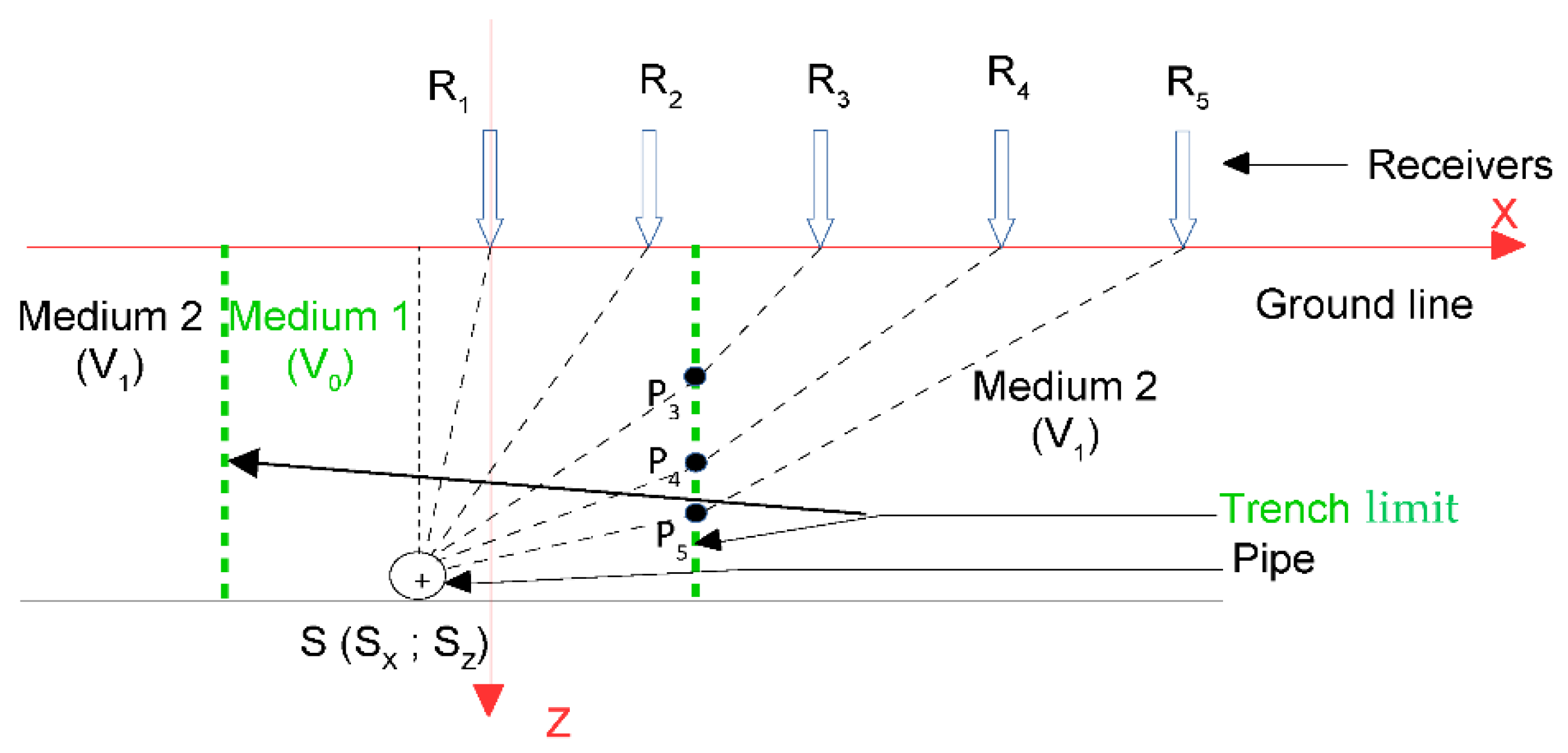
3. Modeling with Two Propagation Media (M2)
3.1. Propagation Time Modeling M2
3.1.1. Presentation of the Propagation Time Model M2
- If Ri is inside the trench, it is returned to the single propagation medium case of Model M1 (Equation (2))
- If Ri is outside the trench, then
3.1.2. Analytical Expression of the Interface Point Pi
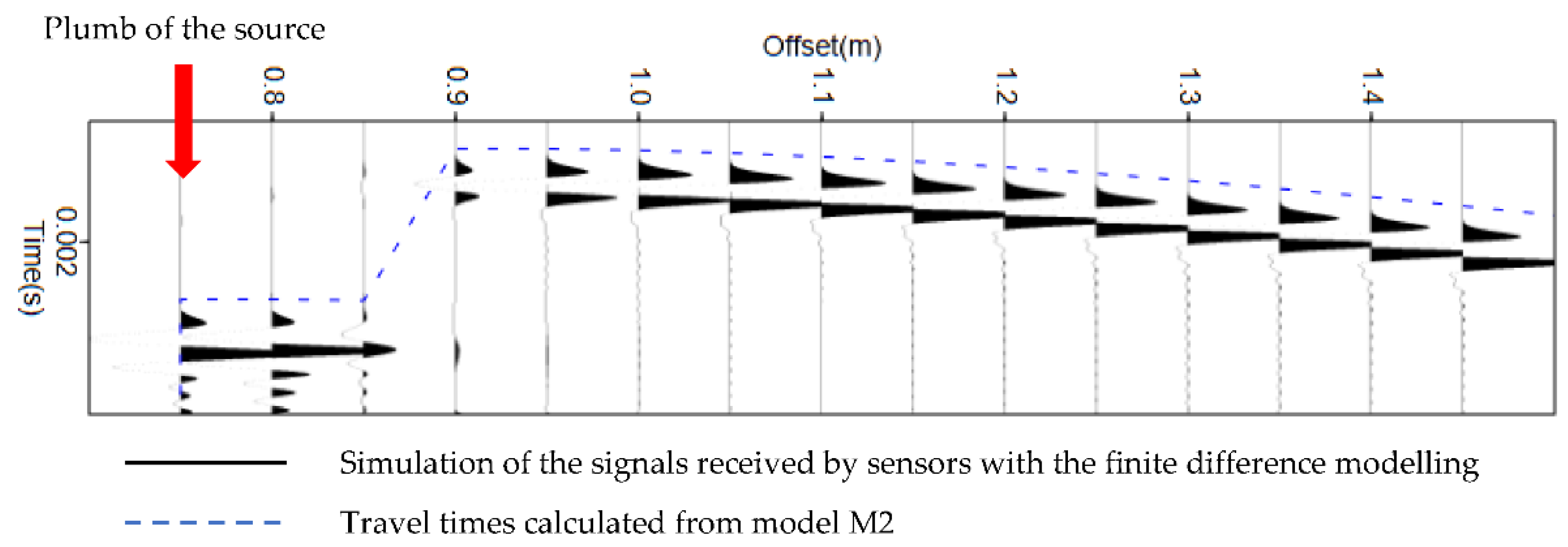
3.2. Validation of Travel Time Estimate of M2 through Comparison with a Finite Difference Modeling of the Full Wavefield
3.3. Cramer–Rao Bound from Model M2
3.3.1. Calculation of the Cramer–Rao Bound from Model M2
3.3.2. Numerical Simulation Using the Cramer–Rao Bound from Model M2
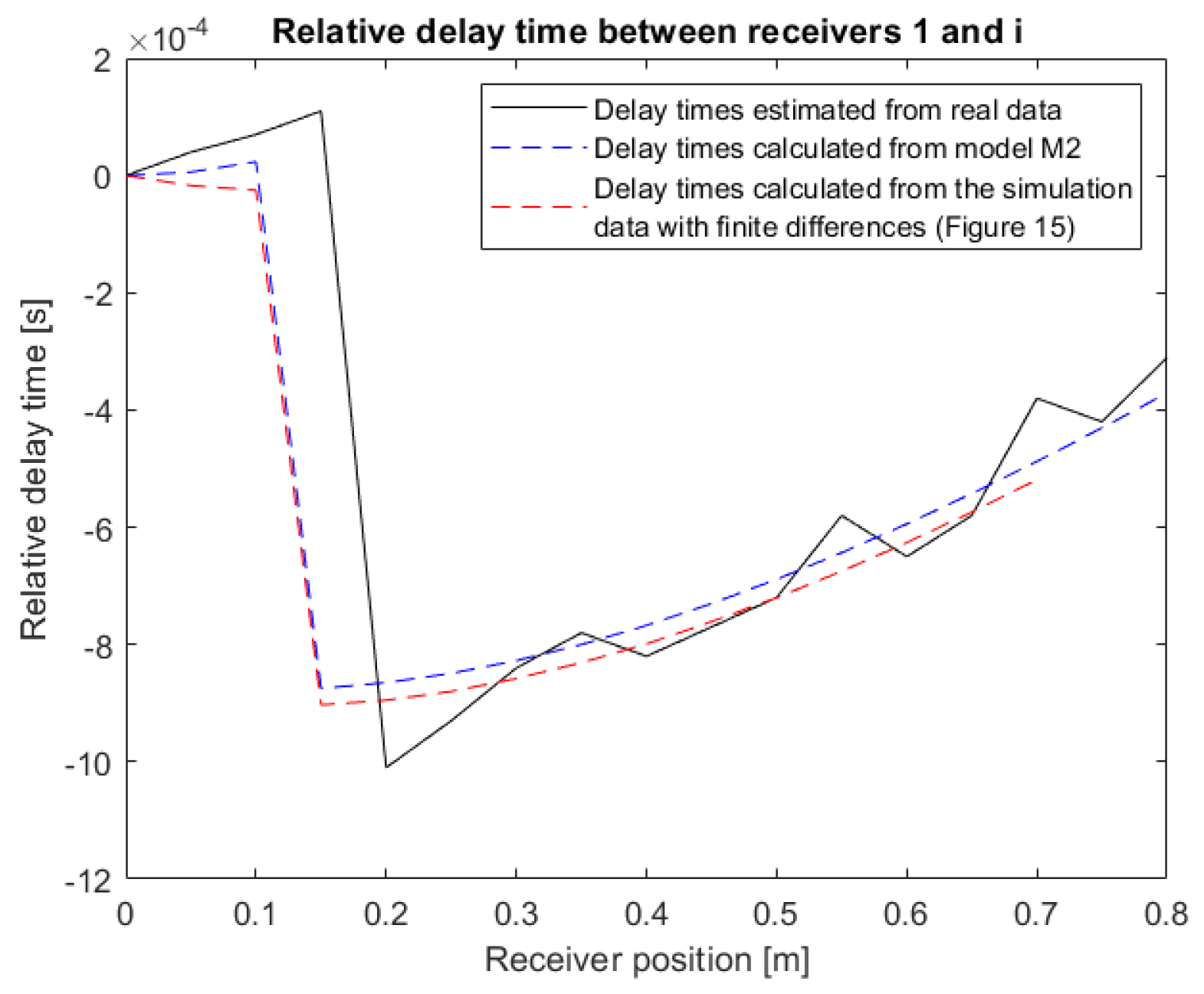
3.4. Validation of the Travel Time Model M2 on Real Data
3.5. Depth Estimation from Model M2
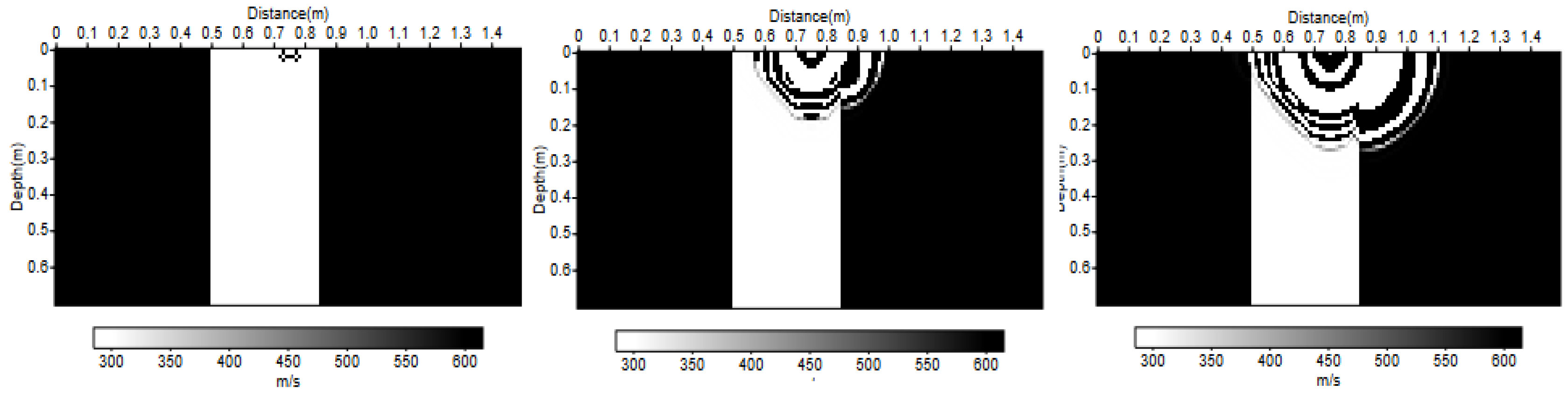
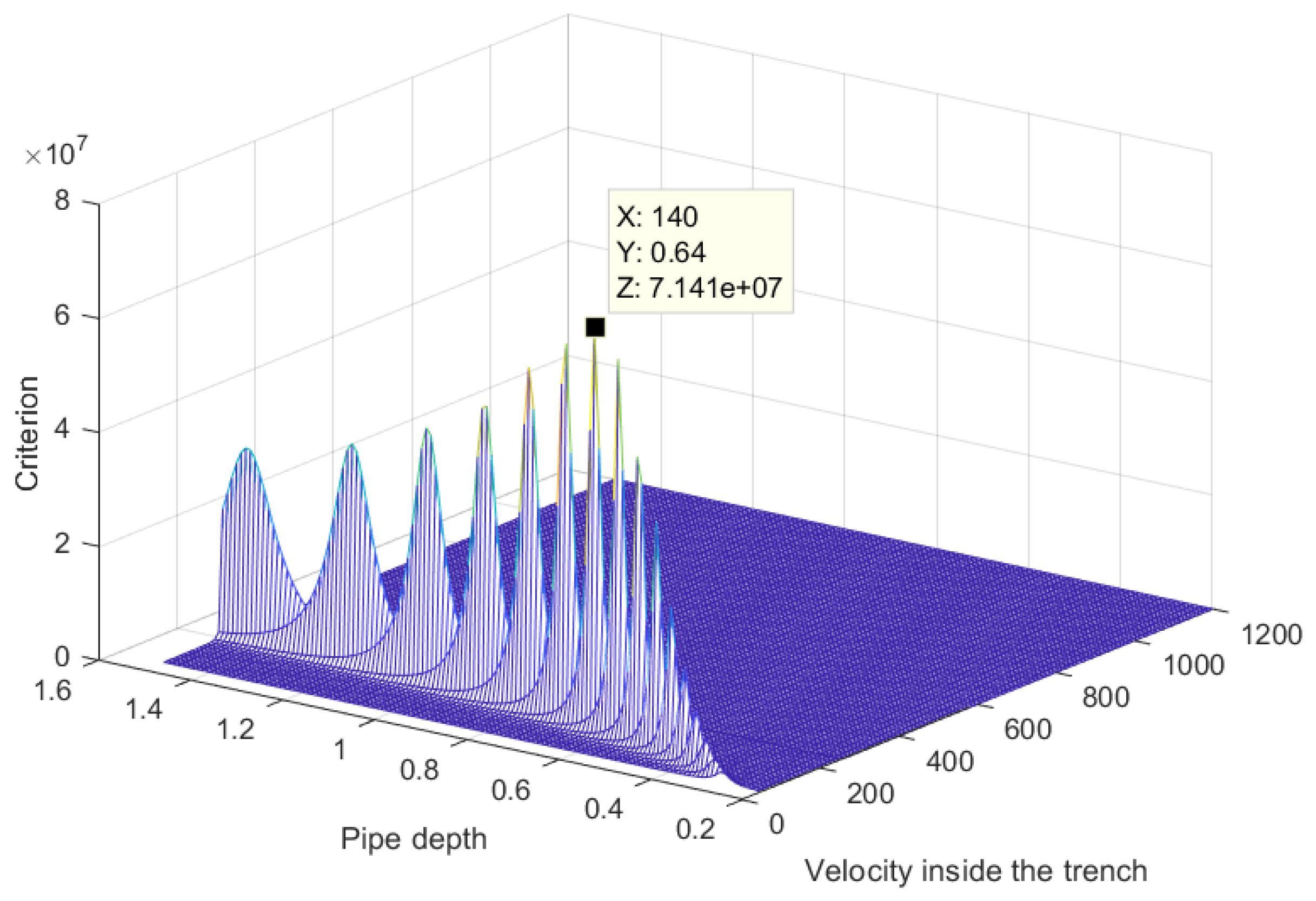
3.5.1. Numerical Simulation with MUSIC Algorithm Adapted to Model M2
3.5.2. Estimation on Real Data
4. Conclusions and Future Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Calculation of the Gradient of PiZ
References
- Liu, Y.; Habibi, D.; Chai, D.; Wang, X.; Chen, H.; Gao, Y.; Li, S. A Comprehensive Review of Acoustic Methods for Locating Underground Pipelines. Appl. Sci. 2020, 10, 1031. [Google Scholar] [CrossRef] [Green Version]
- Jeong, H.S.; Arboleda, C.A.; Abraham, D.M.; Halpin, D.W.; Bernold, L.E. Imaging and Locating Buried Utilities; Joint Transportation Research Program, Indiana Department of Transportation and Purdue University: West Lafayette, IN, USA, 2003. [Google Scholar] [CrossRef]
- Harmankaya, U.; Kaslilar, A.; Thorbecke, J.; Wapenaar, K.; Draganov, D. Locating near-surface scatterers using non-physical scattered waves resulting from seismic interferometry. J. Appl. Geophys. 2013, 91, 66–81. [Google Scholar] [CrossRef]
- Filippi, C.; Leparoux, D.; Grandjean, G.; Bitri, A.; Côte, P. New robust observables on Rayleigh waves affected by an underground cavity: From numerical to experimental modelling. Geophys. J. Int. 2019, 218, 1903–1918. [Google Scholar] [CrossRef]
- Muggleton, M.J.; Rustighi, E. Mapping the Underworld: Recent developments in vibro-acoustic techniques to locate buried infrastructure. Géotech. Lett. 2013, 3, 137–141. [Google Scholar] [CrossRef] [Green Version]
- Hao, T.; Rogers, C.D.F.; Metje, N.; Chapman, D.N.; Muggleton, J.M.; Foo, K.Y.; Wang, P.; Pennock, S.R.; Atkins, P.R.; Swingler, S.G.; et al. Condition assessment of the buried utility service infrastructure. Tunn. Undergr. Space Technol. 2012, 28, 331–344. [Google Scholar] [CrossRef]
- Dou, Q.; Wei, L.; Magee, D.R.; Atkins, P.R.; Chapman, D.N.; Curioni, G.; Goddard, K.F.; Hayati, F.; Jenks, H.; Metje, N.; et al. 3D Buried Utility Location Using a Marching-Cross-Section Algorithm for Multi-Sensor Data Fusion. Sensors 2016, 16, 1827. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Guo, T.; Leung, H.; Xu, H.; Liu, L.; Wang, B.; Liu, Y. Locating Underground Pipe Using Wideband Chaotic Ground Penetrating Radar. Sensors 2019, 19, 2913. [Google Scholar] [CrossRef] [Green Version]
- Pettinelli, E.; di Matteo, A.; Mattei, E.; Crocco, L.; Soldovieri, F.; Redman, J.D.; Annan, A.P. GPR Response from Buried Pipes: Measurement on Field Site and Tomographic Reconstructions. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2639–2645. [Google Scholar] [CrossRef]
- Xerri, W.; Saracco, G.; Gassier, G.; Zomero, L.; Picon, P. Preliminary Acoustic Study of 3D Localization of Buried Polyethylene Pipe. Quantitative Nondestructive Evaluation; American Society of Mechanical Engineers: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Xerri, W.; Saracco, G.; Ribodetti, A.; Zomero, L.; Picon, P. Estimating the depth of buried polyethylene pipe by comparing propagation models. In Proceedings of the French of Congress Acoustics (CFA), Marseille, France, 11–15 April 2022. [Google Scholar]
- Liu, Y.; Habibi, D.; Chai, D.; Wang, X.; Chen, H. A Numerical Study of Axisymmetric Wave Propagation in Buried Fluid-Filled Pipes for Optimizing the Vibro-Acoustic Technique When Locating Gas Pipelines. Energies 2019, 12, 3707. [Google Scholar] [CrossRef] [Green Version]
- Papandreou, B.; Rustighi, E.; Brennan, M.J. Study into the Feasibility of Using Acoustic Techniques to Locate Buried Objects; ISVR Technical Memorandum; Institute of Sound and Vibration Research: Southampton, UK, 2008. [Google Scholar]
- Muggleton, J.M.; Brennan, M.J.; Rogers, C.D.F. Point vibration measurements for the detection of shallow-buried objects. Tunn. Undergr. Space Technol. 2014, 39, 27–33. [Google Scholar] [CrossRef] [Green Version]
- Katz, A.; Karaa, F.; Niver, E. Innovative and Effective Techniques for Locating Underground Conduits; New Jersey Institute of Technology: Newark, NJ, USA, 2011. [Google Scholar]
- McFadden, J.A. Radial Vibrations of Thick-Walled Hollow Cylinders. J. Acoust. Soc. Am. 1954, 26, 714. [Google Scholar] [CrossRef]
- Gazis, D.C. Exact Analysis of the Plane-Strain Vibrations of Thick-Walled Hollow Cylinders. J. Acoust. Soc. Am. 1958, 30, 786–794. [Google Scholar] [CrossRef]
- Sinha, B.K.; Plona, T.J.; Kostek, S.; Chang, S.K. Axisymmetric wave propagation in fluid-loaded cylindrical shells. I: Theory. J. Acoust. Soc. Am. 1992, 92, 1132–1143. [Google Scholar] [CrossRef]
- Operto, S.; Virieux, J.; Ribodetti, A.; Anderson, J.E. Finite-difference frequency-domain modeling of viscoacoustic wave propagation in 2D tilted transversely isotropic media. Geophysics 2009, 74, T75–T95. [Google Scholar] [CrossRef] [Green Version]
- Virieux, J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics 1986, 51, 889–901. [Google Scholar] [CrossRef]
- Virieux, J. SH wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics 1984, 49, 1933–1957. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Scharf, L.L.; McWhorter, L.T. Geometry of the Cramer-Rao bound. Signal Process 1993, 31, 301–311. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple Emitter Location and Signal Parameter Estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Zhao, Y.; Liu, J. Mixed-Order MUSIC Algorithm for Localization of Far-Field and Near-Field Sources. IEEE Signal Process. Lett. 2013, 20, 311–314. [Google Scholar] [CrossRef]
- Fossati, C.; Bourennane, S.; Marot, J. Chapter 3: Localization of Buried Objects in Sediment Using High Resolution Array Processing Methods. In Underwater Acoustics; Bourennane, S., Ed.; InTech: Rijeka, Croatia, 2012; pp. 41–58. [Google Scholar] [CrossRef] [Green Version]
- Han, D.; Fossati, C.; Bourennane, S.; Saidi, Z. Bearing and Range Estimation Algorithm for Buried Object in Underwater Acoustics. Research Letters in Signal Processing; Hindawi: London, UK, 2009. [Google Scholar] [CrossRef]
- Saidi, Z.; Bourennane, S. Cumulant-Based Coherent Signal Subspace Method for Bearing and Range Estimation. EURASIP J. Adv. Signal Process 2007, 2007, 084576. [Google Scholar] [CrossRef] [Green Version]
- Sahin, A.; Miller, E.L. Object-based localization of buried objects using high-resolution array processing techniques. In Proceedings of the SPIE, Orlando, FL, USA, 31 May 1996. [Google Scholar] [CrossRef]
- Choi, J.W.; Kim, Y.H. Spherical beam-forming and MUSIC methods for the estimation of location and stength of spherical sound sources. Mech. Syst. Signal Process 1995, 9, 569–588. [Google Scholar] [CrossRef]





| Mean | Standard Deviation | True Value | ||
|---|---|---|---|---|
| Numerical Simulation 1 with 5 sensors and σnoise = 1 × 10−7 | Depth SZ (m) | 0.7056 | 0.0486 | 0.7 |
| Average velocity V0 (m/s) | 494 | 17 | 500 | |
| Plumb of the pipe SX (m) | 0.0047 | 0.0065 | 0 | |
| Numerical Simulation 2 with 6 sensors and σnoise = 5 × 10−7 | Depth SZ (m) | 0.6658 | 0.0317 | 0.7 |
| Average velocity V0 (m/s) | 499 | 7 | 500 | |
| Plumb of the pipe SX (m) | 0.0172 | 0.0109 | 0 | |
| Numerical Simulation 3 with 7 sensors and σnoise = 1 × 10−6 | Depth SZ (m) | 0.7386 | 0.0466 | 0.7 |
| Average velocity V0 (m/s) | 501 | 9 | 500 | |
| Plumb of the pipe SX (m) | 0.0325 | 0.0315 | 0 |
| Estimate Value | Reference Value | |
|---|---|---|
| Depth (SZ) (m) | 0.39 | 0.42 |
| Average velocity (V0) (m/s) | 360 | unknown |
| Estimate Value | Reference Value | |
|---|---|---|
| Depth (SZ) (m) | 0.75 | 0.70 |
| Average velocity (V0) (m/s) | 540 | unknown |
| Mean | Standard Deviation | True Value | ||
|---|---|---|---|---|
| Numerical Simulation 1 with σnoise = 5 × 10−6 | Depth SZ (m) | 0.7294 | 0.0849 | 0.7 |
| Average velocity V0 (m/s) | 293 | 19 | 300 | |
| Average velocity V1 (m/s) | 592 | 41 | 600 | |
| Numerical Simulation 2 with σnoise = 5 × 10−5 | Depth SZ (m) | 0.6666 | 0.2246 | 0.7 |
| Average velocity V0 (m/s) | 261 | 58 | 300 | |
| Average velocity V1 (m/s) | 638 | 128 | 600 |
| Mean | Standard Deviation | True Value | ||
|---|---|---|---|---|
| Numerical Simulation 1 with σnoise = 5 × 10−6 | Depth SZ (m) | 0.6604 | 0.0704 | 0.7 |
| Average velocity V0 (m/s) | 293 | 18 | 300 | |
| Average velocity V1 (m/s) | 611 | 79 | 600 |
| Estimate Value | Reference Value | |
|---|---|---|
| Depth (SZ) (m) | 0.64 | 0.70 |
| Average velocity inside the trench (V0) (m/s) | 140 | unknown |
| Average velocity outside the trench (V1) (m/s) | 250 | unknown |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xerri, W.; Saracco, G.; Ribodetti, A.; Zomero, L.; Picon, P. Three-Dimensional Localization of Buried Polyethylene Pipes Using Acoustic Method. Sensors 2022, 22, 9433. https://doi.org/10.3390/s22239433
Xerri W, Saracco G, Ribodetti A, Zomero L, Picon P. Three-Dimensional Localization of Buried Polyethylene Pipes Using Acoustic Method. Sensors. 2022; 22(23):9433. https://doi.org/10.3390/s22239433
Chicago/Turabian StyleXerri, William, Gineth Saracco, Alessandra Ribodetti, Laurent Zomero, and Philippe Picon. 2022. "Three-Dimensional Localization of Buried Polyethylene Pipes Using Acoustic Method" Sensors 22, no. 23: 9433. https://doi.org/10.3390/s22239433
APA StyleXerri, W., Saracco, G., Ribodetti, A., Zomero, L., & Picon, P. (2022). Three-Dimensional Localization of Buried Polyethylene Pipes Using Acoustic Method. Sensors, 22(23), 9433. https://doi.org/10.3390/s22239433







