Analytical Modeling and Analysis of Permanent-Magnet Motor with Demagnetization Fault
Abstract
1. Introduction
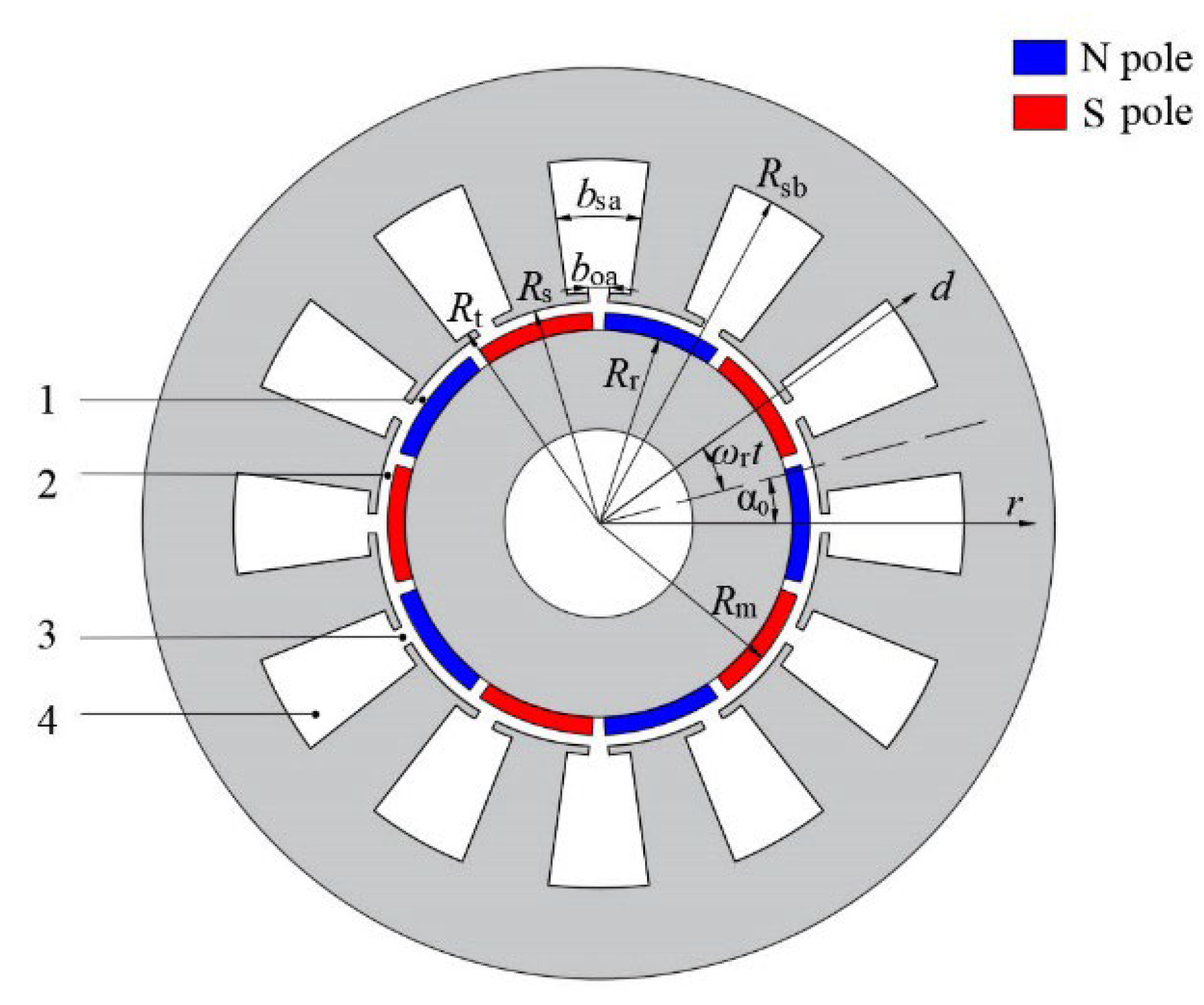
2. Analytical Model for Permanent Magnet
2.1. Uniform Demagnetization
2.1.1. Radial Magnetization
2.1.2. Parallel Magnetization
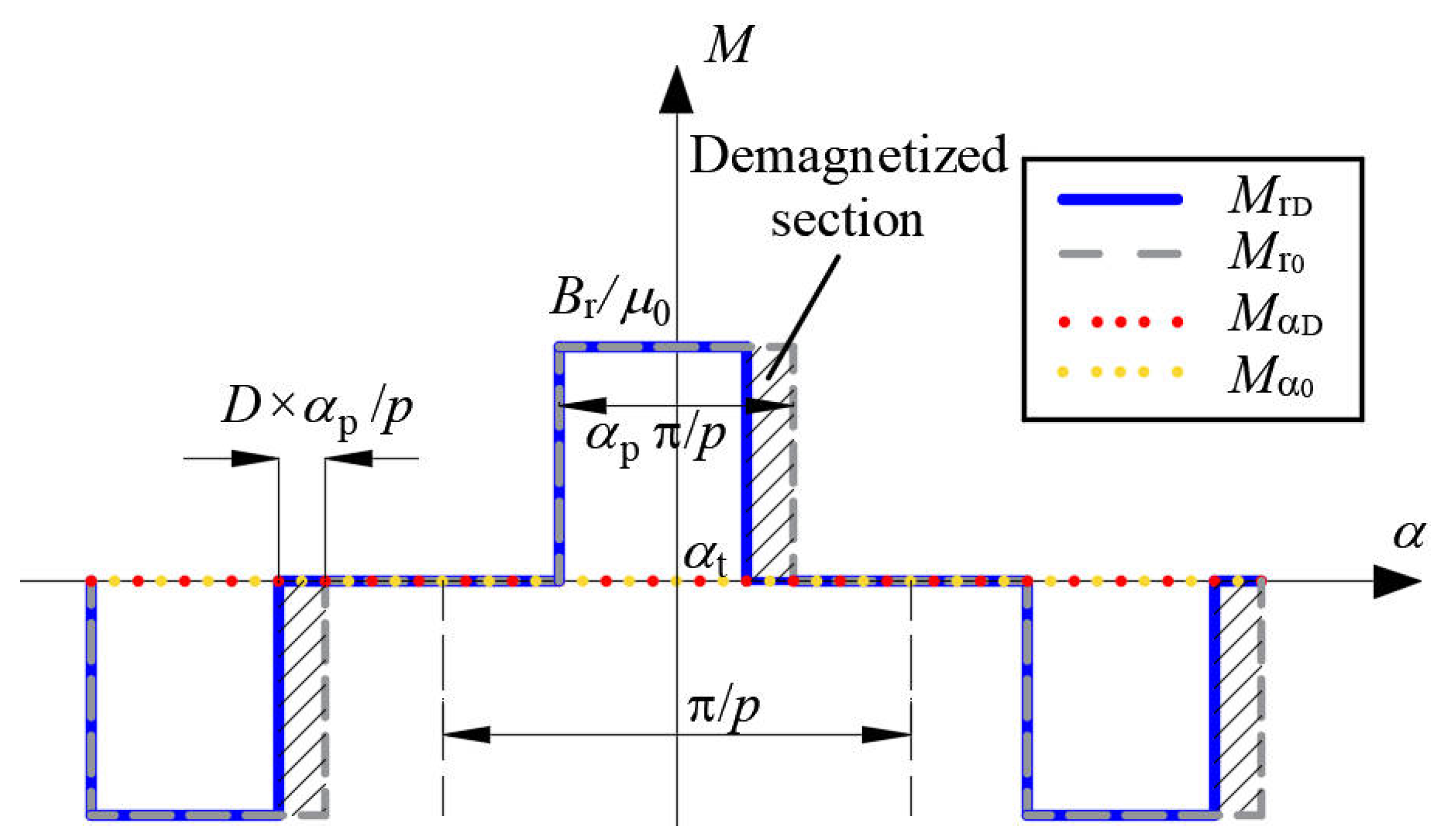
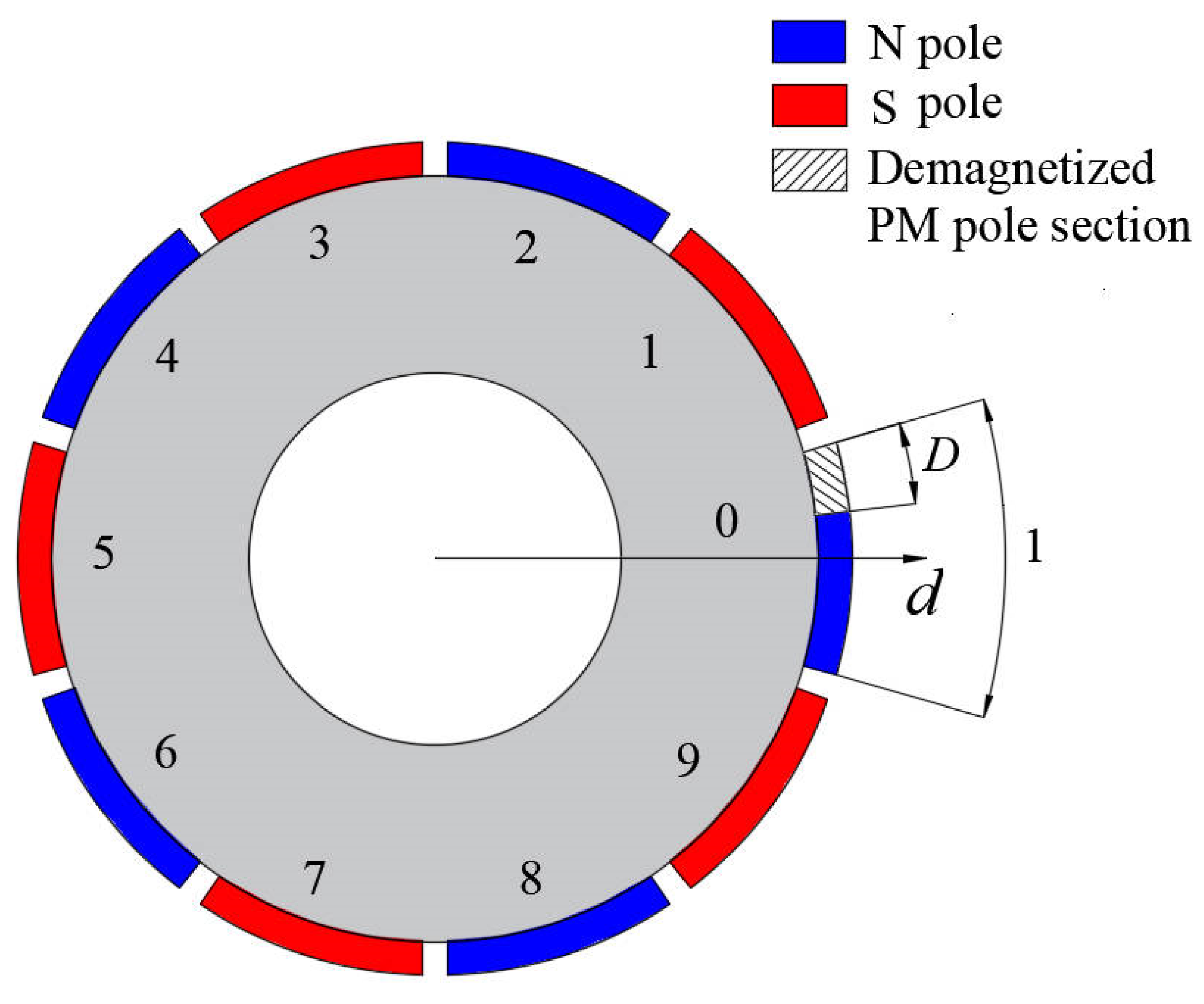
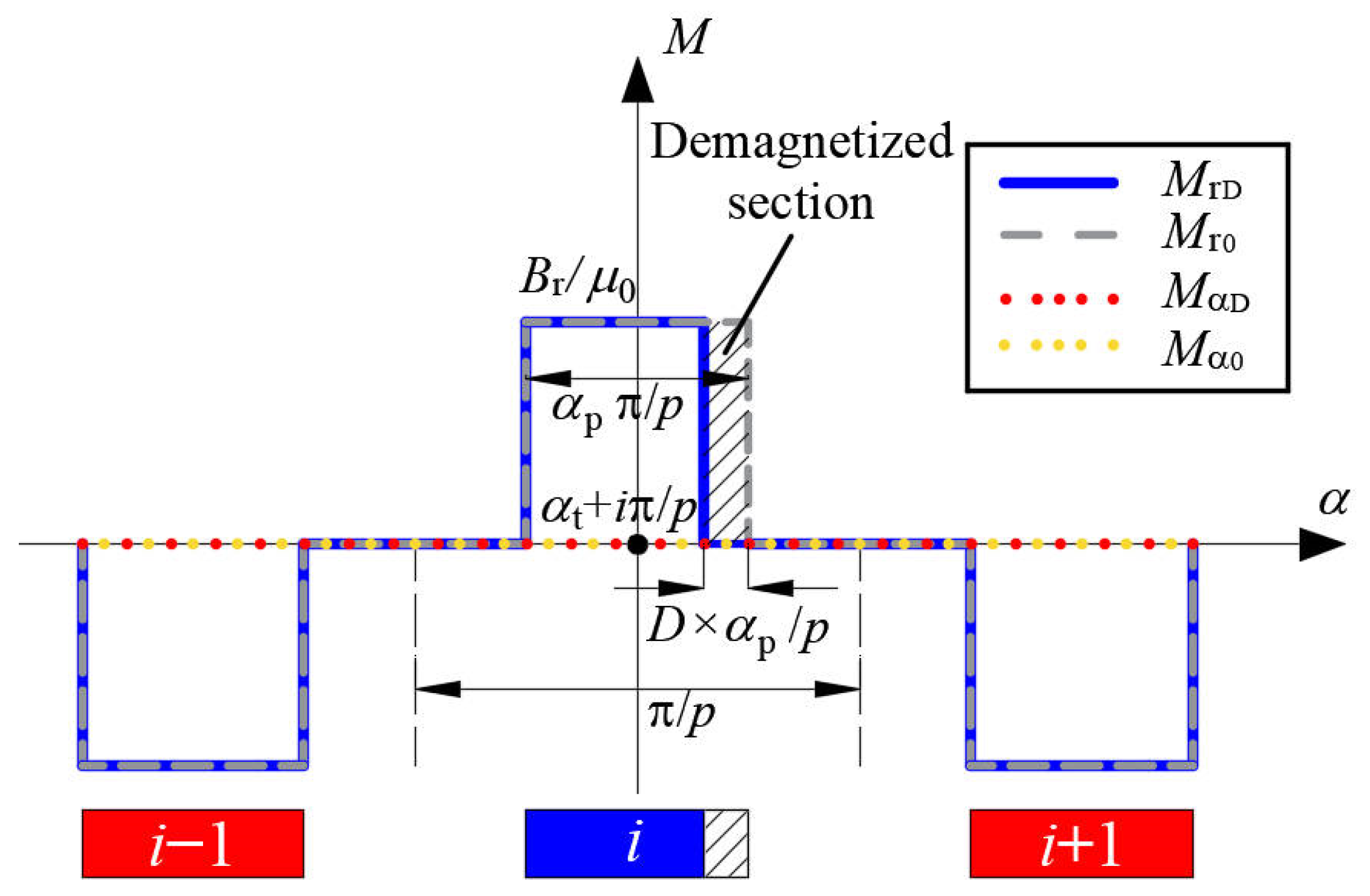
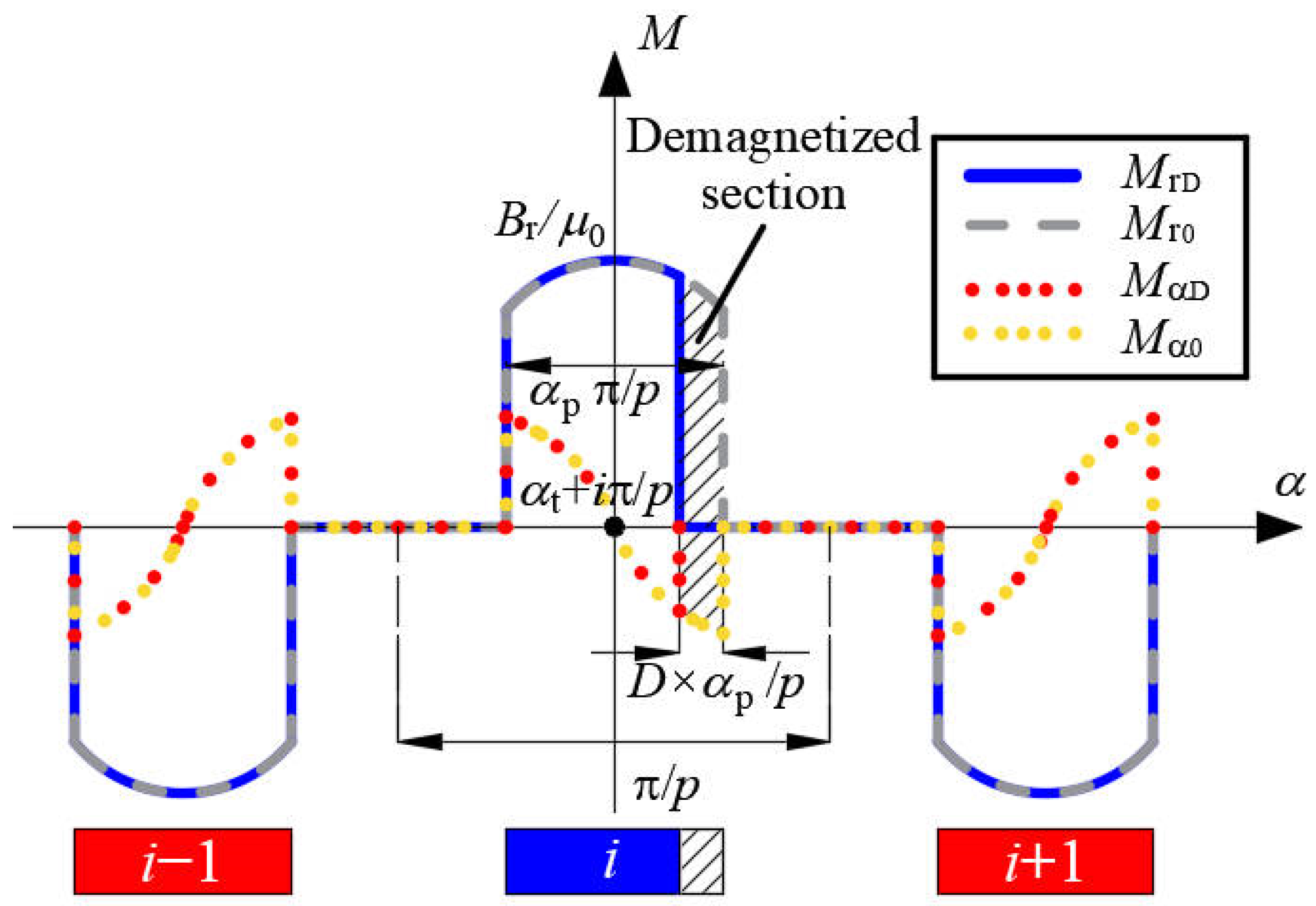
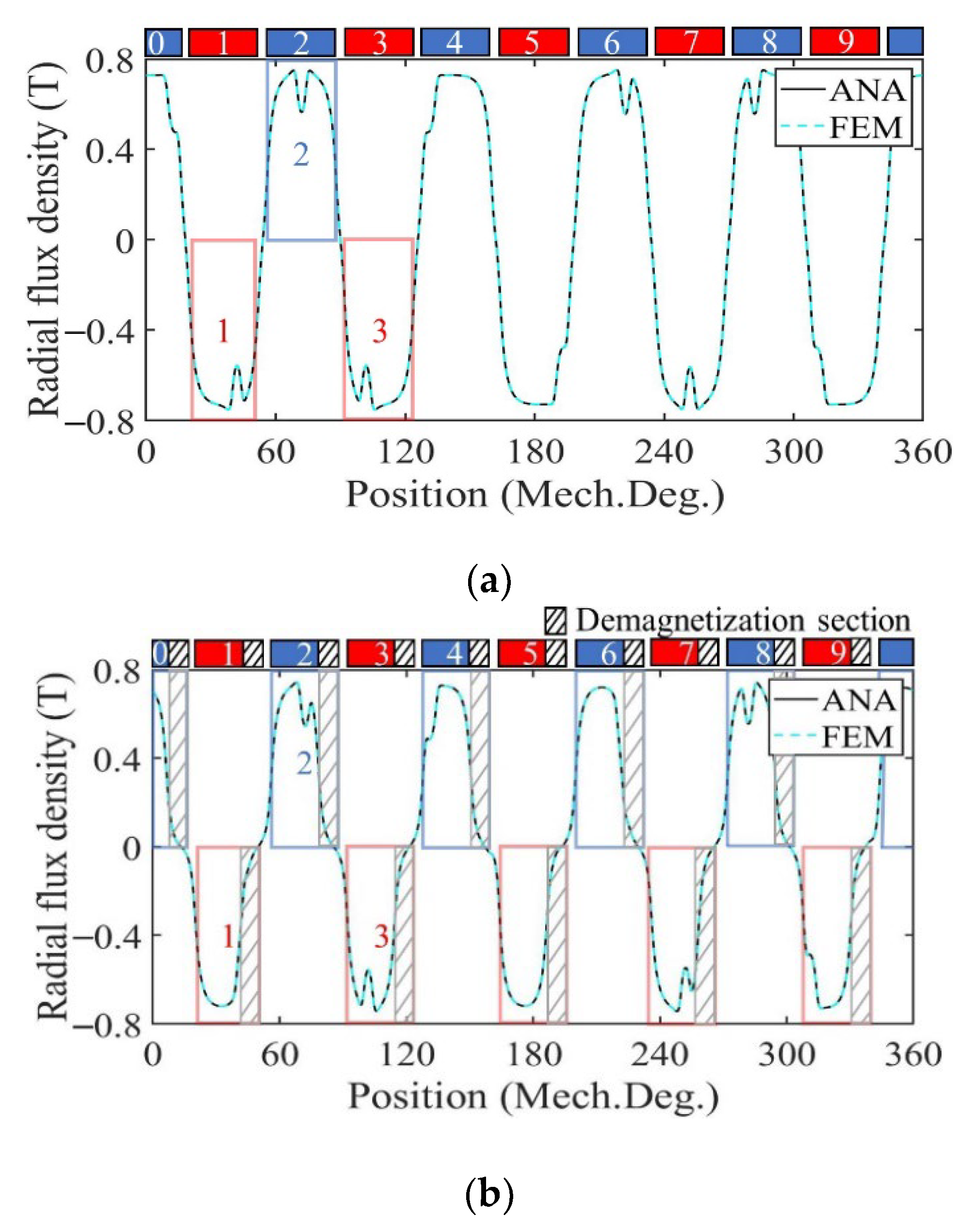
2.2. Partial Demagnetization
2.2.1. Radial Magnetization
2.2.2. Parallel Magnetization
2.3. Motor Performance Calculation
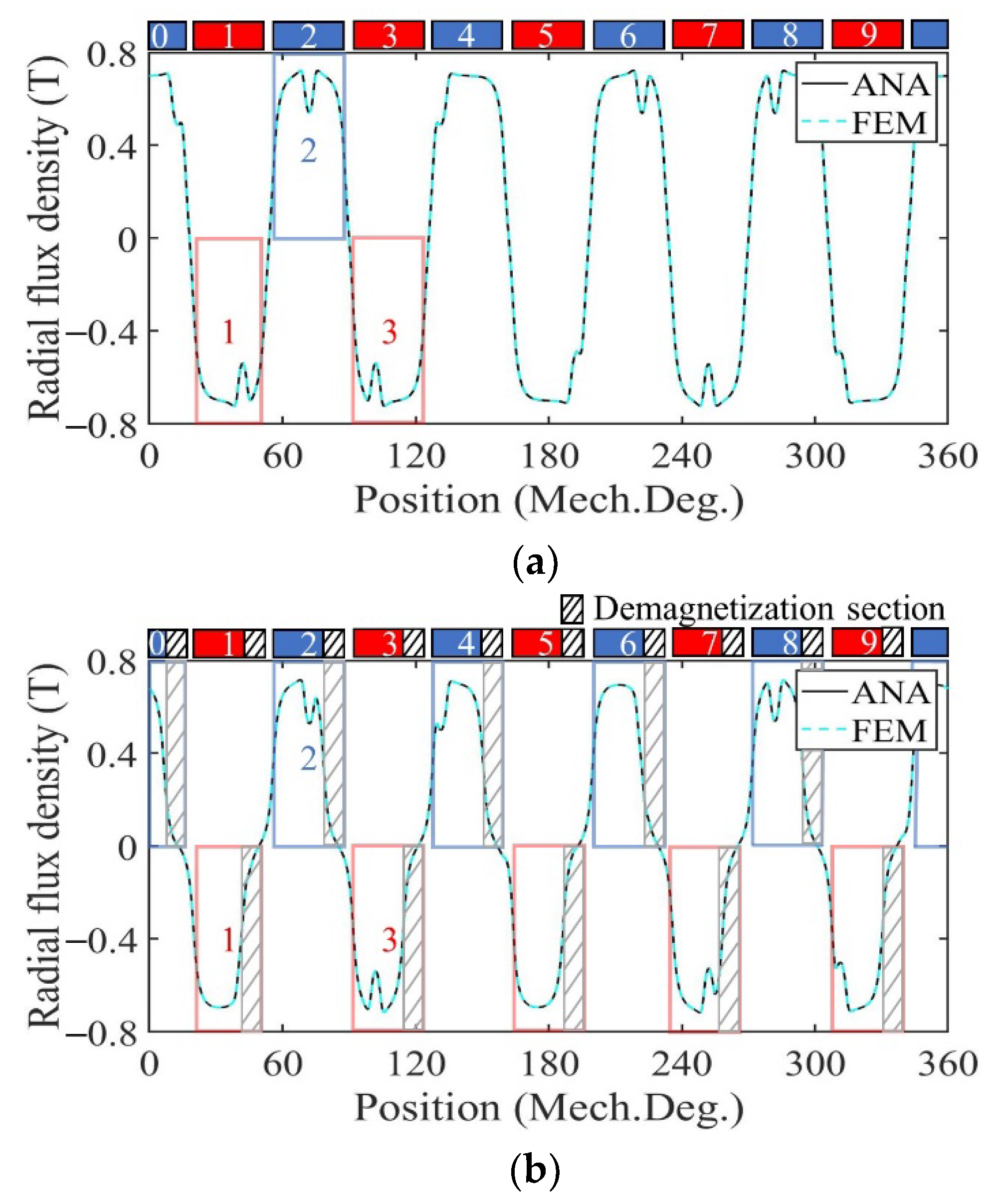
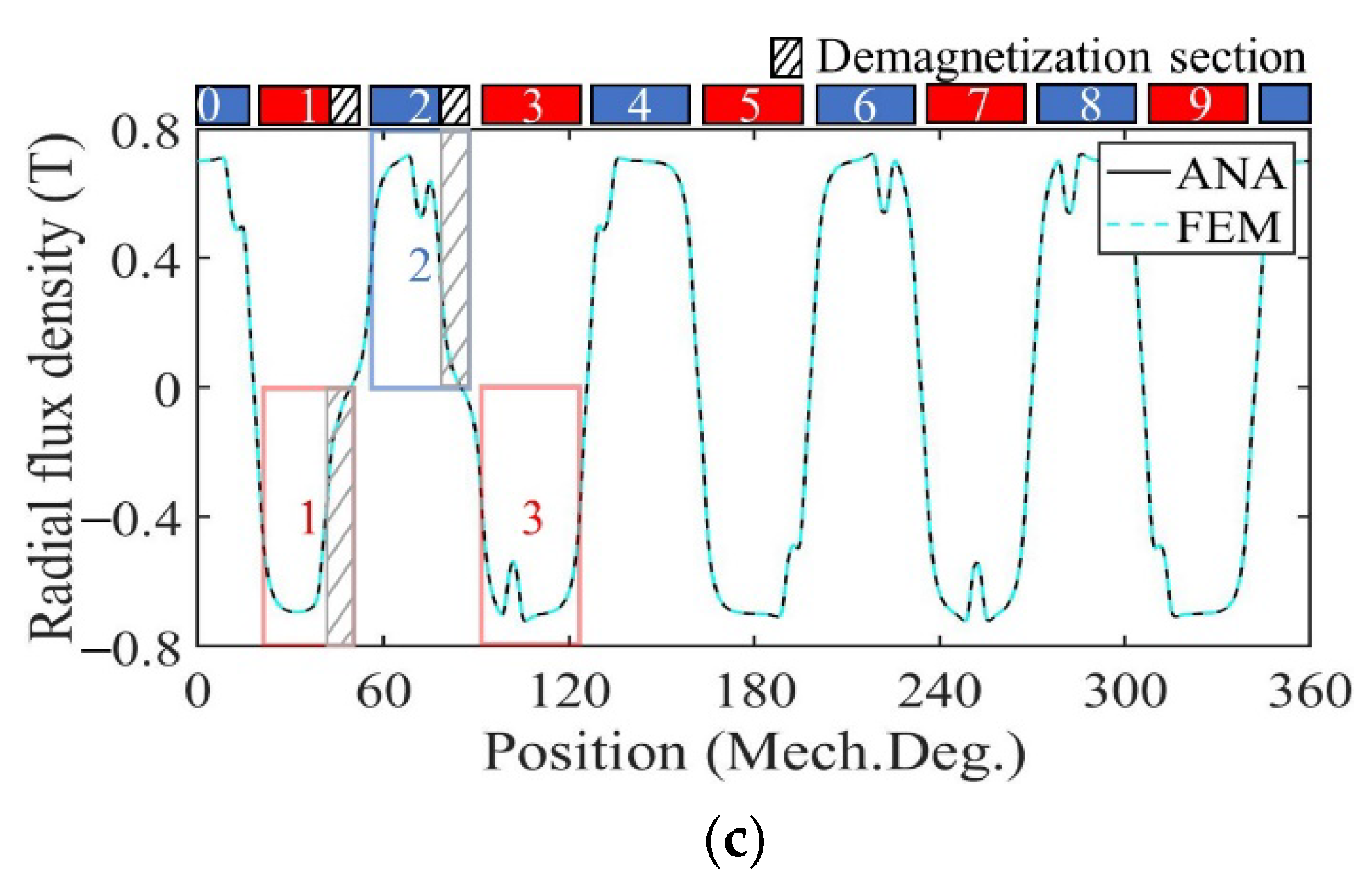
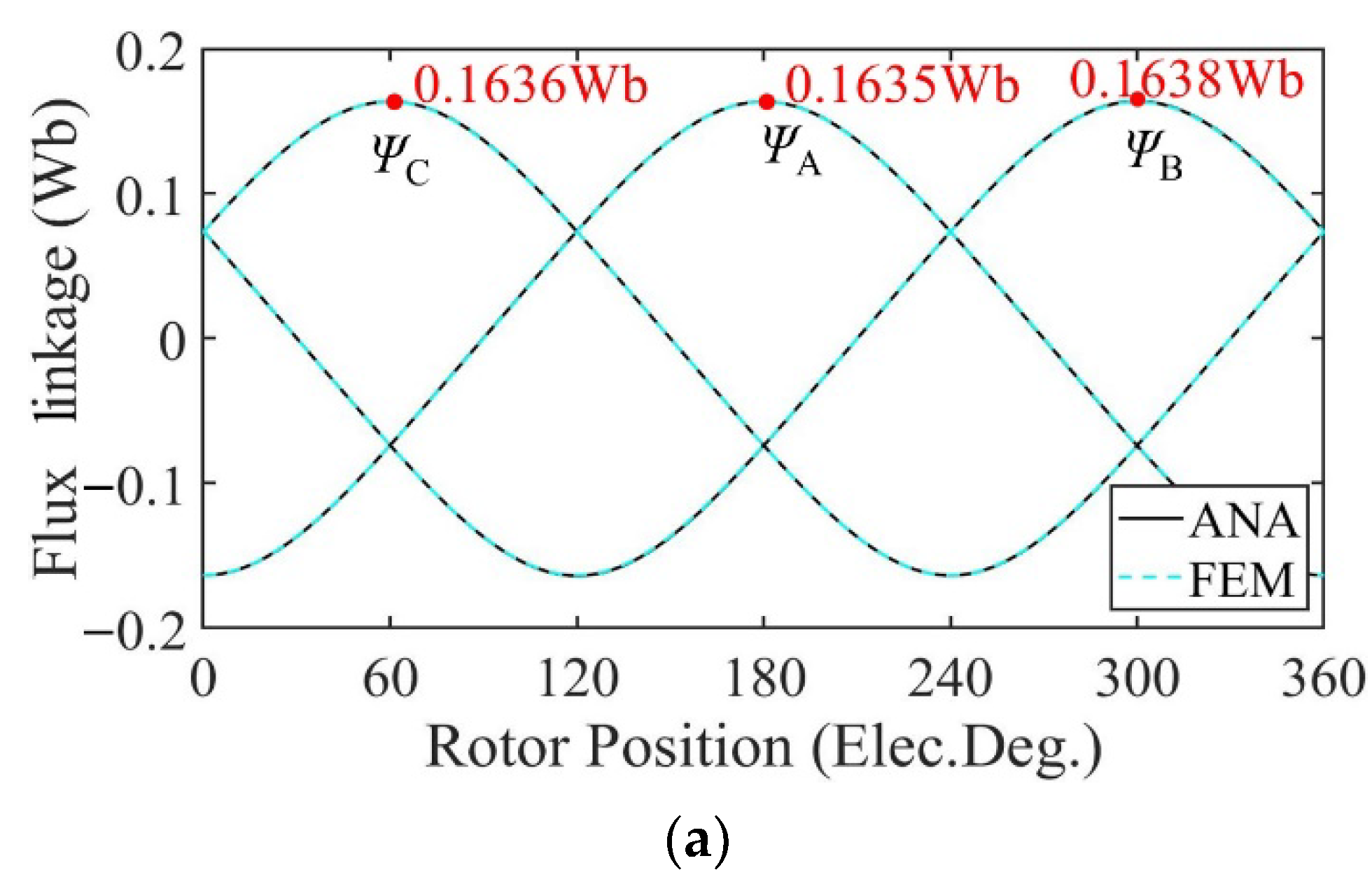
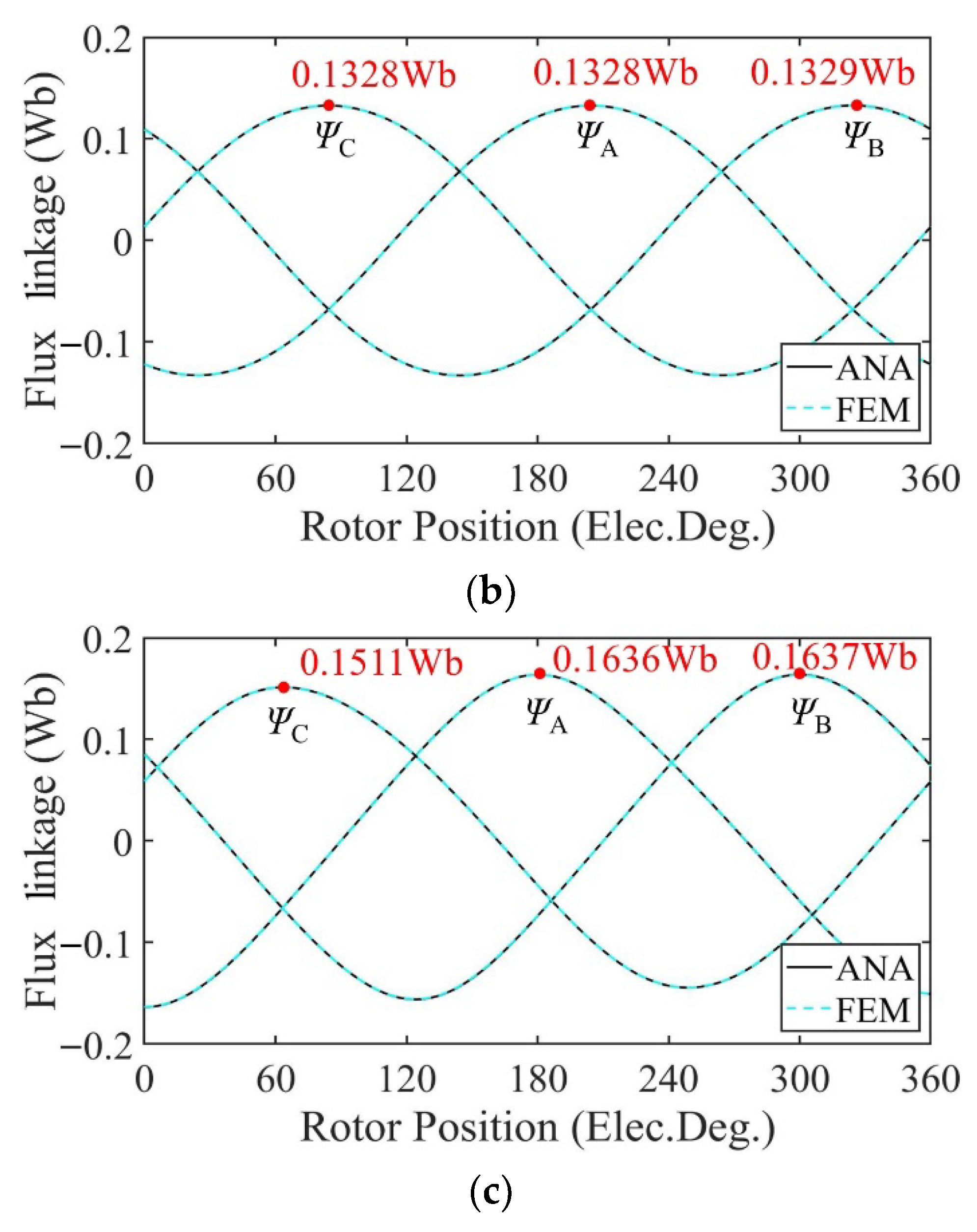
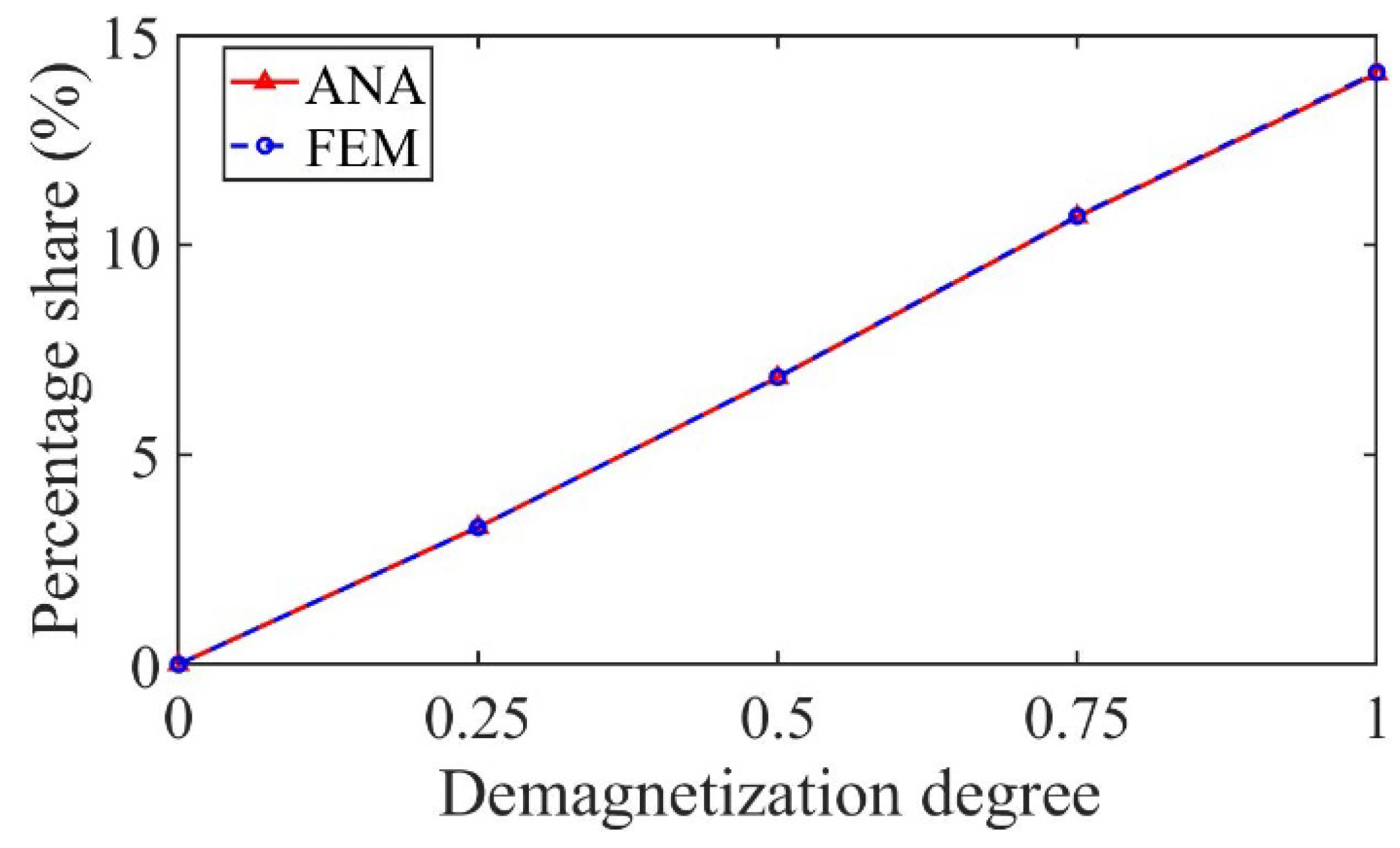
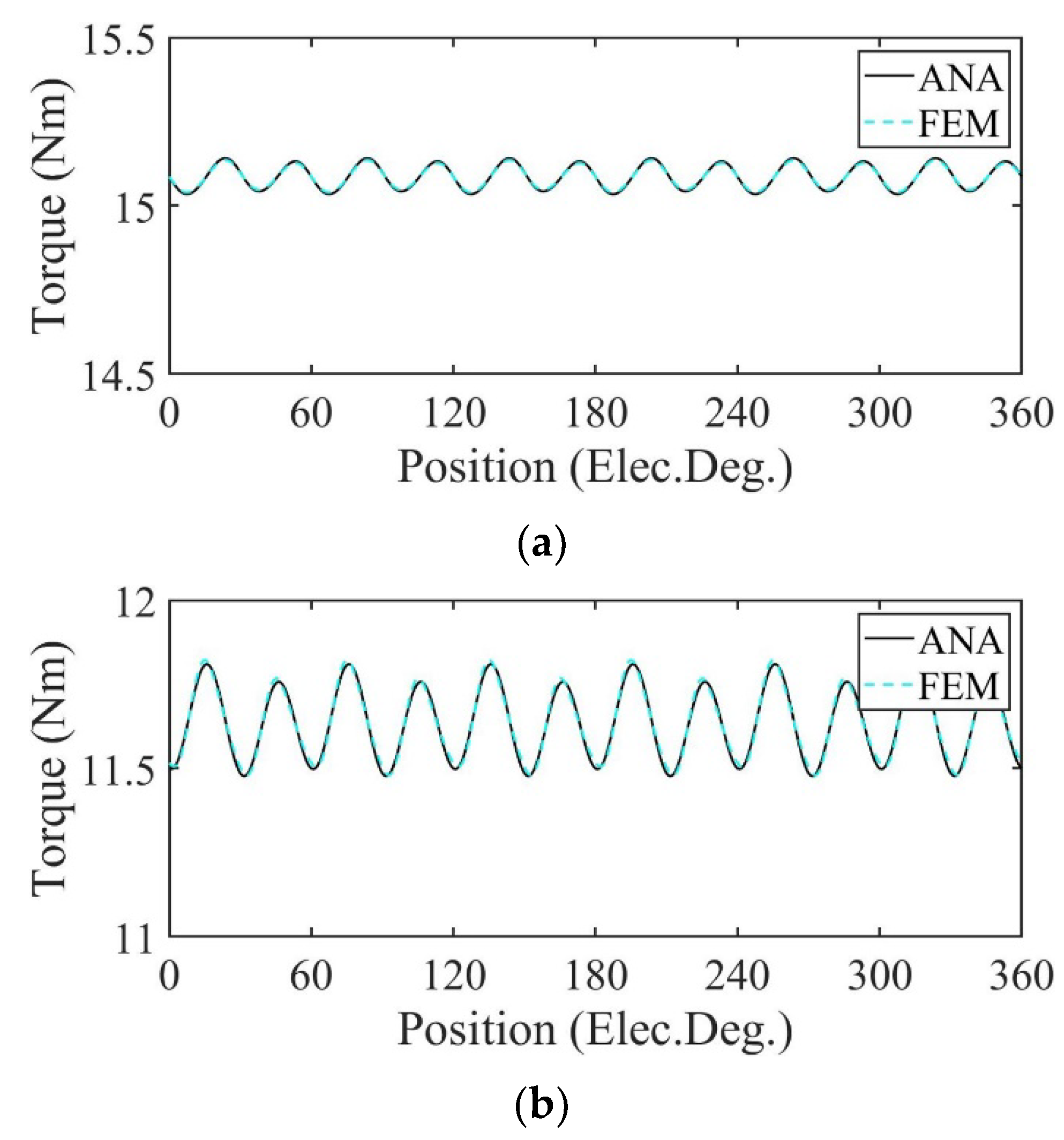
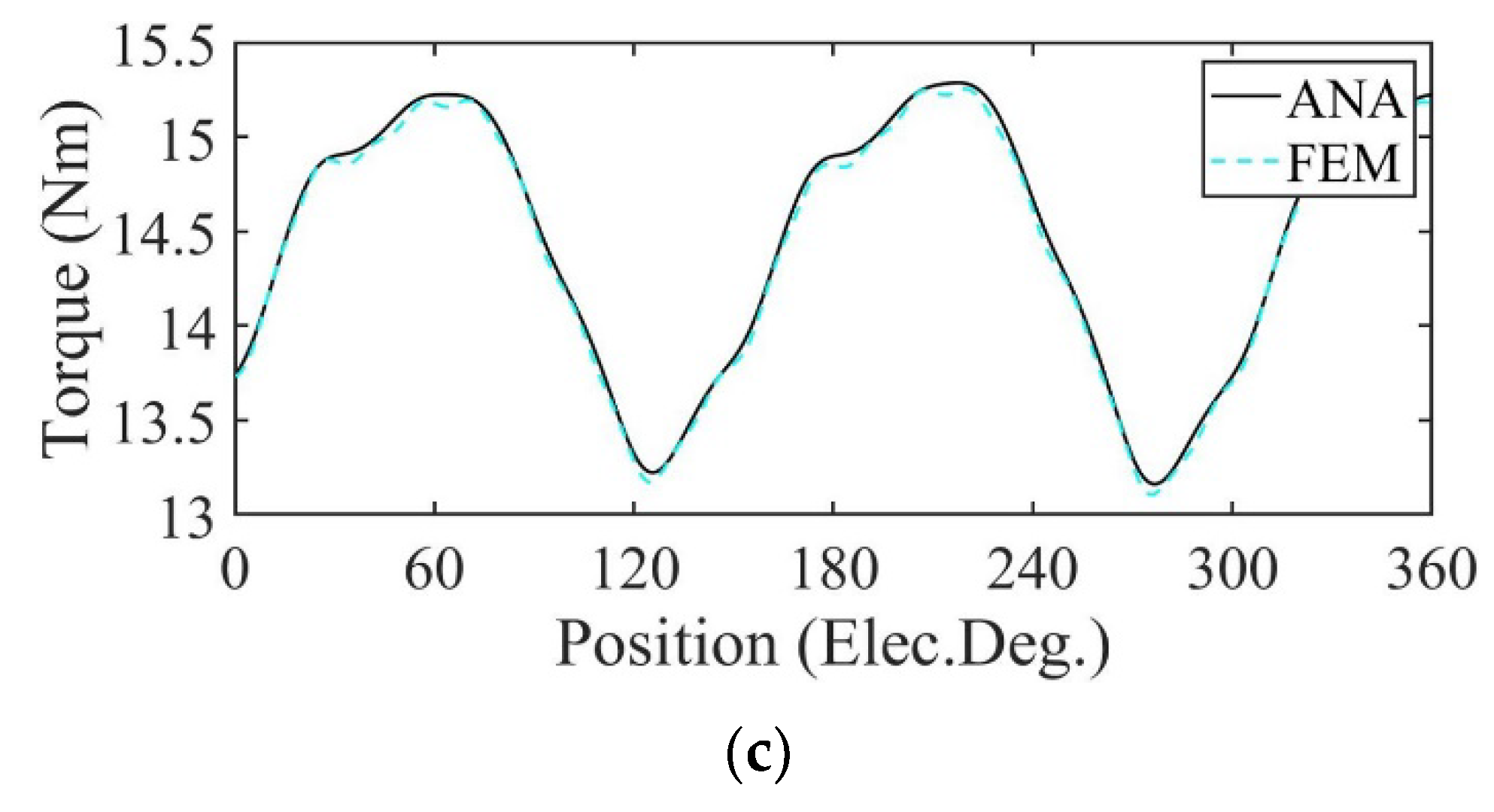
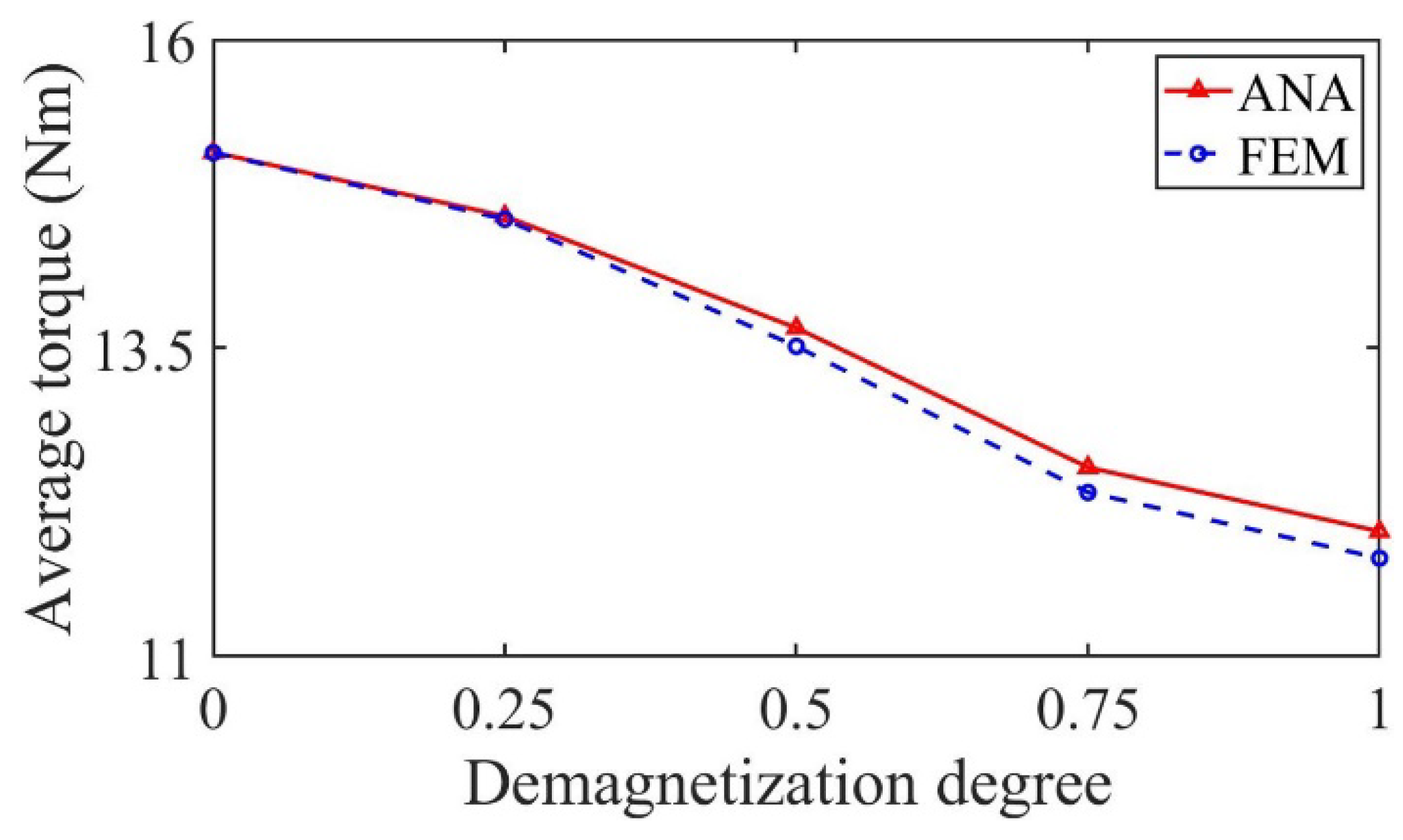
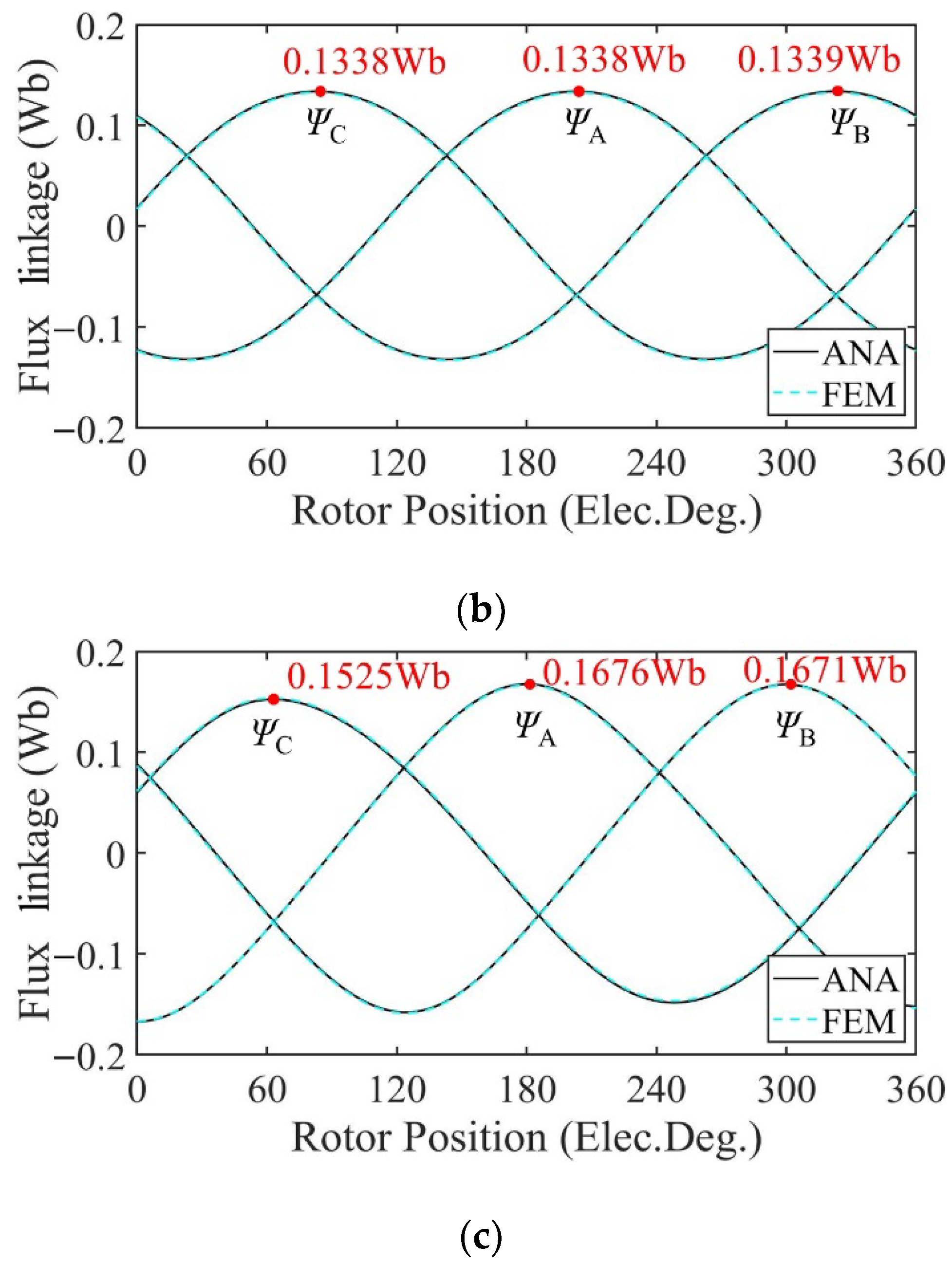
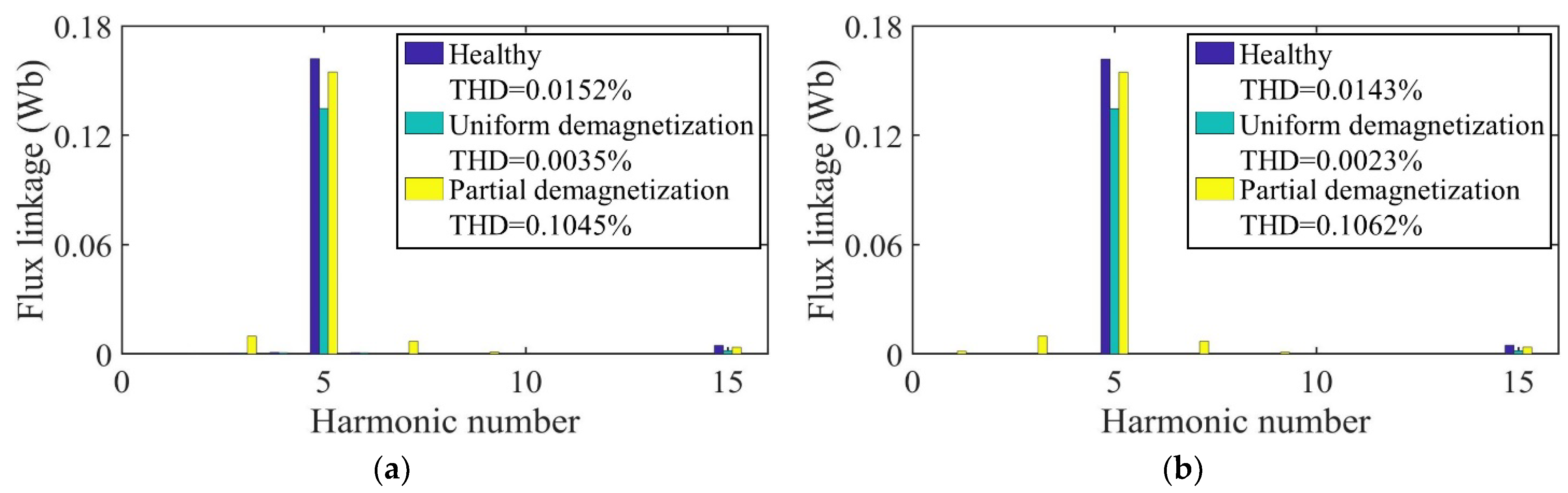
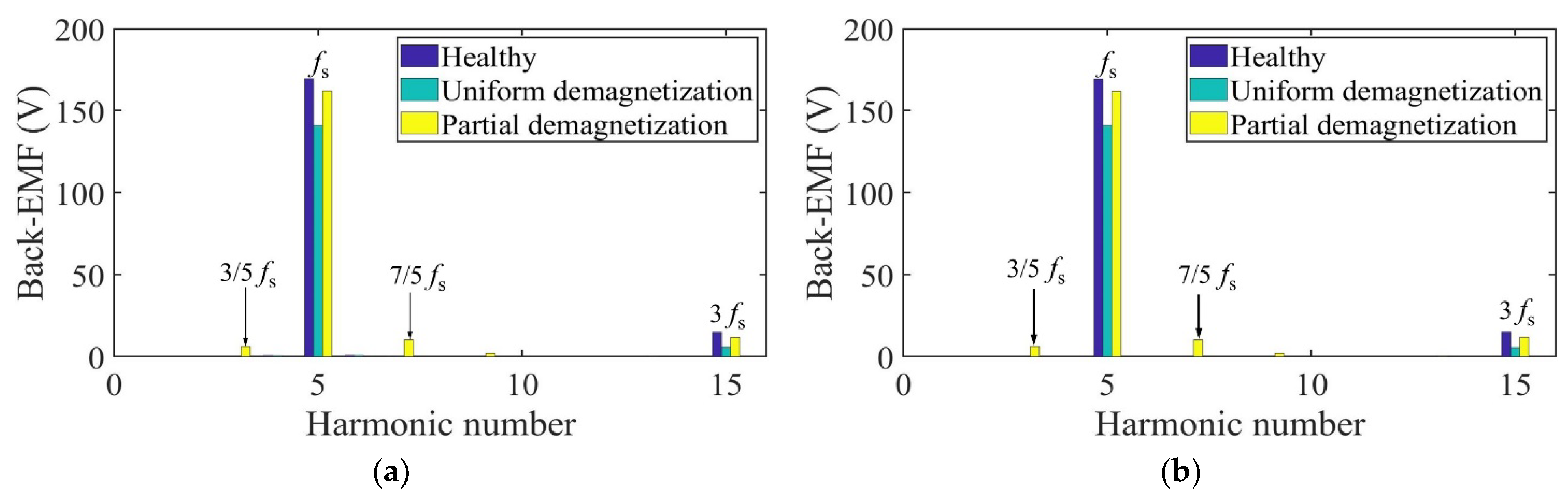
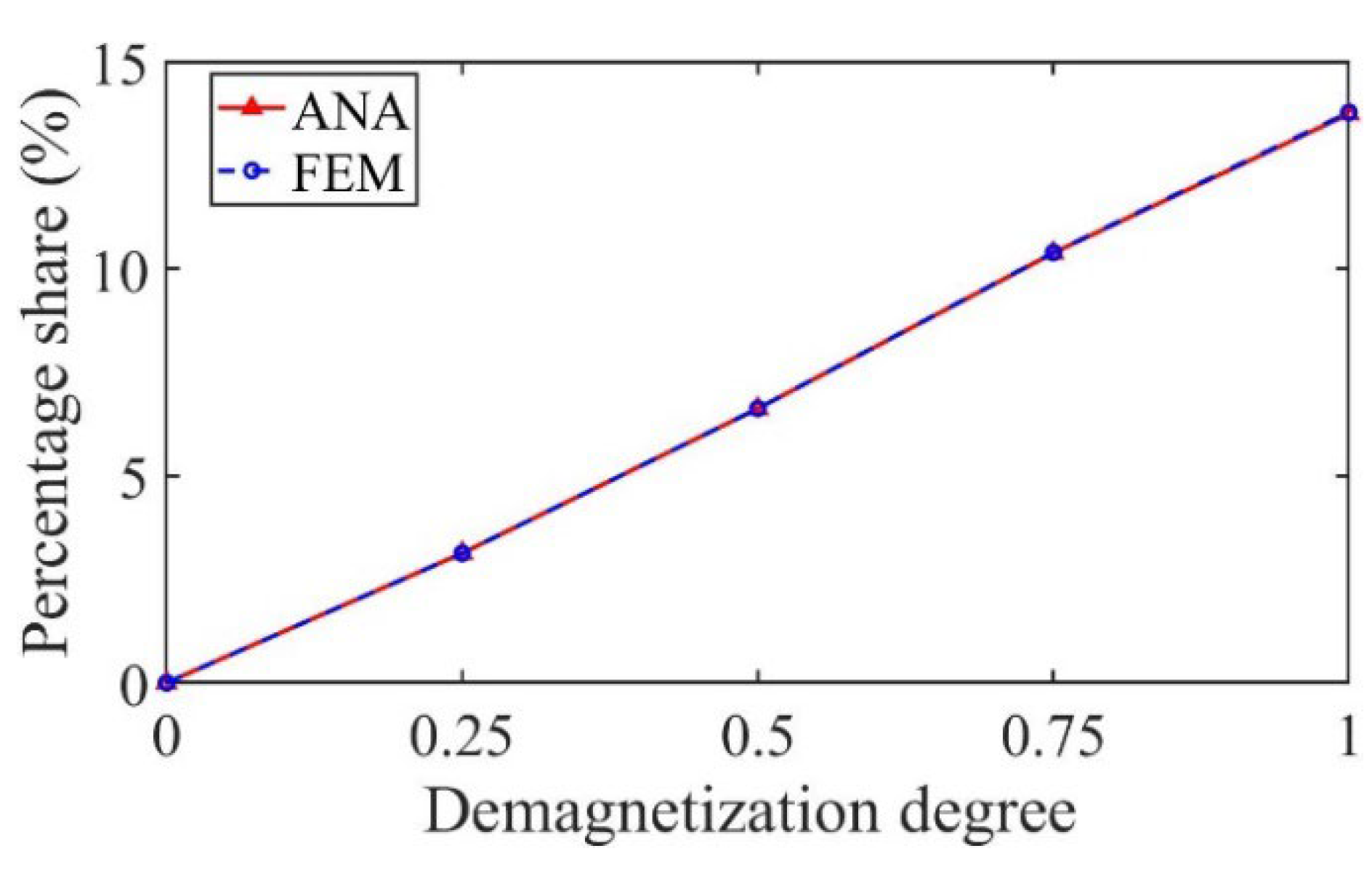
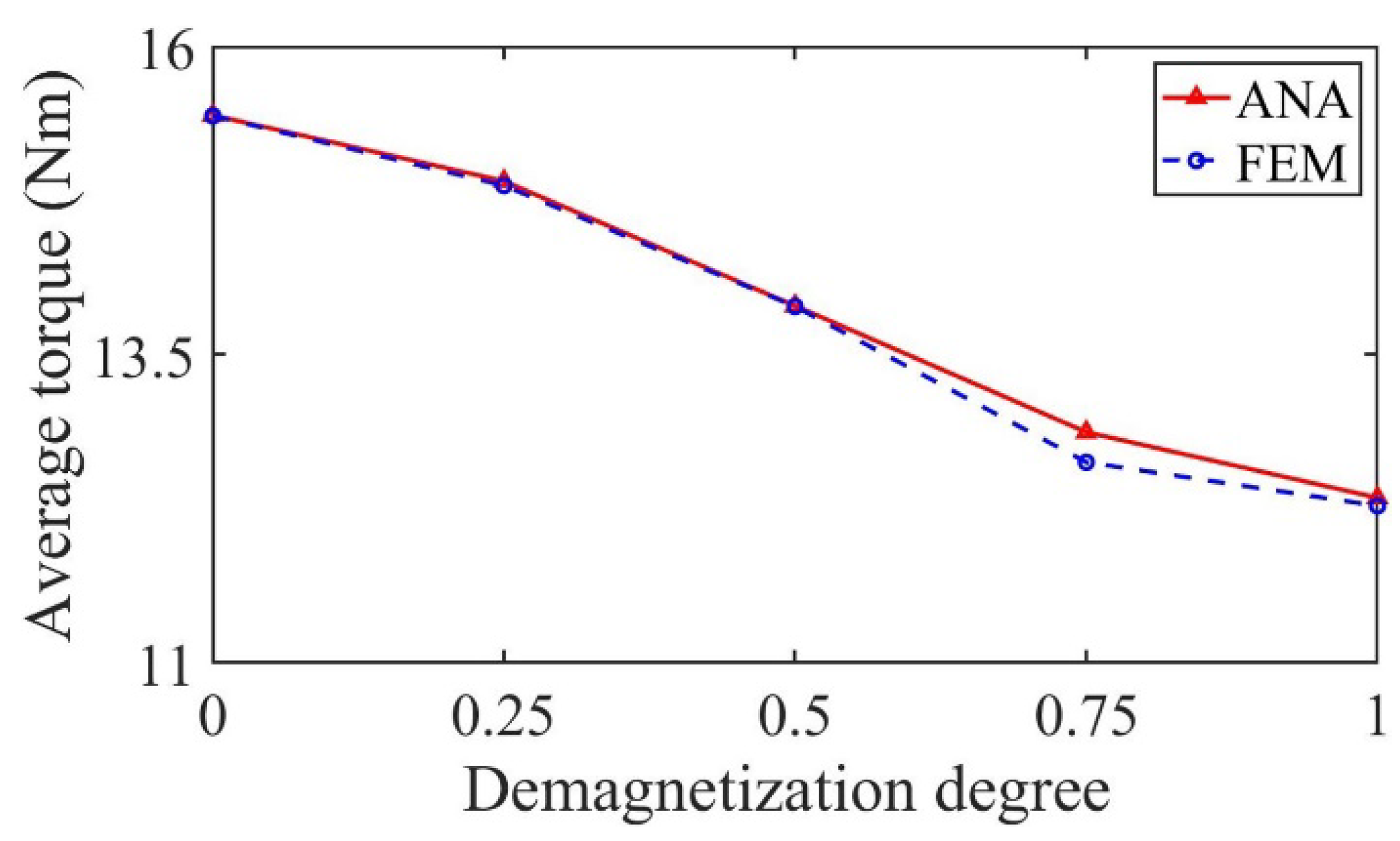
3. Validation and Analysis
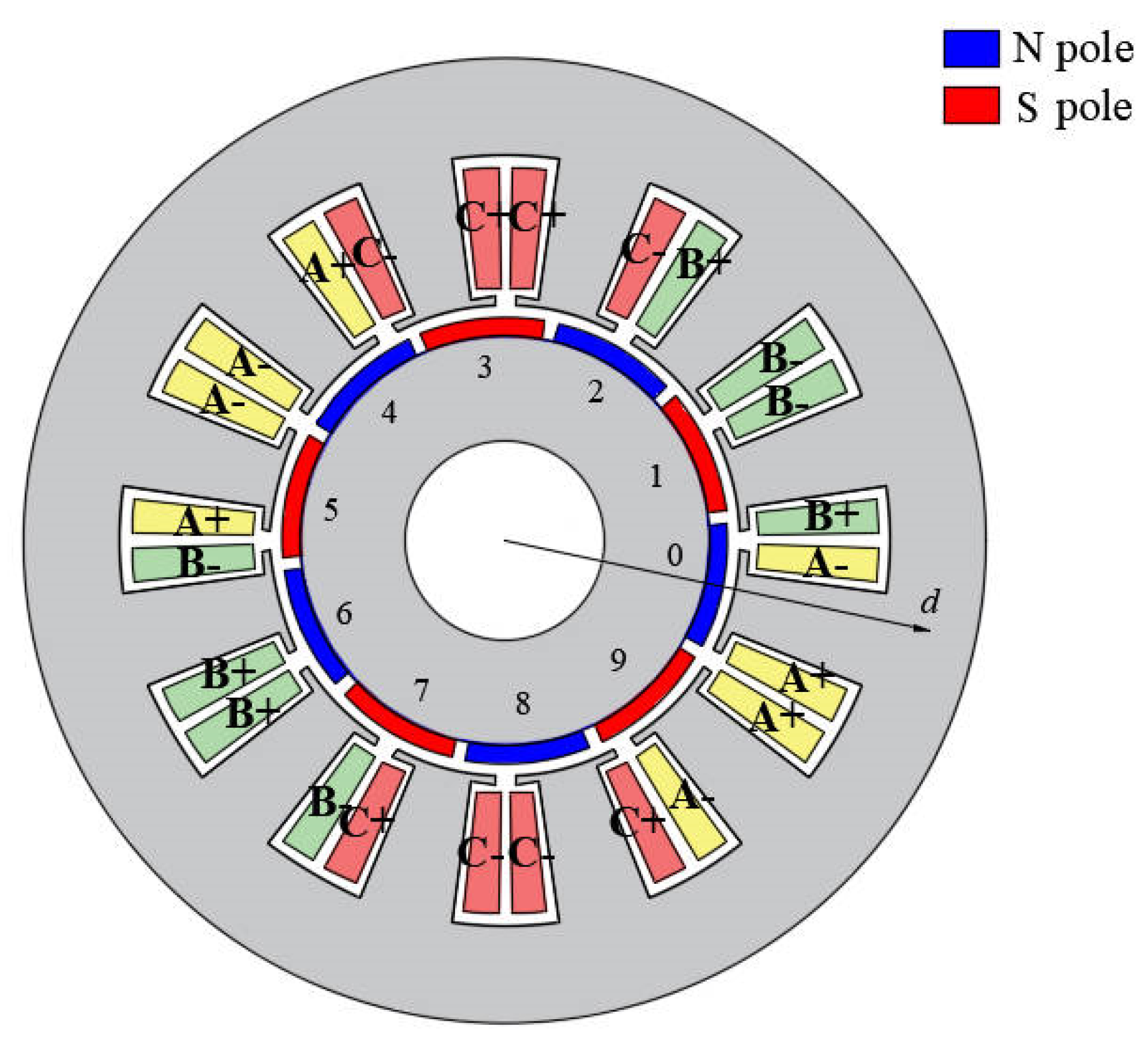
3.1. Performance Analysis of Motor with Radially Magnetized PMs
3.2. Performance Analysis of Motor with Parallel Magnetized PMs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McArdle, M.G.; Morrow, D.J. Noninvasive Detection of Brushless Exciter Rotating Diode Failure. IEEE Trans. Energy Convers. 2004, 19, 378–383. [Google Scholar] [CrossRef]
- Vijayraghavan, P.; Krishnan, R. Noise in Electric Machines: A Review. In Proceedings of the Conference Record of 1998 IEEE Industry Applications Conference. Thirty-Third IAS Annual Meeting (Cat. No.98CH36242), St. Louis, MO, USA, 12–15 October 1998; Volume 1, pp. 251–258. [Google Scholar] [CrossRef]
- Faiz, J.; Nejadi-Koti, H. Demagnetization Fault Indexes in Permanent Magnet Synchronous Motors—An Overview. IEEE Trans. Magn. 2016, 52, 1–11. [Google Scholar] [CrossRef]
- Urresty, J.-C.; Riba, J.-R.; Delgado, M.; Romeral, L. Detection of Demagnetization Faults in Surface-Mounted Permanent Magnet Synchronous Motors by Means of the Zero-Sequence Voltage Component. IEEE Trans. Energy Convers. 2012, 27, 42–51. [Google Scholar] [CrossRef]
- Cheng, M.; Hang, J.; Zhang, J. Overview of Fault Diagnosis Theory and Method for Permanent Magnet Machine. Chin. J. Electr. Eng. 2015, 1, 21–36. [Google Scholar] [CrossRef]
- Candelo-Zuluaga, C.; Riba, J.-R.; Thangamuthu, D.V.; Garcia, A. Detection of Partial Demagnetization Faults in Five-Phase Permanent Magnet Assisted Synchronous Reluctance Machines. Energies 2020, 13, 3496. [Google Scholar] [CrossRef]
- Gritli, Y.; Tani, A.; Rossi, C.; Casadei, D. Assessment of Current and Voltage Signature Analysis for the Diagnosis of Rotor Magnet Demagnetization in Five-Phase AC Permanent Magnet Generator Drives. Math. Comput. Simul. 2019, 158, 91–106. [Google Scholar] [CrossRef]
- Barmpatza, A.C.; Kappatou, J.C. Study of a Combined Demagnetization and Eccentricity Fault in an AFPM Synchronous Generator. Energies 2020, 13, 5609. [Google Scholar] [CrossRef]
- Krichen, M.; Elbouchikhi, E.; Benhadj, N.; Chaieb, M.; Benbouzid, M.; Neji, R. Motor Current Signature Analysis-Based Permanent Magnet Synchronous Motor Demagnetization Characterization and Detection. Machines 2020, 8, 35. [Google Scholar] [CrossRef]
- Gyftakis, K.; Rasid, S.; Skarmoutsos, G.; Mueller, M. The Demagnetization Harmonics Generation Mechanism in Permanent Magnet Machines with Concentrated Windings. IEEE Trans. Energy Convers. 2021, 36, 2934–2944. [Google Scholar] [CrossRef]
- Park, Y.; Fernandez, D.; Lee, S.B.; Hyun, D.; Jeong, M.; Kommuri, S.K.; Cho, C.; Diaz Reigosa, D.; Briz, F. Online Detection of Rotor Eccentricity and Demagnetization Faults in PMSMs Based on Hall-Effect Field Sensor Measurements. IEEE Trans. Ind. Appl. 2019, 55, 2499–2509. [Google Scholar] [CrossRef]
- Goktas, T.; Zafarani, M.; Lee, K.W.; Akin, B.; Sculley, T. Comprehensive Analysis of Magnet Defect Fault Monitoring through Leakage Flux. IEEE Trans. Magn. 2017, 53, 1–10. [Google Scholar] [CrossRef]
- Ullah, Z.; Lee, S.-T.; Hur, J. A Torque Angle-Based Fault Detection and Identification Technique for IPMSM. IEEE Trans. Ind. Appl. 2020, 56, 170–182. [Google Scholar] [CrossRef]
- Burriel-Valencia, J.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Pineda-Sanchez, M.; Perez-Cruz, J.; Riera-Guasp, M. Automatic Fault Diagnostic System for Induction Motors under Transient Regime Optimized with Expert Systems. Electronics 2018, 8, 6. [Google Scholar] [CrossRef]
- Song, J.; Zhao, J.; Dong, F.; Zhao, J.; Xu, L.; Yao, Z. A New Demagnetization Fault Recognition and Classification Method for DPMSLM. IEEE Trans. Ind. Inf. 2020, 16, 1559–1570. [Google Scholar] [CrossRef]
- Fei, S.; Zhang, X. Fault Diagnosis of Power Transformer Based on Support Vector Machine with Genetic Algorithm. Expert Syst. Appl. 2009, 36, 11352–11357. [Google Scholar] [CrossRef]
- Wang, C.-S.; Kao, I.-H.; Perng, J.-W. Fault Diagnosis and Fault Frequency Determination of Permanent Magnet Synchronous Motor Based on Deep Learning. Sensors 2021, 21, 3608. [Google Scholar] [CrossRef]
- Arellano-Espitia, F.; Delgado-Prieto, M.; Martinez-Viol, V.; Saucedo-Dorantes, J.J.; Osornio-Rios, R.A. Deep-Learning-Based Methodology for Fault Diagnosis in Electromechanical Systems. Sensors 2020, 20, 3949. [Google Scholar] [CrossRef]
- Long, J.; Qin, Y.; Yang, Z.; Huang, Y.; Li, C. Discriminative Feature Learning Using a Multiscale Convolutional Capsule Network from Attitude Data for Fault Diagnosis of Industrial Robots. Mech. Syst. Signal Process. 2023, 182, 109569. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Wu, Q.; Yang, Z.; Zhan, Z. A Novel Unsupervised Directed Hierarchical Graph Network with Clustering Representation for Intelligent Fault Diagnosis of Machines. Mech. Syst. Signal Process. 2023, 183, 109615. [Google Scholar] [CrossRef]
- Lee, H.; Jeong, H.; Kim, S.; Kim, S.W. Severity Estimation for Interturn Short-Circuit and Demagnetization Faults through Self-Attention Network. Sensors 2022, 22, 4639. [Google Scholar] [CrossRef]
- Zeng, C.; Huang, S.; Lei, J.; Wan, Z.; Yang, Y. Online Rotor Fault Diagnosis of Permanent Magnet Synchronous Motors Based on Stator Tooth Flux. IEEE Trans. Ind. Appl. 2021, 57, 2366–2377. [Google Scholar] [CrossRef]
- Usman, A.; Rajpurohit, B.S. Modeling and Classification of Stator Inter-Turn Fault and Demagnetization Effects in BLDC Motor Using Rotor Back-EMF and Radial Magnetic Flux Analysis. IEEE Access 2020, 8, 118030–118049. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, X.; Miao, W.; Pong, P.W.T.; Liu, C. Online Detecting Magnet Defect Fault in PMSG With Magnetic Sensing. IEEE Trans. Transp. Electrif. 2021, 7, 2775–2786. [Google Scholar] [CrossRef]
- Guo, B.; Huang, Y.; Peng, F.; Dong, J. General Analytical Modeling for Magnet Demagnetization in Surface Mounted Permanent Magnet Machines. IEEE Trans. Ind. Electron. 2019, 66, 5830–5838. [Google Scholar] [CrossRef]
- Li, Z.; Huang, X.; Yu, Y.; Jiang, D.; Wu, L.; Shi, T. Nonlinear Analytical Modelling for Surface-Mounted Permanent Magnet Motors with Magnet Defect Fault. IEEE Trans. Energy Convers. 2022, 37, 1955–1964. [Google Scholar] [CrossRef]
- De Bisschop, J.; Vansompel, H.; Sergeant, P.; Dupre, L. Demagnetization Fault Detection in Axial Flux PM Machines by Using Sensing Coils and an Analytical Model. IEEE Trans. Magn. 2017, 53, 8203404. [Google Scholar] [CrossRef]
- De Bisschop, J.; Sergeant, P.; Hemeida, A.; Vansompel, H.; Dupré, L. Analytical Model for Combined Study of Magnet Demagnetization and Eccentricity Defects in Axial Flux Permanent Magnet Synchronous Machines. IEEE Trans. Magn. 2017, 53, 8107712. [Google Scholar] [CrossRef]
- Verkroost, L.; De Bisschop, J.; Vansompel, H.; De Belie, F.; Sergeant, P. Active Demagnetization Fault Compensation for Axial Flux Permanent-Magnet Synchronous Machines Using an Analytical Inverse Model. IEEE Trans. Energy Convers. 2020, 35, 591–599. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Roshtkhari, M.J.; Faiz, J.; Khatami, S.V. Advanced Eccentricity Fault Recognition in Permanent Magnet Synchronous Motors Using Stator Current Signature Analysis. IEEE Trans. Ind. Electron. 2014, 61, 2041–2052. [Google Scholar] [CrossRef]
- Zafarani, M.; Goktas, T.; Akin, B. A Comprehensive Analysis of Magnet Defect Faults in Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Appl. 2015, 52, 1331–1339. [Google Scholar] [CrossRef]









| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Pole pair | 5 | - - | |
| Slot/tooth number | 12 | - - | |
| Rated speed | 2000 | rpm | |
| Rated current | 9 | A | |
| Axial length | 125 | mm | |
| Radius of slot bottom | 64 | mm | |
| Radius of slot top | 40.5 | mm | |
| Inner radius of stator | 39 | mm | |
| Outer radius of rotor | 34 | mm | |
| Airgap length | 2 | mm | |
| Slot opening width | /36 | rad | |
| Slot width | 4/45 | rad | |
| Magnet thickness | 3 | mm | |
| Residual flux density of PM | 1.23 | T | |
| Relative permeability of PM | 1.03 | - - | |
| Pole-arc to pole-pitch ratio | 0.9 | - - | |
| Number of turns per coil | 54 | - - | |
| Number of Parallel Branches | 2 | - - |
| Motor Status | Harmonic Frequency (Hz) | ANA (%) | FEM (%) | (%) | |
|---|---|---|---|---|---|
| Healthy | 166.7 (fs) | 5 | 100 | 100 | 0.000 |
| 500 | 15 | 9.875 | 10.078 | 0.203 | |
| Uniform demagnetization | 166.7 (fs) | 5 | 100 | 100 | 0.000 |
| 500 | 15 | 2.376 | 2.231 | 0.145 | |
| Partial demagnetization | 33.3 | 1 | 0.209 | 0.212 | 0.003 |
| 100 | 3 | 3.953 | 3.953 | 0.000 | |
| 166.7 (fs) | 5 | 100 | 100 | 0.000 | |
| 233.3 | 7 | 6.596 | 6.571 | 0.025 | |
| 300 | 9 | 1.257 | 1.248 | 0.009 | |
| 500 | 15 | 8.214 | 8.332 | 0.118 | |
| 566.7 | 17 | 2.934 | 2.922 | 0.012 | |
| 633.3 | 19 | 0.935 | 0.936 | 0.001 |
| Healthy | Uniform Demagnetization | Partial Demagnetization | ||
|---|---|---|---|---|
| (T) | ANA | 0.6067 | 0.5037 | 0.5874 |
| FEM | 0.6065 | 0.5040 | 0.5873 | |
| (%) | 0.0330 | 0.0595 | 0.0170 | |
| (Wb) | ANA | 0.1120 | 0.0947 | 0.1095 |
| FEM | 0.1119 | 0.0947 | 0.1094 | |
| (%) | 0.0894 | 0.0007 | 0.0914 | |
| (V) | ANA | 117.6990 | 99.1365 | 115.0123 |
| FEM | 117.5056 | 99.0559 | 114.8373 | |
| (%) | 0.1646 | 0.0814 | 0.1524 | |
| (Nm) | ANA | 15.0868 | 11.6360 | 14.4665 |
| FEM | 15.0832 | 11.6390 | 14.4315 | |
| (%) | 0.0239 | 0.0258 | 0.2425 | |
| Motor Status | Harmonic Frequency (Hz) | ANA (%) | FEM (%) | (%) | |
|---|---|---|---|---|---|
| Healthy | 166.7 (fs) | 5 | 100 | 100 | 0.000 |
| 500 | 15 | 8.776 | 8.866 | 0.090 | |
| Uniform demagnetization | 166.7 (fs) | 5 | 100 | 100 | 0.000 |
| 500 | 15 | 4.029 | 3.905 | 0.124 | |
| Partial demagnetization | 33.3 | 1 | 0 | 0.002 | 0.002 |
| 100 | 3 | 0.004 | 0.203 | 0.199 | |
| 166.7 (fs) | 5 | 3.792 | 3.792 | 0.000 | |
| 233.3 | 7 | 100 | 100 | 0.000 | |
| 300 | 9 | 6.348 | 6.338 | 0.010 | |
| 500 | 15 | 1.218 | 1.208 | 0.010 | |
| 566.7 | 17 | 7.190 | 7.289 | 0.099 | |
| 633.3 | 19 | 2.922 | 2.906 | 0.016 |
| Healthy | Uniform Demagnetization | Partial Demagnetization | ||
|---|---|---|---|---|
| (T) | ANA | 0.6167 | 0.5082 | 0.5966 |
| FEM | 0.6164 | 0.5083 | 0.5963 | |
| (%) | 0.0487 | 0.0197 | 0.0503 | |
| (Wb) | ANA | 0.1146 | 0.0952 | 0.1121 |
| FEM | 0.1145 | 0.0952 | 0.1120 | |
| (%) | 0.0873 | 0.0219 | 0.0893 | |
| (V) | ANA | 120.3556 | 99.7624 | 117.6695 |
| FEM | 120.1492 | 99.6588 | 117.4150 | |
| (%) | 0.1718 | 0.1040 | 0.2168 | |
| (Nm) | ANA | 15.4431 | 11.8246 | 14.7890 |
| FEM | 15.4383 | 11.8290 | 14.7502 | |
| (%) | 0.0311 | 0.0372 | 0.2630 | |
| Motor Status | Radial Magnetization | Parallel Magnetization | ||
|---|---|---|---|---|
| ANA | FEM | ANA | FEM | |
| Healthy | 33 | 791 | 34 | 826 |
| Uniform demagnetization | 37 | 661 | 37 | 676 |
| Partial demagnetization | 44 | 794 | 45 | 805 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, C.; Peng, L.; Zhang, Z.; Shi, T. Analytical Modeling and Analysis of Permanent-Magnet Motor with Demagnetization Fault. Sensors 2022, 22, 9440. https://doi.org/10.3390/s22239440
Shi C, Peng L, Zhang Z, Shi T. Analytical Modeling and Analysis of Permanent-Magnet Motor with Demagnetization Fault. Sensors. 2022; 22(23):9440. https://doi.org/10.3390/s22239440
Chicago/Turabian StyleShi, Cenwei, Lin Peng, Zhen Zhang, and Tingna Shi. 2022. "Analytical Modeling and Analysis of Permanent-Magnet Motor with Demagnetization Fault" Sensors 22, no. 23: 9440. https://doi.org/10.3390/s22239440
APA StyleShi, C., Peng, L., Zhang, Z., & Shi, T. (2022). Analytical Modeling and Analysis of Permanent-Magnet Motor with Demagnetization Fault. Sensors, 22(23), 9440. https://doi.org/10.3390/s22239440








