Sensing Method Using Dielectric Loss Factor to Evaluate Surface Conditions on Polluted Porcelain Insulator
Abstract
1. Introduction
2. Materials and Methods
3. Results
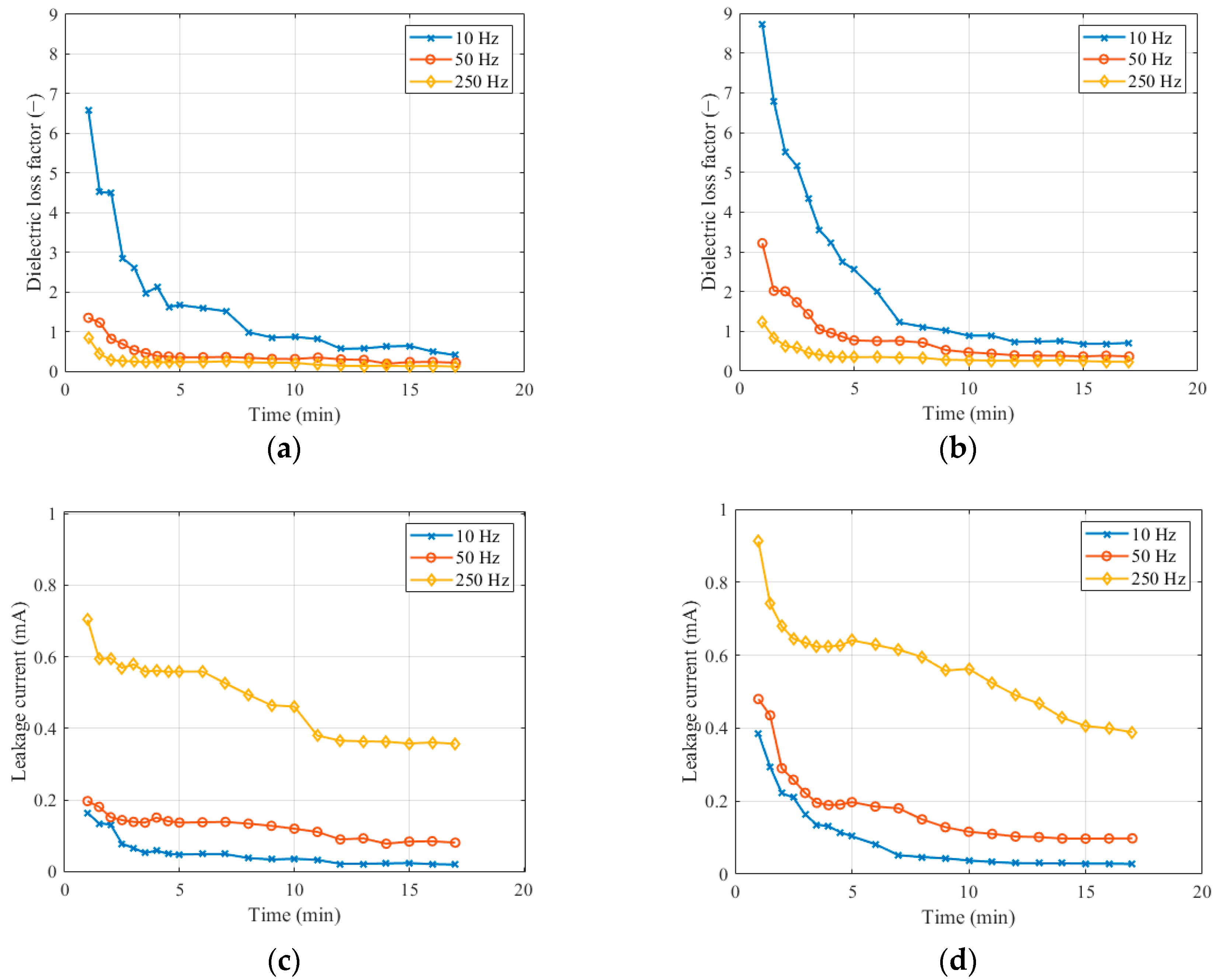
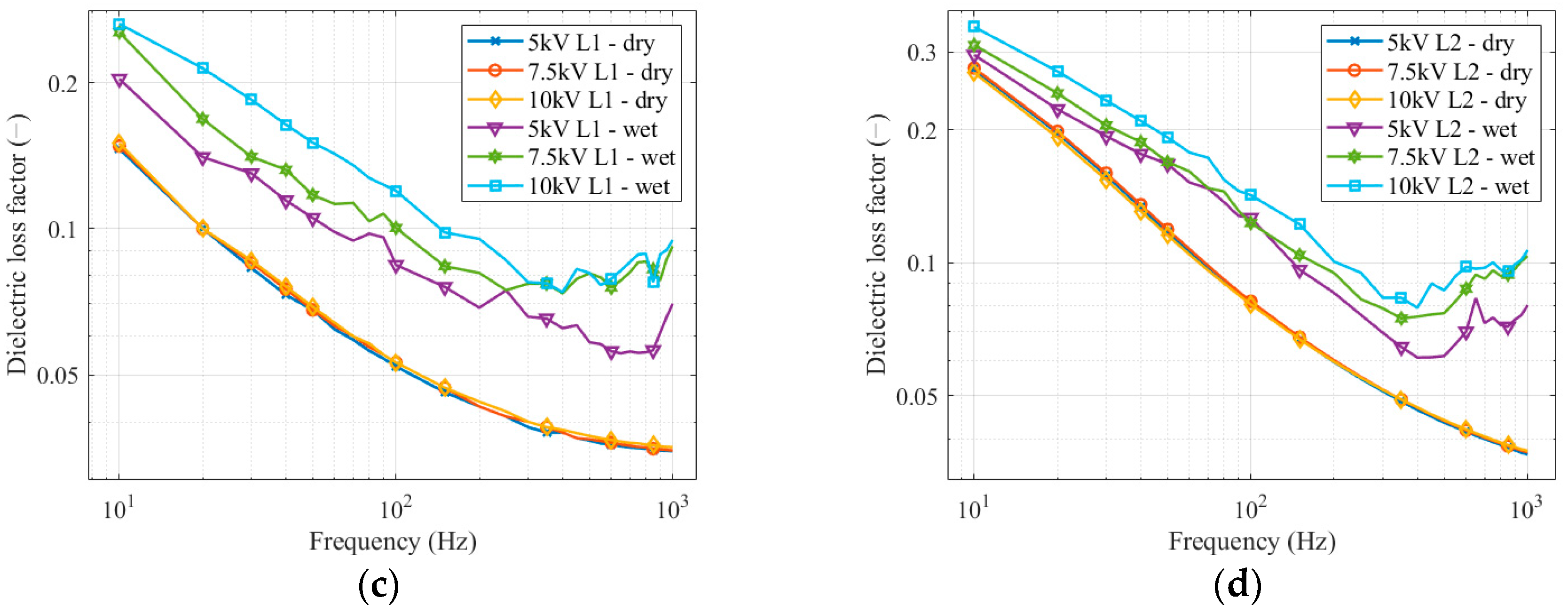
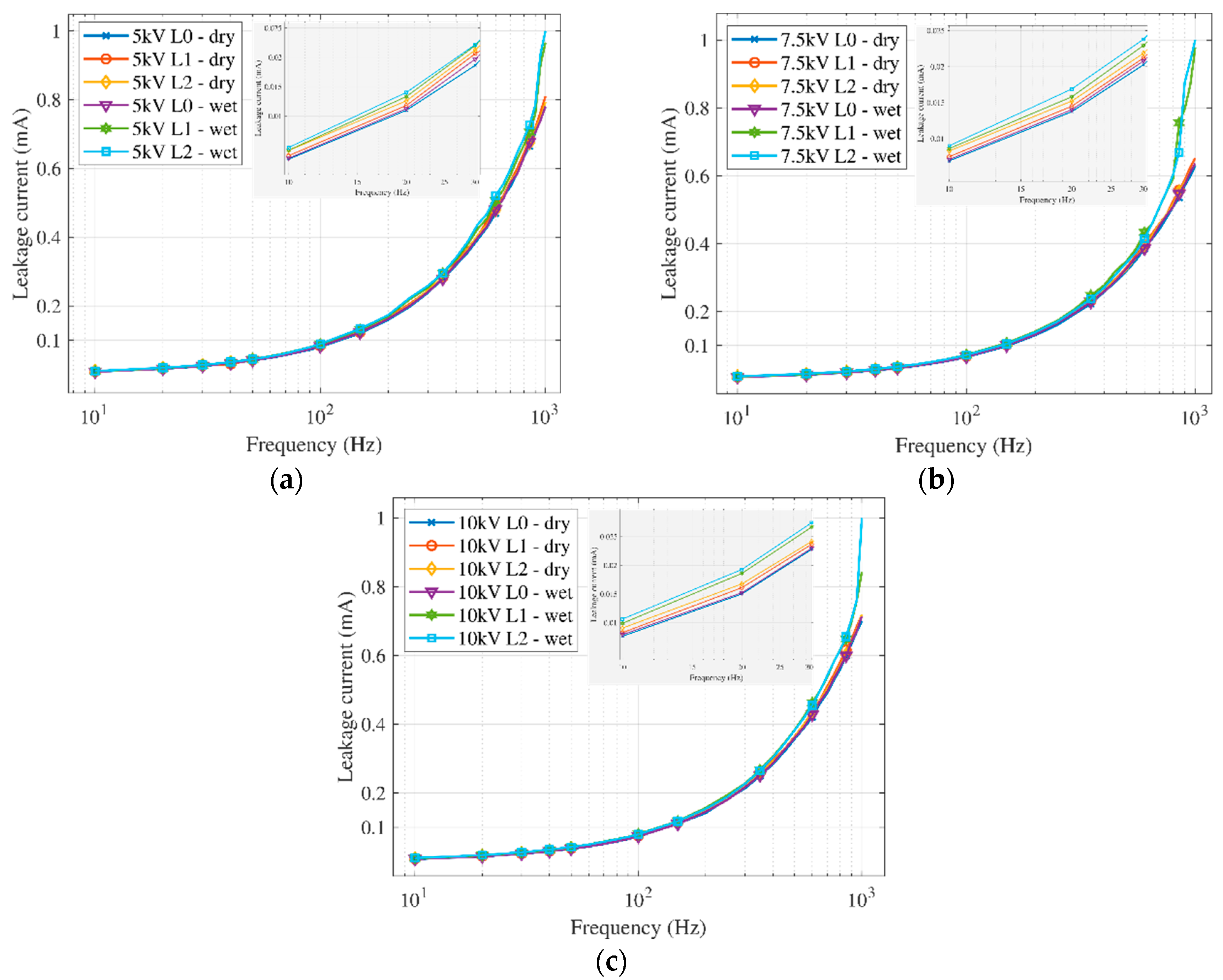
3.1. Dielectric Loss Factor Measurement Result
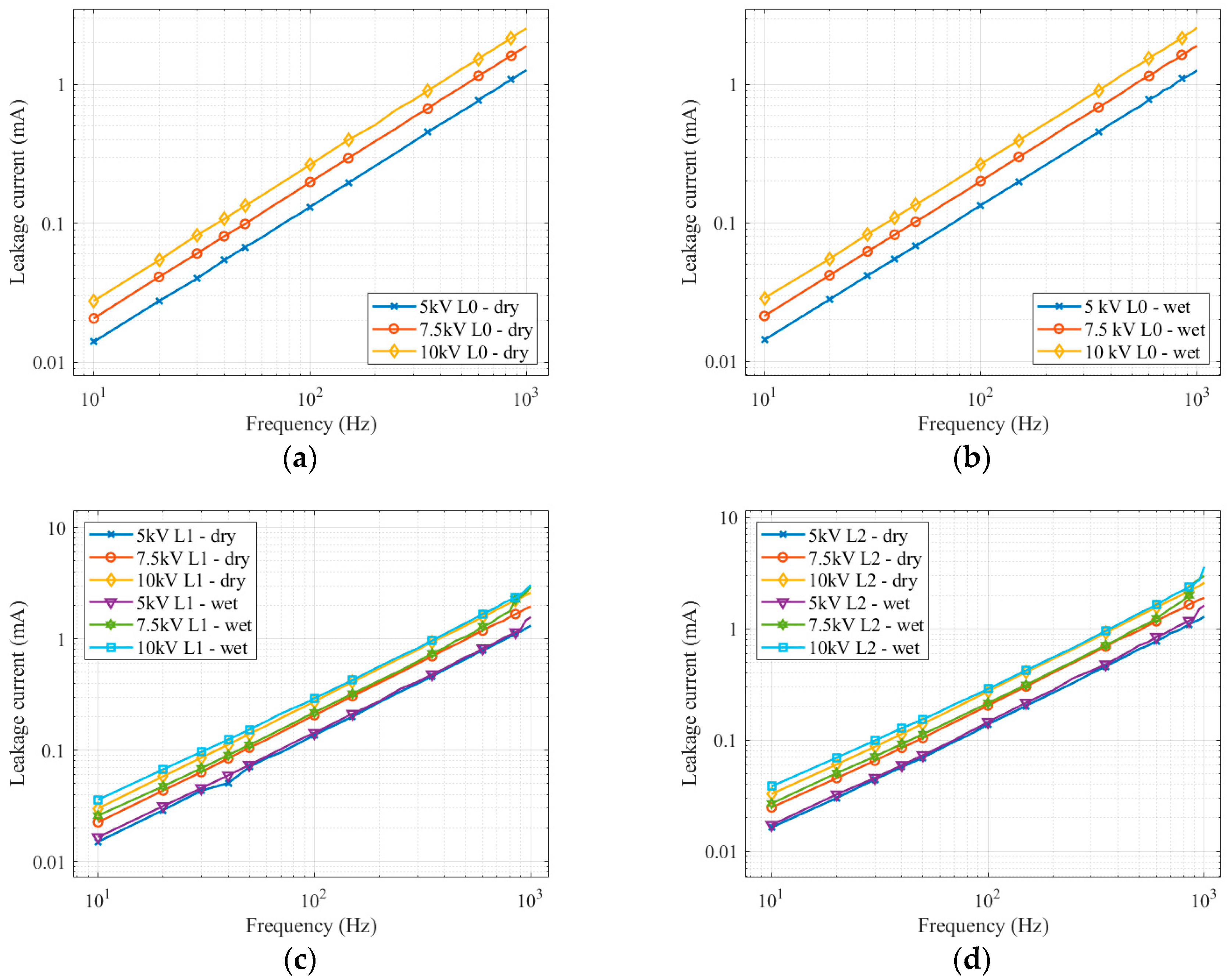
3.2. Leakage Current Measurement Result
4. Discussion
5. Conclusions
- 1.
- Usage for diagnostics of insulators. Our measurements at high voltage confirm the usability of the dielectric loss factor for diagnostics of insulators.
- 2.
- The dielectric loss factor can be used not only for aging process evaluation but has promising results to indicate contamination of insulators. Our measurements in a frequency spectrum widen diagnostic possibilities at various frequency levels. In some applications, it can help to avoid interference with the industrial frequency, which can reduce the accuracy of measurements.
- The dielectric loss factor is more sensitive to changes in the conditions of the insulator surface than the leakage current. When looking at the level of pollution, it showed more significant differences in both dry and wet conditions.
- Measuring the dielectric loss factor in the frequency spectrum or as a single frequency value is a suitable method for diagnosing contamination of the insulator surface.
- In dry conditions, the dielectric loss factor was more stable (with a lower standard deviation), with clearly identifiable changes. The advantage is that dry conditions are more suitable for diagnostics using the dielectric loss factor than a wet environment. In wet conditions, there are frequent changes in the parameters of the polluting layer, which can affect the measured quantities. On the contrary, the results of the leakage current measurements showed that the differences were less pronounced in dry conditions than in wet conditions for all pollution levels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farzaneh, M.; Chisholm, W.A. Insulators for Icing and Polluted Environments; IEEE Press: Piscataway, NJ, USA; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Vosloo, W.L.; Macey, R.E.; de Tourreil, C. The Practical Guide to Outdoor High Voltage Insulators; Crown Publications: Johannesburg, South Africa, 2004. [Google Scholar]
- Haddad, A.; Warne, D.F.; Institution of Electrical Engineers (Eds.) Advances in High Voltage Engineering; Institution of Electrical Engineers: London, UK, 2004. [Google Scholar]
- Kuffel, E.; Zaengl, W.S.; Kuffel, J. High Voltage Engineering: Fundamentals, 2nd ed.; Butterworth-Heinemann: Oxford, UK; Boston, MA, USA, 2000. [Google Scholar]
- Al-Gheilani, A.; Rowe, W.; Li, Y.; Wong, K.L. Stress Control Methods on a High Voltage Insulator: A Review. Energy Procedia 2017, 110, 95–100. [Google Scholar] [CrossRef]
- Montanari, G.C.; Morshuis, P.; Seri, P.; Ghosh, R. Ageing and reliability of electrical insulation: The risk of hybrid AC/DC grids. High Volt. 2020, 5, 620–627. [Google Scholar] [CrossRef]
- Ibrahim, M.E.; Selim, F.; Abd-Elhady, A.M. Partial discharge performance improvement of covered conductor (CC)/high voltage insulator based electrical distribution systems. Electr. Power Syst. Res. 2022, 202, 107601. [Google Scholar] [CrossRef]
- Savadkoohi, E.M.; Mirzaie, M.; Seyyedbarzegar, S.; Mohammadi, M.; Khodsuz, M.; Pashakolae, M.G.; Ghadikolaei, M.B. Experimental investigation on composite insulators AC flashover performance with fan-shaped non-uniform pollution under electro-thermal stress. Int. J. Electr. Power Energy Syst. 2020, 121, 106142. [Google Scholar] [CrossRef]
- Volokhin, V.; Diahovchenko, I. Peculiarities of current sensors used in contemporary electric energy metering devices. Energetika 2017, 63, 8–15. [Google Scholar] [CrossRef]
- IEC 61109:2008; Insulators for Overhead Lines—Composite Suspension and Tension Insulators for a.c. Systems with a Nominal Voltage Greater than 1000 V—Definitions, Test Methods and Acceptance Criteria. IEC: Geneva, Switzerland, 2008.
- Sartika, N.; Naufalarizqa, R.M.P.; Rachmawati; Suwarno. Study on leakage current characteristics and computer simulation of semiconducting glazed insulator under clean and salt fog condition. In Proceedings of the 2018 12th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Xi’an, China, 20–24 May 2018; pp. 82–85. [Google Scholar] [CrossRef]
- Fauziah, D.; Alfiadi, H.; Rachmawati; Suwarno. Performances of long-term coastal field aged silicone-coated ceramic insulators under clean and salt fog conditions. In Proceedings of the 2017 International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Denpasar, Indonesia, 2–5 October 2017; pp. 51–56. [Google Scholar] [CrossRef]
- Suwarno. Understanding of Outdoor Insulator Characteristics through Leakage Current and Electrical Equivalent Circuit. In Proceedings of the 2021 3rd International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Bandung, Indonesia, 5–6 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Sunanda, C.; Dinesh, M.N.; Vasudev, N. Comparison of XRD analysis and leakage current in Ageing study of high voltage SR insulator with nano fillers. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Hernandez-Corona, R.; Ramirez-Vazquez, I. Polymeric insulators characterization aged in salt fog chamber by different techniques. In Proceedings of the 2016 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Toronto, ON, Canada, 17–20 October 2016; pp. 845–848. [Google Scholar] [CrossRef]
- Chatterjee, S.; Banik, A.; Dalai, S.; Chatterjee, B. Identification of salt and salinity level of 11 kV contaminated porcelian disc insulator using STD-MRA analysis of leakage current. In Proceedings of the 2015 International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Bangalore, India, 10–12 December 2015; pp. 242–246. [Google Scholar] [CrossRef]
- Dey, J.; Dutta, S.; Baral, A.; Chakravorti, S. Leakage Current Monitoring of Suspension Insulator for Effective Determination of ESDD. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Haya, S.N.; Jaelani, A.A.; Lumba, L.S.; Suwarno. Accelerated Aging Study on Silicone Rubber Insulator with Contaminant Level and Fog Conductivity Variations. In Proceedings of the 2021 3rd International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Bandung, Indonesia, 5–6 October 2021; pp. 91–95. [Google Scholar] [CrossRef]
- Dolník, B.; Šárpataky, Ľ.; Kolcunová, I.; Havran, P. Sensing Method Using Multiple Quantities for Diagnostic of Insulators in Different Ambient Conditions. Sensors 2022, 22, 1376. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Fan, S.; Deng, Y.; Dong, Y.; Yang, J.; Pan, A. Study on Characteristic Parameters and Influencing Factors of Leakage Current of Polluted Porcelain Insulators. In Proceedings of the 2020 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Rasamsetti, S.S.; Sumathi, N. Leakage current characteristics of 132kV polymeric and porcelain insulator under various polluted conditions. In Proceedings of the 2017 IEEE International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI), Chennai, India, 21–22 September 2017; pp. 1535–1540. [Google Scholar] [CrossRef]
- Murthy, K.R.; Rao, V.V.; Badachi, C.; Dixit, P. Leakage current analysis of porcelain disc insulator subjected to unusual pollutants. In Proceedings of the 2016 International Conference on Circuits, Controls, Communications and Computing (I4C), Bangalore, India, 4–6 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Pandian, R.G.; Subburaj, P. Leakage current and flash over performance analysis of 11 kv pin insulator under Bird excretion pollution. In Proceedings of the 2016 International Conference on Energy Efficient Technologies for Sustainability (ICEETS), Nagercoil, India, 7–8 April 2016; pp. 311–314. [Google Scholar] [CrossRef]
- Putra, N.R.M.; Sartika, N.; Rachmawati; Suwarno. The study on leakage current waveform characteristics and computer simulation of ceramic insulator under artificial tropical condition. In Proceedings of the 2018 12th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Xi’an, China, 20–24 May 2018; pp. 320–323. [Google Scholar] [CrossRef]
- Deb, S.; Ghosh, R.; Dutta, S.; Dalai, S.; Chatterjee, B. Condition monitoring of 11kV porcelain pin insulator extracting surface current from total leakage current. In Proceedings of the 2017 3rd International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Rupnagar, India, 16–18 November 2017; pp. 403–406. [Google Scholar] [CrossRef]
- Wakhidin, M.; Suwarno. Effects of Artificial Tropical Climate Aging on Insulation Performance of Silicone Rubber Polymeric Insulators. In Proceedings of the 2019 2nd International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Denpasar, Indonesia, 1–4 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Fauziah, D.; Alfiadi, H.; Rachmawati; Suwamo. The effect of coating on leakage current characteristic of coast field aged ceramic insulator. In Proceedings of the 2017 4th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Yogyakarta, Indonesia, 19–21 September 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Ahmad, H.; Salam, M.A.; Ying, L.Y.; Bashir, N. Harmonic components of leakage current as a diagnostic tool to study the aging of insulators. J. Electrost. 2008, 66, 156–164. [Google Scholar] [CrossRef]
- Douar, M.A.; Mekhaldi, A.; Bouzidi, M.C. Frequency analysis of the leakage current under non uniform polluted conditions on one insulator plane model. In Proceedings of the 2010 Annual Report Conference on Electrical Insulation and Dielectic Phenomena, West Lafayette, IN, USA, 17–20 October 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Fahimi, N.; Chalaki, M.R.; Baferani, M.A.; Tajik, M.R.; Shayegani, A.A. Investigating the failures of defected silicon rubber insulators in salt-fog chamber. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Araya, J.; Montana, J.; Schurch, R. Electric Field Distribution and Leakage Currents in Glass Insulator Under Different Altitudes and Pollutions Conditions using FEM Simulations. IEEE Latin Am. Trans. 2021, 19, 1278–1285. [Google Scholar] [CrossRef]
- Sardast, R.; Faghihi, F.; Vakilian, M. Study on Different Dimensions of C-type Corona Rings in 400 kV Insulator Strings Based on FEM Analysis of Electric Field Distribution. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; pp. 673–678. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, D.; Yin, J.; Wang, S. Study on Mechanical Properties of Fallen Suspension Porcelain Insulator using FEM Analysis. In Proceedings of the 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Xi’an, China, 15–17 October 2021; pp. 813–817. [Google Scholar] [CrossRef]
- Othman, M.; Isa, M.; Mazlee, M.N.; Piah, M.A.M.; Abd, N.; Rahman. Simulation of 33 kV String Insulators Using Finite Element Method (FEM). In Proceedings of the 2019 IEEE Student Conference on Research and Development (SCOReD), Bandar Seri Iskandar, Malaysia, 15–17 October 2019; pp. 86–89. [Google Scholar] [CrossRef]
- Bhavani, J.; Kumar Ch, S.V.S.P. Finite Element Modeling of Voltage and Electric Field Distribution along the Insulators. In Proceedings of the 2019 4th International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT), Bangalore, India, 17–18 May 2019; pp. 225–229. [Google Scholar] [CrossRef]
- Yalentic, V.; Grzinic, S.; Dobrec, D. Testing the electrical insulation system of power transformer based on mesuring factor of dielectric losses. In Proceedings of the IEEE EUROCON 2017—17th International Conference on Smart Technologies, Ohrid, Macedonia, 6–8 July 2017; pp. 423–427. [Google Scholar] [CrossRef]
- Jaroszewski, M.; Beroual, A.; Golebiowski, D. Effect of temperature on dielectric loss factor of biodegradable transformer oil. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athens, Greece, 10–13 September 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Cheng, X.; Ye, G.; Sun, H.; Li, T.; Sun, C. Analysis of low-frequency dielectric loss of XLPE cable insulation based on extended Debye model. AIP Adv. 2021, 11, 085103. [Google Scholar] [CrossRef]
- Morsalin, S.; Phung, B.T. Modeling of dielectric dissipation factor measurement for XLPE cable based on Davidson-Cole model. IEEE Trans. Dielect. Electr. Insul. 2019, 26, 1018–1026. [Google Scholar] [CrossRef]
- Bashir, N.; Ahmad, H.; Suddin, M.S. Ageing studies on transmission line glass insulators using dielectric dissipation factor test. In Proceedings of the 2010 Conference Proceedings IPEC, Singapore, 27–29 October 2010; pp. 1062–1066. [Google Scholar] [CrossRef]
- Gerdinand, F.; Budde, M.; Kurrat, M. Electrical and mechanical strength of mineral filled epoxy insulators in correlation to power loss factor. In Proceedings of the 2004 IEEE International Conference on Solid Dielectrics, 2004. ICSD 2004, Toulouse, France, 5–9 July 2004; pp. 320–323. [Google Scholar] [CrossRef]
- Ehsani, M.; Borsi, H.; Gockenbach, E.; Morshedian, J.; Bakhshandeh, G.R.; Shayegani, A.A. Effect of aging on dielectric behavior of outdoor polymeric insulators. In Proceedings of the 2004 IEEE International Conference on Solid Dielectrics, 2004. ICSD 2004, Toulouse, France, 5–9 July 2004; pp. 312–315. [Google Scholar] [CrossRef]
- IEC 60305:2021; Insulators for Overhead Lines with a Nominal Voltage above 1000 V—Ceramic or Glass Insulator Units for AC Systems—Characteristics of Insulator Units of the Cap and Pin Type. CEN-CENELEC Management Centre: Brussels, Belgium, 2021.
- IEC TS 60815-1:2008; Selection and Dimensioning of High-Voltage Insulators Intended for Use in Polluted Conditions—Part 1: Definitions, Information and General Principles. IEC: Geneva, Switzerland, 2008.
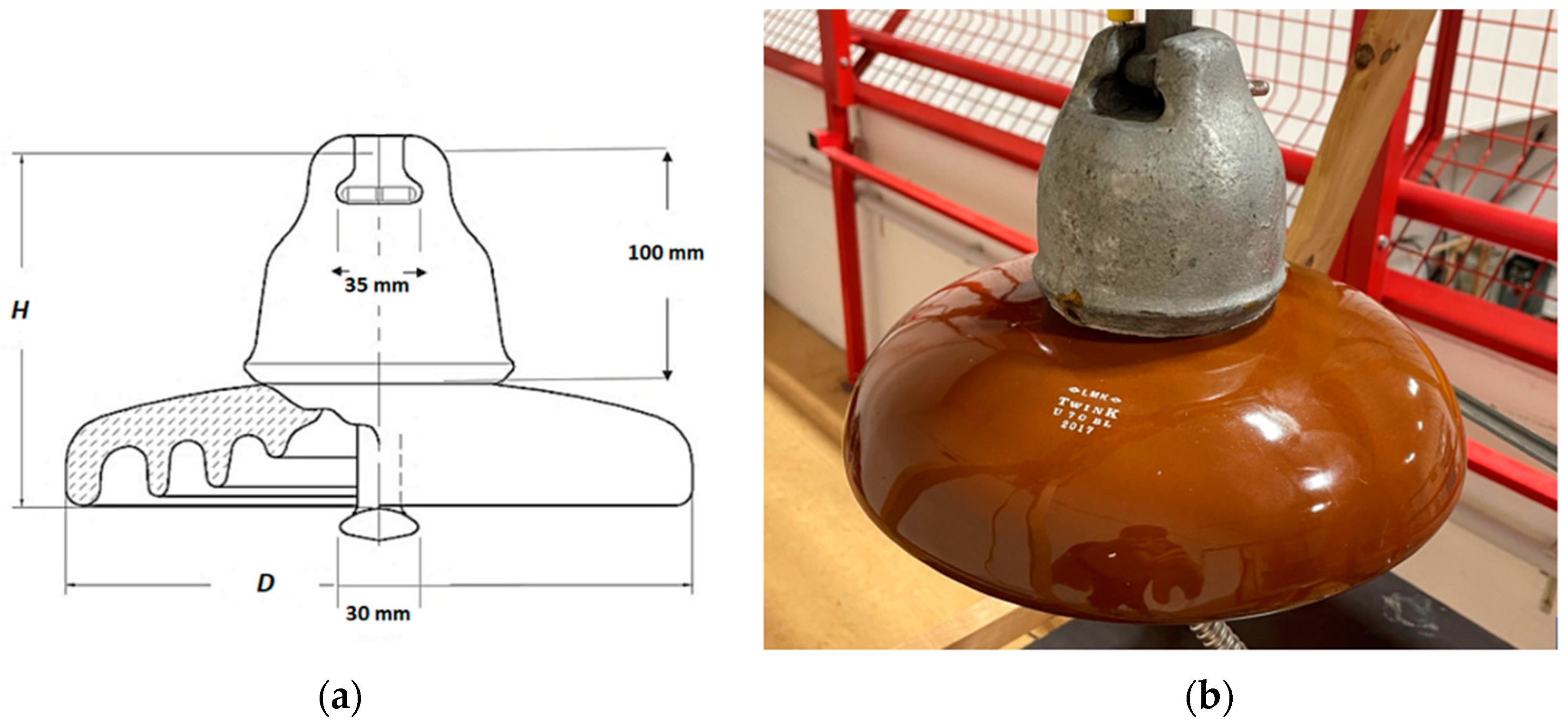
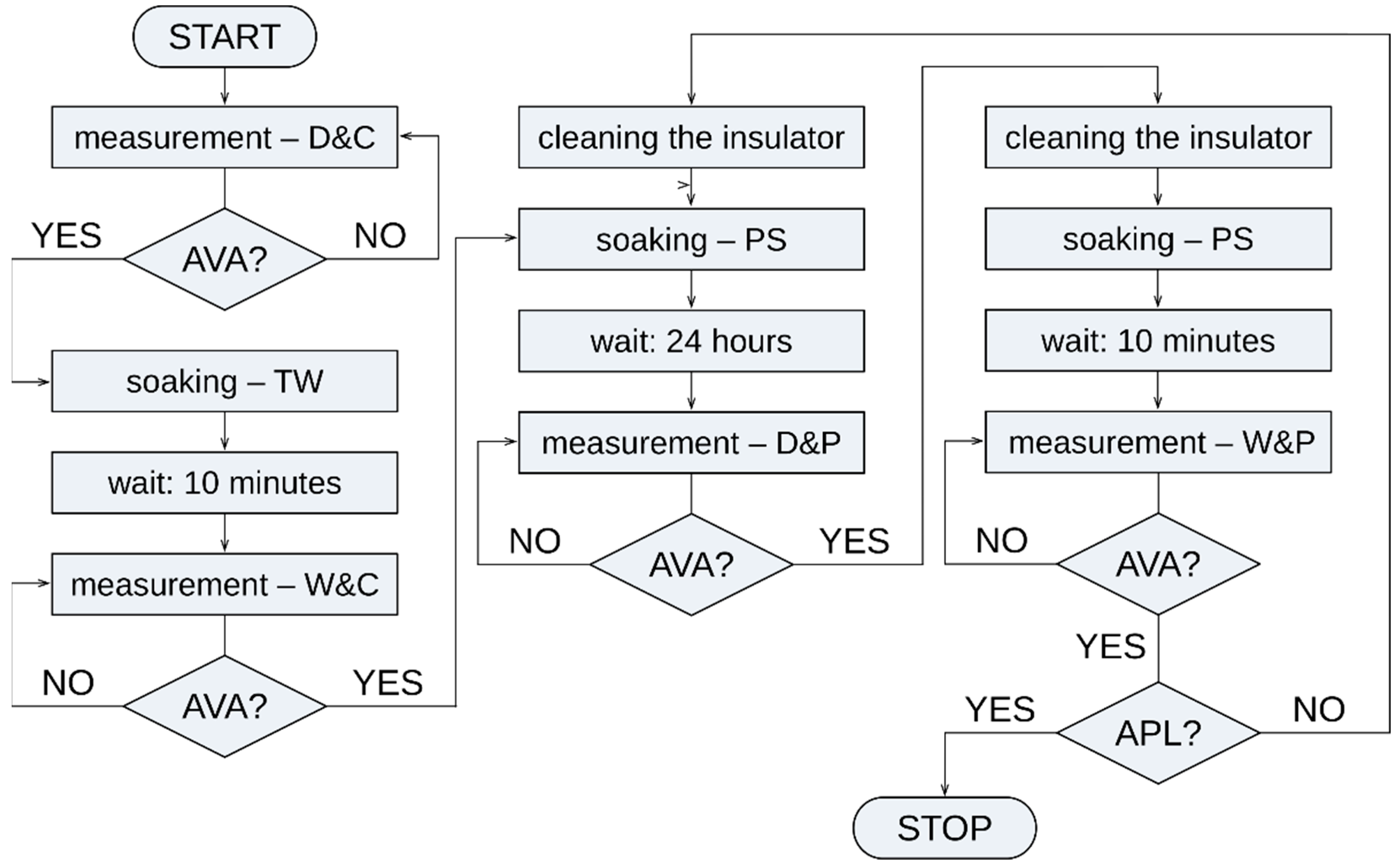




| Pollution Level | NaCl Amount (g/L) | Solution Conductivity (µS/cm) |
|---|---|---|
| L0 | 0 | 50 |
| L1 | 6 | 129 |
| L2 | 16 | 286 |
| Acronym | Acronym Meaning |
|---|---|
| AVA | All Voltages Applied |
| APL | All Pollution Levels |
| D&C | Dry and Clean |
| D&P | Dry and Polluted |
| W&C | Wet and Clean |
| W&P | Wet and Polluted |
| TW | Tap Water |
| PS | Polluting Solution |
| Pollution Level | Average Difference (%) | ||
|---|---|---|---|
| 5–7.5 kV | 5–10 kV | 7.5–10 kV | |
| L0 (dry) | 0.26 | 2.03 | 2.08 |
| L1 (dry) | 1.05 | 2.22 | 1.18 |
| L2 (dry) | 0.93 | 1.29 | 1.31 |
| L0 (wet) | 1.69 | 1.52 | 2.1 |
| L1 (wet) | 18.9 | 26.8 | 9.76 |
| L2 (wet) | 12.96 | 20.26 | 8.83 |
| Comparison | Average Difference (%) | ||
|---|---|---|---|
| Voltage 5 kV | Voltage 7.5 kV | Voltage 10 kV | |
| L1 (dry)—L1 (wet) | 38.7 | 49.8 | 54.2 |
| L2 (dry)—L2 (wet) | 33.8 | 41.1 | 47.0 |
| L1 (dry)—L2 (dry) | 25.1 | 25.0 | 23.7 |
| L1 (wet)—L2 (wet) | 21.3 | 15.8 | 14.5 |
| Pollution Level | Average Difference (%) | ||
|---|---|---|---|
| 5–7.5 kV | 5–10 kV | 7.5–10 kV | |
| L0 (dry) | 33.1 | 50.0 | 25.3 |
| L1 (dry) | 33.6 | 50.3 | 25.1 |
| L2 (dry) | 33.4 | 50.1 | 25.0 |
| L0 (wet) | 33.4 | 49.9 | 24.8 |
| L1 (wet) | 36.7 | 51.0 | 22.1 |
| L2 (wet) | 35.5 | 50.4 | 23.0 |
| Comparison | Average Difference (%) | ||
|---|---|---|---|
| Voltage 5 kV | Voltage 7.5 kV | Voltage 10 kV | |
| L1 (dry)—L1 (wet) | 5.7 | 9.9 | 7.1 |
| L2 (dry)—L2 (wet) | 7.08 | 9.8 | 7.8 |
| L1 (dry)—L2 (dry) | 2.07 | 1.48 | 1.33 |
| L1 (wet)—L2 (wet) | 2.15 | 2.97 | 1.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šárpataky, Ľ.; Dolník, B.; Zbojovský, J.; Schichler, U.; Pischler, O.; Schober, B. Sensing Method Using Dielectric Loss Factor to Evaluate Surface Conditions on Polluted Porcelain Insulator. Sensors 2022, 22, 9442. https://doi.org/10.3390/s22239442
Šárpataky Ľ, Dolník B, Zbojovský J, Schichler U, Pischler O, Schober B. Sensing Method Using Dielectric Loss Factor to Evaluate Surface Conditions on Polluted Porcelain Insulator. Sensors. 2022; 22(23):9442. https://doi.org/10.3390/s22239442
Chicago/Turabian StyleŠárpataky, Ľuboš, Bystrík Dolník, Ján Zbojovský, Uwe Schichler, Oliver Pischler, and Bernhard Schober. 2022. "Sensing Method Using Dielectric Loss Factor to Evaluate Surface Conditions on Polluted Porcelain Insulator" Sensors 22, no. 23: 9442. https://doi.org/10.3390/s22239442
APA StyleŠárpataky, Ľ., Dolník, B., Zbojovský, J., Schichler, U., Pischler, O., & Schober, B. (2022). Sensing Method Using Dielectric Loss Factor to Evaluate Surface Conditions on Polluted Porcelain Insulator. Sensors, 22(23), 9442. https://doi.org/10.3390/s22239442








