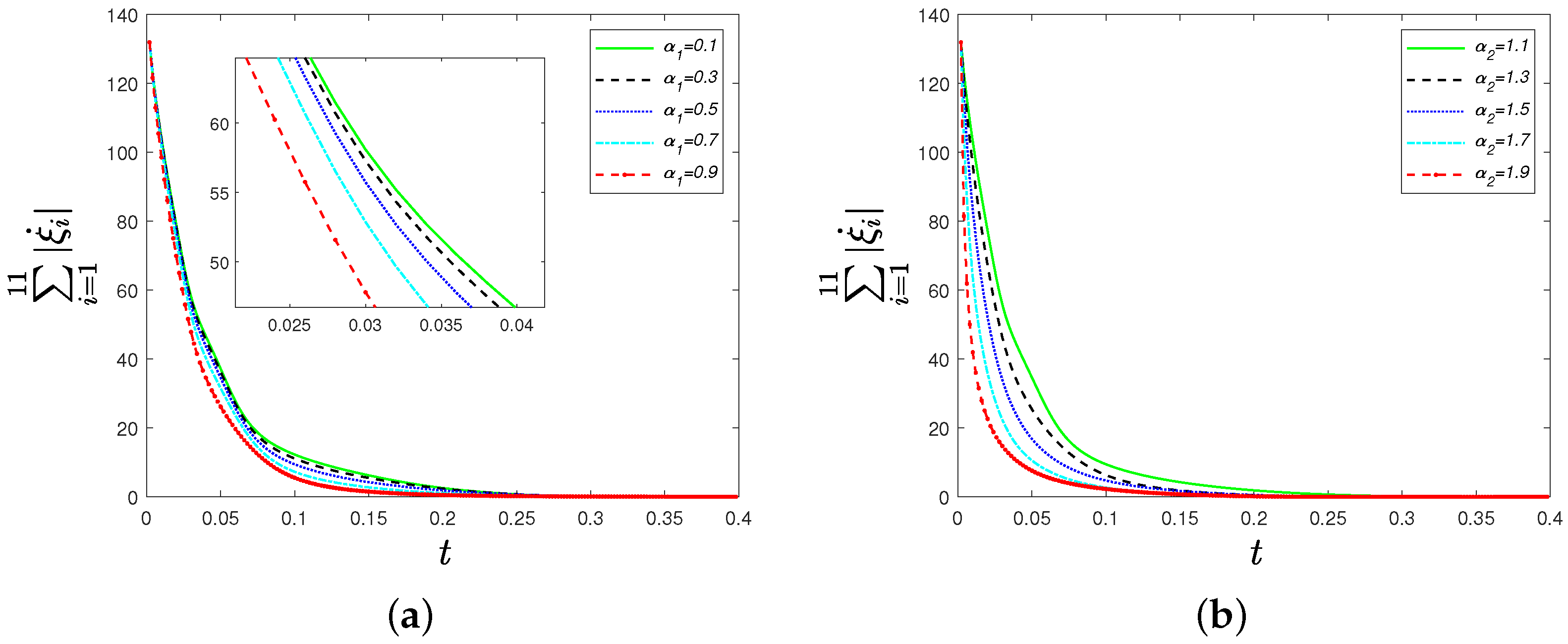Fixed-Time Synchronization of Coupled Oscillator Networks with a Pacemaker
Abstract
:1. Introduction
- Effective criteria are established to deal with fixed-time phase agreement and frequency synchronization for the Kuramoto–oscillator network with a pacemaker, and upper bounds of synchronization time are also provided;
- Compared with our previous results [29], synchronization can be achieved for arbitrary initial phases/ frequencies and the upper bounds of synchronization time are not affected by initial phases/ frequencies;
- The requirement on the connectivity of physical system is relaxed.
2. Model and Preliminaries
3. Fixed-Time Phase Agreement and Frequency Synchronization
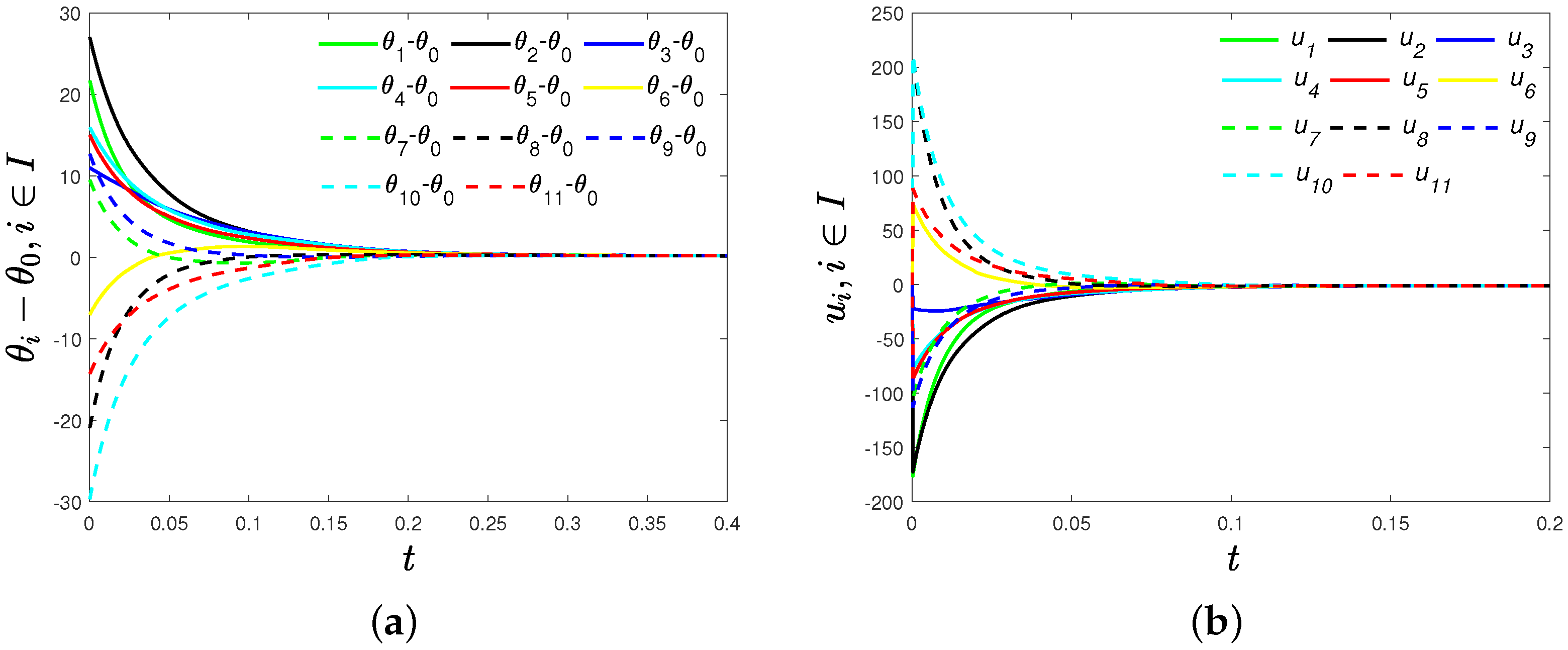
3.1. Fixed-Time Phase Agreement
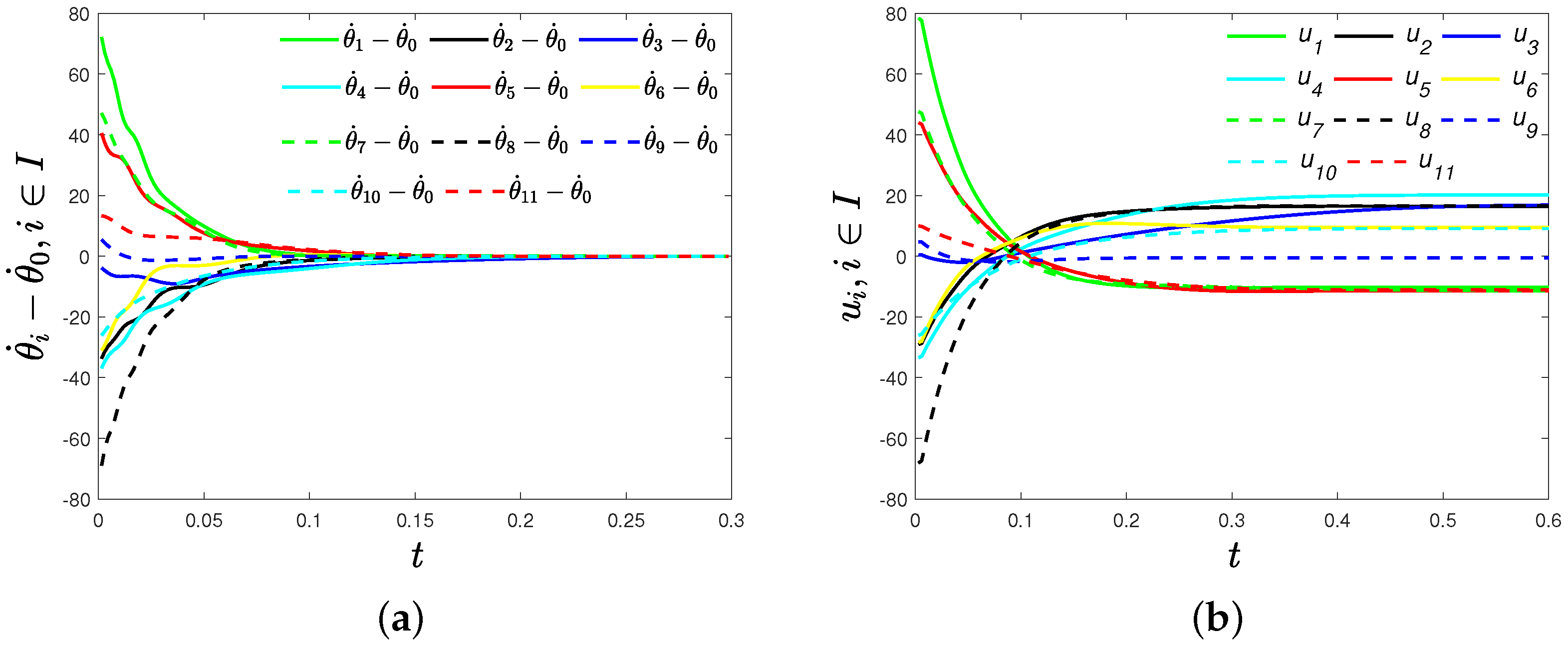
3.2. Fixed-Time Frequency Synchronization
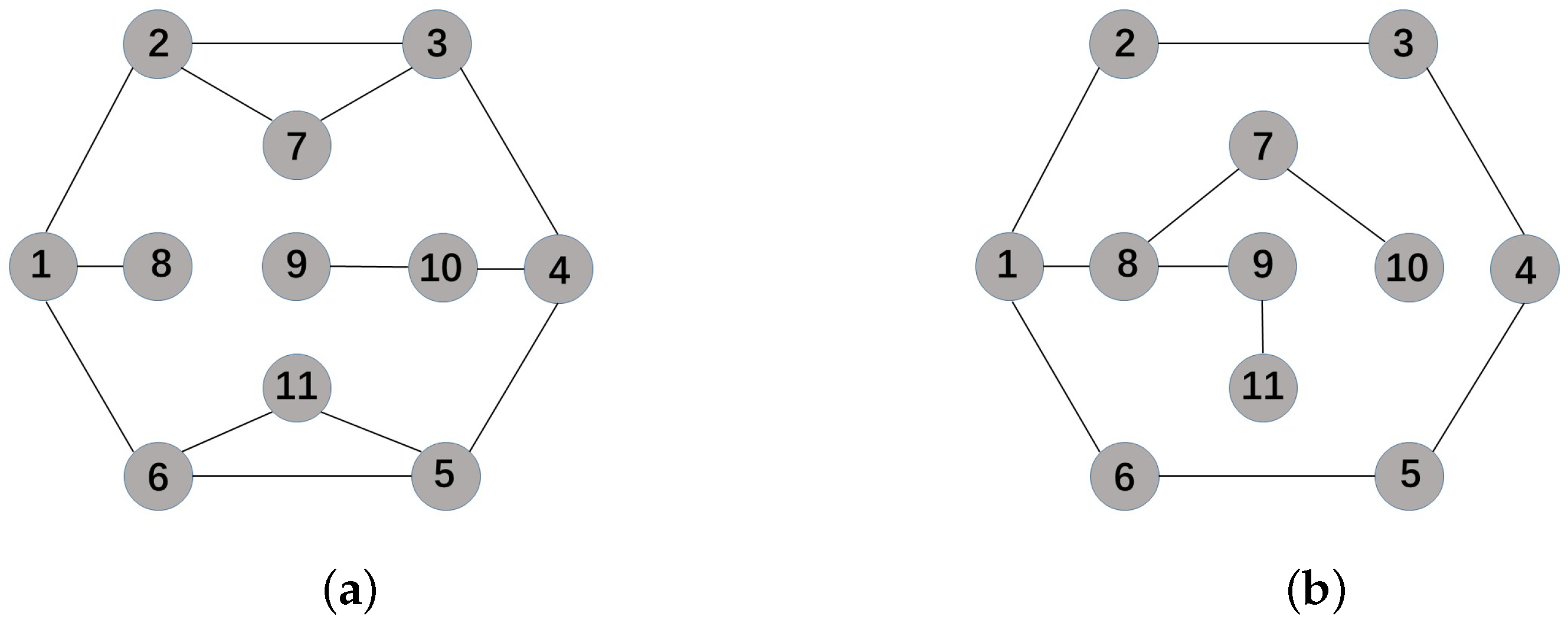
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Theorem 2
References
- Buck, J. Synchronous rhythmic flashing of fireflies. II. Q. Rev. Biol. 1988, 63, 265–289. [Google Scholar] [CrossRef]
- Walker, T.J. Acoustic synchrony: Two mechanisms in the snowy tree cricket. Science 1969, 166, 891–894. [Google Scholar] [CrossRef] [PubMed]
- Dörfler, F.; Chertkov, M.; Bullo, F. Synchronization in complex oscillator networks and smart grids. Proc. Natl. Acad. Sci. USA 2013, 110, 2005–2010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paley, D.A.; Leonard, N.E.; Sepulchre, R.; Grunbaum, D.; Parrish, J.K. Oscillator Models and Collective Motion. IEEE Control Syst. Mag. 2007, 27, 89–105. [Google Scholar]
- Seyboth, G.S.; Wu, J.H.; Qin, J.B.; Yu, C.B.; Allgöwer, F. Collective Circular Motion of Unicycle Type Vehicles with Nonidentical Constant Velocities. IEEE Trans. Control Netw. Syst. 2014, 1, 167–176. [Google Scholar] [CrossRef]
- Rao, P.C.; Li, X. Cooperative Formation of Self-Propelled Vehicles With Directed Communications. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 315–319. [Google Scholar] [CrossRef]
- Wiesenfeld, K.; Colet, P.; Strogatz, S.H. Frequency locking in Josephson arrays: Connection with the Kuramoto model. Phys. Rev. E 1998, 57, 1563–1569. [Google Scholar] [CrossRef] [Green Version]
- Néda, Z.; Ravasz, E.; Brechet, Y.; Vicsek, T.; Barabási, A.-L. Self-organizing processes: The sound of many hands clapping. Nature 2000, 403, 6772. [Google Scholar] [CrossRef] [Green Version]
- Acebrón, J.A.; Bonilla, L.L.; Pérez Vicente, C.J.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77, 137–185. [Google Scholar] [CrossRef] [Green Version]
- Childs, L.M.; Strogatz, S.H. Stability diagram for the forced Kuramoto model. Chaos: Interdiscip. J. Nonlinear Sci. 2008, 18, 043128. [Google Scholar] [CrossRef] [Green Version]
- Jadbabaie, A.; Motee, N.; Barahona, M. On the stability of the Kuramoto model of coupled nonlinear oscillators. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Chopra, N.; Spong, M.W. On exponential synchronization of Kuramoto oscillators. IEEE Trans. Autom. Control 2009, 54, 353–357. [Google Scholar] [CrossRef]
- Kopetz, H.; Ochsenreiter, W. Clock synchronization in distributed real-time systems. IEEE Trans. Comput. 1987, 36, 933–940. [Google Scholar] [CrossRef]
- Li, X.; Rao, P.C. Synchronizing a weighted and weakly-connected Kuramoto oscillator digraph with a pacemaker. IEEE Trans. Circuits Syst. Regul. Pap. 2015, 62, 899–905. [Google Scholar] [CrossRef]
- Rao, P.C.; Li, X.; Ogorzalek, M.J. Stability of synchronous solutions in a directed Kuramoto-Oscillator network with a pacemaker. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 1222–1226. [Google Scholar] [CrossRef]
- Tong, D.B.; Rao, P.C.; Chen, Q.Y.; Ogorzalek, M.J.; Li, X. Exponential synchronization and phase locking of a multilayer Kuramoto–oscillator system with a pacemaker. Neurocomputing 2018, 308, 129–137. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Doyle, F.J. Exponential synchronization rate of Kuramoto oscillators in the presence of a pacemaker. IEEE Trans. Autom. Control. 2013, 58, 989–994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Derler, P.; Lee, E.A.; Vincentelli, A.S. Modeling cyber-physical systems. Proc. IEEE 2011, 100, 13–28. [Google Scholar] [CrossRef]
- Lee, E.A. Computing Foundations and Practice for Cyber-Physical Systems: A Preliminary Report; Technical Report No. UCB/EECS-2007-72; Electrical Engineering Computer Sciences, University of California: Berkeley, CA, USA, 2007. [Google Scholar]
- Zhang, W.-Y.; Yang, C.; Guan, Z.-H.; Liu, Z.-W.; Chi, M.; Zheng, G.-L. Bounded synchronization of coupled Kuramoto oscillators with phase lags via distributed impulsive control. Neurocomputing 2016, 218, 216–222. [Google Scholar] [CrossRef]
- Rao, P.C.; Li, X. Pacemaker-Based Global Synchronization of Kuramoto Oscillators via Distributed Control. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1768–1772. [Google Scholar] [CrossRef]
- Shi, Y.-J.; Ma, Y. Finite/fixed-time synchronization for complex networks via quantized adaptive control. Electron. Res. Arch. 2021, 29, 2047–2061. [Google Scholar] [CrossRef]
- Aouiti, C.; Assali, E.A. Finite-time and fixed-time synchronization of inertial neural networks with mixed delays. J. Syst. Sci. Complex. 2021, 34, 206–235. [Google Scholar]
- Jiang, S.Q.; Qi, Y.K.; Cai, S.M.; Lu, X.B. Light fixed-time control for cluster synchronization of complex networks. Neurocomputing 2020, 424, 63–70. [Google Scholar] [CrossRef]
- Zhang, W.L.; Li, H.F.; Li, C.D.; Li, Z.B.; Yang, X.S. Fixed-time synchronization criteria for complex networks via quantized pinning control. ISA Trans. 2019, 91, 151–156. [Google Scholar] [CrossRef]
- Zheng, C.C.; Hu, C.; Yu, J.; Jiang, H.J. Fixed-time synchronization of discontinuous competitive neural networks with time-varying delays. Neural Netw. 2022, 153, 192–203. [Google Scholar] [CrossRef]
- Wu, J.; Li, X. Finite-Time and Fixed-Time Synchronization of Kuramoto-Oscillator Network with Multiplex Control. IEEE Trans. Control Netw. Syst. 2019, 6, 863–873. [Google Scholar] [CrossRef]
- Dong, J.-G.; Xue, X.P. Finite-time synchronization of Kuramoto-type oscillators. Nonlinear Anal. Real World Appl. 2015, 26, 133–149. [Google Scholar] [CrossRef]
- Rao, P.C.; Guo, X.F. Finite-time synchronization of Kuramoto–oscillator networks with a pacemaker based on cyber-physical system. Front. Phys. 2022, in press. [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef] [Green Version]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Rao, P.; Wu, Z. Fixed-Time Synchronization of Coupled Oscillator Networks with a Pacemaker. Sensors 2022, 22, 9460. https://doi.org/10.3390/s22239460
Guo X, Rao P, Wu Z. Fixed-Time Synchronization of Coupled Oscillator Networks with a Pacemaker. Sensors. 2022; 22(23):9460. https://doi.org/10.3390/s22239460
Chicago/Turabian StyleGuo, Xiufeng, Pengchun Rao, and Zhaoyan Wu. 2022. "Fixed-Time Synchronization of Coupled Oscillator Networks with a Pacemaker" Sensors 22, no. 23: 9460. https://doi.org/10.3390/s22239460
APA StyleGuo, X., Rao, P., & Wu, Z. (2022). Fixed-Time Synchronization of Coupled Oscillator Networks with a Pacemaker. Sensors, 22(23), 9460. https://doi.org/10.3390/s22239460