Design and Research of Chromatic Confocal System for Parallel Non-Coaxial Illumination Based on Optical Fiber Bundle
Abstract
1. Introduction
2. Principles of Parallel Chromatic Confocal System with Non-Coaxial Illumination
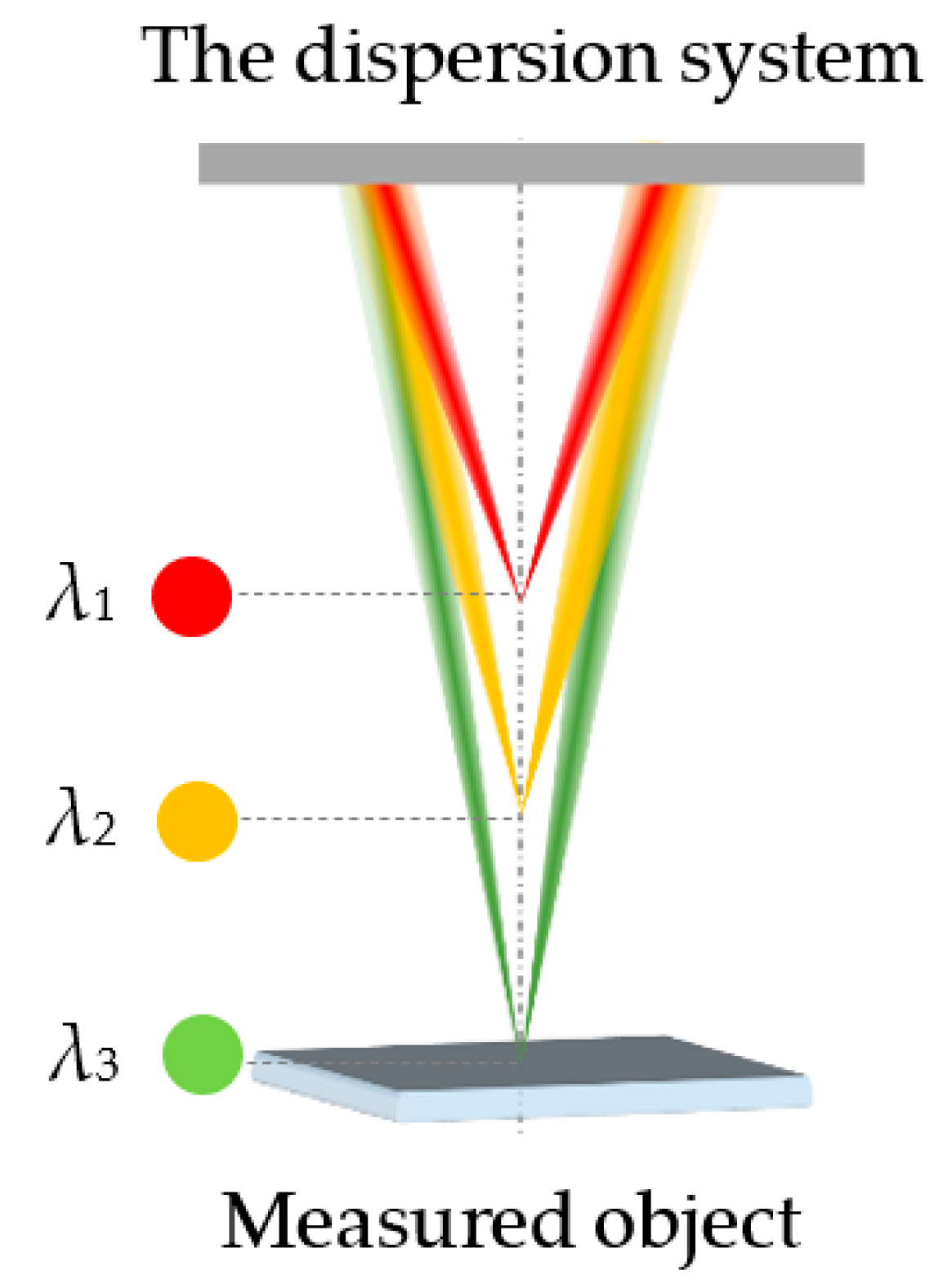
2.1. Principle of Dispersion
2.2. Principle of Single-Point Chromatic Confocal System with Non-Coaxial Illumination
2.3. Principle of the Optical Fiber Bundle
2.4. Principle of Parallel Chromatic Confocal System with Non-Coaxial Illumination
2.5. Principle of the Color-Conversion Algorithm
3. Experiments
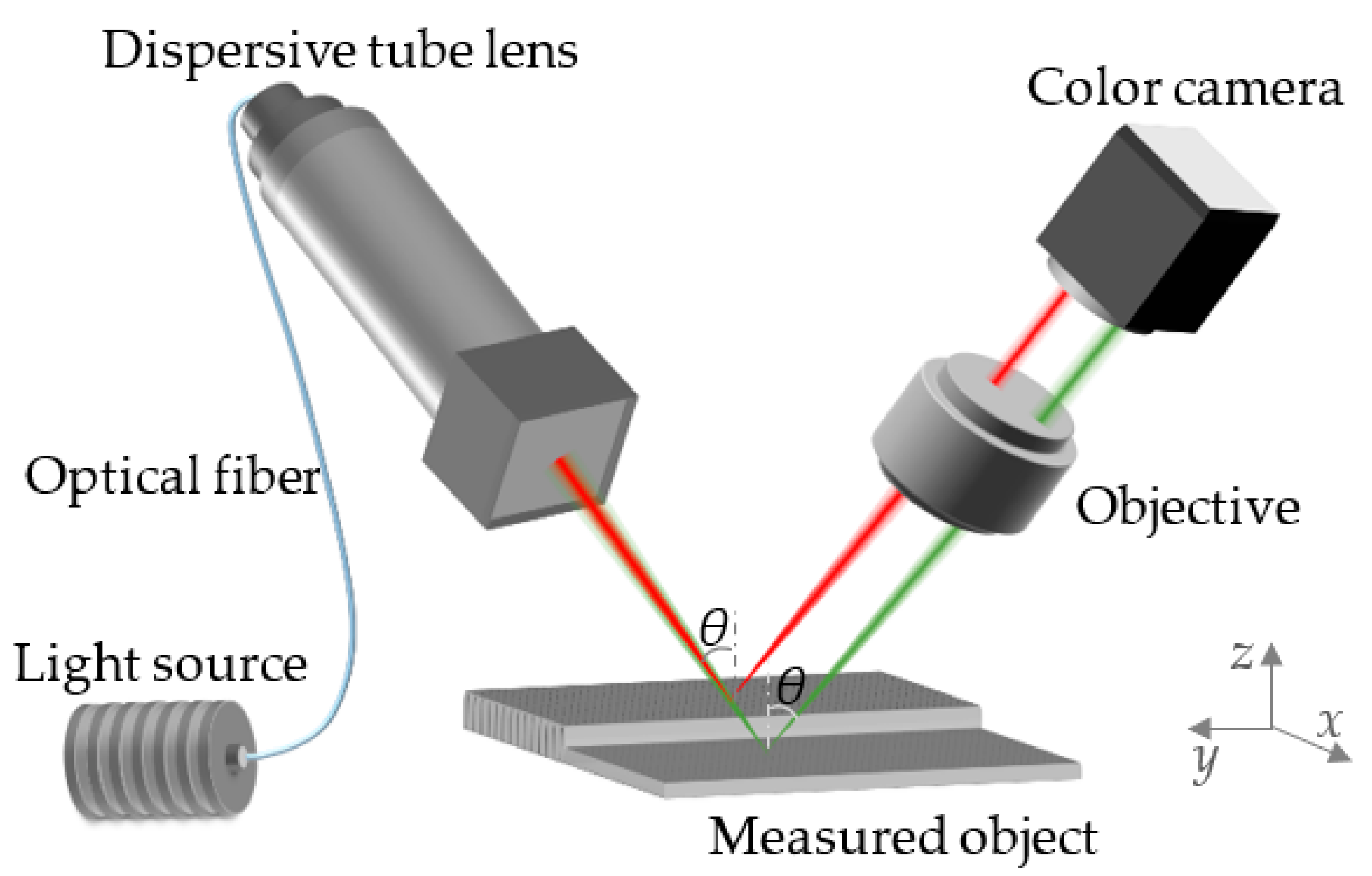
3.1. Construction of the Measurement System
3.2. Calibration Experiment
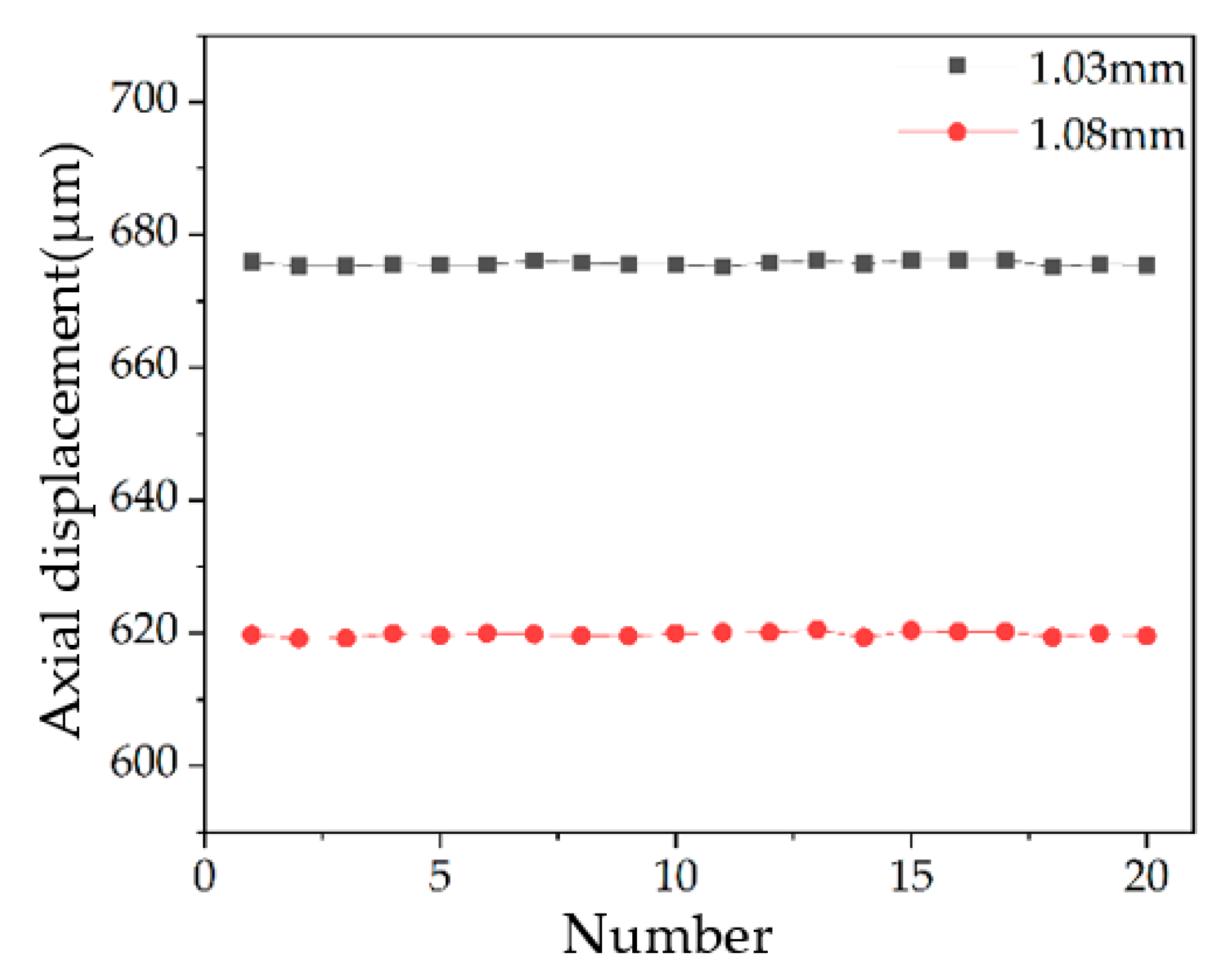
3.3. Measurement of Step Height
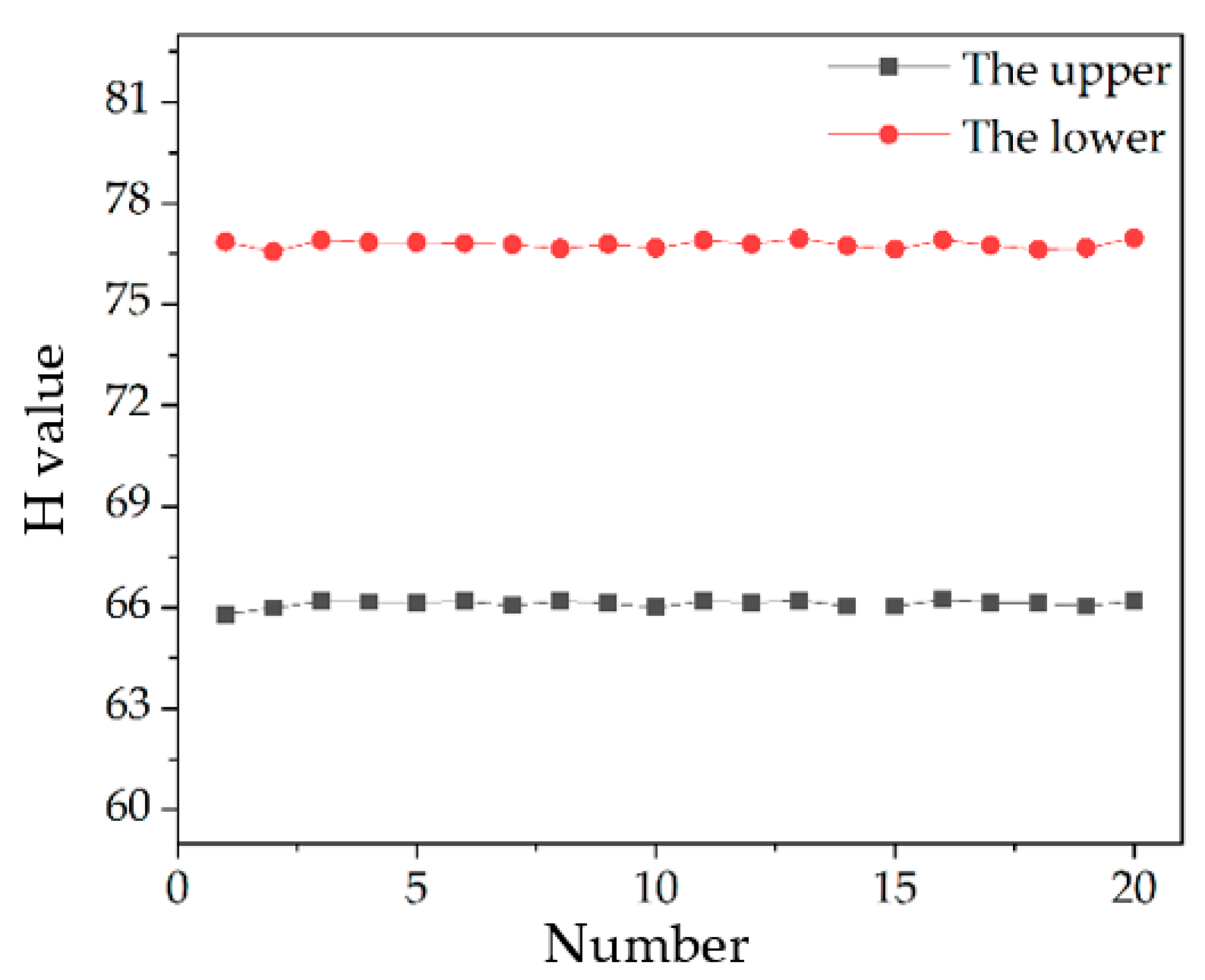
3.4. Measurement of Transparent Specimen Thickness
3.5. Three-Dimensional Topography by Line-Scanning Method
3.6. Contrast Experiment
4. Discussion
- (1)
- By the related theoretical analysis of the non-coaxial-illumination system and the properties of the optical fiber bundle, it is proved that the optical fiber bundle can be applied in the chromatic confocal system. Based on this, the existing single-point non-coaxial-illumination system is optimized using the optical fiber bundle as the light-beam splitter to realize parallel measurements, and this optimization can improve the measurement efficiency of the single-point system.
- (2)
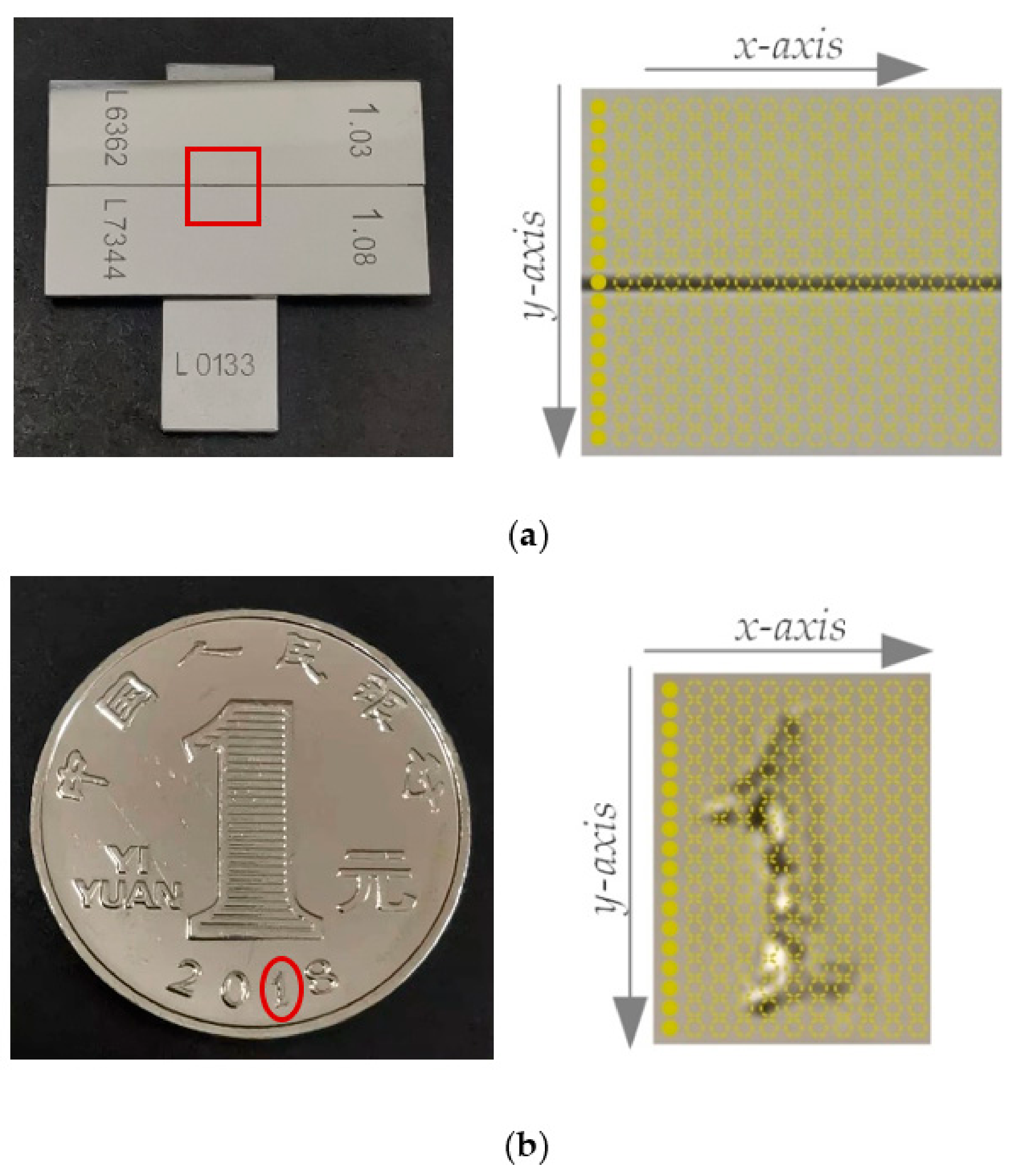
- Combined with the color-conversion algorithm, the conclusion of (1) is verified by corresponding step height measurement, transparent specimen thickness measurement and three-dimensional topography restoration. Three-dimensional topography includes the restoration of the step and character “1” of the coin.
- (3)
- The experimental results show that the measuring range of the system is 200 μm, the repeatability is better than 0.87 μm, the relative error is less than ±4% and the measurement accuracy can reach micron level. Additionally, the measurement efficiency of the proposed system is 18 times higher than that of the single-point non-coaxial-illumination system.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Behrends, G.; Stöbener, D.; Fischer, A. Integrated, Speckle-Based Displacement Measurement for Lateral Scanning White Light Interferometry. Sensors 2021, 21, 2486. [Google Scholar] [CrossRef]
- Im, J.; Kim, H.; Park, W.; Ahn, J.S.; Lee, B.; Choi, S. High-precision white light interferometry based on a color CCD and peak matching algorithm. J. Korean Phys. Soc. 2022, 80, 599–605. [Google Scholar] [CrossRef]
- Pillarz, M.; von Freyberg, A.; Stöbener, D.; Fischer, A. Gear shape measurement potential of laser triangulation and confocal-chromatic distance sensors. Sensors 2021, 21, 937. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Wang, S.; Bai, J.; Zhang, J.; Huang, J.; Zhou, X.; Liu, D.; Liu, C. Confocal laser scanning and 3D reconstruction methods for the subsurface damage of polished optics. Opt. Laser Eng. 2021, 136, 106315. [Google Scholar] [CrossRef]
- Ren, H.; Liu, Y.; Wang, Y.; Liu, N.; Yu, X.; Su, X. Uniaxial 3D Measurement with Auto-Synchronous Phase-Shifting and Defocusing Based on a Tilted Grating. Sensors 2021, 21, 3730. [Google Scholar] [CrossRef] [PubMed]
- Iwasa, T.; Ota, K.; Harada, T.; Muramatsu, R. High-resolution surface shape measurement of parabola antenna reflector by using grating projection method with virtual targets. Acta Astronaut. 2018, 153, 95–108. [Google Scholar] [CrossRef]
- Choi, Y.; Yoo, H.; Kang, D. Large-area thickness measurement of transparent multi-layer films based on laser confocal reflection sensor. Measurement 2020, 153, 107390. [Google Scholar] [CrossRef]
- Vasilev, E.; Wang, J.; Knezevic, M. A structure metric for quantitative assessment of fracture surfaces in 3D conceived based on confocal laser scanning microscopy data. Mater. Charact. 2022, 194, 112369. [Google Scholar] [CrossRef]
- Quinten, M. Thickness Determination of Transparent Coatings: Considering a correction factor, chromatic confocal sensors can easily be used to determine the thickness of a transparent workpiece. PhotonicsViews 2019, 16, 68–71. [Google Scholar] [CrossRef]
- Lu, W.; Chen, C.; Wang, J.; Leach, R.; Zhang, C.; Liu, X.; Lei, Z.; Yang, W.; Jiang, X.J. Characterization of the displacement response in chromatic confocal microscopy with a hybrid radial basis function network. Opt. Express 2019, 27, 22737–22752. [Google Scholar] [CrossRef]
- Fu, S.; Kor, W.S.; Cheng, F.; Seah, L.K. In-situ measurement of surface roughness using chromatic confocal sensor. Procedia CIRP 2020, 94, 780–784. [Google Scholar] [CrossRef]
- Claus, D.; Nizami, M.R. Influence of aberrations and roughness on the chromatic confocal signal based on experiments and wave-optical modeling. Surf. Topogr. Metrol. Prop. 2020, 8, 025031. [Google Scholar] [CrossRef]
- Du, H.; Zhang, W.; Ju, B.; Sun, Z.; Sun, A. A new method for detecting surface defects on curved reflective optics using normalized reflectivity. Rev. Sci. Instrum. 2020, 91, 036103. [Google Scholar] [CrossRef] [PubMed]
- Chouhad, H.; El Mansori, M.; Knoblauch, R.; Corleto, C. Smart data driven defect detection method for surface quality control in manufacturing. Meas. Sci. Technol. 2021, 32, 105403. [Google Scholar] [CrossRef]
- Chun, B.S.; Kim, K.; Gweon, D. Three-dimensional surface profile measurement using a beam scanning chromatic confocal microscope. Rev. Sci. Instrum. 2009, 80, 073706. [Google Scholar] [CrossRef]
- Wertjanz, D.; Kern, T.; Csencsics, E.; Stadler, G.; Schitter, G. Compact scanning confocal chromatic sensor enabling precision 3-D measurements. Appl. Opt. 2021, 60, 7511–7517. [Google Scholar] [CrossRef]
- Yu, Q.; Yu, X.F.; Cui, C.; Ye, R. Survey of parallel light source technology in parallel confocal measurement. Chin. Opt. 2013, 6, 652–659. [Google Scholar]
- Grant, D.M.; McGinty, J.; McGhee, E.J.; Bunney, T.D.; Owen, D.M.; Talbot, C.B.; Zhang, W.; Kumar, S.; Munro, I.; Lanigan, P. High speed optically sectioned fluorescence lifetime imaging permits study of live cell signaling events. Opt. Express 2007, 15, 15656–15673. [Google Scholar] [CrossRef]
- Kagawa, K.; Seo, M.; Yasutomi, K.; Terakawa, S.; Kawahito, S. Multi-beam confocal microscopy based on a custom image sensor with focal-plane pinhole array effect. Opt. Express 2013, 21, 1417–1429. [Google Scholar] [CrossRef]
- Tiziani, H.J.; Achi, R.; Krämer, R.N.; Wiegers, L. Theoretical analysis of confocal microscopy with microlenses. Appl. Opt. 1996, 35, 120–125. [Google Scholar] [CrossRef]
- Lane, P.M.; Dlugan, A.L.; Richards-Kortum, R.; MacAulay, C.E. Fiber-optic confocal microscopy using a spatial light modulator. Opt. Lett. 2000, 25, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Hou, W.; Zhang, Y. Fast parallel 3D profilometer with DMD technology. In Proceedings of the Seventh International Symposium on Precision Engineering Measurements and Instrumentation, Yunnan, China, 7–11 August 2011; Volume 8321, pp. 155–161. [Google Scholar]
- Tiziani, H.J.; Uhde, H. Three-dimensional image sensing by chromatic confocal microscopy. Appl. Opt. 1994, 33, 1838–1843. [Google Scholar] [CrossRef] [PubMed]
- Tiziani, H.J.; Wegner, M.; Steudle, D. Confocal principle for macro-and microscopic surface and defect analysis. Opt. Eng. 2000, 39, 32–39. [Google Scholar] [CrossRef]
- Hillenbrand, M.; Lorenz, L.; Kleindienst, R.; Grewe, A.; Sinzinger, S. Spectrally multiplexed chromatic confocal multipoint sensing. Opt. Lett. 2013, 38, 4694–4697. [Google Scholar] [CrossRef]
- Hillenbrand, M.; Weiss, R.; Endrödy, C.; Grewe, A.; Hoffmann, M.; Sinzinger, S. Chromatic confocal matrix sensor with actuated pinhole arrays. Appl. Opt. 2015, 54, 4927–4936. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Mei, S.; Fan, L.; Wang, H. A line-scanning chromatic confocal sensor for three-dimensional profile measurement on highly reflective materials. Rev. Sci. Instrum. 2021, 92, 053707. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, Y.; Zhang, Y.; Cheng, F.; Shang, W.; Wang, Y. A novel chromatic confocal one-shot 3D measurement system based on DMD. Measurement 2021, 186, 110140. [Google Scholar] [CrossRef]
- Berkovic, G.; Zilberman, S.; Shafir, E.; Rubin, D. Chromatic confocal displacement sensing at oblique incidence angles. Appl. Opt. 2020, 59, 3183–3186. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, Y.; Shang, W.; Dong, S.; Wang, C.; Wang, Y.; Liu, T.; Cheng, F. Thickness measurement for glass slides based on chromatic confocal microscopy with inclined illumination. Photonics 2021, 8, 170. [Google Scholar] [CrossRef]













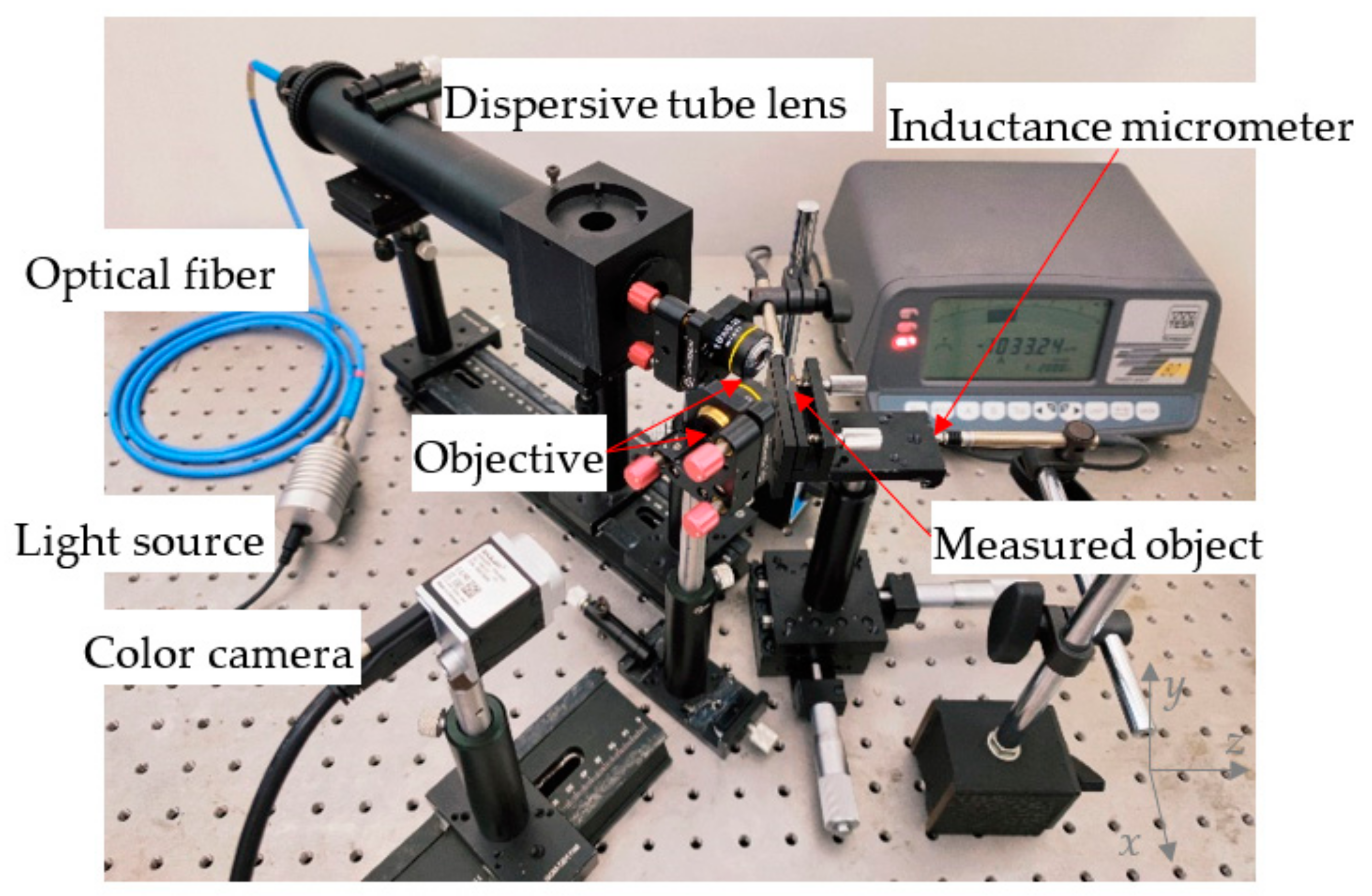

| Components | Manufacturer | Function |
|---|---|---|
| White-light source | Yousheng, (MT-G2 Easy White LED) | Produce polychromatic light source |
| Optical fiber bundle | Yousheng, (Custom-made) | Divide a light beam into several beams |
| Dispersive tube lens | Self-built | Produce chromatic dispersion |
| Objective | Motic, (Magnification:10×; N.A value:0.1) | Focus on the light |
| Platform | Daheng Optics, (GCM-T25MC) | Adjust and provide displacement |
| Gauge block | WD, (32 pieces of level 0) | As the measured object |
| Transparent specimen | Sail brand | As the measured object |
| Inductance micrometer | Tesa, (TT80) | Measure displacement value and true value |
| Color camera | Basler, (a2A5320-23ucBAS) | Capture color images |
| Number | Axial Displacement (μm) | H Value |
|---|---|---|
| 1 | 0 | 26.93 |
| 2 | 50 | 28.58 |
| 3 | 100 | 30.46 |
| 4 | 150 | 32.88 |
| 5 | 200 | 35.89 |
| 6 | 250 | 39.57 |
| 7 | 300 | 44.24 |
| 8 | 350 | 49.94 |
| 9 | 400 | 56.56 |
| 10 | 450 | 65.47 |
| 11 | 500 | 76.23 |
| 12 | 550 | 86.36 |
| 13 | 600 | 93.12 |
| 14 | 650 | 97.70 |
| 15 | 700 | 101.27 |
| 16 | 750 | 104.63 |
| 17 | 800 | 107.28 |
| 18 | 850 | 109.58 |
| 19 | 900 | 112.03 |
| 20 | 950 | 115.20 |
| Number | H Value of Block 1 | Displacement of Block 1 (μm) | H Value of Block 2 | Displacement of Block 2 (μm) | Height of Difference (μm) |
|---|---|---|---|---|---|
| 1 | 89.91 | 675.85 | 79.31 | 619.78 | 56.07 |
| 2 | 89.80 | 675.27 | 79.20 | 619.20 | 56.07 |
| 3 | 89.80 | 675.27 | 79.21 | 619.25 | 56.02 |
| 4 | 89.85 | 675.54 | 79.34 | 619.94 | 55.60 |
| 5 | 89.84 | 675.48 | 79.28 | 619.62 | 55.86 |
| 6 | 89.83 | 675.43 | 79.35 | 619.99 | 55.44 |
| 7 | 89.96 | 676.12 | 79.32 | 619.83 | 56.29 |
| 8 | 89.89 | 675.75 | 79.28 | 619.62 | 56.13 |
| 9 | 89.85 | 675.54 | 79.26 | 619.52 | 56.02 |
| 10 | 89.84 | 675.48 | 79.34 | 619.94 | 55.54 |
| 11 | 89.79 | 675.22 | 79.37 | 620.10 | 55.12 |
| 12 | 89.89 | 675.75 | 79.37 | 620.10 | 55.65 |
| 13 | 89.96 | 676.12 | 79.45 | 620.52 | 55.60 |
| 14 | 89.87 | 675.64 | 79.23 | 619.36 | 56.28 |
| 15 | 89.98 | 676.22 | 79.43 | 620.41 | 55.81 |
| 16 | 89.97 | 676.17 | 79.39 | 620.20 | 55.97 |
| 17 | 89.98 | 676.22 | 79.40 | 620.26 | 55.96 |
| 18 | 89.78 | 675.17 | 79.24 | 619.41 | 55.76 |
| 19 | 89.86 | 675.59 | 79.33 | 619.89 | 55.70 |
| 20 | 89.83 | 675.43 | 79.27 | 619.57 | 55.86 |
| The average value of the step (μm) | 55.84 | ||||
| The difference from the true value (μm) | −2.03 | ||||
| Relative error | −3.51% | ||||
| The standard deviation σ of the step (μm) | 0.29 | ||||
| Number | H Value of Upper | H Value of Lower | H Value of the Difference |
|---|---|---|---|
| 1 | 65.80 | 76.86 | 11.06 |
| 2 | 65.99 | 76.57 | 10.58 |
| 3 | 66.19 | 76.91 | 10.72 |
| 4 | 66.17 | 76.84 | 10.67 |
| 5 | 66.15 | 76.84 | 10.69 |
| 6 | 66.19 | 76.81 | 10.62 |
| 7 | 66.06 | 76.78 | 10.72 |
| 8 | 66.19 | 76.65 | 10.46 |
| 9 | 66.14 | 76.79 | 10.65 |
| 10 | 66.00 | 76.68 | 10.68 |
| 11 | 66.20 | 76.90 | 10.70 |
| 12 | 66.15 | 76.79 | 10.64 |
| 13 | 66.21 | 76.95 | 10.74 |
| 14 | 66.05 | 76.74 | 10.69 |
| 15 | 66.05 | 76.64 | 10.59 |
| 16 | 66.23 | 76.91 | 10.68 |
| 17 | 66.16 | 76.75 | 10.59 |
| 18 | 66.13 | 76.63 | 10.50 |
| 19 | 66.05 | 76.68 | 10.63 |
| 20 | 66.20 | 76.97 | 10.77 |
| The average H value of the difference | 10.67 | ||
| The thickness value of the transparent specimen(μm) | 177.58 | ||
| The difference from the true value(μm) | −6.5 | ||
| Relative error | −3.53% | ||
| The standard deviation σ of the difference(μm) | 0.12 | ||
| Experiment Type | Experiment Results | Our System | The Comparative System |
|---|---|---|---|
| Calibration experiment | Calibration equation | ||
| Measuring range (μm) | 200 | 400 | |
| Linear correlation coefficient | >0.99 | >0.99 | |
| Measurement of transparent specimen thickness | Measured thickness value (μm) | 177.58 | 176.00 |
| Relative error | −3.53% | −4.39% | |
| Standard deviation σ (μm) | 0.12 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yu, Q.; Wang, C.; Zhang, Y.; Cheng, F.; Wang, Y.; Lin, T.; Liu, T.; Xi, L. Design and Research of Chromatic Confocal System for Parallel Non-Coaxial Illumination Based on Optical Fiber Bundle. Sensors 2022, 22, 9596. https://doi.org/10.3390/s22249596
Zhang Y, Yu Q, Wang C, Zhang Y, Cheng F, Wang Y, Lin T, Liu T, Xi L. Design and Research of Chromatic Confocal System for Parallel Non-Coaxial Illumination Based on Optical Fiber Bundle. Sensors. 2022; 22(24):9596. https://doi.org/10.3390/s22249596
Chicago/Turabian StyleZhang, Yali, Qing Yu, Chong Wang, Yaozu Zhang, Fang Cheng, Yin Wang, Tianliang Lin, Ting Liu, and Lin Xi. 2022. "Design and Research of Chromatic Confocal System for Parallel Non-Coaxial Illumination Based on Optical Fiber Bundle" Sensors 22, no. 24: 9596. https://doi.org/10.3390/s22249596
APA StyleZhang, Y., Yu, Q., Wang, C., Zhang, Y., Cheng, F., Wang, Y., Lin, T., Liu, T., & Xi, L. (2022). Design and Research of Chromatic Confocal System for Parallel Non-Coaxial Illumination Based on Optical Fiber Bundle. Sensors, 22(24), 9596. https://doi.org/10.3390/s22249596







