Landmark-Based Scale Estimation and Correction of Visual Inertial Odometry for VTOL UAVs in a GPS-Denied Environment
Abstract
1. Introduction
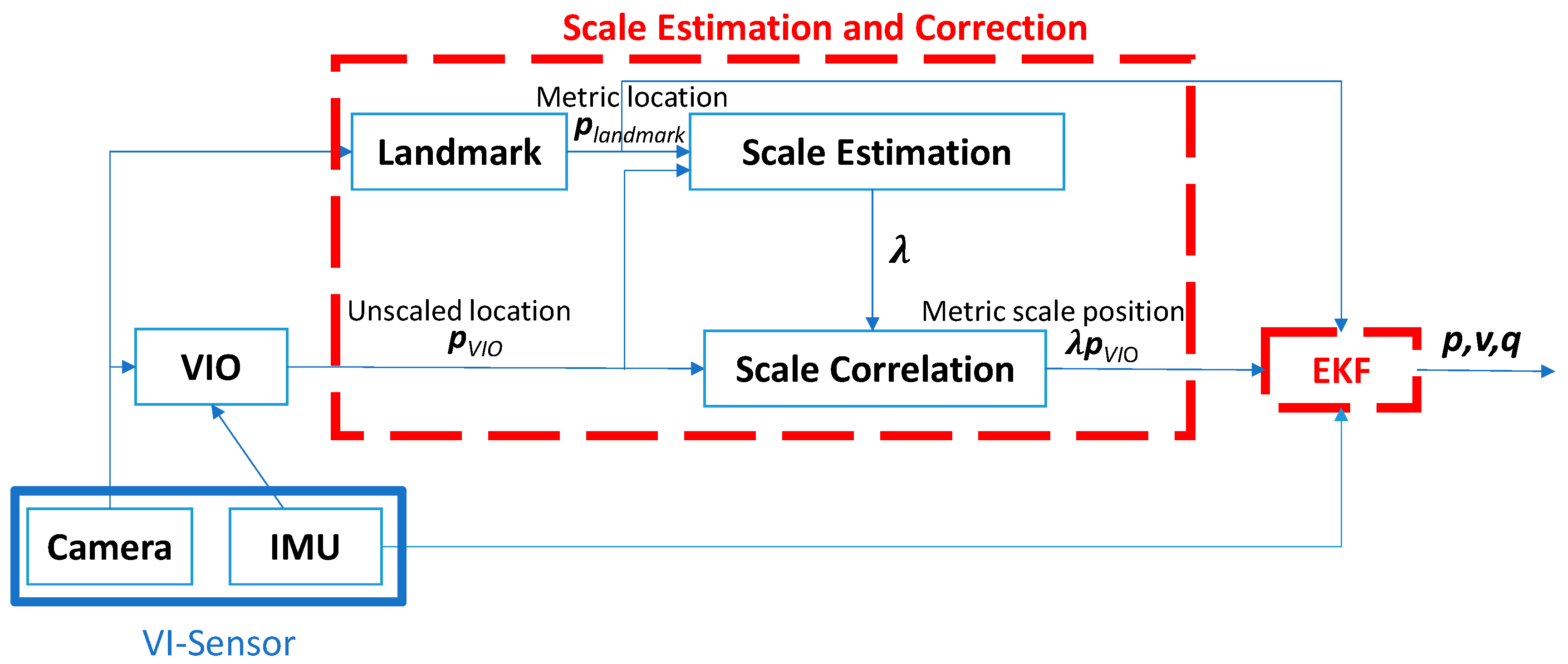
2. Scale Estimation and Correction with a Landmark Assistant
2.1. Flow Chart of the Proposed Approach
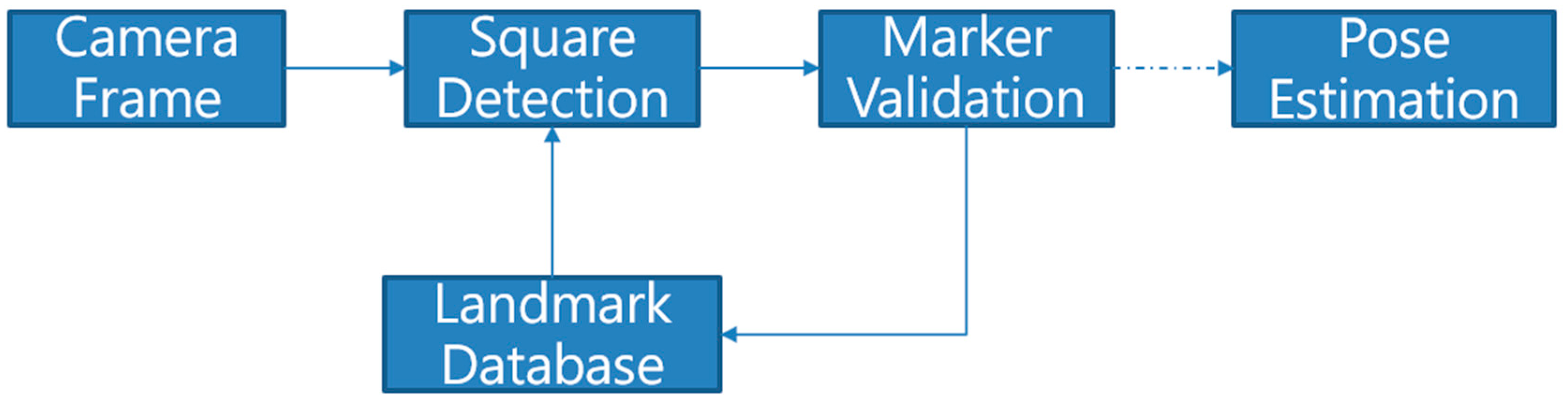
2.2. Coordinate Systems and Landmark Detection
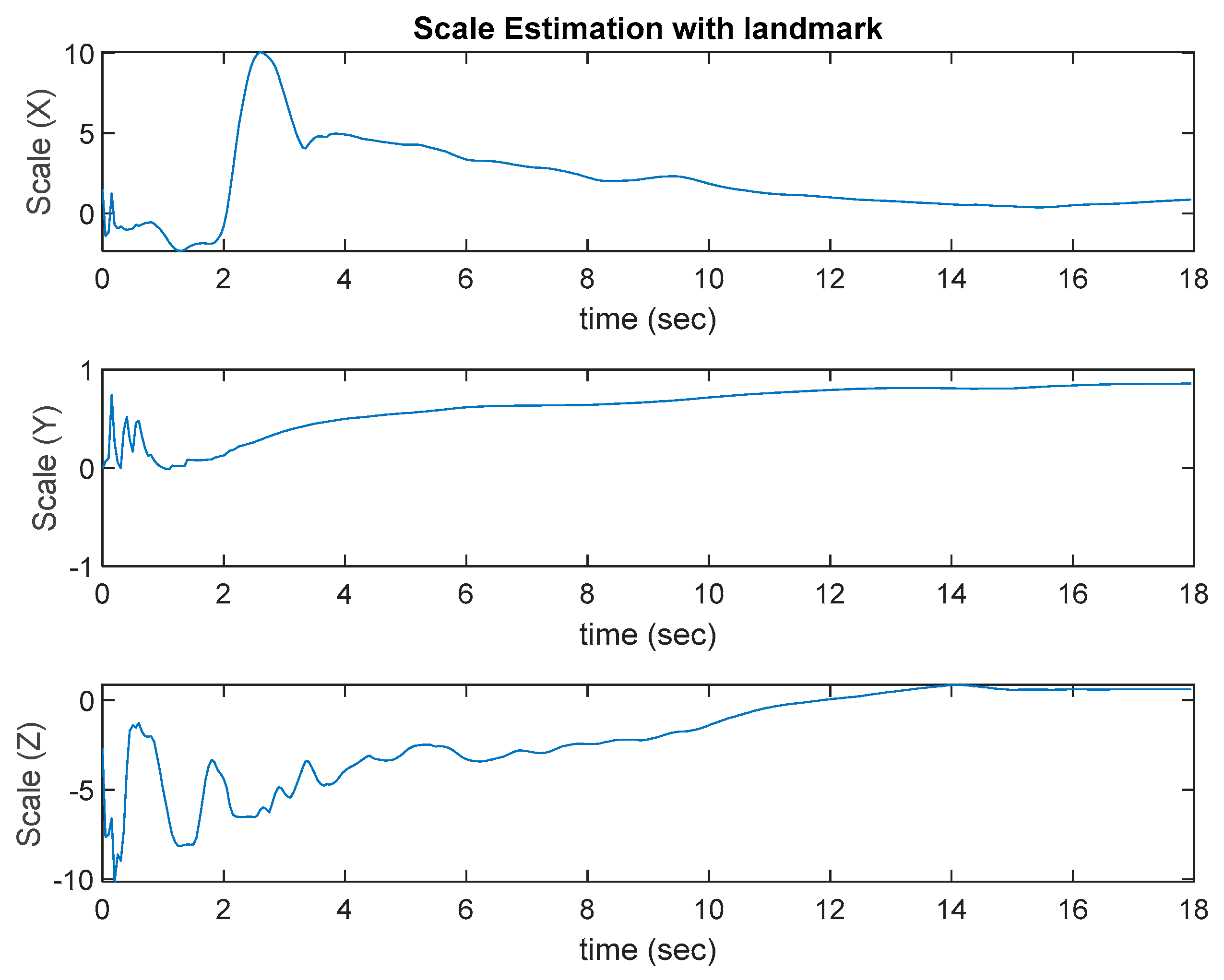
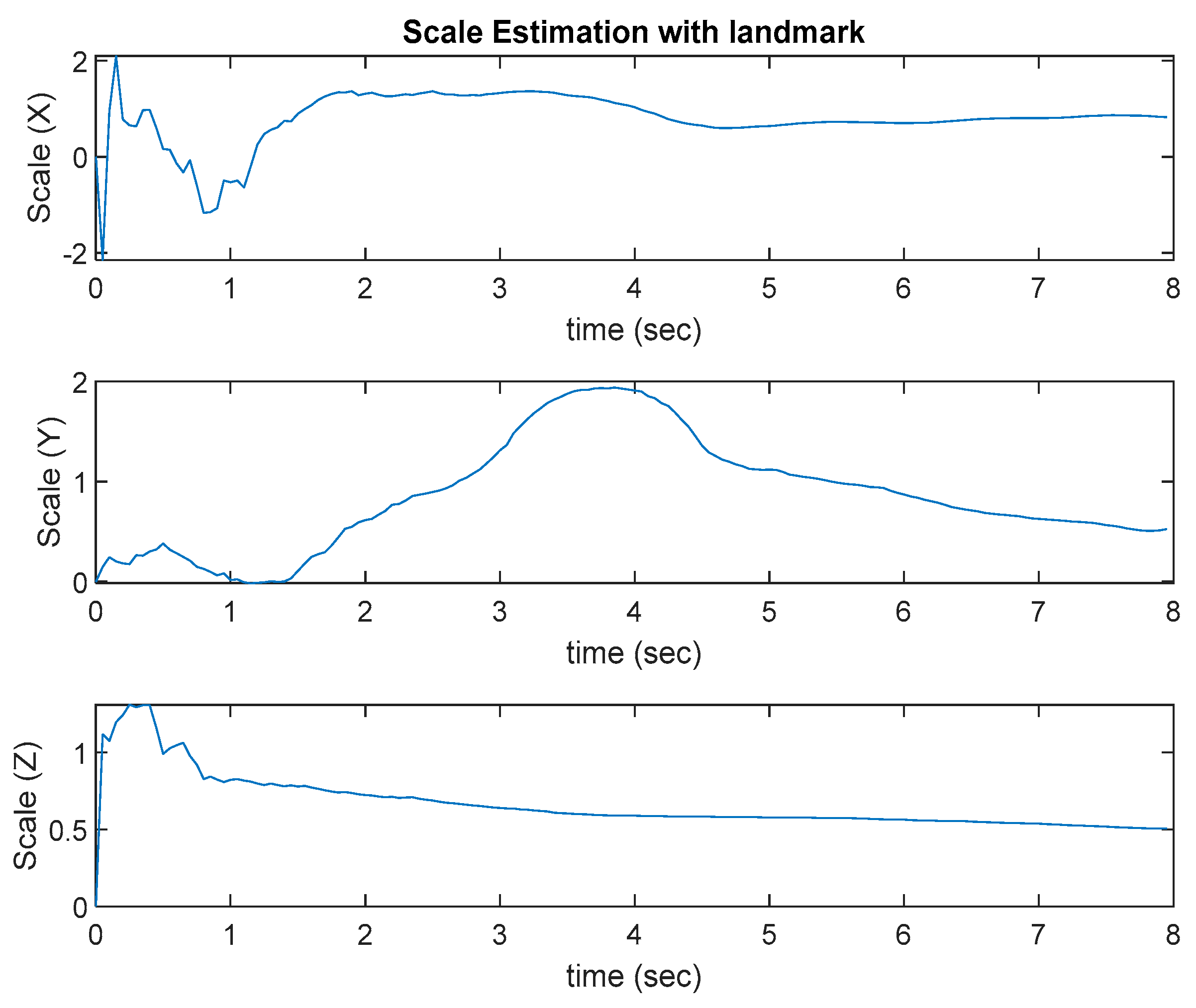
2.3. VIO Algorithm and Scale Estimation
2.4. Sensor Fusion
3. System Setup and Ground Test
3.1. System Setup
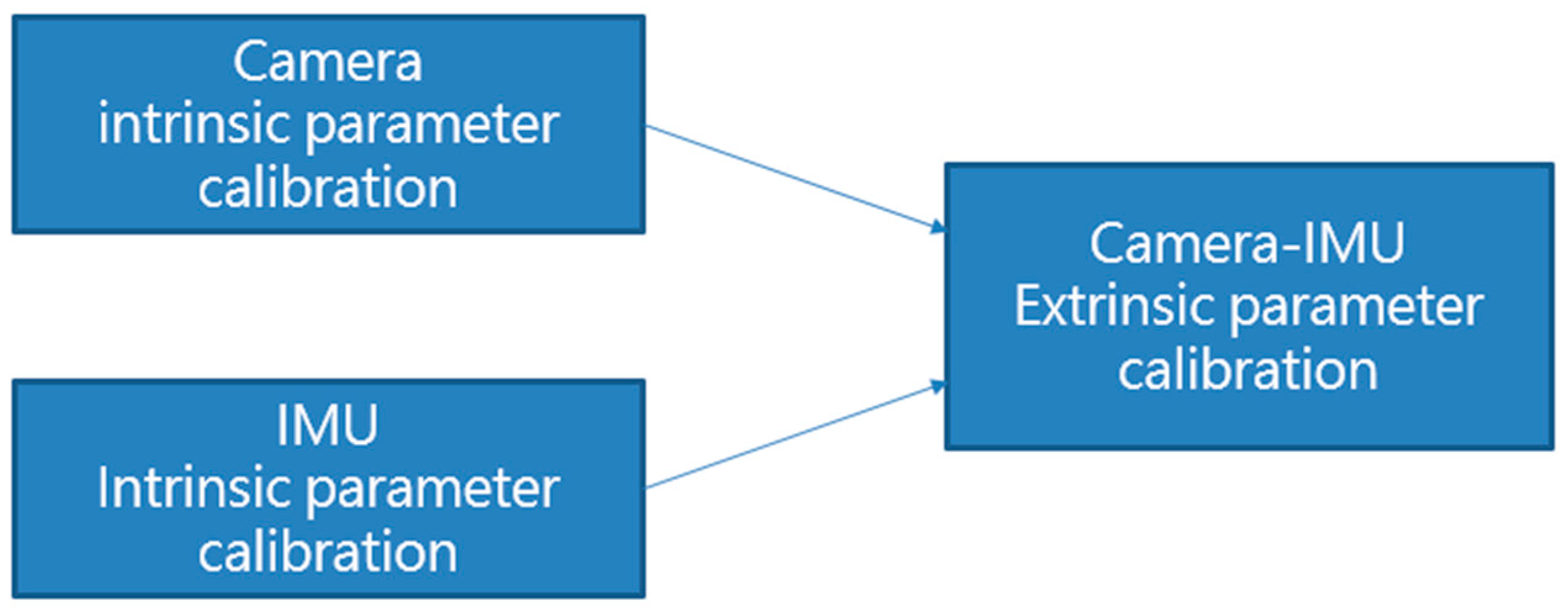
3.2. Sensor Calibration
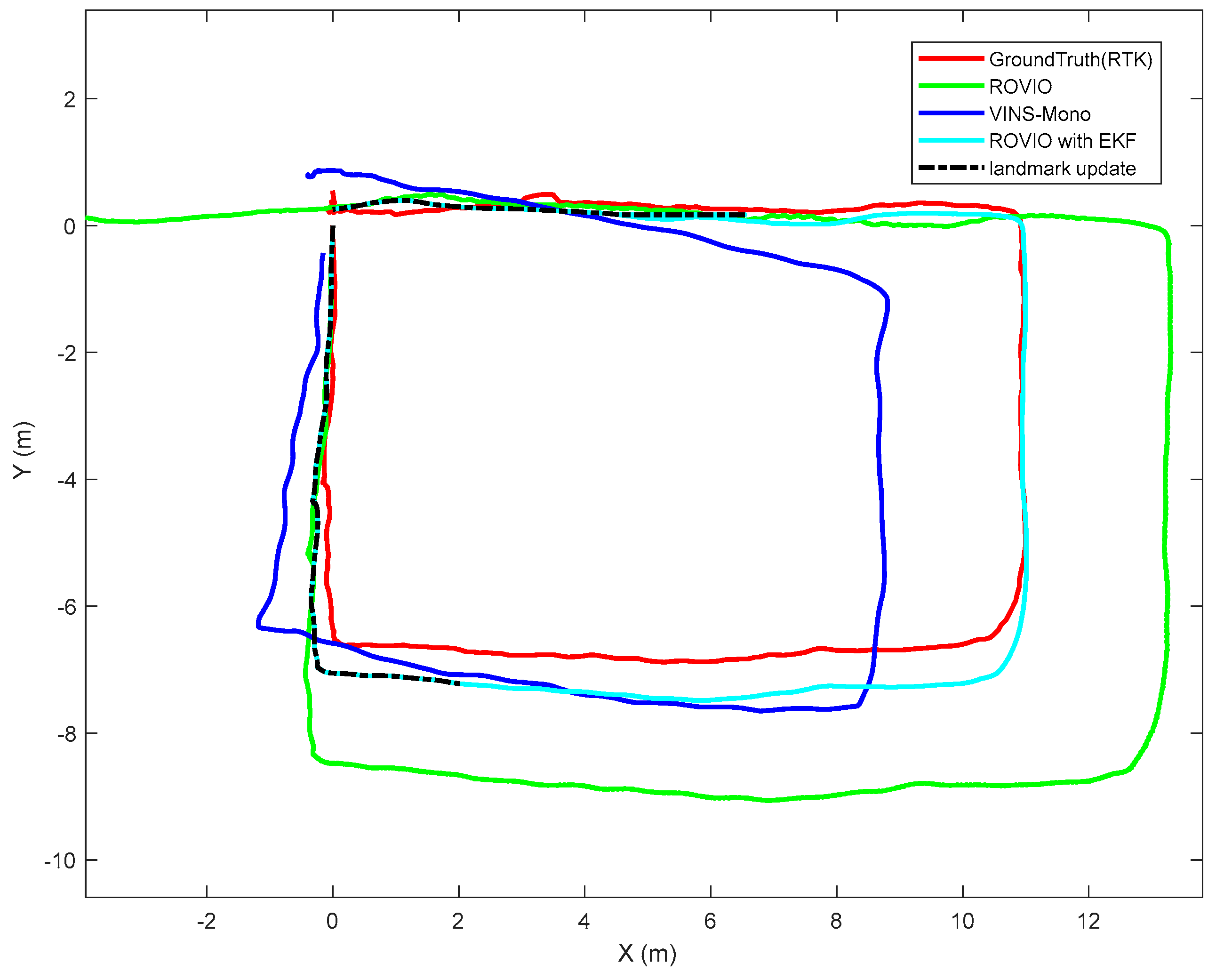
3.3. Ground Test
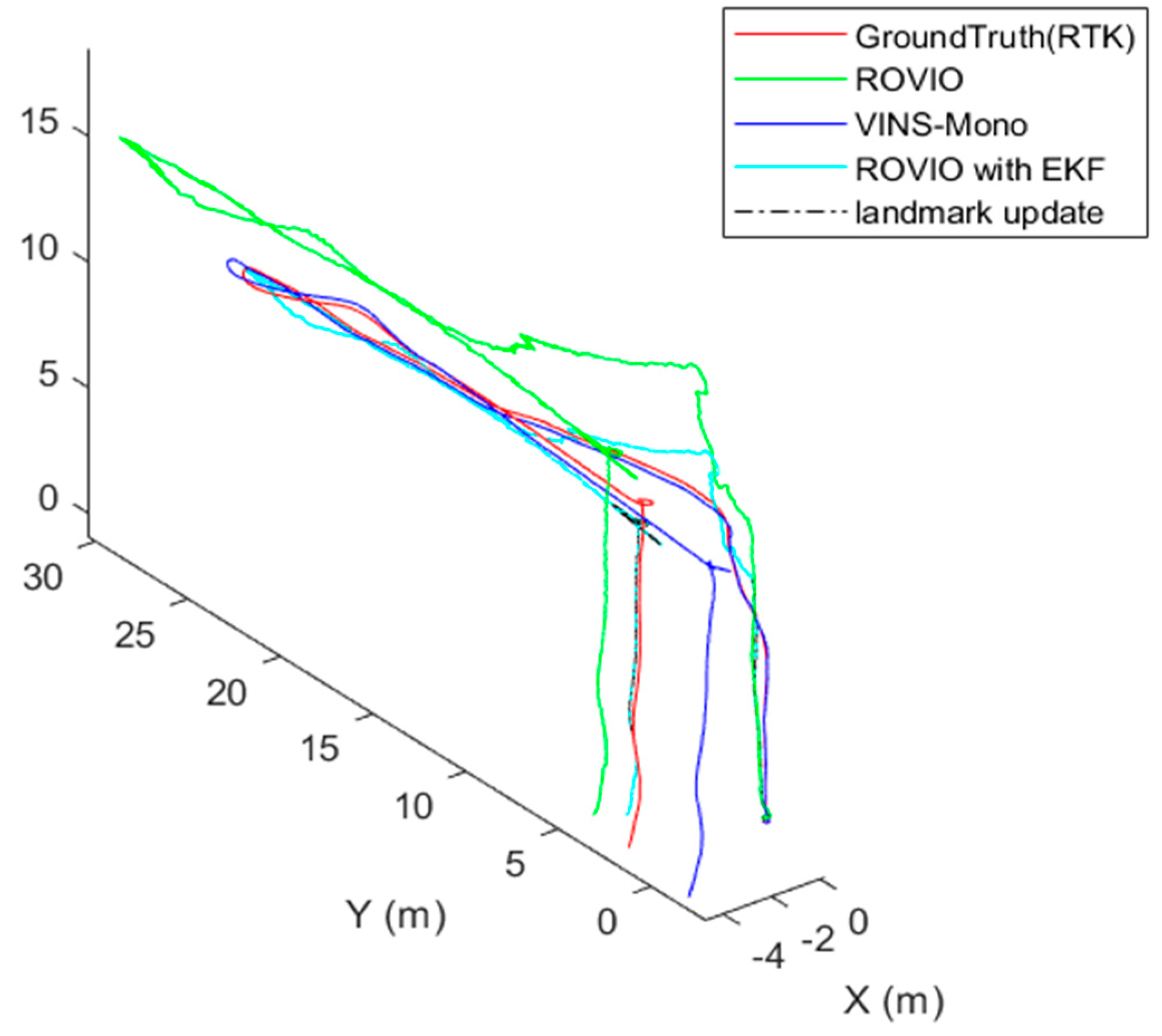
4. Flight Test Results and Discussion
5. Conclusions
- Add more experiment designs to complete full movements in three axes.
- Add external force estimation in the algorithm.
- Use a GPS timestamp to synchronize the time of the camera and IMU.
- Add external pose information in the measurement update process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gyagenda, N.; Hatilima, J.V.; Roth, H.; Zhmud, V. A review of gnss-independent uav navigation techniques. Robot. Auton. Syst. 2022, 152, 104069. [Google Scholar] [CrossRef]
- Chowdhary, G.; Johnson, E.N.; Magree, D.; Wu, A.; Shein, A. Gps-denied indoor and outdoor monocular vision aided navigation and control of unmanned aircraft. J. Field Robot. 2013, 30, 415–438. [Google Scholar] [CrossRef]
- Jeong, N.; Hwang, H.; Matson, E.T. Evaluation of Low-Cost Lidar Sensor for Application in Indoor Uav Navigation. In Proceedings of the 2018 IEEE Sensors Applications Symposium (SAS), Seoul, Republic of Korea, 12–14 March 2018; pp. 1–5. [Google Scholar]
- Laoudias, C.; Moreira, A.; Kim, S.; Lee, S.; Wirola, L.; Fischione, C. A survey of enabling technologies for network localization, tracking, and navigation. IEEE Commun. Surv. Tutor. 2018, 20, 3607–3644. [Google Scholar] [CrossRef]
- Lu, Y.; Xue, Z.; Xia, G.-S.; Zhang, L. A survey on vision-based uav navigation. Geo-Spat. Inf. Sci. 2018, 21, 21–32. [Google Scholar] [CrossRef]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. Monoslam: Real-time single camera slam. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. Orb-slam: A versatile and accurate monocular slam system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. Orb-slam3: An accurate open-source library for visual, visual–inertial, and multimap slam. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. Lsd-Slam: Large-Scale Direct Monocular Slam. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Bustos, A.P.; Chin, T.-J.; Eriksson, A.; Reid, I. Visual Slam: Why Bundle Adjust? In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 2385–2391. [Google Scholar]
- Bloesch, M.; Burri, M.; Omari, S.; Hutter, M.; Siegwart, R. Iterated extended Kalman filter based visual-inertial odometry using direct photometric feedback. Int. J. Robot. Res. 2017, 36, 1053–1072. [Google Scholar] [CrossRef]
- Delmerico, J.; Scaramuzza, D. A Benchmark Comparison of Monocular Visual-Inertial Odometry Algorithms for Flying Robots. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QL, Australia, 21–25 May 2018; pp. 2502–2509. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Kumar, G.A.; Patil, A.K.; Patil, R.; Park, S.S.; Chai, Y.H. A lidar and imu integrated indoor navigation system for uavs and its application in real-time pipeline classification. Sensors 2017, 17, 1268. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Zhang, F. Fast-lio: A fast, robust lidar-inertial odometry package by tightly-coupled iterated Kalman filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Zhang, Z. Visual-inertial odometry of aerial robots. arXiv 2019, arXiv:1906.03289. [Google Scholar]
- Huang, G. Visual-Inertial Navigation: A Concise Review. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9572–9582. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. Visual-inertial monocular slam with map reuse. IEEE Robot. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef]
- Sun, K.; Mohta, K.; Pfrommer, B.; Watterson, M.; Liu, S.; Mulgaonkar, Y.; Taylor, C.J.; Kumar, V. Robust stereo visual inertial odometry for fast autonomous flight. IEEE Robot. Autom. Lett. 2018, 3, 965–972. [Google Scholar] [CrossRef]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust Visual Inertial Odometry Using a Direct Ekf-Based Approach. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar]
- Cortés, S.; Solin, A.; Rahtu, E.; Kannala, J. Advio: An Authentic Dataset for Visual-Inertial Odometry. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 419–434. [Google Scholar]
- Schubert, D.; Goll, T.; Demmel, N.; Usenko, V.; Stückler, J.; Cremers, D. The Tum Vi Benchmark for Evaluating Visual-Inertial Odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1680–1687. [Google Scholar]
- Zhang, Z.; Zhao, R.; Liu, E.; Yan, K.; Ma, Y. Scale estimation and correction of the monocular simultaneous localization and mapping (slam) based on fusion of 1d laser range finder and vision data. Sensors 2018, 18, 1948. [Google Scholar] [CrossRef] [PubMed]
- Lv, Q.; Ma, J.; Wang, G.; Lin, H. Absolute Scale Estimation of Orb-Slam Algorithm Based on Laser Ranging. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 10279–10283. [Google Scholar]
- Caselitz, T.; Steder, B.; Ruhnke, M.; Burgard, W. Monocular Camera Localization in 3D Lidar Maps. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 1926–1931. [Google Scholar]
- Urzua, S.; Munguía, R.; Grau, A. Monocular slam system for mavs aided with altitude and range measurements: A gps-free approach. J. Intell. Robot. Syst. 2019, 94, 203–217. [Google Scholar] [CrossRef]
- Engel, J.; Stückler, J.; Cremers, D. Large-Scale Direct Slam with Stereo Cameras. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September 2015–2 October 2015; pp. 1935–1942. [Google Scholar]
- Liu, P.; Geppert, M.; Heng, L.; Sattler, T.; Geiger, A.; Pollefeys, M. Towards Robust Visual Odometry with a Multi-Camera System. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1154–1161. [Google Scholar]
- Okuyama, K.; Kawasaki, T.; Kroumov, V. Localization and Position Correction for Mobile Robot Using Artificial Visual Landmarks. In Proceedings of the 2011 International Conference on Advanced Mechatronic Systems, Zhengzhou, China, 11–13 August 2011; pp. 414–418. [Google Scholar]
- Lebedev, I.; Erashov, A.; Shabanova, A. Accurate Autonomous Uav Landing Using Vision-Based Detection of Aruco-Marker. In Proceedings of the International Conference on Interactive Collaborative Robotics, St. Petersburg, Russia, 7–9 October 2020; pp. 179–188. [Google Scholar]
- Xing, H.; Liu, Y.; Guo, S.; Shi, L.; Hou, X.; Liu, W.; Zhao, Y. A multi-sensor fusion self-localization system of a miniature underwater robot in structured and gps-denied environments. IEEE Sens. J. 2021, 21, 27136–27146. [Google Scholar] [CrossRef]
- Qin, T. 2018. Available online: https://github.Com/ethz-asl/kalibr (accessed on 15 July 2022).
- Gaowenliang. 2007. Available online: https://github.com/gaowenliang/imu_utils (accessed on 15 July 2022).






| ROVIO | ROVIO with GPS | ROVIO with Landmark | ROVIO with EKF | |
|---|---|---|---|---|
| Target Location | 4.2167 m | 3.9842 m | 3.7498 m | 0.037 m |
| RMSE | 3.7469 m | 1.9756 m | 2.1976 m | 0.3432 m |
| ROVIO | ROVIO with GPS | ROVIO with Landmark | ROVIO with EKF | |
|---|---|---|---|---|
| Case 1 | 1.6687 m | 1.4254 m | 1.4596 m | 1.116 m |
| Case 2 | 7.1529 m | 6.1271 m | 5.9645 m | 2.4478 m |
| ROVIO | ROVIO with GPS | ROVIO with Landmark | ROVIO with EKF | |
|---|---|---|---|---|
| Case 1 | 3.2097 m | 2.2386 m | 1.8626 m | 1.7431 m |
| Case 2 | 8.4588 m | 6.0043 m | 5.7631 m | 5.1649 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-C.; Chen, C.-C.; Shen, C.-T.; Lai, Y.-C. Landmark-Based Scale Estimation and Correction of Visual Inertial Odometry for VTOL UAVs in a GPS-Denied Environment. Sensors 2022, 22, 9654. https://doi.org/10.3390/s22249654
Lee J-C, Chen C-C, Shen C-T, Lai Y-C. Landmark-Based Scale Estimation and Correction of Visual Inertial Odometry for VTOL UAVs in a GPS-Denied Environment. Sensors. 2022; 22(24):9654. https://doi.org/10.3390/s22249654
Chicago/Turabian StyleLee, Jyun-Cheng, Chih-Chun Chen, Chang-Te Shen, and Ying-Chih Lai. 2022. "Landmark-Based Scale Estimation and Correction of Visual Inertial Odometry for VTOL UAVs in a GPS-Denied Environment" Sensors 22, no. 24: 9654. https://doi.org/10.3390/s22249654
APA StyleLee, J.-C., Chen, C.-C., Shen, C.-T., & Lai, Y.-C. (2022). Landmark-Based Scale Estimation and Correction of Visual Inertial Odometry for VTOL UAVs in a GPS-Denied Environment. Sensors, 22(24), 9654. https://doi.org/10.3390/s22249654







