Development of a Flexible Integrated Self-Calibrating MEMS Pressure Sensor Using a Liquid-to-Vapor Phase Change
Abstract
:1. Introduction
2. Modeling and Development
2.1. Governing Physics
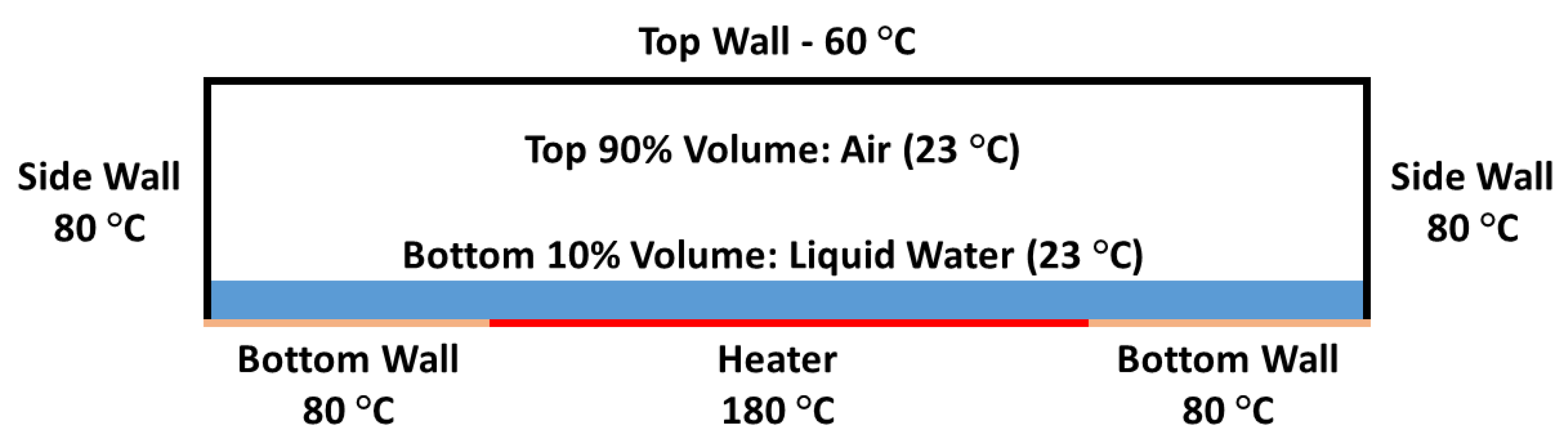
2.2. Sensor Cavity Two-Phase Modeling
3. Two-Phase Sensor Prototype
3.1. Development and Description
3.2. Testing and Calibration Procedures
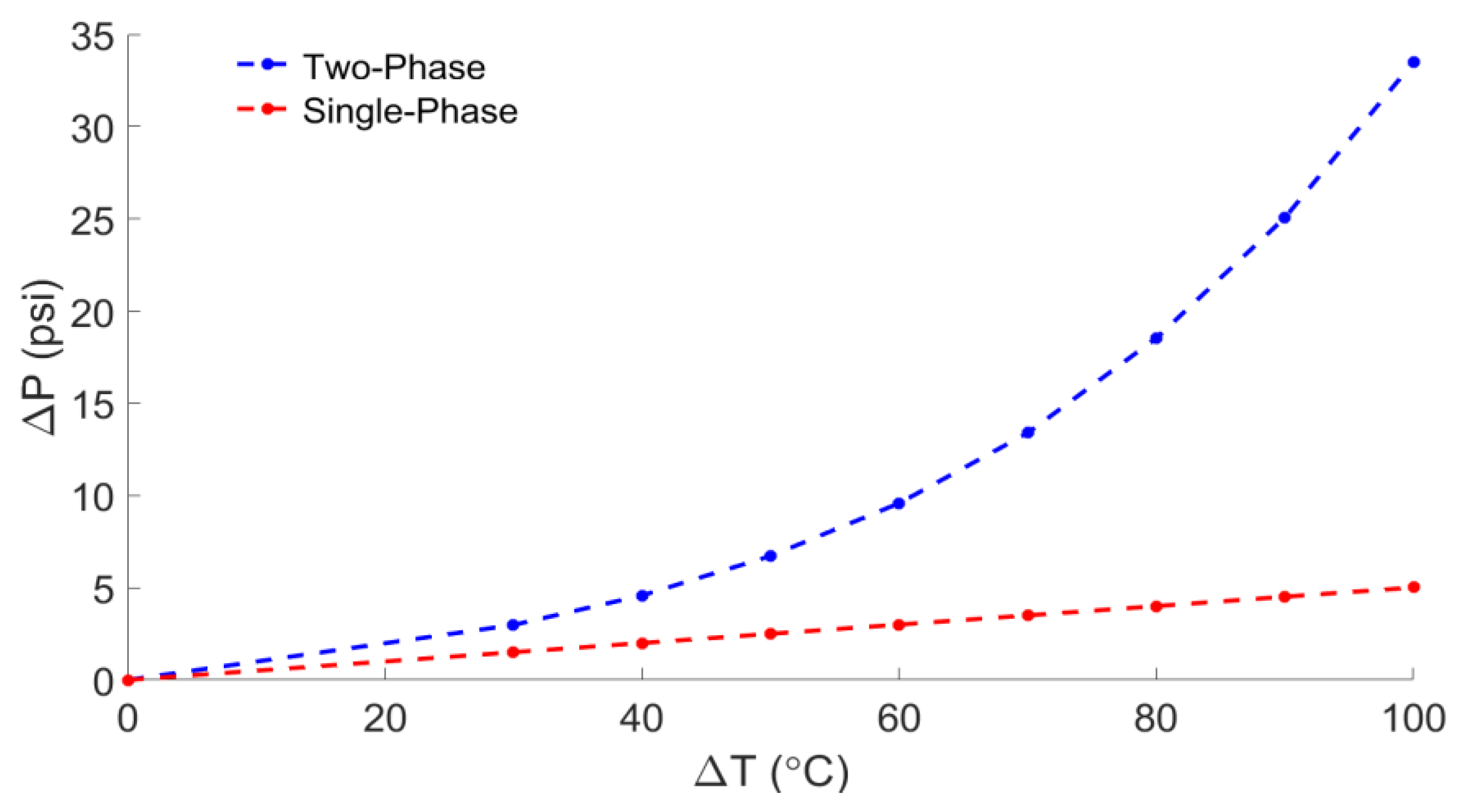
4. Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Evaporation frequency |
| b | Condensation frequency |
| Mass flow rate | |
| P | Absolute pressure |
| T | Temperature |
| α | Phase volume fraction |
| ρ | Phase density |
| Subscripts | |
| a | air |
| f | final |
| i | initial |
| l | liquid |
| sat | saturated |
| T | total |
| v | vapor |
References
- Xu, Y.; Hu, X.; Kundu, S.; Nag, A.; Afsarimanesh, N.; Sapra, S.; Mukhopadhyay, S.C.; Han, T. Silicon-Based Sensors for Biomedical Applications: A Review. Sensors 2019, 19, 2908. [Google Scholar] [CrossRef] [Green Version]
- Javed, Y.; Mansoor, M.; Shah, I.A. A Review of Principles of MEMS Pressure Sensing with its Aerospace Applications. Sens. Rev. 2019, 39, 652–664. [Google Scholar] [CrossRef]
- Bhatt, G.; Manoharan, K.; Chauhan, P.S.; Bhattacharya, S. MEMS Sensors for Automotive Applications: A Review. In Sensors for Automotive and Aerospace Applications; Springer: Singapore, 2019; pp. 223–239. [Google Scholar]
- Foken, T. Springer Handbook of Atmospheric Measurements; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Nag, M.; Singh, J.; Kumar, A.; Alvi, P.A.; Singh, K. Sensitivity Enhancement and Temperature Compatibility of Graphene Piezoresistive MEMS Pressure Sensor. Microsyst. Technol. 2019, 25, 3977–3982. [Google Scholar] [CrossRef]
- Farhath, M.; Samad, M. Design and Simulation of a High Sensitive Stripped-Shaped Piezoresistive Pressure Sensor. J. Comput. Electron. 2020, 19, 310–320. [Google Scholar] [CrossRef]
- Song, P.; Si, C.; Zhang, M.; Zhao, Y.; He, Y.; Liu, W.; Wang, X. A Novel Piezoresistive MEMS Pressure Sensors Based on Temporary Bonding Technology. Sensors 2020, 20, 337. [Google Scholar] [CrossRef] [Green Version]
- Shin, S.; Ko, B.; So, H. Structural Effects of 3D Printing Resolution on the Gauge Factor of Microcrack-Based Strain Gauges for Health Care Monitoring. Microsyst. Nanoeng. 2022, 8, 12. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Jia, W.; Xiao, Y.; Feng, Z.; Wu, G. A Temperature-Stable and Low Impedance Piezoelectric MEMS Resonator for Drop-In Replacement of Quartz Crystals. IEEE Electron Device Lett. 2021, 42, 1382–1385. [Google Scholar] [CrossRef]
- Singh, K.; Alvi, P.A. Influence of the Pressure Range on Temperature Coefficient of Resistivity (TCR) for Polysilicon Piezoresistive MEMS Pressure Sensor. Phys. Scr. 2020, 95, 075005. [Google Scholar]
- Basov, M. High-Sensitivity MEMS Pressure Sensor Utilizing Bipolar Junction Transistor with Temperature Compensation. Sens. Actuators A Phys. 2020, 303, 111705. [Google Scholar] [CrossRef]
- Li, J.; Bao, R.; Tao, J.; Peng, Y.; Pan, C. Recent Progress in Flexible Pressure Sensor Arrays: From Design to Applications. J. Mater. Chem. C. 2018, 6, 11878. [Google Scholar] [CrossRef]
- Sikarwar, S.; Singh, S.; Yadav, B.C. Review on Pressure Sensors for Structural Health Monitoring. Photonic Sens. 2017, 7, 294. [Google Scholar] [CrossRef]
- Luo, N.; Dai, W.; Li, C.; Zhou, Z.; Lu, L.; Poon, C.C.; Chen, S.C.; Zhang, Y.; Zhao, N. Flexible Piezoresistive Sensor Patch Enabling Ultralow Power Cuffless Blood Pressure Measurement. Adv. Funct. Mater. 2016, 26, 1178–1187. [Google Scholar] [CrossRef]
- Yu, R.; Xia, T.; Wu, B.; Yuan, J.; Ma, L.; Cheng, G.J.; Liu, F. Highly Sensitive Flexible Piezoresistive Sensor with 3D Conductive Network. ACS Appl. Mater. Interfaces 2020, 12, 35291–35299. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Panahi-Sarmad, M.; Chen, T.; Wang, A.; Xu, R.; Xiao, X. Highly Sensitive and Flexible Capacitive Pressure Sensor Based on a Dual-Structured Nanofiber Membrane as the Dielectric for Attachable Wearable Electronics. ACS Appl. Electron. Mater. 2022, 4, 469–477. [Google Scholar] [CrossRef]
- Shi, J.; Wang, L.; Dai, Z.; Zhao, L.; Du, M.; Li, H.; Fang, Y. Multiscale Hierarchical Design of a Flexible Piezoresistive Pressure Sensor with High Sensitivity and Wide Linearity Range. Small 2018, 14, 1800819. [Google Scholar] [CrossRef]
- Huang, L.; Zeng, R.; Tang, D.; Cao, X. Bioinspired and Multiscale Hierarchical Design of a Pressure Sensor with High Sensitivity and Wide Linearity Range for High-Throughput Biodetection. Nano Energy 2022, 99, 107376. [Google Scholar] [CrossRef]
- Gao, L.; Zhu, C.; Li, L.; Zhang, C.; Liu, J.; Yu, H.D.; Huang, W. All Paper-Based Flexible and Wearable Piezoresistive Pressure Sensor. ACS Appl. Mater. Interfaces 2019, 11, 25034–25042. [Google Scholar] [CrossRef]
- Guan, X.; Wang, Z.; Zhao, W.; Huang, H.; Wang, S.; Zhang, Q.; Zhong, D.; Lin, W.; Ding, N.; Peng, Z. Flexible Piezoresistive Sensors with Wide-Range Pressure Measurements Based on a Graded Nest-Like Architecture. ACS Appl. Mater. Interfaces 2020, 12, 26137–26144. [Google Scholar] [CrossRef]
- Kamat, A.M.; Pei, Y.; Jayawardhana, B.; Kottapalli, A.G.P. Biomimetic Soft Polymer Microstructures and Piezoresistive Graphene Mems Sensors Using Sacrificial Metal 3D Printing. ACS Appl. Mater. Interfaces 2021, 13, 1094–1104. [Google Scholar] [CrossRef]
- Wang, Y.; Yue, Y.; Cheng, F.; Cheng, Y.; Ge, B.; Liu, N.; Gao, Y. Ti3C2TxMXene-Based Flexible Piezoresistive Physical Sensors. ACS Nano 2022, 16, 1734–1758. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; Zhang, Q.; Li, Z.; Li, Z.; Cheng, L.; Dai, F. Electrospinning Silk Fibroin/Graphene Nanofiber Membrane Used for 3D Wearable Pressure Sensor. Polymers 2022, 14, 3875. [Google Scholar] [CrossRef] [PubMed]
- Basic Principles of Instrument Calibration. Available online: https://www.instrumentationtoolbox.com/2012/12/understanding-instrument-calibration.html (accessed on 13 June 2022).
- Yu, L.; Kim, B.J.; Meng, E. Chronically Implanted Pressure Sensors: Challenges and State of the Field. Sensors 2014, 14, 20620–20644. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Algamili, A.S.; Khir, M.H.M.; Dennis, J.O.; Ahmed, A.Y.; Alabsi, S.S.; Hashwan, S.S.B.; Junaid, M.M. A Review of Actuation and Sensing Mechanisms in MEMS-Based Sensor Devices. Nanoscale Res. Lett. 2021, 12, 16. [Google Scholar] [CrossRef] [PubMed]
- Hantos, G.; Flynn, D.; Desmulliez, M.P.Y. Built-In Self-Test (BIST) Methods for MEMS: A Review. Micromachines 2020, 12, 40. [Google Scholar] [CrossRef] [PubMed]
- Yameogo, P.; Heiba, U.; Bahri, M.A.; Pons, P. Self Calibrating Pressure Sensor for Biomedical Applications. In Proceedings of the IEEE Sensors 2009, Christchurch, New Zealand, 25–28 October 2009; pp. 691–694. [Google Scholar]
- Mindlin, L.; Bart, S.F.; Gu, L. Self-Calibrating Pressure Sensor System with Pressure Sensor and Reference Sensor that Share Common Sealed Chamber. U.S. Patent Application No. 14/101,177, 9 October 2014. [Google Scholar]
- Kang, Y.; Homer, M.; Gladwin, L.; Claus, R.; Sibold, R.; Ng, W.; Ruan, H. Semiconductor Nano and Micro Membrane based Pressure Sensors for Wide Bandwidth Measurements. In Proceedings of the ASME Turbo Expo 2019, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- De Clerck, A.; Kang, Y.; Sibold, R.; Mouring, S.; Ruan, H.; Ng, W. Modeling the Thermal Performance of a MEMS Pressure Sensor with Self-Calibration Capabilities. Sensors 2022, 22, 3828. [Google Scholar] [CrossRef]
- Vitz, E.; Moore, J.W.; Shorb, J.; Prat-Resina, X.; Wendorff, T.; Hahn, A. ChemPRIME; University of Wisconsin: Madison, WI, USA, 2020. [Google Scholar]
- Examples of Corrosive Substances and Their pH Levels. Available online: https://blog.storemasta.com.au/examples-corrosive-substances-ph-levels (accessed on 13 June 2022).
- Huo, M.; Chuai, R.; Yin, L.; Liu, X.; Wang, X. Self-testable Pressure Sensors Based on Phase Change. In Proceedings of the 1st IEEE International Conference on Nano/Micro Engineered and Molecular Systems 2006, Zhuhai, China, 18–21 January 2006. [Google Scholar]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 736–737, 756–757. [Google Scholar]
- Drioli, E.; Giorno, L. Encyclopedia of Membranes; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–3. [Google Scholar]
- Teo, A.J.T.; Li, H.; Tan, S.H.; Yoon, Y. An Optical MEMS Accelerometer Fabricated Using Double-Sided Deep Reactive Ion Etching on Silicon-On-Insulator Wafer. J. Micromech. Microeng. 2017, 27, 067001. [Google Scholar] [CrossRef]
- Kang, Y.; De Clerck, A.; Ruan, H. Method of Wafer-Level Fabrication of Self-Calibrating Pressure Sensors. U.S. Patent Application No. 63,227,511, 2021. [Google Scholar]
- Vapor Pressures Common Liquids. Available online: https://www.engineeringtoolbox.com/vapor-pressure-d_312.html (accessed on 13 June 2022).







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Mouring, S.; de Clerck, A.; Mao, S.; Ng, W.; Ruan, H. Development of a Flexible Integrated Self-Calibrating MEMS Pressure Sensor Using a Liquid-to-Vapor Phase Change. Sensors 2022, 22, 9737. https://doi.org/10.3390/s22249737
Kang Y, Mouring S, de Clerck A, Mao S, Ng W, Ruan H. Development of a Flexible Integrated Self-Calibrating MEMS Pressure Sensor Using a Liquid-to-Vapor Phase Change. Sensors. 2022; 22(24):9737. https://doi.org/10.3390/s22249737
Chicago/Turabian StyleKang, Yuhong, Scott Mouring, Albrey de Clerck, Shuo Mao, Wing Ng, and Hang Ruan. 2022. "Development of a Flexible Integrated Self-Calibrating MEMS Pressure Sensor Using a Liquid-to-Vapor Phase Change" Sensors 22, no. 24: 9737. https://doi.org/10.3390/s22249737
APA StyleKang, Y., Mouring, S., de Clerck, A., Mao, S., Ng, W., & Ruan, H. (2022). Development of a Flexible Integrated Self-Calibrating MEMS Pressure Sensor Using a Liquid-to-Vapor Phase Change. Sensors, 22(24), 9737. https://doi.org/10.3390/s22249737





