Joint Resource Management and Trajectory Optimization for UAV-Enabled Maritime Network
Abstract
1. Introduction
1.1. Background
1.2. Related Works
1.3. Motivations and Contributions
- A multi-UAV enabled maritime network model is proposed to enhance the coverage of the maritime communication. To improve the maritime performance, the user association, power allocation, and the UAV trajectory are jointly optimized. Specially, the maritime two-ray model, which includes the LoS ray and sea-reflected ray, is adopted to analyze the throughput of the maritime user. Then, an optimization problem is formulated to maximize the average achievable data rate, which is an NP-hard mixed integer nonlinear programming (MINLP) problem.
- To achieve the solutions with a low computational complexity, the optimization problem is decomposed into three subproblems, namely user association optimization, power allocation optimization, and UAV trajectory optimization. Consequently, the successive convex approximation (SCA) technique and block coordinate descent (BCD) method are adopted to solve the corresponding subproblems. Based on this, a joint iterative algorithm is developed.
- We provide some analytical results on the computational complexity and convergence of the proposed algorithm. In addition, extensive simulations are carried out to demonstrate the effectiveness of the proposed algorithm, and that the proposed algorithm converges well and improve the performance of the maritime network. The results also demonstrates that the proposed algorithm exhibits a low computational complexity.
1.4. Organization
2. System Model and Problem Formulation
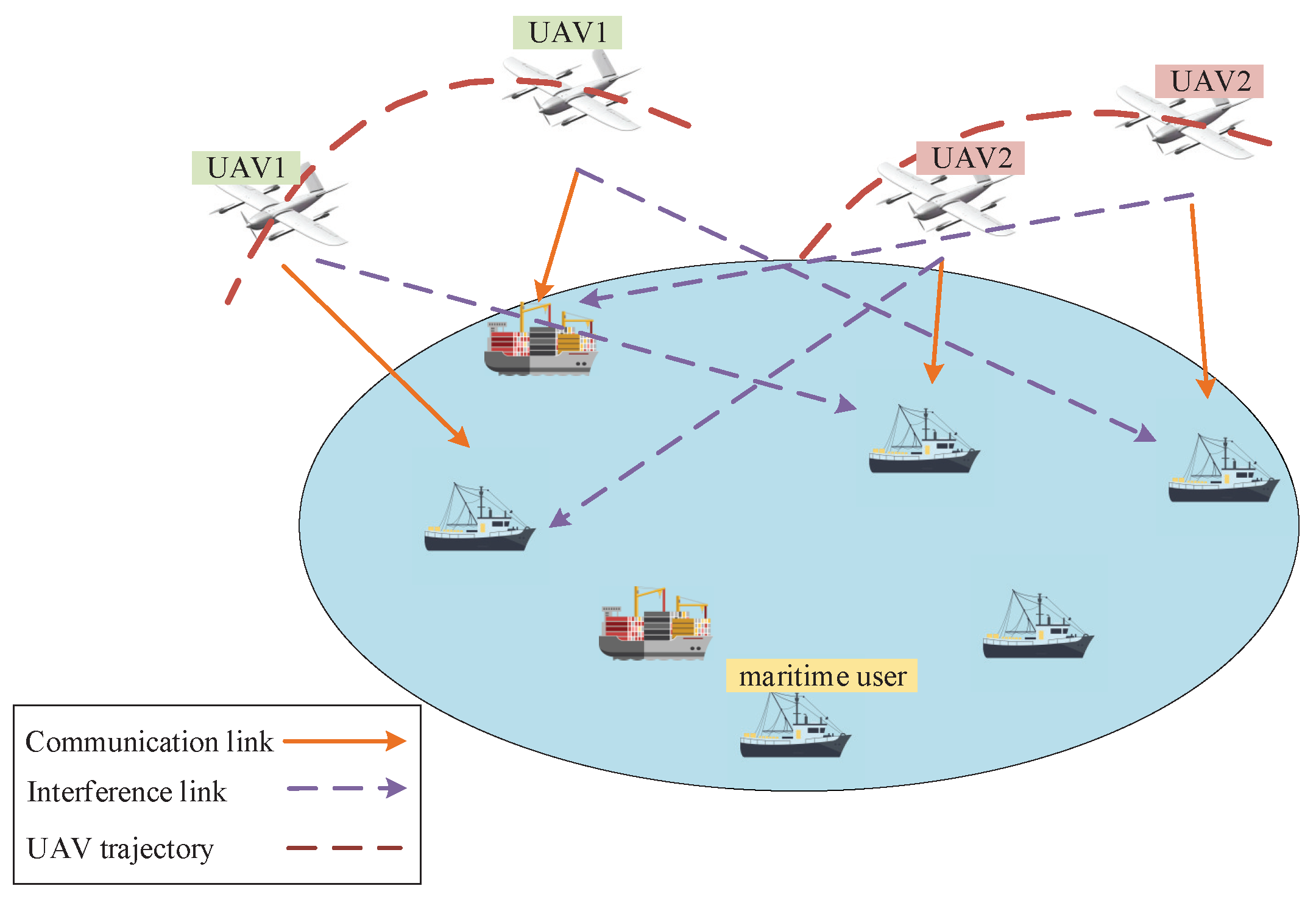
2.1. System Model
2.2. Throughput Analysis
2.3. Problem Formulation
3. Joint User Association, Power Allocation, and Trajectory Optimization
3.1. Problem Decomposition
3.2. User Association Optimization
3.3. Power Allocation Optimization
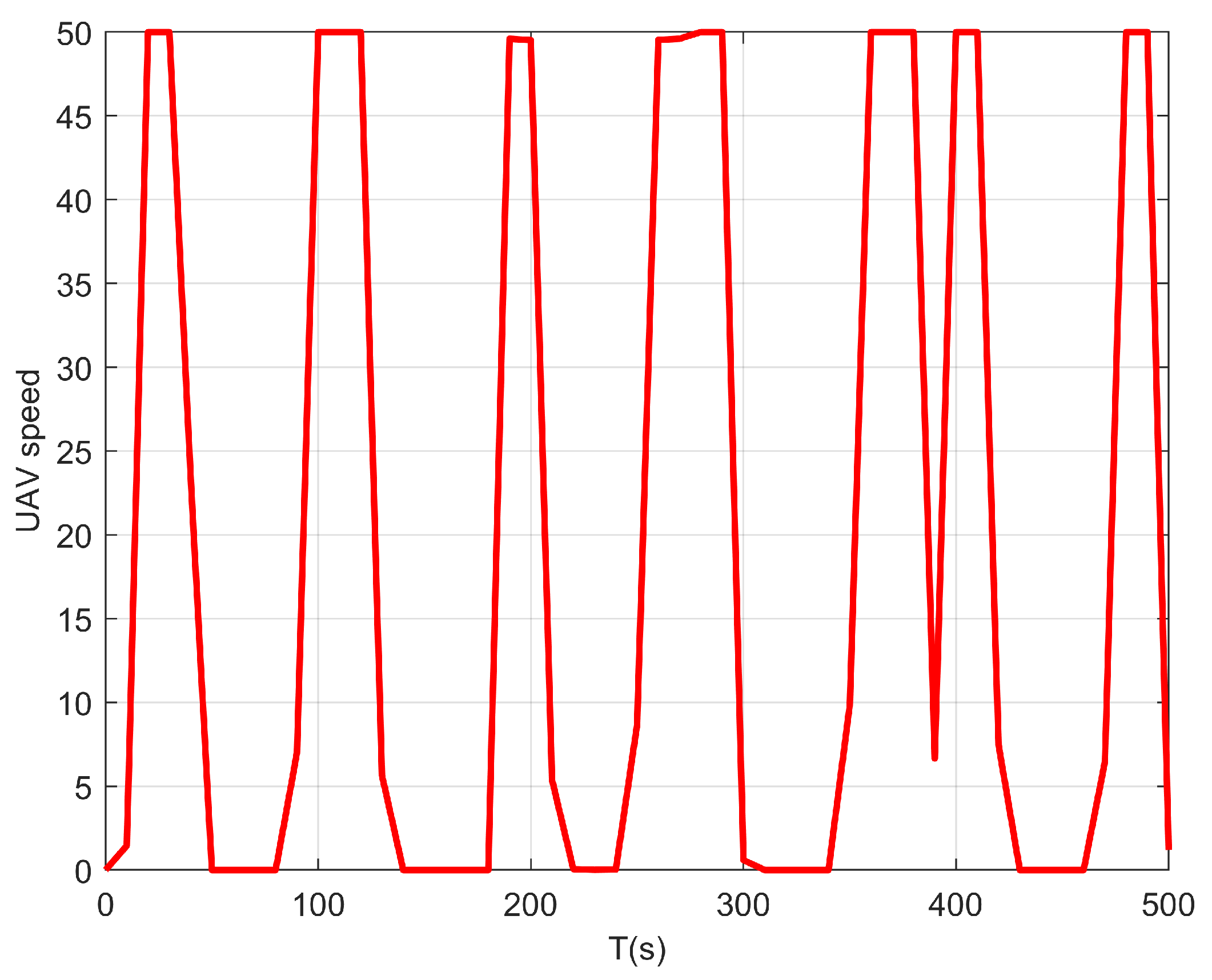
3.4. UAV Trajectory Optimization
4. Proposed Algorithm
4.1. Algorithm Development
| Algorithm 1 Joint user association, power allocation, and UAV trajectory optimization algorithm |
| Input: The iteration index , the maximum number of iteration , and the convergence threshold . |
| Output: The optimal user association , power allocation , UAV trajectory , and the expected throughput R. |
|
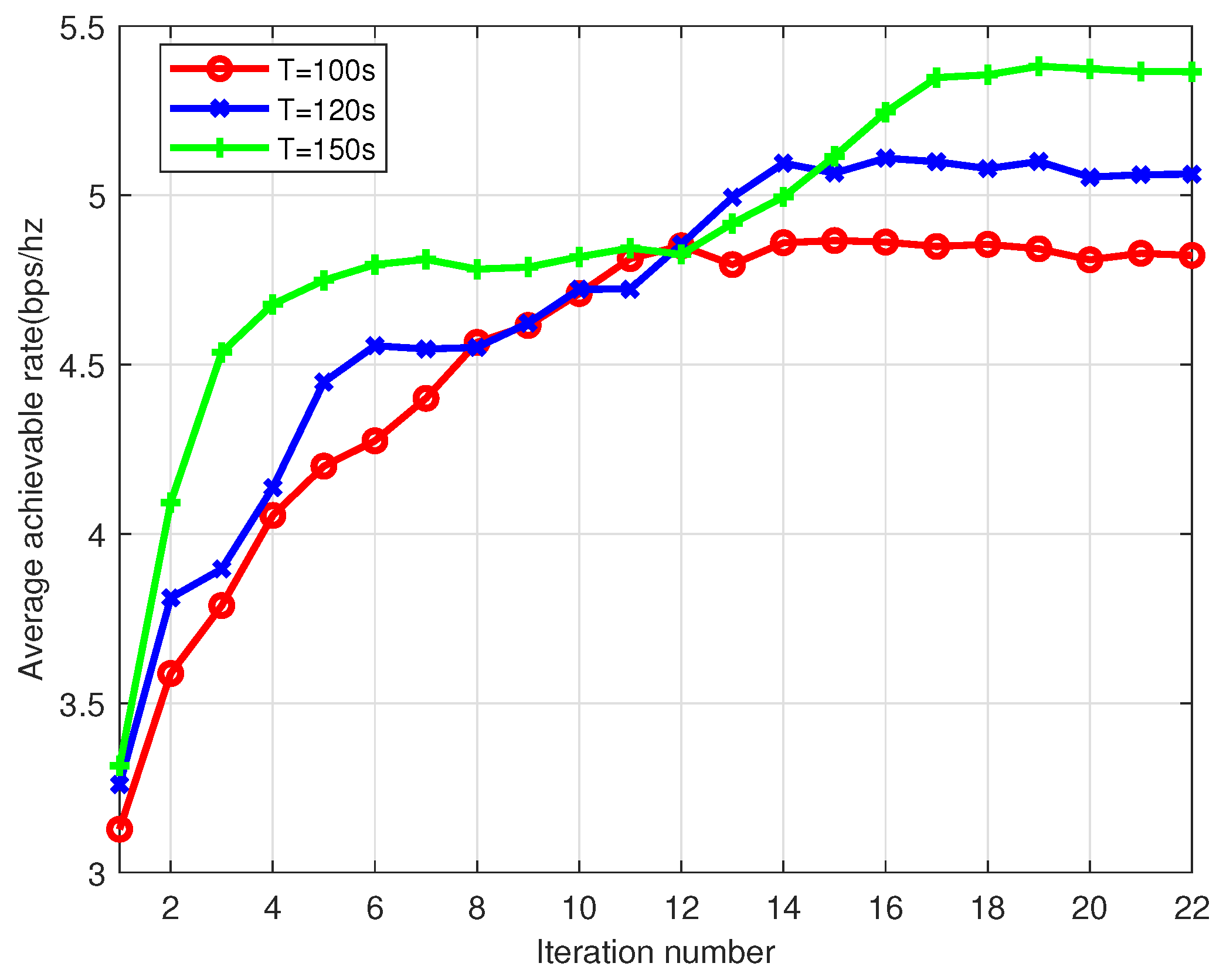
4.2. Convergence Analysis
4.3. Computational Complexity Analysis
5. Numerical Simulation
5.1. Single UAV
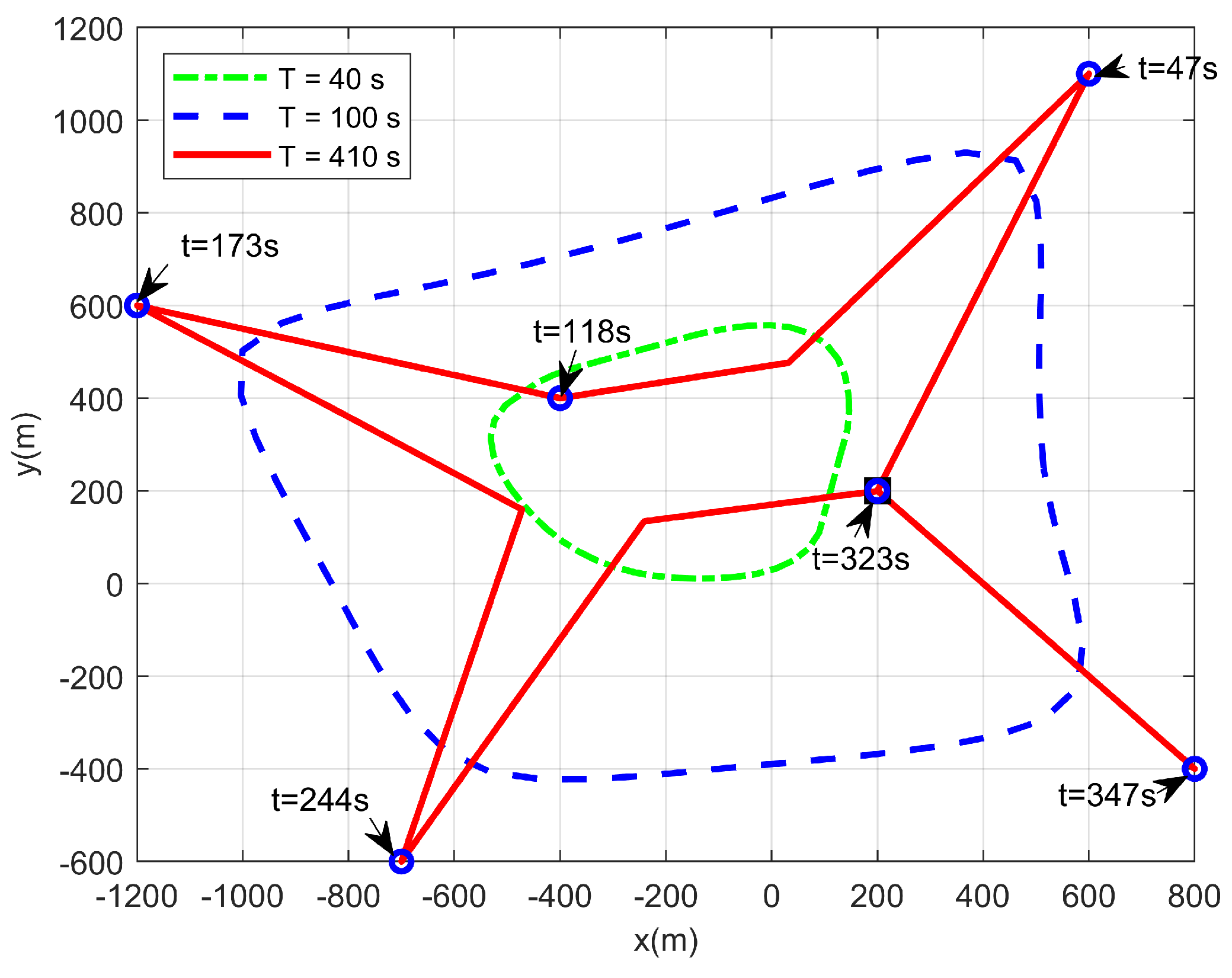
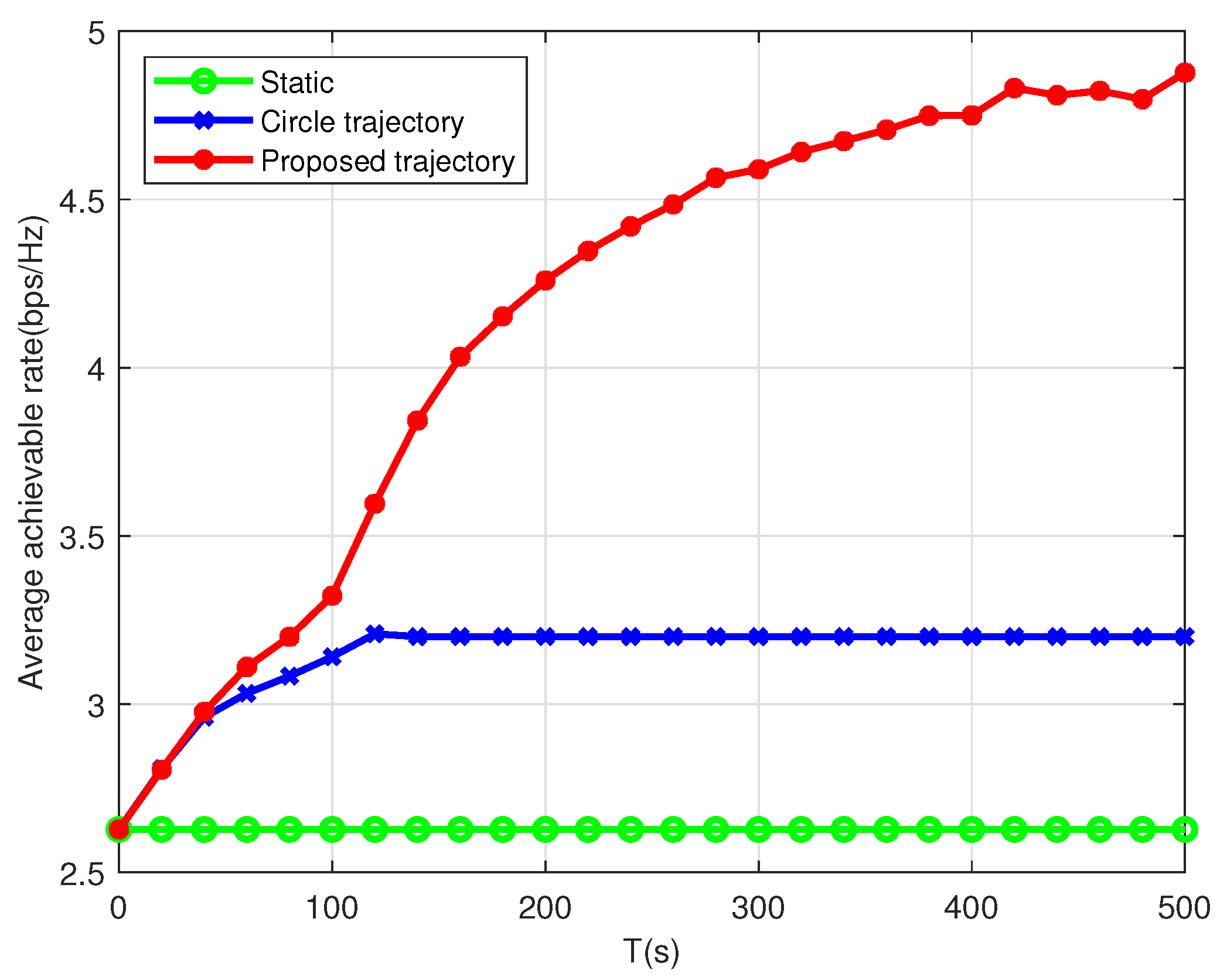
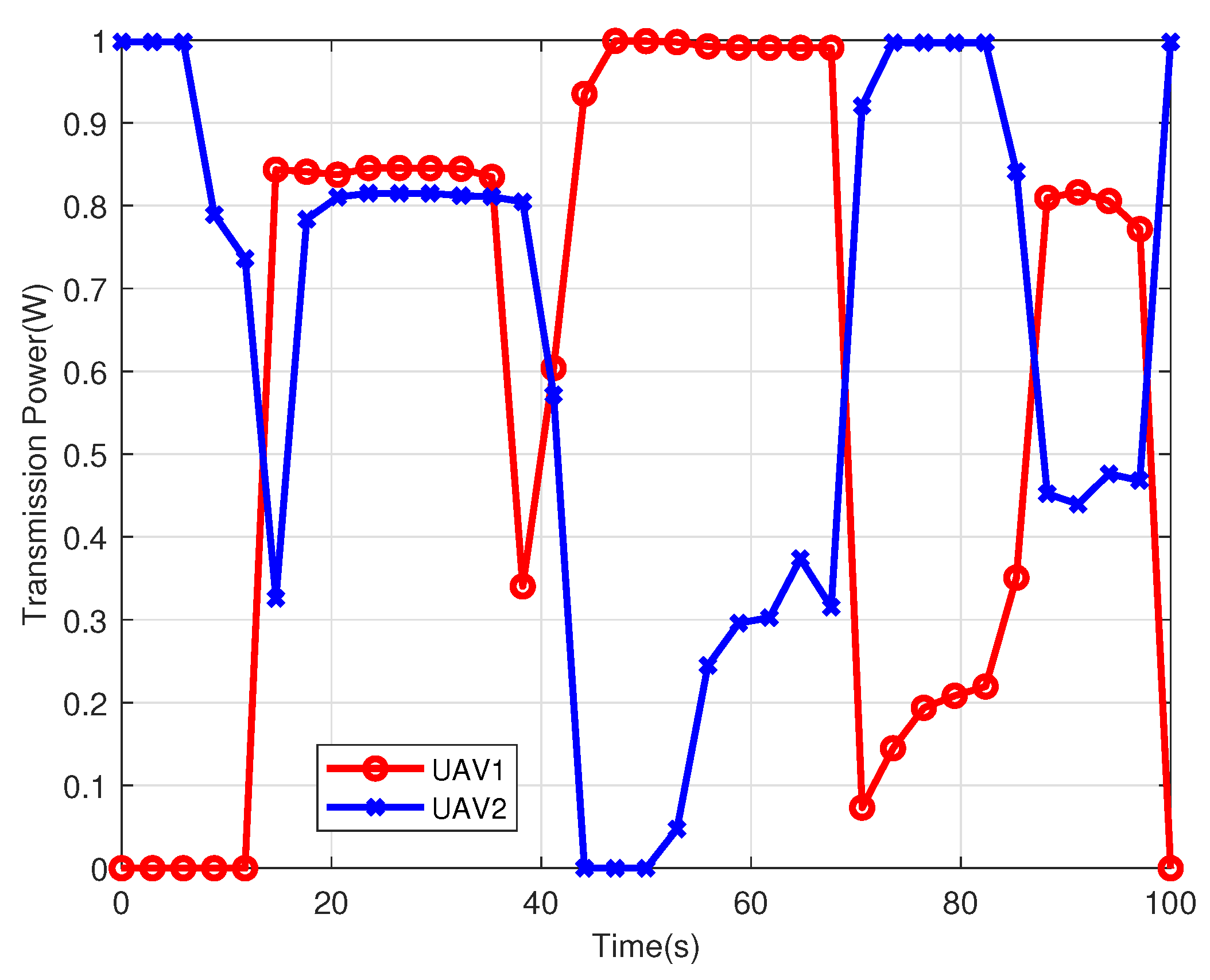
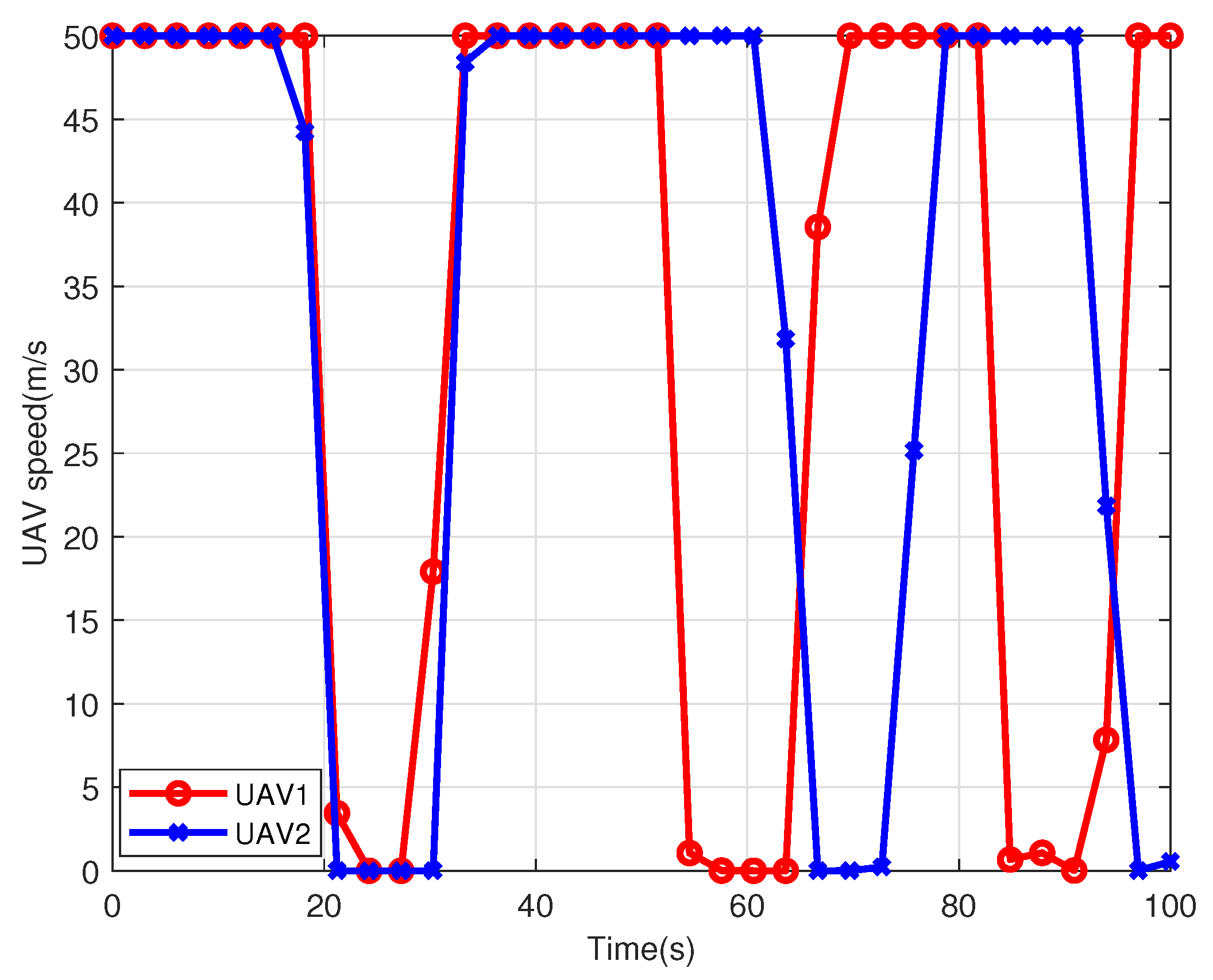
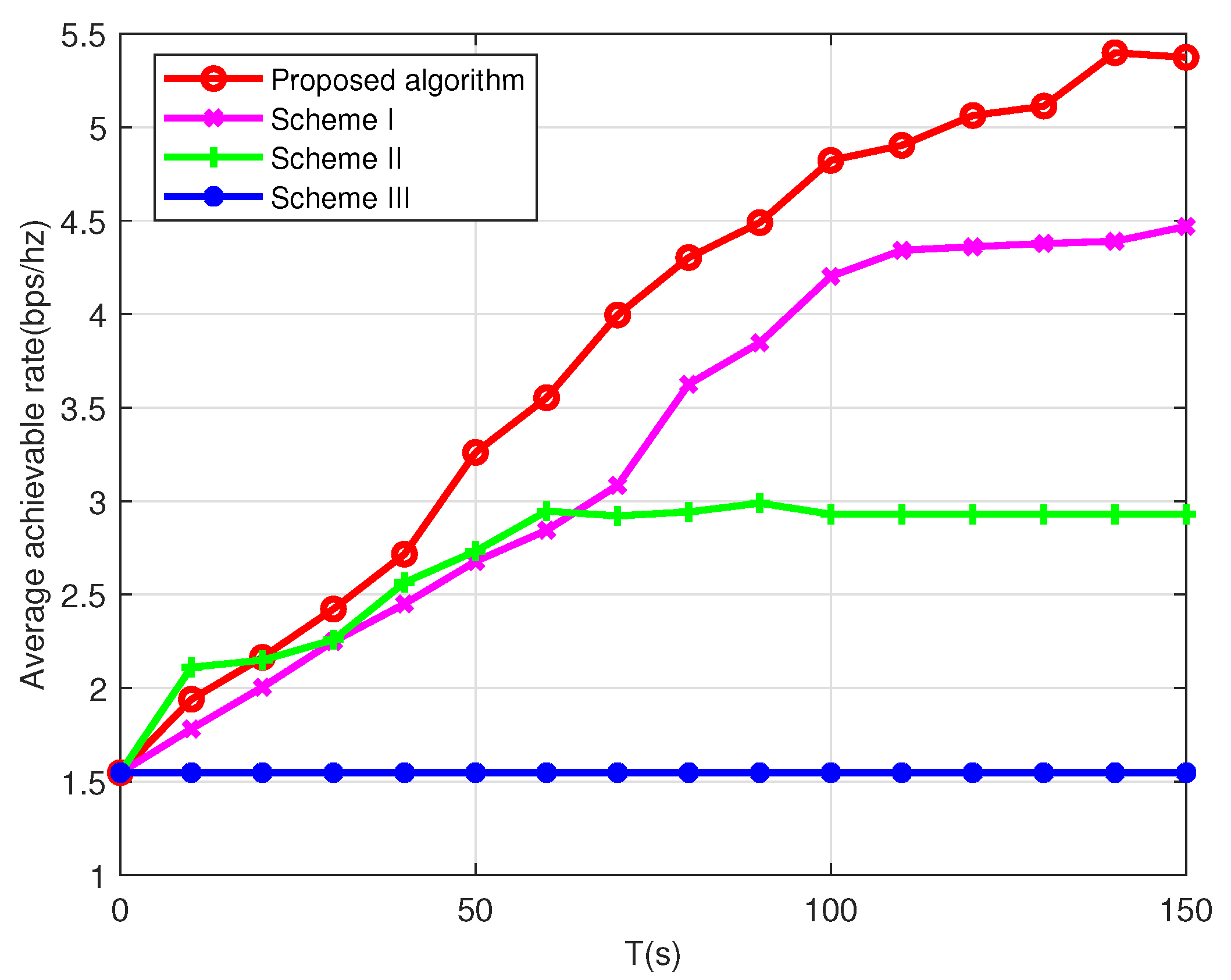
5.2. Multiple UAVs
- Scheme I: The user association and UAV trajectory are jointly optimized but without transmission power allocation optimization (maximum transmission power).
- Scheme II: The user association and power allocation are jointly optimized but without trajectory optimization (the UAVs follow circular paths).
- Scheme III: The user association and power allocation are jointly optimized but with static UAVs, which are placed at the geometric center of the users.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned aerial vehicle |
| LoS | Line-of-sight |
| VHF | Very high frequency |
| TBS | Terrestrial base station |
| CSI | Channel state information |
| NOMA | Non-orthogonal multiple access |
| MCN | Maritime communication network |
| BCD | Block coordinate descent |
| SCA | Successive convex approximation |
| TDMA | Time division multiple access |
Appendix A. Proof of Lemma 1
Appendix B. Proof of Lemma 2
Appendix C. Proof of Lemma 3
References
- Wei, T.; Feng, W.; Chen, Y.; Wang, C.-X.; Ge, N.; Lu, J. Hybrid satellite-terrestrial communication networks for the maritime internet of things: Key technologies, opportunities, and challenges. IEEE Internet Things J. 2021, 8, 8910–8934. [Google Scholar] [CrossRef]
- Li, H.; Yu, C.; Zhang, C.; Jiao, H.; Lin, B.; He, R. Maritime multi-relay communications based on UAV trajectory adjustment and dual Q-learning. In Proceedings of the 2021 International Conference on Security, Pattern Analysis, and Cybernetics, Chengdu, China, 18–20 June 2021; pp. 571–576. [Google Scholar]
- Zeng, C.; Wang, J.B.; Ding, C.; Zhang, H.; Lin, M.; Cheng, J. Joint optimization of trajectory and communication resource allocation for unmanned surface vehicle enabled maritime wireless networks. IEEE Trans. Commun. 2021, 69, 8100–8115. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhang, Y. UAV communications for 5G and beyond: Recent advances and future trends. IEEE Internet Things J. 2019, 6, 2241–2263. [Google Scholar] [CrossRef]
- Li, X.; Feng, W.; Wang, J.; Chen, Y.; Ge, N.; Wang, C.X. Enabling 5G on the ocean: A hybrid satellite-UAV-terrestrial network solution. IEEE Wirel. Commun. 2020, 27, 116–121. [Google Scholar] [CrossRef]
- Tang, R.; Feng, W.; Chen, Y.; Ge, N. NOMA-based UAV communications for maritime coverage enhancement. China Commun. 2021, 18, 230–243. [Google Scholar] [CrossRef]
- Hou, Q.; Cai, Y.; Hu, Q.; Lee, M.; Yu, G. Joint resource allocation and trajectory design for multi-UAV systems with moving Users: Pointer network and unfolding. IEEE Trans. Wirel. Commun. 2022; early access. [Google Scholar]
- Naqvi, S.A.R.; Hassan, S.A.; Pervaiz, H.; Ni, Q. Drone-aided communication as a key enabler for 5G and resilient public safety networks. IEEE Commun. Mag. 2018, 56, 36–42. [Google Scholar] [CrossRef]
- Zeng, Y.; Lyu, J.; Zhang, R. Cellular-connected UAV: Potential, challenges, and promising technologies. IEEE Wirel. Commun. 2019, 26, 120–127. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, H.; Li, Y.; Sun, Q.; Wu, Y.; Jin, S.; Quek, T.Q.S.; Xu, C. Wireless channel models for maritime communications. IEEE Access 2018, 6, 68070–68088. [Google Scholar] [CrossRef]
- Balkees, P.A.S.; Sasidhar, K.; Rao, S. A survey based analysis of propagation models over the sea. In Proceedings of the 6th International Conference on Advances in Computing, Communications and Informatics, Pune, India, 26–27 February 2015; pp. 69–75. [Google Scholar]
- Wei, T.; Feng, W.; Wang, J.; Ge, N.; Lu, J. Exploiting the shipping lane information for energy-efficient maritime communications. IEEE Trans. Veh. Technol. 2019, 68, 7204–7208. [Google Scholar] [CrossRef]
- Liu, C.; Feng, W.; Wei, T.; Ge, N. Fairness-oriented hybrid precoding for massive MIMO maritime downlink systems with large-scale CSIT. China Commun. 2018, 15, 52–61. [Google Scholar] [CrossRef]
- Jo, S.W.; Shim, W.S. LTE-maritime: High-speed maritime wireless communication based on LTE technology. IEEE Access 2019, 7, 53172–53181. [Google Scholar] [CrossRef]
- Su, N.; Wang, J.B.; Zeng, C.; Zhang, H.; Lin, M.; Li, G.Y. Unmanned surface vehicle aided maritime data collection using deep reinforcement learning. IEEE Internet Things J. 2022, 9, 19773–19786. [Google Scholar] [CrossRef]
- Li, X.; Feng, W.; Chen, Y.; Wang, C.X.; Ge, N. Maritime coverage enhancement using UAVs coordinated with hybrid satellite-terrestrial networks. IEEE Trans. Commun. 2020, 68, 2355–2369. [Google Scholar] [CrossRef]
- Yang, T.; Jiang, Z.; Sun, R.; Cheng, N.; Feng, H. Maritime search and rescue based on group mobile computing for unmanned aerial vehicles and unmanned surface vehicles. IEEE Trans. Ind. Informat. 2020, 16, 7700–7708. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Efficient deployment of multiple unmanned aerial vehicles for optimal wireless coverage. IEEE Commun. Lett. 2016, 20, 1647–1650. [Google Scholar] [CrossRef]
- Dai, H.; Bian, H.; Li, C.; Wang, B. UAV-aided wireless communication design with energy constraint in space-air-ground integrated green IoT networks. IEEE Access 2020, 8, 86251–86261. [Google Scholar] [CrossRef]
- Kumar, K.; Kumar, S.; Kaiwartya, O.; Sikandar, A.; Kharel, R.; Mauri, J.L. Internet of unmanned aerial vehicles: QoS provisioning in aerial ad-hoc networks. Sensors 2020, 20, 3160. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; D’Andreagiovanni, F.; Liu, W.; Gutierrez, J.A.; Blefari-Melazzi, N.; Choo, K.K.R.; Alouini, M.S. Multi-area throughput and energy optimization of UAV-aided cellular networks powered by solar panels and grid. IEEE Trans. Mobile Comput. 2021, 20, 2427–2444. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R. Energy-efficient UAV communication with trajectory optimization. IEEE Trans. Wirel. Commun. 2017, 16, 3747–3760. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, W.; Wang, J.; Quek, T.Q.S. Hybrid satellite-UAV-terrestrial networks for 6G ubiquitous coverage: A maritime communications perspective. IEEE J. Sel. Areas Commun. 2021, 39, 3475–3490. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Y.; Ge, N.; Lu, J.; Zhang, J. Virtual MIMO in multi-cell distributed antenna systems: Coordinated transmissions with large-scale CSIT. IEEE J. Sel. Areas Commun. 2013, 31, 2067–2081. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Y.; Lin, D.; Ge, N.; Lu, J.; Li, S. When mmWave communications meet network densification: A scalable interference coordination perspective. IEEE J. Sel. Areas Commun. 2017, 35, 1459–1471. [Google Scholar] [CrossRef]
- Jha, S.K.; Prakash, S.; Rathore, R.S.; Mahmud, M.; Kaiwartya, O.; Lloret, J. Quality-of-service-centric design and analysis of unmanned aerial vehicles. Sensors 2022, 22, 5477. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Roste, T.; Bekkadal, F.; Ekman, T. Channel characterization including path loss and Doppler effects with sea reflections for mobile radio propagation over sea at 2 GHz. In Proceedings of the 2nd International Conference on Wireless Communications and Signal Processing, Suzhou, China, 21–22 October 2010; pp. 1–6. [Google Scholar]
- Mengali, U.; D’Andrea, A.N. Synchronization Techniques for Digital Receivers; Springer Science and Business Media: New York, NY, USA, 2013. [Google Scholar]
- Gueye, S.; Michel, S.; Yassine, A. A 0-1 linear programming formulation for the Berth Assignment Problem. In Proceedings of the 4th International Conference on Logistics, Hammamet, Tunisia, 31 May–3 June 2011; pp. 50–54. [Google Scholar]
- Todd, M.J. A low complexity interior-point algorithm for linear programming. SIAM J. Optim. 1992, 2, 198–209. [Google Scholar] [CrossRef]
- Zhong, C.; Yao, J.; Xu, J. Secure UAV communication with cooperative jamming and trajectory control. IEEE Commun. Lett. 2019, 23, 286–289. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, R.; Zhang, J.; Gao, S.; Yang, L. Cooperative jamming for secure UAV communications with partial eavesdropper information. IEEE Access 2019, 7, 94593–94603. [Google Scholar] [CrossRef]
- Lee, H.; Eom, S.; Park, J.; Lee, I. UAV-aided secure communications with cooperative jamming. IEEE Trans. Veh. Technol. 2018, 67, 9385–9392. [Google Scholar] [CrossRef]
- Larsson, A.; Piotrowski, A.; Giles, T.; Smart, D. Near-earth RF propagation—Path loss and variation with weather. In Proceedings of the 2nd International Conference on Radar, Adelaide, Australia, 9–12 September 2013; pp. 57–63. [Google Scholar]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for multi-UAV enabled wireless networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L.; Faybusovich, L. Convex optimization. IEEE Trans. Autom. Control 2006, 51, 1859. [Google Scholar]

| Symbols | Description |
|---|---|
| Set of maritime users | |
| Set of UAVs | |
| T | Flight duration |
| Coordinate of user k | |
| Coordinate of UAV m in time t | |
| Time slot | |
| Connection between user k and UAV m in time slot n | |
| Transmission power between user k and UAV m in time slot n | |
| Channel power gain between user k and UAV m in time slot n | |
| The antenna height of user k | |
| The antenna height of UAV m | |
| Data rate of user k served by UAV m in time slot n | |
| Set of communication scheduling variables | |
| Set of transmission power variables | |
| Set of UAV trajectory variables | |
| Introduced slack variable | |
| Introduced auxiliary variable | |
| Introduced auxiliary variable | |
| Introduced auxiliary variable |
| Parameters | Values |
|---|---|
| Carrier frequency | 2 GHz |
| Maximum speed | 50 m/s |
| Maximum transmission power | 1 W |
| Noise power | −114 dBm |
| Minimum collision-proof distance | 100 m |
| Maximum iteration number | 50 |
| Threshold |
| UAV Index | UAV1 | UAV2 | ||
|---|---|---|---|---|
| Scheduling | ||||
| User Index | ||||
| user1 | 0–12, 76–100 s | null | ||
| user2 | 13–50 s | null | ||
| user3 | 51–75 s | null | ||
| user4 | null | 0–10, 86–100 s | ||
| user5 | null | 11–48 s | ||
| user6 | null | 49–85 s | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, G.; Ding, X.; Liu, S. Joint Resource Management and Trajectory Optimization for UAV-Enabled Maritime Network. Sensors 2022, 22, 9763. https://doi.org/10.3390/s22249763
Yu G, Ding X, Liu S. Joint Resource Management and Trajectory Optimization for UAV-Enabled Maritime Network. Sensors. 2022; 22(24):9763. https://doi.org/10.3390/s22249763
Chicago/Turabian StyleYu, Guanding, Xin Ding, and Shengli Liu. 2022. "Joint Resource Management and Trajectory Optimization for UAV-Enabled Maritime Network" Sensors 22, no. 24: 9763. https://doi.org/10.3390/s22249763
APA StyleYu, G., Ding, X., & Liu, S. (2022). Joint Resource Management and Trajectory Optimization for UAV-Enabled Maritime Network. Sensors, 22(24), 9763. https://doi.org/10.3390/s22249763







