Extended Energy-Expenditure Model in Soccer: Evaluating Player Performance in the Context of the Game
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Subjects
2.3. Data Acquisition
2.4. Procedures and Variables
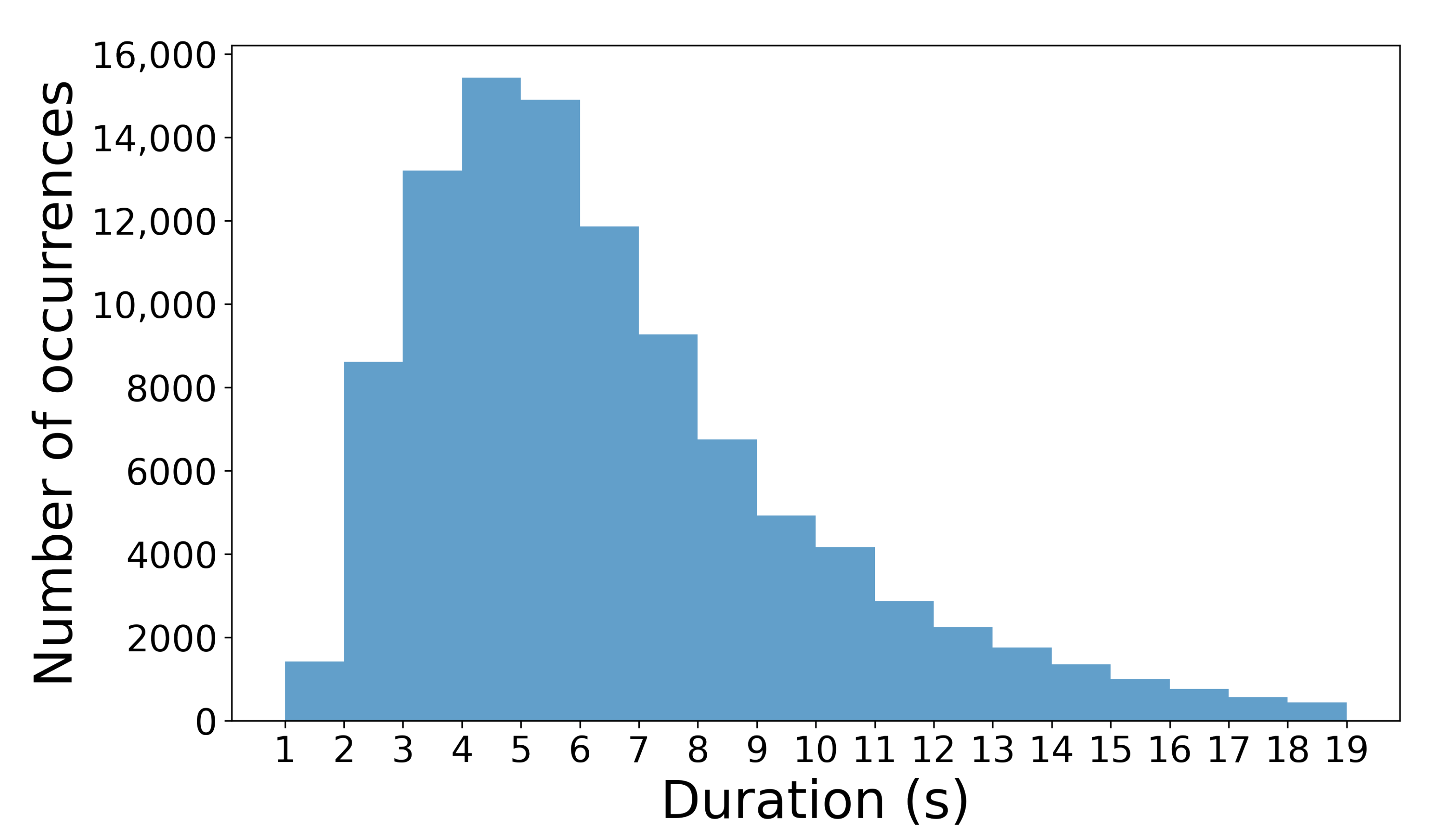
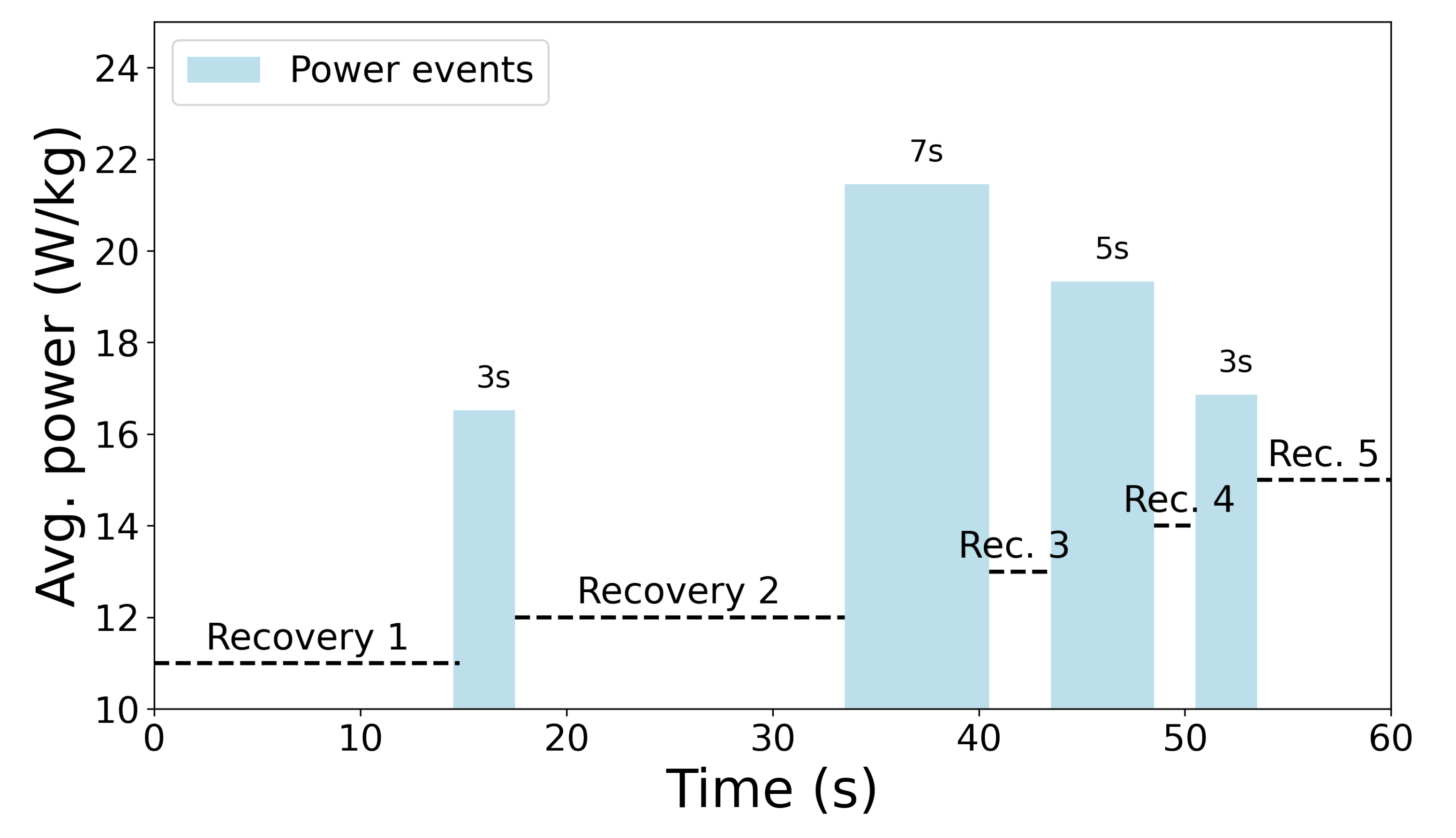
2.4.1. MPE Data
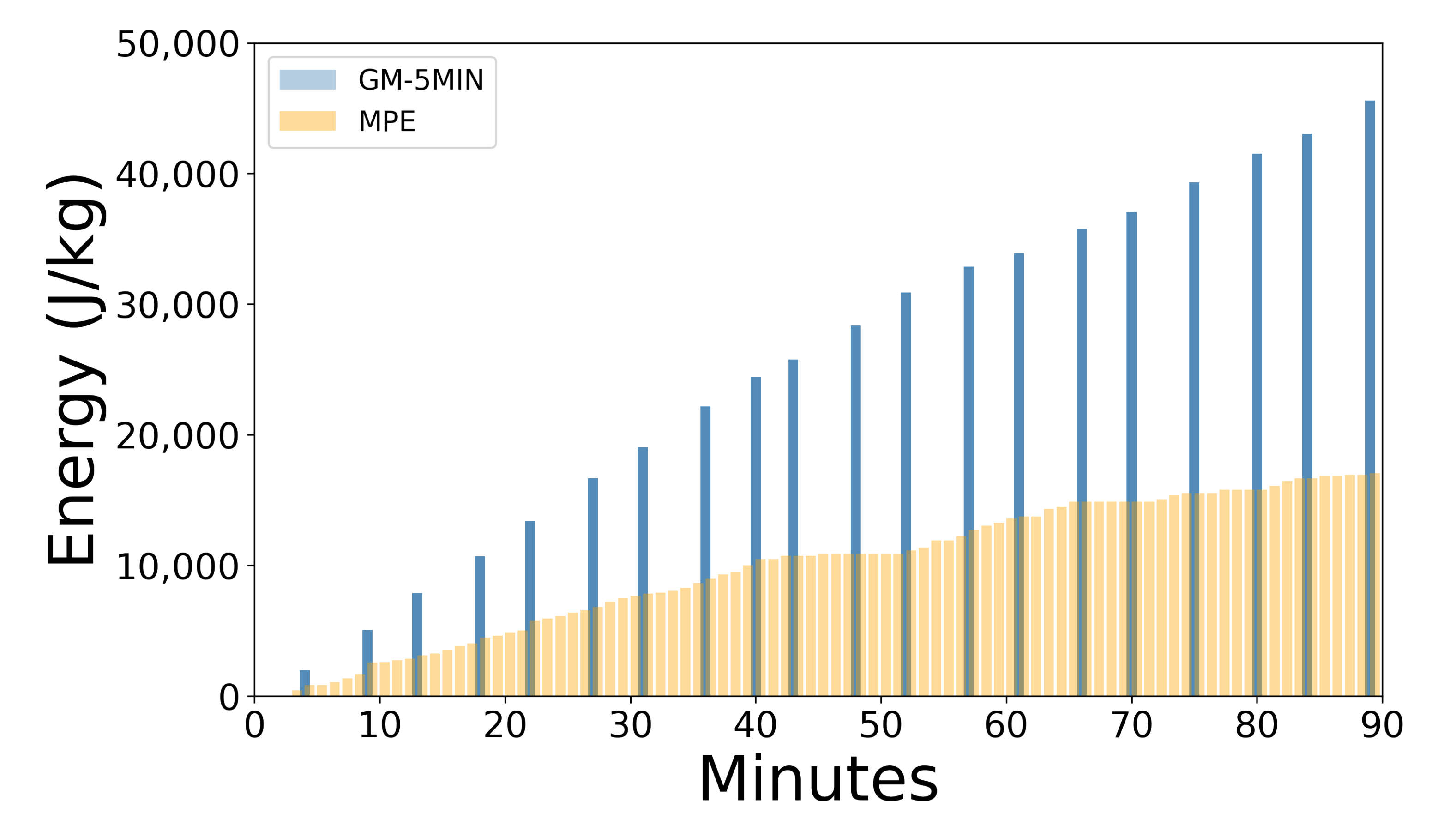
2.4.2. GM-5MIN Data
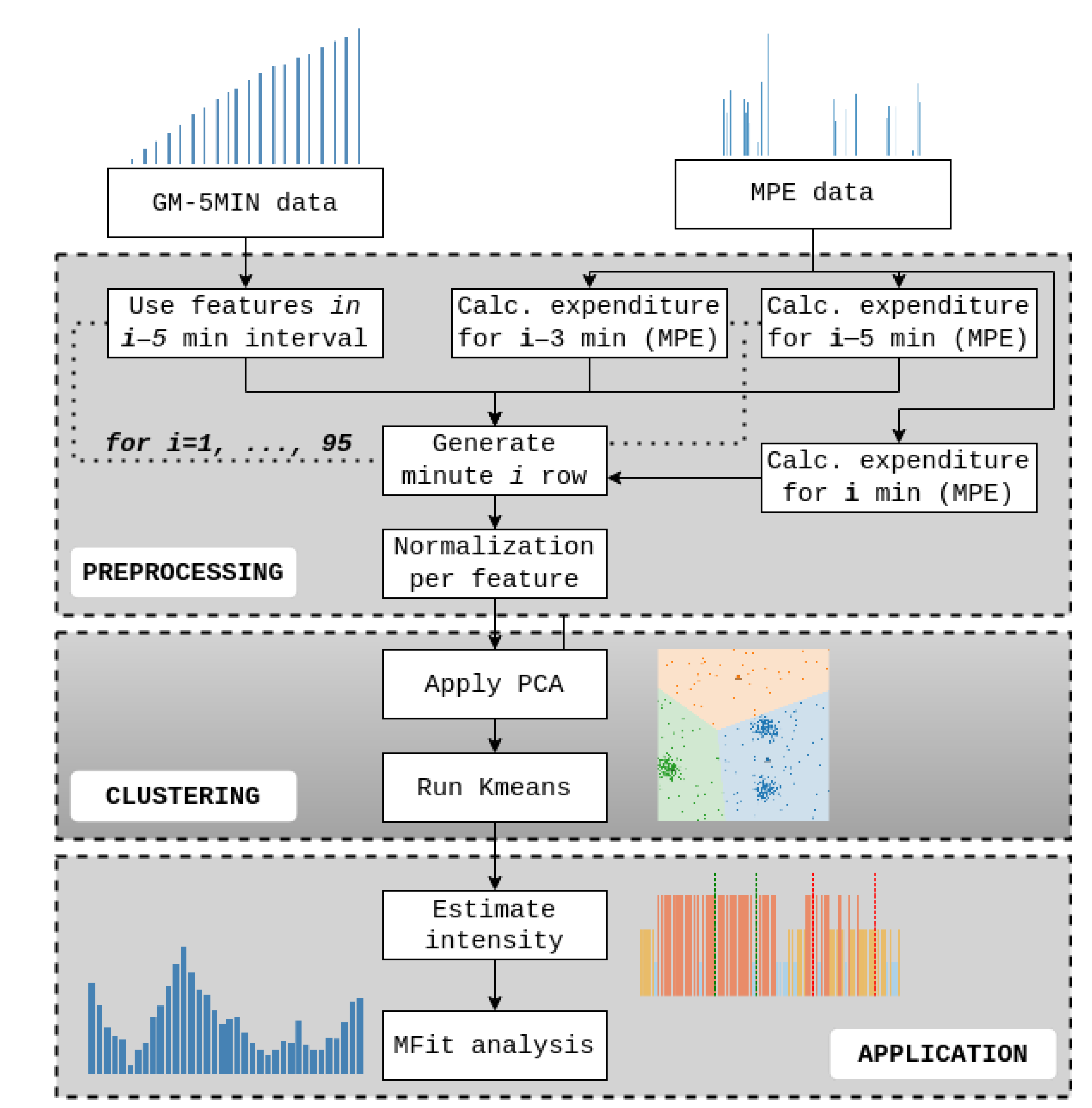
2.5. Data Preprocessing
| Feature Name | Description | |
|---|---|---|
| GM-5MIN-PRIOR | Distance (m) | Distance covered in the last 5 min. |
| MPE count | Number of MPEs in the last 5 min | |
| Anaerobic energy (J/kg) | Anaerobic energy spent in the last 5 min | |
| Average metabolic power (W/kg) | Average metabolic power spent in the last 5 min | |
| Average MPE time (s) | Average MPE duration in the last 5 min | |
| Average MPE recovery time (s) | Average recovery time in the last 5 min | |
| Average MPE recovery power (W/kg) | Average recovery power in the last 5 min | |
| Walk energy (J/kg) | Energy spent walking in the last 5 min | |
| Running energy (J/kg) | Energy spent running in the last 5 min | |
| General energy (J/kg) | Energy spent on all activities in the last 5 min | |
| Total number of MPEs | Number of MPEs up to that moment in the game | |
| Total energy spent (J/kg) | Energy spent up to that moment in the game | |
| MPE-PRIOR | MPE energy (3 min) | Energy spent on MPEs in the last 3 min |
| MPE energy (5 min) | Energy spent on MPEs in the last 5 min | |
| MPE count (3 min) | Number of MPEs in the last 3 min | |
| MPE count (5 min) | Number of MPEs in the last 5 min | |
| Recovery time (s) (3 min) | Recovery time (s) in the last 3 min | |
| Recovery time (s) (5 min) | Recovery time (s) in the last 5 min | |
| Average recovery time (s) (3 min) | Average recovery time (s) in the last 3 min | |
| Average recovery time (s) (5 min) | Average recovery time (s) in the last 5 min | |
| Total recovery time (s) | Recovery time up to that moment in the game | |
| MPE-CURRENT | MPE energy spent (J/kg) | Energy spent on MPEs in the observed minute |
| Event count | Number of MPEs in the observed minute | |
| Average recovery time (s) | Average recovery time in the observed minute | |
| Recovery time (s) | Recovery time in the observed minute |
2.6. Clustering Analysis
2.7. Clustering Application
3. Results
3.1. Clustering Analysis Results
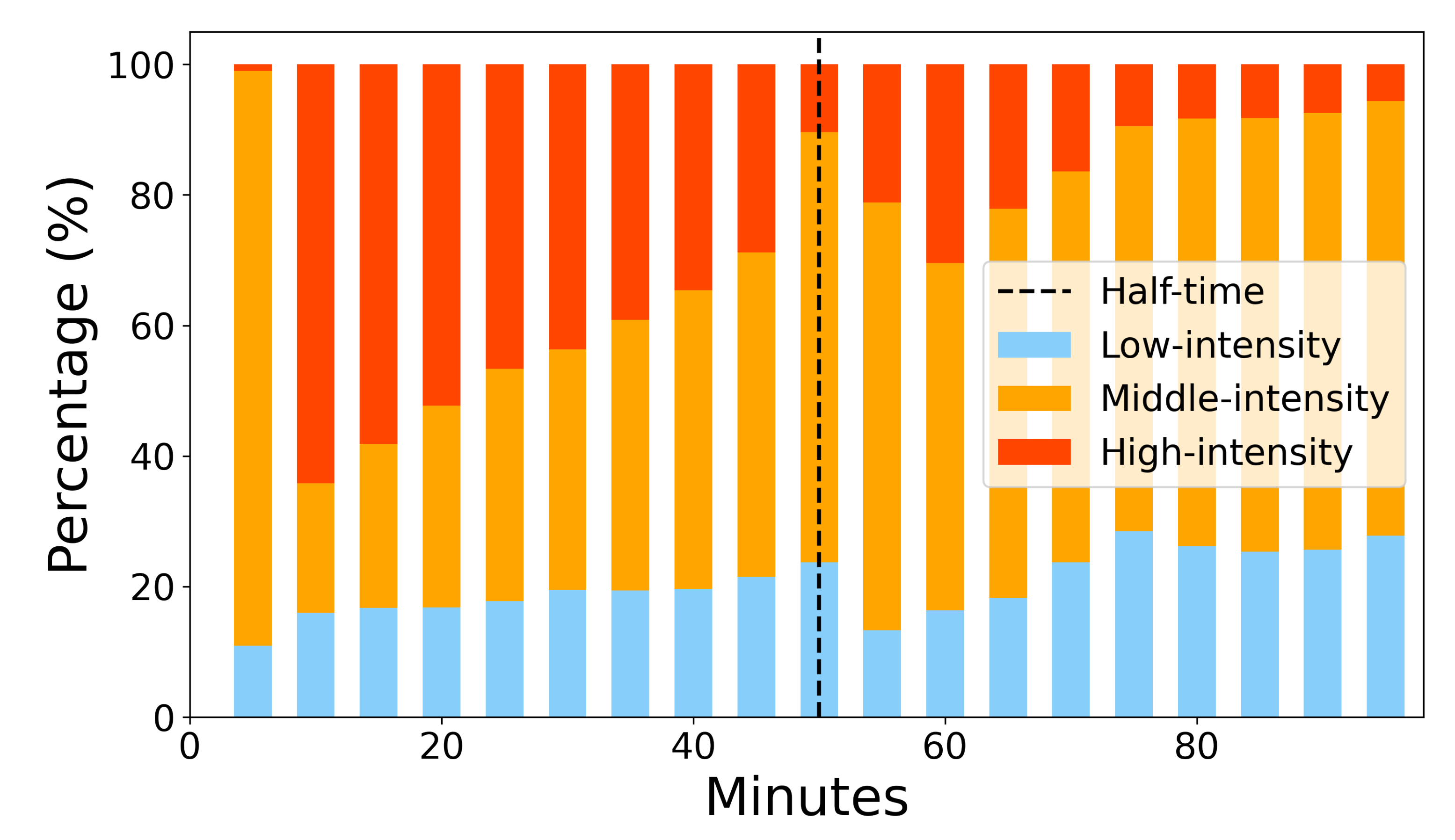
3.2. In-Depth Game Visualization
3.3. Evaluation through Game Load
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GPS | Global Positioning System |
| TD | Total Distance |
| HSR | High-Speed Running |
| MPE | Metabolic Power Event |
| HIA | High Intensity Action |
| CB | Center Back |
| FB | Full Back |
| WB | Wing Back |
| MF | Midfielder |
| WM | Wide Midfielder |
| WF | Wide Forward |
| FW | Forward |
| PCA | Principal Component Analysis |
| WCSS | Within-Cluster Sum of Squares |
| CV | Coefficient of Variation |
| MFit | Markov Fitness |
| GM | GPS Metrics |
References
- Aquino, R.; Munhoz Martins, G.H.; Palucci Vieira, L.H.; Menezes, R.P. Influence of Match Location, Quality of Opponents, and Match Status on Movement Patterns in Brazilian Professional Football Players. J. Strength Cond. Res. 2017, 31, 2155–2161. [Google Scholar] [CrossRef]
- Rago, V.; Silva, J.; Mohr, M.; Randers, M.; Barreira, D.; Krustrup, P.; Rebelo, A. Influence of opponent standard on activity profile and fatigue development during preseasonal friendly soccer matches: A team study. Res. Sport. Med. 2018, 26, 413–424. [Google Scholar] [CrossRef]
- García-Unanue, J.; Pérez-Gómez, J.; Giménez, J.V.; Felipe, J.L.; Gómez-Pomares, S.; Gallardo, L.; Sánchez-Sánchez, J. Influence of contextual variables and the pressure to keep category on physical match performance in soccer players. PLoS ONE 2018, 13, e0204256. [Google Scholar] [CrossRef]
- Palucci Vieira, L.H.; Aquino, R.; Lago-Peñas, C.; Munhoz Martins, G.H.; Puggina, E.F.; Barbieri, F.A. Running Performance in Brazilian Professional Football Players During a Congested Match Schedule. J. Strength Cond. Res. 2018, 32, 313–325. [Google Scholar] [CrossRef]
- Oliva-Lozano, J.M.; Fortes, V.; Krustrup, P.; Muyor, J.M. Acceleration and sprint profiles of professional male football players in relation to playing position. PLoS ONE 2020, 15, e0236959. [Google Scholar] [CrossRef]
- Teixeira, J.E.; Leal, M.; Ferraz, R.; Ribeiro, J.; Cachada, J.M.; Barbosa, T.M.; Monteiro, A.M.; Forte, P. Effects of Match Location, Quality of Opposition and Match Outcome on Match Running Performance in a Portuguese Professional Football Team. Entropy 2021, 23, 973. [Google Scholar] [CrossRef]
- Aquino, R.; Carling, C.; Palucci Vieira, L.H.; Martins, G.; Jabor, G.; Machado, J.; Santiago, P.; Garganta, J.; Puggina, E. Influence of Situational Variables, Team Formation, and Playing Position on Match Running Performance and Social Network Analysis in Brazilian Professional Soccer Players. J. Strength Cond. Res. 2020, 34, 808–817. [Google Scholar] [CrossRef]
- Nobari, H.; Oliveira, R.; Brito, J.P.; Pérez-Gómez, J.; Clemente, F.M.; Ardigò, L.P. Comparison of Running Distance Variables and Body Load in Competitions Based on Their Results: A Full-Season Study of Professional Soccer Players. Int. J. Environ. Res. Public Health 2021, 18, 2077. [Google Scholar] [CrossRef]
- Ponce-Bordón, J.C.; Díaz-García, J.; López-Gajardo, M.A.; Lobo-Triviño, D.; López del Campo, R.; Resta, R.; García-Calvo, T. The Influence of Time Winning and Time Losing on Position-Specific Match Physical Demands in the Top One Spanish Soccer League. Sensors 2021, 21, 6843. [Google Scholar] [CrossRef]
- Lorenzo-Martinez, M.; Kalén, A.; Rey, E.; López-Del Campo, R.; Resta, R.; Lago-Peñas, C. Do elite soccer players cover less distance when their team spent more time in possession of the ball? Sci. Med. Footb. 2021, 5, 310–316. [Google Scholar] [CrossRef]
- Redwood-Brown, A.J.; O’Donoghue, P.G.; Nevill, A.M.; Saward, C.; Dyer, N.; Sunderland, C. Effects of situational variables on the physical activity profiles of elite soccer players in different score line states. Scand. J. Med. Sci. Sports 2018, 28, 2515–2526. [Google Scholar] [CrossRef] [PubMed]
- Trewin, J.; Meylan, C.; Varley, M.C.; Cronin, J. The influence of situational and environmental factors on match-running in soccer: A systematic review. Sci. Med. Footb. 2017, 1, 183–194. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Gómez, M.A.; Gonçalves, B.; Sampaio, J. Technical performance and match-to-match variation in elite football teams. J. Sports Sci. 2016, 34, 509–518. [Google Scholar] [CrossRef]
- Oliveira, R.; Brito, J.P.; Martins, A.; Mendes, B.; Marinho, D.A.; Ferraz, R.; Marques, M.C. In-season internal and external training load quantification of an elite European soccer team. PLoS ONE 2019, 14, e0209393. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, J.H.; Polglaze, T.; Peeling, P. Validity and reliability of a player-tracking device to identify movement orientation in team sports. Int. J. Perform. Anal. Sport 2021, 21, 790–803. [Google Scholar] [CrossRef]
- Prampero, P.E.d.; Osgnach, C. Metabolic Power in Team Sports—Part 1: An Update. Int. J. Sports Med. 2018, 39, 581–587. [Google Scholar] [CrossRef]
- Osgnach, C.; Prampero, P.E.d. Metabolic Power in Team Sports—Part 2: Aerobic and Anaerobic Energy Yields. Int. J. Sport. Med. 2018, 39, 588–595. [Google Scholar] [CrossRef]
- Delves, R.I.M.; Aughey, R.J.; Ball, K.; Duthie, G.M. The Quantification of Acceleration Events in Elite Team Sport: A Systematic Review. Sports Med. 2021, 7, 45. [Google Scholar] [CrossRef]
- Prampero, P.; Fusi, S.; Sepulcri, L.; Morin, J.B.; Belli, A.; Antonutto, G. Sprint running: A new energetic approach. J. Exp. Biol. 2005, 208, 2809–2816. [Google Scholar] [CrossRef] [Green Version]
- Klemp, M.; Memmert, D.; Rein, R. The influence of running performance on scoring the first goal in a soccer match. Int. J. Sport. Sci. Coach. 2021, 17, 17479541211035382. [Google Scholar] [CrossRef]
- Hennessy, L.; Jeffreys, I. The Current Use of GPS, Its Potential, and Limitations in Soccer. Strength Cond. J. 2018, 40, 83–94. [Google Scholar] [CrossRef]
- Cian, C. Macrocycle Overview—Does Player Tracking aid Periodized Peak Performance? Available online: https://pro.statsports.com/macrocycle-overview-does-player-tracking-aid-periodized-peak-performance/ (accessed on 1 December 2022).



| Feature | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 |
|---|---|---|---|---|---|---|---|
| Distance (m) | ✓ | ||||||
| MPE count | ✓ | ||||||
| Anaerobic energy (J/kg) | ✓ | ||||||
| Average metabolic power (W/kg) | ✓ | ✓ | |||||
| Average MPE time (s) | ✓ | ||||||
| Average MPE recovery time (s) | ✓ | ||||||
| Walk energy (J/kg) | ✓ | ✓ | |||||
| Running energy (J/kg) | ✓ | ||||||
| General energy (J/kg) | ✓ | ||||||
| Total event count | ✓ | ||||||
| Total energy spent (J/kg) | ✓ | ✓ | |||||
| MPE energy (3 min) | ✓ | ✓ | ✓ | ||||
| MPE energy (5 min) | ✓ | ||||||
| Average recovery time (s) (3 min) | ✓ | ||||||
| Average recovery time (s) (5 min) | ✓ | ✓ | |||||
| Total recovery time (s) | ✓ | ||||||
| MPE energy spent (J/kg) | ✓ | ||||||
| Event count | ✓ | ✓ | |||||
| Average recovery time (s) | ✓ | ✓ |
| Parameter Name | Low Group | Middle Group | High Group |
|---|---|---|---|
| MPE features (1 min) | |||
| Energy (J) | 0 0 | 180 150 | 230 280 |
| Event count | 0 0 | 1.8 0.9 | 2 1 |
| Average recovery time (s) | 60 0 | 20 7 | 18 8 |
| MPE features (3 min before) | |||
| Energy (J/kg) 3 min | 400 350 | 400 330 | 700 350 |
| MPE count (3 min) | 3.8 2.2 | 4.0 2.2 | 6 2 |
| Recovery time (s) (3 min) | 155 16 | 154 15 | 140 16 |
| GM-5MIN features (5 min before) | |||
| Energy (J/kg) | 2900 1000 | 1300 1000 | 2800 500 |
| MPE count | 6 3.5 | 4 3.5 | 9 2.5 |
| Anaerobic energy (J/kg) | 750 400 | 500 400 | 1000 150 |
| Avg. MPE recovery time (s) | 60 80 | 50 60 | 23 8 |
| Running energy (J/kg) | 1400 800 | 1000 800 | 2250 450 |
| Game Id | Clustering with K-Means | GM-GAME Data | ||||
|---|---|---|---|---|---|---|
| High | Middle | Low | High | Middle | Low | |
| 1 | 0.3572 | 0.4042 | 0.2538 | 0.0743 | 0.5845 | 0.4497 |
| 2 | 0.2456 | 0.5178 | 0.2507 | 0.0881 | 0.5116 | 0.4089 |
| 3 | 0.3300 | 0.5092 | 0.1737 | 0.0511 | 0.5717 | 0.4257 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 79 | 0.4338 | 0.3946 | 0.1863 | 0.0679 | 0.6124 | 0.4352 |
| 80 | 0.2611 | 0.3997 | 0.3487 | 0.0695 | 0.5011 | 0.3963 |
| CV | 45.91% | 30.66% | 24.41% | 21.32% | 16.82% | 19.12% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skoki, A.; Rossi, A.; Cintia, P.; Pappalardo, L.; Štajduhar, I. Extended Energy-Expenditure Model in Soccer: Evaluating Player Performance in the Context of the Game. Sensors 2022, 22, 9842. https://doi.org/10.3390/s22249842
Skoki A, Rossi A, Cintia P, Pappalardo L, Štajduhar I. Extended Energy-Expenditure Model in Soccer: Evaluating Player Performance in the Context of the Game. Sensors. 2022; 22(24):9842. https://doi.org/10.3390/s22249842
Chicago/Turabian StyleSkoki, Arian, Alessio Rossi, Paolo Cintia, Luca Pappalardo, and Ivan Štajduhar. 2022. "Extended Energy-Expenditure Model in Soccer: Evaluating Player Performance in the Context of the Game" Sensors 22, no. 24: 9842. https://doi.org/10.3390/s22249842
APA StyleSkoki, A., Rossi, A., Cintia, P., Pappalardo, L., & Štajduhar, I. (2022). Extended Energy-Expenditure Model in Soccer: Evaluating Player Performance in the Context of the Game. Sensors, 22(24), 9842. https://doi.org/10.3390/s22249842










