The Influence of Temperature on Frequency Modulation Spectroscopy in Atom Gravimeter
Abstract
:1. Introduction
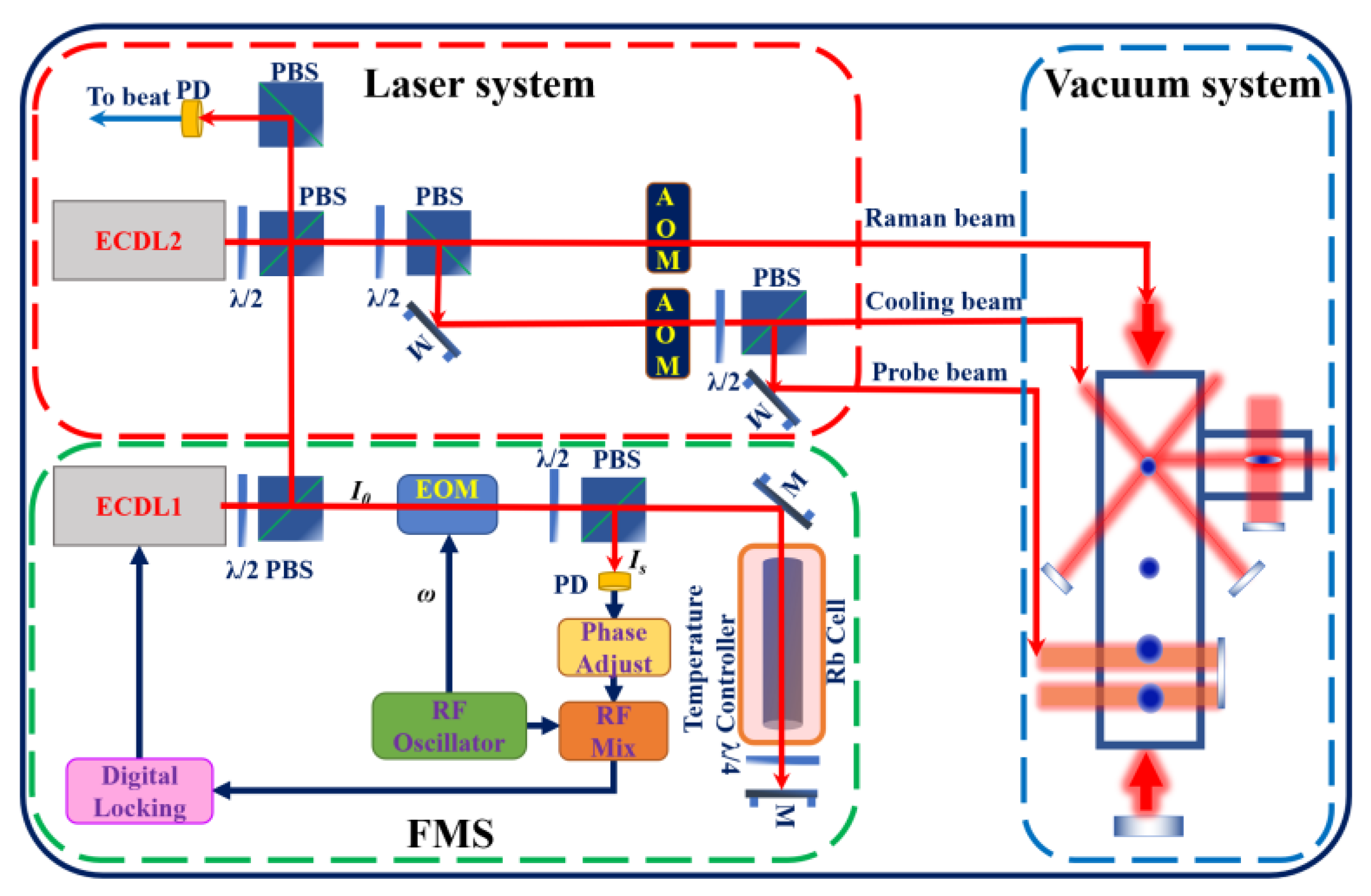
2. Experimental Setup
3. Theory
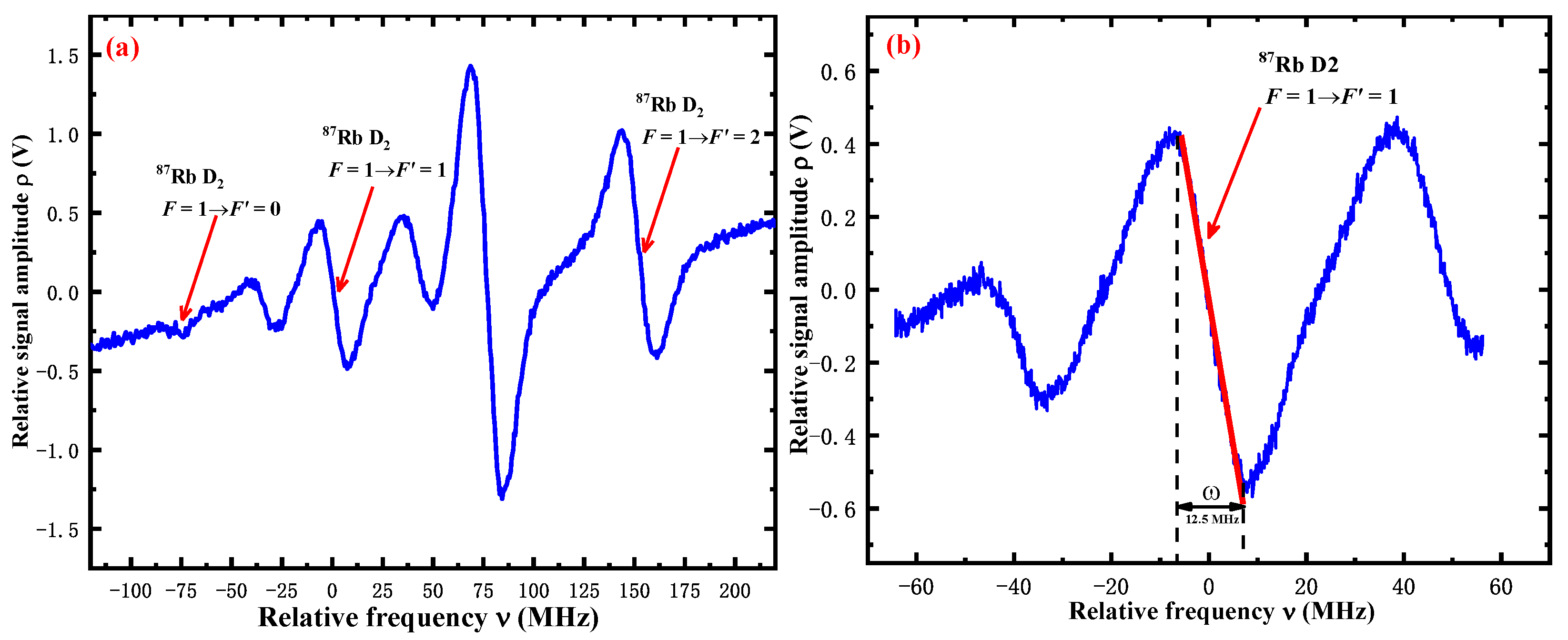
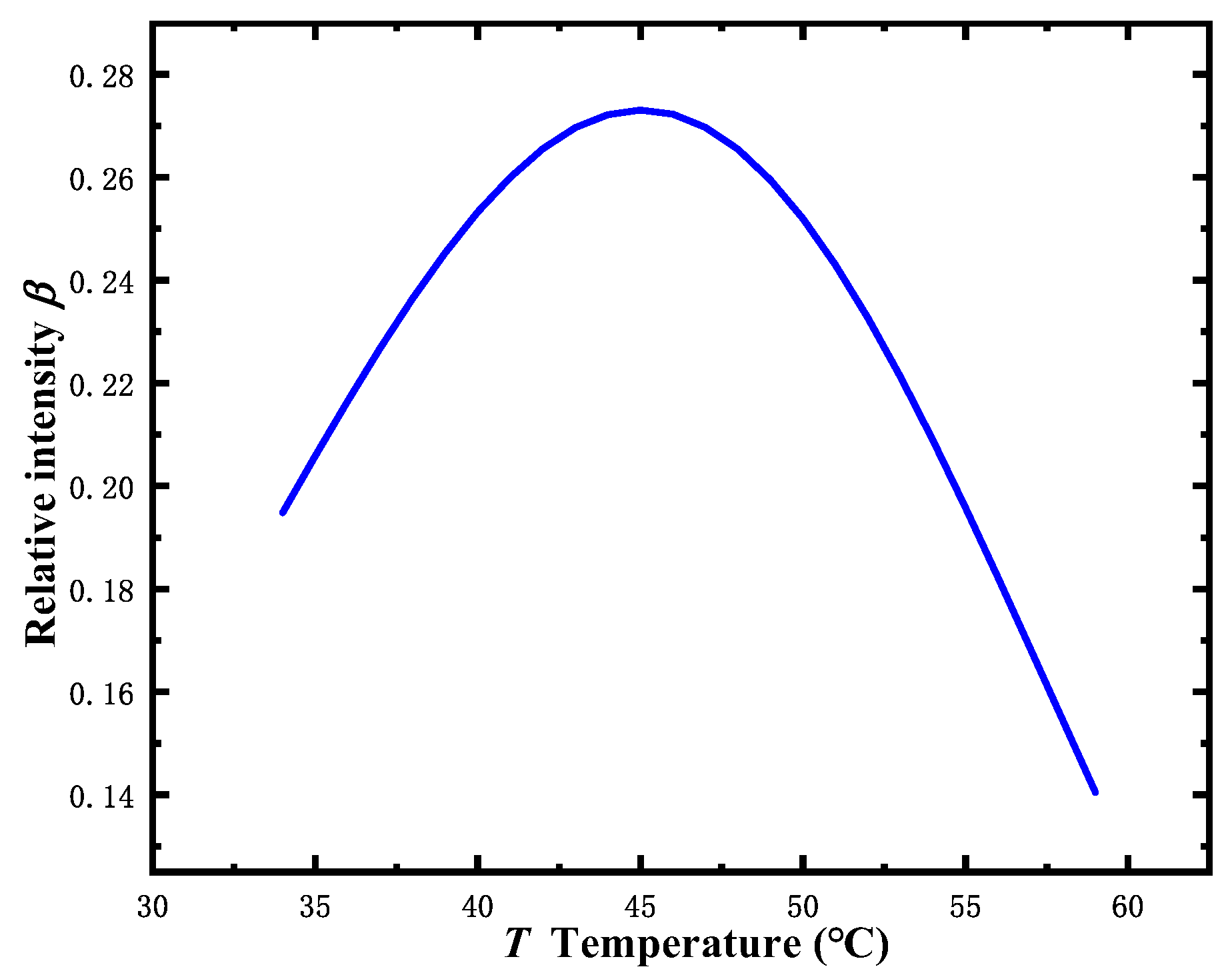
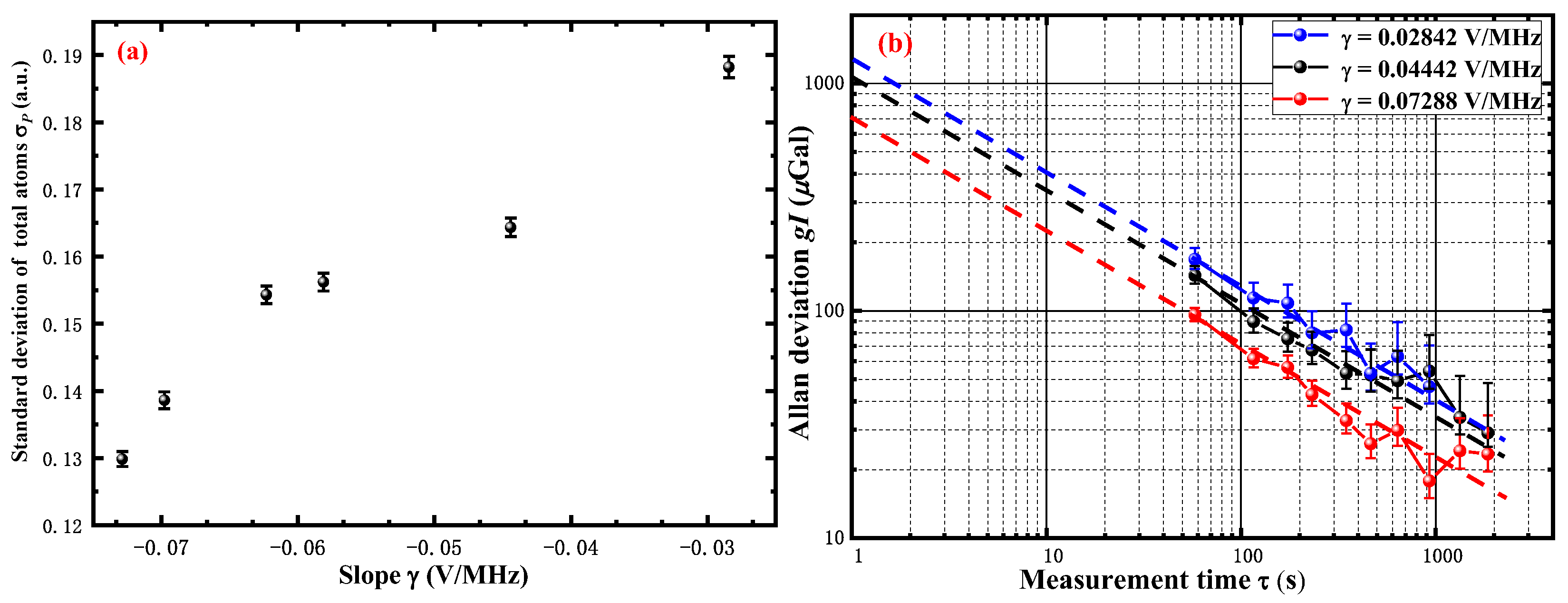
4. Experimental Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Keith, D.W.; Schattenburg, M.L.; Smith, H.I.; Pritchard, D.E. Diffraction of Atoms by a Transmission Grating. Phys. Rev. Lett. 1988, 61, 1580–1583. [Google Scholar] [CrossRef] [PubMed]
- Clauser, J.F. Ultra-high sensitivity accelerometers and gyroscopes using neutral atom matter-wave interferometry. Phys. B+C 1988, 151, 262–272. [Google Scholar] [CrossRef]
- Kasevich, M.; Chu, S. Atomic interferometry using stimulated Raman transitions. Phys. Rev. Lett. 1991, 67, 181–184. [Google Scholar] [CrossRef] [PubMed]
- Parker, R.H.; Yu, C.; Zhong, W.; Estey, B.; Müller, H. Measurement of the fine-structure constant as a test of the Standard Model. Science 2018, 360, 191–195. [Google Scholar] [CrossRef] [Green Version]
- Bouchendira, R.; Cladé, P.; Guellati-Khélifa, S.; Nez, F.; Biraben, F. New Determination of the Fine Structure Constant and Test of the Quantum Electrodynamics. Phys. Rev. Lett. 2011, 106, 080801. [Google Scholar] [CrossRef] [Green Version]
- Fixler, J.B.; Foster, G.T.; McGuirk, J.M.; Kasevich, M.A. Atom Interferometer Measurement of the Newtonian Constant of Gravity. Science 2007, 315, 74–77. [Google Scholar] [CrossRef]
- Rosi, G.; Sorrentino, F.; Cacciapuoti, L.; Prevedelli, M.; Tino, G.M. Precision measurement of the Newtonian gravitational constant using cold atoms. Nature 2014, 510, 518–521. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Zhao, Y.; Cheng, B.; Zhang, C.; Li, D.; Zhu, D.; Yue, Y.; Li, J.; Zhang, K.; Lin, Q.; et al. A Simplified Laser System for Atom Interferometry Based on a Free-Space EOM. Photonics 2022, 9, 301. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Zimmermann, M.; Efremov, M.A.; Schleich, W.P.; Shemer, L.; Arie, A. Amplitude and Phase of Wave Packets in a Linear Potential. Phys. Rev. Lett. 2019, 122, 124302. [Google Scholar] [CrossRef] [Green Version]
- Gonçalves, M.R.; Rozenman, G.G.; Zimmermann, M.; Efremov, M.A.; Case, W.B.; Arie, A.; Shemer, L.; Schleich, W.P. Bright and dark diffractive focusing. Appl. Phys. A 2022, 128, 1–23. [Google Scholar] [CrossRef]
- Asenbaum, P.; Overstreet, C.; Kim, M.; Curti, J.; Kasevich, M.A. Atom-interferometric test of the equivalence principle at the 10–12 level. Phys. Rev. Lett. 2020, 125, 191101. [Google Scholar] [CrossRef] [PubMed]
- Gustavson, T.L.; Bouyer, P.; Kasevich, M.A. Precision Rotation Measurements with an Atom Interferometer Gyroscope. Phys. Rev. Lett. 1997, 78, 2046–2049. [Google Scholar] [CrossRef] [Green Version]
- Savoie, D.; Altorio, M.; Fang, B.; Sidorenkov, L.A.; Geiger, R.; Landragin, A. Interleaved atom interferometry for high-sensitivity inertial measurements. Sci. Adv. 2018, 4, eaau7948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tackmann, G.; Berg, P.; Schubert, C.; Abend, S.; Gilowski, M.; Ertmer, W.; Rasel, E.M. Self-alignment of a compact large-area atomic Sagnac interferometer. New J. Phys. 2012, 14, 015002. [Google Scholar] [CrossRef]
- Fang, J.; Qin, J. Advances in Atomic Gyroscopes: A View from Inertial Navigation Applications. Sensors 2012, 12, 6331–6346. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Gao, W.; Li, Q.; Li, R.; Yao, Z.; Lu, S. A Novel Monitoring Navigation Method for Cold Atom Interference Gyroscope. Sensors 2019, 19, 222. [Google Scholar] [CrossRef] [Green Version]
- Kasevich, M.; Chu, S. Measurement of the gravitational acceleration of an atom with a light-pulse atom interferometer. Appl. Phys. A 1992, 54, 321–332. [Google Scholar] [CrossRef]
- Peters, A.; Chung, K.Y.; Chu, S. High-precision gravity measurements using atom interferometry. Metrologia 2001, 38, 25–61. [Google Scholar] [CrossRef]
- Le Gouët, J.; Mehlstäubler, T.; Kim, J.; Merlet, S.; Clairon, A.; Landragin, A.; Dos Santos, F.P. Limits to the sensitivity of a low noise compact atomic gravimeter. Appl. Phys. B Laser Opt. 2008, 92, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Xu, V.; Jaffe, M.; Panda, C.D.; Kristensen, S.L.; Clark, L.W.; Müller, H. Probing gravity by holding atoms for 20 s. Science 2019, 366, 745–749. [Google Scholar] [CrossRef]
- Margalit, Y.; Dobkowski, O.; Zhou, Z.; Amit, O.; Japha, Y.; Moukouri, S.; Rohrlich, D.; Mazumdar, A.; Bose, S.; Henkel, C.; et al. Realization of a complete Stern-Gerlach interferometer: Toward a test of quantum gravity. Sci. Adv. 2021, 7, eabg2879. [Google Scholar] [CrossRef] [PubMed]
- Snadden, M.J.; McGuirk, J.M.; Bouyer, P.; Haritos, K.G.; Kasevich, M.A. Measurement of the Earth’s gravity gradient with an atom interferometer-based gravity gradiometer. Phys. Rev. Lett. 1998, 81, 971–974. [Google Scholar] [CrossRef]
- Sorrentino, F.; Bodart, Q.; Cacciapuoti, L.; Lien, Y.-H.; Prevedelli, M.; Rosi, G.; Salvi, L.; Tino, G.M. Sensitivity limits of a Raman atom interferometer as a gravity gradiometer. Phys. Rev. A 2014, 89, 023607. [Google Scholar] [CrossRef] [Green Version]
- Sorrentino, F.; Lien, Y.-H.; Rosi, G.; Cacciapuoti, L.; Prevedelli, M.; Tino, G.M. Sensitive gravity-gradiometry with atom interferometry: Progress towards an improved determination of the gravitational constant. New J. Phys. 2010, 12, 095009. [Google Scholar] [CrossRef]
- Duan, X.-C.; Zhou, M.-K.; Mao, D.-K.; Yao, H.-B.; Deng, X.-B.; Luo, J.; Hu, Z.-K. Operating an atom-interferometry-based gravity gradiometer by the dual-fringe-locking method. Phys. Rev. A 2014, 90, 023617. [Google Scholar] [CrossRef]
- Caldani, R.; Weng, K.X.; Merlet, S.; Dos Santos, F.P. Simultaneous accurate determination of both gravity and its vertical gradient. Phys. Rev. A 2019, 99, 033601. [Google Scholar] [CrossRef] [Green Version]
- Perrin, I.; Bidel, Y.; Zahzam, N.; Blanchard, C.; Bresson, A.; Cadoret, M. Proof-of-principle demonstration of vertical-gravity-gradient measurement using a single-proof-mass double-loop atom interferometer. Phys. Rev. A 2019, 99, 013601. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.-K.; Sun, B.-L.; Duan, X.-C.; Zhou, M.-K.; Chen, L.-L.; Zhan, S.; Zhang, Q.-Z.; Luo, J. Demonstration of an ultrahigh-sensitivity atom-interferometry absolute gravimeter. Phys. Rev. A 2013, 88, 043610. [Google Scholar] [CrossRef]
- Narducci, F.A.; Black, A.T.; Burke, J.H. Advances toward fieldable atom interferometers. Adv. Phys. X 2022, 7, 043610. [Google Scholar] [CrossRef]
- Amit, O.; Margalit, Y.; Dobkowski, O.; Zhou, Z.; Japha, Y.; Zimmermann, M.; Efremov, M.A.; Narducci, F.A.; Rasel, E.M.; Schleich, W.P. T 3 Stern-Gerlach matter-wave interferometer. Phys. Rev. Lett. 2019, 123, 083601. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, Y.; Weng, K.; Zhu, D.; Fu, Z.; Cheng, B.; Wang, X.; Lin, Q. Modulation transfer spectroscopy for D1 transition line of rubidium. J. Opt. Soc. Am. B 2018, 35, 2705–2710. [Google Scholar] [CrossRef]
- Le Gouët, J.; Kim, J.; Bourassin-Bouchet, C.; Lours, M.; Landragin, A.; Dos Santos, F.P. Wide bandwidth phase-locked diode laser with an intra-cavity electro-optic modulator. Opt. Commun. 2009, 282, 977–980. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, O.; Knaak, K.-M.; Wynands, R.; Meschede, D. Cesium saturation spectroscopy revisited: How to reverse peaks and observe narrow resonances. Appl. Phys. A 1994, 59, 167–178. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, X.; Liu, S.; Yu, J.; Chen, X. Laser frequency stabilization using a dispersive line shape induced by Doppler Effect. Opt. Express 2015, 23, 2982–2990. [Google Scholar] [CrossRef] [PubMed]
- Shirley, J.H. Modulation transfer processes in optical heterodyne saturation spectroscopy. Opt. Lett. 1982, 7, 537–539. [Google Scholar] [CrossRef]
- Hong, Y.; Hou, X.; Chen, D.; Zhou, C.; Huang, M.; Song, T.; Wang, G.; Zhao, J.; Chen, W. Research on Frequency Stabilization Technology of Modulation Transfer Spectroscopy Based on Rb~(87). Chin. J. Lasers 2021, 48, 27–34. [Google Scholar]
- Bjorklund, G.C. Frequency-modulation spectroscopy: A new method for measuring weak absorptions and dispersions. Opt. Lett. 1980, 5, 15–17. [Google Scholar] [CrossRef]
- Mandon, J.; Guelachvili, G.; Picqué, N. Frequency-modulation Fourier transform spectroscopy: A broadband method for measuring weak absorptions and dispersions. Opt. Lett. 2007, 32, 2206–2208. [Google Scholar] [CrossRef]
- Zi, F.; Wu, X.; Zhong, W.; Parker, R.H.; Yu, C.; Budker, S.; Lu, X.; Müller, H. Laser frequency stabilization by combining modulation transfer and frequency modulation spectroscopy. Appl. Opt. 2017, 56, 2649–2652. [Google Scholar] [CrossRef]
- Bjorklund, G.C.; Levenson, M.D.; Lenth, W.; Ortiz, C. Frequency modulation (FM) spectroscopy. Theory of lineshapes and signal-to-noise analysis. Appl. Phys. B (Photophys. Laser Chem.) 1983, B32, 145–152. [Google Scholar] [CrossRef]
- Supplee, J.M.; Whittaker, E.A.; Lenth, W. Theoretical description of frequency modulation and wavelength modulation spectroscopy. Appl. Opt. 1994, 33, 6294–6302. [Google Scholar] [CrossRef] [PubMed]
- Petrov, K.P.; Waltman, S.; Dlugokencky, E.J.; Arbore, M.; Fejer, M.M.; Tittel, F.K.; Hollberg, L.W. Precise measurement of methane in air using diode-pumped 3.4-μm difference-frequency generation in PPLN. Appl. Phys. B-Lasers Opt. 1997, 64, 567–572. [Google Scholar] [CrossRef]
- Merlet, S.; Volodimer, L.; Lours, M.; Dos Santos, F.P. A simple laser system for atom interferometry. Appl. Phys. A 2014, 117, 749–754. [Google Scholar] [CrossRef] [Green Version]
- Fu, Z.F.Z.; Wang, Q.W.Q.; Wang, Z.W.Z.; Bin Wu, B.W.; Cheng, B.C.B.; Lin, Q.L.Q. Participation in the absolute gravity comparison with a compact cold atom gravimeter. Chin. Opt. Lett. 2019, 17, 011204. [Google Scholar] [CrossRef] [Green Version]
- Nakayama, S. Theoretical Analysis of Rb and Cs D2 Lines in Saturation Spectroscopy with Optical Pumping. Jpn. J. Appl. Phys. 1984, 23, 879–883. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weng, K.; Wu, B.; Wang, F.; Zhang, X.; Zhou, Y.; Cheng, B.; Lin, Q. The Influence of Temperature on Frequency Modulation Spectroscopy in Atom Gravimeter. Sensors 2022, 22, 9935. https://doi.org/10.3390/s22249935
Weng K, Wu B, Wang F, Zhang X, Zhou Y, Cheng B, Lin Q. The Influence of Temperature on Frequency Modulation Spectroscopy in Atom Gravimeter. Sensors. 2022; 22(24):9935. https://doi.org/10.3390/s22249935
Chicago/Turabian StyleWeng, Kanxing, Bin Wu, Feichen Wang, Xiaohui Zhang, Yin Zhou, Bing Cheng, and Qiang Lin. 2022. "The Influence of Temperature on Frequency Modulation Spectroscopy in Atom Gravimeter" Sensors 22, no. 24: 9935. https://doi.org/10.3390/s22249935
APA StyleWeng, K., Wu, B., Wang, F., Zhang, X., Zhou, Y., Cheng, B., & Lin, Q. (2022). The Influence of Temperature on Frequency Modulation Spectroscopy in Atom Gravimeter. Sensors, 22(24), 9935. https://doi.org/10.3390/s22249935



