Design and Fabrication of a Novel Wheel-Ring Triaxial Gyroscope
Abstract
:1. Introduction
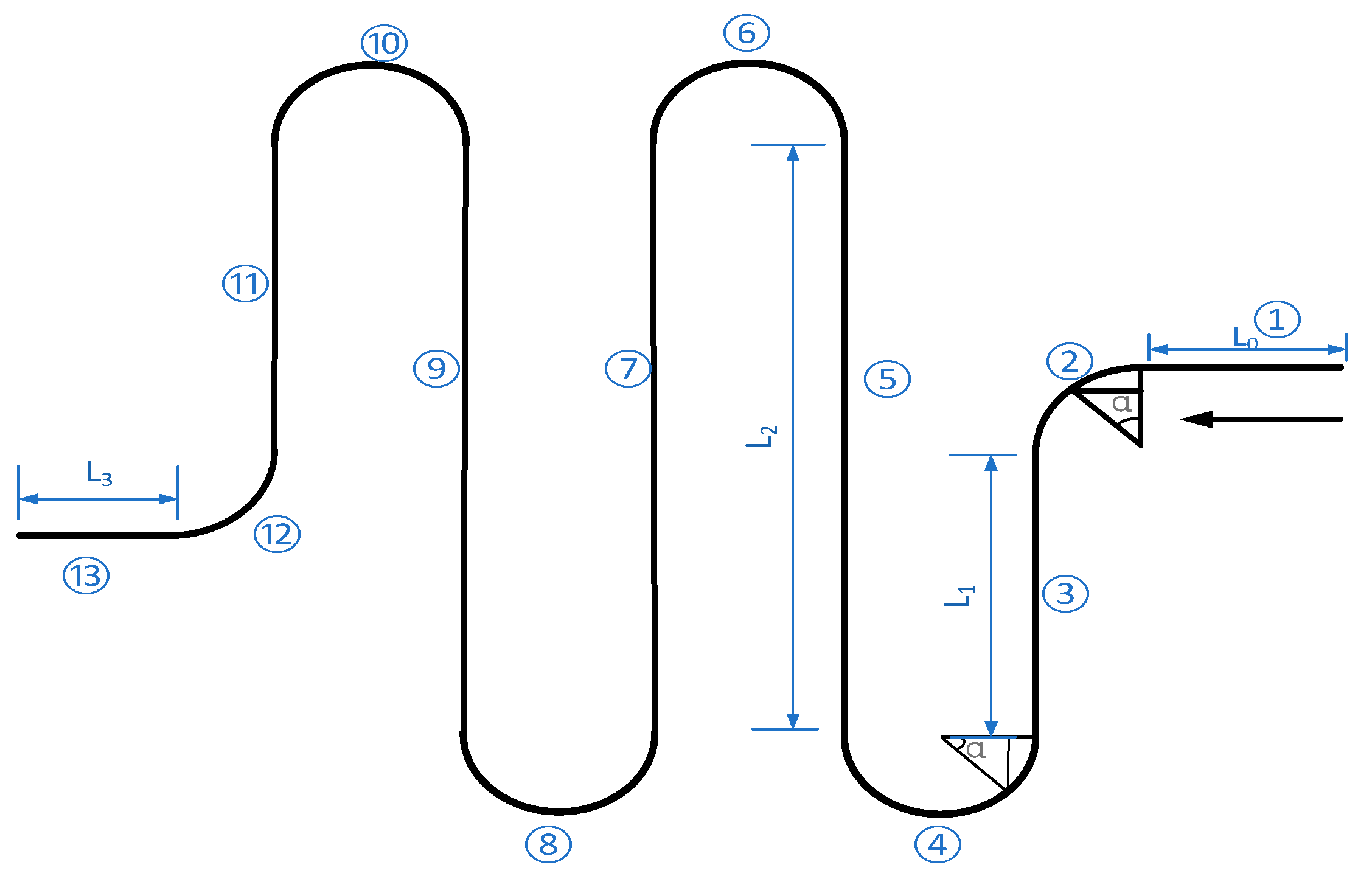
2. Structure Design
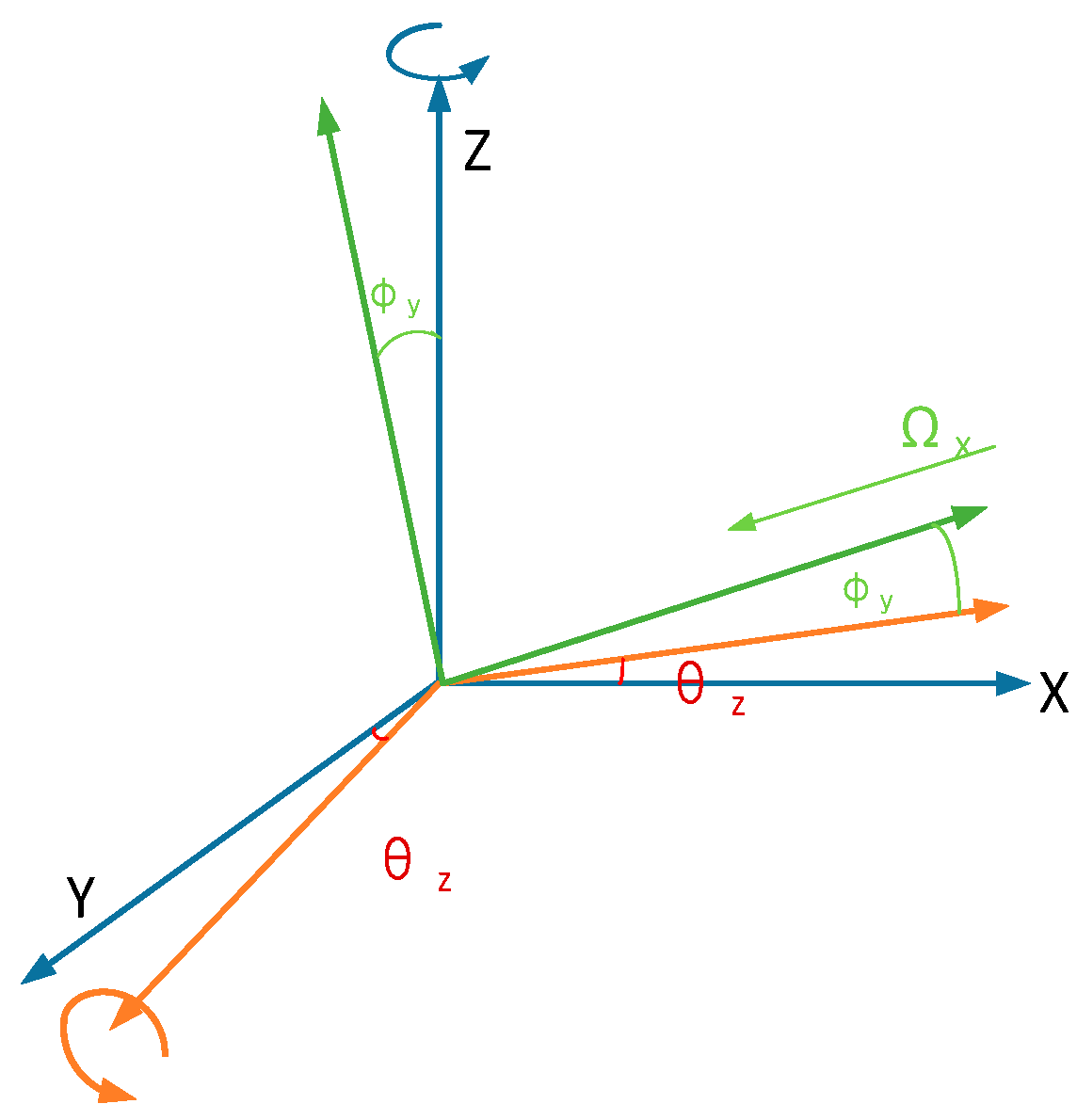
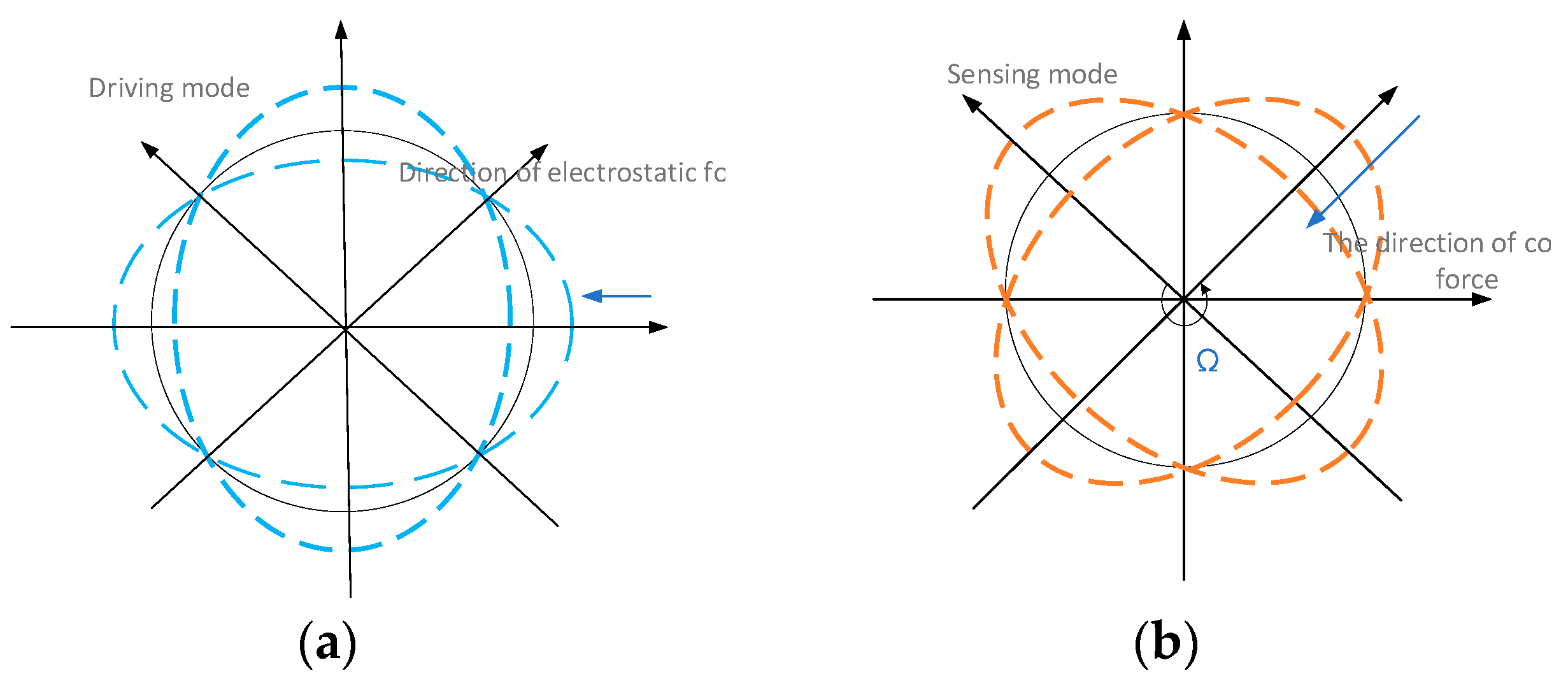
2.1. Operating Principle
2.2. Mathematical Model
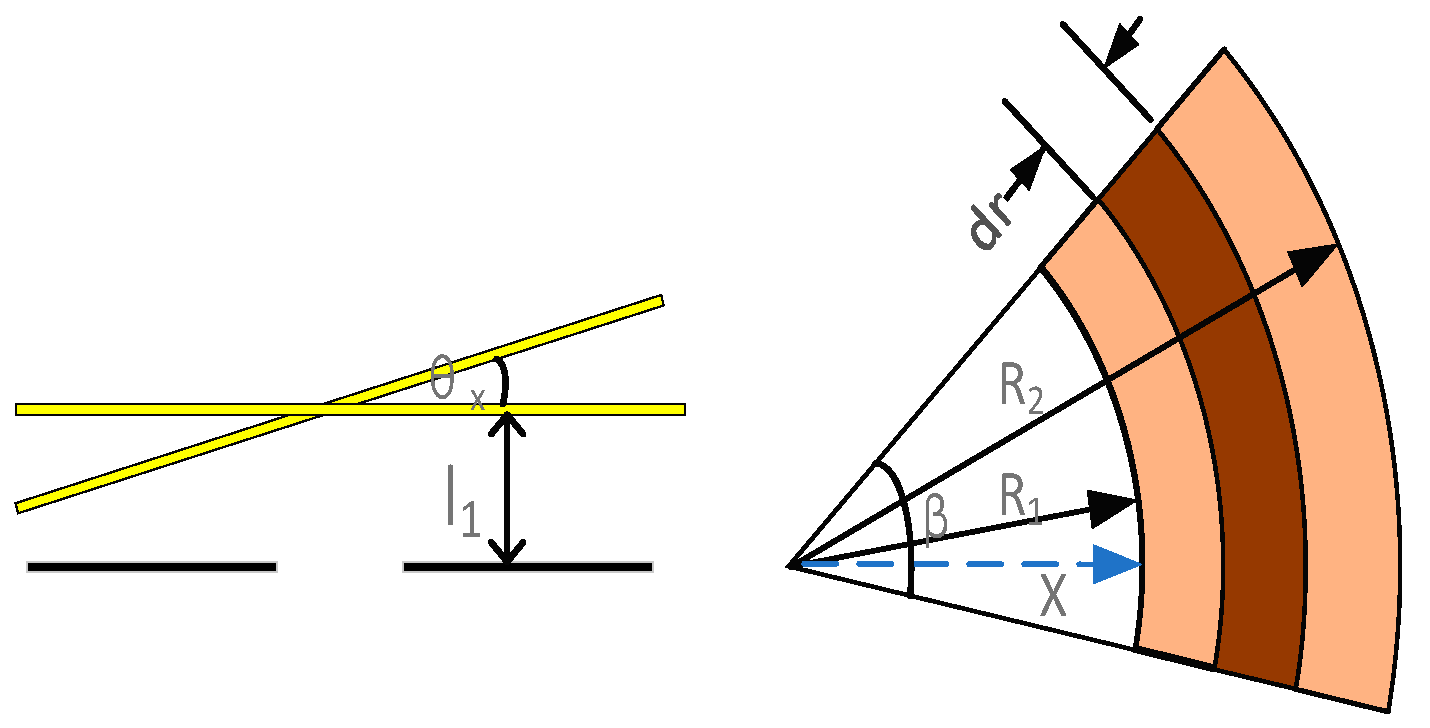
2.3. Stiffness Calculation of S-Shaped Springs
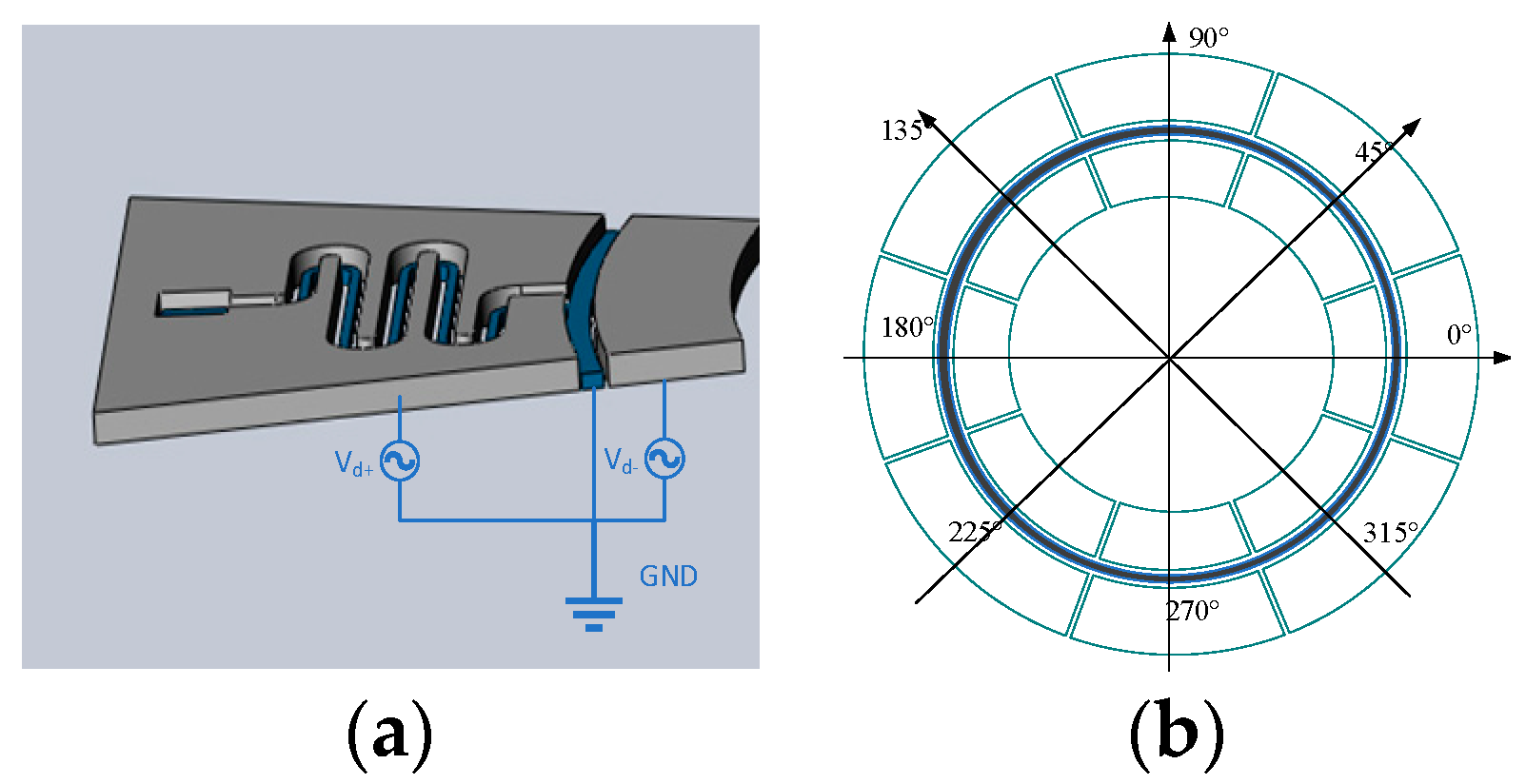
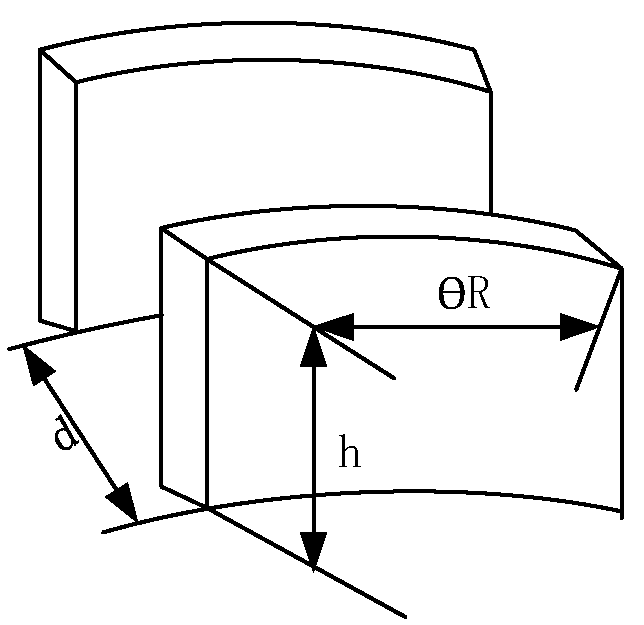
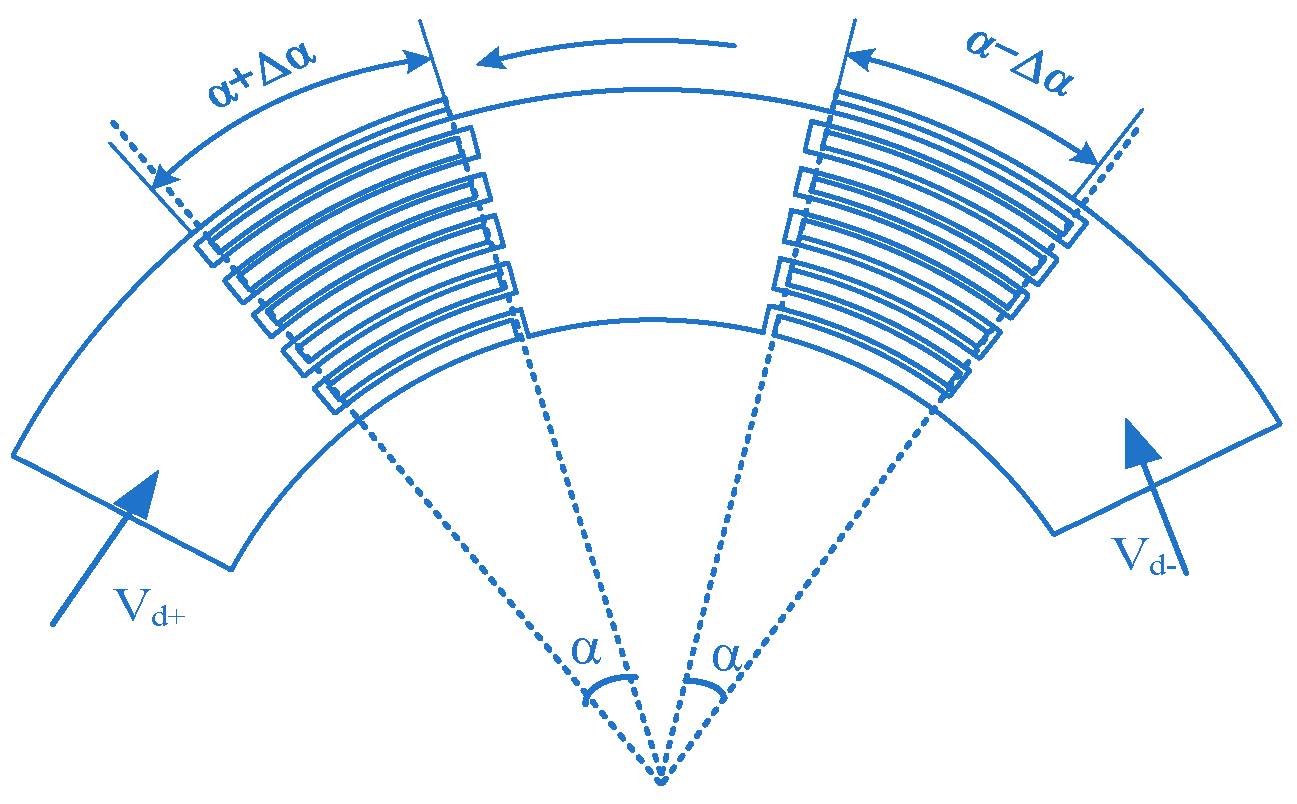
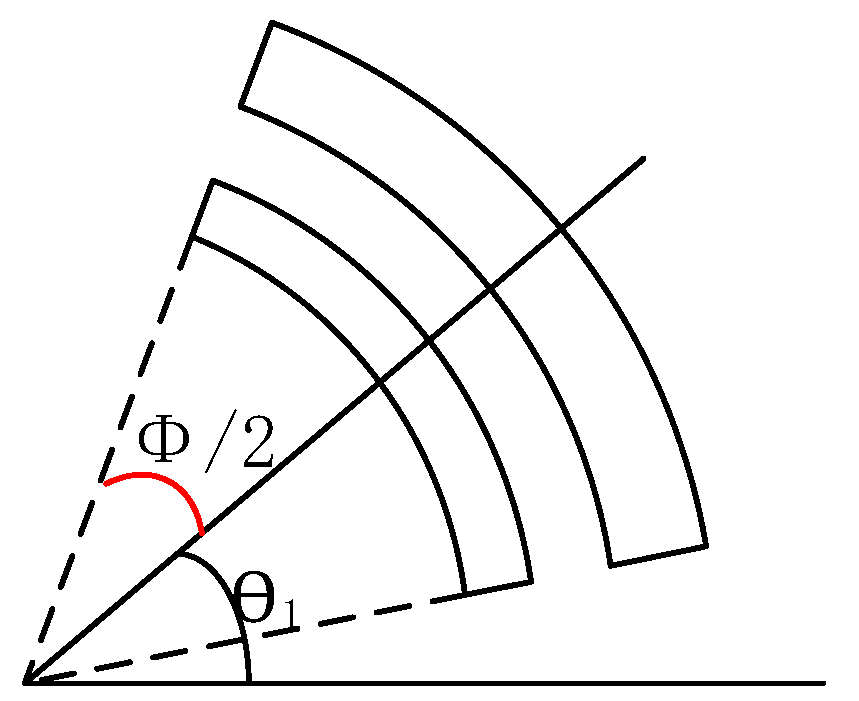
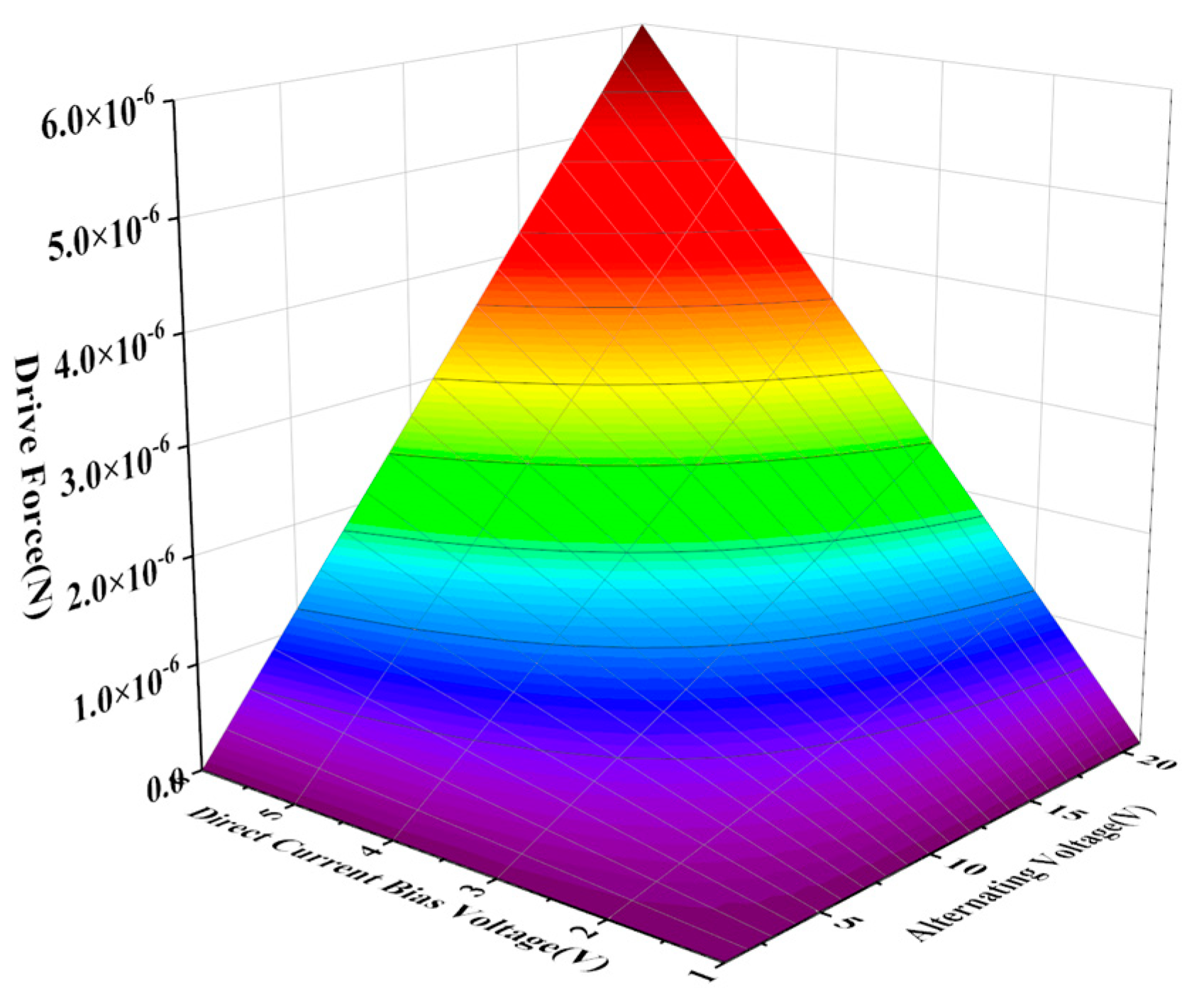
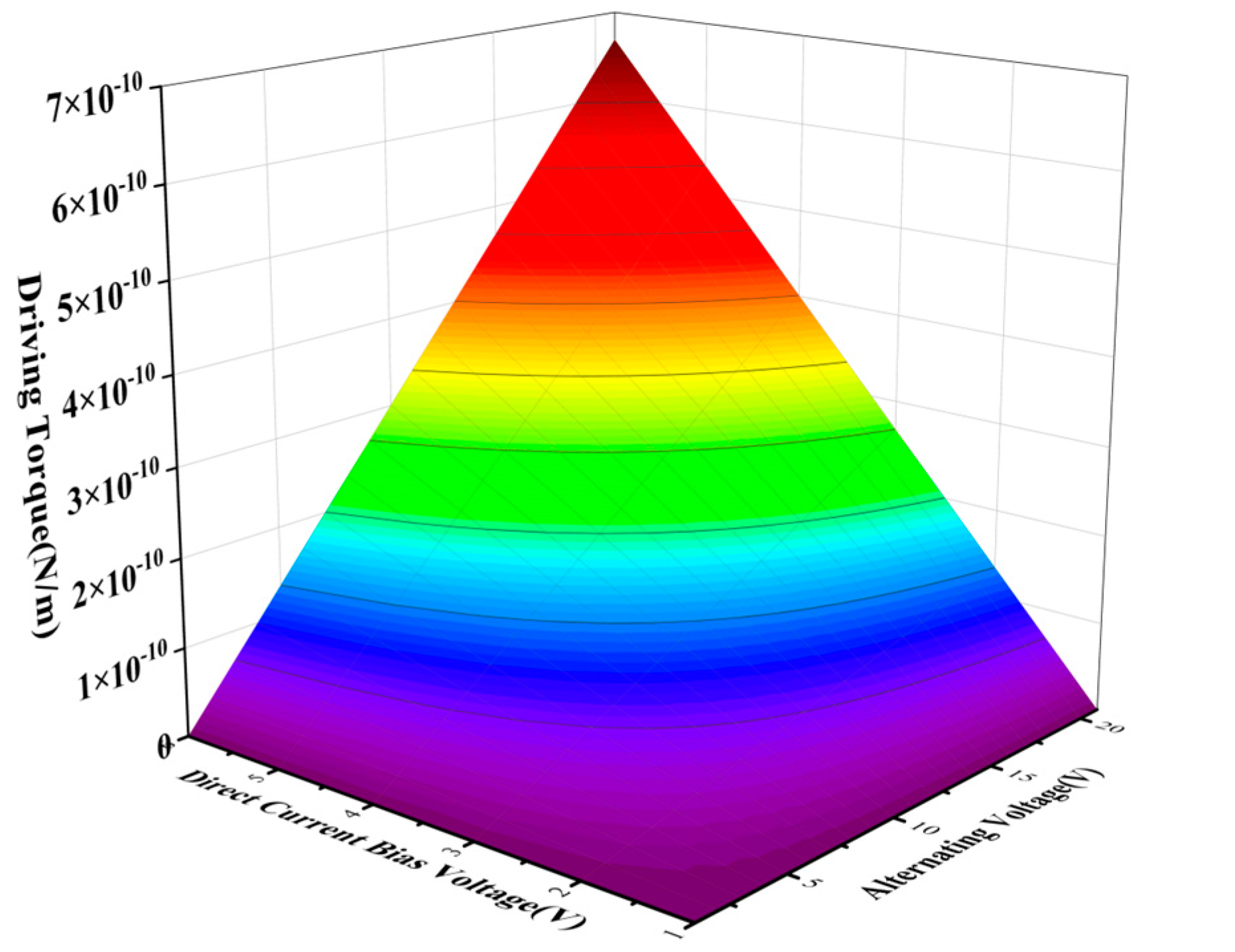
2.4. Drive Force Calculation
2.5. Sensing Capacitance
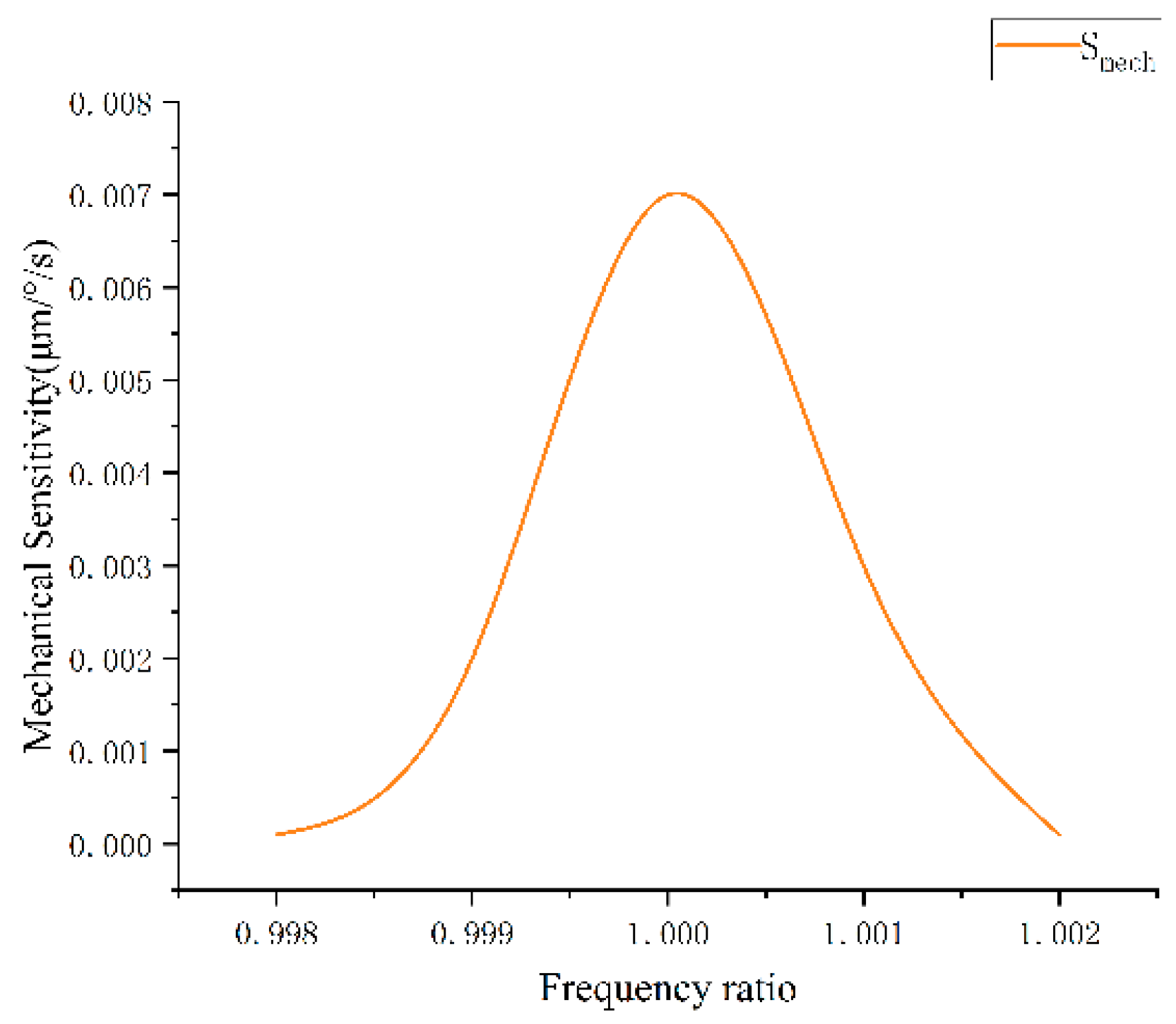
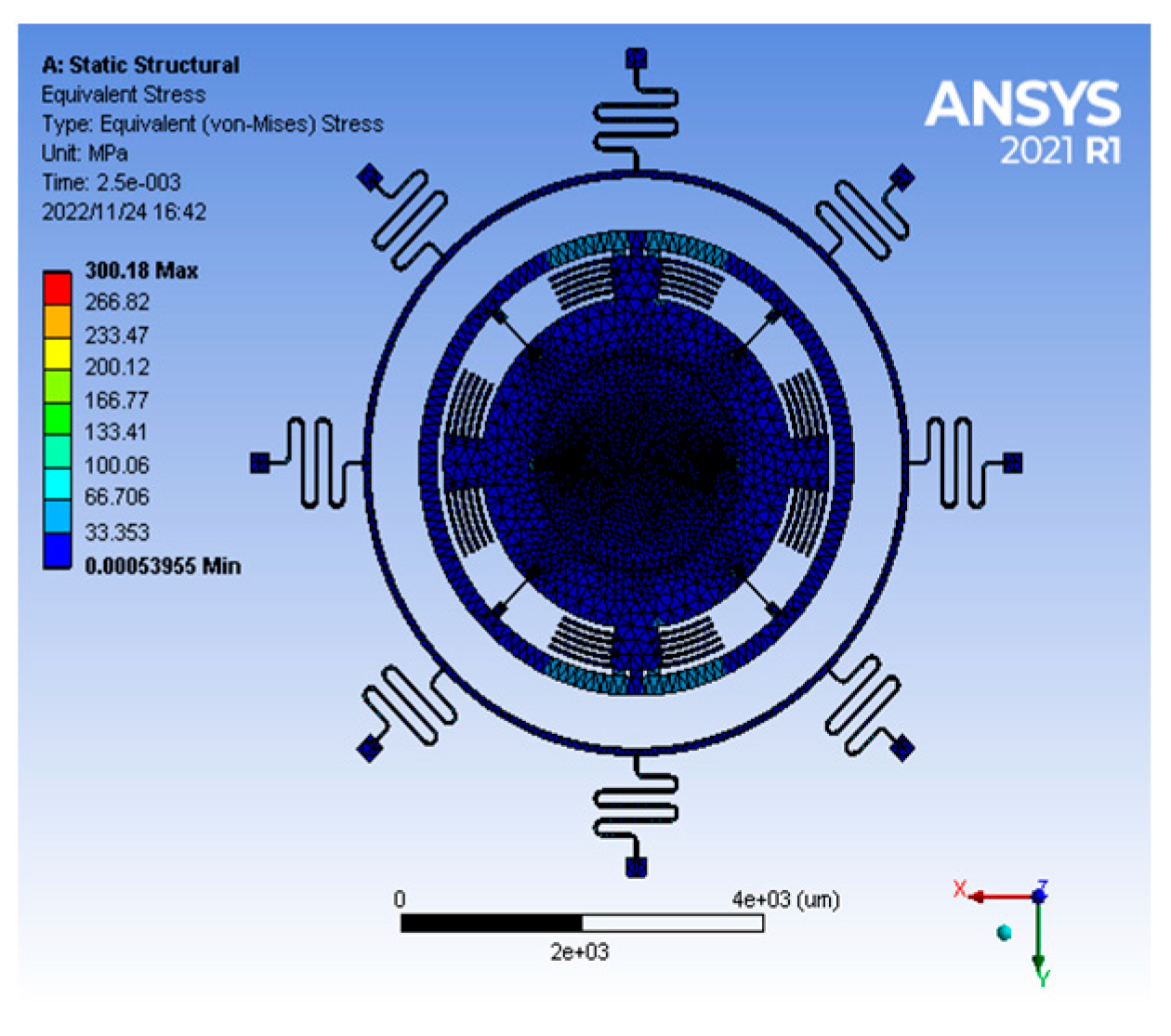
3. Performance Analysis
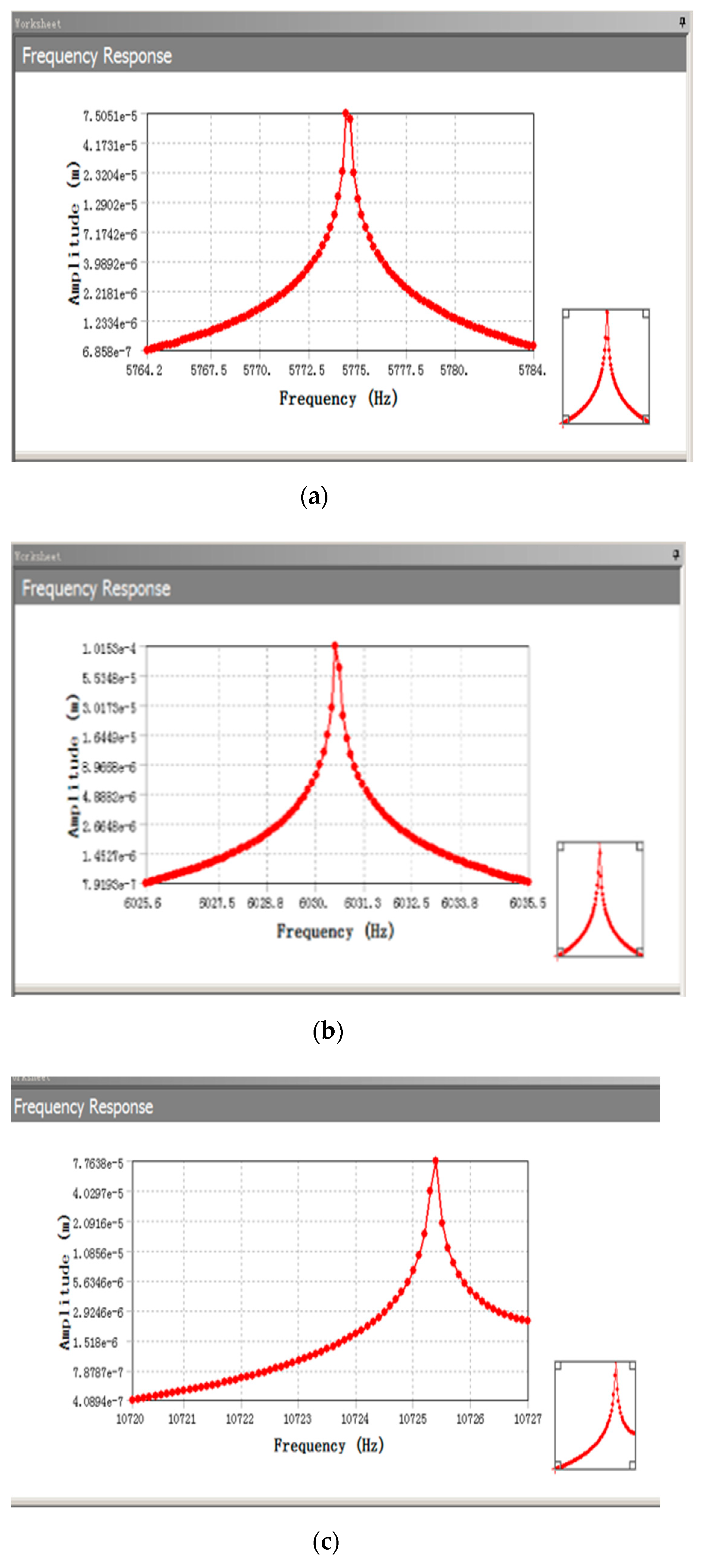
3.1. Modal Analysis and Harmonic Response Analysis
3.2. Transient Shock Response Analysis
4. Fabrication
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, D.; Kong, L.; Gao, H. Design and analysis of a novel fully decoupled tri-axis linear vibratory gyroscope with matched modes. Sensors 2015, 15, 16929–16955. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Challoner, A.D.; Howard, H.G.; Liu, J.Y. Boeing disc resonator gyroscope. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 504–514. [Google Scholar]
- Cao, H.; Liu, Y.; Zhang, Y.; Shao, X.; Gao, J.; Huang, K.; Shi, Y.; Tang, J.; Shen, C.; Liu, J. Design and experiment of dual-mass MEMS gyroscope sense closed system based on bipole compensation method. IEEE Access 2019, 7, 49111–49124. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, Y.; Shen, C.; Liu, Y.; Wang, X. Temperature Energy Influence Compensation for MEMS Vibration Gyroscope Based on RBF NN-GA-KF Method. Shock Vib. 2018, 2018, 2830686. [Google Scholar] [CrossRef]
- Cao, H.; Zhao, R.; Cai, Q.; Shi, Y.; Liu, L. Structural design and simulation analysis of silicon micro triaxial wheel-ring gyroscope. In Proceedings of the 2020 International Conference on Sensing, Measurement & Data Analytics in the era of Artificial Intelligence (ICSMD), Xi’an, China, 15–17 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 130–132. [Google Scholar]
- Giomi, E.; Fanucci, L.; Rocchi, A. Analog-CMDA based interfaces for MEMS gyroscopes. Microelectron. J. 2014, 45, 78–88. [Google Scholar] [CrossRef]
- Seok, S.; Moon, S.; Kim, K.; Kim, S.; Yang, S.; Lim, G. Design and Vibration Analysis of Tri-axis Linear Vibratory MEMS Gyroscope. J. Sens. Sci. Technol. 2017, 26, 235–238. [Google Scholar]
- Takahashi, H.; Abe, K.; Takahata, T.; Shimoyama, I. MEMS triaxial gyroscope using surface and sidewall doping piezoresistors. J. Micromech. Microeng. 2020, 30, 105012. [Google Scholar] [CrossRef]
- Wang, M.C.; Jiao, J.W.; Yan, P.L.; Mi, B.W.; Qin, S. A novel tri-axis MEMS gyroscope with in-plane tetra-pendulum proof masses and enhanced sensitive springs. J. Micromech. Microeng. 2014, 24, 045002. [Google Scholar] [CrossRef]
- Sonmezoglu, S.; Taheri-Tehrani, P.; Valzasina, C.; Falorni, L.G.; Zerbini, S.; Nitzan, S.; Horsley, D.A. Single-structure micromachined three-axis gyroscope with reduced drive-force coupling. IEEE Electron Device Lett. 2015, 36, 953–956. [Google Scholar] [CrossRef]
- Fan, Q.; Zhou, Y.; Liu, M.; Lin, C.; Su, Y. A MEMS Rate-Integrating Gyroscope (RIG) With In-Run Automatic Mode-Matching. IEEE Sens. J. 2021, 22, 2282–2291. [Google Scholar] [CrossRef]
- Eley, R.; Fox, C.H.J.; McWilliam, S. The dynamics of a vibrating-ring multi-axis rate gyroscope. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2000, 214, 1503–1513. [Google Scholar] [CrossRef]
- Yoon, S.; Park, U.; Rhim, J.; Yang, S.S. Tactical grade MEMS vibrating ring gyroscope with high shock reliability. Microelectron. Eng. 2015, 142, 22–29. [Google Scholar] [CrossRef]
- Liang, D.D.; Yang, X.D.; Zhang, W.; Ren, Y.; Yang, T. Linear, nonlinear dynamics, and sensitivity analysis of a vibratory ring gyroscope. Theor. Appl. Mech. Lett. 2018, 8, 393–403. [Google Scholar] [CrossRef]
- Indeitsev, D.A.; Belyaev, Y.V.; Lukin, A.V.; Popov, I.A.; Igumnova, V.S.; Mozhgova, N.V. Analysis of imperfections sensitivity and vibration immunity of MEMS vibrating wheel gyroscope. Nonlinear Dyn. 2021, 105, 1273–1296. [Google Scholar] [CrossRef]
- Cao, H.; Li, H.; Kou, Z.; Shi, Y.; Tang, J.; Ma, Z.; Shen, C.; Liu, J. Optimization and Experimentation of Dual-Mass MEMS Gyroscope Quadrature Error Correction Methods. Sensors 2016, 16, 71. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Cai, Q.; Zhang, Y.; Shen, C.; Shi, Y.; Liu, J. Design, Fabrication, and Experiment of a Decoupled Multi-Frame Vibration MEMS Gyroscope. IEEE Sens. J. 2021, 21, 19815–19824. [Google Scholar] [CrossRef]
- Cao, H.; Wei, W.; Liu, L.; Ma, T.; Zhang, Z.; Zhang, W.; Shen, C.; Duan, X. A Temperature Compensation Approach for Dual-Mass MEMS Gyroscope Based on PE-LCD and ANFIS. IEEE Access 2021, 9, 95180–95193. [Google Scholar] [CrossRef]
- Ma, T.; Cao, H.; Shen, C. A Temperature Error Parallel Processing Model for MEMS Gyroscope based on a Novel Fusion Algorithm. Electronics 2020, 9, 499. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Xue, R.; Cai, Q.; Gao, J.; Zhao, R.; Shi, Y.; Huang, K.; Shao, X.; Shen, C. Design and Experiment for Dual-Mass MEMS Gyroscope Sensing Closed-Loop System. IEEE Access 2020, 8, 48074–48087. [Google Scholar] [CrossRef]
- Tsai, D.H.; Fang, W. Design and simulation of a dual-axis sensing decoupled vibratory wheel gyroscope. Sens. Actuators A Phys. 2006, 126, 33–40. [Google Scholar] [CrossRef]
- Hossain, S.T.; McWilliam, S.; Popov, A.A. An investigation on thermoelastic damping of high-Q ring resonators. Int. J. Mech. Sci. 2016, 106, 209–219. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Liu, Y.; Kou, Z.; Zhang, Y.; Shao, X.; Gao, J.; Huang, K.; Shi, Y.; Tang, J.; Shen, C.; et al. Design, fabrication and experiment of double U-beam MEMS vibration ring gyroscope. Micromachines 2019, 10, 186. [Google Scholar] [CrossRef]
- Kou, Z.; Liu, J.; Cao, H.; Feng, H.; Ren, J.; Kang, Q.; Shi, Y. Design and fabrication of a novel MEMS vibrating ring gyroscope. In Proceedings of the 2017 IEEE 3rd Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 3–5 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 131–134. [Google Scholar]
- Obitani, K.; Araya, K.; Yachi, M.; Tsuchiya, T. Piezoelectric disk gyroscope fabricated with single-crystal lithium niobate. Journal of Microelectromechanical Systems 2021, 30, 384–391. [Google Scholar] [CrossRef]
- Gallacher, B.J. Principles of a micro-rate integrating ring gyroscope. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 658–672. [Google Scholar] [CrossRef]
- Yeh, J.A.; Chen, C.N.; Lui, Y.S. Large rotation actuated by in-plane rotary comb-drives with serpentine spring suspension. J. Micromech. Microeng. 2004, 15, 201. [Google Scholar] [CrossRef]
- Larkin, K.; Ghommem, M.; Serrano, M.; Abdelkefi, A. A review on vibrating beam-based micro/nano-gyroscopes. Microsyst. Technol. 2021, 27, 4157–4181. [Google Scholar] [CrossRef]
- Nie, W.; Cheng, J.; Xi, Z.; Zhou, Z.; Yin, L. Elastic coefficient analysis on planar S-shaped micro spring under high impact load. Microsyst. Technol. 2017, 23, 1367–1375. [Google Scholar] [CrossRef]
- Bao, M.H. Micro Mechanical Transducers: Pressure Sensors, Accelerometers and Gyroscopes; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Yu, H.; Jin, X.; Liu, X.; Liu, D.; Li, Z.; Li, S.; Duan, J.; Zhang, J.; Li, C. Pose error identification algorithm based on hemispherical resonant gyroscope assembly capacitance uniformity. Measurement 2022, 198, 111426. [Google Scholar] [CrossRef]
- Jalil, J.; Ruan, Y.; Zhu, Y. Room-temperature sensing of single electrons using vibrating-reed electrometer in silicon-on-glass technology. IEEE Electron. Device Lett. 2018, 39, 1928–1931. [Google Scholar] [CrossRef] [Green Version]
- Dutta, S.; Pandey, A. Overview of residual stress in MEMS structures: Its origin, measurement, and control. J. Mater. Sci. Mater. Electron. 2021, 32, 6705–6741. [Google Scholar] [CrossRef]
- Fan, B.; Chen, A.; Hu, W.; Zheng, F.; Xu, D.; Guo, S. Investigation of air damping in different vibrational modes of lateral-axis gyroscopes. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–3. [Google Scholar]
- Herth, E.; Baranski, M.; Berlharet, D.; Edmond, S.; Bouville, D.; Calvet, L.E.; Gorecki, C. Fast ultra-deep silicon cavities: Toward isotropically etched spherical silicon molds using an ICP-DRIE. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2019, 37, 021206. [Google Scholar] [CrossRef]
- Herth, E.; Edmond, S.; Bouville, D.; Cercus, J.L.; Bayle, F.; Cambril, E. Micro-/Nanopillars for Micro-and Nanotechnologies Using Inductively Coupled Plasmas. Phys. Status Solidi A 2019, 216, 1900324. [Google Scholar] [CrossRef]





| Institutions | Size (mm × mm) | Z-Axis Shock Resistance | Year |
|---|---|---|---|
| SEU [1] | 9.80 × 9.80 | Unknown | 2015 |
| FSL [7] | 2.90 × 2.25 | Unknown | 2017 |
| KEIO [8] | 5.00 × 5.00 | Unknown | 2020 |
| UCAS [9] | 3.57 × 3.47 | Unknown | 2014 |
| UCD [10] | 3.20 × 3.20 | Unknown | 2015 |
| Property | Value |
|---|---|
| Density | 2330 kg/m3 |
| Young’s Modulus | 169 GPa |
| Poisson’s Ratio | 0.27 |
| Design Parameter | Value |
| Ring Radius, R | 3000 μm |
| Central Angle, θ | 40° |
| Thickness, h | 80 μm |
| Plate Spacing, d | 5 μm |
| Overlapping Angle, α | 18° |
| Comb Gap, hd | 5 μm |
| Moving Comb Radius, ri | (1665 + 80i) μm (i = 1,2..,6) |
| Direct Current Bias Voltage, VD | 5 V |
| Quality Factor Q | 3000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, T.; Wei, W.; Cai, Q.; Cui, R.; Shen, C.; Cao, H. Design and Fabrication of a Novel Wheel-Ring Triaxial Gyroscope. Sensors 2022, 22, 9978. https://doi.org/10.3390/s22249978
Guo T, Wei W, Cai Q, Cui R, Shen C, Cao H. Design and Fabrication of a Novel Wheel-Ring Triaxial Gyroscope. Sensors. 2022; 22(24):9978. https://doi.org/10.3390/s22249978
Chicago/Turabian StyleGuo, Tianqi, Wenqiang Wei, Qi Cai, Rang Cui, Chong Shen, and Huiliang Cao. 2022. "Design and Fabrication of a Novel Wheel-Ring Triaxial Gyroscope" Sensors 22, no. 24: 9978. https://doi.org/10.3390/s22249978
APA StyleGuo, T., Wei, W., Cai, Q., Cui, R., Shen, C., & Cao, H. (2022). Design and Fabrication of a Novel Wheel-Ring Triaxial Gyroscope. Sensors, 22(24), 9978. https://doi.org/10.3390/s22249978







