A Convolutional Neural Network-Based Method for Discriminating Shadowed Targets in Frequency-Modulated Continuous-Wave Radar Systems
Abstract
:1. Introduction
2. State of the Art
3. Problem Statement
3.1. FMCW Radar Device
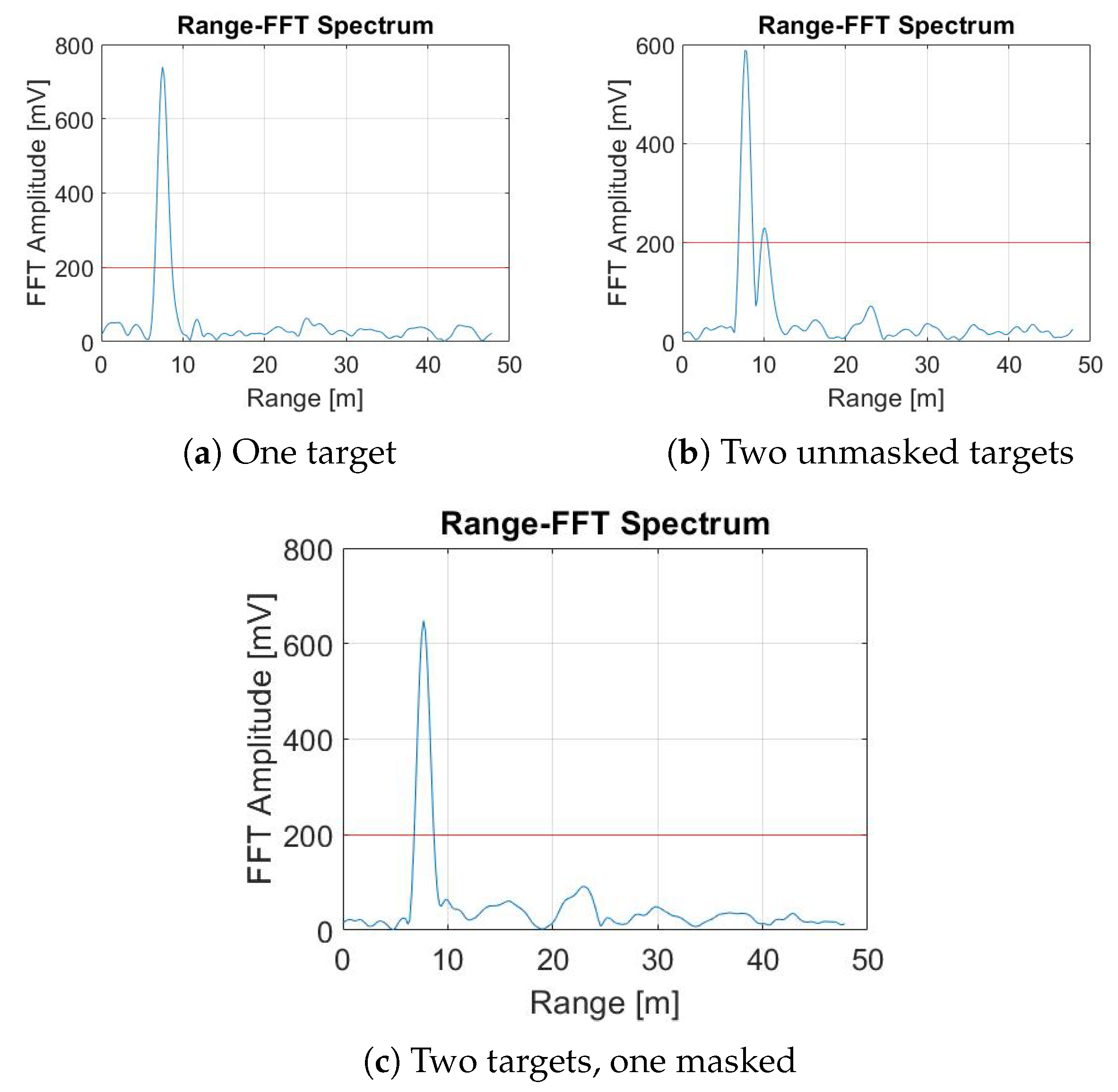
3.2. Shadow Effect
4. Methodology
4.1. Time Frequency Analysis
4.2. Deep Neural Network Models
5. Experimental Setup
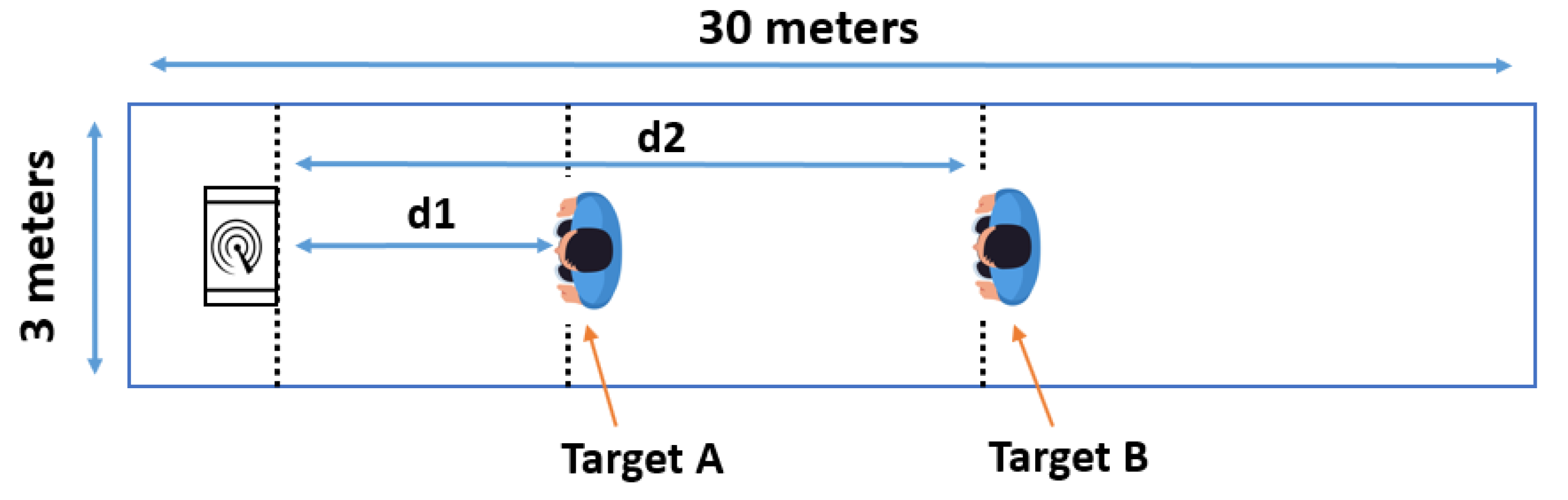
5.1. Data Acquisition
5.2. Spectrogram
5.3. Training
6. Experimental Results and Discussion
7. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thi Phuoc Van, N.; Tang, L.; Demir, V.; Hasan, S.F.; Duc Minh, N.; Mukhopadhyay, S. Microwave radar sensing systems for search and rescue purposes. Sensors 2019, 19, 2879. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, H.; Liu, M.; Zhang, Y.; Liang, F.; Qi, F.; Chen, F.; Lv, H.; Wang, J. An Algorithm based wavelet entropy for shadowing effect of human detection using ultra-wideband bio-radar. Sensors 2017, 17, 2255. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, K.; Zhong, J.; Zhu, J.; Zhang, X.; Zhao, F.; Xie, H.; Gu, F.; Zhou, B.; Wu, M. The method of forest fires recognition by using Doppler weather radar. In Proceedings of the 8Symposium on Fire and Forest Meteorology, Kalispell, MT, USA, 13–15 October 2007; pp. 1–7. [Google Scholar]
- Capria, A.; Giusti, E.; Moscardini, C.; Conti, M.; Petri, D.; Martorella, M.; Berizzi, F. Multifunction imaging passive radar for harbour protection and navigation safety. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 30–38. [Google Scholar] [CrossRef]
- Lemaitre, F.; Poussieres, J.C. Method and System for Sensing and Locating a Person, eg under an Avalanche. US Patent 6,031,482, 29 February 2000. [Google Scholar]
- Rizik, A.; Randazzo, A.; Vio, R.; Delucchi, A.; Chible, H.; Caviglia, D.D. Low-Cost FMCW Radar Human-Vehicle Classification Based on Transfer Learning. In Proceedings of the 2020 32nd International Conference on Microelectronics (ICM), Aqaba, Jordan, 14–17 December 2020; pp. 1–4. [Google Scholar]
- Kocur, D.; Rovňáková, J.; Urdzík, D. Experimental analyses of mutual shadowing effect for multiple target tracking by UWB radar. In Proceedings of the 2011 IEEE 7th International Symposium on Intelligent Signal Processing, Floriana, Malta, 19–21 September 2011; pp. 1–4. [Google Scholar]
- Kocur, D.; Rovňáková, J.; Urdzík, D. Mutual shadowing effect of people tracked by the short-range UWB radar. In Proceedings of the 2011 34th International Conference on Telecommunications and Signal Processing (TSP), Budapest, Hungary, 18–20 August 2011; pp. 302–306. [Google Scholar]
- Maaref, N.; Millot, P.; Pichot, C.; Picon, O. FMCW ultra-wideband radar for through-the-wall detection of human beings. In Proceedings of the 2009 International Radar Conference" Surveillance for a Safer World"(RADAR 2009), Bordeaux, France, 12–16 October 2009; pp. 1–5. [Google Scholar]
- Mitomo, T.; Ono, N.; Hoshino, H.; Yoshihara, Y.; Watanabe, O.; Seto, I. A 77 GHz 90 nm CMOS transceiver for FMCW radar applications. IEEE J. Solid-State Circuits 2010, 45, 928–937. [Google Scholar] [CrossRef]
- Lin Jr, J.; Li, Y.P.; Hsu, W.C.; Lee, T.S. Design of an FMCW radar baseband signal processing system for automotive application. SpringerPlus 2016, 5, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Wen, B.; Ma, Z.; Wu, S. Range/Doppler ambiguity elimination in high-frequency chirp radars. IEE Proc.-Radar Sonar Navig. 2006, 153, 467–472. [Google Scholar] [CrossRef]
- Kulpa, K.; Czekała, Z. Masking effect and its removal in PCL radar. IEE Proc.-Radar Sonar Navig. 2005, 152, 174–178. [Google Scholar] [CrossRef]
- Urdzík, D.; Zetík, R.; Kocur, D.; Rovnáková, J. Shadowing effect investigation for the purposes of person detection and tracking by UWB radars. In Proceedings of the 2012 The 7th German Microwave Conference, Ilmenau, Germany, 12–14 March 2012; pp. 1–4. [Google Scholar]
- Xue, H.; Liu, M.; Lv, H.; Jiao, T.; Li, Z.; Qi, F.; Wang, P.; Wang, J.; Zhang, Y. A dynamic clutter interference suppression method for multiple static human targets detection using ultra-wideband radar. Microw. Opt. Technol. Lett. 2019, 61, 2854–2865. [Google Scholar] [CrossRef]
- Claudepierre, L.; Douvenot, R.; Chabory, A.; Morlaas, C. Assessment of the Shadowing Effect between Windturbines at VOR and Radar frequencies. Forum Electromagn. Res. Methods Appl. Technol. (FERMAT) 2016, 13, 1464–1476. [Google Scholar]
- Perez Fontan, F.; Espiñeira, P. Shadowing Effects; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 29–60. [Google Scholar]
- Zetik, R.; Jovanoska, S.; Thomä, R. Simple Method for Localisation of Multiple Tag-Free Targets Using UWB Sensor Network. In Proceedings of the 2011 IEEE International Conference on Ultra-Wideband (ICUWB), Bologna, Italy, 14–16 September 2011; pp. 268–272. [Google Scholar] [CrossRef]
- Radar Shadow. In Dictionary Geotechnical Engineering/Wörterbuch GeoTechnik: English-German/Englisch-Deutsch; Springer: Berlin/Heidelberg, Germany, 2014; p. 1069. [CrossRef]
- O’Mahony, N.; Campbell, S.; Carvalho, A.; Harapanahalli, S.; Hernandez, G.V.; Krpalkova, L.; Riordan, D.; Walsh, J. Deep learning vs. traditional computer vision. In Proceedings of the Science and Information Conference, Las Vegas, NV, USA, 25–26 April 2019; pp. 128–144. [Google Scholar]
- Heuel, S.; Rohling, H. Pedestrian classification in automotive radar systems. In Proceedings of the 2012 13th International RADAR Symposium, Warsaw, Poland, 23–25 May 2012; pp. 39–44. [Google Scholar]
- Mukhtar, A.; Xia, L.; Tang, T.B. Vehicle detection techniques for collision avoidance systems: A review. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2318–2338. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, Z.; Zhou, M. Latern: Dynamic continuous hand gesture recognition using FMCW radar sensor. IEEE Sens. J. 2018, 18, 3278–3289. [Google Scholar] [CrossRef]
- Hussain, M.; Bird, J.J.; Faria, D.R. A study on cnn transfer learning for image classification. In Proceedings of the UK Workshop on computational Intelligence, Nottingham, UK, 5–7 September 2018; pp. 191–202. [Google Scholar]
- Lee, H.; Kwon, H. Going deeper with contextual CNN for hyperspectral image classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huh, M.; Agrawal, P.; Efros, A.A. What makes ImageNet good for transfer learning? arXiv 2016, arXiv:1608.08614. [Google Scholar]
- Rizik, A.; Tavanti, E.; Chible, H.; Caviglia, D.D.; Randazzo, A. Cost-Efficient FMCW Radar for Multi-Target Classification in Security Gate Monitoring. IEEE Sens. J. 2021, 21, 20447–20461. [Google Scholar] [CrossRef]
- Sacco, G.; Piuzzi, E.; Pittella, E.; Pisa, S. An FMCW radar for localization and vital signs measurement for different chest orientations. Sensors 2020, 20, 3489. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Ran, L.; Li, C. A K-Band Portable FMCW Radar With Beamforming Array for Short-Range Localization and Vital-Doppler Targets Discrimination. IEEE Trans. Microw. Theory Tech. 2017, 65, 3443–3452. [Google Scholar] [CrossRef]
- Han, K.; Hong, S. Vocal Signal Detection and Speaking-Human Localization With MIMO FMCW Radar. IEEE Trans. Microw. Theory Tech. 2021, 69, 4791–4802. [Google Scholar] [CrossRef]
- Cong, J.; Wang, X.; Lan, X.; Huang, M.; Wan, L. Fast Target Localization Method for FMCW MIMO Radar via VDSR Neural Network. Remote Sens. 2021, 13, 1956. [Google Scholar] [CrossRef]
- Stephan, M.; Hazra, S.; Santra, A.; Weigel, R.; Fischer, G. People Counting Solution Using an FMCW Radar with Knowledge Distillation From Camera Data. In Proceedings of the 2021 IEEE Sensors, Sydney, Australia, 31 October–3 November 2021. [Google Scholar]
- Will, C.; Vaishnav, P.; Chakraborty, A.; Santra, A. Human Target Detection, Tracking, and Classification Using 24-GHz FMCW Radar. IEEE Sens. J. 2019, 19, 7283–7299. [Google Scholar] [CrossRef]
- Vaishnav, P.; Santra, A. Continuous Human Activity Classification With Unscented Kalman Filter Tracking Using FMCW Radar. IEEE Sens. Lett. 2020, 4, 1–4. [Google Scholar] [CrossRef]
- Wang, G.; Gu, C.; Inoue, T.; Li, C. A hybrid FMCW-interferometry radar for indoor precise positioning and versatile life activity monitoring. IEEE Trans. Microw. Theory Tech. 2014, 62, 2812–2822. [Google Scholar] [CrossRef]
- Angelov, A.; Robertson, A.; Murray-Smith, R.; Fioranelli, F. Practical classification of different moving targets using automotive radar and deep neural networks. IET Radar Sonar Navig. 2018, 12, 1082–1089. [Google Scholar] [CrossRef] [Green Version]
- Abdulatif, S.; Wei, Q.; Aziz, F.; Kleiner, B.; Schneider, U. Micro-doppler based human-robot classification using ensemble and deep learning approaches. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 1043–1048. [Google Scholar]
- Khanna, R.; Oh, D.; Kim, Y. Through-wall remote human voice recognition using doppler radar with transfer learning. IEEE Sens. J. 2019, 19, 4571–4576. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Vaughan, R. Deep learning radar design for breathing and fall detection. IEEE Sens. J. 2020, 20, 5072–5085. [Google Scholar] [CrossRef]
- Huang, X.; Ding, J.; Liang, D.; Wen, L. Multi-person recognition using separated micro-Doppler signatures. IEEE Sens. J. 2020, 20, 6605–6611. [Google Scholar] [CrossRef]
- Kim, S.; Lee, K.; Doo, S.; Shim, B. Automotive radar signal classification using bypass recurrent convolutional networks. In Proceedings of the 2019 IEEE/CIC International Conference on Communications in China (ICCC), Changchun, China, 11–13 August 2019; pp. 798–803. [Google Scholar]
- Kim, Y.; Alnujaim, I.; You, S.; Jeong, B.J. Human detection based on time-varying signature on range-Doppler diagram using deep neural networks. IEEE Geosci. Remote Sens. Lett. 2020, 18, 426–430. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Infenion POSITION2GO Board. Available online: https://www.infineon.com/cms/en/product/evaluation-boards/demo-position2go/ (accessed on 17 December 2021).
- Nicolaescu, L.; Oroian, T. Radar cross section. In Proceedings of the 5th International Conference on Telecommunications in Modern Satellite, Cable and Broadcasting Service. TELSIKS 2001. Proceedings of Papers (Cat. No. 01EX517), Nis, Yugoslavia, 19–21 September 2001; Volume 1, pp. 65–68. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 1314–1324. [Google Scholar]
- Deep Neural Networks. Available online: https:/keras.io/api/applications/ (accessed on 17 December 2021).




| Parameters | Value |
|---|---|
| Sweep Bandwidth | 200 MHz |
| Center Frequency | 24 GHz |
| Up-Chirp Time | 300 s |
| Number of Samples/Chirp (Ns) | 128 |
| Number of Chirps/Frame (Nc) | 32 |
| Maximum Range | 50 m |
| Maximum Velocity | 5.4 km/h |
| Range Resolution | 0.75 m |
| Velocity Resolution | 0.4 km/h |
| Sampling Rate | 42 KHz |
| Model | Num of Params (Million) | Top Accuracy (%) | Size (MB) | Inference Time (ms) on GPU |
|---|---|---|---|---|
| ResNet50 | 25.6 | 74.9 | 98 | 4.55 |
| VGG19 | 143.6 | 71.3 | 549 | 4.38 |
| MobileNet_V2 | 3.53 | 71.3 | 14 | 3.83 |
| Small MobileNet_V3 | 2.0 | 73.8 | 12 | 3.57 |
| Class | Distance of Target A () [m] | Distance of Target B () [m] | Num of Meas. per Comb. |
|---|---|---|---|
| One Target | 3 | - | 30 |
| 5 | - | 30 | |
| 7 | - | 30 | |
| 9 | - | 30 | |
| 11 | - | 30 | |
| Two Targets | 3 | 5 | 20 |
| 5 | 7 | 20 | |
| 7 | 9 | 20 | |
| 9 | 11 | 20 | |
| 11 | 13 | 20 |
| Model | Num of Params | Average Test | Inference Time | Size |
|---|---|---|---|---|
| (Million) | Acc (%) ± STD | (ms) on GPU | (MB) | |
| MobileNet_V2 | 2.3 | 81.5 ± 4.36 | 2.35 | 7.2 |
| MobileNet_V3 Large | 3.2 | 92.2 ± 2.86 | 2.23 | 18.2 |
| MobileNet_V3 Small | 1.6 | 90.9 ± 1.4 | 1.91 | 6.8 |
| MobileNet_V3 Small Minimalistic | 1.06 | 88.7 ± 2.39 | 1.64 | 5.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohanna, A.; Gianoglio, C.; Rizik, A.; Valle, M. A Convolutional Neural Network-Based Method for Discriminating Shadowed Targets in Frequency-Modulated Continuous-Wave Radar Systems. Sensors 2022, 22, 1048. https://doi.org/10.3390/s22031048
Mohanna A, Gianoglio C, Rizik A, Valle M. A Convolutional Neural Network-Based Method for Discriminating Shadowed Targets in Frequency-Modulated Continuous-Wave Radar Systems. Sensors. 2022; 22(3):1048. https://doi.org/10.3390/s22031048
Chicago/Turabian StyleMohanna, Ammar, Christian Gianoglio, Ali Rizik, and Maurizio Valle. 2022. "A Convolutional Neural Network-Based Method for Discriminating Shadowed Targets in Frequency-Modulated Continuous-Wave Radar Systems" Sensors 22, no. 3: 1048. https://doi.org/10.3390/s22031048
APA StyleMohanna, A., Gianoglio, C., Rizik, A., & Valle, M. (2022). A Convolutional Neural Network-Based Method for Discriminating Shadowed Targets in Frequency-Modulated Continuous-Wave Radar Systems. Sensors, 22(3), 1048. https://doi.org/10.3390/s22031048







