A Dynamic Algorithm for Interference Management in D2D-Enabled Heterogeneous Cellular Networks: Modeling and Analysis
Abstract
:1. Introduction
- We propose a dynamic algorithm called Acceptance Interference Region (AIR) to provide a solution to the problem of guaranteeing a strict QoS for all links in D2D-enabled heterogeneous cellular networks. A distance-based approach is used to achieve guaranteed link quality. The proof of AIR is provided in Appendix A;
- We propose an efficient ON/OFF algorithm to provide a solution to the problem of achieving maximum transmission capacity in the network;
- We develop a mathematical model containing the network, SINR, and small cell density models for system performance modeling and analysis. To this end, we derive the outage probabilities of D2D links, macro-cell links, and small cell links for system performance analysis. We also provide analysis and proof (see Appendix B) to show how small cell density and the number of D2D pairs affect the communication link quality. We validate our analytical models using a MATLAB-based simulation.
2. Related Work
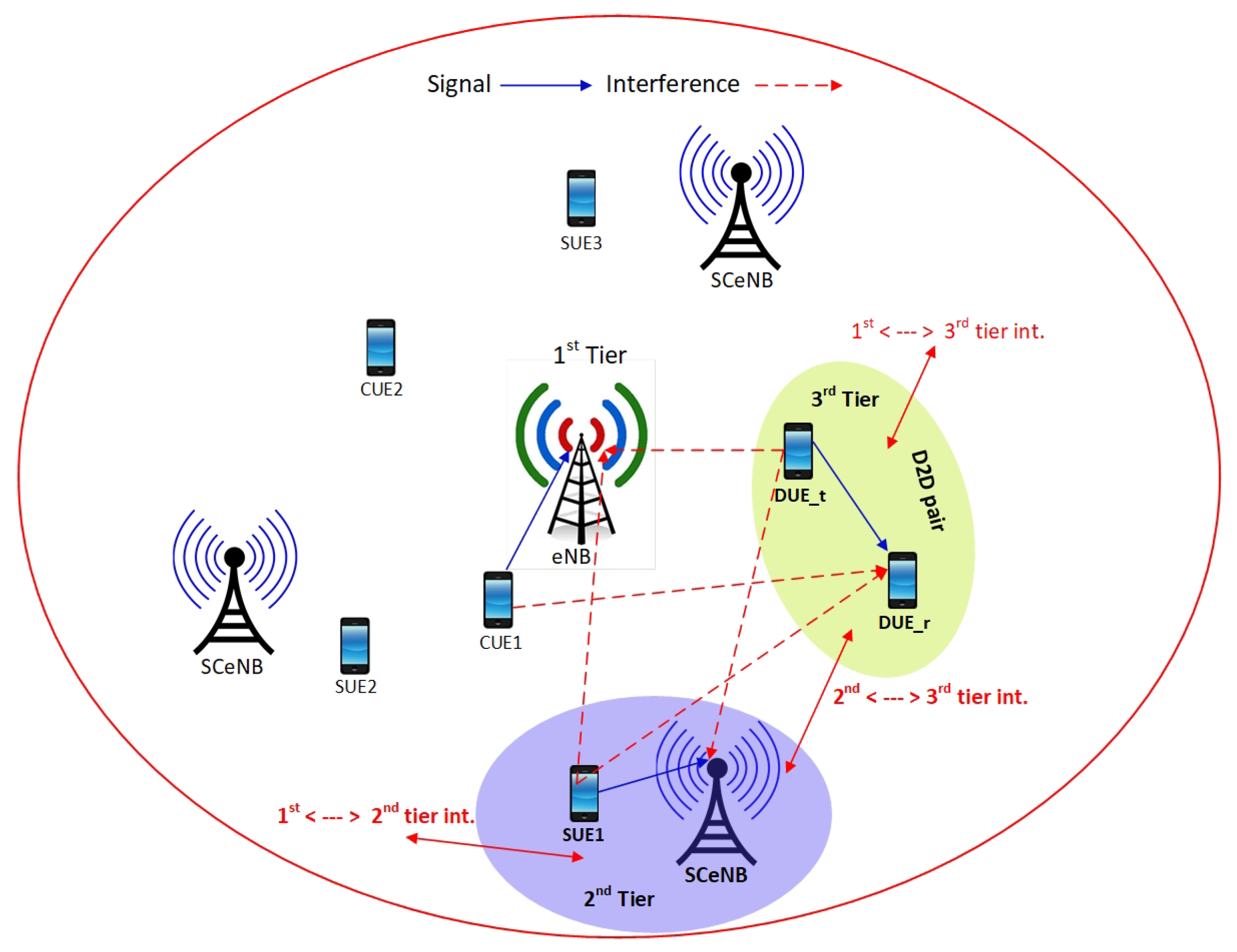
3. System Model
3.1. Network Model
3.2. SINR Model
| Algorithm 1: The proposed AIR dynamic algorithm. |
 |
3.3. Small Cell Density Model
| Algorithm 2. ON-OFF algorithm for interference minimization. |
 |
4. Performance Evaluation
4.1. Simulation Environment and Parameters
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of AIR Algorithm
Appendix B. Proof of Small Cell Density and D2D Pairs Affecting Communication Link Quality
Appendix C. Proof of Small Cell Density of Communications Mode
References
- Kamruzzaman, M.; Sarkar, N.I.; Gutierrez, J.; Ray, S.K. A mode selection algorithm for mitigating interference in D2D enabled next-generation heterogeneous cellular networks. In Proceedings of the 2019 International Conference on Information Networking (ICOIN), Kuala Lumpur, Malaysia, 9–11 January 2019; pp. 131–135. [Google Scholar]
- Forecast, G. Cisco visual networking index: Global mobile data traffic forecast update, 2017–2022. Update 2019, 2017, 2022. [Google Scholar]
- Kuruvatti, N.P.; Hernandez, R.; Schotten, H.D. Interference Aware Power Management in D2D Underlay Cellular Networks. In Proceedings of the 2019 IEEE AFRICON, Accra, Ghana, 25–27 September 2019; pp. 1–5. [Google Scholar]
- Kazmi, S.A.; Tran, N.H.; Saad, W.; Han, Z.; Ho, T.M.; Oo, T.Z.; Hong, C.S. Mode selection and resource allocation in device-to-device communications: A matching game approach. IEEE Trans. Mob. Comput. 2017, 16, 3126–3141. [Google Scholar] [CrossRef]
- Araniti, G.; Raschellà, A.; Orsino, A.; Militano, L.; Condoluci, M. Device-to-device communications over 5G systems: Standardization, challenges and open issues. In 5G Mobile Communications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 337–360. [Google Scholar]
- Lin, X.; Andrews, J.G.; Ghosh, A.; Ratasuk, R. An overview of 3GPP device-to-device proximity services. IEEE Commun. Mag. 2014, 52, 40–48. [Google Scholar] [CrossRef] [Green Version]
- Attaul Mustafa, H.; Imran, M.A.; Zeeshan Shakir, M.; Imran, A.; Tafazolli, R. Separation Framework: An Enabler for Cooperative and D2D Communication for Future 5G Networks. arXiv 2016, arXiv:1604.02636. [Google Scholar]
- Cai, X.; Zheng, J.; Zhang, Y. A graph-coloring based resource allocation algorithm for D2D communication in cellular networks. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 5429–5434. [Google Scholar]
- Xu, S.; Kwak, K.S.; Rao, R. Interference-aware resource sharing in D2D underlaying LTE-A networks. Trans. Emerg. Telecommun. Technol. 2015, 26, 1306–1322. [Google Scholar] [CrossRef]
- Bithas, P.S.; Maliatsos, K.; Foukalas, F. An SINR-aware joint mode selection, scheduling, and resource allocation scheme for D2D communications. IEEE Trans. Veh. Technol. 2019, 68, 4949–4963. [Google Scholar] [CrossRef] [Green Version]
- Zhi, Y.; Tian, J.; Deng, X.; Qiao, J.; Lu, D. Deep reinforcement learning-based resource allocation for D2D communications in heterogeneous cellular networks. Digit. Commun. Netw. 2021; in press. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, F.; Wu, P. Interference management for D2D communications in heterogeneous cellular networks. Pervasive Mob. Comput. 2018, 51, 138–149. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Z.; Xiao, H.; Xing, C. Uplink interference coordination management with power control for D2D underlaying cellular networks: Modeling, algorithms, and analysis. IEEE Trans. Veh. Technol. 2018, 67, 8582–8594. [Google Scholar] [CrossRef]
- Alzoubi, K.H.; Roslee, M.B.; Elgamati, M.A.A. Interference Management of D2D Communication in 5G Cellular Network. In Proceedings of the 2019 Symposium on Future Telecommunication Technologies (SOFTT), Kuala Lumpur, Malaysia, 18–19 November 2019; Volume 1, pp. 1–7. [Google Scholar]
- Sarma, S.S.; Hazra, R. Interference management for D2D communication in mmWave 5G network: An Alternate Offer Bargaining Game theory approach. In Proceedings of the 2020 7th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 27–28 February 2020; pp. 202–207. [Google Scholar]
- Yang, J.; Ding, M.; Mao, G.; Lin, Z. Interference Management in In-Band D2D Underlaid Cellular Networks. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 873–885. [Google Scholar] [CrossRef]
- Shamaei, S.; Bayat, S.; Hemmatyar, A.M.A. Interference management in D2D-enabled heterogeneous cellular networks using matching theory. IEEE Trans. Mob. Comput. 2018, 18, 2091–2102. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, H.; Chronopoulos, A.T. Joint Mode Selection and Power Control for Interference Management in D2D-Enabled Heterogeneous Cellular Networks. IEEE Trans. Veh. Technol. 2020, 69, 9707–9719. [Google Scholar] [CrossRef]
- Albasry, H.; Zhu, H.; Wang, J. In-Band Emission Interference in D2D-Enabled Cellular Networks: Modeling, Analysis, and Mitigation. IEEE Trans. Wirel. Commun. 2018, 17, 7395–7410. [Google Scholar] [CrossRef]
- Hassan, Y.; Hussain, F.; Hossen, S.; Choudhury, S.; Alam, M.M. Interference minimization in D2D communication underlaying cellular networks. IEEE Access 2017, 5, 22471–22484. [Google Scholar] [CrossRef]
- Huynh, T.; Onuma, T.; Kuroda, K.; Hasegawa, M.; Hwang, W.J. Joint downlink and uplink interference management for device to device communication underlaying cellular networks. IEEE Access 2016, 4, 4420–4430. [Google Scholar] [CrossRef]
- Chen, W.; Li, T.; Xiao, Z.; Wang, D. On mitigating interference under device-to-device communication in macro-small cell networks. In Proceedings of the 2016 International Conference on Computer, Information and Telecommunication Systems (CITS), Kunming, China, 6–8 July 2016; pp. 1–5. [Google Scholar]
- Celik, A.; Radaydeh, R.M.; Al-Qahtani, F.S.; Alouini, M.S. Resource allocation and interference management for D2D-enabled DL/UL decoupled Het-Nets. IEEE Access 2017, 5, 22735–22749. [Google Scholar] [CrossRef] [Green Version]
- Jiang, F.; Wang, B.; Sun, C.; Liu, Y.; Wang, R. Mode selection and resource allocation for device-to-device communications in 5G cellular networks. China Commun. 2016, 13, 32–47. [Google Scholar] [CrossRef]
- Librino, F.; Quer, G. Distributed mode and power selection for non-orthogonal D2D communications: A stochastic approach. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 232–243. [Google Scholar] [CrossRef]
- Chen, H.; Deng, X.; Gao, M.; Yang, L.; Guo, L.; Chi, M. Location related communication mode selection and spectrum sharing for D2D communications in cellular networks. In Proceedings of the 2018 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Xiamen, China, 25–26 January 2018; pp. 169–173. [Google Scholar]
- Haneggi, M. Stochastic Geometry for Wireless Networks; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Xu, Y. On the performance of device-to-device communications with delay constraint. IEEE Trans. Veh. Technol. 2016, 65, 9330–9344. [Google Scholar] [CrossRef]
- Gupta, P.; Kumar, P.R. The capacity of wireless networks. IEEE Trans. Inf. Theory 2000, 46, 388–404. [Google Scholar] [CrossRef] [Green Version]








| Notation | Definition |
|---|---|
| PPP constituted by the macro-BSs (eNB) | |
| PPP constituted by the small cell BSs (SCeNB) | |
| PPP constituted by DUEs | |
| Intensity of SCeNBs | |
| Intensity of DUES | |
| Transmission power of a typical UE operating in cellular mode | |
| Transmission power of a typical UE operating in D2D mode | |
| Transmission power of a typical SUE | |
| The set of CUEs, DUEs, and SUEs | |
| Path loss exponent | |
| Required SINR for cellular and D2D links | |
| Thermal noise | |
| Channel coefficient between x and y | |
| D2D | Device-to-device |
| SINR | Signal-to-noise-plus-interference ratio |
| UE | User equipment |
| CUE | Cellular user equipment |
| DUE | Device-to-device user equipment |
| MS | Mode selection |
| PPP | Poison point process |
| SUE | Small cell user equipment |
| eNB | Evolved node B, i.e., LTE macro-base station |
| SCeNB | Small cell evolved node B, i.e., small cell |
| AIR | Accepted interference region |
| QoS | Quality of Service |
| Simulation Parameters | Values |
|---|---|
| Intensity of SCeNBs, | |
| Intensity of DUES, | |
| CUE transmission power, | 23 (dBm) |
| Transmission power of DUEs, | 20 (dBm) |
| Transmission power of SUEs, | 20 (dBm) |
| Path loss exponent, | 3 and 4 |
| Required SINR threshold, | −2.6 dB |
| Noise power, | −118 dBm |
| Cellular UE numbers, | 150 |
| D2D pairs numbers, | 50 |
| Small cell UE numbers, | 250 |
| Maximum allowable outages, i.e., QoS, | 0.1, 0.01 and 0.001 |
| Channel bandwidth, B | 180 KHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamruzzaman, M.; Sarkar, N.I.; Gutierrez, J. A Dynamic Algorithm for Interference Management in D2D-Enabled Heterogeneous Cellular Networks: Modeling and Analysis. Sensors 2022, 22, 1063. https://doi.org/10.3390/s22031063
Kamruzzaman M, Sarkar NI, Gutierrez J. A Dynamic Algorithm for Interference Management in D2D-Enabled Heterogeneous Cellular Networks: Modeling and Analysis. Sensors. 2022; 22(3):1063. https://doi.org/10.3390/s22031063
Chicago/Turabian StyleKamruzzaman, Md, Nurul I. Sarkar, and Jairo Gutierrez. 2022. "A Dynamic Algorithm for Interference Management in D2D-Enabled Heterogeneous Cellular Networks: Modeling and Analysis" Sensors 22, no. 3: 1063. https://doi.org/10.3390/s22031063
APA StyleKamruzzaman, M., Sarkar, N. I., & Gutierrez, J. (2022). A Dynamic Algorithm for Interference Management in D2D-Enabled Heterogeneous Cellular Networks: Modeling and Analysis. Sensors, 22(3), 1063. https://doi.org/10.3390/s22031063








