Modeling and Verification of Asynchronous Systems Using Timed Integrated Model of Distributed Systems
Abstract
:1. Introduction
- timed specification and verification: distributed systems are asynchronous in nature, and time dependencies may substantially change their observed features; as in the Russian fairy tale: the crane offered the heron a marriage; the heron initially refused, but later changed her mind and offered to charm the crane when he took offense …; as a result, they see each other often, but each of them is proud and refuses when the latter is ready to propose; the tale has no end, because its characters act exactly in counter-phase, they do not synchronize in any way; in particular, some deadlocks can disappear due to time dependencies, while others can arise.
- communication duality: expressing the distributed system in terms of nodes with their states and agents with their messages, emphasizing communication duality in distributed systems: message passing versus resource sharing; the system specification can be switched between two system views: node view and agent view, yet with both in a uniform structure;
- locality: the node’s action is executed based on the current situation of the node (without any association with other nodes); no event outside the node (except for messages sent to it) can affect the behavior of the node;
- autonomy: each decision regarding the execution of the actions of the node (including the choice between many possible actions) is taken autonomously; the only way to influence the behavior of a node is to send a message to it (the message may enable an action that was previously disabled); no order is established in the set of pending messages, such as a stack or queue, the node autonomously decides which message will initiate the next action;
- asynchrony: the synchronization of nodes with agents is hidden inside processes (in actions belonging to processes); therefore, processes are perceived as asynchronous from the outside; also the communication channels are asynchronous: the message is sent irrespective of the local situation of the target node, in particular, whether it is waiting for this message or performing completely different operations;
- automated verification: expressing essential features of the distributed system’s behavior using general temporal formulas [2], not related to the internal structure of the system being verified.
- The specification is real-time aware, which is not novel between formalisms, but is an important step in IMDS evolution.
- It is based on a relation between two pairs of a distributed node state and the distributed computation (called an agent) message. The input pair only triggers a system action and produces a new pair that simply waits for its occasion (the consecutive actions of the node and the agent need not even be enabled at this moment). This counters the requirements for synchrony and non-locality of actions. The description models asynchronous actions, in which nothing depends on the synchronous delivery of any items needed to fire the actions. Distributed components make their autonomous moves based only on their local elements, and they do not depend on any global or non-local features of the distributed system.
- Communication duality (client–server versus RPC) is incorporated in the model; the views are only the decompositions or cuts of the system, the given view is achieved by a specific grouping of the actions; however, the set of actions remains the same.
- Identification of partial deadlocks and the partial distributed termination, as well as total–general temporal formulas are defined for this purpose, related to the features of the formalism, rather than to the features of the given verified system. The developed verification algorithms (which are beyond the scope of this article) allow both timeless and timed verification. The compatibility with Uppaal timed automata allows for verification under the external verifier Uppaal [13,14].
- interface to the specifications of the distributed system, text or graphic,
- a simple built-in temporal verifier (based on the TempoRG verifier [15]) for checking models of small and medium systems,
- simulator,
- Progress transition (or: transition): If the Boolean expression on the automaton’s transition is true, the progress transition (or transition) is executed. This expression is composed of integers and clock values. TA actions are symbols associated with transitions (not to be confused with IMDS actions, we will use the term symbol for TA actions). When two or more automata have the same action symbol, the transitions are synchronous. The transitions are otherwise executed in an interleaving way [24].
- Timed transition can be executed if all of the automata in the set have time invariants (relationships between clock values and integers) in their current locations. All the clocks are simultaneously shifted by the same value (not exceeding any invariant).
2. Related Work: Timed Automata and Other Timed Formalisms
- If a Boolean expression on a progress transition (or simply: transition, also termed action transition [37]) outgoing from a current location of a timed automaton TA is fulfilled, the transition can be executed. This expression is made up of integer constants and clocks. A difference is only allowed when two clocks are utilized in the expression. If more than one transition (in the same automaton or different automata) can be executed in a set of TA, the choice is nondeterministic. Transitions are denoted by symbols known as actions (do not confuse with IMDS actions, we use the term symbol for TA action). When two or more automata have the same action symbol, the transitions are executed synchronously. Otherwise, the transitions interleave.
- The timed transition can be executed if all of the automata in the set have their time invariants fulfilled in their current locations. The execution is based on synchronously advancing all clocks (by the same, real value > 0). The smallest difference between the maximum value of a clock used in an invariant and the present value used in this invariant is the maximum value to which the clocks can be advanced. If the invariants x < 2 and y ≤ 3 are present, and the current clock values are x = 1.5 and y = 2.6, the highest value is 0.4, which advances x to 1.9 and y to 3.
2.1. Timed Automaton-Syntax
- L = {l0, l1, …} is a finite set of locations,
- l0 ∈ L is an initial location,
- Z = {c0, c1, …} is the set of clocks,
- Q denotes a set of labels (interpreted as actions on transitions, do not confuse with IMDS actions),
- every location l ∈ L is mapped by Jl(l) to a set of valuations of clocks in Z, over a Cartesian product of , for example, Jl(l) = {c1-c2 > 2},
- E ⊆ L × Q × Jll × 2Z × L—set of transitions: e = (l, q, Jll(l,l′), r, l′) ∈ E
- Jll is a set of functions for pairs l,l′ ∈ L, every transition (l,l′), is mapped by Jll(l,l′) to a set of valuations of clocks in Z over a Cartesian product of , just as Jl(l) for a location l,
- r ∈ 2Z indicates a subset of clocks in Z that are reset on transition.
2.2. Timed Automaton-Semantics
- Vertices ⊆ L × is the set of LTS vertices for the automaton TA (because the term state is reserved for IMDS node states, we use the term vertex instead),
- vertex0 = (l0, u0) ∈ Vertices is the initial vertex, u0 maps all clocks c ∈ Z to 0.
- ▶ = ▶t ∪ ▶p is the transition relation such that:
- (l, u) ▶t (l, u + d) if ∀d′: 0 ≤ d′ ≤ d ⇒ u + d′ ∈ Jl(l) – timed transition,
- (l, u) ▶p (l′, u′) if there exists e = (l, q, Jll(l,l′), r, l′) ∈ E
2.3. Network of TA
- A set of locations is a Cartesian product L = L1 × … × Ln, l ∈ L is a location vector l = (l1, …, ln), li ∈ Li.
- l0 ∈ L is an initial location vector l0 = (l10, …, ln0), li0 ∈ Li.
- Z is a common set of clocks—a union of sets of clocks Z = Z1 ∪ … ∪ Zn.
- Q is a common set of labels—symbols on transitions Q = Q1 ∪ … ∪ Qn.
- Location invariant functions are composed into a common function over location vectors Jl(l) = Jl1(l1) ∧ … ∧ Jln(ln).
2.4. The Semantics of the Network of TA
- Vertices = (L1 × … × Ln) × is the set of global LTS vertices,
- vertex0 = (l0; u0) ∈Vertices is the initial vertex, u0 maps all clocks c ∈ Z to 0,
- ▶ = ▶t ∪ ▶p is the transition relation defined by:
- -
- (l, u) ▶t (l, u + d) if ∀d′ 0 ≤ d′ ≤ d ⇒ u + d′ ∈ Jl(l)—timed transition,
- -
- if there exists a symbol q ∈ Q, for which there exist transitions ei, ej, … in TAi, TAj, … (at least one, but if more, then in distinct automata): ei = (l1i, q, Jlli(l1i,l2i), ri, l2i) ∈ Ei, ej = (l1j, q, Jllj(l1j,l2j), rj, l2j) ∈ Ej, …then there exists the transition e = (l1, q, Jll(l1,l2), r, l2) ∈ ▶p such thatu ∈ Jll(l[l1i/l2i, l1j/l2j, …]), u′ = [ri ∪ rj ∪ …↳ 0]u—progress transition, Comment: There is a synchronization transition if more than one transition in distinct TA have the same q label on their transitions.
2.5. The Uppaal Extesion to TA
3. Integrated Model of Distributed Systems (IMDS)
- the current state matches some pending messages in the node—at least one action is ready to be executed; the node process is running;
- the current state does not match any pending messages in the node (or no messages are pending on the node)—a matching message may arrive in the node in the future; the node process is waiting;
- no messages are pending in the node, and none will appear in the future; the node process is idle;
- there are pending messages in the node, but the present state does not match any of them, and there may not be any matching messages in the node in the future; the node process has reached a deadlock.
- the agent’s message is pending in the node and matches the current state of this node—the action is ready to fire; the agent runs;
- the agent’s message is pending in the node and does not match the current state of this node, but a matching state may occur in the future; the agent is waiting;
- the agent’s message is pending in the node, and neither the current state of this node nor such a condition may occur in the future; the agent is deadlocked;
- the agent process has terminated, since no agent’s messages are pending in any node.
3.1. Basic IMDS Definition
- P = {p1, p2, …, pNp}—finite set of states (of nodes)
- M = {m1, m2, …, mNm}—finite set of messages (of agents)
- Λ ⊂ (M × P) × (M × P)—set of actions
- the pair (m,p) match (1,31);
- (m,p) is the input pair, (m′,p′) is the output pair (2,32);
- the state p is current, the message m is pending;
- p′ is the next state, m′ is the next message.
- Pini ⊂ P – set of initial states
- Mini ⊂ M – states of initial messages.
3.2. IMDS System Behavior
- H = P ∪ M—set of items
- Tini = Pini ∪ Mini—initial configuration
- T ⊆ H—configuration
- ∀λ∈Λ λ = ((m,p),(m′,p′)) Tinp(λ) ⊃ {m,p}, Tout(λ) = Tinp(λ)\{m,p} ∪ {m′,p′}—obtaining Tout(λ) from Tinp(λ) for an action (31,1)→(32,2)
- LTS = ⟨N,N0,W⟩, where
- N is a set of vertices (configurations {T0, T1, …}, Tini = T0);
- N0 = Tini is the root;
- W is the set of directed labeled transitions, W ⊆ N × Λ × N, W = {(Tinp(λ),λi,Tout(λ) | λi∈ Λ, i = 1, …, ord(Λ)}.
3.3. IMDS Processes
- S = {s1, s2, …, sNs}—finite set of nodes
- A = {a1, a2, …, sNa}—finite set of agents
- V = {v1, v2, …, vNv}—finite set of values
- R = {r1, r2, …, rNr}—finite set of services
- P ⊂ S × V—set of states,
- M ⊂ A × S × R—set of messages,
- H = P ∪ M—set of items,
- Initial sets Pini and Mini, set of items H, configurations T and Tini are defined over P and M, as before.
- Λ ⊂ (M × P) × (M × P) ∪ (M × P) × (P) | (m,p)Λ(m′,p′) ∨ (m,p)Λ(p′), m = (a,s,r) ∈ M, p = (s1,v1) ∈ P, m′ = (a2,s2,r2) ∈ M, p′ = (s3,v3) ∈ P, s1 = s, s3 = s, a2 = a
- B(s) = {λ ∈ Λ | λ = (((a,s,r),(s,v)), ((a,s′,r′),(s,v′))) ∨ λ = (((a,s,r),(s,v)), ((s,v′))), s′ ∈ S, a ∈ A, v,v′ ∈ V, r,r′ ∈ R}—node process of the node s ∈ S,
- C(a) = {λ ∈ Λ | λ = (((a,s,r),(s,v)), ((a,s′,r′),(s,v′))) ∨ λ = (((a,s,r),(s,v)), ((s,v′))), s,s′ ∈ S, v,v′ ∈ V, r,r′ ∈ R}—agent process of the agent a ∈ A,
- B = {B(s1),B(s2),…,B(sNs) | si ∈ S}—the node view (decomposition of the system to node processes),
- C = {C(a1),C(a2),…,C(aNa) | ai ∈ A}—the agent view (decomposition of the system to agent processes).
3.4. Automated Deadlock and Termination Identification in IMDS
- Ds—true in all configurations, where at least one message is pending at the node s,
- Es—true in all configurations, where at least one action is prepared at the node s.
- Da—true in all configurations, where a message of the agent a is pending,
- Ea—true in all configurations, where the action is prepared with a message of the agent a,
- Fa—true in all configurations, where a terminating action (with a message of the agent a on input) is prepared.
- communication deadlock in node s: EF AG(Ds ∧ ¬Es)—a configuration is reachable in which a message is pending at the node s, but from this configuration on, no action will be prepared on node s;
- node s idle: AF AG(¬Ds)—there is a configuration after which no message will arrive at s;
- resource deadlock in the agent a: EF AG(Da ∧ ¬Ea)—a configuration is reachable in which a message of the agent a is pending but from this configuration on, the message will not match any state;
- termination of agent a: AF(Fa)—a terminating action of agent a is inevitable.
- communication duality: Any system can be broken down into node processes that communicate via messages (the output state of the action is the carrier of the node process, while the output message is the means of communication) or agent processes communicating through the states of the nodes (the output message is the carrier agent process, while the output state is the means of communication);
- locality: Each action on a node is dependent on the node’s current state, and one of a set of pending messages on that node; no incident from outside (except messages received by the node) can affect the behavior of the node;
- autonomy: each node independently decides which of the defined actions can be performed in the current situation; in other words, the nodes decide for themselves if, and when, the messages are accepted and what actions they will cause;
- asynchrony: the node receives a message when it is ready for it; otherwise the message is pending; there are no synchronous operations in the model, such as simultaneous transitions on shared symbols in Büchi automata [3] or timed automata [18], and no joint operations of nodes or agents; synchronous sending and receiving operations in CSP [44], Occam [45], or Uppaal Timed Automata [14], synchronous operations on the complementary input and output ports in CCS [44]; node and agent autonomy is implemented using asynchronous operations: sending a message to a node or setting a new node state for subsequent agent operations are the only ways to influence the behavior of nodes and agents;
- asynchronous channels: communication between nodes is one-way (communication in the opposite direction has its separate channel) and may appear synchronous because the message appears on the receiving node immediately after it is sent; however, asynchrony is modeled by the possibility of deferring the message’s acceptance; the message can wait a long time, even forever, before being accepted;
- automated verification: the four above-mentioned temporal formulas are used to locate communication deadlocks in the processes of individual nodes, idleness of nodes, deadlocks over resources in agent processes, and agent termination, regardless of the structure of the verified system; therefore, they form the basis of the design of the automatic Dedan verifier, which can be used without knowledge of time logic and model checking.
4. Timed IMDS (T-IMDS)
- time durations of actions (fixed or range),
- time delays of inter-node channels (fixed or range).
4.1. Syntax
4.2. Semantics
- The current input state pinp (1) and pending input message minp (31) match; therefore, they can invoke the action λ = ((minp,pinp),(m,p)): (31,1)→(32d,2c). If multiple actions are enabled in a node, the choice is nondeterministic. The first phase (31,1)→(32a,2a) is a reception of the message minp and invocation of the action.
- Time duration of the action begins, which lasts between tλ min(λ) and tλ max(λ). Counting the time duration is the second phase (32a,2a)→(32b,2b).
- When the time duration ends, the new pair of (m,p) is generated (32b,2b)→(32c,2c). From this moment, the state p is available for invoking the next action in the node. The message m is sent to the target node, and it must be propagated to become accessible.
- The last phase is message delivery, in which the channel delay between tch min(ch) and tch max(ch) is counted (32c)→(32d). After the delay, the message m becomes available for invocation of the next agent action, in the target node with its current state.
- For every action λ = ((minp,pinp),(m,p)) (3), the range bounds of action duration tλ min(λ) and tλ max(λ) are defined.
- The set of channels CH of the form ch = (a,sinp→s) are defined: ∀λ = ((minp,pinp),(m,p)): ∃ ch: ch = (Ma(minp), Ms(minp)→Ms(m)). Totally K channels, indexed 1, …, K. The channel transmitting the output message of the action λ is denoted chλ.
- For every ch, the range bounds of channel delay tch min(ch), tch max(ch) are defined.
- Delay time is defined for a channel between given nodes; therefore, for all agents sending messages along the channel, the range of delay is equal: ∀a1,a2: ∀ch1 = (a1, sinp→s), ch2 = (a2, sinp→s): tch min(ch1) = tch min(ch2) ∧ tch max(ch1) = tch max(ch2); however, this does not influence the shape of the LTS.
- A timed configuration consists of messages, states, their derivatives, node time values cts, and channel time values ctch: Tt = (T = {mtai, ptsj | i = 1, …, Na, j = 1, …, Ns, mtai ∈ Mt, ptsi ∈ Pt}, cts1, …, ctsNs, ctch1, …, ctchK), where Na is the number of agents and Ns is the number of nodes. T is called a set of items.
- The set of states p (1,2b) and derivatives pλt (2a), pλ (2b)e: Pt = {pi, piλjt, piλje | I = 1, …, card(P), j = 1, …, card(λ), λj = ((minp,pinp),(m,pi)) ∈ Λ, piλjt = (pi,λj), piλje = (pi,λj)}
- The set of messages m (31,32d) and derivatives mλt (32a), mλe (32b), mchλ (32c): Mt = {mi, miλjt, miλje, michλj | i = 1, …, card(M), j = 1, …, card(Λ), k = 1, …, K, λj = ((minp,pinp),(mi,p)) ∈ Λ, miλjt = (mi,λj), miλje = (mi,λj), michλj= (mi,chλj,λj) }.
- For λ = ((minp,pinp),(m,p)) we define that Ps(pλt) = Ps(pλe) = Ps(p), Ms(mλt) = Ms(mλe) = Ms(mchλ) = Ms(m), Ma(mλt) = Ma(mλe) = Ma(mchλ) = Ma(m).
- Each pλt has two attributes: tλ min(pλt) and tλ max(pλt).
- Each mchλ has two attributes: tch min(mchλ) = tch min(chλ) and tch max(mchλ) = tch max(chλ).
- The root vertex in the LTS is the initial timed configuration is T0t = (T0 = {m0a1, …, m0aNa, p0s1, …, p0sNs | m0ai∈M0, p0si ∈ P0}, 0, …, 0, 0, …, 0).
- 12.
- (minp,pinp) (31,1) is the input pair of an action λ,
- 13.
- (minpλt,pλt) (32a,2a) for a transition ending the time duration of the action λ,
- 14.
- (mλe,pλe) (32b,2b) for generation of the output pair (m,p) of the action λ,
- 15.
- (mchλ) (32c) for a transition ending the time delay of the message m generated in the action λ.
- 16.
- (minpλt,pλt) (32a,2a) for a timed transition modeling sub-periods of time in the action duration of the action λ,
- 17.
- (mchλ) (32c) for a timed transition modeling sub-periods of time in the time delay of the message m generated in the action λ;
- 18.
- reception/invocation transition (31,2)→(32a,2a)—for Tt: (∃{minp,pinp} ⊂ T: ∃λ ∈ Λ: λ = ((minp,pinp),(m,p))) ⇒ T’t = (T\{minp,pinp} ∪ {minpλt,pλt}, previous cts1,…,ctsNs except cPs(p inp) := 0, previous ctch1,…,ctchK);
- 19.
- generation/send transition (of a new m and p) (32b,2b)→(32c,2c)—for Tt: (∃{mλe,pλe} ⊂ T: λ = ((minp,pinp),(m,p))) ⇒ T’t = (T\{mλe,pλe} ∪ {mchλ,p}, previous cts1, …, ctsNs, previous ctch1, …, ctchK except cchλ := 0);
- 20.
- two transitions—action duration timed transition (32b,2b)→(32b,2b) and duration end timeless transition (32b,2b)→(32c,2c)—for Tt: ¬(∃ {minp,pinp} ⊂ T: ∃λ ∈ Λ: λ = ((minp,pinp),(m,p))) ∧ //no action to invoke ¬(∃ {mλe,pλe} ⊂ T: λ = ((minp,pinp),(m,p))) ∧ // no message to generate (∃ {minpλt,pλt} ⊂ T) | s=Ps(pλt) ⇒ (tλ min(λ) < cts < tλ max(λ) ⇒ T’t = (T\{minpλt,pλt} ∪ {mλe,pλe}, previous cts1,…,ctsNs except cs := 0, previous ctch1,…,ctchK), //action duration ended (cts<tλ max(λ) ⇒ T″t = (T, csi := previous ctsi + δ, i = 1..Ns, cchj := previous ctchj + δ, j = 1..K));
- 21.
- two transitions—channel delay timed transition (32c)→(32c) and delay end timeless transition (32c)→(32d)—for Tt: ¬(∃ {minp,pinp} ⊂ T: ∃λ ∈ Λ: λ = ((minp,pinp),(m,p))) ∧ //no action to start ¬(∃ {mλe,pλe} ⊂ T: λ = ((minp,pinp),(m,p))) ∧ // no message to generate (∃ mchλ∈T ) ⇒ (tch min(chλ) < ctch < tch max(chλ) ⇒ T’t = (T\{mchλ} ∪ {m}, previous cts1, …, ctsNs, previous ctch1,…,ctchK except cchλ := 0)), //channel delay ended (ctch < tch max(mchλ) ⇒ T″t = (T, csi:= previous ctsi + δ, i = 1..Ns, cchj := previous ctchj + δ, j = 1..K)).
- 22.
- If multiple transitions come out of an LTS vertex, the choice is nondeterministic. However, if both reception/generation transition and duration/delay end transition are possible in the current configuration, the latter is not included into LTS.
- 23.
- The general limit for δ in the parallel timed transitions is that for all ctsi in Tt, λ1 = ((m1inp,p1inp),(m1,p1)), Ps(p1inp) = si, pλ1t ∈ T, and all ctchλ2 in Tt, λ2 = ((m2inp,p2inp),(m2,p2)), mchλ2 ∈T, δ < min(tλ max(pλ1t)–ctsi, tch max(chλ2)–ctchλ2). In every inequality tmin < ct, ct < tmax, the relation should be replaced by ≤ if the corresponding range bound is closed. If all tλ max(pλ1t) and all tch max(mchλ2) in Tt are for closed upper bounds of time ranges, then the relation in the inequality < for δ should be replaced by ≤.
5. Uppaal Timed Automata
5.1. The Syntax of Uppaal TA
- L= {l0, l1, …} is a finite set of locations,
- l0 ∈ L is an initial location,
- Z = {c0, c1, …} is the set of clocks,
- CH is a set of symbols called channels,
- Q denotes a set of labels (interpreted as actions on transitions, do not confuse with IMDS actions), they represent send and receive operations on a channel: ch!, ch?, ch ∈ CH; outside the automaton, internal labels are ignored and replaced by τ,
- every location l ∈ L is mapped by Jl(l) to a set of valuations of clocks in Z, over a Cartesian product of , for example, Jl(l) = {c1-c2 > 2}; Restriction. As in verification tools, e.g., Uppaal [14], we limit location invariants to downwards closed constraints of the form: x ≤ n or x < n where n is a natural number,
- O = {o1, o2, …} finite set of variables, for which we define:Vi = {vi1, vi2, …}—finite, integral set of values of variable oi ∈ O,PV = V1 × V2 × … × Vord(O)—a Cartesian product of values of variables o1, o2, …, oord(O) ∈ O,Ō = (v1, v2, …, vord(O)); vi ∈ Vi; Ō ∈ PV—vector of values of variables in O,
- Ō0 = (v10, v20, …, vord(O)0)—initial vector of values of variables in O,
- E ⊆ L × Q × Jll × 2Z × 2PV× F × L—set of transitions: e = (l, q, Jll(l,l′), r, b, f, l′) ∈ E
- Jll is a set of functions for pairs l,l’∈L, every transition (l,l’) is mapped by Jll(l,l′) to a set of valuations of clocks in Z over a Cartesian product of , just as Jl(l) for a location l,
- r ∈ 2Z indicates a subset of clocks in Z that are reset on transition,
- b ∈ 2PV—set of vectors of variable values enabling a transition; Comment: typically b is presented as equalities and inequalities between variables in O and constants, connected by Boolean operators, for example (o1 < 3) ∧ (o2 ≥ 6),
- F is a set of functions on variables in O, f ∈ F, f: PV → PV—unction assigning new values to the variables in O; f/i restricts this function to the value of variable oi. Comment: In Uppaal TA, the function is given as a set of assignments oi = expression over variables in O and integer constants (all other variables are left unchanged).
5.2. The Semantics of UTA
- Vertices ⊆ L × PV × is the set of LTS vertices for the automaton UTA (because the term state is reserved for IMDS node states, we use the term vertex instead),
- vertex0 = (l0, Ō0, u0) ∈ Vertices is the initial vertex, u0 maps all clocks c ∈ Z to 0.
- ▶ = ▶t ∪ ▶p is the transition relation such that:
- (l, Ō, u) ▶t (l, Ō, u+d) if ∀d’: 0 ≤ d′ ≤ d ⇒ u + d′ ∈ Jl(l)—timed transition,
- (l, Ō, u) ▶p (l′, Ō′, u′) if there exists e = (l, q, Jll(l,l′), r, b, f, l′) ∈ E such that u ∈ Jll(l,l′); u′ = [r ↳ 0]u and Ō ∈ b and Ō′ = F(Ō)—progress transition;
5.3. Network of UTA
- A set of locations is a Cartesian product L = L1 × … × Ln, l ∈ L is a location vector l = (l1, …, ln), li ∈ Li.
- l0 ∈ L is an initial location vector l0 = (l10, …, ln0), li0 ∈ Li.
- Z is a common set of clocks—a union of sets of clocks Z = Z1 ∪ … ∪ Zn.
- CH is a common set of channels—a union of sets of channels CH = CH1 ∪ … ∪ CHn, it can be ignored because the labels in Q disappear in the construction of NUTA.
- Q is a common set of labels—symbols on transitions: the labels on channels (ch!, ch?) disappear on the construction on NUTA (they are replaced by τ) according to the semantic rules given below.
- Location invariant functions are composed into a common function over location vectors Jl(l) = Jl1(l1) ∧ … ∧ Jln(ln).
- O is a common set of variables (union of sets of variables O1 ∪ … ∪ On), Ō—vector of their values, PV—the Cartesian product of sets of values of all variables in O, Ō0—a common vector of their initial values.
5.4. The Semantics of the Network of UTA
- Vertices = (L1 × …× Ln) × PV × is the set of global LTS vertices,
- vertex0 = (l0; Ō0; u0) ∈ Vertices is the initial vertex, u0 maps all clocks c ∈ Z to 0,
- ▶ = ▶t ∪ ▶p ∪ ▶!? is the transition relation defined by:
- 3a.
- (l, Ō, u) ▶t (l, Ō, u + d) if ∀d′ 0 ≤ d’ ≤ d ⇒ u + d′ ∈ Jl(l)—timed transition,
- 3b.
- (l, Ō, u) ▶p (l[li/li′], Ō′, u′); if there exists (li, τ; Jlli(li,li′), ri, bi, fi, li′) ∈ Ei such that u ∈ Jlli(l[li/li′]); u′ = [ri ↳ 0]u and Ō ∈ bi and Ō′ = fi(Ō)—progress transition,
- 3c.
- (l, Ō, u) ▶!? (l[lj/lj′, li/li′], Ō′, u′) if there exist two transitions (li, ch?, Jlli(li,li′), ri, bi, fi, li′) ∈ Ei and (lj, ch!, Jllj(lj,lj′), rj, bj, fj, lj′) ∈ Ej such that u ∈ Jll(l[lj/lj′, li/li′]), u′ = [ri ∪ rj ↳ 0]u and Ō ∈ bi and Ō ∈ bj—synchronization transition (a special kind of progress transition), new values of variables in O are calculated:
- for every ok ∈ O, fi(ok) = vk and fj(ok) = vk′ or fj(ok) = vk and fi(ok) = vk′ Comment: At least one of the functions fi, fj must be an identity function for a given variable that returns the same value as its argument (it is disregarded); the other must be in effect (it gives the variable’s new value). This criterion prohibits incoherent assignments to the same variable in the automata UTAj and UTAk; it is met by the construction in the translation of T-IMDS to UTA, as an assignment is applied in only one of the pair’s automata;
- If both ▶t and ▶!? are possible from given vertex (l; Ō; u), then ▶t is not inserted into LTS,
- If both ▶p and ▶!? are possible from given vertex (l; Ō; u), then ▶p is not inserted into LTS; Comment: In this way, Uppaal urgent channels are achieved; only such channels are applied in the translation of T-IMDS to UTA,
- If two transitions are possible, the choice is non-deterministic (however, both are inserted into LTS because it defines all possible behaviors).
6. Translation of T-IMDS to Timed Automata
6.1. Example
- (31,1) location down: initial location—no, time invariant—no (4),
- -
- (31,1)→(32a,2a) transition: next location—upλ2t, condition—a1_sem==sem_signal, assignments—no, time constraint—no, clock reset—csem:=0, channel synchronization: ch_a1_sem? (4)→(8)→(5)
- -
- (31,1)→(32a,2a) transition: next location—upλ4t, condition—a2_sem==sem_signal, assignments—no, time constraint—no, clock reset—csem:=0, channel synchronization: ch_a2_sem? (4)→(8)→(5)
- (32a,2a) location upλ2t: initial location—no, time invariant—csem ≤ 3 (5),
- -
- (32a,2a)→(32b,2b) transition: next location—upλ2e, condition—no, assignments—a1_sem:=none, a1_sa1:=sa1_ok_up, time constraint—2 < csem ≤ 3, clock reset—csem:=0, channel synchronization—no (5)→(9)→(6)
- (32b,2b) location upλ2e: initial location—no, time invariant—no (6),
- -
- (32b,2b)→(32c,2c) transition: next location—up; condition—no, assignments—no, time constraint—no, clock reset—csem:=0, channel synchronization: ch_a1_sem_sa1! (6)→(10)→(7)
- (32a,2a) location upλ4t: initial location—no, time invariant—csem ≤ 3 (5),
- -
- (32a,2a)→(32b,2b) transition: next location—upλ4e, condition—no, assignments—a2_sem:=none, a2_sa2:=sa2_ok_up, time constraint—2 < csem ≤ 3, clock reset—csem:=0, channel synchronization—no (5)→(9)→(6)
- (32b,2b) location upλ4e: initial location—no, time invariant—no,
- -
- (32b,2b)→(32c,2c) transition: next location—up; condition—no, assignments—no, time constraint—no, clock reset—csem:=0, channel synchronization: ch_a2_sem_sa2! (6)→(10)→(7)
- (2c) location up: initial location—no, time invariant—no (7),
- …etc.
6.2. Translation Rules
- sever s ⇒ timed node automaton s with clock cs (reset on every transition, used to count actions duration),
- state p of automaton s (1,2c) and derivatives (pλt, pλe) (2a,2b) ⇒ locations p, pλt, pλe in timed node automaton s (4,5,6,7),
- message m (32,32d) and derivatives (mλt, mλe, mchλ) (32a,32b,32c) ⇒ pairs of message variable a_s values and locations of automaton s and automaton ch, details below,
- agent a → set of variables (for every node visited by the agent) {a_s1, a_s2, …} (8),
- channel ch ⇒ automaton ch (Figure 3) with clock cch (reset on every transition, used to count channel delay),
- message minp pending at the node s (1) ⇒ a_s == s_r (8), all other a_sx == none, sx ≠ s, channel ch in location send (11,18,24), variable a_s has a set of values {none, s_r, s_r1, s_r2, …} (8) (services r, r1, r2 distinguish between messages sent to the node s by the agent a),
- derivative item pλt for action λ (duration running) (2a) ⇒ location pλt (5),
- derivative item pλe for action λ (duration ended) (2b) ⇒ location pλe (6),
- message minp (stable message minp) (32) ⇒ pair (send,a_s==s_r); (8) location send in channel (a,→s) (11,18,24),
- derivative item minpλt for action λ ⇒ pair (pλt, a_s == s_r) (5,8,14/19/29); note that a_sout==none,
- derivative item mλe for action λ ⇒ pair (pλe, a_sout == sout_rout) (6,9); note that a_s == none,
- derivative item mchλ for action λ ⇒ location wait of the channel ch automaton (15/20/25/26); note than a_s == none, a_sout == sout_rout (9),
- configuration T ⇒ set of locations of node automata representing node states and derivatives and values of pairs (location of a node automaton sx/channel automaton chz, value of ay_sx) representing messages and derivatives,
- actual value of action duration in node s/channel ch delay in Tt—the value of the clock cs/clock cch (9/27/28),
- duration range lower bound tλ min(λ) ⇒ lower bound of time constraint of the transition pλt→pλe: tλ min(λ) < cs (9),
- duration range upper bound tλ max(λ) ⇒ upper bound of time constraint of the transition pλt→pλe: cs < tλ max(λ) (9) and of time invariant of location pλt: cs < tλ max(λ) (5),
- delay range lower bound tch min(ch) ⇒ lower bound of time constraint of the transition wait→send of the channel automaton, tch min(ch) < cch (16/27/28),
- delay range upper bound tch max(ch) ⇒ upper bound of time constraint of the transition wait→send of the channel automaton, cch < tch max(ch) (16/27/28) and of time invariant of wait location: cch < tλ max(ch) (13/21/22),
- action λ (3), (31,1)→(32a,2a)→(32b,2c)→(32c,2c), (32c)→(32d) ⇒ sequence: message and state(minp,pinp)-receive transition(minp,pinp)→(minpλt,pλt)-duration location(pλt)-timed transitions(action duration in pλt)-end of duration transition(minpλt,pλt)→(mλe,pλe)-end of duration location(pλe)-send transition(mλe,pλe)→(mchλ,p), (11/18/24,4) → (14/19/29,8) → (12/17/23,5) → (9) → (12/17/23,6) → (15/20/25/26,10) → (13/18/21/22,7),
- receive transition (minp,pinp)→(minpλt,pλt) (31,1)→(32a,2a) ⇒ channel automaton chas = (a,→s) in location send, node s automaton in location pinp, urgent channel synchronization (ch_a_s! on (minp,pinp)→(minpλt,pλt), ch_a_s? on send→idle), condition a_s == s_r fulfilled, on transition cs is reset to 0, (11/18/24,4) → (14/19/29,8) → (12/17/23,5),
- end of action duration transition (minpλt,pλt)→(mλe,pλe) (32a,2a)→(32b,2b) ⇒ node s automaton in location pλt, clock cs value tλ min(λ) < cs < tλ max(λ), on transition a_s := none, a_sout == sout_rout, cs is reset to 0, (12/17/23,5) → (9) → (12/17/23,6),
- generation of next m,p and send transition (mλe,pλe)→(p,mchλ) (32b,2b)→(32c,2c) ⇒ node s automaton in location pλe, channel ch automaton in location idle, urgent channel synchronization (ch_a_s_sout! on (mλe,pλe)→(p,mchλ), ch_a_s_sout? on idle→wait), (12/17/23,6) → (15/20/25/26,10) → (13/18/21/22,7),
- advancing duration of an action (32b,2b)→(32b,2b) or channel delay (32c)→(32d) ⇒ timed transitions—within time invariants of all locations with time invariant—to a next time region, limited by outgoing transitions time range upper bounds, tλ max for action durations in pλt locations (5–9), and tch max for channel delays in wait locations (13–16/21–27/22–28),
- asynchronous channel between nodes ch (32c)→(32d) ⇒ an asynchronous channel is compound of two synchronous urgent channels (Figure 5); asynchronous channel is inactive in the idle location (12/17/23); the signal that the message is ready is obtained from the sending automaton via input urgent channel ch_a_sout: urgent channel synchronization (ch_a_sout!, ch_a_sout?) (15/20/25/26); then, the time delay is counted in the wait location (13/21/22); it lasts between tch min and tch max, as the transition ending the channel delay is followed for clock values cch tch min(ch) < cch < tch max(ch) (16/27/28); finally, the signal sending the message to the target automaton via output urgent channel ch_a_s_sout is issued: urgent channel synchronization (ch_a_s_sout!, ch_a_s_sout?) (14/19/27/28); if the receiving s automaton is not ready to accept the message—the synchronization on ch_a_s is deferred: a message is pending (11/18/24); an own local clock cch is used to count the time delay of an asynchronous channel (13–16/21-–27/22–28).
6.3. Translation of the Example
6.4. Equivalence between T-IMDS and UTA
- The configuration Tt (states and derivatives, messages and derivatives, the current time region determining abstraction class of node clocks and channel clocks) entirely defines the situation in T-IMDS. In UTA, locations of node and channel automata, values of variables (there are only a_s variables), and current time region define the situation (we do not use the term ‘state’ for unambiguity) (4.2.5, 5.4.1, 6.2.2, 6.2.9, 6.2.10, 6.2.11, 6.2.12). Finally, every set of items in Tt corresponds to a separate set of UTA locations and variable values. Every reachable set of locations and variable values maps to a set of T-IMDS items. Moreover, the region succession graph agrees with advancing the time according to minimum and maximum time bounds (of action duration and channel delay) (4.2.5, 5.4.3a, 6.2.14).
- The same concerns the initial configuration of T-IMDS and the initial situation in UTA (4.2.11, 5.4.2).
- Every one of the T-IMDS transitions (minp,pinp)→(minpλt,pλt)→(mλe,pλe)→(mchλ,p) depends only on items enumerated in pairs, independently of any other item present in Tt (4.2.18–4.2.21, 6.2.20–6.2.22). Only the transition mchλ→m does not depend on the state of the message issuing node (it can be p or some other item if the next action is invoked) (4.2.21, 6.2.23). In UTA, corresponding transitions depend only on the current location and values of variables representing pending messages. The variables are local to the pairs of messages sending and messages receiving automata, and only the sending automaton can change the variable value (4.2.20, 6.2.21). The automaton collaborates with channel automata, and by construction, the input channel is in the synchronizing location send (synchronous channel put (!) on a transition outgoing from send location) if minp is pending (4.2.18, 6.2.20). The output channel is in the idle location (with synchronous channel get (?) on a transition outgoing from idle) while the action producing the output message is in progress (4.2.21, 6.2.24).
- Timed transitions in T-IMDS are concurrent for every clock (node clocks and channel clocks) (4.2.20, 4.2.21, 6.2.23). The same is true for UTA (4.4.3a).
- Timed transition in T-IMDS is possible if no progress transition is enabled (minp,pinp)→(minpλt,pλt), (mλe,pλe)→(mchλ,p) (4.2.20, 4.2.21). The same concerns duration ending and delay ending transitions (minpλt,pλt)→(mλe,pλe), mλe→m (4.2.20, 4.2.21). In UTA, all channels are urgent, whose effect is the same: precedence of progress transitions (they correspond to T-IMDS progress transitions) over timed transitions, and over transitions outgoing from time-counting locations (corresponding to duration ending and delay ending transitions) (5.4.4, 6.4.23).
- In both models, the nondeterministic choice is performed if multiple transitions are enabled (4.2.22, 5.4.6).
7. Examples
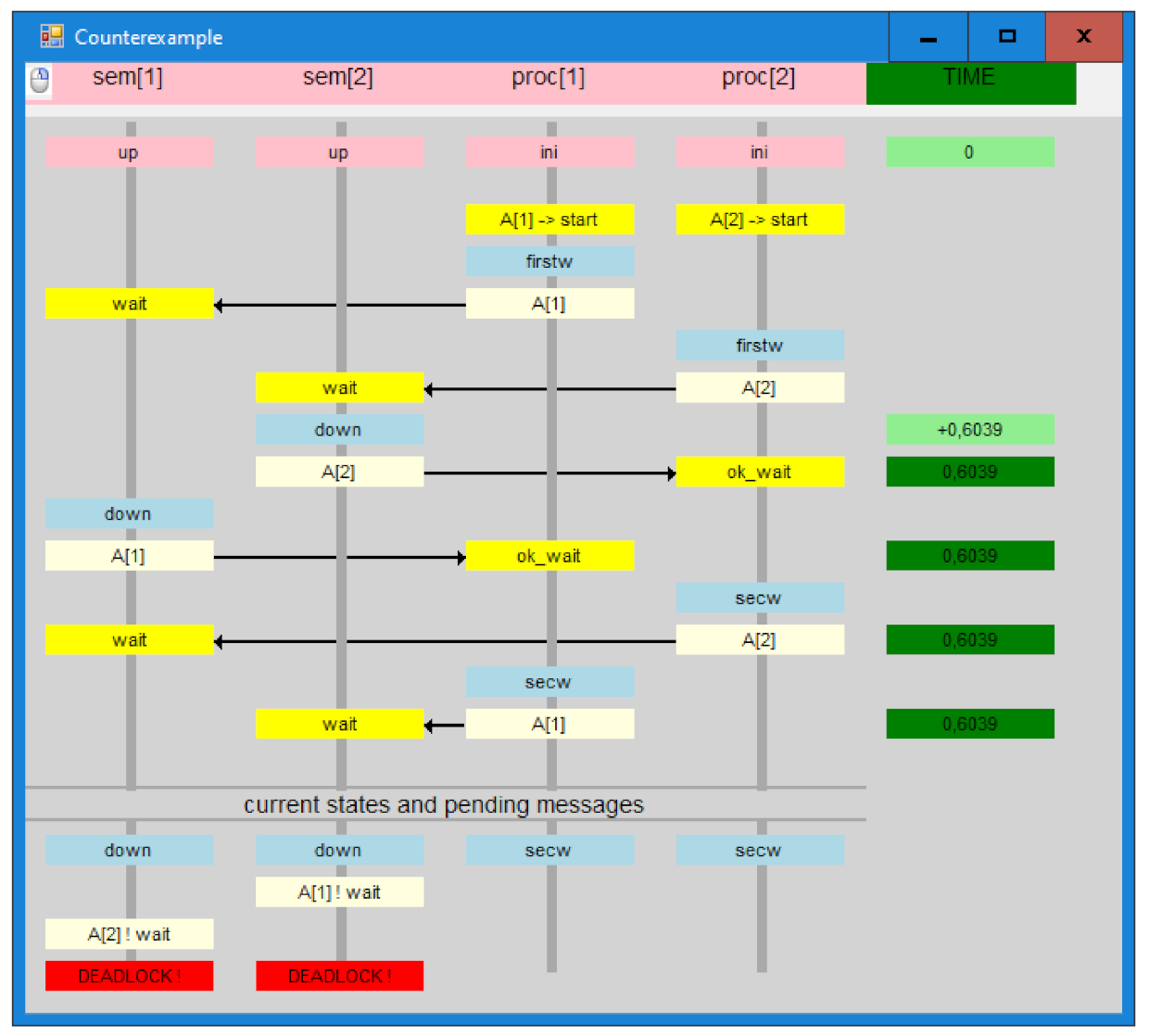
7.1. Simple Example—Two Semaphores
7.2. Practical Example: Automated Vehicle Guidance System
7.2.1. Timeless Verification
7.2.2. Timed Verification
- Time of movement between segments (issuing the take message) is between 1 and 10.
- The channel delay is assumed (1,10).
8. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Proof of Equivalence between T-IMDS and UTA Implementation
- The initial T-IMDS configuration Tt0 includes the states of all nodes (4.2.11). The initial compound location of the set of all UTA node automata contains all initial locations, and every initial location p0 = (s,v0) corresponds to the initial state of the implemented node s. Consequently, initial states of all nodes are implemented.
- The initial T-IMDS configuration Tt0 includes the messages of all agents (4.2.11). The initial compound location of the set of all UTA channel automata contains the idle locations, except one channel automaton for every agent, whose initial location is send.
- The initial T-IMDS configuration Tt0 includes the messages of all agents (4.2.11). The UTA variables storing the called services of the agents, directed to individual node automata, are equal to none, except one variable for every agent, whose initial name appoints the initial node of the agent and the value corresponds to the service contained in the initial message (6.2.6). This feature, along with the previous point, ensures that each agent has its initial message directed to the node of its origin. Thus, initial messages of all agents are implemented.
- All UTA channel automata, except those holding initial agent messages are in idle location (6.2.24), and the transition outgoing from this location has the channel receive operation ch_a_s1_s2? enabled, so all those channels are ready to accept messages for their transfer.
- In every UTA channel automaton implementing T-IMDS channel (a,→s), that is in send location, the UTA channel send operation ch(a,→s)_a_s! is enabled on the transition outgoing from the send location (6.2.24).
- All the time values in Tt0 are 0 (4.2.11). UTA clock values: the value of every UTA cs implementing cts is initially 0, the value of every UTA cch implementing ctch is initially 0 (5.4.2).
- If there is a matching pair (minp,pinp) then the action λ = ((minp,pinp),(m,p)) triggered by the pair (minp,pinp) can be executed, i.e., a progress transition replaces pinp with pλt, and minp with minpλt (4.2.18). Likewise, in UTA, minp denotes that the variable a_s == s_r and channel send operation ch(a,→s)_a_s! in channel (a,→s) automaton is enabled (6.2.9). Matching (minp,pinp) denotes that channel receive operation ch(a,→s)_a_s? in node s automaton is enabled (6.2.20). There are simultaneous transitions executed from send to idle in channel (a,→s) automaton and from pinp to pλt in node s automaton. The value of the variable a_s remains s_r (6.2.20). The location pλt implements the pλt derivative of the state p (5.2.7) and the pair (pλt,a_s == s_r) implements minpλt (6.2.10); therefore, the transition replaces (minp,pinp) with (minpλt,pλt). As the channel (a,→s) automaton location becomes idle and channel send operation ch(a,→s)_a_s! is no longer enabled, the minp message disappears (6.2.9). Instead, the channel automaton in its idle location has the channel receive operations ch(a,→s)_a_si_s? enabled, which means that the channel is ready to accept the next message to transfer (6.2.24).
- If a pair (mλe,pλe) exists in T-IMDS configuration Tt, then the progress transition can be executed that replaces mλe with mchλ and pλe with p (6.2.22). The state derivative pλe is implemented in UTA as the location pλe (6.2.8) and the mλe is implemented as the pair (pλe, a_s == s_r) (6.2.11). The transition in UTA is enabled by the channel send operation ch(a,→sout)_a_si_s!, where the output message of the action λ is m = (a,sout,rout) (6.2.24). As all the channels for agent a are ready to accept a message (they are in idle location so their channel receive operations ch(a,→sout)_a_s_sj! are enabled), the channel automaton transferring messages to the node sout is among them. Thus, the transition implementing replacement of (mλe,pλe) with (mchλ,p) can be executed (6.2.22). Once executed, the location p implementing the output state p (6.2.2) is reached and the implementation of the message m is inserted into a channel, i.e., the pair (p,a_sout == sout_rout) occurs (the variable sout is set on the duration end transition 6.2.21). The channel automaton left the idle location and reached the wait location in which a channel delay is counted (6.2.24). If the delay is 0, the channel automaton reaches the send location immediately (location wait does not appear in the channel automaton).
- If there are more than one T-IMDS progress transitions enabled (previous points 8 and 9), one of them is chosen in a non-deterministic way (4.2.22). The same rule applies to non-deterministic choice between the corresponding progress transitions in UTA (5.4.6).
- If a pair (minpλt,pλt) exists in T-IMDS configuration Tt, then either the timed transition is followed that advances all the time values (of nodes and channels) at least by the value of a least lower time constraint minus the time already spent in the derivative pλt/mchλ (all action durations and all channel delays), at most by the value of a greatest upper time constraint, leaving the pair (minpλt,pλt) unchanged (6.2.23); or the progress transition can be executed that replaces minpλt with mλe and pλt with pλe, if the node time value is between the lower and upper time constraint of the action λ (6.2.21). In UTA, the situation is alike: for all locations with time invariant (there are only pλt and wait such locations) either a timed transition less than minimum time invariant minus its clock value (5.4.3a), or the progress transition to pλe is executed (5.4.3b). The progress transition assigns a_sout == sout_rout (6.2.21); therefore, the pair (pλt,a_sout == sout_rout) is reached which implements mλe (6.2.11).
- If a derivative mchλ exists in T-IMDS configuration Tt, then either the timed transition is followed that advances all the time values (of nodes and channels), at least by the value of a least lower time constraint minus the time already spent in the derivative pλt/mchλ (all action durations and all channel delays), at most by the value of a greatest upper time constraint, leaving the pair (minpλt,pλt) unchanged (6.2.23); or the progress transition can be executed that replaces mchλ with m, if the node time value is between the lower and upper time constraint of the channel ch delay (6.2.24). In UTA, the situation is the same: for all locations with time invariant (there are only pλt and wait such locations) either a timed transition less than minimum time invariant minus its clock value (5.4.3a), or the progress transition to pλe is executed (5.4.3b). The progress transition changes the location of the channel ch automaton from wait to send (6.2.24); therefore, the implementation of m is reached (send,a_sout == sout_rout) (6.2.9—m is minp for the next action).
- In both T-IMDS timed transitions mentioned in points 10 and 11, the UTA timed transition can be made by the value that leaves the time region the same or advances the region to its successor, which does not reach the lower bound of any progress transition (4.2.23, 6.2.23). In such a situation, only the next timed transition must be executed. A sequence of such timed transition in UTA implements a minimum time shift in T-IMDS, after which at least one progress transition can be executed.
- If at least one progress transition is enabled in T-IMDS, it has a priority over any timed transition (6.2.22). Therefore, it is in UTA, because urgent channels are used on every progress transition (5.4.4, 5.4.5).
References
- Daszczuk, W.B. Communication and Resource Deadlock Analysis using IMDS Formalism and Model Checking. Comput. J. 2017, 60, 729–750. [Google Scholar] [CrossRef]
- Daszczuk, W.B. Specification and Verification in Integrated Model of Distributed Systems (IMDS). Computers 2018, 7, 65. [Google Scholar] [CrossRef] [Green Version]
- Holzmann, G.J. Tutorial: Proving properties of concurrent systems with SPIN. In Proceedings of the 6th International Conference on Concurrency Theory, CONCUR’95, Philadelphia, PA, USA, 21–24 August 1995; Springer: Berlin/Heidelberg, Germany, 1995; pp. 453–455. [Google Scholar] [CrossRef]
- Zielonka, W. Notes on finite asynchronous automata. RAIRO-Theor. Inform. Appl. 1987, 21, 99–135. [Google Scholar] [CrossRef]
- Jia, W.; Zhou, W. Distributed Network Systems. From Concepts to Implementations; Springer: Berlin/Heidelberg, Germany, 2005; Volume 15. [Google Scholar] [CrossRef]
- Clarke, E.M.; Grumberg, O.; Peled, D.A. Model Checking; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Kern, C.; Greenstreet, M.R. Formal verification in hardware design: A survey. ACM Trans. Des. Autom. Electron. Syst. 1999, 4, 123–193. [Google Scholar] [CrossRef]
- Inverso, O.; Nguyen, T.L.; Fischer, B.; La Torre, S.; Parlato, G. Lazy-CSeq: A Context-Bounded Model Checking Tool for Multi-threaded C-Programs. In Proceedings of the 30th IEEE/ACM International Conference on Automated Software Engineering (ASE), Lincoln, NE, USA, 9–13 November 2015; IEEE: New York, NY, USA, 2015; pp. 807–812. [Google Scholar] [CrossRef] [Green Version]
- Kaveh, N. Using Model Checking to Detect Deadlocks in Distributed Object Systems. In Proceedings of the 2nd International Workshop on Distributed Objects, Davis, CA, USA, 2–3 November 2000; Emmerich, W., Tai, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 1999, pp. 116–128. [Google Scholar] [CrossRef] [Green Version]
- Arcaini, P.; Gargantini, A.; Riccobene, E. AsmetaSMV: A Model Checker for AsmetaL Models–Tutorial; Report, Università degli Studi di Milano, Dipartimento di Tecnologie dell’Informazione; 2009; Available online: https://air.unimi.it/retrieve/handle/2434/69105/96882/Tutorial_AsmetaSMV.pdf (accessed on 30 January 2022).
- Yang, Y.; Chen, X.; Gopalakrishnan, G. Inspect: A Runtime Model Checker for Multithreaded C Programs; Report UUCS-08-004; University of Utah: Salt Lake City, UT, USA, 2008; Available online: http://www.cs.utah.edu/docs/techreports/2008/pdf/UUCS-08-004.pdf (accessed on 1 February 2022).
- Podelski, A.; Rybalchenko, A. Software Model Checking of Liveness Properties via Transition Invariants; Research Report MPI–I–2003–2–00; Max Planck Institut für Informatik: Saarbrücken, Germany, 2003; Available online: https://pure.mpg.de/pubman/faces/ViewItemOverviewPage.jsp?itemId=item_1819221 (accessed on 30 January 2022).
- Behrmann, G.; David, A.; Larsen, K.G.; Pettersson, P.; Yi, W. Developing UPPAAL over 15 years. Softw. Pract. Exp. 2011, 41, 133–142. [Google Scholar] [CrossRef]
- Behrmann, G.; David, A.; Larsen, K.G. A Tutorial on Uppaal 4.0; Aalborg University: Aalborg, Denmark, 2006; Available online: http://www.it.uu.se/research/group/darts/papers/texts/new-tutorial.pdf (accessed on 30 January 2022).
- Daszczuk, W.B. Evaluation of temporal formulas based on “Checking By Spheres”. In Proceedings of the Euromicro Symposium on Digital Systems Design, Warsaw, Poland, 4–6 September 2001; IEEE: New York, NY, USA, 2001; pp. 158–164. [Google Scholar] [CrossRef] [Green Version]
- Holzmann, G.J. The model checker SPIN. IEEE Trans. Softw. Eng. 1997, 23, 279–295. [Google Scholar] [CrossRef] [Green Version]
- Cimatti, A.; Clarke, E.M.; Giunchiglia, F.; Roveri, M. NUSMV: A new symbolic model checker. Int. J. Softw. Tools Technol. Transf. 2000, 2, 410–425. [Google Scholar] [CrossRef]
- Alur, R.; Dill, D.L. A theory of timed automata. Theor. Comput. Sci. 1994, 126, 183–235. [Google Scholar] [CrossRef] [Green Version]
- Bérard, B.; Cassez, F.; Haddad, S.; Lime, D.; Roux, O.H. Comparison of the Expressiveness of Timed Automata and Time Petri Nets. In Proceedings of the Third International Conference, FORMATS 2005, Uppsala, Sweden, 26–28 September 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 211–225. [Google Scholar] [CrossRef] [Green Version]
- Popescu, C.; Martinez Lastra, J.L. Formal Methods in Factory Automation. In Factory Automation; Silvestre-Blanes, J., Ed.; InTech: Rijeka, Croatia, 2010; pp. 463–475. [Google Scholar] [CrossRef] [Green Version]
- Daszczuk, W.B. Threefold Analysis of Distributed Systems: IMDS, Petri Net and Distributed Automata DA3. In Proceedings of the 37th IEEE Software Engineering Workshop, Federated Conference on Computer Science and Information Systems, FEDCSIS’17, Prague, Czech Republic, 3–6 September 2017; IEEE Computer Society Press: New York, NY, USA, 2017; pp. 377–386. [Google Scholar] [CrossRef] [Green Version]
- Daszczuk, W.B. Siphon-based deadlock detection in Integrated Model of Distributed Systems (IMDS). In Proceedings of the Federated Conference on Computer Science and Information Systems, 3rd Workshop on Constraint Programming and Operation Research Applications (CPORA’18), Poznań, Poland, 9–12 September 2018; IEEE: New York, NY, USA, 2018; pp. 425–435. [Google Scholar] [CrossRef] [Green Version]
- Bérard, B. An Introduction to Timed Automata. In Control of Discrete-Event Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 169–187. [Google Scholar] [CrossRef]
- Glabbeek, R.J.; Goltz, U. Equivalences and refinement. In Proceedings of the LITP Spring School on Theoretical Computer Science La Roche Posay, France, 23–27 April 1990; Springer: Berlin/Heidelberg, Germany, 1990; pp. 309–333. [Google Scholar] [CrossRef]
- Lime, D.; Roux, O.H. Model Checking of Time Petri Nets Using the State Class Timed Automaton. Discret. Event Dyn. Syst. 2006, 16, 179–205. [Google Scholar] [CrossRef] [Green Version]
- Cassez, F.; Roux, O.H. Structural translation from Time Petri Nets to Timed Automata. J. Syst. Softw. 2006, 79, 1456–1468. [Google Scholar] [CrossRef] [Green Version]
- Henzinger, T.A.; Ho, P.-H.; Wong-Toi, H. A user guide to HyTech. In Proceedings of the TACAS 95: International Workshop on Tools and Algorithms for the Construction and Analysis of Systems, Aarhus, Denmark, 19–20 May 1995; Springer: Berlin/Heidelberg, Germany, 1995; pp. 41–71. [Google Scholar] [CrossRef] [Green Version]
- André, É.; Fribourg, L.; Kühne, U.; Soulat, R. IMITATOR 2.5: A Tool for Analyzing Robustness in Scheduling Problems. In Proceedings of the FM 2012: International Symposium on Formal Methods, Paris, France, 27–31 August 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 33–36. [Google Scholar] [CrossRef]
- Laroussinie, F.; Markey, N.; Schnoebelen, P. Efficient timed model checking for discrete-time systems. Theor. Comput. Sci. 2006, 353, 249–271. [Google Scholar] [CrossRef]
- Krystosik, A.; Turlej, D. Emlan: A Language for model checking of embedded systems software. IFAC Proc. Vol. 2006, 39, 126–131. [Google Scholar] [CrossRef]
- Emerson, E.A.; Mok, A.K.; Sistla, A.P.; Srinivasan, J. Quantitative temporal reasoning. Real-Time Syst. 1992, 4, 331–352. [Google Scholar] [CrossRef]
- Gluchowski, P. Languages of CTL and RTCTL Calculi in Real-Time Analysis of a System Described by a Fault Tree with Time Dependencies. In Proceedings of the 2009 Fourth International Conference on Dependability of Computer Systems, DepCoS-RELCOMEX’09, Brunów, Poland, 30 June–2 July 2009; IEEE: New York, NY, USA, 2009; pp. 33–41. [Google Scholar] [CrossRef]
- Frossl, J.; Gerlach, J.; Kropf, T. An efficient algorithm for real-time symbolic model checking. In Proceedings of the ED&TC European Design and Test Conference, Paris, France, 11–14 March 1996; IEEE Computer Society Press: New York, NY, USA, 1996; pp. 15–20. [Google Scholar] [CrossRef] [Green Version]
- Audemard, G.; Cimatti, A.; Kornilowicz, A.; Sebastiani, R. Bounded Model Checking for Timed Systems. In Proceedings of the FORTE 2002: International Conference on Formal Techniques for Networked and Distributed Systems, Houston, TX, USA, 11–14 November 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 243–259. [Google Scholar] [CrossRef] [Green Version]
- Ruf, J.; Kropf, T. Symbolic Verification and Analysis of Discrete Timed Systems. Form. Methods Syst. Des. 2003, 23, 67–108. [Google Scholar] [CrossRef]
- Winskel, G.; Nielsen, M. Models for Concurrency. Handbook of Logic in Computer Science; Oxford University Press: Oxford, UK, 1995; Volume 4. [Google Scholar]
- Bowman, H. Time and Action Lock Freedom Properties for Timed Automata. In Proceedings of the 21st International Conference on Formal Techniques for Networked and Distributed Systems, FORTE 2001, Cheju Island, Korea, 28–31 August 2001; Kluwer Academic Publishers: Boston, MA, USA, 2001; pp. 119–134. [Google Scholar] [CrossRef] [Green Version]
- Keller, R.M. Formal verification of parallel programs. Commun. ACM 1976, 19, 371–384. [Google Scholar] [CrossRef]
- Reniers, M.A.; Willemse, T.A.C. Folk Theorems on the Correspondence between State-Based and Event-Based Systems. In Proceedings of the 37th Conference on Current Trends in Theory and Practice of Computer Science, Nový Smokovec, Slovakia, 22–28 January 2011; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6543, pp. 494–505. [Google Scholar] [CrossRef] [Green Version]
- Daszczuk, W.B. Graphic modeling in Distributed Autonomous and Asynchronous Automata (DA3). Softw. Syst. Model. 2021, 20, 36. [Google Scholar] [CrossRef]
- Chrobot, S. Modelling communication in distributed systems. In Proceedings of the International Conference on Parallel Computing in Electrical Engineering PARELEC 2002, Warsaw, Poland, 25 September 2002; IEEE Computer Society: New York, NY, USA, 2002; pp. 55–60. [Google Scholar] [CrossRef]
- Daszczuk, W.B.; Bielecki, M.; Michalski, J. Rybu: Imperative-style Preprocessor for Verification of Distributed Systems in the Dedan Environment. In Proceedings of the KKIO’17–Software Engineering Conference, Rzeszów, Poland, 14–16 September 2017; Polish Information Processing Society: Warshaw, Poland, 2017; pp. 135–150. [Google Scholar]
- Penczek, W.; Szreter, M.; Gerth, R.; Kuiper, R. Improving Partial Order Reductions for Universal Branching Time Properties. Fundam. Inform. 2000, 43, 245–267. [Google Scholar] [CrossRef]
- Lanese, I.; Montanari, U. Hoare vs Milner: Comparing Synchronizations in a Graphical Framework With Mobility. Electron. Notes Theor. Comput. Sci. 2006, 154, 55–72. [Google Scholar] [CrossRef] [Green Version]
- May, D. Occam. ACM Sigplan Not. 1983, 18, 69–79. [Google Scholar] [CrossRef]
- Daszczuk, W.B. Asynchronous Specification of Production Cell Benchmark in Integrated Model of Distributed Systems. In Proceedings of the 23rd International Symposium on Methodologies for Intelligent Systems, ISMIS 2017, Warsaw, Poland, 26–29 June 2017; Bembenik, R., Skonieczny, L., Protaziuk, G., Kryszkiewicz, M., Rybinski, H., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 40, pp. 115–129. [Google Scholar] [CrossRef]
- Daszczuk, W.B. Static and Dynamic Verification of Space Systems Using Asynchronous Observer Agents. Sensors 2021, 21, 4541. [Google Scholar] [CrossRef]
- Czejdo, B.; Bhattacharya, S.; Baszun, M.; Daszczuk, W.B. Improving Resilience of Autonomous Moving Platforms by real-time analysis of their Cooperation. Autobusy-TEST 2016, 17, 1294–1301. Available online: http://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-6ab8a90d-13a7-429b-9ecd33cce2801f6f/c/10_L_CZEJDO_BHATTACHARYA_BASZUN_DASZCZUK.pdf (accessed on 30 January 2022).
- Lee, G.M.; Crespi, N.; Choi, J.K.; Boussard, M. Internet of Things. In Evolution of Telecommunication Services; Springer: Berlin/Heidelberg, Germany, 2013; pp. 257–282. [Google Scholar] [CrossRef]
- Grosskopf, A.; Decker, G.; Weske, M. The Process: Business Process Modeling Using BPMN; Meghan-Kiffer Press: Tampa, FL, USA, 2018; p. 182. ISBN 9780929652269. [Google Scholar]
- Jałowiec, J. Translation of Business Process Model and Notation into Integrated Model of Distributed Systems. Available online: https://repo.pw.edu.pl/info/bachelor/WUT31de757656da422c87be61e7ede00630/?r=diploma&tab=&lang=pl (accessed on 30 January 2022).












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daszczuk, W.B. Modeling and Verification of Asynchronous Systems Using Timed Integrated Model of Distributed Systems. Sensors 2022, 22, 1157. https://doi.org/10.3390/s22031157
Daszczuk WB. Modeling and Verification of Asynchronous Systems Using Timed Integrated Model of Distributed Systems. Sensors. 2022; 22(3):1157. https://doi.org/10.3390/s22031157
Chicago/Turabian StyleDaszczuk, Wiktor B. 2022. "Modeling and Verification of Asynchronous Systems Using Timed Integrated Model of Distributed Systems" Sensors 22, no. 3: 1157. https://doi.org/10.3390/s22031157
APA StyleDaszczuk, W. B. (2022). Modeling and Verification of Asynchronous Systems Using Timed Integrated Model of Distributed Systems. Sensors, 22(3), 1157. https://doi.org/10.3390/s22031157





