Electrical and Low Frequency Noise Characterization of Graphene Chemical Sensor Devices Having Different Geometries
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
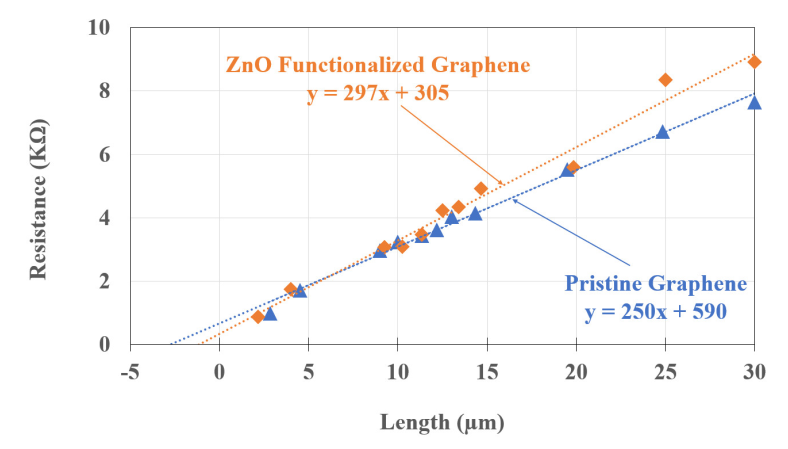
3.1. Resistance Measurements
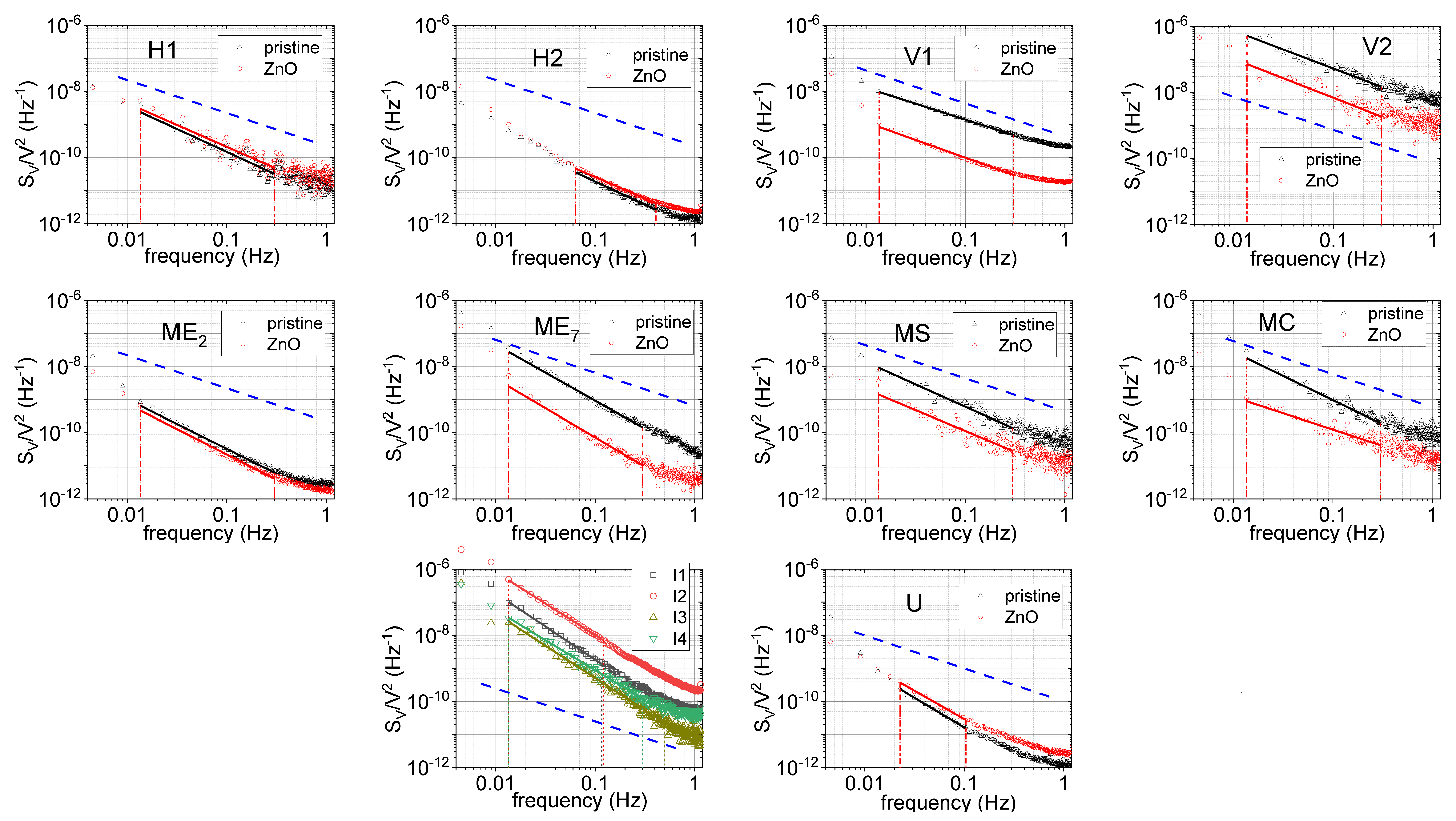
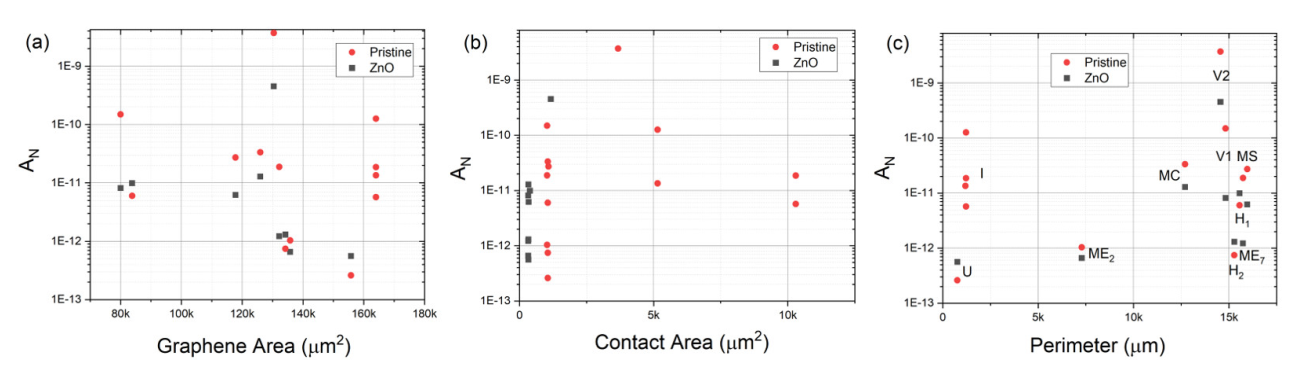
3.2. Low Frequency Noise in Graphene Devices
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ratinac, K.R.; Yang, W.; Ringer, S.P.; Braet, F. Toward Ubiquitous Environmental Gas Sensors—Capitalizing on the Promise of Graphene. Environ. Sci. Technol. 2010, 44, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Potyrailo, R.A.; Surman, C.; Nagraj, N.; Burns, A. Materials and Transducers Toward Selective Wireless Gas Sensing. Chem. Rev. 2011, 111, 7315–7354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of Individual Gas Molecules Adsorbed on Graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef]
- Rumyantsev, S.; Liu, G.; Stillman, W.; Shur, M.; Balandin, A.A. Electrical and Noise Characteristics of Graphene Field-Effect Transistors: Ambient Effects, Noise Sources and Physical Mechanisms. J. Phys. Condens. Matter 2010, 22, 395302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, G.; Rumyantsev, S.; Shur, M.S.; Balandin, A.A. Origin of 1/f Noise in Graphene Multilayers: Surface vs. Volume. Appl. Phys. Lett. 2013, 102, 093111. [Google Scholar] [CrossRef] [Green Version]
- Xia, F.; Perebeinos, V.; Lin, Y.-ming; Wu, Y.; Avouris, P. The Origins and Limits of Metal–Graphene Junction Resistance. Nat. Nanotechnol. 2011, 6, 179–184. [Google Scholar] [CrossRef] [PubMed]
- Chae, H.K.; Siberio-Pérez, D.Y.; Kim, J.; Go, Y.B.; Eddaoudi, M.; Matzger, A.J.; O’Keeffe, M.; Yaghi, O.M. A Route to High Surface Area, Porosity and Inclusion of Large Molecules in Crystals. Nature 2004, 427, 523–527. [Google Scholar] [CrossRef] [PubMed]
- Yavari, F.; Koratkar, N. Graphene-Based Chemical Sensors. J. Phys. Chem. Lett. 2012, 3, 1746–1753. [Google Scholar] [CrossRef]
- Boukhvalov, D.W.; Katsnelson, M.I. Chemical Functionalization of Graphene. J. Phys. Condens. Matter 2009, 21, 344205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuila, T.; Bose, S.; Mishra, A.K.; Khanra, P.; Kim, N.H.; Lee, J.H. Chemical Functionalization of Graphene and Its Applications. Prog. Mater. Sci. 2012, 57, 1061–1105. [Google Scholar] [CrossRef]
- Yan, L.; Zheng, Y.B.; Zhao, F.; Li, S.; Gao, X.; Xu, B.; Weiss, P.S.; Zhao, Y. Chemistry and Physics of a Single Atomic Layer: Strategies and Challenges for Functionalization of Graphene and Graphene-Based Materials. Chem. Soc. Rev. 2012, 41, 97–114. [Google Scholar] [CrossRef]
- Liu, J.; Tang, J.; Gooding, J.J. Strategies for Chemical Modification of Graphene and Applications of Chemically Modified Graphene. J. Mater. Chem. 2012, 22, 12435. [Google Scholar] [CrossRef]
- Sreeprasad, T.S.; Berry, V. How Do the Electrical Properties of Graphene Change with Its Functionalization? Small 2012, 9, 341–350. [Google Scholar] [CrossRef]
- Parrish, K.N.; Akinwande, D. Impact of Contact Resistance on the Transconductance and Linearity of Graphene Transistors. Appl. Phys. Lett. 2011, 98, 183505. [Google Scholar] [CrossRef]
- Lee, J.; Kim, Y.; Shin, H.-J.; Lee, C.S.; Lee, D.; Moon, C.-Y.; Lim, J.; Chan Jun, S. Clean Transfer of Graphene and Its Effect on Contact Resistance. Appl. Phys. Lett. 2013, 103, 103104. [Google Scholar] [CrossRef]
- Pirkle, A.; Chan, J.; Venugopal, A.; Hinojos, D.; Magnuson, C.W.; McDonnell, S.; Colombo, L.; Vogel, E.M.; Ruoff, R.S.; Wallace, R.M. The Effect of Chemical Residues on the Physical and Electrical Properties of Chemical Vapor Deposited Graphene Transferred to SiO2. Appl. Phys. Lett. 2011, 99, 122108. [Google Scholar] [CrossRef] [Green Version]
- Venugopal, A.; Colombo, L.; Vogel, E.M. Contact Resistance in Few and Multilayer Graphene Devices. Appl. Phys. Lett. 2010, 96, 013512. [Google Scholar] [CrossRef]
- Russo, S.; Craciun, M.F.; Yamamoto, M.; Morpurgo, A.F.; Tarucha, S. Contact Resistance in Graphene-Based Devices. Phys. E Low Dimens. Syst. Nanostruct. 2010, 42, 677–679. [Google Scholar] [CrossRef] [Green Version]
- Robinson, J.A.; LaBella, M.; Zhu, M.; Hollander, M.; Kasarda, R.; Hughes, Z.; Trumbull, K.; Cavalero, R.; Snyder, D. Contacting Graphene. Appl. Phys. Lett. 2011, 98, 053103. [Google Scholar] [CrossRef]
- Li, W.; Liang, Y.; Yu, D.; Peng, L.; Pernstich, K.P.; Shen, T.; Hight Walker, A.R.; Cheng, G.; Hacker, C.A.; Richter, C.A.; et al. Ultraviolet/Ozone Treatment to Reduce Metal-Graphene Contact Resistance. Appl. Phys. Lett. 2013, 102, 183110. [Google Scholar] [CrossRef] [Green Version]
- Gahoi, A.; Wagner, S.; Bablich, A.; Kataria, S.; Passi, V.; Lemme, M.C. Contact Resistance Study of Various Metal Electrodes with CVD Graphene. Solid-State Electron. 2016, 125, 234–239. [Google Scholar] [CrossRef]
- Moon, J.S.; Antcliffe, M.; Seo, H.C.; Curtis, D.; Lin, S.; Schmitz, A.; Milosavljevic, I.; Kiselev, A.A.; Ross, R.S.; Gaskill, D.K.; et al. Ultra-Low Resistance Ohmic Contacts in Graphene Field Effect Transistors. Appl. Phys. Lett. 2012, 100, 203512. [Google Scholar] [CrossRef]
- Rumyantsev, S.; Liu, G.; Shur, M.S.; Potyrailo, R.A.; Balandin, A.A. Selective Gas Sensing with a Single Pristine Graphene Transistor. Nano Lett. 2012, 12, 2294–2298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balandin, A.A. Low-Frequency 1/f Noise in Graphene Devices. Nat. Nanotechnol. 2013, 8, 549–555. [Google Scholar] [CrossRef]
- von Haartman, M. Low-Frequency Noise Characterization, Evaluation and Modeling of Advanced Si- and SiGe-Based CMOS Transistors. Doctoral Dissertation, Royal Institute of Technology (KTH), Stockholm, Sweden, 2006. [Google Scholar]
- Hooge, F.N. 1/f Noise Sources. IEEE Trans. Electron Devices 1994, 41, 1926–1935. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.; Jin, Z.; Ma, P.; Zhang, D.; Shi, J.; Niu, J.; Wang, X.; Wang, S.; Li, M.; Liu, X.; et al. The Sheet Resistance of Graphene under Contact and Its Effect on the Derived Specific Contact Resistivity. Carbon 2015, 82, 500–505. [Google Scholar] [CrossRef]
- Ishigami, M.; Chen, J.H.; Cullen, W.G.; Fuhrer, M.S.; Williams, E.D. Atomic Structure of Graphene on SiO2. Nano Lett. 2007, 7, 1643–1648. [Google Scholar] [CrossRef] [Green Version]
- Der Ziel, A.V. Noise: Sources, Characterization, Measurement; Prentice-Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Navale, Y.H.; Navale, S.T.; Ramgir, N.S.; Stadler, F.J.; Gupta, S.K.; Aswal, D.K.; Patil, V.B. Zinc Oxide Hierarchical Nanostructures as Potential NO2 Sensors. Sens. Actuators B Chem. 2017, 251, 551–563. [Google Scholar] [CrossRef]
- Galstyan, V.; Comini, E.; Kholmanov, I.; Faglia, G.; Sberveglieri, G. Reduced Graphene Oxide/Zno Nanocomposite for Application in Chemical Gas Sensors. RSC Adv. 2016, 6, 34225–34232. [Google Scholar] [CrossRef]
- Fu, H.; Jiang, Y.; Ding, J.; Zhang, J.; Zhang, M.; Zhu, Y.; Li, H. Zinc Oxide Nanoparticle Incorporated Graphene Oxide as Sensing Coating for Interferometric Optical Microfiber for Ammonia Gas Detection. Sens. Actuators B Chem. 2018, 254, 239–247. [Google Scholar] [CrossRef]
- Nyakiti, L.O.; Wheeler, V.D.; Garces, N.Y.; Myers-Ward, R.L.; Eddy, C.R.; Gaskill, D.K. Enabling Graphene-Based Technologies: Toward Wafer-Scale Production of Epitaxial Graphene. MRS Bull. 2012, 37, 1149–1157. [Google Scholar] [CrossRef]
- Nath, A.; Koehler, A.D.; Jernigan, G.G.; Wheeler, V.D.; Hite, J.K.; Hernández, S.C.; Robinson, Z.R.; Garces, N.Y.; Myers-Ward, R.L.; Eddy, C.R.; et al. Achieving Clean Epitaxial Graphene Surfaces Suitable for Device Applications by Improved Lithographic Process. Appl. Phys. Lett. 2014, 104, 224102. [Google Scholar] [CrossRef]
- Nath, A.; Currie, M.; Boyd, A.K.; Wheeler, V.D.; Koehler, A.D.; Tadjer, M.J.; Robinson, Z.R.; Sridhara, K.; Hernandez, S.C.; Wollmershauser, J.A.; et al. In Search of Quantum-Limited Contact Resistance: Understanding the Intrinsic and Extrinsic Effects on the Graphene–Metal Interface. 2D Mater. 2016, 3, 025013. [Google Scholar] [CrossRef]
- Lock, E.H.; Prestigiacomo, J.C.; Dev, P.; Nath, A.; Myers-Ward, R.L.; Reinecke, T.L.; Gaskill, D.K.; Osofsky, M.S. Quantum Transport in Functionalized Epitaxial Graphene without Electrostatic Gating. Carbon 2021, 175, 490–498. [Google Scholar] [CrossRef]
- Lock, E.H.; Perkins, F.K.; Boyd, A.K.; Myers-ward, R.L.; Gaskill, D.K.; Nath, A. Graphene-Based ppb Level Sulfur Detector in Fuels. U.S. Patent WO 20190107524, 11 April 2019. [Google Scholar]
- Zhang, X.; Wu, Z.; Zheng, H.; Ren, Q.; Zou, Z.; Mei, L.; Zhang, Z.; Xia, Y.; Lin, C.-T.; Zhao, P.; et al. High-Quality Graphene Transfer via Directional Etching of Metal Substrates. Nanoscale 2019, 11, 16001–16006. [Google Scholar] [CrossRef]
- Chen, J.; Gao, X. Directional Dependence of Electrical and Thermal Properties in Graphene-Nanoplatelet-Based Composite Materials. Results Phys. 2019, 15, 102608. [Google Scholar] [CrossRef]
- Cho, J.; Lee, H.; Nam, K.-H.; Yeo, H.; Yang, C.-M.; Seong, D.G.; Lee, D.; Kim, S.Y. Enhanced Electrical Conductivity of Polymer Nanocomposite Based on Edge-Selectively Functionalized Graphene Nanoplatelets. Compos. Sci. Technol. 2020, 189, 108001. [Google Scholar] [CrossRef]
- Schroder, D.K. Semiconductor Material and Device Characterization; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Wang, L.; Meric, I.; Huang, P.Y.; Gao, Q.; Gao, Y.; Tran, H.; Taniguchi, T.; Watanabe, K.; Campos, L.M.; Muller, D.A.; et al. One-Dimensional Electrical Contact to a Two-Dimensional Material. Science 2013, 342, 614–617. [Google Scholar] [CrossRef] [Green Version]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Horowitz, P.; Hill, W. The Art of Electronics; Cambridge University Press: Cambridge, 2014. [Google Scholar]
- Shao, Q.; Liu, G.; Teweldebrhan, D.; Balandin, A.A.; Rumyantsev, S.; Shur, M.S.; Yan, D. Flicker Noise in Bilayer Graphene Transistors. IEEE Electron. Device Lett. 2009, 30, 288–290. [Google Scholar] [CrossRef] [Green Version]
- Kalmbach, C.-C.; Ahlers, F.J.; Schurr, J.; Müller, A.; Feilhauer, J.; Kruskopf, M.; Pierz, K.; Hohls, F.; Haug, R.J. Nonequilibrium Mesoscopic Conductance Fluctuations as the Origin of 1/f Noise in Epitaxial Graphene. Phys. Rev. B 2016, 94, 205430. [Google Scholar] [CrossRef]
- Heller, I.; Chatoor, S.; Männik, J.; Zevenbergen, M.A.; Oostinga, J.B.; Morpurgo, A.F.; Dekker, C.; Lemay, S.G. Charge Noise in Graphene Transistors. Nano Lett. 2010, 10, 1563–1567. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.S.; Curtis, D.; Zehnder, D.; Kim, S.; Gaskill, D.K.; Jernigan, G.G.; Myers-Ward, R.L.; Eddy, C.R.; Campbell, P.M.; Lee, K.-M.; et al. Low-Phase-Noise Graphene FETs in Ambipolar RF Applications. IEEE Electron. Device Lett. 2011, 32, 270–272. [Google Scholar] [CrossRef]
- Li, X.; Lu, X.; Li, T.; Yang, W.; Fang, J.; Zhang, G.; Wu, Y. Noise in Graphene Superlattices Grown on Hexagonal Boron Nitride. ACS Nano 2015, 9, 11382–11388. [Google Scholar] [CrossRef] [PubMed]
- Snow, E.S.; Novak, J.P.; Lay, M.D.; Perkins, F.K. 1/f Noise in Single-Walled Carbon Nanotube Devices. Appl. Phys. Lett. 2004, 85, 4172–4174. [Google Scholar] [CrossRef]
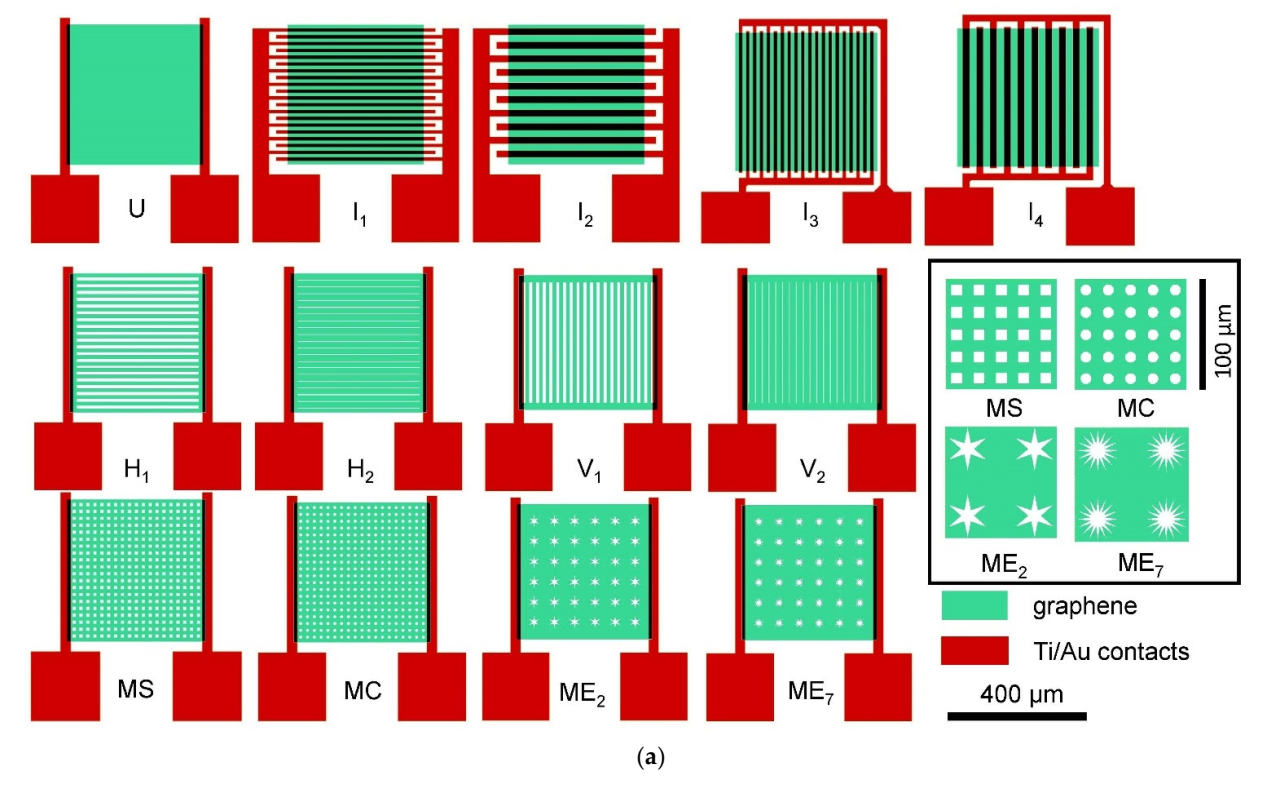



| Channel Structure Type | Device Designation | Channel Length, µm | Channel Width, µm (Constricted) | Detailed Description |
|---|---|---|---|---|
| Group 1: Unpatterned | U | 380 | 410 | Horizontal transport |
| I1 | 10 | 7600 | Vertical transport | |
| I2 | 20 | 3600 | ||
| I3 | 10 | 7600 | Horizontal transport | |
| I4 | 20 | 3600 | ||
| Group 2: Horizontal Slots | H1 | 380 | 210 | 21 ea. 10 µm strips |
| H2 | 380 | 350 | 20 ea. 17 µm strips, 2 ea. 5 µm strips | |
| Group 3: Vertical Slots | V1 | 380 | 40 | 2 ea. 20 µm wide strips at either end of set of slots, strips 360 µm long, 10 µm and 17 µm wide, respectively |
| V2 | 380 | 40 | ||
| Group 4: 2D Patterns | MS | 380 | 220 | 10 × 10 µm2 squares on regular 20 µm pitch grid |
| MC | 380 | 210 | 10 µm dia. Circles on regular 20 µm pitch grid | |
| ME7 | 380 | 160 | 416 µm2 area, 425 µm coded perimeter, on regular 60 µm pitch grid | |
| ME2 | 380 | 160 | 480 µm2 area, 180 µm coded perimeter, on regular 60 µm pitch grid |
| Parameter | Pristine | Functionalized | Ref [16] | Ref [35] |
|---|---|---|---|---|
| Rc, Ω-µm | 5900 ± 800 | 3050 ± 1800 | 1497 | 1075 ± 285 |
| Rsh, kΩ/□ | 5.0 ± 0.1 | 5.9 ± 0.3 | 0.952 | 0.84 |
| LT, µm | 1.2 ± 0.2 | 0.53 ± 0.1 | 1.57 | 1.28 |
| ρc, Ω-cm2 | 7.2 × 10−5 ± 2.2 × 10−5 | 2.2 × 10−5 ± 2.5 × 10−5 | 2.35 × 10−5 | 1.38 × 10−5 |
| Groups | Device Designation | Total Resistance RT (kΩ) | |
|---|---|---|---|
| Pristine Graphene | ZnO Functionalized | ||
| Group 1 | U | 4.49 | 5.10 |
| I1 | 0.03 ± 0.003 | ||
| I2 | 0.05 ± 0.004 | ||
| I3 | 0.06 ± 0.002 | ||
| I4 | 0.08 ± 0.007 | ||
| Group 2 | H1 | 8.14 ± 1.46 | 9.07 |
| H2 | 5.36 ± 1.80 | 4.93 | |
| Group 3 | V1 | 50.5 ± 15.4 | 48.9 ± 3.69 |
| V2 | 59.1 ± 19.7 | 46.6 ± 1.58 | |
| Group 4 | MS | 7.73 ± 2.51 | 7.24 |
| MC | 6.95 ± 1.89 | 8.63 ± 0.18 | |
| ME7 | 8.84 ± 1.82 | 11.2 ± 1.26 | |
| ME2 | 5.27 ± 0.63 | 8.31 ± 1.90 | |
| Group | Device Designation | Pristine Graphene | Functionalized Graphene | ||||
|---|---|---|---|---|---|---|---|
| Effective Contact Area (µm2) | Contact Resistance RC (kΩ) | Sheet Resistance Rsh (kΩ/□) | Effective Contact Area (µm2) | Contact Resistance RC (kΩ) | Sheet Resistance Rsh (kΩ/□) | ||
| Group 1 | U | 492 | 0.03 | 4.8 | 217 | 0.02 | 5.5 |
| I1 | 4800 | 0.003 | 16.7 | 2120 | |||
| I2 | 2400 | 0.006 | 6.8 | 1060 | |||
| I3 | 4800 | 0.003 | 38.8 | 2120 | |||
| I4 | 2400 | 0.006 | 12.4 | 1060 | |||
| Group 2 | H1 | 492 | 0.03 | 4.5 | 217 | 0.02 | 5.0 |
| H2 | 492 | 0.03 | 4.9 | 217 | 0.02 | 4.5 | |
| Group 3 | V1 | 480 | 0.03 | 5.3 | 212 | 0.021 | 5.1 |
| V2 | 480 | 0.03 | 6.2 | 212 | 0.021 | 4.9 | |
| Group 4 | MS | 492 | 0.03 | 4.4 | 217 | 0.02 | 4.2 |
| MC | 492 | 0.03 | 3.8 | 217 | 0.02 | 4.7 | |
| ME7 | 480 | 0.03 | 3.7 | 212 | 0.021 | 4.7 | |
| ME2 | 480 | 0.03 | 2.2 | 212 | 0.021 | 3.5 | |
| Effective Width (µm) | ||||
|---|---|---|---|---|
| Group | Device | Coded Width (µm) | Pristine Graphene Films | ZnO Functionalized Graphene Films |
| Group 1 | U | 410 | 387 | 389 |
| Group 2 | H1 | 210 | 211 | 200 |
| H2 | 350 | 323 | 373 | |
| Group 3 | V1 | 40 | 34 | 37 |
| V2 | 40 | 29 | 40 | |
| Group 4 | MS | 220 | 222 | 256 |
| MC | 210 | 248 | 214 | |
| ME7 | 160 | 194 | 68 | |
| ME2 | 160 | 329 | 94 | |
| AN | γ | SV/V2 · L · Weff. @ 10 Hz (µm2/Hz) | |||||
|---|---|---|---|---|---|---|---|
| Group | Device | Pristine | Functionalized | Pristine | Functionalized | Pristine | Functionalized |
| Group 1 | U | 2.61 × 10−13 | 5.59 × 10−13 | 1.8 | 1.7 | 5.96 × 10−10 | 1.61 × 10−9 |
| I1 | 1.86 × 10−11 | 2 | 3.68 × 10−9 | ||||
| I2 | 1.26 × 10−10 | 1.9 | 6.57 × 10−8 | ||||
| I3 | 5.72 × 10−12 | 2 | 4.91 × 10−10 | ||||
| I4 | 1.35 × 10−11 | 1.8 | 5.14 × 10−9 | ||||
| Group 2 | H1 | 6.02 × 10−12 | 9.92 × 10−12 | 1.4 | 1.3 | 1.90 × 10−8 | 3.94 × 10−8 |
| H2 | 7.46 × 10−13 | 1.30 × 10−12 | 1.4 | 1.3 | 3.58 × 10−9 | 7.85 × 10−9 | |
| Group 3 | V1 | 1.49 × 10−10 | 8.18 × 10−12 | 1 | 1.1 | 1.90 × 10−7 | 8.27 × 10−9 |
| V2 | 3.71 × 10−9 | 4.51 × 10−10 | 1.1 | 1.2 | 3.22 × 10−6 | 3.11 × 10−7 | |
| Group 4 | MS | 2.73 × 10−11 | 6.22 × 10−12 | 1.4 | 1.3 | 9.07 × 10−8 | 2.60 × 10−08 |
| MC | 3.34 × 10−11 | 1.29 × 10−11 | 1.5 | 1 | 9.81 × 10−8 | 1.20 × 10−7 | |
| ME7 | 1.88 × 10−11 | 1.22 × 10−12 | 1.7 | 1.8 | 2.74 × 10−8 | 1.41 × 10−9 | |
| ME2 | 1.04 × 10−12 | 6.60 × 10−13 | 1.5 | 1.5 | 4.03 × 10−9 | 2.56 × 10−9 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nah, J.; Perkins, F.K.; Lock, E.H.; Nath, A.; Boyd, A.; Myers-Ward, R.L.; Gaskill, D.K.; Osofsky, M.; Rao, M.V. Electrical and Low Frequency Noise Characterization of Graphene Chemical Sensor Devices Having Different Geometries. Sensors 2022, 22, 1183. https://doi.org/10.3390/s22031183
Nah J, Perkins FK, Lock EH, Nath A, Boyd A, Myers-Ward RL, Gaskill DK, Osofsky M, Rao MV. Electrical and Low Frequency Noise Characterization of Graphene Chemical Sensor Devices Having Different Geometries. Sensors. 2022; 22(3):1183. https://doi.org/10.3390/s22031183
Chicago/Turabian StyleNah, JongBong, Frank Keith Perkins, Evgeniya H. Lock, Anindya Nath, Anthony Boyd, Rachael L. Myers-Ward, David Kurt Gaskill, Michael Osofsky, and Mulpuri V. Rao. 2022. "Electrical and Low Frequency Noise Characterization of Graphene Chemical Sensor Devices Having Different Geometries" Sensors 22, no. 3: 1183. https://doi.org/10.3390/s22031183
APA StyleNah, J., Perkins, F. K., Lock, E. H., Nath, A., Boyd, A., Myers-Ward, R. L., Gaskill, D. K., Osofsky, M., & Rao, M. V. (2022). Electrical and Low Frequency Noise Characterization of Graphene Chemical Sensor Devices Having Different Geometries. Sensors, 22(3), 1183. https://doi.org/10.3390/s22031183






