Incomplete Region Estimation and Restoration of 3D Point Cloud Human Face Datasets
Abstract
:1. Introduction
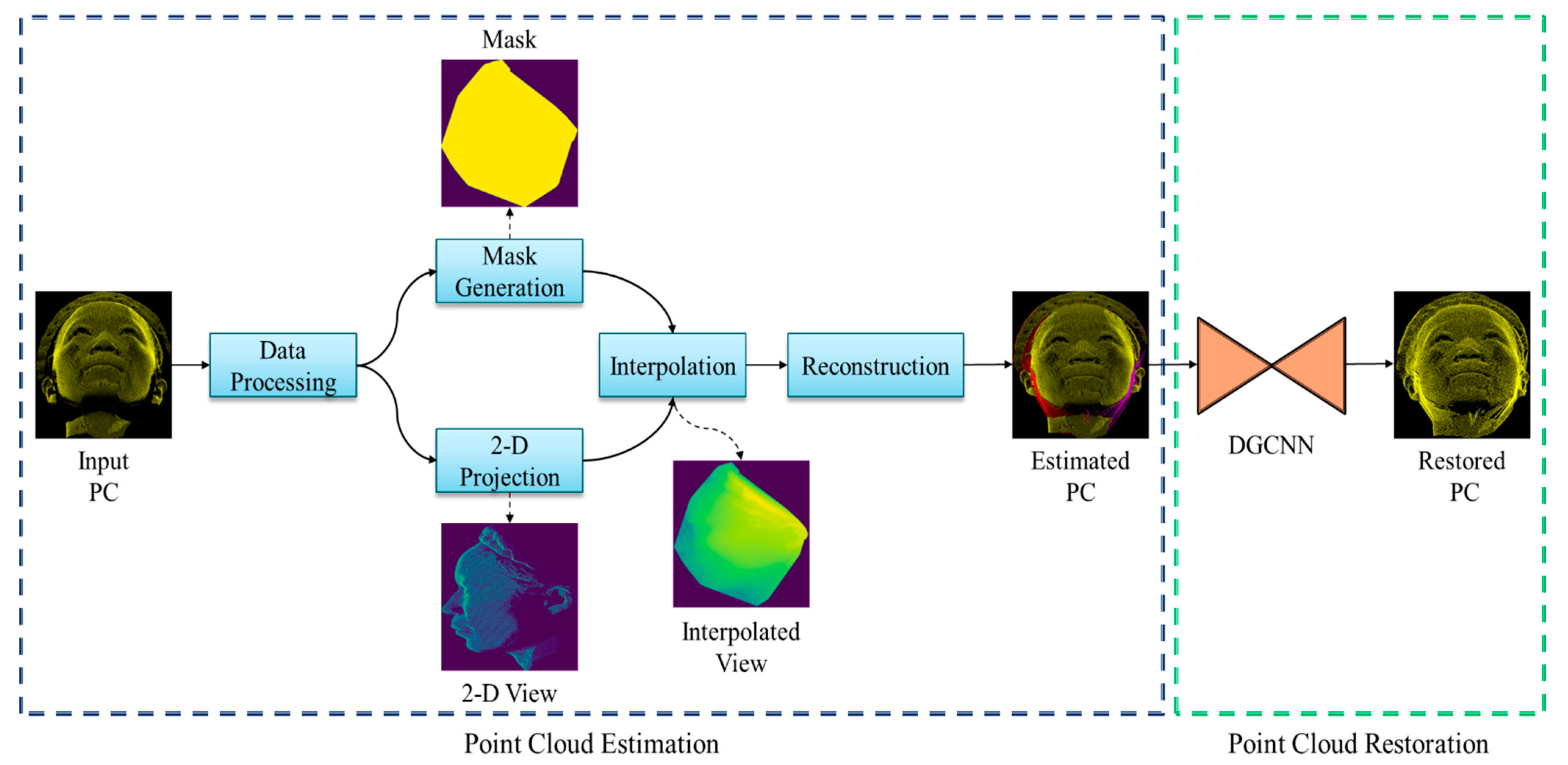
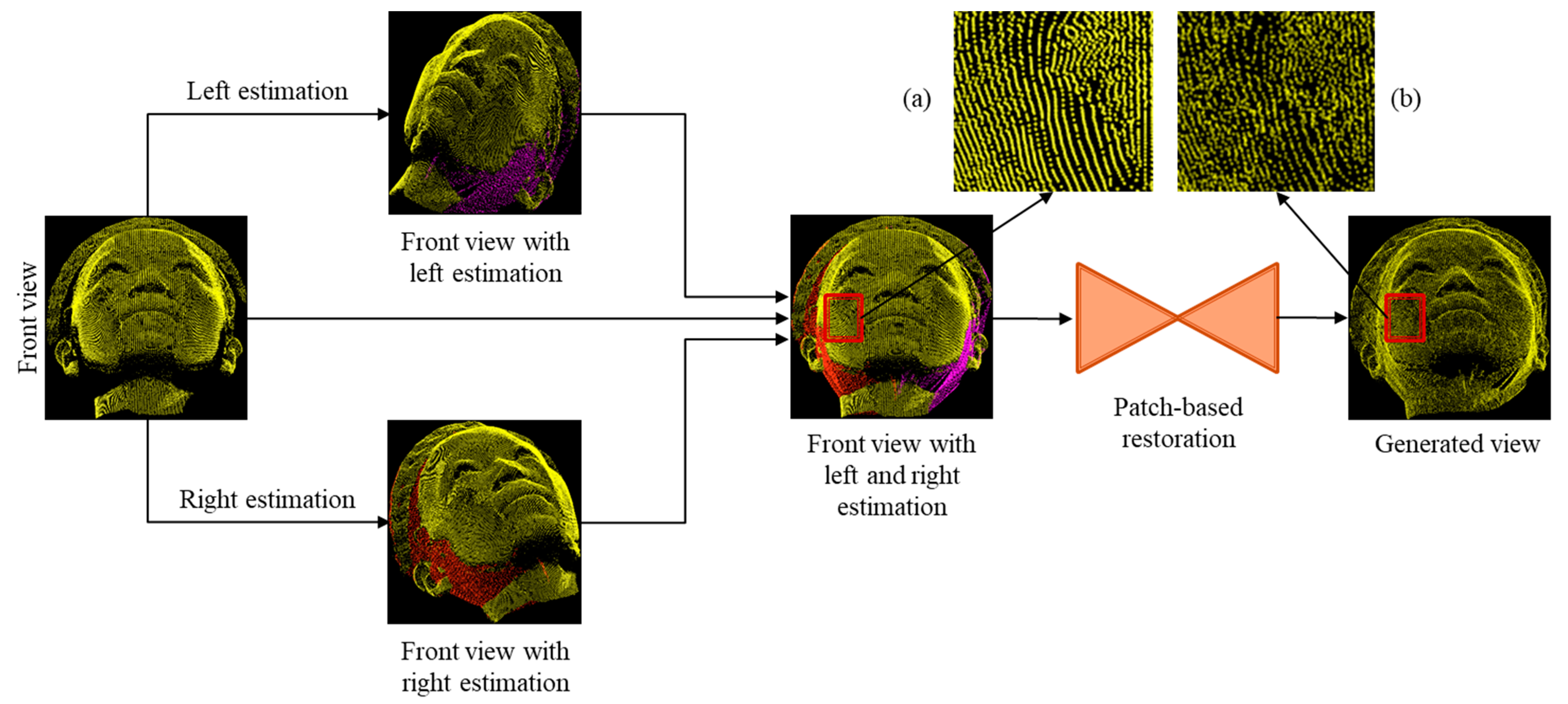
- First, we perform preprocessing, such as rotation along the left and right angles of the input point cloud. From the rotated view, we generate a mask and project it onto the 2D surface. The generated mask and the 2D projection are interpolated to propagate the interpolated output. Then, we perform reconstruction to generate the estimated point cloud.
- To improve the quality of the estimated regions, we apply a deep learning model to restore the point cloud. We consider a dynamic graph convolutional neural network (DGCNN) that introduces edge convolution to accomplish the restoration.
- We evaluated the proposed method on our own and LSFM datasets to show the robustness of the proposed system. The proposed method can considerably improve the quality of the estimated point cloud.
- We also compared the proposed method with state-of-the-art point cloud processing systems to show the effectiveness and robustness. The proposed method achieved better results than previous methods.
2. Related Works
3. Proposed Methodology
3.1. Architectural Overview of the Proposed Method
3.2. Point Cloud Estimation of Incomplete Regions
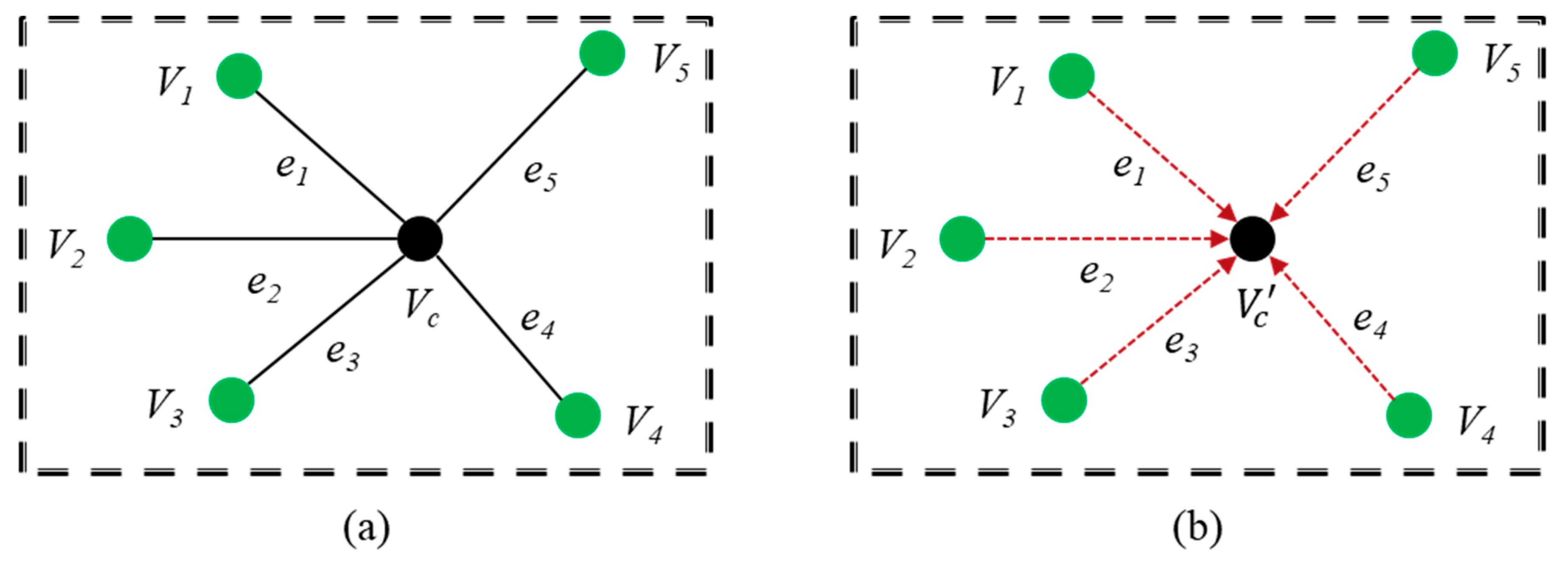
3.3. Deep Learning-Based Point Cloud Restoration
3.3.1. Architecture of the Proposed DGCNN Model
3.3.2. Loss Function for the Point Cloud Restoration
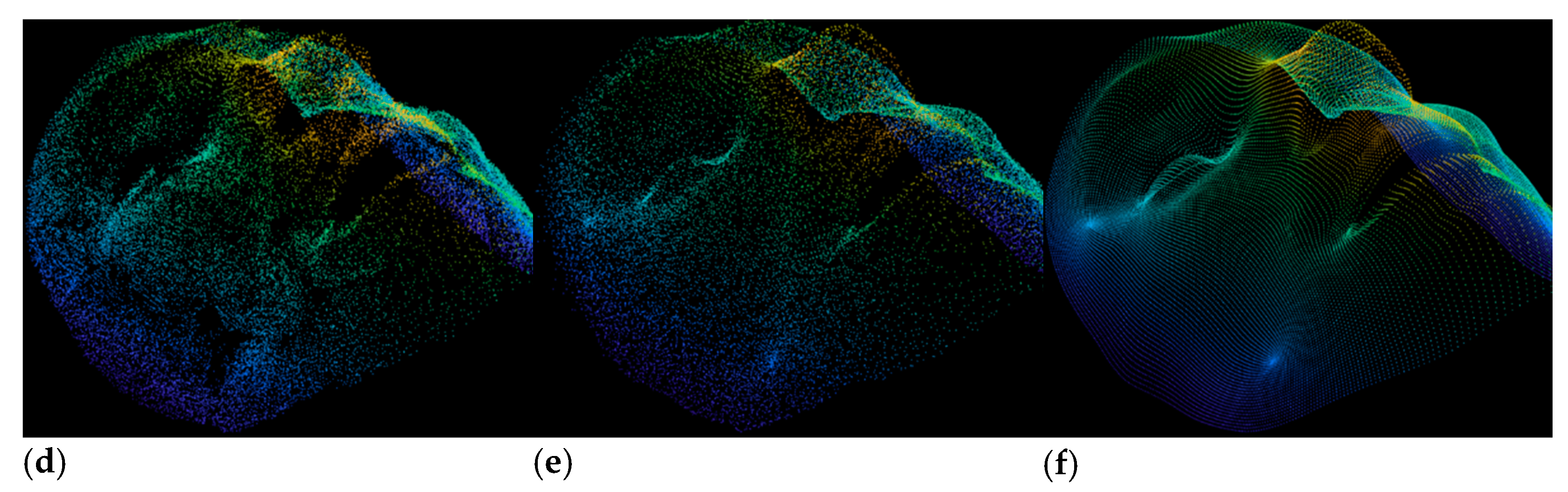
4. Experimental Results
4.1. Environmental Setups
4.2. Evaluation Metrics
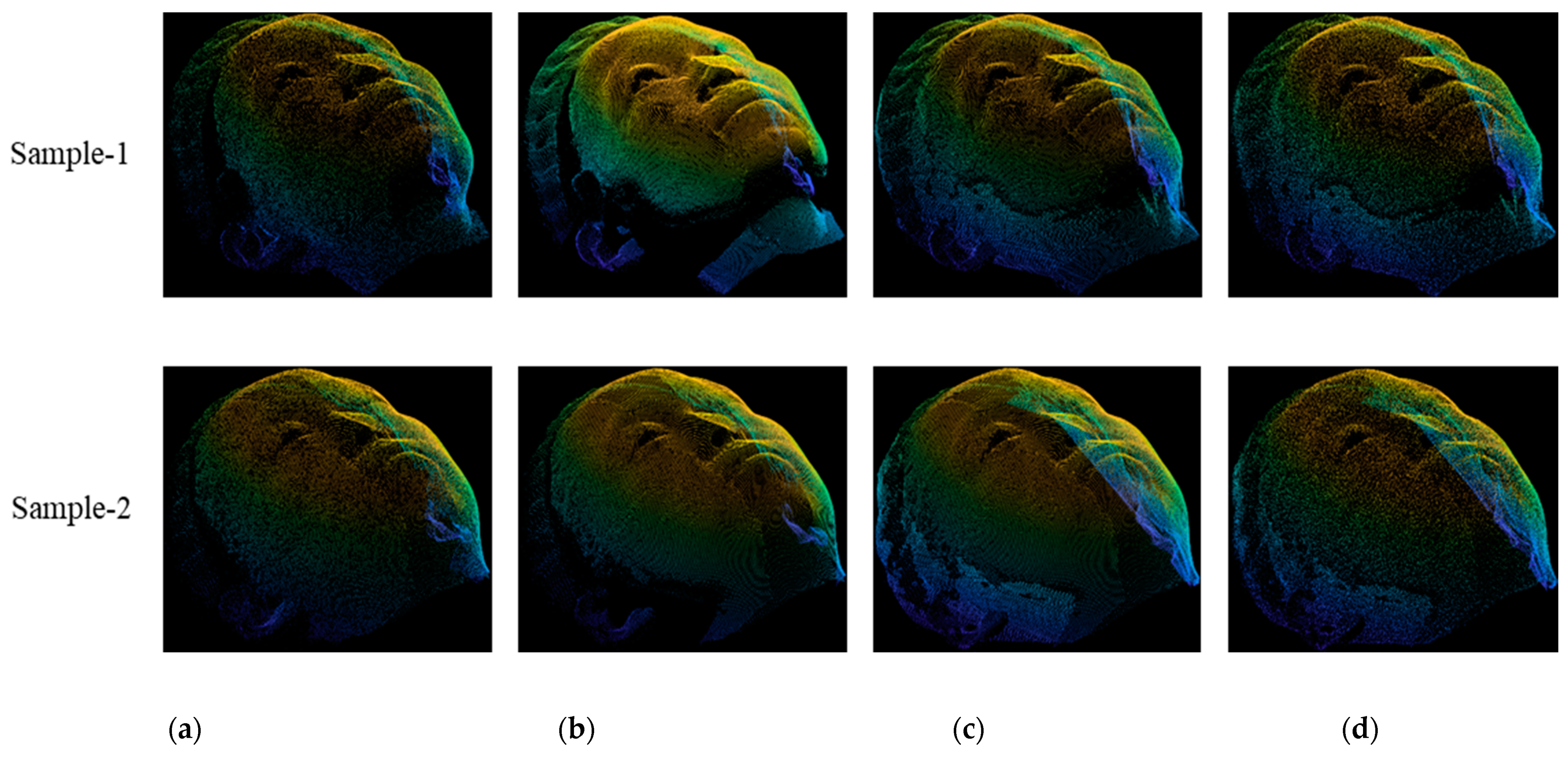
4.3. Performance Evaluations and State-of-the-Arts Comparsons
4.4. Complexity Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Pang, G.; Neumann, U. 3D point cloud object detection with multi-view convolutional neural network. In Proceedings of the 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 585–590. [Google Scholar] [CrossRef]
- Garcia, A.G.; Alberto, F.D.; Rodriguez, J.R.; Orts, S.E.; Cazaorla, M.; Azorin, J.L. PointNet: A 3d convolutional neural network for real-time object class recognition. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1578–1584. [Google Scholar] [CrossRef]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-end learning for point cloud based 3d object detection. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4490–4499. [Google Scholar]
- Li, D.; Wang, H.; Liu, N.; Wang, X.; Xu, J. 3D object recognition and pose estimation from point cloud using stably observed point pair feature. IEEE Access 2020, 8, 44335–44345. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. Advan. Neural Inform. Process. Syst. 2017, 30, 5099–5108. [Google Scholar] [CrossRef]
- Zhang, Y.; Rabbat, M. A graph-cnn for 3d point cloud classification. In Proceedings of the International Conference on Acoustics, Speech and Signal Proceedings (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 6279–6283. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Chen, H.; Cui, Z.; Timofte, R.; Pollefeys, M.; Chirikjian, G.; Van, L.G. Towards Efficient Graph Convolutional Networks for Point Cloud Handling. arXiv 2021, arXiv:2104.05706. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph CNN for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Li, X.; Fu, C.W.; Cohen, D.O.; Heng, P.A. PU-Net: Point cloud upsampling network. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 2790–2799. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Li, X.; Fu, C.W.; Cohen, D.O.; Heng, P.A. PU-GAN: A point cloud upsampling adversarial network. In Proceedings of the International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 7203–7212. [Google Scholar]
- Yifan, W.; Wu, S.; Huang, H.; Cohen, D.O.; Sorkine, O.H. Patch-based progressive 3d point set upsampling. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 5958–5967. [Google Scholar] [CrossRef] [Green Version]
- Qian, G.; Abualshour, A.; Li, G.; Thabet, A.; Ghanem, B. PU-GCN: Point cloud upsampling using graph convolutional networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 19–25 June 2021; pp. 11683–11692. [Google Scholar] [CrossRef]
- Setty, S.; Ganihar, S.A.; Mudenagudi, U. Framework for 3D object hole filling. In Proceedings of the Fifth National Conference on Computer Vision, Pattern Recognition, Image Proceedings and Graphics (NCVPRIPG), Patna, India, 16–19 December 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Attene, M.; Campen, M.; Kobbelt, L. Polygon mesh repairing: An application perspective. ACM Comput. Surv. 2013, 45, 1–33. [Google Scholar] [CrossRef]
- Li, Z.; Meek, D.S.; Walton, D.J. Polynomial blending in a mesh hole filling application. Comp. Aided Design 2010, 42, 340–349. [Google Scholar] [CrossRef]
- Zhao, W.; Gao, S.; Lin, H. A robust hole-filling algorithm for triangular mesh. Visual Comp. 2007, 23, 987–997. [Google Scholar] [CrossRef]
- Wei, Z.L.; Zhong, Y.X.; Yuan, C.L.; Li, R. Research on Smooth Filling Algorithm of Large Holes in Triangular Mesh Model. China Mech. Engin. 2008, 19, 949–954. [Google Scholar]
- Wang, X.; Cao, J.; Liu, X.; Li, B. Advancing Front Method in Triangular Meshes Hole-Filling Application. J. Comp. Aided Des. Comp. Graph. 2011, 23, 1048–1054. [Google Scholar]
- Altantsetseg, E.; Khorloo, O.; Matsuyama, K.; Konno, K. Complex hole filling algorithm for 3D models. In Proceedings of the Computer Graphics International Conference (CGI), Yokohama, Japan, 27–30 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Oliveira, M.M. Filling holes on locally smooth surfaces reconstructed from point clouds. Image Vis. Comp. 2007, 25, 103–113. [Google Scholar] [CrossRef]
- Wang, Y.H.; Wei, W.U.Y. Holes repairing algorithm of scattered data based on the fitting of partial subdivision curved surface. J. Mach. Des. 2009, 12, 72–74. [Google Scholar]
- Tran, M.H.; Nhan, B.C. A Complete Method for Reconstructing an Elevation Surface of 3D Point Clouds. REV J. Elect. Commun. 2015, 4, 91–97. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.S.; Manh, H.T.; Tien, T.N. Filling holes on the surface of 3D point clouds based on tangent plane of hole boundary points. In Proceedings of the Seventh Symposium on Information and Communication Technology, Ho Chi Minh, Vietnam, 8–9 December 2016; pp. 331–338. [Google Scholar] [CrossRef]
- Quinsat, Y. Filling holes in digitized point cloud using a morphing-based approach to preserve volume characteristics. Intern. J. Adv. Manufact. Technol. 2015, 81, 411–421. [Google Scholar] [CrossRef]
- Chalmoviansky, P.; Jttler, B. Filling holes in point clouds. In Mathematics of Surfaces; Springer: Berlin/Heidelberg, Germany, 2003; pp. 196–212. [Google Scholar] [CrossRef]
- Qiu, Z.Y.; Song, X.Y.; Zhang, D.H. Reparation of Holes in Discrete Data Points. J. Eng. Graph. 2004, 25, 85–89. [Google Scholar]
- Chen, F.; Chen, Z.; Ding, Z.; Ye, X.; Zhang, S. Filling holes in point cloud with radial basis function. J. Comp. Aided Des. Comp. Graph. 2006, 18, 1414–1419. [Google Scholar]
- Wu, X.; Chen, W. A scattered point set hole-filling method based on boundary extension and convergence. In Proceedings of the Eleventh World Congress on Intelligent Control and Automation (WCICA), Shenyang, China, 29 June–4 July 2014; pp. 5329–5334. [Google Scholar] [CrossRef]
- Lin, H.; Wang, W. Feature preserving holes filling of scattered point cloud based on tensor voting. In Proceedings of the International Conference on Signal and Image Proceedings (ICIP), Beijing, China, 17–20 September 2017; pp. 402–406. [Google Scholar] [CrossRef]
- Dinesh, C.; Ivan, V.B.; Cheung, G. Exemplar-based framework for 3D point cloud hole filling. In Proceedings of the Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, J.; Zhao, Y.; Hao, W.; Ning, X.; Lv, K. Point cloud hole filling based on feature lines extraction. In Proceedings of the International Conference on Virtual Reality and Visualization (ICVRV), Zhengzhou, China, 21–22 October 2017; pp. 61–66. [Google Scholar] [CrossRef]
- Luo, S.; Hu, W. Differentiable manifold reconstruction for point cloud denoising. In Proceedings of the 28th ACM International Conference on Multimedia, New York, NY, USA, 12–16 October 2020; pp. 1330–1338. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E.; Masters, B.R. Digital Image Processing; Prentice Hall: Hoboken, NJ, USA, 2009; p. 029901. [Google Scholar]
- Booth, J.; Roussos, A.; Zafeiriou, S.; Ponniah, A.; Dunaway, D. A 3d morphable model learnt from 10,000 faces. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 5543–5552. [Google Scholar] [CrossRef] [Green Version]
- Onscans Inc. Available online: http://onscans.com/en/ (accessed on 30 November 2021).
- Hu, W.; Fu, Z.; Guo, Z. Local frequency interpretation and non-local self-similarity on graph for point cloud inpainting. IEEE Trans. Image Process. 2019, 28, 4087–4100. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Methods | Sample-1 | Sample-2 | Sample-3 | Sample-4 | Average | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| CD | HD | CD | HD | CD | HD | CD | HD | CD | HD | |
| Proposed [Estimation] | 2.38 | 20.52 | 2.22 | 20.83 | 2.31 | 13.19 | 2.55 | 36.73 | 2.37 | 22.82 |
| PU-Net [10] | 9.12 | 25.30 | 8.96 | 27.66 | 10.49 | 20.32 | 10.01 | 28.80 | 9.65 | 25.52 |
| PU-GAN [11] | 2.11 | 19.81 | 2.02 | 23.00 | 2.10 | 14.42 | 2.43 | 29.32 | 2.17 | 21.64 |
| DRMD [33] | 2.48 | 22.37 | 2.40 | 23.34 | 2.38 | 14.43 | 2.82 | 28.66 | 2.52 | 22.20 |
| Proposed [Restoration] | 1.37 | 19.82 | 1.22 | 21.97 | 1.11 | 14.58 | 1.51 | 29.47 | 1.30 | 21.46 |
| Methods | Proposed [Estimation] | PU-Net [10] | PU-GAN [11] | DRMD [33] | Proposed [Restoration] | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| CD | HD | CD | HD | CD | HD | CD | HD | CD | HD | |
| Ground Truth versus Restoration | 2.59 | 14.41 | 8.81 | 16.68 | 1.53 | 8.38 | 2.32 | 11.39 | 1.35 | 9.08 |
| SL. No | Layer (Type) | Output Shape | Parameters |
|---|---|---|---|
| 1 | Linear, ReLU Linear, ReLU Linear, ReLU DynamEdgeConv | (32) (64) (64) (64) | 224 2112 4160 - |
| 2 | Linear, ReLU Linear, ReLU DynamEdgeConv | (64) (64) (64) | 8256 4160 - |
| 3 | Linear, ReLU Linear, ReLU DynamEdgeConv | (64) (64) (64) | 8256 4160 - |
| 4 | Linear, ReLU Linear, ReLU DynamEdgeConv | (64) (64) (64) | 8256 4160 - |
| 5 | Linear, ReLU | (128) | 32,896 |
| 6 | Conv1d, ReLU Conv1d | (64,512) (3512) | 8256 195 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uddin, K.; Jeong, T.H.; Oh, B.T. Incomplete Region Estimation and Restoration of 3D Point Cloud Human Face Datasets. Sensors 2022, 22, 723. https://doi.org/10.3390/s22030723
Uddin K, Jeong TH, Oh BT. Incomplete Region Estimation and Restoration of 3D Point Cloud Human Face Datasets. Sensors. 2022; 22(3):723. https://doi.org/10.3390/s22030723
Chicago/Turabian StyleUddin, Kutub, Tae Hyun Jeong, and Byung Tae Oh. 2022. "Incomplete Region Estimation and Restoration of 3D Point Cloud Human Face Datasets" Sensors 22, no. 3: 723. https://doi.org/10.3390/s22030723
APA StyleUddin, K., Jeong, T. H., & Oh, B. T. (2022). Incomplete Region Estimation and Restoration of 3D Point Cloud Human Face Datasets. Sensors, 22(3), 723. https://doi.org/10.3390/s22030723






