Breast Cancer Classification from Ultrasound Images Using Probability-Based Optimal Deep Learning Feature Fusion
Abstract
:1. Introduction
- We modified a pre-trained deep model named DarkNet53 and trained it on augmented ultrasound images using transfer learning.
- The best features are selected using reformed deferential evolution (RDE) and reformed gray wolf (RGW) optimization algorithms.
- The best selected features are fused using a probability-based approach and classified using machine learning algorithms.
2. Related Work
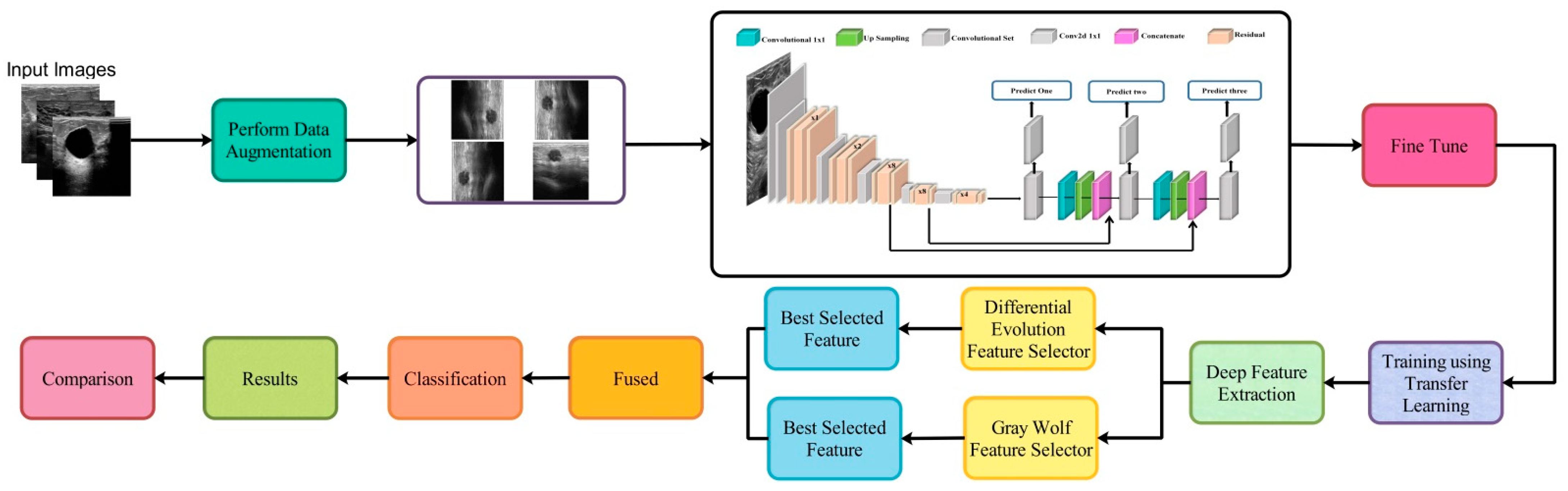
3. Proposed Methodology
3.1. Dataset Augmentation
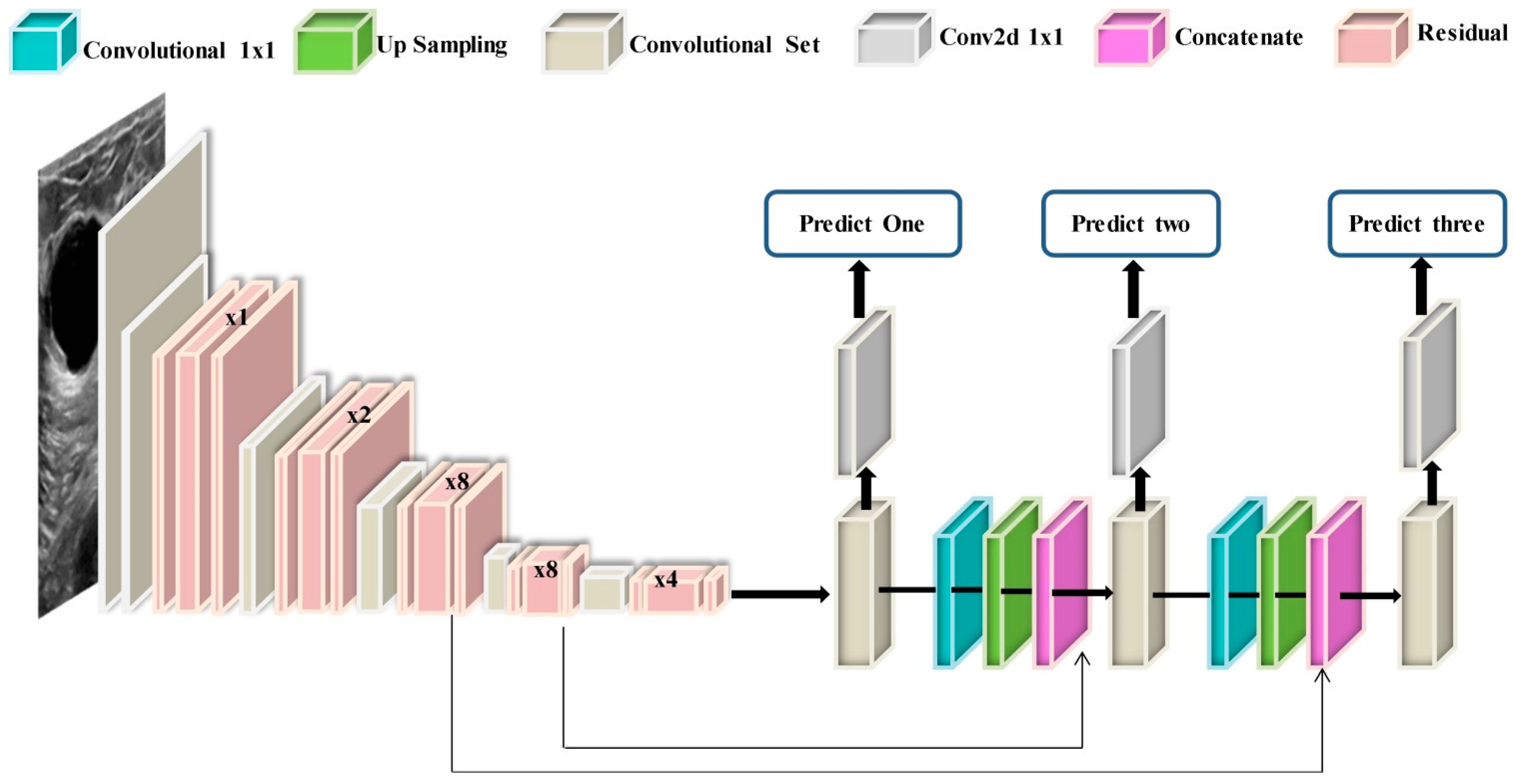
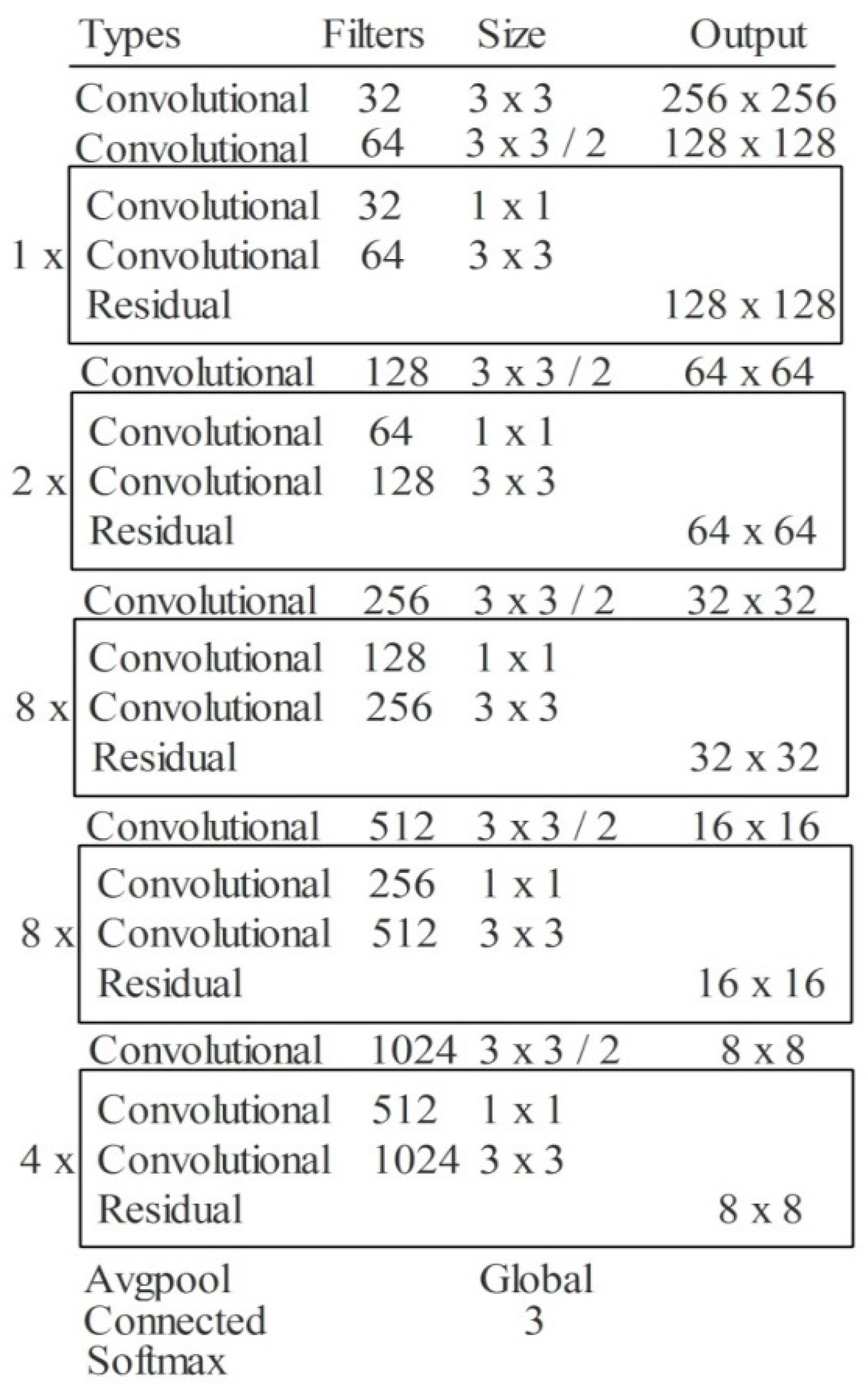
3.2. Modified DarkNet-53 Model
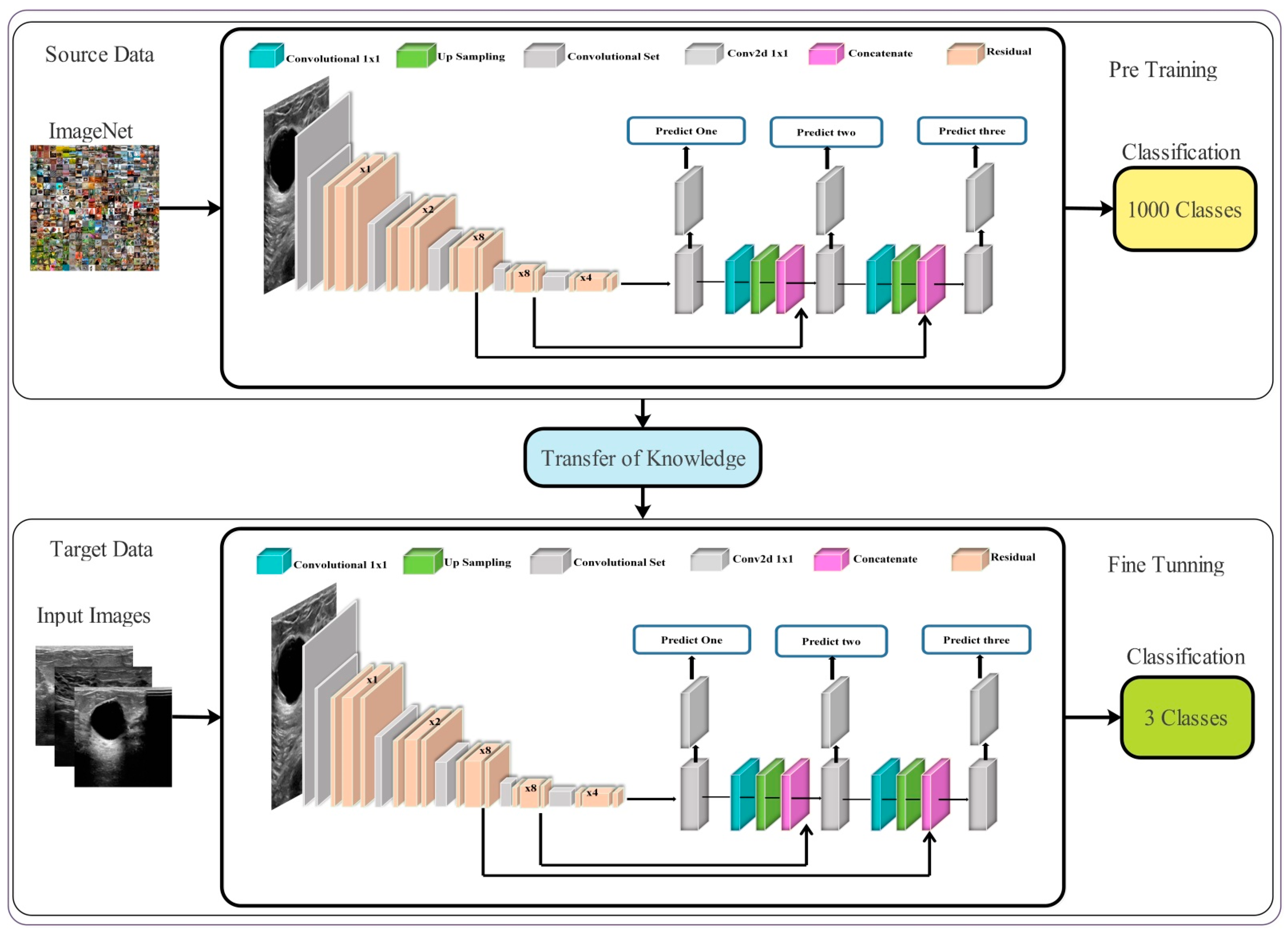
3.3. Transfer Learning
3.4. Best Features Selection
3.4.1. Reformed Differential Evolution (RDE) Algorithm
3.4.2. Reformed Binary Gray Wolf (RBGW) Optimization
| Algorithm 1. Reformed Features Optimization Algorithm |
| Input: the pack’s total number of grey wolves, the number of optimization iterations. Output: Binary position of the grey wolf that is optimal, Best fitness value Begin
|
3.5. Feature Fusion and Classification
4. Experimental Results and Analysis
- (i)
- Classification using modified DarkNet53 features in training/testing ratio of 50:50;
- (ii)
- Classification using modified DarkNet53 features in training/testing ratio 70:30;
- (iii)
- Classification using modified DarkNet53 features in training/testing ratio 60:40;
- (iv)
- Classification using DE based best feature selection on training/testing ratio 50:50;
- (v)
- Classification using the Gray Wolf algorithm based best feature selection in training/testing ratio 50:50, and
- (vi)
- Fusion of best selected features and classification using several classifiers, including the support vector machine (SVM), KNN, decision trees (DT), etc.
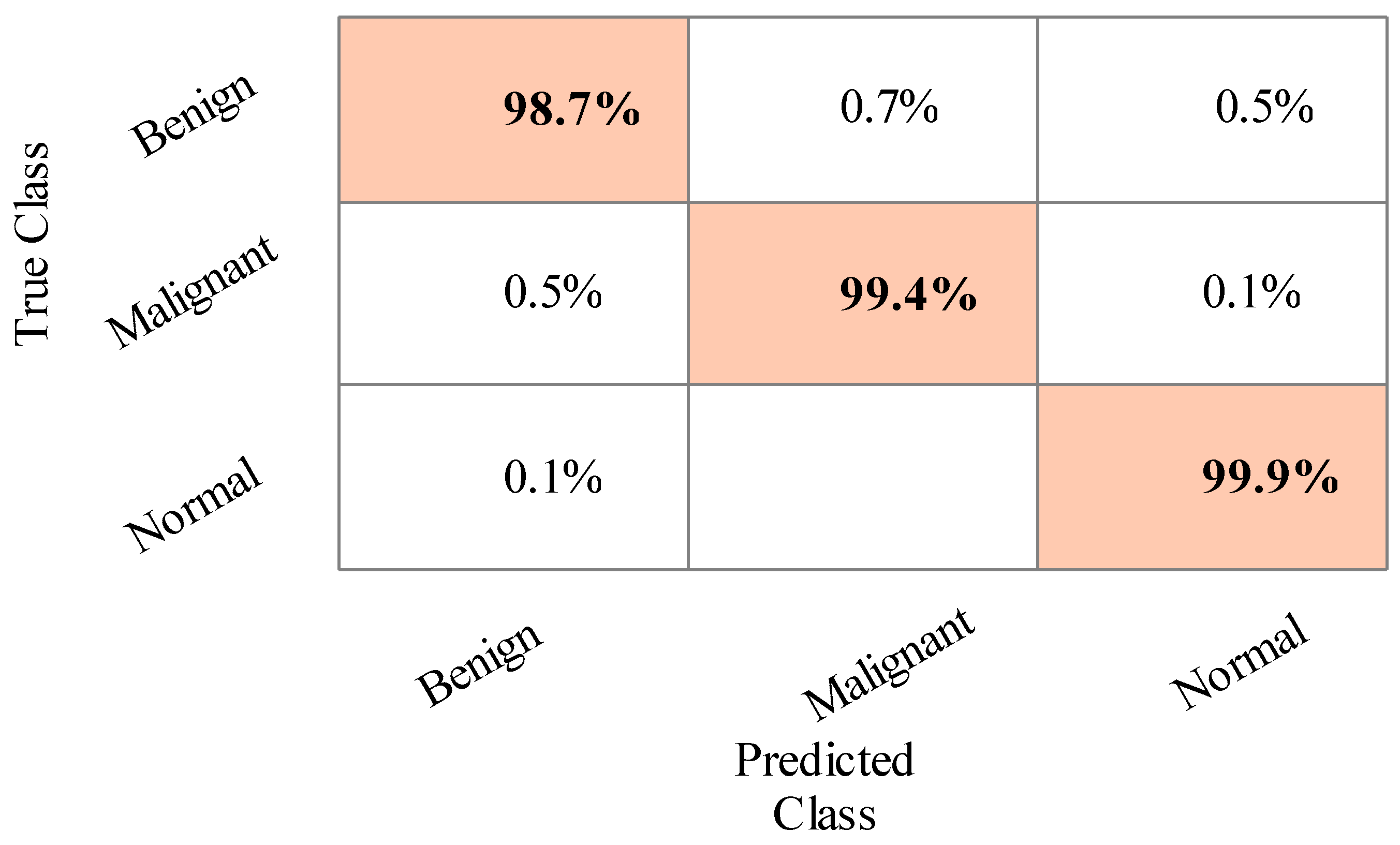
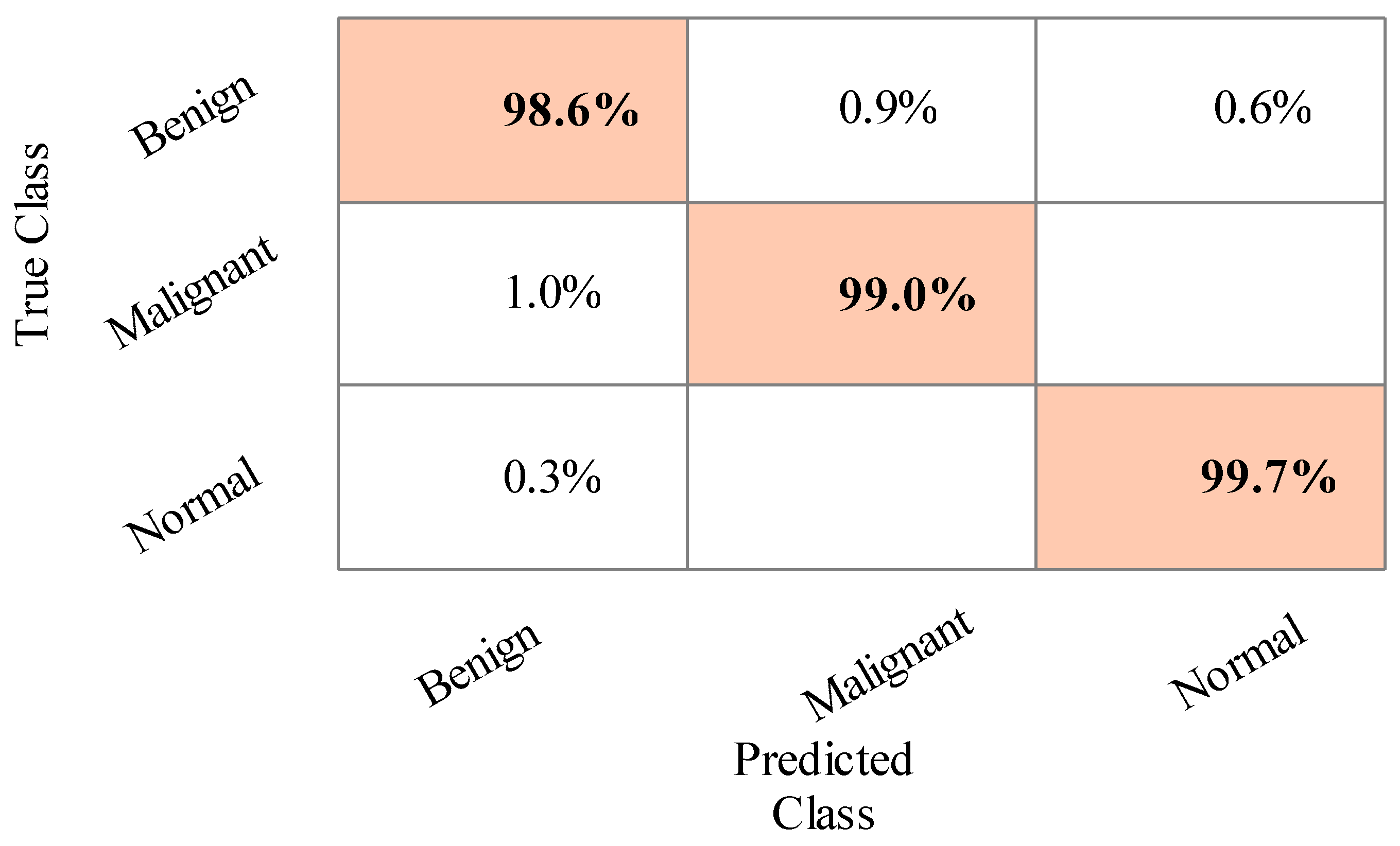
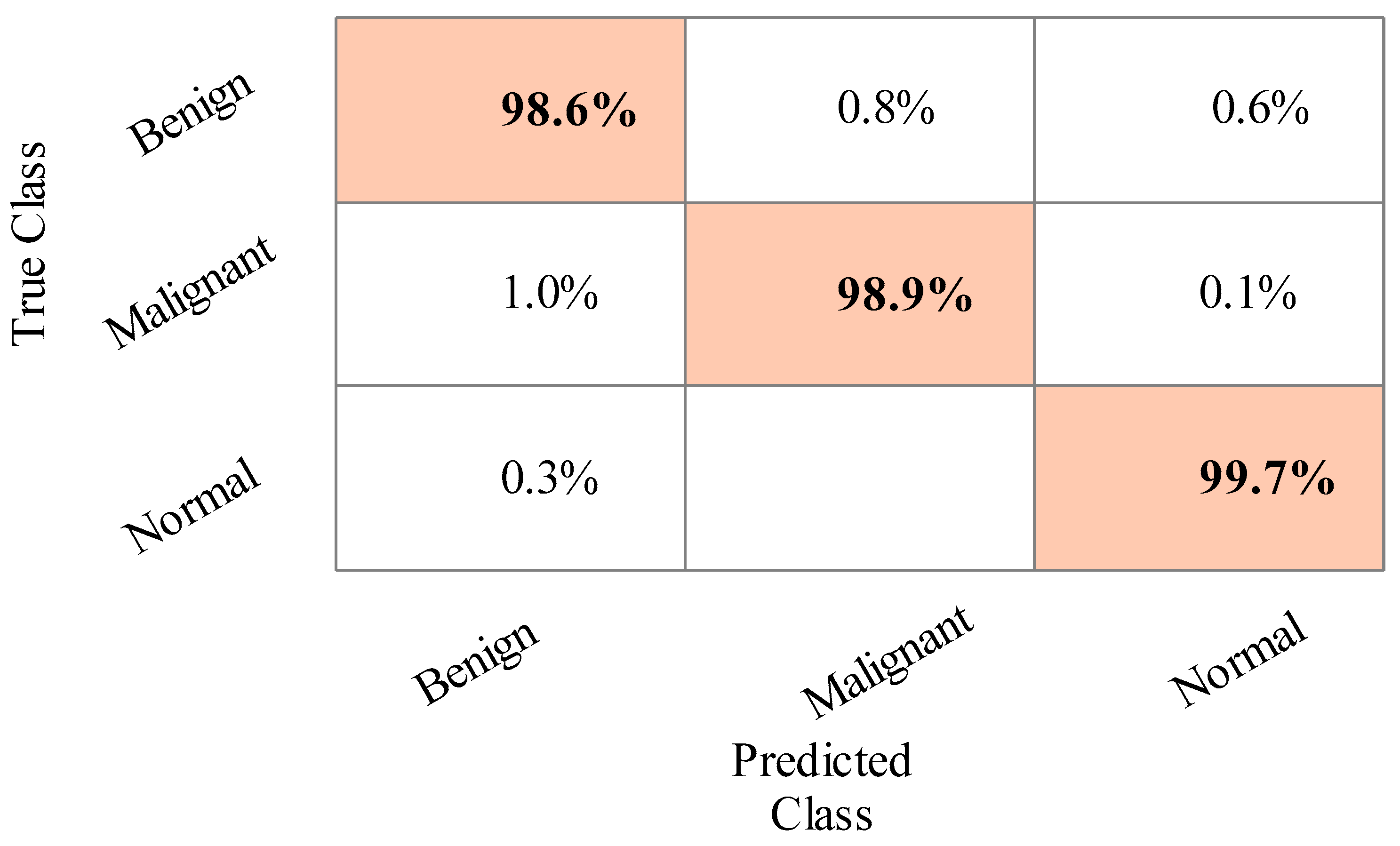
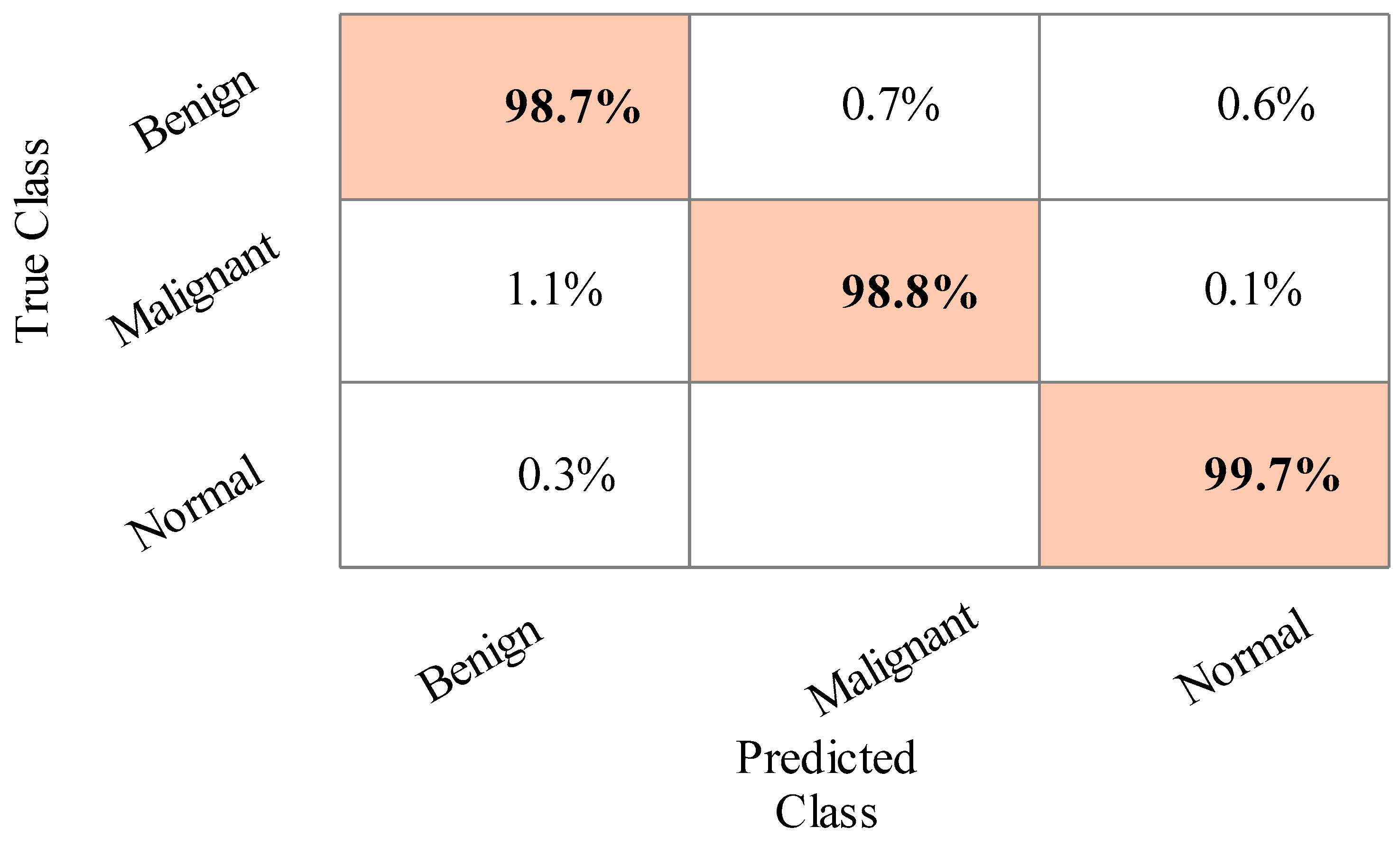
4.1. Results
4.2. Statistical Analysis
4.3. Comparison with the State of the Art
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional neural network |
| RDE | Reformed differential evaluation |
| RGW | Reformed differential evaluation |
| MRI | Magnetic resonance imaging |
| CAD | Computer-aided diagnosis |
| AI | Artificial intelligence |
| GA | Genetic algorithm |
| PSO | Particle swarm optimization |
| HT | Hilbert transform |
| KNN | K-Nearest neighbor |
| ML | Machine learning |
| ROI | Region of interest |
| TL | Transfer learning |
| DRS | Deep representation scaling |
| Di-CNN | Dilated semantic segmentation network |
| LUPI | Learning using privileged information |
| MMD | Maximum mean discrepancy |
| DDSTN | Doubly supervised TL network |
| BTS | Breast tumor section |
| ELM | Extreme learning machine |
| DT | Decision tree |
| SVM | Support vector machine |
| WKNN | Weighted KNN |
| QSVM | Quadratic SVM |
| CGSVM | Cubic gaussian SVM |
| LD | Linear discriminant |
| ESKNN | Ensemble subspace KNN |
| ESD | Ensemble subspace discriminant |
| FNR | False negative rate |
References
- Yu, K.; Chen, S.; Chen, Y. Tumor Segmentation in Breast Ultrasound Image by Means of Res Path Combined with Dense Connection Neural Network. Diagnostics 2021, 11, 1565. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Spezia, M.; Huang, S.; Yuan, C.; Zeng, Z.; Zhang, L.; Ji, X.; Liu, W.; Huang, B.; Luo, W. Breast cancer development and progression: Risk factors, cancer stem cells, signaling pathways, genomics, and molecular pathogenesis. Genes Dis. 2018, 5, 77–106. [Google Scholar] [CrossRef] [PubMed]
- Badawy, S.M.; Mohamed, A.E.-N.A.; Hefnawy, A.A.; Zidan, H.E.; GadAllah, M.T.; El-Banby, G.M. Automatic semantic segmentation of breast tumors in ultrasound images based on combining fuzzy logic and deep learning—A feasibility study. PLoS ONE 2021, 16, e0251899. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.-C.; Hu, Z.-Q.; Long, J.-H.; Zhu, G.-M.; Wang, Y.; Jia, Y.; Zhou, J.; Ouyang, Y.; Zeng, Z. Clinical implications of tumor-infiltrating immune cells in breast cancer. J. Cancer 2019, 10, 6175. [Google Scholar] [CrossRef] [PubMed]
- Irfan, R.; Almazroi, A.A.; Rauf, H.T.; Damaševičius, R.; Nasr, E.; Abdelgawad, A. Dilated Semantic Segmentation for Breast Ultrasonic Lesion Detection Using Parallel Feature Fusion. Diagnostics 2021, 11, 1212. [Google Scholar] [CrossRef]
- Faust, O.; Acharya, U.R.; Meiburger, K.M.; Molinari, F.; Koh, J.E.W.; Yeong, C.H.; Ng, K.H. Comparative assessment of texture features for the identification of cancer in ultrasound images: A review. Biocybern. Biomed. Eng. 2018, 38, 275–296. [Google Scholar] [CrossRef] [Green Version]
- Pourasad, Y.; Zarouri, E.; Salemizadeh Parizi, M.; Salih Mohammed, A. Presentation of Novel Architecture for Diagnosis and Identifying Breast Cancer Location Based on Ultrasound Images Using Machine Learning. Diagnostics 2021, 11, 1870. [Google Scholar] [CrossRef]
- Sainsbury, J.; Anderson, T.; Morgan, D. Breast cancer. BMJ 2000, 321, 745–750. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Lin, X.; Zhao, Y.; Li, L.; Yan, K.; Liang, D.; Sun, D.; Li, Z.-C. Deep learning vs. radiomics for predicting axillary lymph node metastasis of breast cancer using ultrasound images: Don’t forget the peritumoral region. Front. Oncol. 2020, 10, 53. [Google Scholar] [CrossRef] [Green Version]
- Almajalid, R.; Shan, J.; Du, Y.; Zhang, M. Development of a deep-learning-based method for breast ultrasound image segmentation. In Proceedings of the 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; IEEE: New York, NY, USA, 2018; pp. 1103–1108. [Google Scholar]
- Ouahabi, A. Signal and Image Multiresolution Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ahmed, S.S.; Messali, Z.; Ouahabi, A.; Trepout, S.; Messaoudi, C.; Marco, S. Nonparametric denoising methods based on contourlet transform with sharp frequency localization: Application to low exposure time electron microscopy images. Entropy 2015, 17, 3461–3478. [Google Scholar] [CrossRef] [Green Version]
- Sood, R.; Rositch, A.F.; Shakoor, D.; Ambinder, E.; Pool, K.-L.; Pollack, E.; Mollura, D.J.; Mullen, L.A.; Harvey, S.C. Ultrasound for breast cancer detection globally: A systematic review and meta-analysis. J. Glob. Oncol. 2019, 5, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Byra, M. Breast mass classification with transfer learning based on scaling of deep representations. Biomed. Signal Process. Control 2021, 69, 102828. [Google Scholar] [CrossRef]
- Chen, D.-R.; Hsiao, Y.-H. Computer-aided diagnosis in breast ultrasound. J. Med. Ultrasound 2008, 16, 46–56. [Google Scholar] [CrossRef] [Green Version]
- Moustafa, A.F.; Cary, T.W.; Sultan, L.R.; Schultz, S.M.; Conant, E.F.; Venkatesh, S.S.; Sehgal, C.M. Color doppler ultrasound improves machine learning diagnosis of breast cancer. Diagnostics 2020, 10, 631. [Google Scholar] [CrossRef] [PubMed]
- Shen, W.-C.; Chang, R.-F.; Moon, W.K.; Chou, Y.-H.; Huang, C.-S. Breast ultrasound computer-aided diagnosis using BI-RADS features. Acad. Radiol. 2007, 14, 928–939. [Google Scholar] [CrossRef]
- Lee, J.-H.; Seong, Y.K.; Chang, C.-H.; Park, J.; Park, M.; Woo, K.-G.; Ko, E.Y. Fourier-based shape feature extraction technique for computer-aided b-mode ultrasound diagnosis of breast tumor. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; IEEE: New York, NY, USA, 2012; pp. 6551–6554. [Google Scholar]
- Ding, J.; Cheng, H.-D.; Huang, J.; Liu, J.; Zhang, Y. Breast ultrasound image classification based on multiple-instance learning. J. Digit. Imaging 2012, 25, 620–627. [Google Scholar] [CrossRef] [PubMed]
- Bing, L.; Wang, W. Sparse representation based multi-instance learning for breast ultrasound image classification. Comput. Math. Methods Med. 2017, 2017, 7894705. [Google Scholar] [CrossRef] [Green Version]
- Prabhakar, T.; Poonguzhali, S. Automatic detection and classification of benign and malignant lesions in breast ultrasound images using texture morphological and fractal features. In Proceedings of the 2017 10th Biomedical Engineering International Conference (BMEiCON), Hokkaido, Japan, 31 August–2 September 2017; IEEE: New York, NY, USA, 2017; pp. 1–5. [Google Scholar]
- Zhang, Q.; Suo, J.; Chang, W.; Shi, J.; Chen, M. Dual-modal computer-assisted evaluation of axillary lymph node metastasis in breast cancer patients on both real-time elastography and B-mode ultrasound. Eur. J. Radiol. 2017, 95, 66–74. [Google Scholar] [CrossRef]
- Gao, Y.; Geras, K.J.; Lewin, A.A.; Moy, L. New frontiers: An update on computer-aided diagnosis for breast imaging in the age of artificial intelligence. Am. J. Roentgenol. 2019, 212, 300–307. [Google Scholar] [CrossRef]
- Geras, K.J.; Mann, R.M.; Moy, L. Artificial intelligence for mammography and digital breast tomosynthesis: Current concepts and future perspectives. Radiology 2019, 293, 246–259. [Google Scholar] [CrossRef]
- Fujioka, T.; Mori, M.; Kubota, K.; Oyama, J.; Yamaga, E.; Yashima, Y.; Katsuta, L.; Nomura, K.; Nara, M.; Oda, G. The utility of deep learning in breast ultrasonic imaging: A review. Diagnostics 2020, 10, 1055. [Google Scholar] [CrossRef] [PubMed]
- Zahoor, S.; Lali, I.U.; Javed, K.; Mehmood, W. Breast cancer detection and classification using traditional computer vision techniques: A comprehensive review. Curr. Med. Imaging 2020, 16, 1187–1200. [Google Scholar] [CrossRef] [PubMed]
- Kadry, S.; Rajinikanth, V.; Taniar, D.; Damaševičius, R.; Valencia, X.P.B. Automated segmentation of leukocyte from hematological images—A study using various CNN schemes. J. Supercomput. 2021, 1–21. [Google Scholar] [CrossRef]
- Abayomi-Alli, O.O.; Damaševičius, R.; Misra, S.; Maskeliūnas, R.; Abayomi-Alli, A. Malignant skin melanoma detection using image augmentation by oversampling in nonlinear lower-dimensional embedding manifold. Turk. J. Electr. Eng. Comput. Sci. 2021, 29, 2600–2614. [Google Scholar] [CrossRef]
- Maqsood, S.; Damaševičius, R.; Maskeliūnas, R. Hemorrhage detection based on 3d cnn deep learning framework and feature fusion for evaluating retinal abnormality in diabetic patients. Sensors 2021, 21, 3865. [Google Scholar] [CrossRef]
- Hussain, N.; Kadry, S.; Tariq, U.; Mostafa, R.R.; Choi, J.-I.; Nam, Y. Intelligent Deep Learning and Improved Whale Optimization Algorithm Based Framework for Object Recognition. Hum. Cent. Comput. Inf. Sci. 2021, 11, 34. [Google Scholar]
- Kadry, S.; Parwekar, P.; Damaševičius, R.; Mehmood, A.; Khan, J.A.; Naqvi, S.R.; Khan, M.A. Human gait analysis for osteoarthritis prediction: A framework of deep learning and kernel extreme learning machine. Complex Intell. Syst. 2021, 1–19. [Google Scholar] [CrossRef]
- Dhungel, N.; Carneiro, G.; Bradley, A.P. The automated learning of deep features for breast mass classification from mammograms. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; Springer: Cham, Switzerland, 2016; pp. 106–114. [Google Scholar]
- Alhaisoni, M.; Tariq, U.; Hussain, N.; Majid, A.; Damaševičius, R.; Maskeliūnas, R. COVID-19 Case Recognition from Chest CT Images by Deep Learning, Entropy-Controlled Firefly Optimization, and Parallel Feature Fusion. Sensors 2021, 21, 7286. [Google Scholar]
- Odusami, M.; Maskeliūnas, R.; Damaševičius, R.; Krilavičius, T. Analysis of features of alzheimer’s disease: Detection of early stage from functional brain changes in magnetic resonance images using a finetuned resnet18 network. Diagnostics 2021, 11, 1071. [Google Scholar] [CrossRef]
- Nawaz, M.; Nazir, T.; Masood, M.; Mehmood, A.; Mahum, R.; Kadry, S.; Thinnukool, O. Analysis of Brain MRI Images Using Improved CornerNet Approach. Diagnostics 2021, 11, 1856. [Google Scholar] [CrossRef]
- Farzaneh, N.; Williamson, C.A.; Jiang, C.; Srinivasan, A.; Bapuraj, J.R.; Gryak, J.; Najarian, K.; Soroushmehr, S. Automated segmentation and severity analysis of subdural hematoma for patients with traumatic brain injuries. Diagnostics 2020, 10, 773. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; Zhang, Q.; Bu, S. Two-Stage Liver and Tumor Segmentation Algorithm Based on Convolutional Neural Network. Diagnostics 2021, 11, 1806. [Google Scholar] [CrossRef] [PubMed]
- Khaldi, Y.; Benzaoui, A.; Ouahabi, A.; Jacques, S.; Taleb-Ahmed, A. Ear recognition based on deep unsupervised active learning. IEEE Sens. J. 2021, 21, 20704–20713. [Google Scholar] [CrossRef]
- Majid, A.; Nam, Y.; Tariq, U.; Roy, S.; Mostafa, R.R.; Sakr, R.H. COVID19 classification using CT images via ensembles of deep learning models. Comput. Mater. Contin. 2021, 69, 319–337. [Google Scholar] [CrossRef]
- Sharif, M.I.; Alhussein, M.; Aurangzeb, K.; Raza, M. A decision support system for multimodal brain tumor classification using deep learning. Complex Intell. Syst. 2021, 1–14. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Y.; Li, S.; Li, W.; Wang, L. Fusion of handcrafted and deep features for medical image classification. J. Phys. Conf. Ser. 2019, 1345, 022052. [Google Scholar] [CrossRef]
- Alinsaif, S.; Lang, J.; Alzheimer’s Disease Neuroimaging Initiative. 3D shearlet-based descriptors combined with deep features for the classification of Alzheimer’s disease based on MRI data. Comput. Biol. Med. 2021, 138, 104879. [Google Scholar] [CrossRef]
- Khan, M.A.; Muhammad, K.; Sharif, M.; Akram, T.; de Albuquerque, V.H.C. Multi-Class Skin Lesion Detection and Classification via Teledermatology. IEEE J. Biomed. Health Inform. 2021, 25, 4267–4275. [Google Scholar] [CrossRef]
- Masud, M.; Rashed, A.E.E.; Hossain, M.S. Convolutional neural network-based models for diagnosis of breast cancer. Neural Comput. Appl. 2020, 1–12. [Google Scholar] [CrossRef]
- Jiménez-Gaona, Y.; Rodríguez-Álvarez, M.J.; Lakshminarayanan, V. Deep-Learning-Based Computer-Aided Systems for Breast Cancer Imaging: A Critical Review. Appl. Sci. 2020, 10, 8298. [Google Scholar] [CrossRef]
- Zeebaree, D.Q. A Review on Region of Interest Segmentation Based on Clustering Techniques for Breast Cancer Ultrasound Images. J. Appl. Sci. Technol. Trends 2020, 1, 78–91. [Google Scholar]
- Huang, K.; Zhang, Y.; Cheng, H.; Xing, P. Shape-adaptive convolutional operator for breast ultrasound image segmentation. In Proceedings of the 2021 IEEE International Conference on Multimedia and Expo (ICME), Shenzhen, China, 5–9 July 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Sadad, T.; Hussain, A.; Munir, A.; Habib, M.; Ali Khan, S.; Hussain, S.; Yang, S.; Alawairdhi, M. Identification of breast malignancy by marker-controlled watershed transformation and hybrid feature set for healthcare. Appl. Sci. 2020, 10, 1900. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.K.; Roy, P.; Bandyopadhyay, S.; Das, S.K. Breast ultrasound tumour classification: A Machine Learning—Radiomics based approach. Expert Syst. 2021, 38, e12713. [Google Scholar] [CrossRef]
- Hussain, S.; Xi, X.; Ullah, I.; Wu, Y.; Ren, C.; Lianzheng, Z.; Tian, C.; Yin, Y. Contextual level-set method for breast tumor segmentation. IEEE Access 2020, 8, 189343–189353. [Google Scholar] [CrossRef]
- Xiangmin, H.; Jun, W.; Weijun, Z.; Cai, C.; Shihui, Y.; Jun, S. Deep Doubly Supervised Transfer Network for Diagnosis of Breast Cancer with Imbalanced Ultrasound Imaging Modalities. arXiv 2020, arXiv:2007.066342020. [Google Scholar]
- Moon, W.K.; Lee, Y.-W.; Ke, H.-H.; Lee, S.H.; Huang, C.-S.; Chang, R.-F. Computer-aided diagnosis of breast ultrasound images using ensemble learning from convolutional neural networks. Comput. Methods Programs Biomed. 2020, 190, 105361. [Google Scholar] [CrossRef]
- Byra, M.; Jarosik, P.; Szubert, A.; Galperin, M.; Ojeda-Fournier, H.; Olson, L.; O’Boyle, M.; Comstock, C.; Andre, M. Breast mass segmentation in ultrasound with selective kernel U-Net convolutional neural network. Biomed. Signal Process. Control 2020, 61, 102027. [Google Scholar] [CrossRef]
- Kadry, S.; Damaševičius, R.; Taniar, D.; Rajinikanth, V.; Lawal, I.A. Extraction of tumour in breast MRI using joint thresholding and segmentation–A study. In Proceedings of the 2021 Seventh International conference on Bio Signals, Images, and Instrumentation (ICBSII), Chennai, India, 25–27 March 2021; IEEE: New York, NY, USA, 2021; pp. 1–5. [Google Scholar]
- Lahoura, V.; Singh, H.; Aggarwal, A.; Sharma, B.; Mohammed, M.; Damaševičius, R.; Kadry, S.; Cengiz, K. Cloud computing-based framework for breast cancer diagnosis using extreme learning machine. Diagnostics 2021, 11, 241. [Google Scholar] [CrossRef]
- Maqsood, S.; Damasevicius, R.; Shah, F.M. An Efficient Approach for the Detection of Brain Tumor Using Fuzzy Logic and U-NET CNN Classification, International Conference on Computational Science and Its Applications; Springer: Cham, Switzerland, 2021; pp. 105–118. [Google Scholar]
- Rajinikanth, V.; Kadry, S.; Taniar, D.; Damasevicius, R.; Rauf, H.T. Breast-cancer detection using thermal images with marine-predators-algorithm selected features. In Proceedings of the 2021 Seventh International conference on Bio Signals, Images, and Instrumentation (ICBSII), Noida, India, 26–27 August 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Ouahabi, A.; Taleb-Ahmed, A. Deep learning for real-time semantic segmentation: Application in ultrasound imaging. Pattern Recognit. Lett. 2021, 144, 27–34. [Google Scholar] [CrossRef]
- Al-Dhabyani, W.; Gomaa, M.; Khaled, H.; Fahmy, A. Dataset of breast ultrasound images. Data Brief 2020, 28, 104863. [Google Scholar] [CrossRef]
- Khan, M.A.; Kadry, S.; Zhang, Y.-D.; Akram, T.; Sharif, M.; Rehman, A.; Saba, T. Prediction of COVID-19-pneumonia based on selected deep features and one class kernel extreme learning machine. Comput. Electr. Eng. 2021, 90, 106960. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Sharif, M.I.; Raza, M.; Anjum, A.; Saba, T.; Shad, S.A. Skin lesion segmentation and classification: A unified framework of deep neural network features fusion and selection. Expert Syst. 2019, e12497. [Google Scholar] [CrossRef]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Cao, Z.; Yang, G.; Chen, Q.; Chen, X.; Lv, F. Breast tumor classification through learning from noisy labeled ultrasound images. Med. Phys. 2020, 47, 1048–1057. [Google Scholar] [CrossRef] [PubMed]
- Ilesanmi, A.E.; Chaumrattanakul, U.; Makhanov, S.S. A method for segmentation of tumors in breast ultrasound images using the variant enhanced deep learning. Biocybern. Biomed. Eng. 2021, 41, 802–818. [Google Scholar] [CrossRef]
- Zhuang, Z.; Yang, Z.; Raj, A.N.J.; Wei, C.; Jin, P.; Zhuang, S. Breast ultrasound tumor image classification using image decomposition and fusion based on adaptive multi-model spatial feature fusion. Comput. Methods Programs Biomed. 2021, 208, 106221. [Google Scholar] [CrossRef]
- Pang, T.; Wong, J.H.D.; Ng, W.L.; Chan, C.S. Semi-supervised GAN-based Radiomics Model for Data Augmentation in Breast Ultrasound Mass Classification. Comput. Methods Programs Biomed. 2021, 203, 106018. [Google Scholar] [CrossRef]







| Reference | Methods | Features | Dataset |
|---|---|---|---|
| [47], 2021 | Shape Adaptive CNN | Deep learning | Breast Ultrasound Images (BUSI) |
| [48], 2020 | Hilbert transform and Watershed | Textural features | BUSI |
| [3], 2021 | Fuzzy Logic and Semantic Segmentation | Deep features | BUSI |
| [49], 2021 | Machine learning and radiomics | Textural and geometric features | BUSI |
| [14], 2021 | CNN and deep representation scaling | Deep features through scaling layers | BUSI |
| [50], 2020 | U-Net Encoder-Decoder CNN architecture | High level contextual features | BUSI |
| [56], 2021 | U-Net and Fuzzy logic | CNN features | BUSI |
| Classifier | Sensitivity (%) | Precision (%) | F1 Score (%) | Accuracy (%) | FNR | Classification Time (s) |
|---|---|---|---|---|---|---|
| CSVM | 99.2 | 99.2 | 99.2 | 99.3 | 0.8 | 200.697 |
| MGSVM | 99.2 | 99.2 | 99.2 | 99.2 | 0.8 | 207.879 |
| QSVM | 99.16 | 99.16 | 99.16 | 99.2 | 0.84 | 159.21 |
| ESD | 98.8 | 98.8 | 98.8 | 98.9 | 1.2 | 198.053 |
| LSVM | 98.93 | 98.93 | 98.93 | 98.9 | 1.07 | 122.98 |
| ESKNN | 98.6 | 98.6 | 98.6 | 98.7 | 1.4 | 189.79 |
| FKNN | 98.7 | 98.7 | 98.7 | 98.7 | 1.3 | 130.664 |
| LD | 98.6 | 98.6 | 98.6 | 98.6 | 1.4 | 120.909 |
| CGSVM | 98.16 | 98.2 | 98.17 | 98.2 | 1.84 | 133.085 |
| WKNN | 97.9 | 97.93 | 97.91 | 97.9 | 2.1 | 129.357 |
| Classifier | Sensitivity (%) | Precision (%) | F1 Score (%) | Accuracy (%) | FNR (%) | Classification Time (s) |
|---|---|---|---|---|---|---|
| CSVM | 99.3 | 99.3 | 99.3 | 99.3 | 0.7 | 111.112 |
| MGSVM | 99.2 | 99.2 | 99.2 | 99.3 | 0.8 | 113.896 |
| QSVM | 99.16 | 99.2 | 99.17 | 99.2 | 0.84 | 125.304 |
| ESD | 99.0 | 99.03 | 99.01 | 99.0 | 1.0 | 167.126 |
| LSVM | 99.06 | 99.1 | 99.07 | 99.1 | 0.94 | 120.608 |
| ESKNN | 98.06 | 98.03 | 98.04 | 98.1 | 1.94 | 141.71 |
| FKNN | 97.73 | 97.76 | 97.74 | 97.7 | 2.27 | 124.324 |
| LD | 97.6 | 97.6 | 97.6 | 97.7 | 2.4 | 131.507 |
| CGSVM | 98.06 | 98.06 | 98.06 | 98.1 | 1.94 | 155.501 |
| WKNN | 96.03 | 96.13 | 96.07 | 96.0 | 3.97 | 127.675 |
| Classifier | Sensitivity (%) | Precision (%) | F1 Score (%) | Accuracy (%) | FNR (%) | Classification Time (s) |
|---|---|---|---|---|---|---|
| CSVM | 98.9 | 98.9 | 98.9 | 98.9 | 1.1 | 107.697 |
| MGSVM | 98.7 | 98.7 | 98.7 | 98.7 | 1.3 | 103.149 |
| QSVM | 98.7 | 98.7 | 98.7 | 98.7 | 1.3 | 89.049 |
| ESD | 98.6 | 98.7 | 98.65 | 98.7 | 1.4 | 94.31 |
| LSVM | 98.5 | 98.5 | 98.5 | 98.6 | 1.5 | 68.827 |
| ESKNN | 97.9 | 98 | 97.95 | 98.0 | 2.1 | 79.34 |
| FKNN | 97.8 | 97.8 | 98.24 | 97.8 | 2.2 | 84.537 |
| LD | 98.1 | 98.1 | 98.1 | 98.1 | 1.9 | 85.317 |
| CGSVM | 97.8 | 97.9 | 98.34 | 97.9 | 2.2 | 76.2 |
| WKNN | 97.2 | 97.2 | 97.2 | 97.2 | 2.8 | 81.191 |
| Classifier | Sensitivity (%) | Precision (%) | F1 Score (%) | Accuracy (%) | FNR | Classification Time (s) |
|---|---|---|---|---|---|---|
| CSVM | 99.10 | 99.06 | 99.08 | 99.1 | 0.9 | 28.082 |
| MGSVM | 99.13 | 99.13 | 99.13 | 99.1 | 0.87 | 41.781 |
| QSVM | 99.10 | 99.10 | 99.1 | 99.1 | 0.9 | 35.448 |
| ESD | 98.70 | 98.70 | 98.7 | 98.7 | 1.3 | 42.74 |
| LSVM | 98.90 | 98.86 | 98.88 | 98.9 | 1.1 | 33.073 |
| ESKNN | 98.40 | 98.36 | 98.38 | 98.4 | 1.6 | 37.555 |
| FKNN | 98.26 | 98.30 | 98.28 | 98.3 | 1.74 | 35.349 |
| LD | 98.50 | 98.50 | 98.5 | 98.5 | 1.5 | 35.213 |
| CGSVM | 98.43 | 98.43 | 98.43 | 98.4 | 1.57 | 39.686 |
| WKNN | 97.00 | 97.10 | 97.05 | 97.0 | 3.0 | 42.829 |
| Classifier | Sensitivity (%) | Precision (%) | F1 Score (%) | Accuracy (%) | FNR | Classification Time (s) |
|---|---|---|---|---|---|---|
| CSVM | 99.06 | 99.1 | 99.08 | 99.1 | 0.94 | 25.239 |
| MGSVM | 98.96 | 98.96 | 98.96 | 99.0 | 1.04 | 29.732 |
| QSVM | 98.96 | 98.96 | 98.96 | 99.0 | 1.04 | 33.632 |
| ESD | 98.5 | 98.5 | 98.5 | 98.5 | 1.5 | 30.823 |
| LSVM | 98.7 | 98.7 | 98.7 | 98.7 | 1.3 | 35.774 |
| ESKNN | 98.5 | 98.5 | 98.5 | 98.5 | 1.5 | 31.585 |
| FKNN | 98.36 | 98.36 | 98.36 | 98.4 | 1.64 | 40.854 |
| LD | 98.2 | 98.2 | 98.2 | 98.3 | 1.8 | 38.5073 |
| CGSVM | 98.06 | 98.1 | 98.08 | 98.1 | 1.94 | 32.396 |
| WKNN | 97.2 | 97.2 | 97.2 | 97.2 | 2.8 | 30.698 |
| Classifier | Sensitivity (%) | Precision (%) | F1 Score (%) | Accuracy (%) | FNR (%) | Classification Time (s) |
|---|---|---|---|---|---|---|
| CSVM | 99.06 | 99.06 | 99.06 | 99.18 | 0.94 | 13.599 |
| MGSVM | 99.10 | 99.10 | 99.10 | 99.16 | 0.9 | 15.659 |
| QSVM | 98.96 | 98.96 | 98.96 | 99.30 | 1.04 | 17.601 |
| ESD | 98.76 | 98.80 | 98.78 | 98.90 | 1.24 | 26.240 |
| LSVM | 98.93 | 98.90 | 98.91 | 99.00 | 1.07 | 19.185 |
| ESKNN | 98.56 | 98.60 | 98.58 | 98.90 | 1.44 | 22.425 |
| FKNN | 98.36 | 98.36 | 98.36 | 98.74 | 1.64 | 24.508 |
| LD | 98.40 | 98.40 | 98.40 | 98.40 | 1.60 | 21.045 |
| CGSVM | 98.20 | 98.20 | 98.20 | 98.30 | 1.80 | 20.627 |
| WKNN | 97.46 | 97.53 | 97.49 | 98.10 | 2.54 | 18.734 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabeen, K.; Khan, M.A.; Alhaisoni, M.; Tariq, U.; Zhang, Y.-D.; Hamza, A.; Mickus, A.; Damaševičius, R. Breast Cancer Classification from Ultrasound Images Using Probability-Based Optimal Deep Learning Feature Fusion. Sensors 2022, 22, 807. https://doi.org/10.3390/s22030807
Jabeen K, Khan MA, Alhaisoni M, Tariq U, Zhang Y-D, Hamza A, Mickus A, Damaševičius R. Breast Cancer Classification from Ultrasound Images Using Probability-Based Optimal Deep Learning Feature Fusion. Sensors. 2022; 22(3):807. https://doi.org/10.3390/s22030807
Chicago/Turabian StyleJabeen, Kiran, Muhammad Attique Khan, Majed Alhaisoni, Usman Tariq, Yu-Dong Zhang, Ameer Hamza, Artūras Mickus, and Robertas Damaševičius. 2022. "Breast Cancer Classification from Ultrasound Images Using Probability-Based Optimal Deep Learning Feature Fusion" Sensors 22, no. 3: 807. https://doi.org/10.3390/s22030807
APA StyleJabeen, K., Khan, M. A., Alhaisoni, M., Tariq, U., Zhang, Y.-D., Hamza, A., Mickus, A., & Damaševičius, R. (2022). Breast Cancer Classification from Ultrasound Images Using Probability-Based Optimal Deep Learning Feature Fusion. Sensors, 22(3), 807. https://doi.org/10.3390/s22030807







