A Fast Two-Stage Bilateral Filter Using Constant Time O(1) Histogram Generation
Abstract
:1. Introduction
- We improve the range kernel in BF based on an edge-preserving noise-reduced guidance image, where isolated noisy pixels are removed to avoid erroneously judging those noisy pixels as edges;
- We adopt mean filtering based on column histogram construction to approximate the spatial kernel, achieving constant-time filtering regardless of the kernel radius’ size and better smoothing;
- We conducted an extensive experiment on multiple benchmark datasets for denoising and demonstrated that the proposed DHBF performs favorably against other state-of-the-art BF methods.
2. Related Works
2.1. Classic Methods
2.2. CI-Based Methods
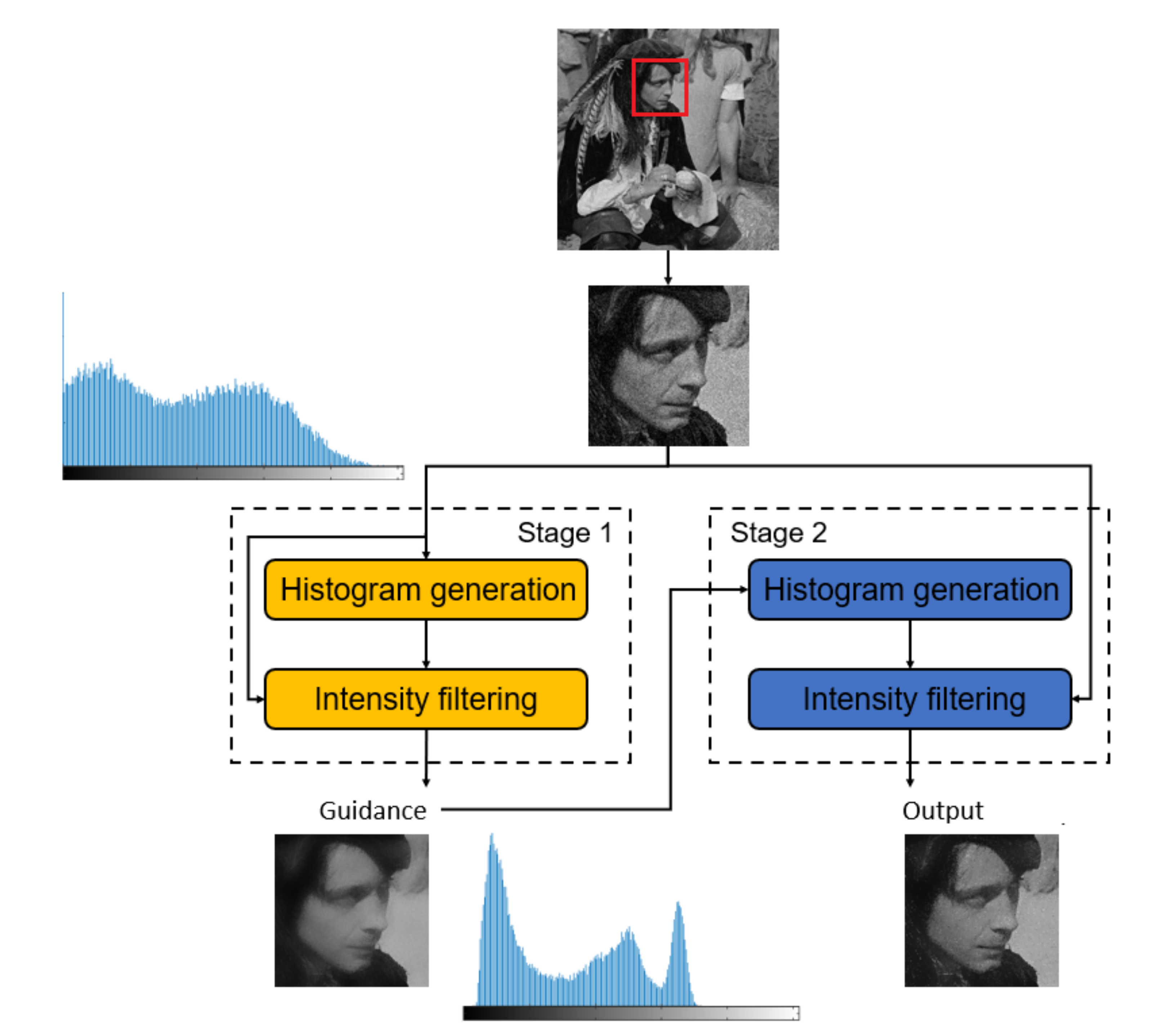
3. Proposed Method
3.1. Local Histogram Generation
3.2. Two-Stage Filtering
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Yang, Q.; Tan, K.-H.; Ahuja, N. Shadow removal using bilateral filtering. IEEE Trans. Image Process. 2012, 21, 4361–4368. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Ardabilian, M.; Chen, L. A fast trilateral filter-based adaptive support weight method for stereo matching. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 730–743. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Ngan, K.N. Unsupervized video segmentation with low depth of field. IEEE Trans. Circuits Syst. Video Technol. 2007, 17, 1742–1751. [Google Scholar] [CrossRef]
- Xie, J.; Feris, R.S.; Sun, M.-T. Edge-guided single depth image super resolution. IEEE Trans. Image Process. 2016, 25, 428–438. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Yin, J.; Chen, B.; Li, Y. Highly accurate image reconstruction for multimodal noise suppression using semi-supervised learning on big data. IEEE Trans. Multimed. 2018, 20, 3045–3056. [Google Scholar] [CrossRef]
- Licciardo, G.D.; D’Arienzo, A.; Rubino, A. Stream processor for real-time inverse tone mapping of Full-HD images. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 23, 2531–2539. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, J.; Zhu, Z.; Wu, S. Selectively detail-enhanced fusion of differently exposed images with moving objects. IEEE Trans. Image Process. 2014, 23, 4372–4382. [Google Scholar] [CrossRef]
- Ghosh, S.; Chaudhury, K.N. Fast bright-pass bilateral filtering for low-light enhancement. In Proceedings of the International Conference on Image Processing, Taipei, Taiwan, 22–25 September 2019; pp. 205–209. [Google Scholar]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 839–846. [Google Scholar]
- Caponetto, R.; Fortuna, L.; Nunnari, G.; Occhipinti, L.; Xibilia, M.G. Soft computing for greenhouse climate control. IEEE Trans. Fuzzy Syst. 2000, 8, 753–760. [Google Scholar] [CrossRef] [Green Version]
- Pal, S.K.; Talwar, V.; Mitra, P. Web mining in soft computing framework: Relevance, state of the art and future directions. IEEE Trans. Neural Netw. 2002, 13, 1163–1177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tseng, V.S.; Ying, J.J.-C.; Wong, S.T.C.; Cook, D.J.; Liu, J. Computational intelligence techniques for combating COVID-19: A survey. IEEE Comput. Intell. Mag. 2020, 15, 10–22. [Google Scholar] [CrossRef]
- Porikli, F. Constant time O(1) bilateral filtering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 24–26 June 2008; pp. 1–8. [Google Scholar]
- He, S.; Yang, Q.; Lau, R.W.H.; Yang, M.-H. Fast weighted histograms for bilateral filtering and nearest neighbor searching. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 891–902. [Google Scholar] [CrossRef]
- Yang, Q.; Tan, K.-H.; Ahuja, N. Real-time O(1) bilateral filtering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Fontainebleau Resort, FL, USA, 20–25 June 2009; pp. 557–564. [Google Scholar]
- Yu, W.; Franchetti, F.; Hoe, J.C.; Chang, Y.-J.; Chen, T. Fast bilateral filtering by adapting block size. In Proceedings of the IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 3281–3284. [Google Scholar]
- Chaudhury, K.N.; Sage, D.; Unser, M. Fast O(1) bilateral filtering using trigonometric range kernels. IEEE Trans. Image Process. 2011, 20, 3376–3382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chaudhury, K.N. Constant-time filtering using shiftable kernels. IEEE Singal Process. Lett. 2011, 18, 651–654. [Google Scholar] [CrossRef] [Green Version]
- Sugimoto, K.; Kamata, S.-I. Compressive bilateral filtering. IEEE Trans. Image Process. 2015, 24, 3357–3369. [Google Scholar] [CrossRef]
- Chaudhury, K.N.; Ghosh, S. On fast bilateral filtering using Fourier kernels. IEEE Singal Process. Lett. 2016, 23, 570–573. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Nair, P.; Chaudhury, K.N. Optimized Fourier bilateral filtering. IEEE Signal Process. Lett. 2018, 25, 1555–1559. [Google Scholar] [CrossRef] [Green Version]
- Gavaskar, R.G.; Kunal, N.; Chaudhury, K.N. Fast adaptive bilateral filtering. IEEE Trans. Image Process. 2019, 28, 779–790. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Tang, L.; Tang, J. Speed up bilateral filtering via sparse approximation on a learned cosine dictionary. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 603–617. [Google Scholar] [CrossRef]
- Chen, B.-H.; Tseng, Y.-S.; Yin, J.-L. Gaussian-adaptive bilateral filter. IEEE Signal Process. Lett. 2020, 27, 1670–1674. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, L. Fast bilateral filtering. Electron. Lett. 2019, 55, 258–260. [Google Scholar] [CrossRef]
- Guo, J.; Chen, C.; Xiang, S.; Ou, Y.; Li, B. A fast bilateral filtering algorithm based on rising cosine function. Neural. Comput. Appl. 2019, 31, 5097–5108. [Google Scholar] [CrossRef]
- Huang, T.S.; Yang, G.J.; Tang, G.Y. A fast two-dimensional median filtering algorithm. IEEE Trans. Acoust. Speech Signal Process. 1979, 27, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Porikli, F. Integral histogram: A fast way to extract histograms in Cartesian spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005; pp. 829–836. [Google Scholar]
- Perreault, S.; Hebert, P. Median filtering in constant time. IEEE Trans. Image Process. 2007, 16, 2389–2394. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Tao, L. Efficient histogram-based sliding window. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3003–3010. [Google Scholar]
- Peng, Y.-T.; Chen, F.-C.; Ruan, S.-J. An efficient O(1) contrast enhancement algorithm using parallel column histograms. IEICE Trans. Inf. Syst. 2013, 96, 2724–2725. [Google Scholar] [CrossRef] [Green Version]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 416–423. [Google Scholar]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; AlberiMorel, M.L. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the British Machine Vision Conference, Surrey, UK, 3–7 September 2012. [Google Scholar]
- Zeyde, R.; Protter, M.; Elad, M. On single image scale-up using sparse-representation. In Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Huang, J.-B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- The USC-SIPI Image Database. Available online: https://sipi.usc.edu/database/ (accessed on 31 August 2021).
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it?—A new look at signal fidelity measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [Green Version]
- Xue, W.; Zhang, L.; Mou, X.; Bovik, A.C. Gradient magnitude similarity deviation: A highly efficient perceptual image quality index. IEEE Trans. Image Process. 2014, 23, 684–695. [Google Scholar] [CrossRef] [Green Version]











| Dataset | Metrics | Methods | |||
|---|---|---|---|---|---|
| BF [10] | OFBF [22] | GABF [25] | DHBF | ||
| BSDS100 [33] | PSNR↑ [38] | 21.8311 | 21.7637 | 22.4537 | 23.6162 |
| SSIM↑ [39] | 0.4358 | 0.4335 | 0.5255 | 0.5601 | |
| FSIM↑ [40] | 0.7500 | 0.7479 | 0.7612 | 0.8123 | |
| GMSD↓ [41] | 0.1296 | 0.1306 | 0.1300 | 0.1075 | |
| Set5 [34] | PSNR↑ [38] | 22.1226 | 22.0191 | 22.7614 | 24.1221 |
| SSIM↑ [39] | 0.3349 | 0.3311 | 0.4531 | 0.4859 | |
| FSIM↑ [40] | 0.8400 | 0.8375 | 0.8436 | 0.8817 | |
| GMSD↓ [41] | 0.1367 | 0.1384 | 0.1326 | 0.1071 | |
| Set14 [35] | PSNR↑ [38] | 21.8147 | 21.7265 | 21.9705 | 23.3298 |
| SSIM↑ [39] | 0.4333 | 0.4302 | 0.5017 | 0.5373 | |
| FSIM↑ [40] | 0.8444 | 0.8421 | 0.8265 | 0.8695 | |
| GMSD↓ [41] | 0.1304 | 0.1318 | 0.1330 | 0.1107 | |
| Urban100 [36] | PSNR↑ [38] | 21.6105 | 21.5481 | 20.8885 | 22.7292 |
| SSIM↑ [39] | 0.5506 | 0.5484 | 0.5739 | 0.6284 | |
| FSIM↑ [40] | 0.8122 | 0.8107 | 0.7824 | 0.8455 | |
| GMSD↓ [41] | 0.1293 | 0.1305 | 0.1331 | 0.1057 | |
| USC-SIPI [37] | PSNR↑ [38] | 22.1064 | 22.0483 | 22.9213 | 24.4111 |
| SSIM↑ [39] | 0.3826 | 0.3806 | 0.5019 | 0.5364 | |
| FSIM↑ [40] | 0.8154 | 0.8140 | 0.8243 | 0.8631 | |
| GMSD↓ [41] | 0.1408 | 0.1416 | 0.1271 | 0.1068 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.-W.; Lin, Y.-T.; Peng, Y.-T. A Fast Two-Stage Bilateral Filter Using Constant Time O(1) Histogram Generation. Sensors 2022, 22, 926. https://doi.org/10.3390/s22030926
Cheng S-W, Lin Y-T, Peng Y-T. A Fast Two-Stage Bilateral Filter Using Constant Time O(1) Histogram Generation. Sensors. 2022; 22(3):926. https://doi.org/10.3390/s22030926
Chicago/Turabian StyleCheng, Sheng-Wei, Yi-Ting Lin, and Yan-Tsung Peng. 2022. "A Fast Two-Stage Bilateral Filter Using Constant Time O(1) Histogram Generation" Sensors 22, no. 3: 926. https://doi.org/10.3390/s22030926
APA StyleCheng, S.-W., Lin, Y.-T., & Peng, Y.-T. (2022). A Fast Two-Stage Bilateral Filter Using Constant Time O(1) Histogram Generation. Sensors, 22(3), 926. https://doi.org/10.3390/s22030926







