Simultaneous ThermoBrachytherapy: Electromagnetic Simulation Methods for Fast and Accurate Adaptive Treatment Planning
Abstract
:1. Introduction
2. Materials and Methods
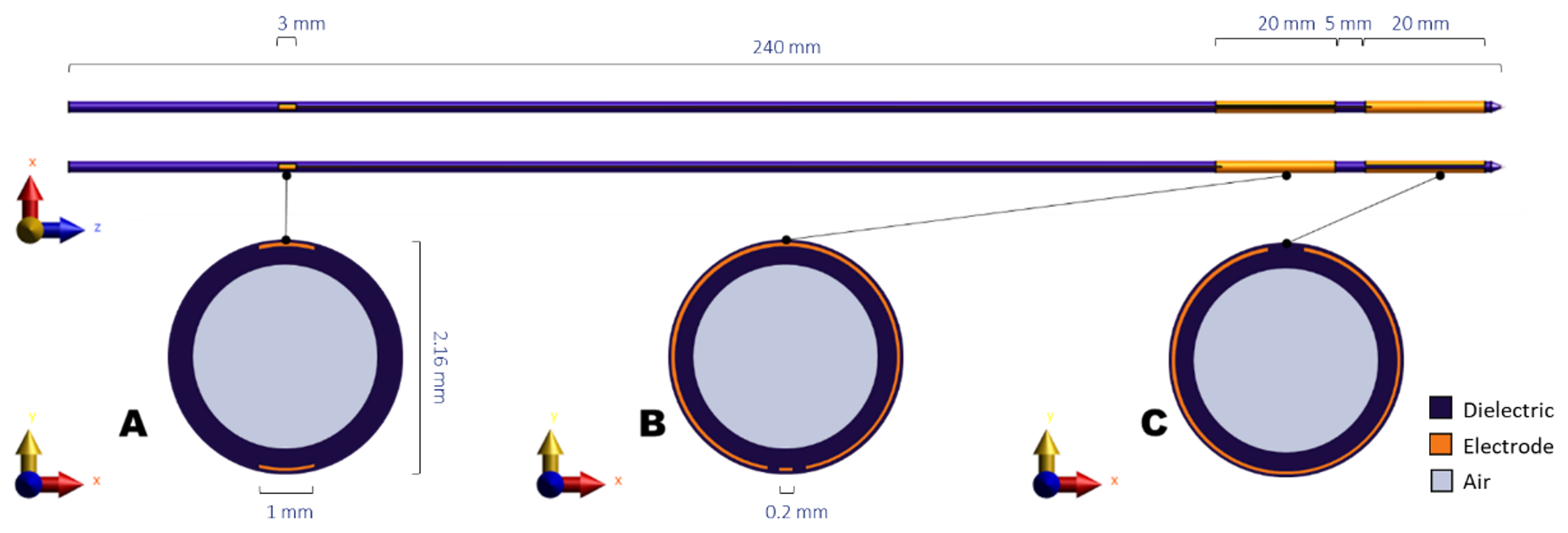
2.1. Hyperthermia System
2.2. SAR Calculation
- Single calculation with a full-wave Finite-Difference Time-Domain (FDTD) solver, applied on a detailed model of the electrodes in the phantom setup;
- Single calculation with an electro-quasistatic (EQS) solver applied on a detailed model of the electrodes in the phantom setup;
- Single calculation with an EQS solver applied on a simplified model of the electrodes in the phantom setup;
- A superpositioning of all electric fields, calculated separately with the EQS solver for each electrode, using the simplified model of the electrodes in the phantom setup.
2.2.1. Calculation Method 1: FDTD Solver Applied on the Detailed Model
2.2.2. Calculation Method 2: EQS Solver Applied on Detailed Model
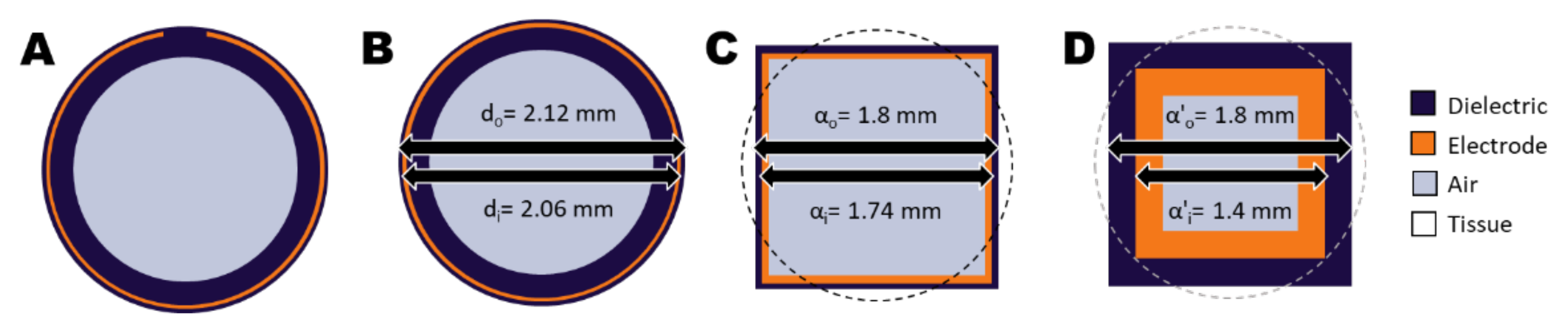
2.2.3. Calculation Method 3: EQS Solver Applied on a Simplified Model
2.2.4. Calculation Method 4: Superpositioning of EQS Solver Results Applied on a Simplified Model
2.3. Validation of SAR Calculations
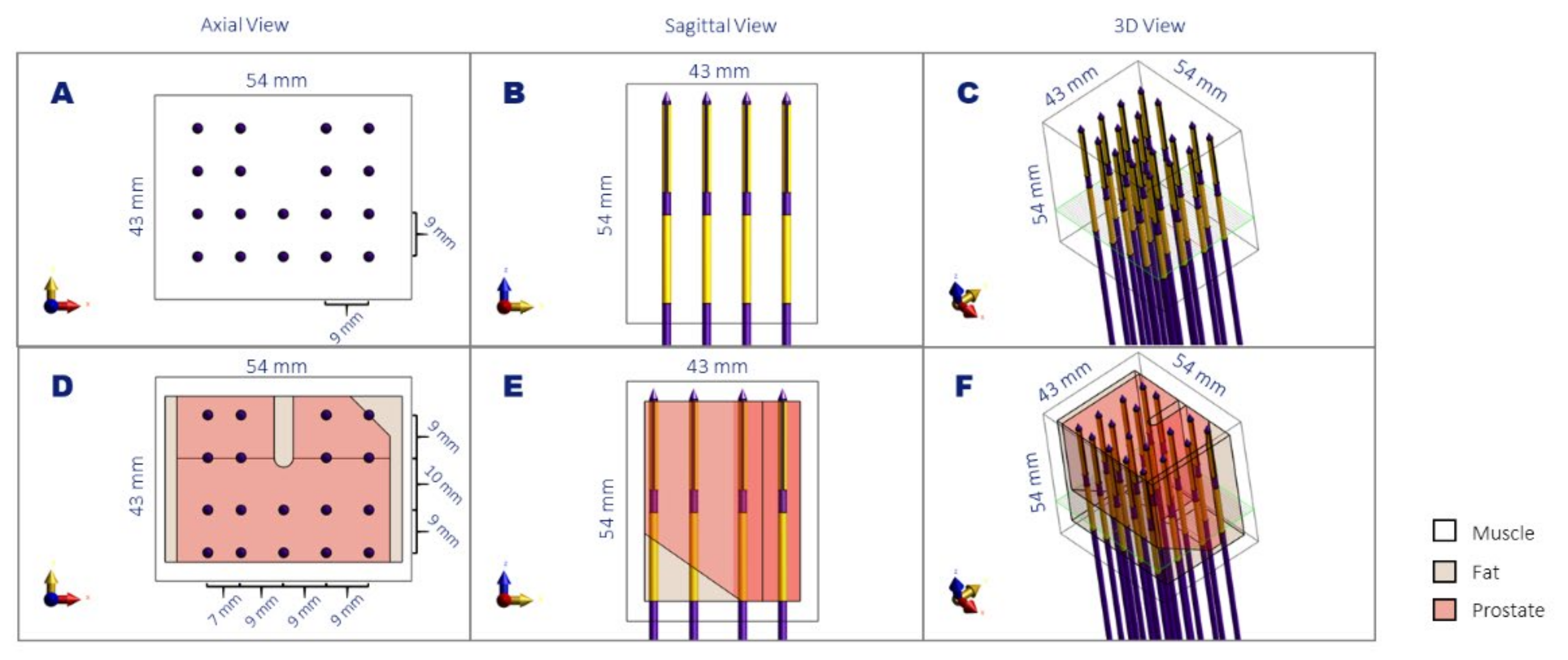
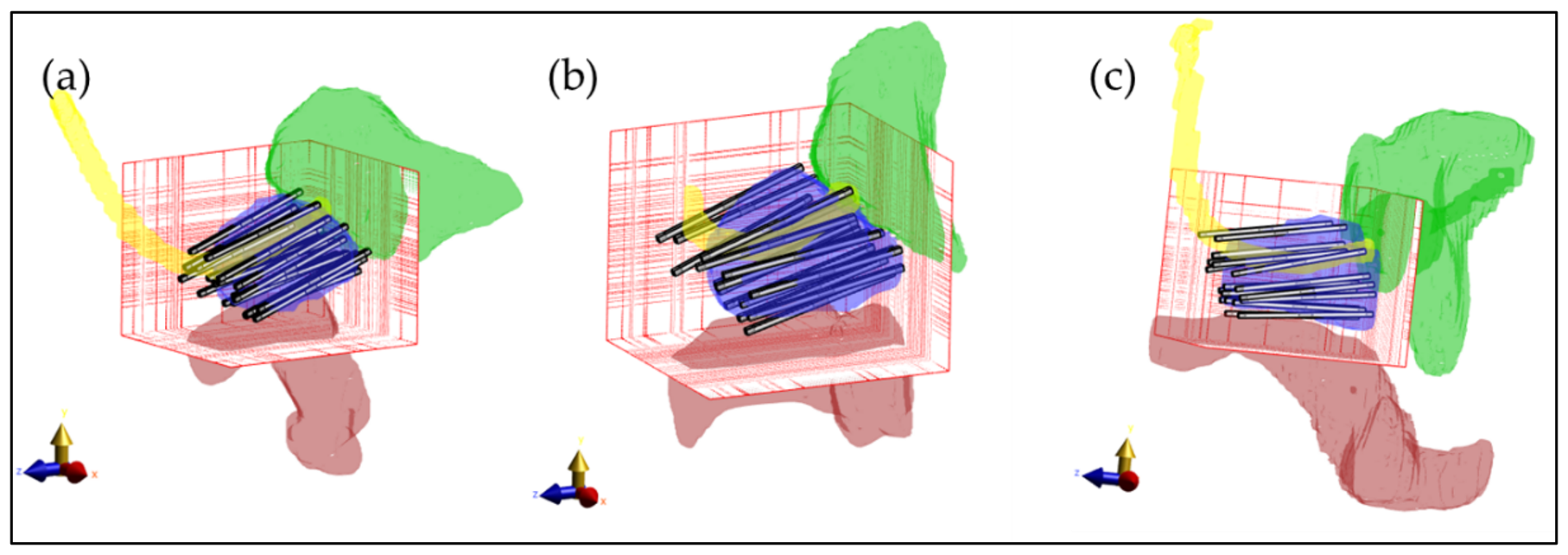
2.4. Application on Real Patient Scenarios
3. Results
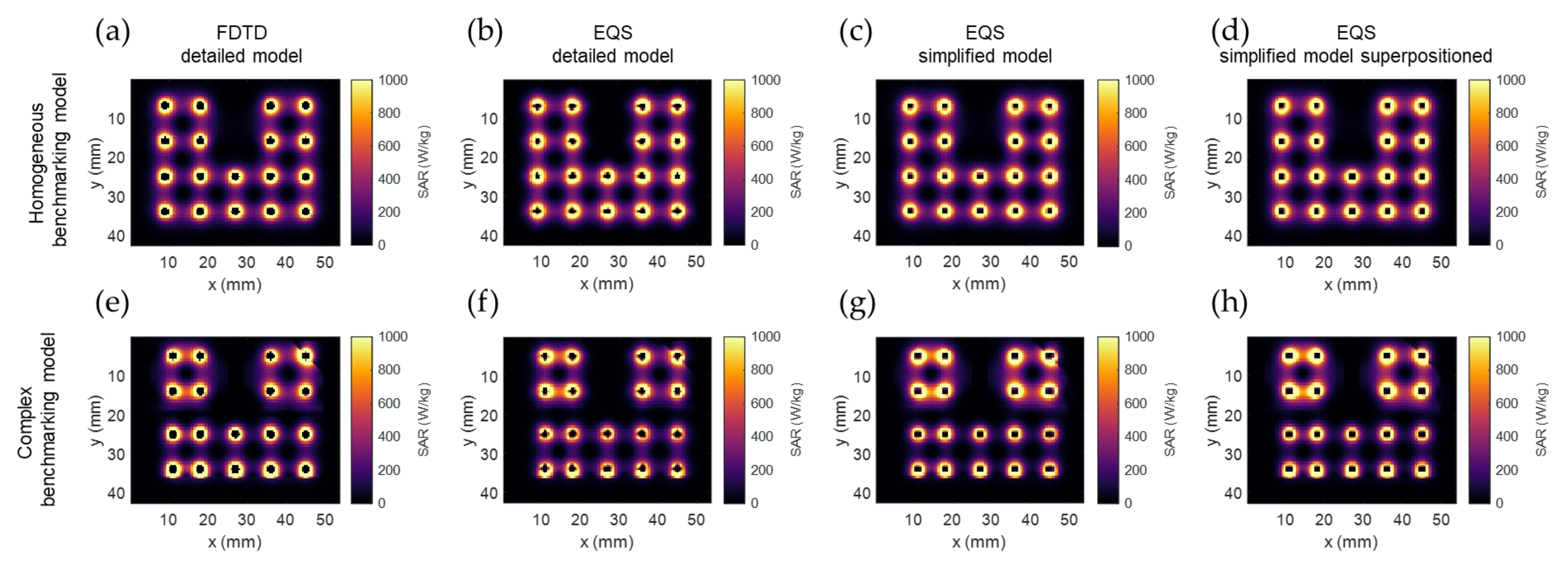
3.1. SAR Calculation Benchmarking Results
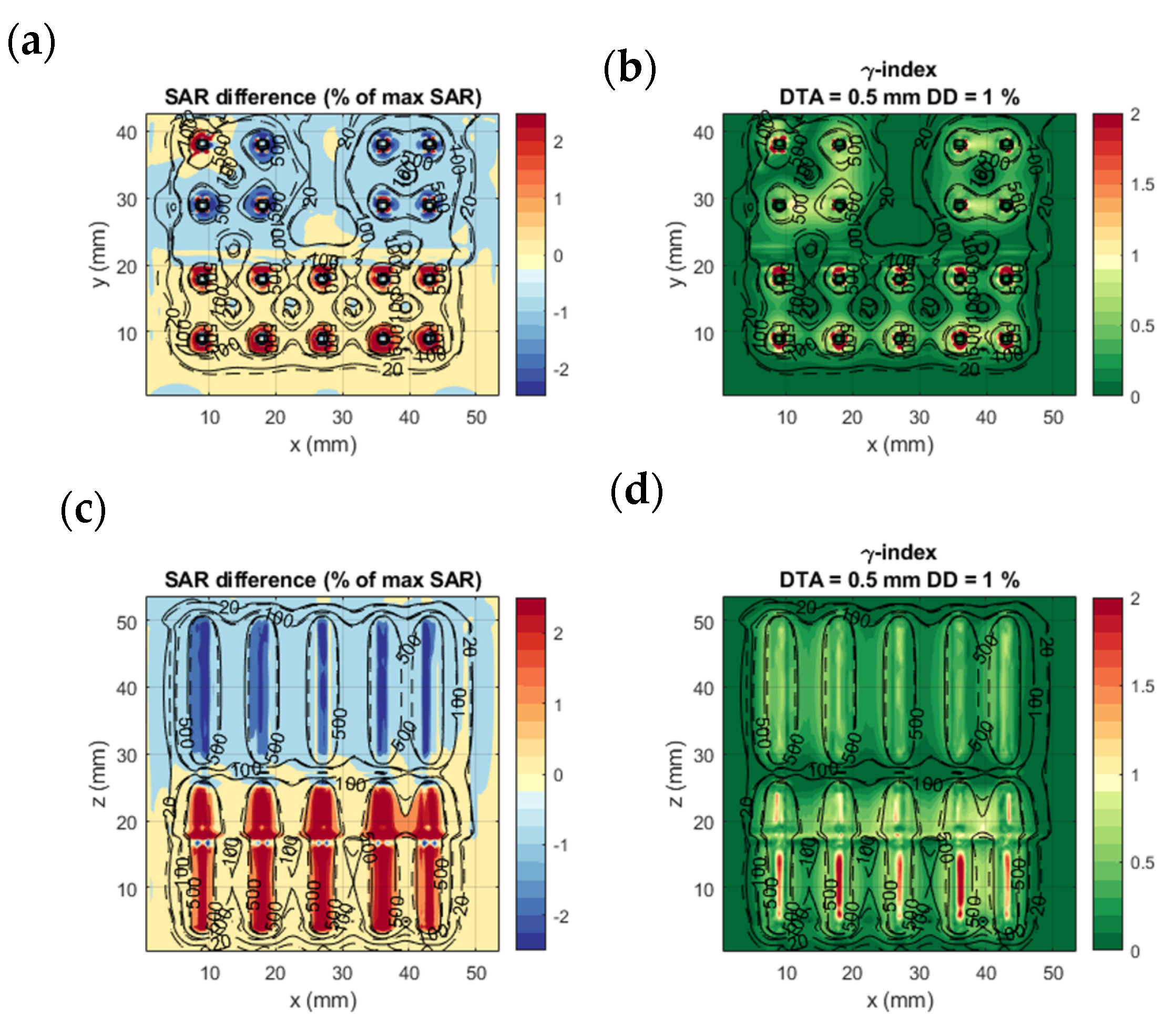
3.2. Evaluation of SAR Calculations
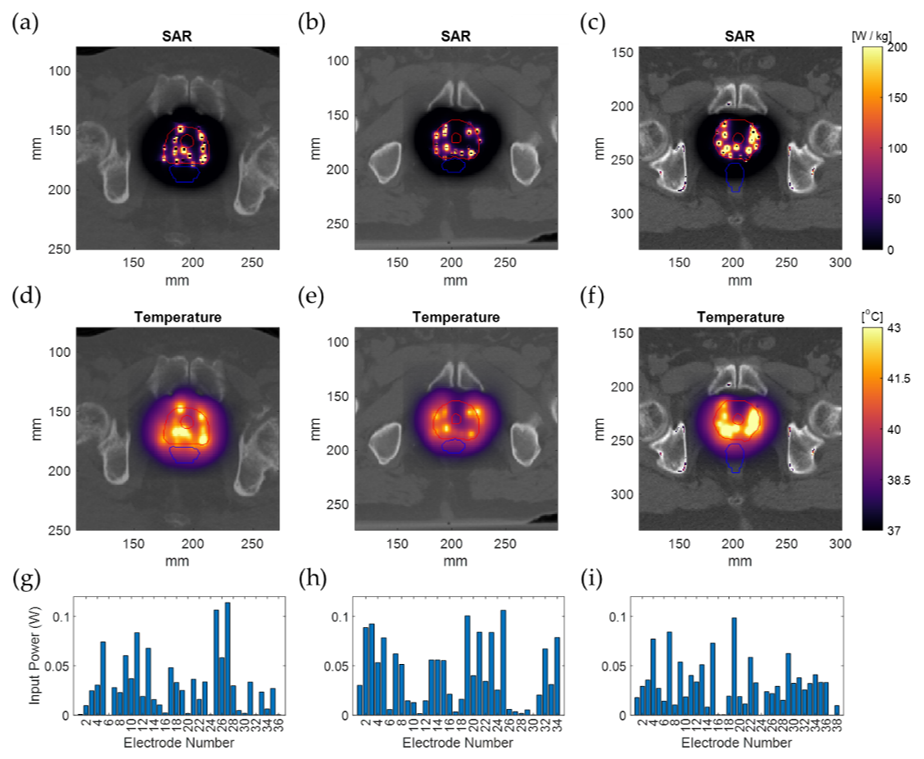
3.3. Treatment Planning Results in Patient Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hoskin, P.J.; Colombo, A.; Henry, A.; Niehoff, P.; Hellebust, T.P.; Siebert, F.A.; Kovacs, G. GEC/ESTRO recommendations on high dose rate afterloading brachytherapy for localised prostate cancer: An update. Radiother. Oncol. 2013, 107, 325–332. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tselis, N.; Hoskin, P.; Baltas, D.; Strnad, V.; Zamboglou, N.; Rödel, C.; Chatzikonstantinou, G. High dose rate brachytherapy as monotherapy for localised prostate cancer: Review of the current status. Clin. Oncol. 2017, 29, 401–411. [Google Scholar] [CrossRef] [PubMed]
- Mendez, L.C.; Ravi, A.; Chung, H.; Tseng, C.L.; Wronski, M.; Paudel, M.; McGuffin, M.; Cheung, P.; Loblaw, A.; Morton, G. Pattern of relapse and dose received by the recurrent intraprostatic nodule in low-to intermediate-risk prostate cancer treated with single fraction 19 Gy high-dose-rate brachytherapy. Brachytherapy 2018, 17, 291–297. [Google Scholar] [CrossRef] [PubMed]
- Tharmalingam, H.; Tsang, Y.; Ostler, P.; Wylie, J.; Bahl, A.; Lydon, A.; Ahmed, I.; Elwell, C.; Nikapota, A.R.; Hoskin, P.J. Single dose high-dose rate (HDR) brachytherapy (BT) as monotherapy for localised prostate cancer: Early results of a UK national cohort study. Radiother. Oncol. 2020, 143, 95–100. [Google Scholar] [CrossRef]
- Horsman, M.R.; Overgaard, J. Hyperthermia: A potent enhancer of radiotherapy. Clin. Oncol. 2007, 19, 418–426. [Google Scholar] [CrossRef]
- Nakahara, S.; Ohguri, T.; Kakinouchi, S.; Itamura, H.; Morisaki, T.; Tani, S.; Yahara, K.; Fujimoto, N. Intensity-modulated radiotherapy with regional hyperthermia for high-risk localized prostate carcinoma. Cancers 2022, 14, 400. [Google Scholar] [CrossRef] [PubMed]
- Overgaard, J. Simultaneous and sequential hyperthermia and radiation treatment of an experimental tumor and its surrounding normal tissue in vivo. Int. J. Radiat. Oncol. Biol. Phys. 1980, 6, 1507–1517. [Google Scholar] [CrossRef]
- Van Leeuwen, C.M.; Oei, A.L.; Ten Cate, R.; Franken, N.A.P.; Bel, A.; Stalpers, L.J.A.; Crezee, J.; Kok, H.P. Measurement and analysis of the impact of time-interval, temperature and radiation dose on tumour cell survival and its application in thermoradiotherapy plan evaluation. Int. J. Hyperth. 2018, 34, 30–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Overgaard, J. The heat is (still) on–the past and future of hyperthermic radiation oncology. Radiother. Oncol. 2013, 109, 185–187. [Google Scholar] [CrossRef]
- Ruifrok, A.C.; Levendag, P.C.; Lakeman, R.F.; Deurloo, I.K.K.; Visser, A.G. Combined treatment with interstitial hyperthermia and interstitial radiotheraphy in an animal tumor model. Int. J. Radiat. Oncol. Biol. Phys. 1991, 20, 1281–1286. [Google Scholar] [CrossRef]
- Kukiełka, A.M.; Hetnał, M.; Bereza, K. Evaluation of tolerance and toxicity of high-dose-rate brachytherapy boost combined with interstitial hyperthermia for prostate cancer. Int. J. Hyperth. 2016, 32, 324–330. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Androulakis, I.; Mestrom, R.M.; Christianen, M.E.; Kolkman-Deurloo, I.K.K.; van Rhoon, G.C. Design of the novel ThermoBrachy applicators enabling simultaneous interstitial hyperthermia and high dose rate brachytherapy. Int. J. Hyperth. 2021, 38, 1660–1671. [Google Scholar] [CrossRef]
- Dobšíček Trefná, H.; Schmidt, M.; Van Rhoon, G.C.; Kok, H.P.; Gordeyev, S.S.; Lamprecht, U.; Marder, D.; Nadobny, J.; Ghadjar, P.; Abdel-Rahman, S.; et al. Quality assurance guidelines for interstitial hyperthermia. Int. J. Hyperth. 2019, 36, 277–294. [Google Scholar] [CrossRef] [Green Version]
- Das, S.K.; Clegg, S.T.; Samulski, T.V. Computational techniques for fast hyperthermia temperature optimization. Med. Phys. 1999, 26, 319–328. [Google Scholar] [CrossRef]
- De Bree, J.; van der Koijk, J.F.; Lagendijk, J.J.W. A 3-D SAR model for current source interstitial hyperthermia. IEEE Trans. Biomed. Eng. 1996, 43, 1038–1045. [Google Scholar] [CrossRef] [PubMed]
- Prakash, P.; Salgaonkar, V.A.; Diederich, C.J. Modelling of endoluminal and interstitial ultrasound hyperthermia and thermal ablation: Applications for device design, feedback control and treatment planning. Int. J. Hyperth. 2013, 29, 296–307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paulides, M.M.; Rodrigues, D.B.; Bellizzi, G.G.; Sumser, K.; Curto, S.; Neufeld, E.; Montanaro, H.; Kok, H.P.; Dobsicek Trefna, H. ESHO benchmarks for computational modeling and optimization in hyperthermia therapy. Int. J. Hyperth. 2021, 38, 1425–1442. [Google Scholar] [CrossRef] [PubMed]
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Steinmetz, T.; Kurz, S.; Clemens, M. Domains of validity of quasistatic and quasistationary field approximations. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2011, 30, 1237–1247. [Google Scholar] [CrossRef]
- Coggon, J.H. Electromagnetic and electrical modeling by the finite element method. Geophysics 1971, 36, 132–155. [Google Scholar] [CrossRef]
- Kaatee, R.S.J.P.; Crezee, H.; Visser, A.G. Temperature measurement errors with thermocouples inside 27 MHz current source interstitial hyperthermia applicators. Phys. Med. Biol. 1999, 44, 1499. [Google Scholar] [CrossRef]
- Khawaji, I.H.; Chindam, C.; Awadelkarim, O.O.; Lakhtakia, A. Dielectric properties of and charge transport in columnar microfibrous thin films of Parylene C. IEEE Trans. Electron Devices 2017, 64, 3360–3367. [Google Scholar] [CrossRef]
- Kahouli, A.; Sylvestre, A.; Jomni, F.; Yangui, B.; Legrand, J. Experimental and theoretical study of AC electrical conduction mechanisms of semicrystalline parylene C thin films. J. Phys. Chem. A 2012, 116, 1051–1058. [Google Scholar] [CrossRef] [PubMed]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues; Version 4.0; IT’IS Foundation: Zurich, Switzerland, 2018. [Google Scholar] [CrossRef]
- Van der Koijk, J.F.; De Bree, J.; Crezee, J.; Lagendijk, J.J.W. Numerical analysis of capacitively coupled electrodes for interstitial hyperthermia. Int. J. Hyperth. 1997, 13, 607–619. [Google Scholar] [CrossRef] [PubMed]
- Low, D.A.; Harms, W.B.; Mutic, S.; Purdy, J.A. A technique for the quantitative evaluation of dose distributions. Med. Phys. 1998, 25, 656–661. [Google Scholar] [CrossRef]
- Petrokokkinos, L.; Zourari, K.; Pantelis, E.; Moutsatsos, A.; Karaiskos, P.; Sakelliou, L.; Seimenis, I.; Georgiou, E.; Papagiannis, P. Dosimetric accuracy of a deterministic radiation transport based brachytherapy treatment planning system. Part II: Monte Carlo and experimental verification of a multiple source dwell position plan employing a shielded applicator. Med. Phys. 2011, 38, 1981–1992. [Google Scholar] [CrossRef]
- Logothetis, A.; Pantelis, E.; Zoros, E.; Pappas, E.P.; Dimitriadis, A.; Paddick, I.; Garding, J.; Johansson, J.; Kollias, G.; Karaiskos, P. Dosimetric evaluation of the Leksell GammaPlan™ Convolution dose calculation algorithm. Phys. Med. Biol. 2020, 65, 045011. [Google Scholar] [CrossRef] [PubMed]
- De Bruijne, M.; Samaras, T.; Chavannes, N.; van Rhoon, G.C. Quantitative validation of the 3D SAR profile of hyperthermia applicators using the gamma method. Phys. Med. Biol. 2007, 52, 3075. [Google Scholar] [CrossRef]
- Sumser, K.; Drizdal, T.; Bellizzi, G.G.; Hernandez-Tamames, J.A.; van Rhoon, G.C.; Paulides, M.M. Experimental validation of the MRcollar: An MR compatible applicator for deep heating in the head and neck region. Cancers 2021, 13, 5617. [Google Scholar] [CrossRef]
- Beaulieu, L.; Carlsson Tedgren, Å.; Carrier, J.F.; Davis, S.D.; Mourtada, F.; Rivard, M.J.; Thomson, R.M.; Verhaegen, F.; Wareing, T.A.; Williamson, J.F. Report of the task group 186 on model-based dose calculation methods in brachytherapy beyond the TG-43 formalism: Current status and recommendations for clinical implementation. Med. Phys. 2012, 39, 6208–6236. [Google Scholar] [CrossRef] [Green Version]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Kok, H.P.; Kotte, A.; Crezee, J. Planning, optimisation and evaluation of hyperthermia treatments. Int. J. Hyperth. 2017, 33, 593–607. [Google Scholar] [CrossRef] [Green Version]
- Bellizzi, G.G.; Drizdal, T.; van Rhoon, G.C.; Crocco, L.; Isernia, T.; Paulides, M.M. The potential of constrained SAR focusing for hyperthermia treatment planning: Analysis for the head & neck region. Phys. Med. Biol. 2018, 64, 015013. [Google Scholar] [PubMed]
- Rijnen, Z.; Bakker, J.F.; Canters, R.A.; Togni, P.; Verduijn, G.M.; Levendag, P.C.; Van Rhoon, G.C.; Paulides, M.M. Clinical integration of software tool VEDO for adaptive and quantitative application of phased array hyperthermia in the head and neck. Int. J. Hyperth. 2013, 29, 181–193. [Google Scholar] [CrossRef] [PubMed]
- Breedveld, S.; Bennan, A.B.; Aluwini, S.; Schaart, D.R.; Kolkman-Deurloo, I.K.K.; Heijmen, B.J. Fast automated multi-criteria planning for HDR brachytherapy explored for prostate cancer. Phys. Med. Biol. 2019, 64, 205002. [Google Scholar] [CrossRef]
- Fionda, B.; Boldrini, L.; D’Aviero, A.; Lancellotta, V.; Gambacorta, M.A.; Kovács, G.; Patarnello, S.; Valentini, V.; Tagliaferri, L. Artificial intelligence (AI) and interventional radiotherapy (brachytherapy): State of art and future perspectives. J. Contemp. Brachytherapy 2020, 12, 497–500. [Google Scholar] [CrossRef] [PubMed]

| Tissue | Mass Density (kg/m3) | Electric Conductivity at 27 MHz (S/m) | Relative Permittivity at 27 MHz | Specific Heat Capacity (J/kg/K) | Thermal Conductivity k (W/m/K) | Perfusion Rate (ml/kg/min) |
|---|---|---|---|---|---|---|
| POM [21] | 1150 | 2.7 × 10−5 | 3.6 | 1670 | 0.230 | - |
| Parylene C [22,23] | 1289 | 1 × 10−5 | 2.4 | 712 | 0.084 | - |
| Air [24] | 1.164 | 0 | 1 | 1004 | 0.0273 | - |
| Muscle [24] | 1090.4 | 0.654 | 95.764 | 3421 | 0.495 | 39.74 |
| Fat [24] | 911 | 0.061 | 17.928 | 2348 | 0.211 | 32.71 |
| Prostate [24] | 1045 | 0.838 | 120.056 | 3760 | 0.512 | 394.12 |
| Rectum [24] | 1045 | 0.654 | 95.8 | 3801 | 0.557 | 0 |
| Urethra [24] | 1102 | 0.375 | 88.8 | 3306 | 0.462 | 394 |
| Bladder [24] | 1086 | 0.276 | 31.5 | 3581 | 0.522 | 78 |
| Calculation Method 1 | Calculation Method 2 | Calculation Method 3 | Calculation Method 4 | |
|---|---|---|---|---|
| Numerical computation method | FDTD | FEM | FEM | FEM |
| Physics model | Maxwell’s curl equations | Electroquasistatic approximation | Electroquasistatic approximation | Electroquasistatic approximation—E-fields Superpositioning |
| Geometric model | Detailed TBT structure | Detailed TBT structure | Rectangular simplified TBT model | Rectangular simplified TBT model |
| Evaluated quantity | SAR | SAR | SAR | SAR |
| Calculation Method | Single FDTD Detailed Model (Calculation Method 1) | Single EQS Detailed Model (Calculation Method 2) | Single EQS Simplified Model (Calculation Method 3) | Superpositioned EQS Simplified Model (Calculation Method 4) | ||||
|---|---|---|---|---|---|---|---|---|
| Model | Homogeneous | Complex | Homogeneous | Complex | Homogeneous | Complex | Homogeneous | Complex |
| simulation domain (cm3) | 2 880 | 2 880 | 345 | 345 | 345 | 345 | 345 | 345 |
| number of voxels (106) | 41.789 | 42.322 | 31.370 | 32.173 | 1.14 | 1.12 | 36 × 1.14 | 36 × 1.12 † |
| model generation time | 10.06 s | 10.10 s | 7.61 s | 8.79 s | 0.30 s | 0.29 s | 36 × 0.30 s † | 36 × 29 s † |
| simulation time | 11 h 43 min * | 11 h 45 min * | 8 min 35 s ** | 9 min 37 s ** | 13 s ** | 13 s ** | 36 × 13 s †‡** | 36 × 13 s †‡** |
| Calculation Method | Single EQS Detailed Model (Calculation Method 2) | Single EQS Simplified Model (Calculation Method 3) | Superpositioned EQS Simplified Model (Calculation Method 4) | |||
|---|---|---|---|---|---|---|
| Model | Homogeneous | Complex | Homogeneous | Complex | Homogeneous | Complex |
| Accuracy (% of max SAR) | 0.52 | 0.30 | 0.50 | 0.34 | 0.50 | 0.34 |
| Bias (% of max SAR) | −0.01 | 0.13 | 0.22 | 0.08 | 0.22 | 0.08 |
| 2%/2 mm γ-index passing rate (%) | 99.8 | 99.8 | 99.6 | 99.7 | 99.6 | 99.7 |
| 1%/0.5 mm γ-index passing rate (%) | 99.6 | 99.3 | 99.2 | 99.2 | 99.2 | 99.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Androulakis, I.; Mestrom, R.M.C.; Christianen, M.E.M.C.; Kolkman-Deurloo, I.-K.K.; van Rhoon, G.C. Simultaneous ThermoBrachytherapy: Electromagnetic Simulation Methods for Fast and Accurate Adaptive Treatment Planning. Sensors 2022, 22, 1328. https://doi.org/10.3390/s22041328
Androulakis I, Mestrom RMC, Christianen MEMC, Kolkman-Deurloo I-KK, van Rhoon GC. Simultaneous ThermoBrachytherapy: Electromagnetic Simulation Methods for Fast and Accurate Adaptive Treatment Planning. Sensors. 2022; 22(4):1328. https://doi.org/10.3390/s22041328
Chicago/Turabian StyleAndroulakis, Ioannis, Rob M. C. Mestrom, Miranda E. M. C. Christianen, Inger-Karine K. Kolkman-Deurloo, and Gerard C. van Rhoon. 2022. "Simultaneous ThermoBrachytherapy: Electromagnetic Simulation Methods for Fast and Accurate Adaptive Treatment Planning" Sensors 22, no. 4: 1328. https://doi.org/10.3390/s22041328
APA StyleAndroulakis, I., Mestrom, R. M. C., Christianen, M. E. M. C., Kolkman-Deurloo, I.-K. K., & van Rhoon, G. C. (2022). Simultaneous ThermoBrachytherapy: Electromagnetic Simulation Methods for Fast and Accurate Adaptive Treatment Planning. Sensors, 22(4), 1328. https://doi.org/10.3390/s22041328







