Unfolded Coprime Linear Array with Three Subarrays for Non-Gaussian Signals: Configuration Design and DOA Estimation
Abstract
:1. Introduction
- We design the structure of UCLATS, whose cDOF of 2-DC is also provided. The problem of sparse array design with non-Gaussian signals is investigated from GPSP perspective and the structure of UCLATS.
- We divide the process of obtaining the location of physical sensors into two steps, which optimizes the array location step by step, resulting in lower design difficulty.
- We devise DFT-MUSIC algorithm for a better balance between computational complexity and DOA estimation performance, which can be utilized for the non-Gaussian signals with the proposed array geometry.
2. Preliminaries
2.1. 2-DC, 2-SC, 2-DCSC, FODC
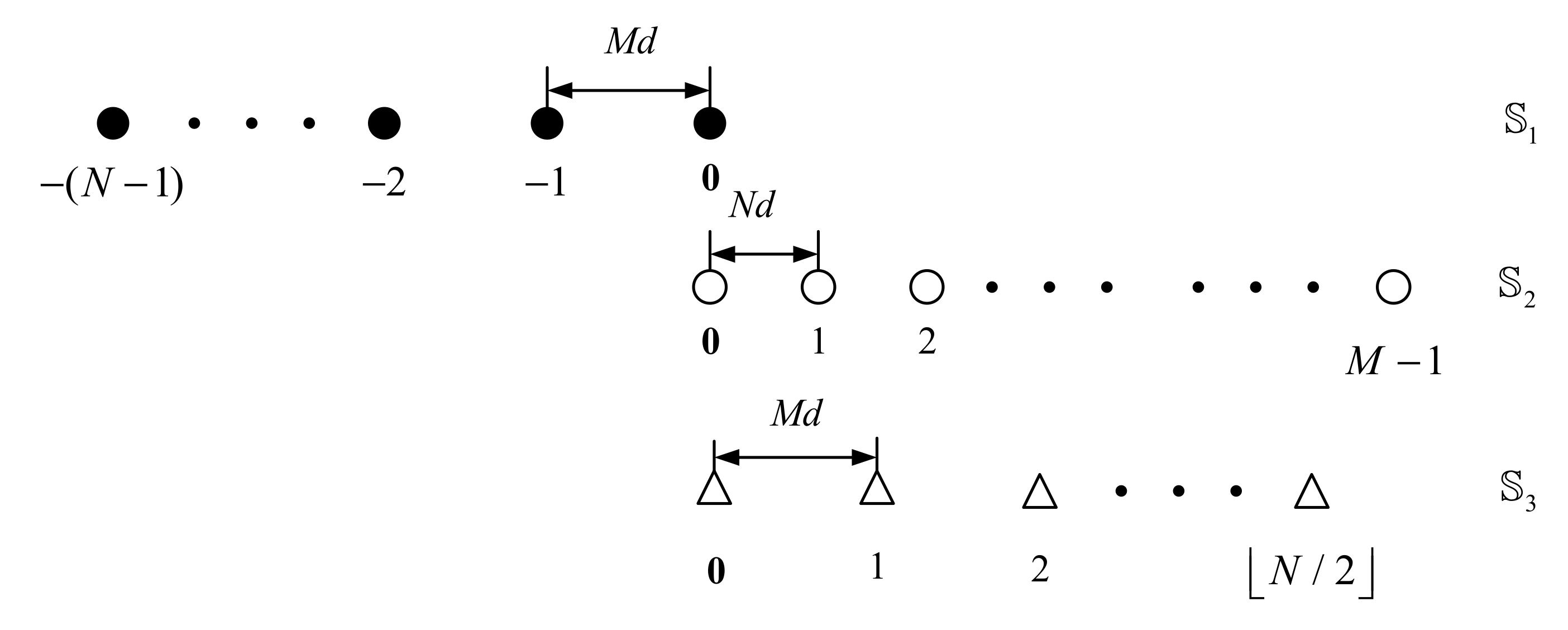
2.2. The Properties of UCLATS
- (a)
- (b)
- contains the consecutive lags in the range ofwith inter-element spacing, where the positive consecutive lags of cross-difference co-arrayare distributed in rangeand.
2.3. Received Signal Model
3. Sparse Array Design Principle
3.1. Global Postage-Stamp Problem (GPSP)
3.2. Sparse Array Design Principle Based on UCLATS
4. DOA Estimation Method
4.1. Initial Estimation by DFT Algorithm
4.2. Fine Estimation by PSS-MUSIC Method
5. Performance Analysis
5.1. Achievable Consecutive DOF
5.2. Computational Complexity
6. Simulations Results
6.1. RMSE Performance Comparison versus Snapshots
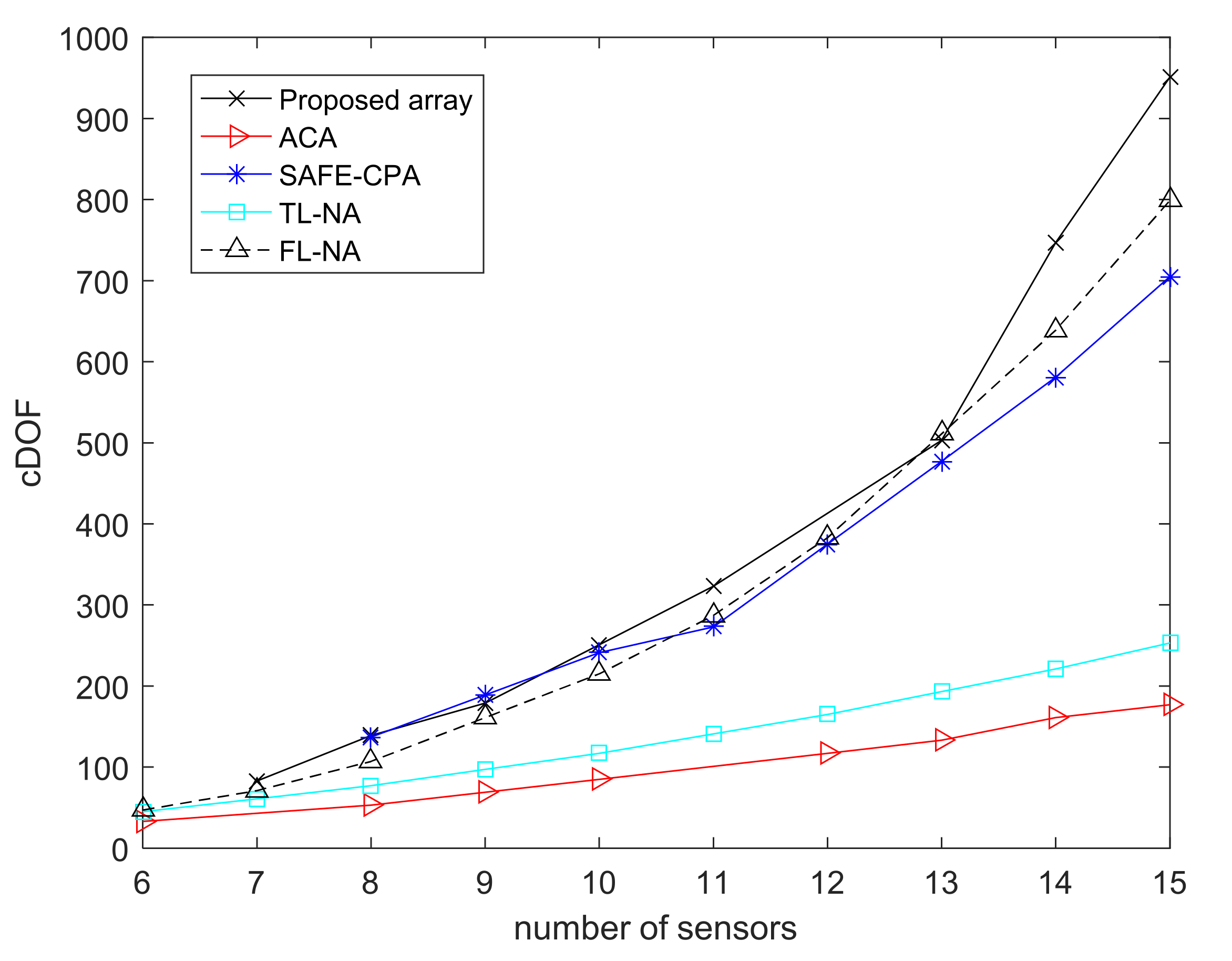
6.2. RMSE Performance Comparison versus Sensors
6.3. RMSE Performance Comparison of Different Arrays with DFT-MUSIC Method
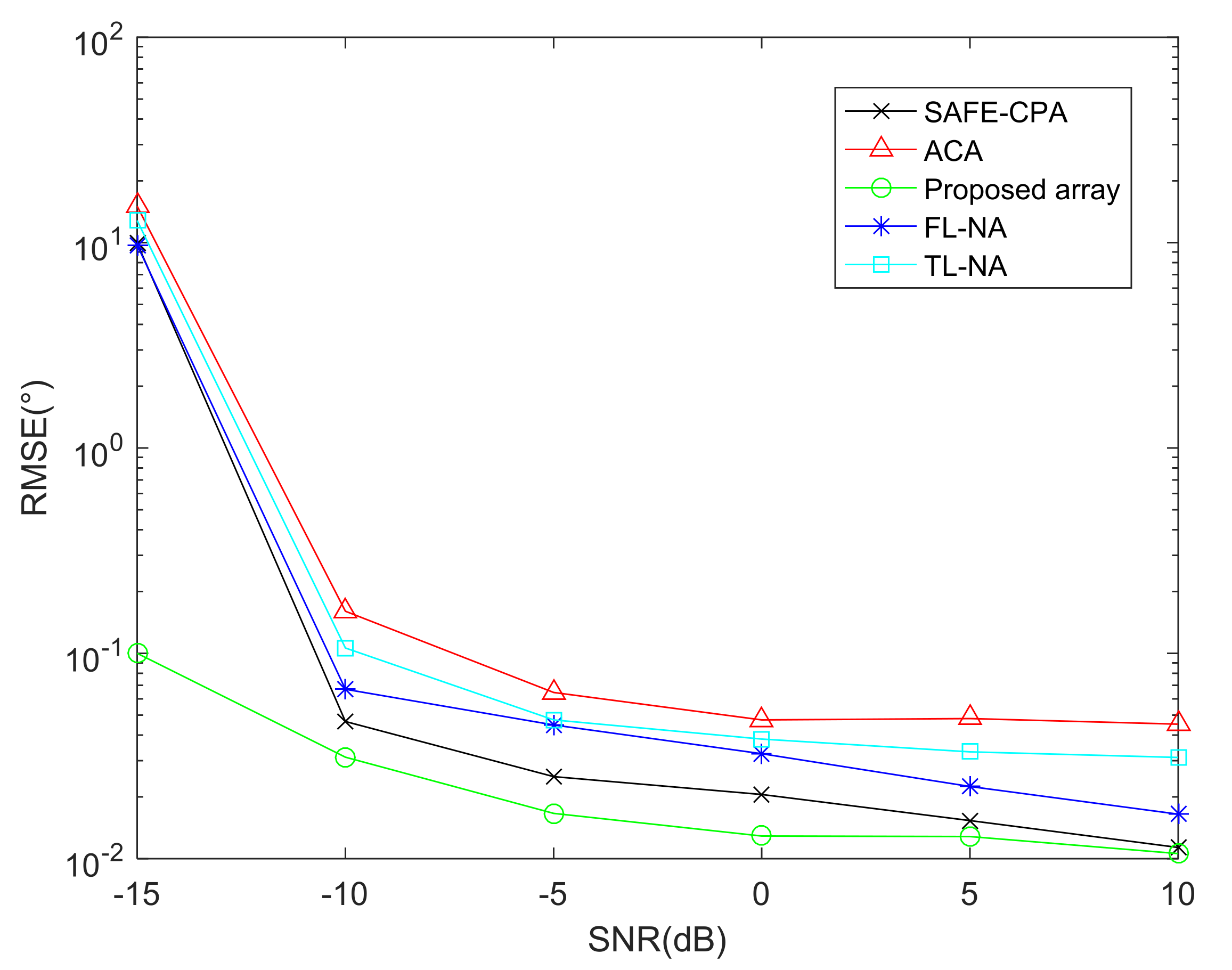
6.4. RMSE Performance Comparison of Different Algorithms
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
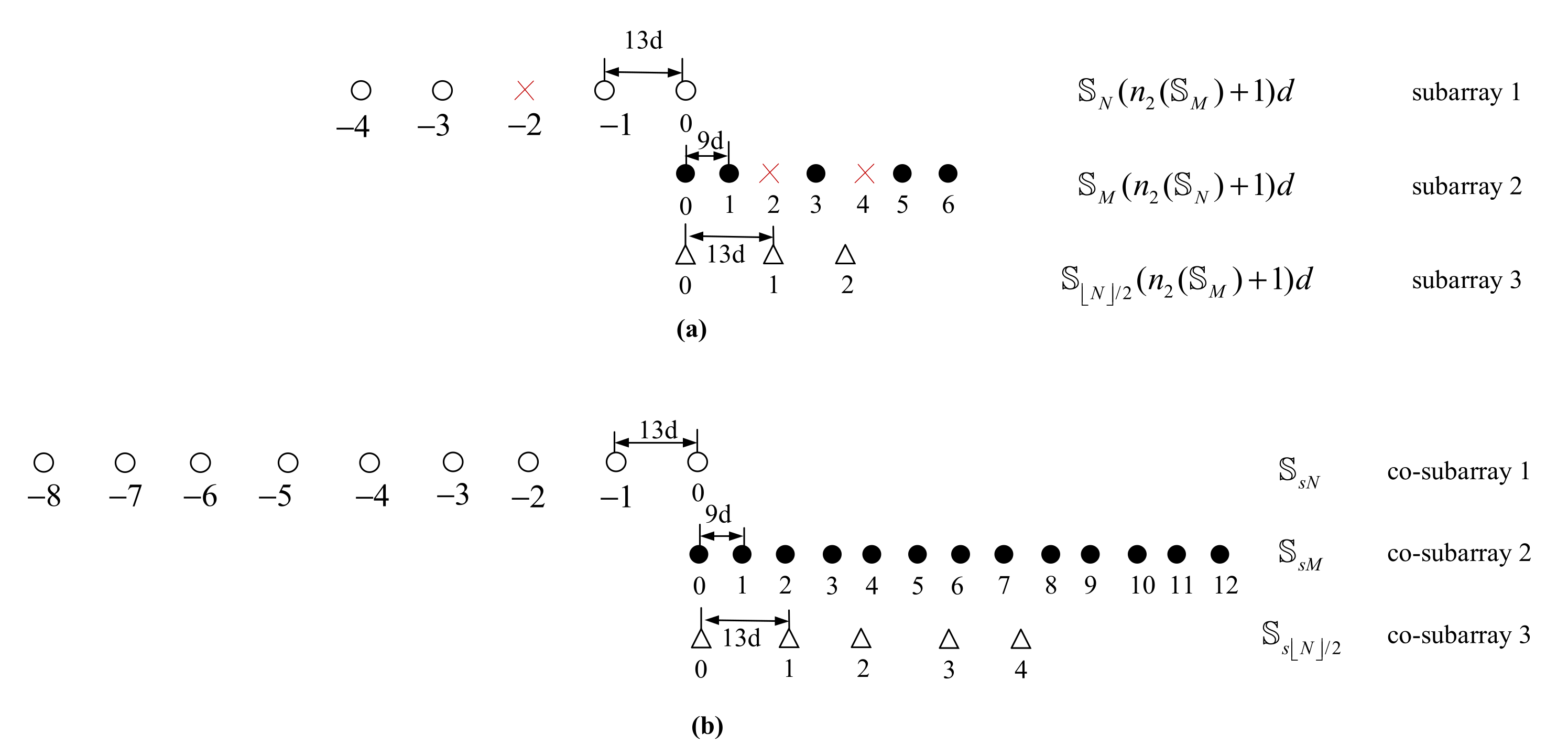
Appendix A
- (a)
- Considering the coprime relationship between M and N, the structure of UCLATS can be rewritten as
- (b)
- It is necessary to prove that there exists such that contains all consecutive elements in the set . Because , we consider first, and the contains consecutive lags in range . Considering the symmetry of , whose continuity of positive part can be employed to denote the whole range, which can be proved from two aspects, i.e., .
Appendix B
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Foschini, G.J.; Golden, G.D.; Valenzuela, R.A.; Wolniansky, P.W. Simplified processing for high spectral efficiency wireless communication employing multi-element arrays. IEEE J. Sel. Areas Commun. 1999, 17, 1841–1852. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.I.; Lau, S.-K.; Wong, K.T.; Tang, S.-K. Beacon-Aided Adaptive Localization of Noise Sources Aboard a Pass-By Railcar Using a Trackside Microphone Array. IEEE Trans. Veh. Technol. 2010, 59, 3720–3727. [Google Scholar] [CrossRef]
- Merino-Martínez, R.; Sijtsma, P.; Snellen, M.; Ahlefeldt, T.; Antoni, J.; Bahr, C.J.; Blacodon, D.; Ernst, D.; Finez, A.; Funke, S.; et al. A review of acoustic imaging methods using phased microphone arrays. CEAS Aeronaut. J. 2019, 10, 197–230. [Google Scholar] [CrossRef] [Green Version]
- Godara, L. Application of antenna arrays to mobile communications. II. Beam-forming and direction-of-arrival considerations. Proc. IEEE 1997, 85, 1195–1245. [Google Scholar] [CrossRef] [Green Version]
- Shamsunder, S.; Giannakis, G.B. Modeling of non-Gaussian array data using cumulants: DOA estimation of more sources with less sensors. Signal Process. 1993, 30, 279–297. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Roy, R.; Paulraj, A.; Kailath, T. ESPRIT—A subspace rotation approach to estimation of parameters of cisoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1340–1342. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing with Co-Prime Samplers and Arrays. IEEE Trans. Signal Process. 2010, 59, 573–586. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Theory of Sparse Coprime Sensing in Multiple Dimensions. IEEE Trans. Signal Process. 2011, 59, 3592–3608. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing with Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.; He, Y.; Li, J. An Array Switching Strategy for Direction of Arrival Estimation with Coprime Linear Array in the Presence of Mutual Coupling. Sensors 2020, 20, 1629. [Google Scholar] [CrossRef] [Green Version]
- Moffet, A. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 2003, 16, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Shen, C.; Li, H.; Li, Z.; Wang, H.; Chen, X.; Chen, J. Direction of Arrival Estimation and Robust Adaptive Beamforming with Unfolded Augmented Coprime Array. IEEE Access 2020, 8, 22314–22323. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Lu, Y.; Ren, S.; Cao, S. Augmented Nested Arrays with Enhanced DOF and Reduced Mutual Coupling. IEEE Trans. Signal Process. 2017, 65, 5549–5563. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X. Direction of Arrival Estimation of Quasi-Stationary Signals Using Unfolded Coprime Array. IEEE Access 2017, 5, 6538–6545. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, X.; Gong, P.; Zhai, H. DOA Estimation for Coprime Linear Arrays: An Ambiguity-Free Method Involving Full DOFs. IEEE Commun. Lett. 2017, 22, 562–565. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized Coprime Array Configurations for Direction-of-Arrival Estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Zhang, X.; Zhou, H. Generalized Nested Array: Optimization for Degrees of Freedom and Mutual Cou-pling. IEEE Commun. Lett. 2018, 22, 1208–1211. [Google Scholar] [CrossRef]
- Tugnait, J.K. On time delay estimation with unknown spatially correlated Gaussian noise using fourth-order cumulants and cross cumulants. IEEE Trans. Signal Process. 1991, 39, 1258–1267. [Google Scholar] [CrossRef]
- Dogan, M.; Mendel, J. Applications of cumulants to array processing. II. Non-Gaussian noise suppression. IEEE Trans. Signal Process. 1995, 43, 1663–1676. [Google Scholar] [CrossRef]
- Porat, B.; Friedlander, B. Direction finding algorithms based on high-order statistics. IEEE Trans. Signal Process. 1991, 39, 2016–2024. [Google Scholar] [CrossRef]
- Zhang, Y.; Ng, B.P. MUSIC-Like DOA Estimation Without Estimating the Number of Sources. IEEE Trans. Signal Process. 2009, 58, 1668–1676. [Google Scholar] [CrossRef]
- Yuen, N.; Friedlander, B. Asymptotic performance analysis of ESPRIT, higher order ESPRIT, and virtual ESPRIT algorithms. IEEE Trans. Signal Process. 1996, 44, 2537–2550. [Google Scholar] [CrossRef]
- Dogan, M.C.; Mendel, J.M. Joint array calibration and direction-finding with virtual-ESPRIT algorithm. In Proceedings of the IEEE Signal Processing Workshop on Higher-Order Statistics, South Lake Tahoe, CA, USA, 7 June 1993. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Multiple Level Nested Array: An Efficient Geometry for 2q-th Order Cumulant Based Array Pro-cessing. IEEE Trans. Signal Process. 2012, 60, 1253–1269. [Google Scholar] [CrossRef]
- Shen, Q.; Liu, W.; Cui, W.; Wu, S.; Pal, P. Simplified and Enhanced Multiple Level Nested Arrays Exploiting High-Order Dif-ference Co-Arrays. IEEE Trans. Signal Process. 2019, 67, 3502–3515. [Google Scholar] [CrossRef]
- Shen, Q.; Liu, W.; Cui, W.; Wu, S. Extension of Co-Prime Arrays Based on the Fourth-Order Difference Co-Array Concept. IEEE Signal Process. Lett. 2016, 23, 615–619. [Google Scholar] [CrossRef]
- Cai, J.; Liu, W.; Zong, R.; Shen, Q. An Expanding and Shift Scheme for Constructing Fourth-Order Difference Coarrays. IEEE Signal Process. Lett. 2017, 24, 480–484. [Google Scholar] [CrossRef] [Green Version]
- Ye, C.; Chen, L.; Zhu, B. Sparse Array Design for DOA Estimation of Non-Gaussian Signals: From Global Postage-Stamp Problem Perspective. Wirel. Commun. Mob. Comput. 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Mossige, S. Algorithms for Computing the h-Range of the Postage Stamp Problem. Math. Comput. 1981, 36, 575. [Google Scholar] [CrossRef]
- Challis, M.F.; Robinson, J.P. Some extremal postage stamp bases. J. Integer Seq. 2010, 13, 1–15. [Google Scholar]
- Cao, R.; Liu, B.; Gao, F.; Zhang, X. A Low-Complex One-Snapshot DOA Estimation Algorithm with Massive ULA. IEEE Commun. Lett. 2017, 21, 1071–1074. [Google Scholar] [CrossRef]
- Fu, Z.; Charge, P.; Wang, Y. A Virtual Nested MIMO Array Exploiting Fourth Order Difference Coarray. IEEE Signal Process. Lett. 2020, 27, 1140–1144. [Google Scholar] [CrossRef]
- Shan, T.-J.; Wax, M.; Kailath, T. On spatial smoothing for direction-of-arrival estimation of coherent signals. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 806–811. [Google Scholar] [CrossRef]






| M | N | |
|---|---|---|
| Odd | Odd | |
| Even | Odd | |
| Odd | Even | |
| Even | Even |
| k | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 8 | 0 | 1 | 3 | 4 | |||||||||
| 5 | 12 | 0 | 1 | 3 | 5 | 6 | ||||||||
| 6 | 16 | 0 | 1 | 3 | 5 | 7 | 8 | |||||||
| 7 | 20 | 0 | 1 | 2 | 5 | 8 | 9 | 10 | ||||||
| 7 | 20 | 0 | 1 | 3 | 4 | 8 | 9 | 11 | ||||||
| 7 | 20 | 0 | 1 | 3 | 4 | 9 | 11 | 16 | ||||||
| 7 | 20 | 0 | 1 | 3 | 5 | 6 | 13 | 14 | ||||||
| 7 | 20 | 0 | 1 | 3 | 5 | 7 | 9 | 10 | ||||||
| 8 | 26 | 0 | 1 | 2 | 5 | 8 | 11 | 12 | 13 | |||||
| 8 | 26 | 0 | 1 | 3 | 4 | 9 | 10 | 12 | 13 | |||||
| 8 | 26 | 0 | 1 | 3 | 5 | 7 | 8 | 17 | 18 | |||||
| 9 | 32 | 0 | 1 | 2 | 5 | 8 | 11 | 14 | 15 | 16 | ||||
| 9 | 32 | 0 | 1 | 3 | 5 | 7 | 9 | 10 | 21 | 22 | ||||
| 10 | 40 | 0 | 1 | 3 | 4 | 9 | 11 | 16 | 17 | 19 | 20 | |||
| 11 | 46 | 0 | 1 | 2 | 3 | 7 | 11 | 15 | 19 | 21 | 22 | 24 | ||
| 11 | 46 | 0 | 1 | 2 | 5 | 7 | 11 | 15 | 19 | 21 | 22 | 24 | ||
| 12 | 54 | 0 | 1 | 2 | 3 | 7 | 11 | 15 | 19 | 23 | 25 | 26 | 28 | |
| 12 | 54 | 0 | 1 | 2 | 5 | 7 | 11 | 15 | 19 | 23 | 25 | 26 | 28 | |
| 12 | 54 | 0 | 1 | 3 | 4 | 9 | 11 | 16 | 18 | 23 | 24 | 26 | 27 | |
| 12 | 54 | 0 | 1 | 3 | 5 | 6 | 13 | 14 | 21 | 22 | 24 | 26 | 27 | |
| 13 | 64 | 0 | 1 | 3 | 4 | 9 | 11 | 16 | 21 | 23 | 28 | 29 | 31 | 32 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Arrays Structure | Number of Sensors T | Consecutive DOF | |
|---|---|---|---|
| TL-NA | |||
| FL-NA | |||
| ACA | |||
| SAFE-CPA | |||
| Proposed array |
| T | 6 | 7 | 8 | 9 | 10 | ||
|---|---|---|---|---|---|---|---|
| cDOF | |||||||
| Array | |||||||
| Proposed array | / | 83 (5, 2, 2) | 139 (5, 3, 2) | 179 (6, 3, 2) | 251 (5, 4, 3) | ||
| ACA | 33 (2, 3) | / | 53 (2, 5) | 69 (3, 4) | 85 (3, 5) | ||
| SAFE-CPA | / | / | 137 (2, 3, 2) | 189 (2, 3, 3) | 241 (2, 3, 4) | ||
| TL-NA | 45 (3, 3) | 61 (3, 4) | 77 (4, 4) | 97 (4, 5) | 117 (5, 5) | ||
| FL-NA | 47 (3, 2, 2, 2) | 71 (3, 3, 2, 2) | 107 (3, 3, 3, 2) | 161 (3, 3, 3, 3) | 215 (4, 3, 3, 3) | ||
| T | 11 | 12 | 13 | 14 | 15 | ||
|---|---|---|---|---|---|---|---|
| cDOF | |||||||
| Array | |||||||
| Proposed array | 323 (6, 4,3) | / | 503 (8, 4, 3) | 747 (7, 6, 4) | 951 (8, 6, 4) | ||
| ACA | / | 117 (4, 5) | 133 (3, 8) | 161 (4, 7) | 177 (5, 6) | ||
| SAFE-CPA | 273 (3, 4, 2) | 375 (3, 4, 3) | 477 (3, 4, 4) | 581 (3, 5, 4) | 705 (3, 5, 5) | ||
| TL-NA | 141 (5, 6) | 165 (6, 6) | 193 (6, 7) | 221 (7, 7) | 253 (7, 8) | ||
| FL-NA | 287 (4, 4, 3, 3) | 383 (4, 4, 4, 3) | 511 (4, 4, 4, 4) | 639 (5, 4, 4, 4) | 799 (5, 5, 4, 4) | ||
| Methods | Computational Complexity | Complex Multiplications |
|---|---|---|
| DFT-MUSIC | ||
| TSS-MUSIC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Li, J.; Ye, C.; Li, J. Unfolded Coprime Linear Array with Three Subarrays for Non-Gaussian Signals: Configuration Design and DOA Estimation. Sensors 2022, 22, 1339. https://doi.org/10.3390/s22041339
Yang M, Li J, Ye C, Li J. Unfolded Coprime Linear Array with Three Subarrays for Non-Gaussian Signals: Configuration Design and DOA Estimation. Sensors. 2022; 22(4):1339. https://doi.org/10.3390/s22041339
Chicago/Turabian StyleYang, Meng, Jingming Li, Changbo Ye, and Jianfeng Li. 2022. "Unfolded Coprime Linear Array with Three Subarrays for Non-Gaussian Signals: Configuration Design and DOA Estimation" Sensors 22, no. 4: 1339. https://doi.org/10.3390/s22041339
APA StyleYang, M., Li, J., Ye, C., & Li, J. (2022). Unfolded Coprime Linear Array with Three Subarrays for Non-Gaussian Signals: Configuration Design and DOA Estimation. Sensors, 22(4), 1339. https://doi.org/10.3390/s22041339








