Aircraft Landing Gear Retraction/Extension System Fault Diagnosis with 1-D Dilated Convolutional Neural Network
Abstract
:1. Introduction
- Analyze the aircraft landing gear R/E system’s main fault mode with its working principle.
- A conventional 1-DCNN was constructed to classify faults based on the actuator’s displacement; experimental results show the average accuracy of the test set reached 91.80%.
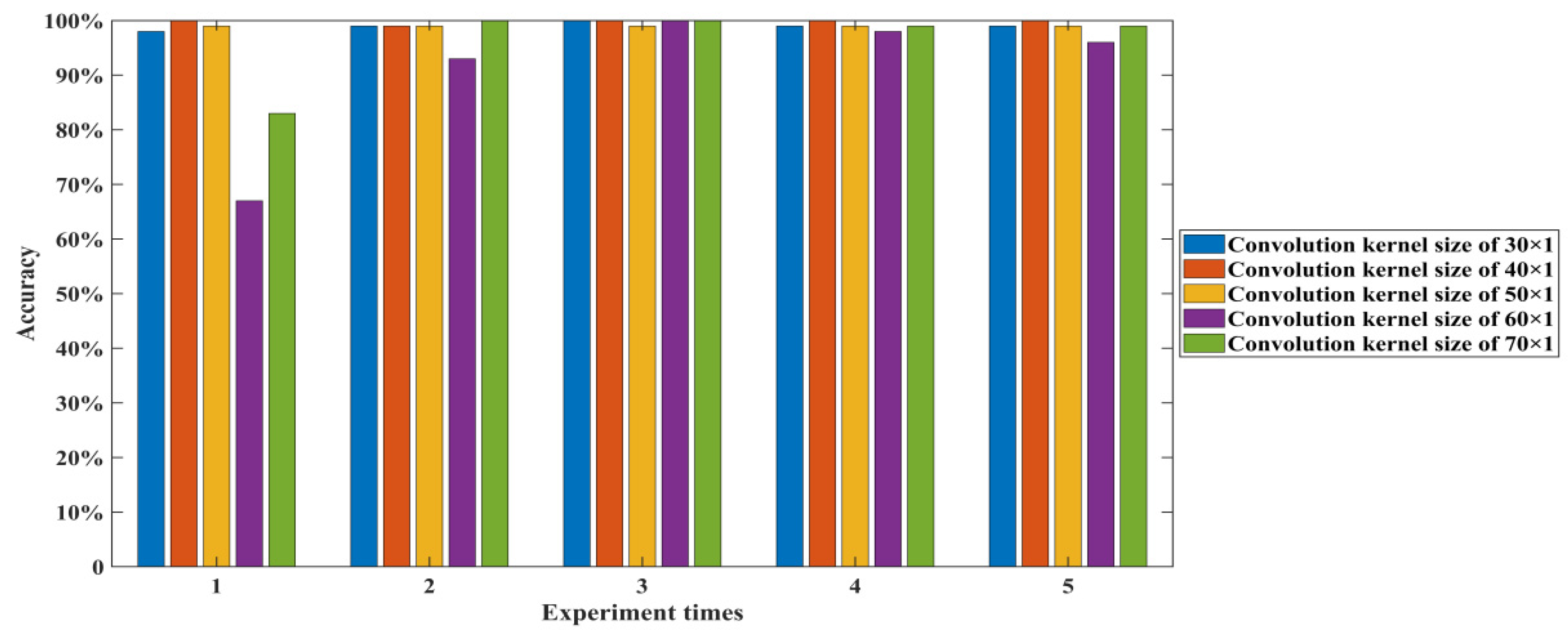
- The receptive field size affects the extraction of the original information by the model. There is a nonlinear relationship between the receptive field and the convolution kernel size for the expanded convolution. The convolution kernel size’s influence on classification accuracy is explored.
- There is a low classification result with a single feature; consequently, 1-DDCNNselects multi-feature parameters with the system pressure, the pressure at the right and left end of the actuator cylinder. Experimental results reveal that the average test accuracy of the model reaches 99.80%.
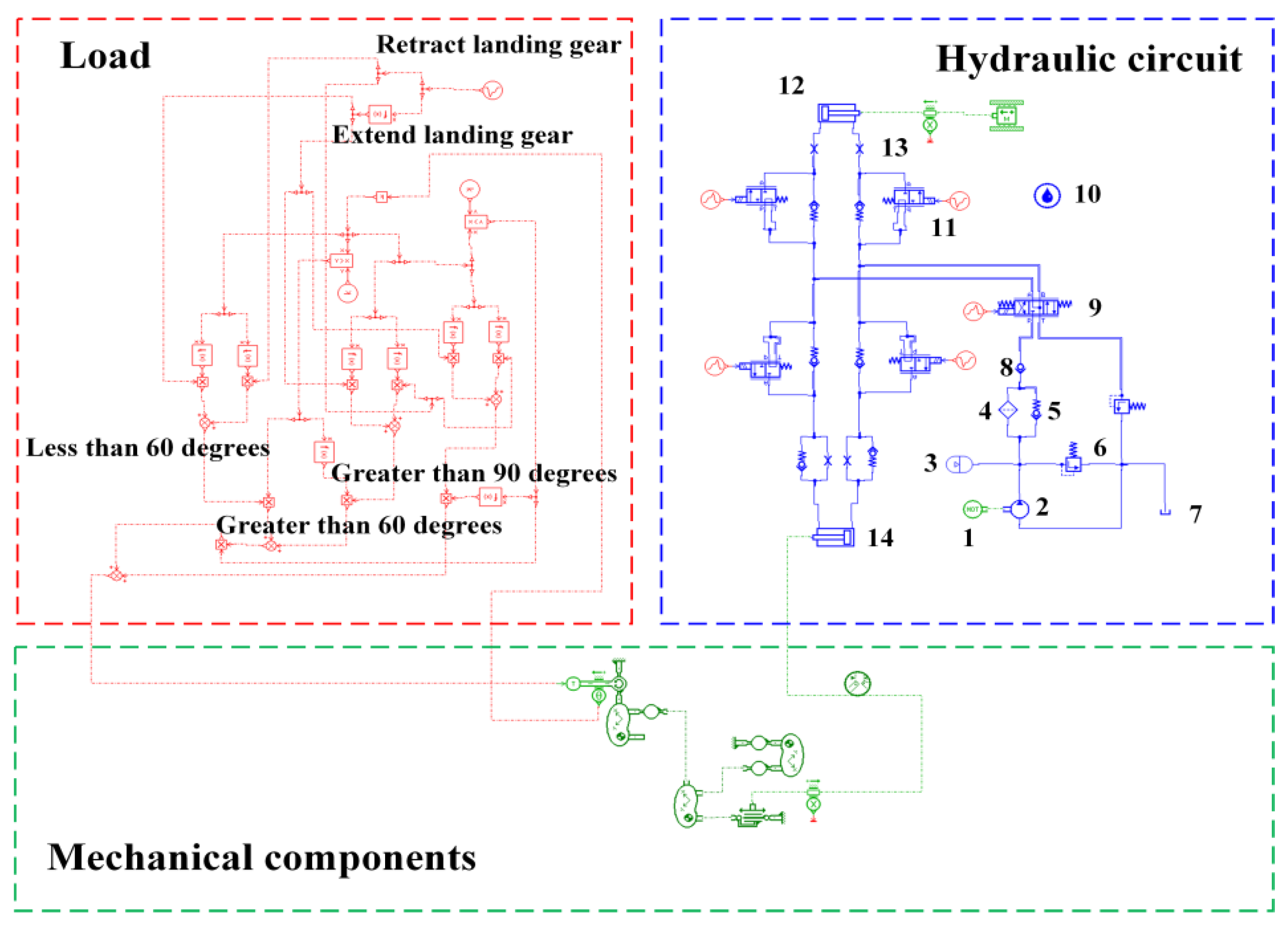
2. The Typical Aircraft Landing Gear R/E System Analysis
2.1. System Working Principle and Composition
2.2. Failure Mode and Effect Analysis
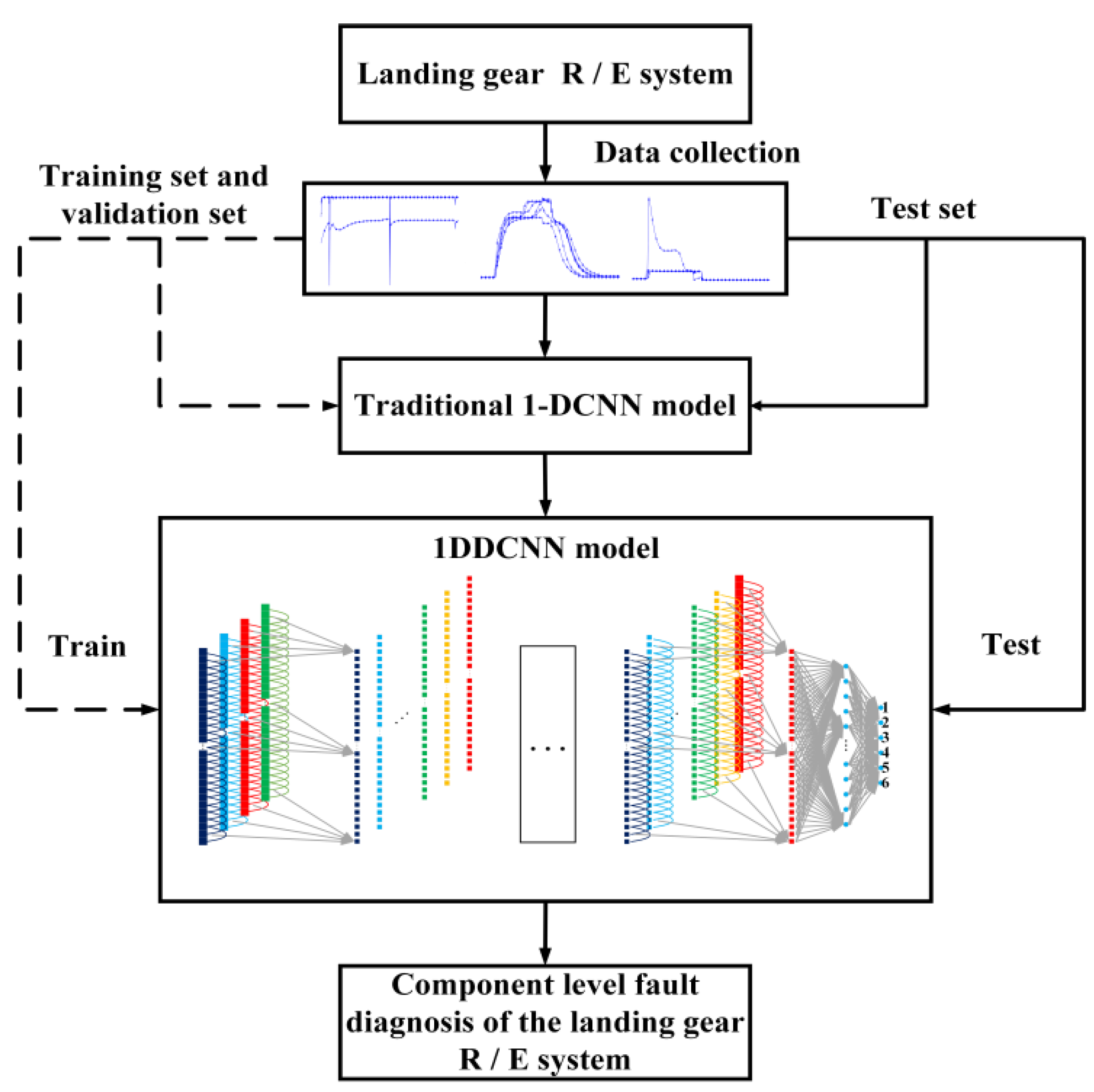
3. 1-DDCNN Fault Diagnosis Model
3.1. 1-DCNN
3.2. 1-DDCNN
3.3. 1-DDCNN Fault Diagnosis Model Framework
4. Experimental Implementations
4.1. Data Description and Operating Environment
4.2. Experimental Model
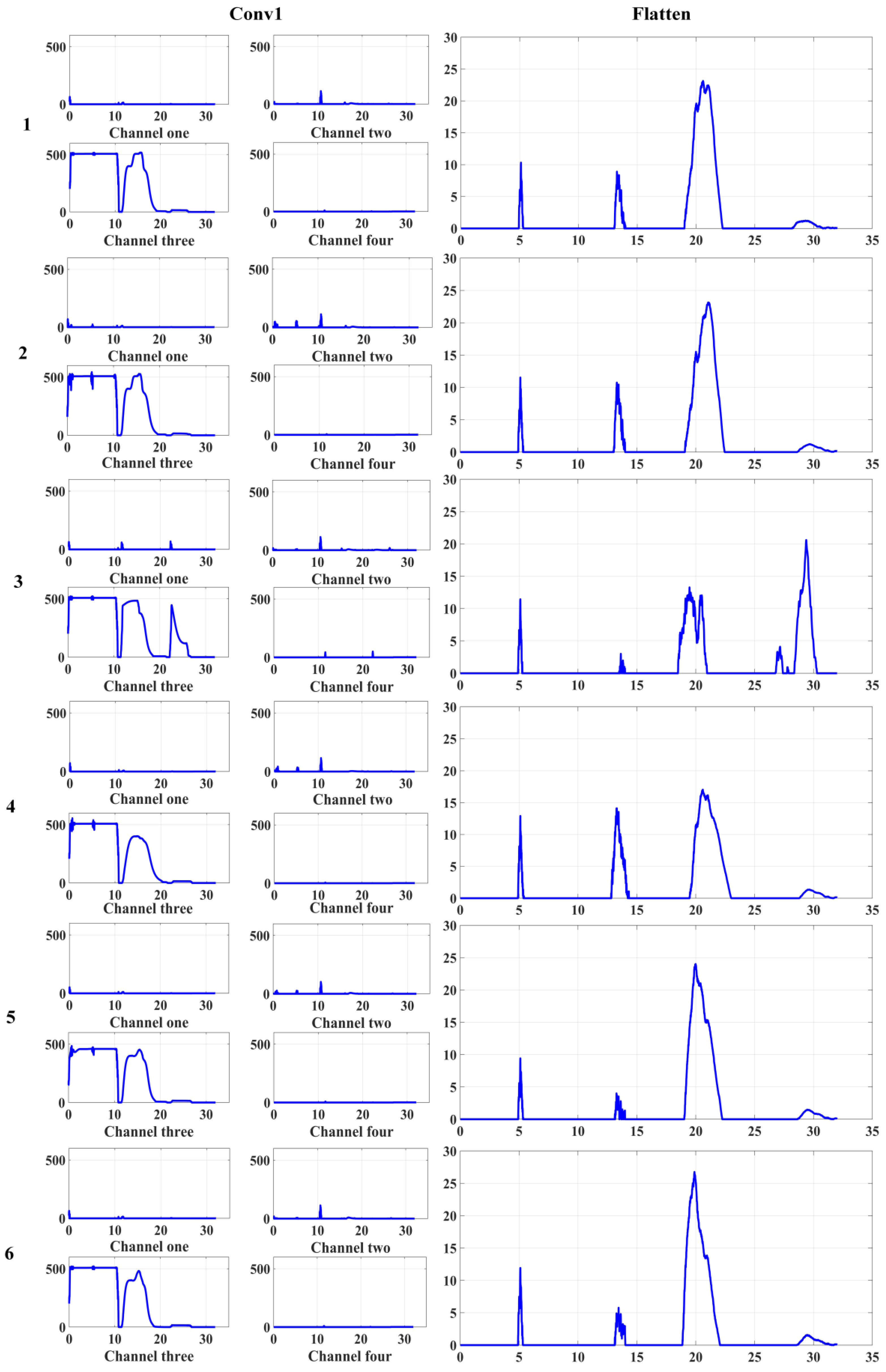
4.3. Experimental Results and Analysis
4.3.1. Research on the Size of Convolution Kernel of 1-DDCNN Model
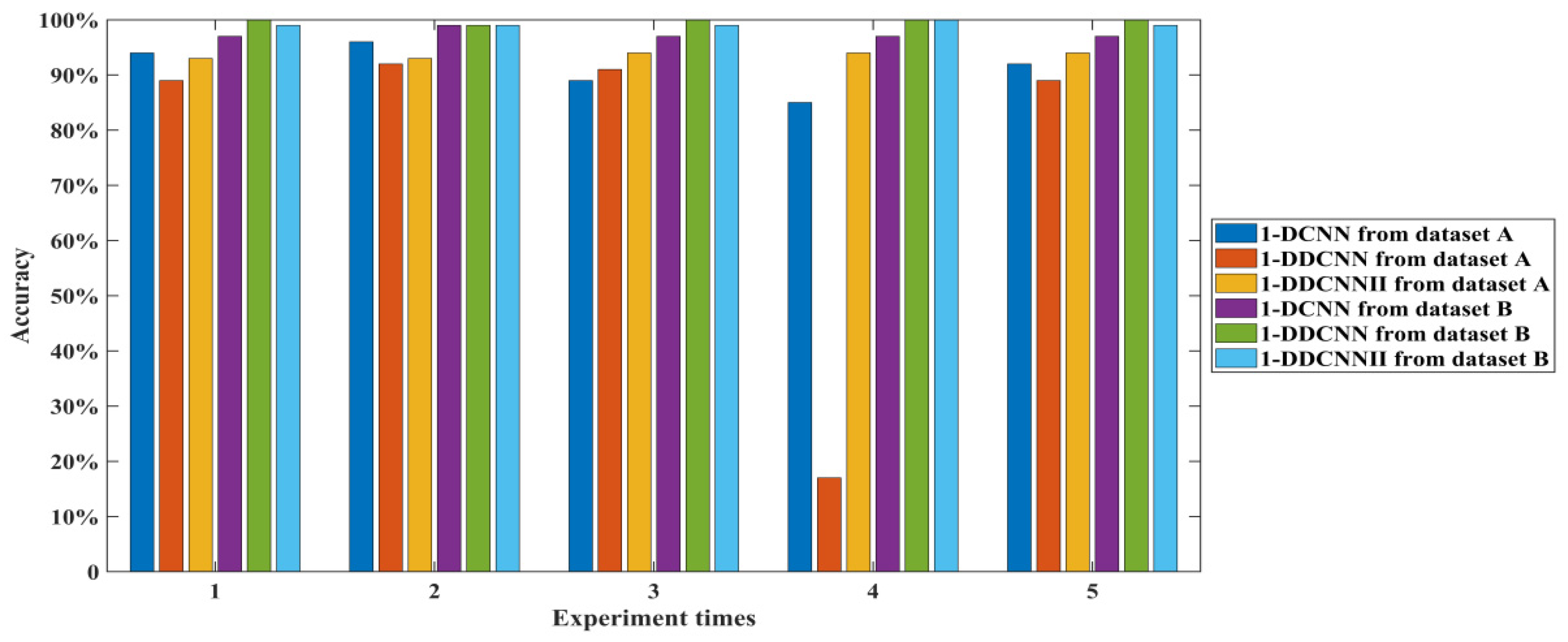
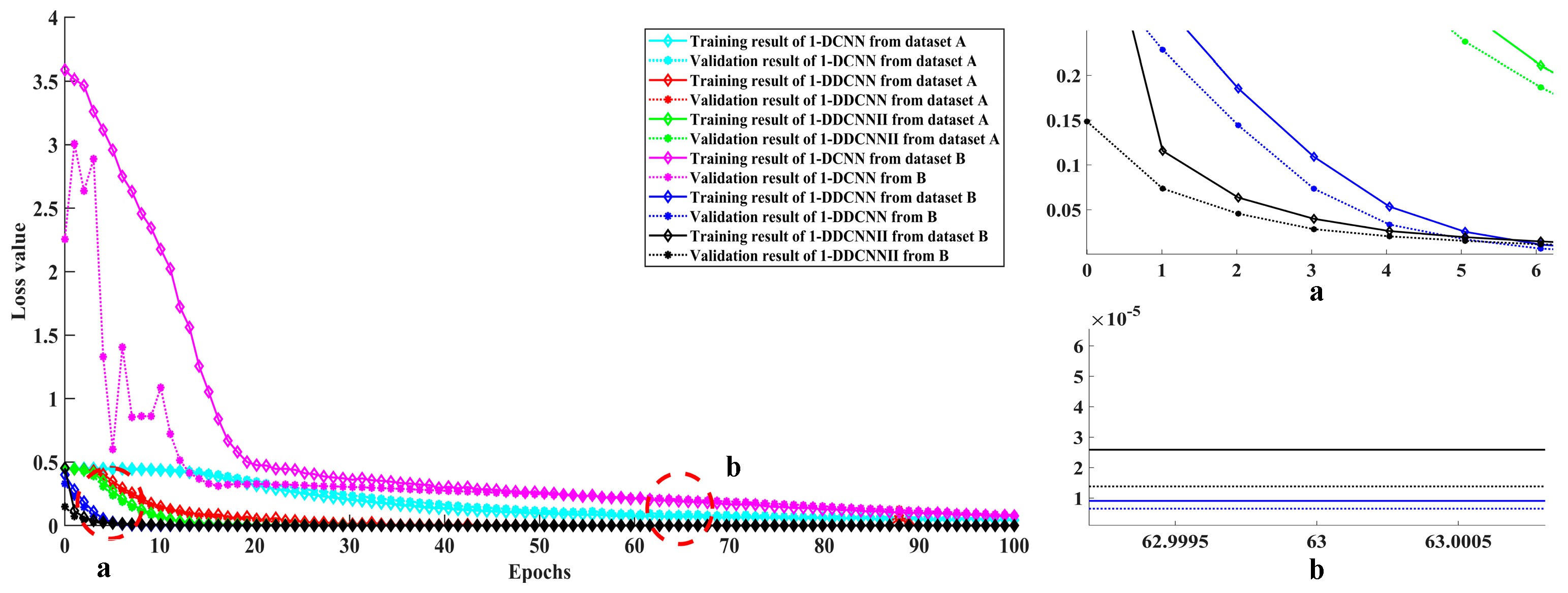
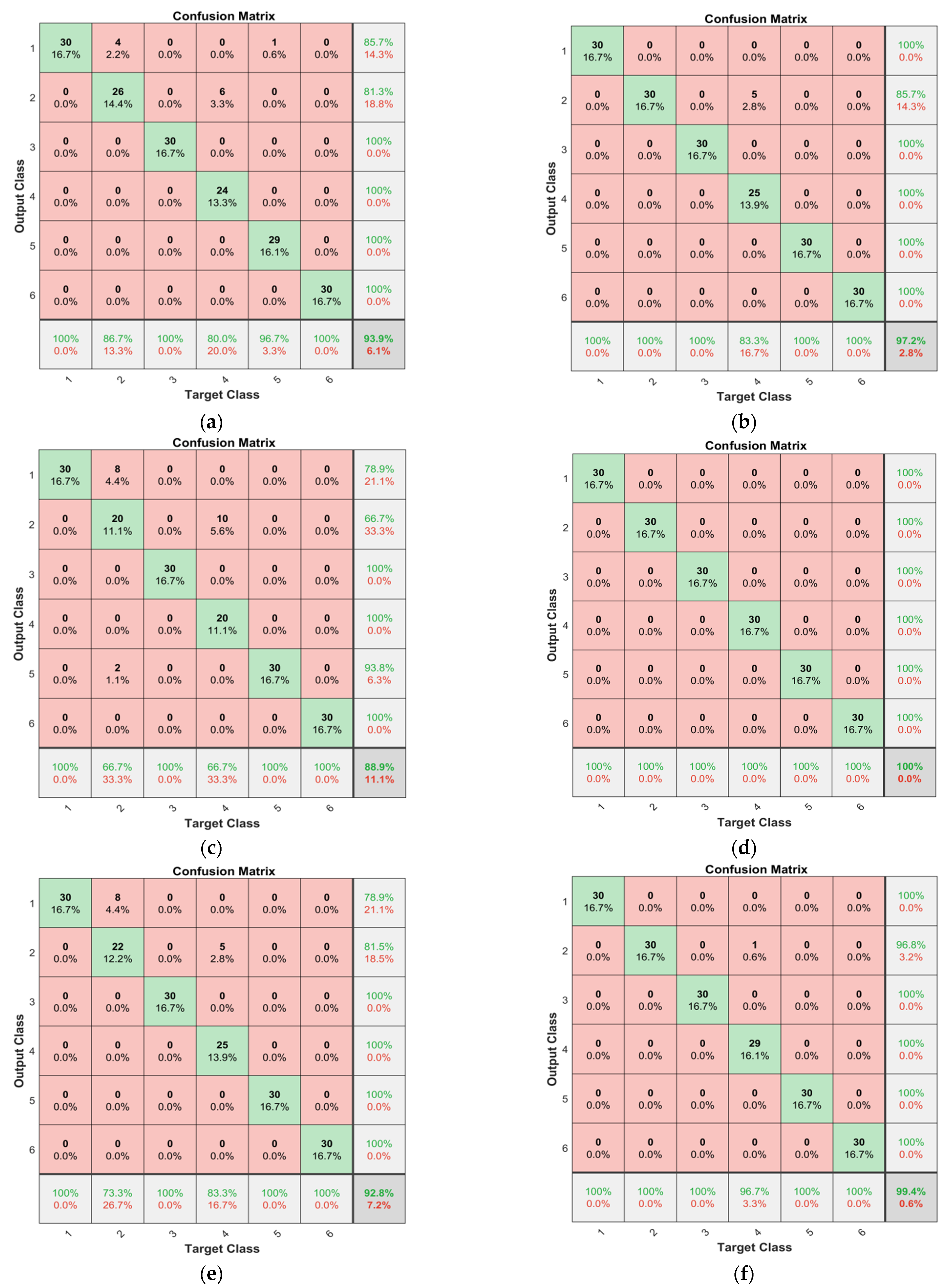
4.3.2. Comparative Experiment of Three Models under Different Datasets
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LeCun, Y. Generalization and network design strategies. Connect. Perspect. 1989, 19, 143–155. [Google Scholar]
- Gligorijevic, J.; Gajic, D.; Brkovic, A. Online Condition Monitoring of Bearings to Support Total Productive Maintenance in the Packaging Materials Industry. Sensors 2016, 16, 316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Janssens, O. Convolutional neural network based fault detection for rotating machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Jing, L. An adaptive multi-sensor data fusion method based on deep convolutional neural networks for fault diagnosis of planetary gearbox. Sensors 2017, 17, 414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, L. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- Wu, C.; Jiang, P.; Ding, C. Intelligent fault diagnosis of rotating machinery based on one-dimensional convolutional neural network. Comput. Ind. 2019, 108, 53–61. [Google Scholar] [CrossRef]
- Huang, W.; Cheng, J.; Yang, Y. An improved deep convolutional neural network with multi-scale information for bearing fault diagnosis. Neurocomputing 2019, 359, 77–92. [Google Scholar] [CrossRef]
- Pan, H. An Improved Bearing Fault Diagnosis Method using One-Dimensional CNN and LSTM. J. Mech. Eng. 2018, 64, 443–452. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Zhuang, Z. A deep learning method for bearing fault diagnosis through stacked residual dilated convolutions. Appl. Sci. 2019, 9, 1823. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Feng, J.R. An Intelligent Fault Diagnosis Method of Rolling Bearing Under Variable Working Loads Using 1-D Stacked Dilated Convolutional Neural Network. IEEE Access 2020, 8, 63027–63042. [Google Scholar] [CrossRef]
- Liang, Y.; Li, B.B.; Jiao, B. A deep learning method for motor fault diagnosis based on a capsule network with gate-structure dilated convolutions. Neural Comput. Appl. 2021, 33, 1401–1418. [Google Scholar] [CrossRef]
- Wang, H.T. Aircraft Hydraulic Components and Systems; National Defense Industry Press: Beijing, China, 2012. [Google Scholar]
- Shi, X.D.; Ying, F.J. Performance simulation and fault analysis of aircraft landing gear extension and retraction system. Comput. Appl. Softw. 2021, 38, 65–71. [Google Scholar]
- Zhou, F.Y.; Jin, L.P.; Dong, J. Review of convolutional neural network. Chin. J. Comput. 2017, 40, 1229–1251. [Google Scholar]







| Components | Failure Mode | Failure Cause |
|---|---|---|
| Constant pressure variable pump | Insufficient oil output and pressure of the pump | Severe pump leakage or low pump speed |
| Excessive noise from the pump | The pump is severely worn or air mixed in the oil | |
| Higher temperature | Abnormal wear in the pump | |
| Actuatorcylinder | Piston rod stuck | The actuator cylinder is leaking seriouslyor press control is faulty |
| The speed did not reach the standard value | The actuator cylinder is leaking seriously and it is subjected to excessive external load | |
| Creeping phenomenon | Air entered the actuatorcylinder | |
| Directional control valve | Insufficient flow after reversing spool | Insufficient valve opening |
| Spool stands still | Spool stuck or electromagnet failed | |
| Excessive pressure drops | Improper setting of some parameters | |
| Filter | Filter clogging | Oil is contaminated |
| Throttle valve | The range of flow regulation is limited | Clogged throttle hole |
| Sub-Model | Parameter | Value |
|---|---|---|
| Hydraulic fluid | Density | 850 kg/m3 |
| Bulk modulus | 1.7 × 104 bar | |
| Temperature | 40 °C | |
| Air/gas content | 0.1% | |
| Constant pressure variable pump | Pump displacement | 5 cc/rev |
| Hydraulic motor | Shaft speed | 5000 rev/min |
| Filter | Equivalent orifice diameter | 6 mm |
| Critical flow number | 2320 | |
| Maximum flow coefficient | 0.7 | |
| Accumulator | Polytrophic index | 1.4 |
| Gas pre-charge pressure | 118 bar | |
| Initial pressure | 152 bar | |
| Accumulator volume | 2 L | |
| Actuatorcylinder | Piston diameter | 69.596 mm |
| Rod diameter | 30.099 mm | |
| Length of stroke | 276.1 mm | |
| Leakage coefficient | 0 L/min/bar | |
| Unlock actuator | Piston diameter | 25.12 mm |
| Rod diameter | 11.049 mm | |
| Length of stroke | 70.84 mm | |
| Press control | Relief value cracking pressure | 206.843 bar |
| Relief value flow rate pressure gradient | 20 L/min/bar | |
| Throttle valve | Diameter | 2 mm |
| Three-position four-way directional control valve | Valve natural frequency | 80 Hz |
| Valve damping ratio | 0.8 | |
| Flow rate | 39 L/min | |
| Pressure drop | 2.5 bar | |
| Valve rated current | 40 mA |
| Failure Status | Labels | Failure Threshold |
|---|---|---|
| Normal | 1 | - |
| Excessive noise from the pump | 2 | Content of air in the hydraulic fluidis more than 5% |
| Throttle valve blocking at right end of actuating cylinder | 3 | The diameter of the throttle valve is less than 2.5 mm |
| Throttle valve blockingat left end of actuating cylinder | 4 | The diameter of the throttle valve is less than 2 mm |
| Constant pressure variable pump leakage | 5 | The diameter of the throttle valve is more than 3 mm |
| Actuator cylinder leakage | 6 | Leakage coefficient of actuator cylinder is greater than 0.01 |
| Data Division | Failure Status | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Training set | 240 | 240 | 240 | 240 | 240 | 240 |
| Validation set | 30 | 30 | 30 | 30 | 30 | 30 |
| Test set | 30 | 30 | 30 | 30 | 30 | 30 |
| Data Division | Feature Parameters | Failure Status | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Training set | System pressure | 240 | 240 | 240 | 240 | 240 | 240 |
| The pressure at the right end of actuating cylinder | 240 | 240 | 240 | 240 | 240 | 240 | |
| The pressure at the left end of actuating cylinder | 240 | 240 | 240 | 240 | 240 | 240 | |
| Validation set | System pressure | 30 | 30 | 30 | 30 | 30 | 30 |
| The pressure at the right end of actuating cylinder | 30 | 30 | 30 | 30 | 30 | 30 | |
| The pressure at the left end of actuating cylinder | 30 | 30 | 30 | 30 | 30 | 30 | |
| Test set | System pressure | 30 | 30 | 30 | 30 | 30 | 30 |
| The pressure at the right end of actuating cylinder | 30 | 30 | 30 | 30 | 30 | 30 | |
| The pressure at the left end of actuating cylinder | 30 | 30 | 30 | 30 | 30 | 30 | |
| Operating Environment | Version |
|---|---|
| CPU | Intel(R) Core(TM) i5-9300H 2.40GHz |
| System | Windows 10 Home Chinese Version |
| Interpreter | Anaconda2.0.3 |
| Compiler | PyCharm2019.3.4 |
| Deep learning framework | Tensorflow2.0 |
| No. | Layer Type | Kernel Size/Stride | Kernel Number | Output Size (Width × Depth) | Padding | Dropout Rate |
|---|---|---|---|---|---|---|
| 1 | Convolution1 | 50 × 1/1 × 1 | 4 | 3201 × 4 | Yes | - |
| 2 | MaxPooling1 | 2 × 1/2 × 1 | 4 | 1600 × 4 | No | - |
| 3 | Convolution2 | 3 × 1/1 × 1 | 16 | 1600 × 16 | Yes | - |
| 4 | MaxPooling2 | 2 × 1/2 × 1 | 16 | 800 × 16 | No | - |
| 5 | Dropout1 | - | - | 800 × 16 | - | 0.2 |
| 6 | Convolution3 | 3 × 1/1 × 1 | 16 | 800 × 16 | Yes | - |
| 7 | MaxPooling3 | 2 × 1/2 × 1 | 16 | 400 × 16 | No | - |
| 8 | Convolution4 | 3 × 1/1 × 1 | 32 | 400 × 32 | Yes | - |
| 9 | MaxPooling4 | 2 × 1/2 × 1 | 32 | 200 × 32 | No | - |
| 10 | Dropout2 | - | - | 200 × 32 | - | 0.2 |
| 11 | Convolution5 | 3 × 1/1 × 1 | 32 | 200 × 32 | Yes | - |
| 12 | MaxPooling5 | 2 × 1/2 × 1 | 32 | 100 × 32 | No | - |
| 13 | Dropout3 | - | - | 100 × 32 | - | 0.2 |
| 14 | Convolution6 | 3 × 1/1 × 1 | 64 | 100 × 64 | Yes | - |
| Activation function of the convolution layer: Relu | ||||||
| Activation function of fully-connected layer:Softmax | ||||||
| Optimization: Adam(1.0 × 10−5) | ||||||
| Iteration: 100 | ||||||
| No. | Layer Type | Kernel Size/Stride | Kernel Number | Expansion Factor | Output Size (Width × Depth) | Padding | Receptive Field |
|---|---|---|---|---|---|---|---|
| 1 | Convolution 1 | 50 × 1/1 × 1 | 4 | 1 | 3201 × 4 | Yes | 50 |
| 2 | Convolution 2 | 50 × 1/1 × 1 | 16 | 2 | 3201 × 16 | Yes | 148 |
| 3 | Convolution 3 | 50 × 1/1 × 1 | 16 | 4 | 3201 × 16 | Yes | 344 |
| 4 | Convolution 4 | 50 × 1/1 × 1 | 32 | 8 | 3201 × 32 | Yes | 736 |
| 5 | Convolution 5 | 50 × 1/1 × 1 | 32 | 16 | 3201 × 32 | Yes | 1520 |
| 6 | Convolution 6 | 50 × 1/1 × 1 | 1 | 32 | 3201 × 1 | Yes | 3088 |
| 7 | Fully-connected | 256 | 1 | - | 256 × 1 | - | - |
| 8 | Softmax | 6 | 1 | - | 6 | - | - |
| The Convolution Kernel Size | Average Accuracy (%) | Standard Deviation | Total Parameter | Average Running Time/s |
|---|---|---|---|---|
| 30 | 99.00 | 0.0071 | 878355 | 187.2152 |
| 40 | 99.80 | 0.0045 | 897355 | 211.7023 |
| 50 | 99.00 | 0.0000 | 916355 | 231.7082 |
| 60 | 90.80 | 0.1355 | 935355 | 262.0429 |
| 70 | 96.20 | 0.0740 | 953355 | 280.4578 |
| No. | Layer Type | Kernel Size/Stride | Kernel Number | Expansion Factor | Output Size (Width×Depth) | Padding | Receptive Field |
|---|---|---|---|---|---|---|---|
| 1 | Convolution 1 | 50 × 1/1 × 1 | 4 | 1 | 3151 × 4 | No | 51 |
| 2 | Convolution 2 | 50 × 1/1 × 1 | 16 | 2 | 3051 × 16 | No | 151 |
| 3 | Convolution 3 | 50 × 1/1 × 1 | 16 | 4 | 2851 × 16 | No | 351 |
| 4 | Convolution 4 | 50 × 1/1 × 1 | 32 | 8 | 2451 × 32 | No | 751 |
| 5 | Convolution 5 | 50 × 1/1 × 1 | 32 | 16 | 1651 × 32 | No | 1551 |
| 6 | Convolution 6 | 50 × 1/1 × 1 | 64 | 32 | 51 × 64 | No | 3151 |
| 7 | Fully-connected | 256 | 1 | - | 256 × 1 | - | - |
| 8 | Softmax | 6 | 1 | - | 6 | - | - |
| Models | Datasets | Average Accuracy (%) | Standard Deviation | Total Parameter | Average Running Time/s |
|---|---|---|---|---|---|
| 1-DCNN | A | 91.80 | 0.0399 | 833074 | 60.9052 |
| 1-DDCNN | 75.60 | 0.3278 | 897035 | 191.7420 | |
| 1-DDCNNⅡ | 93.60 | 0.0055 | 1036854 | 153.4254 | |
| 1-DCNN | B | 97.40 | 0.0089 | 833474 | 76.4105 |
| 1-DDCNN | 99.80 | 0.0045 | 897355 | 211.7023 | |
| 1-DDCNN Ⅱ | 99.20 | 0.0045 | 1037262 | 171.7298 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Xu, Q.; Guo, Y.; Chen, R. Aircraft Landing Gear Retraction/Extension System Fault Diagnosis with 1-D Dilated Convolutional Neural Network. Sensors 2022, 22, 1367. https://doi.org/10.3390/s22041367
Chen J, Xu Q, Guo Y, Chen R. Aircraft Landing Gear Retraction/Extension System Fault Diagnosis with 1-D Dilated Convolutional Neural Network. Sensors. 2022; 22(4):1367. https://doi.org/10.3390/s22041367
Chicago/Turabian StyleChen, Jie, Qingshan Xu, Yingchao Guo, and Runfeng Chen. 2022. "Aircraft Landing Gear Retraction/Extension System Fault Diagnosis with 1-D Dilated Convolutional Neural Network" Sensors 22, no. 4: 1367. https://doi.org/10.3390/s22041367
APA StyleChen, J., Xu, Q., Guo, Y., & Chen, R. (2022). Aircraft Landing Gear Retraction/Extension System Fault Diagnosis with 1-D Dilated Convolutional Neural Network. Sensors, 22(4), 1367. https://doi.org/10.3390/s22041367





