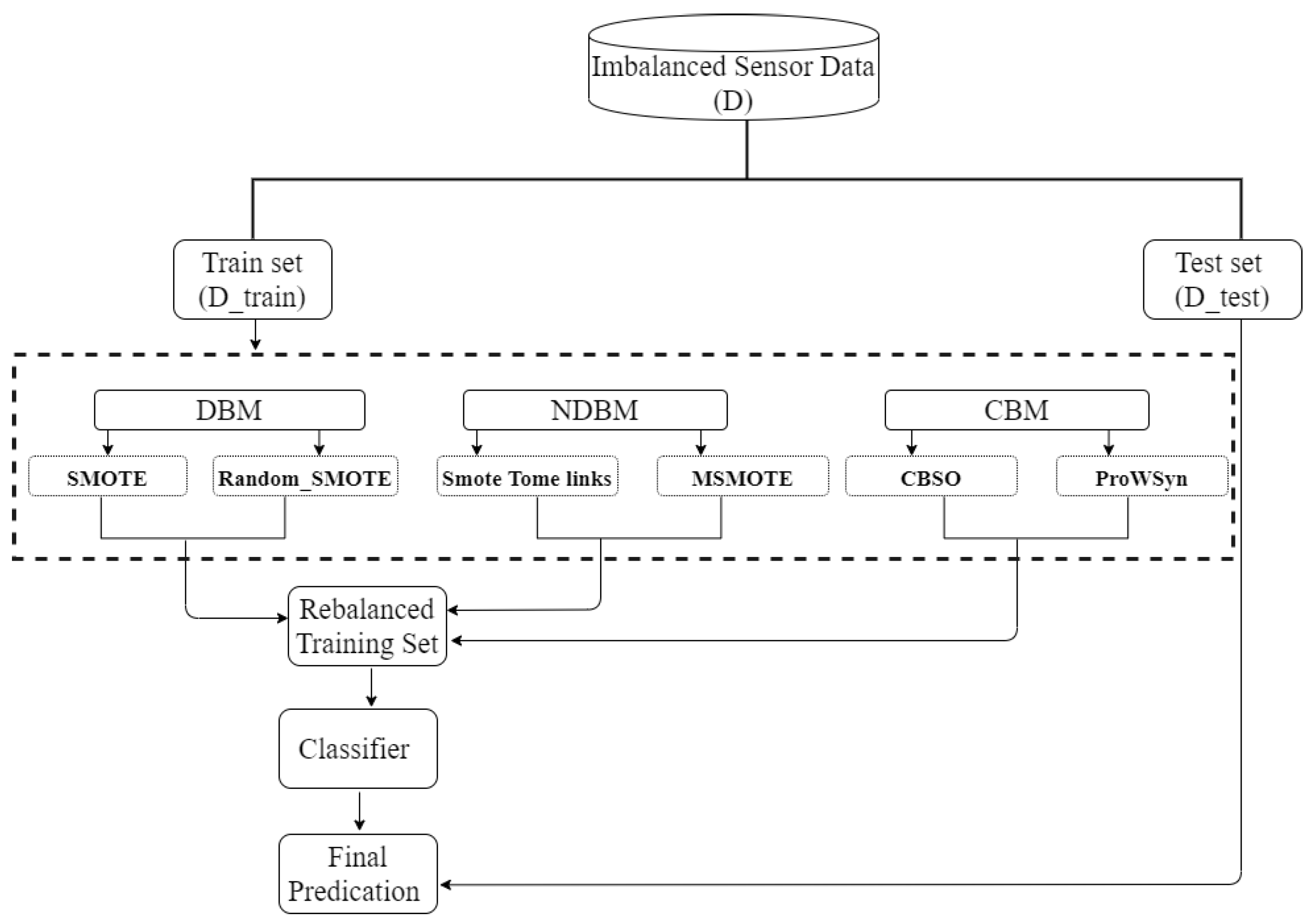
Figure 1.
Overview of the process used for splitting, oversampling, and evaluating the data.
Figure 1.
Overview of the process used for splitting, oversampling, and evaluating the data.
Figure 2.
Activity distribution of the Opportunity dataset.
Figure 2.
Activity distribution of the Opportunity dataset.
Figure 3.
Activity distribution of the PAMAP2 dataset.
Figure 3.
Activity distribution of the PAMAP2 dataset.
Figure 4.
Activity distribution of the ADL dataset.
Figure 4.
Activity distribution of the ADL dataset.
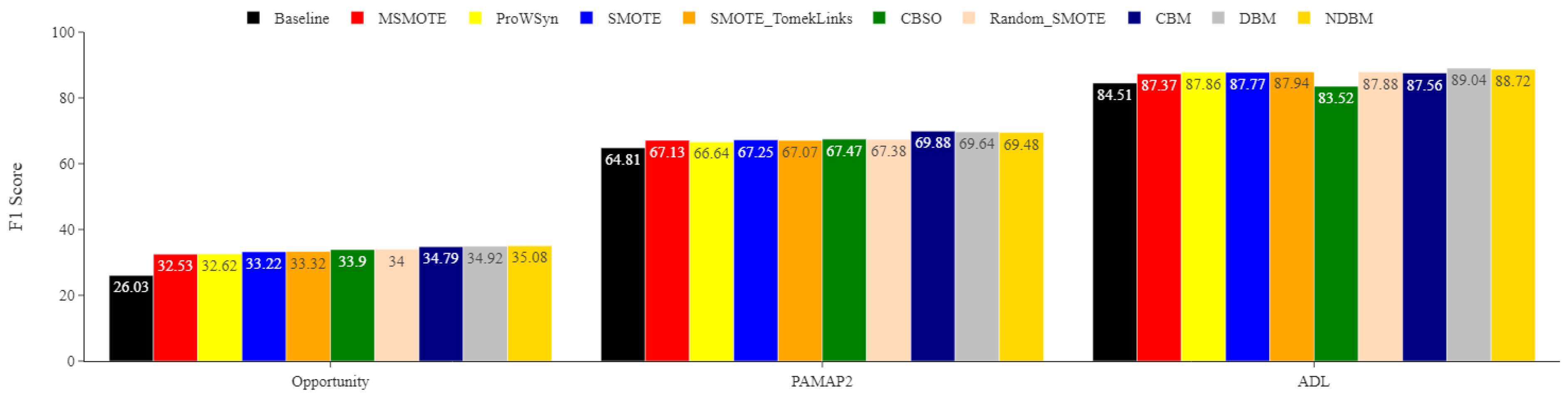
Figure 5.
Opportunity minority classes. Comparing the impact of DBM, NDBM, and CBM on activity recognition performance, using MLP for the most underrepresented activities Open_Fridge, Open_Drawer3, and Close_Drawer3. The reported means of F1 scores are obtained from 30 repetitions. The F1 score is in %.
Figure 5.
Opportunity minority classes. Comparing the impact of DBM, NDBM, and CBM on activity recognition performance, using MLP for the most underrepresented activities Open_Fridge, Open_Drawer3, and Close_Drawer3. The reported means of F1 scores are obtained from 30 repetitions. The F1 score is in %.
Figure 6.
ADL minority classes. Comparing the impact of DBM, NDBM, and CBM on activity recognition performance, using MLP for the most underrepresented activities (Going Up/Downstairs (GUDS), Standing Up, Walking and Going Up/Downstairs (SWGUDS), and Walking and Talking with Someone (WATWS)). The reported means of F1 scores are obtained from 30 repetitions. The F1 score is in %.
Figure 6.
ADL minority classes. Comparing the impact of DBM, NDBM, and CBM on activity recognition performance, using MLP for the most underrepresented activities (Going Up/Downstairs (GUDS), Standing Up, Walking and Going Up/Downstairs (SWGUDS), and Walking and Talking with Someone (WATWS)). The reported means of F1 scores are obtained from 30 repetitions. The F1 score is in %.
Figure 7.
PAMAP2 minority classes. Comparing the impact of DBM, NDBM, and CBM on activity recognition performance, using MLP for the most underrepresented activities (ascending stairs, descending stairs, rope jumping, and running). The reported means of F1 scores are obtained from 30 repetitions. The F1 score is in %.
Figure 7.
PAMAP2 minority classes. Comparing the impact of DBM, NDBM, and CBM on activity recognition performance, using MLP for the most underrepresented activities (ascending stairs, descending stairs, rope jumping, and running). The reported means of F1 scores are obtained from 30 repetitions. The F1 score is in %.
Figure 8.
Comparing run times in seconds of the proposed DBM and CBM for all training datasets. The number of samples in the training sets for the ADL, Opportunity, and PAMAP2 datasets were 11,776, 1569, and 6450, respectively.
Figure 8.
Comparing run times in seconds of the proposed DBM and CBM for all training datasets. The number of samples in the training sets for the ADL, Opportunity, and PAMAP2 datasets were 11,776, 1569, and 6450, respectively.
Table 1.
Datasets details.
Table 1.
Datasets details.
| Dataset | Number of Subjects | Sample Rate | Window Size (s) | Sensor Position | Number of Sensors Used |
|---|
| Opportunity | 4 | 32 | 2 | Right Arm | 1 accelerometer |
| PAMAP2 | 8 | 100 | 3 | Dominant Wrist | 1 accelerometer |
| ADL | 15 | 52 | 10 | Chest | 1 accelerometer |
Table 2.
Features description [
18,
43].
Table 2.
Features description [
18,
43].
| Feature | Description |
|---|
| Mean | It provides the average value of sensor data within a segment |
| Standard deviation | It describes how much sensor data are spread around the mean |
| Minimum | The minimum value of sensor data within a segment |
| Maximum | The maximum value of sensor data within a segment |
| Median | It finds the middle number of a sample within a segment |
| Range | The difference between the maximum and the minimum of sensor data within a segment |
Table 3.
MLP architecture details.
Table 3.
MLP architecture details.
Hidden
Layers | Activation
Function | Optimizer | Loss
Function | Learning
Rate | Regularization | Epochs |
|---|
| 100 | Relu | Adam | Cross-entropy | 0.001 | L2 penalty | 200 |
Table 4.
Distance-based method results. Comparing the performance of MLP on DBM, SMOTE, and Random_SMOTE for multiple datasets. The reported mean of F1 score and standard deviation), recall, and precision are obtained from 30 repetitions. The F1 score, recall, and precision are in %. Highest scores are shown in bold.
Table 4.
Distance-based method results. Comparing the performance of MLP on DBM, SMOTE, and Random_SMOTE for multiple datasets. The reported mean of F1 score and standard deviation), recall, and precision are obtained from 30 repetitions. The F1 score, recall, and precision are in %. Highest scores are shown in bold.
| Data | Method | F1 Score | Recall | Precision |
|---|
| ADL | Baseline | 87.2 (±0.047) | 87.03 | 89.02 |
| | SMOTE | 92.24 (±0.069) | 91.44 | 94.21 |
| | Random_SMOTE | 91.07 (±0.086) | 90.31 | 93.22 |
| | DBM | 92.59 (±0.081) | 91.9 | 94.26 |
| Opportunity | Baseline | 28.85 (±0.017) | 34.1 | 29.57 |
| | SMOTE | 42.95 (±0.043) | 42.45 | 45.73 |
| | Random_SMOTE | 42.74 (±0.04) | 42.19 | 45.75 |
| | DBM | 48.49 (±0.052) | 48.18 | 50.63 |
| PAMAP2 | Baseline | 71.85 (±0.081) | 72.73 | 75.49 |
| | SMOTE | 74.73 (±0.055) | 74.93 | 77.69 |
| | Random_SMOTE | 74.59 (±0.055) | 74.64 | 77.83 |
| | DBM | 80.15 (±0.046) | 80.23 | 81.93 |
Table 5.
Noise detection-based results. Comparing the performance of MLP for NDBM, MSMOTE, and SMOTE_TomekLinks on multiple datasets. The reported mean of F1 score and standard deviation), recall, and precision are obtained from 30 repetitions. The F1 score, recall, and precision are in %. Highest scores are shown in bold.
Table 5.
Noise detection-based results. Comparing the performance of MLP for NDBM, MSMOTE, and SMOTE_TomekLinks on multiple datasets. The reported mean of F1 score and standard deviation), recall, and precision are obtained from 30 repetitions. The F1 score, recall, and precision are in %. Highest scores are shown in bold.
| Data | Method | F1 Score | Recall | Precision |
|---|
| ADL | Baseline | 87.2 (±0.047) | 87.03 | 89.02 |
| | SMOTE_TomekLinks | 91.41 (±0.071) | 90.52 | 93.56 |
| | MSMOTE | 90.7 (±0.067) | 89.65 | 92.66 |
| | NDBM | 92.7 (±0.065) | 91.69 | 94.77 |
| Opportunity | Baseline | 28.85 (±0.017) | 34.1 | 29.57 |
| | SMOTE_TomekLinks | 42.89 (±0.039) | 43.15 | 45.34 |
| | MSMOTE | 39.71 (±0.074) | 39.58 | 42.07 |
| | NDBM | 46.95 (±0.067) | 46.97 | 48.86 |
| PAMAP2 | Baseline | 71.85 (±0.081) | 72.73 | 75.49 |
| | SMOTE_TomekLinks | 74.24 (±0.054) | 74.51 | 77.13 |
| | MSMOTE | 73.73 (±0.059) | 73.78 | 77.03 |
| | NDBM | 79.43 (±0.054) | 79.46 | 81.35 |
Table 6.
Cluster-based results. Comparing the performance of MLP using CBM, CBSO, and ProWsyn on multiple datasets. The reported mean of F1 scores and (±standard deviation), recall, and precision are obtained from 30 repetitions. The F1 score, recall, and precision are in %. Highest scores are shown in bold.
Table 6.
Cluster-based results. Comparing the performance of MLP using CBM, CBSO, and ProWsyn on multiple datasets. The reported mean of F1 scores and (±standard deviation), recall, and precision are obtained from 30 repetitions. The F1 score, recall, and precision are in %. Highest scores are shown in bold.
| Data | Method | F1 Score | Recall | Precision |
|---|
| ADL | Baseline | 87.2 (±0.047) | 87.03 | 89.02 |
| | CBSO | 91.16 (±0.09) | 90.22 | 93.66 |
| | ProWSyn | 91.56 (±0.091) | 90.98 | 93.7 |
| | CBM | 92.96 (0.087) | 91.93 | 95.29 |
| Opportunity | Baseline | 28.85 (±0.017) | 34.1 | 29.57 |
| | CBSO | 42.92 (±0.023) | 42.96 | 45.12 |
| | ProWSyn | 42.78 (±0.055) | 43.47 | 44.99 |
| | CBM | 48.87 (±0.045) | 48.82 | 50.67 |
| PAMAP2 | Baseline | 71.85 (±0.081) | 72.73 | 75.49 |
| | CBSO | 75.69 (±0.042) | 75.43 | 78.19 |
| | ProWSyn | 74.42 (±0.054) | 74.4 | 77.5 |
| | CBM | 80.98 (±0.051) | 80.9 | 82.54 |
Table 7.
Comparing performance of DBM, NDBM, and CBM on multiple datasets. The reported mean of F1 scores and (±standard deviation), recall, and precision were obtained from 30 repetitions. The F1 score, recall, and precision are in %. Highest scores are shown in bold.
Table 7.
Comparing performance of DBM, NDBM, and CBM on multiple datasets. The reported mean of F1 scores and (±standard deviation), recall, and precision were obtained from 30 repetitions. The F1 score, recall, and precision are in %. Highest scores are shown in bold.
| Data | Method | F1 Score | Recall | Precision |
|---|
| ADL | Baseline | 87.2 (±0.047) | 87.03 | 89.02 |
| | DBM | 92.59 (±0.081) | 91.9 | 94.26 |
| | NDBM | 92.7 (±0.065) | 91.69 | 94.77 |
| | CBM | 92.96 (±0.087) | 91.93 | 95.29 |
| Opportunity | Baseline | 28.85 (±0.017) | 34.1 | 29.57 |
| | DBM | 48.49 (±0.052) | 48.18 | 50.63 |
| | NDBM | 46.95 (±0.067) | 46.97 | 48.86 |
| | CBM | 48.87 (±0.045) | 48.82 | 50.67 |
| PAMAP2 | Baseline | 71.85 (±0.081) | 72.73 | 75.49 |
| | DBM | 80.15 (±0.046) | 80.23 | 81.93 |
| | NDBM | 79.43 (±0.054) | 79.46 | 81.35 |
| | CBM | 80.98 (±0.051) | 80.9 | 82.54 |
Table 8.
Anderson–Darling normality test on sampling methods based on the 5 classifiers results × 9 sampling methods (5 × 9 = 45 sample size) on each dataset. The p-value is less than 0.05 ( = 0.05) for ADL and Opportunity which suggests that ADL and Opportunity are not normally distributed compared to PAMPA2.
Table 8.
Anderson–Darling normality test on sampling methods based on the 5 classifiers results × 9 sampling methods (5 × 9 = 45 sample size) on each dataset. The p-value is less than 0.05 ( = 0.05) for ADL and Opportunity which suggests that ADL and Opportunity are not normally distributed compared to PAMPA2.
| Data | Mean | Standard Deviation | Sample Size | p-Value |
|---|
| ADL | 0.8840 | 0.0399 | 45 | 0.0007 |
| Opportunity | 0.3773 | 0.0548 | 45 | 0.0000 |
| PAMAP2 | 0.7272 | 0.0406 | 45 | 0.0680 |
Table 9.
ANOVA for PAMAP2 dataset.
Table 9.
ANOVA for PAMAP2 dataset.
| Data | Degrees of Freedom | Sum of Squares | Mean Square | F Value | p-Value |
|---|
| PAMAP2 | 8 | 0.0067 | 0.0008 | 0.4602 | 0.8757 |
Table 10.
Friedman test results indicate that the p-value is less than 0.05 ( = 0.05) for the ADL and Opportunity datasets. This means that one or more of the sampling methods is more effective than the others.
Table 10.
Friedman test results indicate that the p-value is less than 0.05 ( = 0.05) for the ADL and Opportunity datasets. This means that one or more of the sampling methods is more effective than the others.
| Data | Degrees of Freedom | Chi-Square | p-Value |
|---|
| ADL | 8 | 21.8133 | 0.0053 |
| Opportunity | 8 | 24.2133 | 0.0021 |
Table 11.
Friedman sum-of-ranks test on ADL-based results for all methods and classifiers. CBM is the overall highest ranking method.
Table 11.
Friedman sum-of-ranks test on ADL-based results for all methods and classifiers. CBM is the overall highest ranking method.
| Classifier | CBSO | NDBM | CBM | DBM | MSMOTE | Pro-WSyn | Random_SMOTE | SMOTE_TomekLinks | SMOTE |
|---|
| KNN | 1 | 7 | 9 | 4 | 5 | 8 | 2 | 6 | 3 |
| LR | 1 | 8 | 3 | 9 | 2 | 5 | 6 | 7 | 4 |
| MLP | 3 | 8 | 9 | 7 | 1 | 5 | 2 | 4 | 6 |
| RF | 1 | 6 | 9 | 4 | 7 | 8 | 3 | 5 | 2 |
| SVM | 1 | 8 | 7 | 9 | 2 | 3 | 6 | 4 | 5 |
| Sum of ranks | 7 | 37 | 37 | 33 | 17 | 29 | 19 | 26 | 20 |
Table 12.
Friedman sum-of-ranks test on Opportunity-based results for all methods and classifiers. CBM is the overall highest ranking method.
Table 12.
Friedman sum-of-ranks test on Opportunity-based results for all methods and classifiers. CBM is the overall highest ranking method.
| Classifier | CBSO | NDBM | CBM | DBM | MSMOTE | Pro-WSyn | Random_SMOTE | SMOTE_TomekLinks | SMOTE |
|---|
| KNN | 5 | 6 | 9 | 7 | 1 | 4 | 8 | 3 | 2 |
| LR | 5 | 9 | 7 | 8 | 1 | 2 | 6 | 4 | 3 |
| MLP | 5 | 7 | 9 | 8 | 1 | 3 | 2 | 4 | 6 |
| RF | 4 | 5 | 8 | 3 | 1 | 9 | 7 | 6 | 2 |
| SVM | 2 | 7 | 8 | 9 | 1 | 4 | 3 | 5 | 6 |
| Sum of ranks | 21 | 34 | 41 | 35 | 5 | 22 | 26 | 22 | 19 |