Sensing Method Using Multiple Quantities for Diagnostic of Insulators in Different Ambient Conditions
Abstract
:1. Introduction
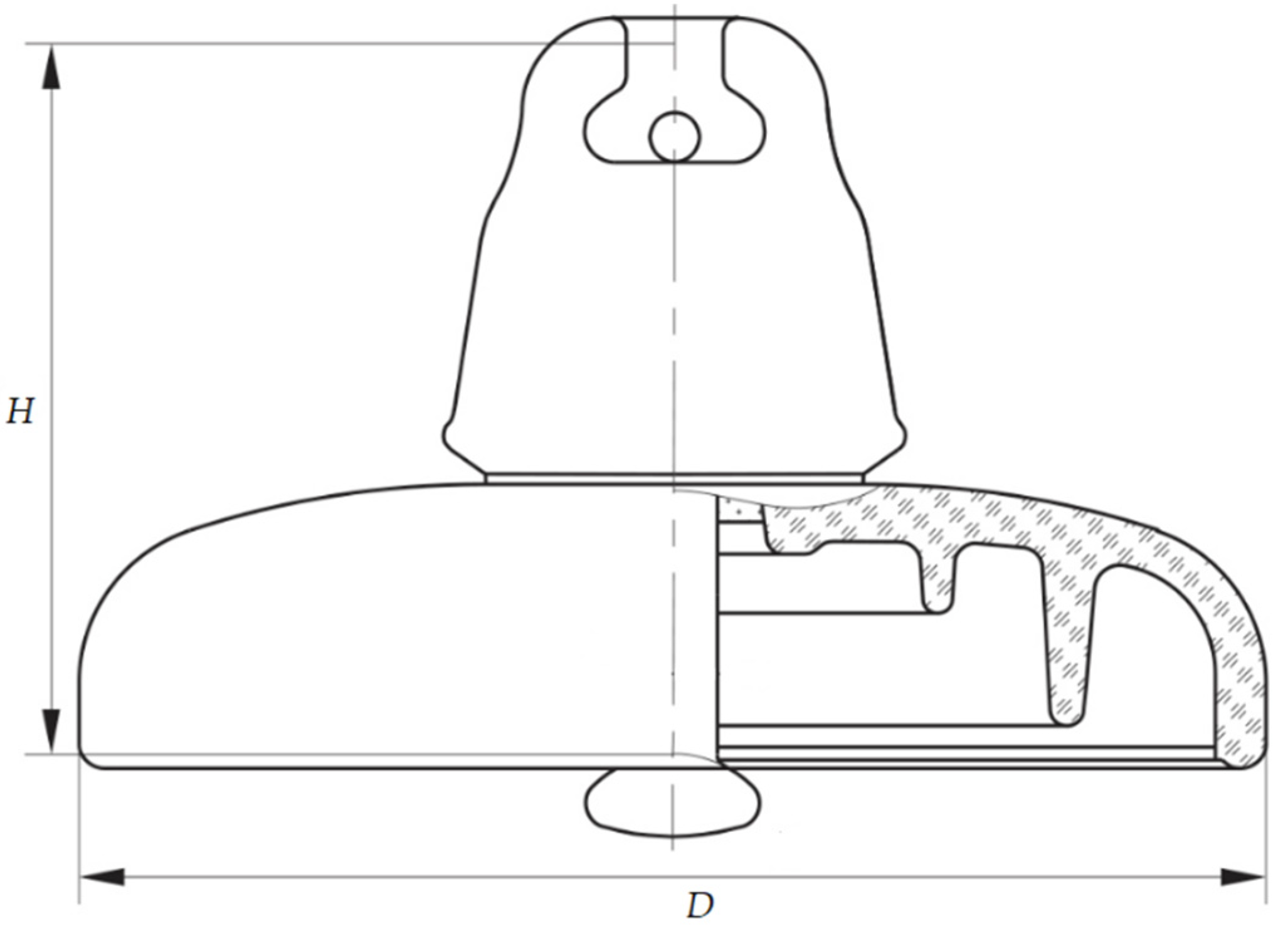
2. Materials and Methods
3. Results
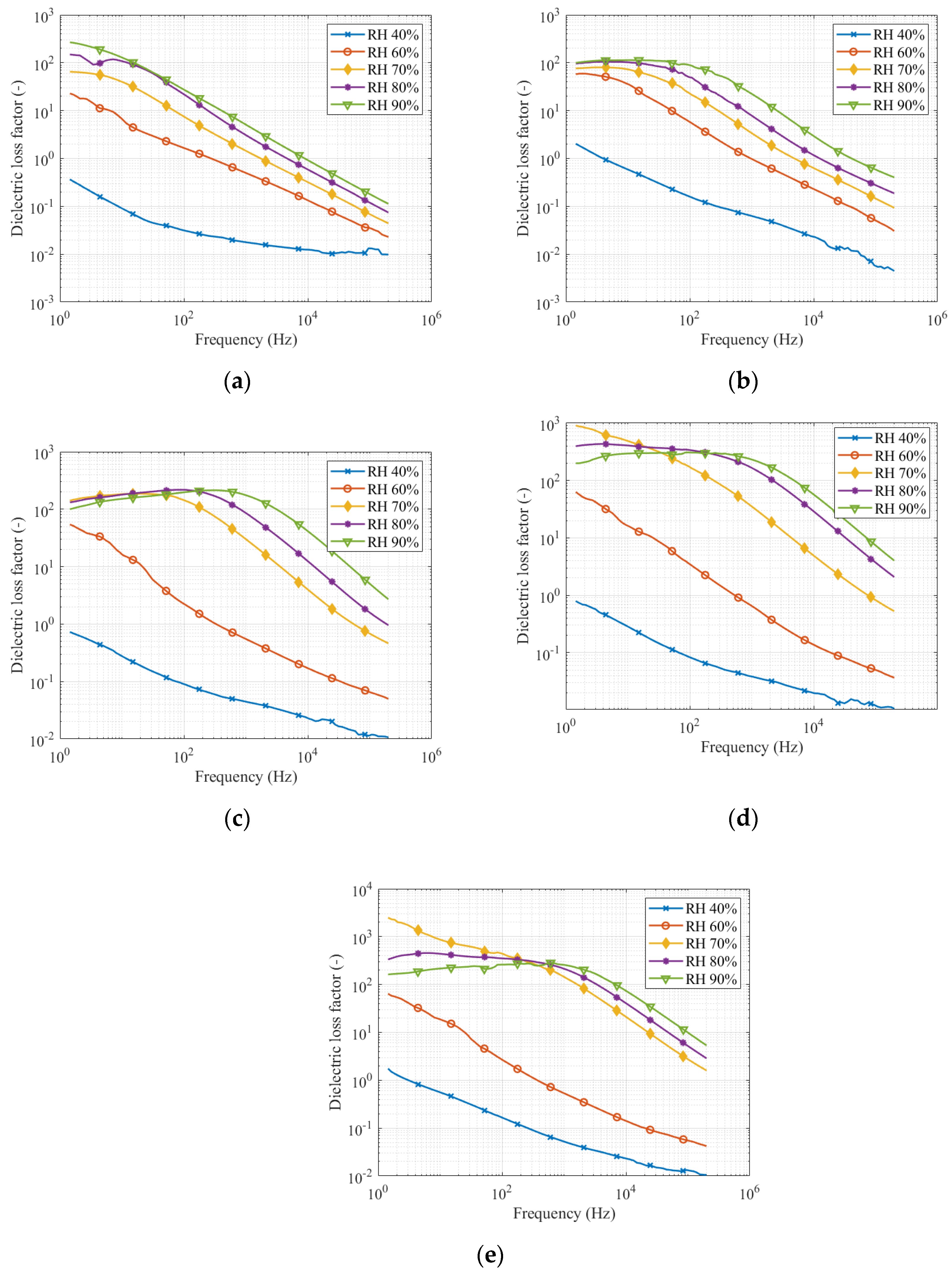
3.1. Measurement of Dielectric Loss Ffactor in the Frequency Range from 1 Hz to 200 kHz
3.2. Measurement of Capacity in the Frequency Range from 1 Hz to 200 kHz
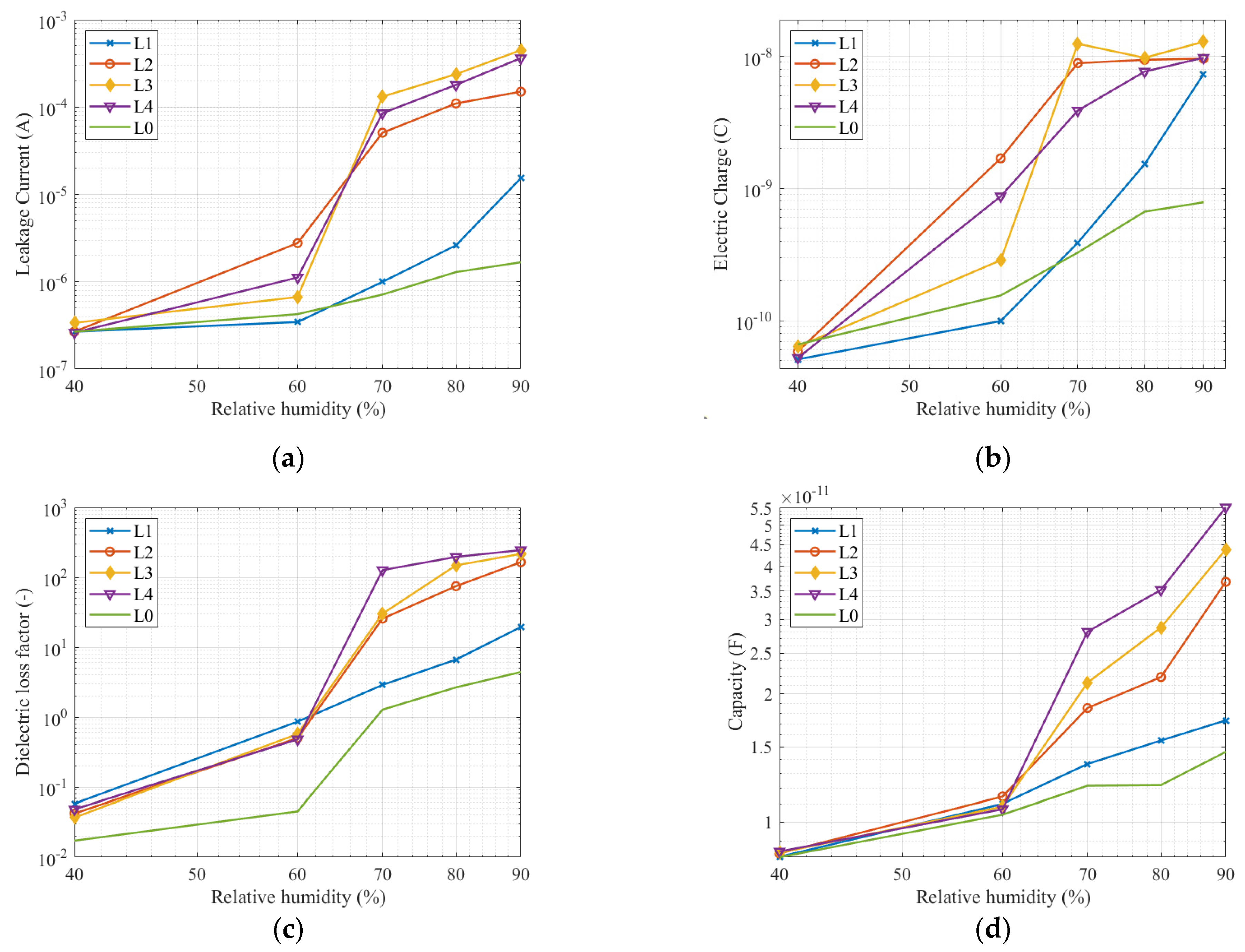
3.3. Comparison of All Quantities at the Frequency 113 Hz and 1 kHz
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farzaneh, M.; Chisholm, W.A. Insulators for Icing and Polluted Environments; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Vosloo, W.L.; Macey, R.E.; de Tourreil, C. The Practical Guide to Outdoor High Voltage Insulators; Crown Publications: Johannesburg, South Africa, 2004. [Google Scholar]
- Haddad, A.; Warne, D.F. Advances in High Voltage Engineering; Institution of Electrical Engineers: London, UK, 2004. [Google Scholar]
- Kuffel, E.; Zaengl, W.S.; Kuffel, J. High Voltage Engineering: Fundamentals, 2nd ed.; Butterworth-Heinemann: Boston, MA, USA; Oxford, UK, 2000. [Google Scholar]
- Taherian, R. 6-Application of Polymer-Based Composites: Polymer-Based Composite Insulators. Electr. Conduct. Polym. Based Compos. 2019, 131–181. [Google Scholar] [CrossRef]
- Papailiou, K.; Schmuck, F. Composite Long Rod Insulators. In Silicone Composite Insulators; Springer: Berlin/Heidelberg, Germany, 2013; pp. 9–51. [Google Scholar] [CrossRef]
- Jiao, J.; Li, L.; Wu, B.; He, C. Novel capacitive proximity sensors for assessing the aging of composite insulators. Sens. Actuators A Phys. 2017, 253, 75–84. [Google Scholar] [CrossRef]
- Suen, M.-S.; Chen, R. Capacitive Tactile Sensor with Concentric-Shape Electrodes for Three-Axial Force Measurement. Proceedings 2018, 2, 708. [Google Scholar] [CrossRef] [Green Version]
- Othman, N.; Piah, M.; Adzis, Z. Contamination effects on charge distribution measurement of high voltage glass insulator string. Measurement 2017, 105, 34–40. [Google Scholar] [CrossRef]
- Qiao, Z.; Cheng, L.; Zhang, S.; Yang, L.; Guo, C. Detection of composite insulators inner defects based on flash thermography. In Proceedings of the 2017 1st International Conference on Electrical Materials and Power Equipment (ICEMPE), Xi’an, China, 14–17 May 2017; pp. 359–363. [Google Scholar] [CrossRef]
- Li, M.; Jing, Y.; Zhang, L.; Li, X.; Huang, G.; Wang, Z. Insulator Defect Detection Based on Ultraviolet Imaging and Acoustic Emission Signal. In Proceedings of the 2020 IEEE 3rd Student Conference on Electrical Machines and Systems (SCEMS), Jinan, China, 4–6 December 2020; pp. 472–475. [Google Scholar] [CrossRef]
- Lasalvia, L.A.B.; Florentine, M.T.B.; Ferreira, T.V.; Germano, A.D.; da Costa, E.G. Intelligent acoustic detection of defective porcelain station post insulators. In Proceedings of the 2015 IEEE Electrical Insulation Conference (EIC), Seattle, WA, USA, 7–10 June 2015; pp. 118–122. [Google Scholar] [CrossRef]
- Liu, L.; Mei, H.; Guo, C.; Zhao, C.; Wang, L. Nondestructive Testing of Porcelain Post Insulators Using Active Infrared Thermography. In Proceedings of the 2017 IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Honolulu, HI, USA, 31 July–4 August 2017; pp. 68–71. [Google Scholar] [CrossRef]
- Ibrahim, M.E.; Selim, F.; Abd-Elhady, A.M. Partial discharge performance improvement of covered conductor (CC)/high voltage insulator based electrical distribution systems. Electr. Power Syst. Res. 2022, 202, 107601. [Google Scholar] [CrossRef]
- Liu, L.; Mei, H.; Wang, L.; Zhao, C.; Guan, Z. Pulsed infrared thermography to inspect the internal defects of composite insulators. In Proceedings of the 2017 IEEE Electrical Insulation Conference (EIC), Baltimore, MD, USA, 11–14 June 2017; pp. 467–470. [Google Scholar] [CrossRef]
- Zhang, B.; Cui, Y.; Zhang, W.; Liu, S.; Zheng, Q.; Yang, S.; Gao, S. Voltage and electric field distribution along porcelain long rod insulator string in AC 500kV transmission line. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 19–22 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Mateus, C.; Barata, F.A.; Luis, R. Effects of Broken Skirts and Pollution on Voltage Distribution for Cap and Pin Glass Insulators. In Proceedings of the 2020 IEEE 14th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Setubal, Portugal, 8–10 July 2020; pp. 30–35. [Google Scholar] [CrossRef]
- Ramesh, M.; Cui, L.; Gorur, R.S. Impact of superficial and internal defects on electric field of composite insulators. Int. J. Electr. Power Energy Syst. 2018, 106, 327–334. [Google Scholar] [CrossRef]
- Ramesh, M.; Gorur, R. Stretched grid finite difference method for computation of electric field in composite insulators with defects. Electr. Power Syst. Res. 2021, 192, 106875. [Google Scholar] [CrossRef]
- Stefenon, S.F.; Corso, M.P.; Nied, A.; Perez, F.L.; Yow, K.; Gonzalez, G.V.; Leithardt, V.R.Q. Classification of insulators using neural network based on computer vision. IET Gener. Transm. Distrib. 2021, gtd2.12353. [Google Scholar] [CrossRef]
- Stefenon, S.F.; Ribeiro, M.H.D.M.; Nied, A.; Mariani, V.C.; Coelho, L.D.S.; Leithardt, V.R.Q.; Silva, L.A.; Seman, L.O. Hybrid Wavelet Stacking Ensemble Model for Insulators Contamination Forecasting. IEEE Access 2021, 9, 66387–66397. [Google Scholar] [CrossRef]
- Stefenon, S.F.; Seman, L.O.; Neto, N.F.S.; Meyer, L.H.; Nied, A.; Yow, K.-C. Echo state network applied for classification of medium voltage insulators. Int. J. Electr. Power Energy Syst. 2022, 134, 107336. [Google Scholar] [CrossRef]
- Othman, N.A.; Piah, M.A.M.; Adzis, Z. Leakage current and trapped charge characteristics for glass insulator string under contaminated conditions. In Proceedings of the 2015 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 19–20 October 2015; pp. 259–262. [Google Scholar] [CrossRef]
- Deb, S.; Ghosh, R.; Dutta, S.; Dalai, S.; Chatterjee, B. Effect of humidity on leakage current of a contaminated 11 kV Porcelain Pin Insulator. In Proceedings of the 2017 6th International Conference on Computer Applications in Electrical Engineering-Recent Advances (CERA), Roorkee, India, 5–7 October 2017; pp. 215–219. [Google Scholar] [CrossRef]
- Fauziah, D.; Alfiadi, H.; Rachmawati; Suwamo. The effect of coating on leakage current characteristic of coast field aged ceramic insulator. In Proceedings of the 2017 4th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Yogyakarta, Indonesia, 19–21 September 2017; pp. 1–7. [Google Scholar] [CrossRef]
- De Santos, H.; Bobi, M.A.S. A Cumulative Pollution Index for the Estimation of the Leakage Current on Insulator Strings. IEEE Trans. Power Deliv. 2020, 35, 2438–2446. [Google Scholar] [CrossRef]
- Samakosh, J.D.; Mirzaie, M. Analysis of leakage current characteristics during aging process of SiR insulator under uniform and longitudinal non-uniform pollution conditions. Measurement 2019, 147, 106862. [Google Scholar] [CrossRef]
- Kim, T.; Yi, J. Application of hydrophobic coating to reduce leakage current through surface energy control of high voltage insulator. Appl. Surf. Sci. 2022, 578, 151820. [Google Scholar] [CrossRef]
- Mohammadnabi, S.; Rahmani, K. Influence of humidity and contamination on the leakage current of 230-kV composite insulator. Electr. Power Syst. Res. 2021, 194, 107083. [Google Scholar] [CrossRef]
- Castillo-Sierra, R.; Oviedo-Trespalacios, O.; Candelo-Becerra, J.E.; Soto, J.D.; Calle, M. A novel method for prediction of washing cycles of electrical insulators in high pollution environments. Int. J. Electr. Power Energy Syst. 2021, 130, 107026. [Google Scholar] [CrossRef]
- Putra, N.R.M.; Sartika, N.; Rachmawati; Suwarno. The study on leakage current waveform characteristics and computer simulation of ceramic insulator under artificial tropical condition. In Proceedings of the 2018 12th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Xi’an, China, 20–24 May 2018; pp. 320–323. [Google Scholar] [CrossRef]
- Rasamsetti, S.S.; Sumathi, N. Leakage current characteristics of 132kV polymeric and porcelain insulator under various polluted conditions. In Proceedings of the 2017 IEEE International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI), Chennai, India, 21–22 September 2017; pp. 1535–1540. [Google Scholar] [CrossRef]
- Kordkheili, H.H.; Abravesh, H.; Tabasi, M.; Dakhem, M.; Abravesh, M.M. Determining the probability of flashover occurrence in composite insulators by using leakage current harmonic components. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 502–512. [Google Scholar] [CrossRef]
- Ahmad, H.; Salam, M.; Ying, L.Y.; Bashir, N. Harmonic components of leakage current as a diagnostic tool to study the aging of insulators. J. Electrost. 2008, 66, 156–164. [Google Scholar] [CrossRef] [Green Version]
- Salem, A.A.; Abd-Rahman, R.; Al-Gailani, S.A.; Salam, Z.; Kamarudin, M.S.; Zainuddin, H.; Yousof, M.F.M. Risk Assessment of Polluted Glass Insulator Using Leakage Current Index Under Different Operating Conditions. IEEE Access 2020, 8, 175827–175839. [Google Scholar] [CrossRef]
- Palangar, M.F.; Mirzaie, M. Detection of Critical Conditions in Ceramic Insulators Based on Harmonic Analysis of Leakage Current. Electr. Power Compon. Syst. 2016, 44, 1854–1864. [Google Scholar] [CrossRef]
- Salem, A.A.; Abd-Rahman, R.; Al-Gailani, S.A.; Kamarudin, M.S.; Ahmad, H.; Salam, Z. The Leakage Current Components as a Diagnostic Tool to Estimate Contamination Level on High Voltage Insulators. IEEE Access 2020, 1. [Google Scholar] [CrossRef]
- Bashir, N.; Ahmad, H.; Suddin, M.S. Ageing studies on transmission line glass insulators using dielectric dissipation factor test. In Proceedings of the 2010 Conference Proceedings IPEC, Singapore, 27–29 October 2010; pp. 1062–1066. [Google Scholar] [CrossRef]
- Gerdinand, F.; Budde, M.; Kurrat, M. Electrical and mechanical strength of mineral filled epoxy insulators in correlation to power loss factor. In Proceedings of the 2004 IEEE International Conference on Solid Dielectrics, 2004. ICSD 2004, Toulouse, France, 5–9 July 2004; pp. 320–323. [Google Scholar] [CrossRef]
- Hu, R.; Zhao, A.; Yu, C.; Shi, Y.; Zhang, X. Measurement of dielectric loss factor based on LabVIEW signal processing module. In Proceedings of the 2020 2nd International Conference on Machine Learning, Big Data and Business Intelligence (MLBDBI), Taiyuan, China, 23–25 October 2020; pp. 557–560. [Google Scholar] [CrossRef]
- Levitskaya, T.M.; Sternberg, B.K. Parameters describing the material behavior in an electromagnetic field. In Electrical Spectroscopy of Earth Materials; Elsevier: Amsterdam, The Netherlands, 2019; pp. 3–15. [Google Scholar] [CrossRef]
- Chrzan, K.; Pohl, Z.; Kowalak, T. Hygroscopic properties of pollutants on HV insulators. IEEE Trans. Electr. Insul. 1989, 24, 107–112. [Google Scholar] [CrossRef] [Green Version]
- Chrzan, K. Conductivuty of Aqueous Dust Solutions. IEEE Trans. Electr. Insul. 1987, EI-22, 241–244. [Google Scholar] [CrossRef]







| Pollution Level | NaCl Amount (g/L) | Solution Conductivity (µS/cm) |
|---|---|---|
| L1 | 1 | 28 |
| L2 | 6 | 129 |
| L3 | 10 | 173 |
| L4 | 16 | 286 |
| Leakage Current (μA) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Clean insulator | L1 | L2 | L3 | L4 | ||||||
| RH (%) | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz |
| 40 | 0.004 | 0.368 | 0.004 | 0.228 | 0.004 | 0.268 | 0.005 | 0.338 | 0.004 | 0.261 |
| 60 | 0.150 | 0.426 | 0.01 | 0.346 | 2.62 | 2.77 | 0.546 | 0.670 | 0.998 | 1.12 |
| 70 | 0.530 | 0.714 | 0.64 | 0.996 | 47.7 | 50.7 | 124 | 131 | 82.2 | 85.0 |
| 80 | 1.18 | 1.29 | 2.35 | 2.61 | 98.2 | 109 | 228 | 238 | 173 | 179 |
| 90 | 1.34 | 1.66 | 13.4 | 15.3 | 149 | 149 | 417 | 448 | 338 | 362 |
| Electric Charge (nC) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Clean insulator | L1 | L2 | L3 | L4 | ||||||
| RH (%) | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz |
| 40 | 0.367 | 0.066 | 0.113 | 0.051 | 0.175 | 0.058 | 0.139 | 0.064 | 0.122 | 0.052 |
| 60 | 0.804 | 0.155 | 0.411 | 0.096 | 16.4 | 1.69 | 0.286 | 0.287 | 7.06 | 0.872 |
| 70 | 2.49 | 0.328 | 3.05 | 0.389 | 82.3 | 8.87 | 88.4 | 12.4 | 37.6 | 3.86 |
| 80 | 4.99 | 0.668 | 13.8 | 1.524 | 89.4 | 9.4 | 992 | 9.73 | 128 | 7.66 |
| 90 | 6.71 | 0.785 | 65 | 7.329 | 107 | 9.6 | 1728 | 12.9 | 1615 | 9.74 |
| Dielectric Loss Factor (-) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Clean insulator | L1 | L2 | L3 | L4 | ||||||
| RH (%) | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz |
| 40 | 0.029 | 0.017 | 0.14 | 0.058 | 0.08 | 0.042 | 0.073 | 0.037 | 0.14 | 0.048 |
| 60 | 1.46 | 0.045 | 4.63 | 0.86 | 1.88 | 0.5 | 2.84 | 0.572 | 2.18 | 0.48 |
| 70 | 6.1 | 1.28 | 18.6 | 2.88 | 128 | 25.6 | 146 | 30.1 | 367 | 126 |
| 80 | 17.3 | 2.66 | 40.9 | 6.64 | 212 | 74.6 | 322 | 148 | 345 | 196 |
| 90 | 22.6 | 4.41 | 73.4 | 19.4 | 202 | 164 | 308 | 216 | 248 | 244 |
| Capacity (pF) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Clean insulator | L1 | L2 | L3 | L4 | ||||||
| RH (%) | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz | 113 Hz | 1 kHz |
| 40 | 8.48 | 8.25 | 9.07 | 8.27 | 9.01 | 8.45 | 8.97 | 8.46 | 9.22 | 8.51 |
| 60 | 16.6 | 10.4 | 14.5 | 11 | 15.8 | 11.5 | 14.3 | 10.9 | 13.8 | 10.7 |
| 70 | 19 | 12.1 | 18.6 | 13.7 | 33.7 | 18.5 | 40.4 | 21.3 | 89.2 | 28 |
| 80 | 17.4 | 12.2 | 23.4 | 15.5 | 70.6 | 21.9 | 122 | 28.7 | 184 | 35.2 |
| 90 | 24.8 | 14.6 | 41.8 | 17.3 | 273 | 36.8 | 283 | 43.9 | 498 | 55.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolník, B.; Šárpataky, Ľ.; Kolcunová, I.; Havran, P. Sensing Method Using Multiple Quantities for Diagnostic of Insulators in Different Ambient Conditions. Sensors 2022, 22, 1376. https://doi.org/10.3390/s22041376
Dolník B, Šárpataky Ľ, Kolcunová I, Havran P. Sensing Method Using Multiple Quantities for Diagnostic of Insulators in Different Ambient Conditions. Sensors. 2022; 22(4):1376. https://doi.org/10.3390/s22041376
Chicago/Turabian StyleDolník, Bystrík, Ľuboš Šárpataky, Iraida Kolcunová, and Peter Havran. 2022. "Sensing Method Using Multiple Quantities for Diagnostic of Insulators in Different Ambient Conditions" Sensors 22, no. 4: 1376. https://doi.org/10.3390/s22041376
APA StyleDolník, B., Šárpataky, Ľ., Kolcunová, I., & Havran, P. (2022). Sensing Method Using Multiple Quantities for Diagnostic of Insulators in Different Ambient Conditions. Sensors, 22(4), 1376. https://doi.org/10.3390/s22041376








