1. Introduction
Angle-only filtering in 2D and 3D finds many important applications in passive tracking [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13]. The advantage of passive tracking over active tracking is that the presence of the passive sensor cannot be detected by the target. Passive tracking arises in submarine tracking using a passive sonar [
1,
11], passive ranging using an infrared search and track (IRST) sensor [
2,
4,
5,
8,
12], passive radar tracking [
4], satellite-to-satellite passive tracking [
14], video tracking [
15], etc. In this paper, we focus on tracking an aircraft using an IRST sensor on another aircraft. This problem is more difficult than the case where multiple sensors are used. The bearings-only filtering (BOF) problem in 2D has been extensively studied, and a vast number of publications exist in the research literature [
1,
10,
16,
17,
18,
19], Chapter 6 of [
11,
20]. However, research in the angle-only filtering (AOF) problem in 3D is limited compared to that in the bearings-only filtering problem.
Observability is a major issue for the BOF problem in 2D [
21] and AOF problem in 3D. In the 2D problem, a four or five-dimensional state is estimated from bearings-only measurements for a non-maneuvering and maneuvering target, respectively. To observe the state of the target, the sensor must perform maneuvers with a motion of higher order than that of the target [
18]. If a four-dimensional Cartesian state is used for the BOF problem in 2D for a non-maneuvering target, it has been observed that the extended Kalman filter (EKF) [
22,
23] diverges. Modified polar coordinates (MPC) [
1,
24,
25] were formulated to overcome the divergence of the EKF. The components of the MPC are bearing, bearing-rate, range-rate divided by range, and the inverse of range [
1]. The first three components of MPC are observable even before an ownship maneuver. MPC decouple the observable and unobservable components of the state vector and provide improved performance of the EKF. Use of MPC makes the dynamic model for the nearly constant velocity (NCV) model nonlinear and complex, but the measurement model becomes linear. In addition to the EKF, the unscented Kalman filter (UKF) [
26], cubature Kalman filter (CKF) [
27], Gaussian sum filter (GSF) [
28], particle filter (PF) [
11], uncorrelated conversion based filter (UCF) [
20], etc. have also been applied to the BOF problem in 2D. In order to address the observability problem, the multiple model-based range-parametrized (RP) EKF (RP-EKF) was proposed by Peach [
19] and Kronhamn [
16]. In addition to the EKF, other filters can also be used in the RP framework.
Most of the existing work on the angle-only filtering problem in 3D is for a non-maneuvering target using the NCV model. The sensor must perform a maneuver to observe the target state. For a non-maneuvering target, the EKF using the Cartesian state for the AOF problem in 3D does not diverge [
8], even though the filter diverges for the corresponding BOF in 2D [
11]. In analogy with the MPC in 2D, Stallard proposed the modified spherical coordinates (MSC) in 3D [
12,
13]. The components of the MSC are elevation, elevation-rate, bearing, bearing-rate times cosine of elevation, the inverse of range, and range-rate divided by range. As in the case of MPC, the dynamic model for the NCV motion using MSC is nonlinear and complex. However, the measurement model is linear since bearing and elevation are components of MSC. The log spherical coordinates (LSC) [
29] can also be used as an alternate to the MSC. The first five components of the LSC are the same as those of the MSC, but the inverse of range (sixth component) is replaced by the logarithm of the range. Many studies have shown that the EKF using the MSC (EKF-MSC) provides a better state estimation accuracy than the Cartesian EKF (CEKF) for the NCV motion [
2,
12,
13].
Starting with the work of Stallard, the EKF-MSC was used in [
2,
12,
13,
30]. Karlsson and Gustafsson used the PF and compared the PF-based algorithms with the multiple model-based range-parametrized EKF (RP-EKF) using the Cartesian state and MSC in a number of tracking scenarios [
6,
7]. Their results showed the superiority of the PF-based algorithms over the RP-EKF-based algorithms.
In our previous work [
29], we compared the EKF-MSC and EKF-LSC using the continuous-discrete filtering approach with the discrete-time CEKF. The results of this study show that the EKF-MSC and EKF-LSC have comparable accuracy and perform better than the discrete-time CEKF for low measurement accuracy. For high measurement accuracy, the discrete-time CEKF has higher state estimation accuracy than the EKF-MSC and EKF-LSC. Prior to our work in [
8,
31,
32], the process noise using the MSC was modeled approximately. We proposed new algorithms using the MSC to model the process noise exactly. The AOF for the NCV motion can be solved in the following three possible ways [
8,
31,
32]:
Use the discrete-time NCV model with the Cartesian state vector (with linear dynamic model) and nonlinear measurement model;
Use the exact discrete-time NCV model with the MSC (with nonlinear dynamic model) and linear measurement model;
Use the MSC with approximate discretization of the continuous-time dynamic model (with nonlinear dynamic model) and linear measurement model.
In [
8], we performed a comprehensive study of the AOF problem for a non-maneuvering target in 3D using the EKF, UKF, and PF with Cartesian state vector and MSC. In this study, new algorithms using the EKF, UKF, and PF with the MSC were formulated, and improved filter initialization algorithms for the Cartesian state and MSC were presented. Four versions of the PF were used in this work: the Cartesian bootstrap filter (CBF), bootstrap filter using MSC with exact dynamic model (BF-MSC(E)), bootstrap filter using MSC with an approximate dynamic model (BF-MSC(A)), and the optimal importance density-based PF using MSC with an approximate dynamic model (ODIPF-MSC(A)). The initial range between the target and the sensor in the scenarios in [
8] is higher than that in [
6,
7]. Numerical results from this study indicate that the state estimation accuracy of the PF-based algorithms is inferior compared with that of the EKF and UKF-based algorithms. For the BOF problem in 2D Chapter 6 of [
11], the measurement SD is of the order of a degree and the measurement time interval is about 30–60 s. In this scenario, a PF has one of the best state estimation accuracies Chapter 6 of [
11,
20]. Secondly, compared to the EKF, the PF-based algorithms have about two orders of magnitude higher computational cost. Thirdly, It is now well established that, when the measurement accuracy and data rate are high (which is true for the current problem), PFs do not offer any advantage over the EKF, UKF, and CKF [
33,
34,
35]. Therefore, we did not consider the PF in this study.
A novel batch Bayesian weighted instrumental variable estimator for the 3D target motion analysis problem using bearing and elevation measurements is presented in [
36]. Results of this study show that the proposed algorithm outperforms its non-Bayesian counterpart. The CEKF, Cartesian UKF (CUKF), Cartesian CKF (CCKF), and the Cartesian new sigma point Kalman filter (CNSKF) were used in [
3] to analyze the AOF problem in 3D for a non-maneuvering target. Results of this study shows that these five filters have nearly the same accuracy in operational scenarios. The particle flow filter (PFF), ensemble Kalman filter (EnKF), EKF, UKF, and PF were compared for the AOF problem in 3D for a non-maneuvering target in [
37]. It was observed that the EKF-MSC, UKF-MSC, deterministic EnKF-MSC, and Cartesian PFF had the best performance in operational conditions.
In [
38], we studied the passive sonar tracking problem when the submarine and the ownship move in different planes using the EKF, UKF, RP-UKF, and PF. Our results showed that the depth of the non-maneuvering target can be estimated accurately, and the PF had the best performance in the scenarios studied. The 3D instrumental variable-based Kalman filter (3D-IVKF) is applied to an underwater passive sonar tracking scenario in [
39] for a non-maneuvering target using bearing and elevation measurements. It is observed that at low measurement standard deviations (SDs) (<6°) the performance of the 3D-IVKF is comparable to that of the UKF and CKF. However, at higher measurement SDs, the 3D-IVKF outperforms the UKF and CKF with lower computational cost.
To compare the accuracies of the filters used in the AOF problem with the best achievable accuracy, we computed the posterior Cramér-Rao lower bound (PCRLB) [
40] for a non-maneuvering target using the NCV model in [
41]. Our results show that when the measurement accuracy is high, the root mean square (RMS) position and velocity errors are close to the corresponding PCRLBs. The difference between RMS position and velocity errors and corresponding PCRLBs increases with a decrease in the measurement accuracy. In [
42], a globally valid posterior Cramér–Rao lower bound was derived for the AOF problem. The authors claim the von Mises–Fisher distribution to be superior to the conventional approach using additive Gaussian noise in measured angular coordinates.
A maneuvering target refers to an accelerating target [
43]. Common accelerated motions considered in tracking are the nearly constant acceleration (NCA), nearly constant turn (NCT), and jerk [
4,
22,
43]. The NCA and jerk models are linear, whereas the NCT model is nonlinear in the target state. The number of publications for a maneuvering target in the AOF problem is quite limited. In [
5], the NCT model was used in the passive ranging problem using an IRST sensor in air-to-air tracking scenarios. The authors used the RP-UKF using the multiple model method. However, algorithm details are not presented in the paper. The NCT model in the
plane has been studied extensively where the angular rate is estimated [
4,
22,
43,
44,
45,
46]. This problem arises in the air-traffic control (ATC) scenario [
4,
22,
27,
43,
47]. In most cases, the conventional discrete-time NCT model is approximate, since the state transition matrix and process noise covariance matrix cannot be derived from the continuous-time model using a consistent procedure.
We consider the tracking of a maneuvering aircraft in 3D and assume that the aircraft moves in the
-plane with the NCT motion and has a NCV motion along the
Z-axis. The speed and angular rate are constant for the constant turn motion (CT) in the
-plane. Thus, it is natural to perturb the speed and angular rate in the NCT motion with the continuous-time white noise (Wiener processes) [
22]. We follow this approach from [
45] to obtain the nonlinear stochastic differential equation (SDE) [
48,
49] for the NCT motion. Since the SDE is nonlinear, it cannot be discretized exactly. We discretize the SDE using the first and second-order weak Taylor (TS2) approximations [
50] to obtain approximate discrete-time dynamic models. The first-order stochastic Taylor series approximation is also known as the Euler approximation. Two types of states for the NCT motion in the
-plane, namely the polar velocity and the Cartesian velocity-based states [
43,
44,
45,
46], are used. The NCV motion along the
Z-axis is discretized exactly. The Cartesian velocity state in NCT comprises the 2D position, 2D velocity, and angular rate. In the polar velocity state, the speed and heading replace the 2D Cartesian velocity.
An IRST sensor on another maneuvering aircraft collects azimuth and elevation measurements. The accuracy of the angle measurements by an IRST sensor is usually high (1 mrad). The data rate of an IRST sensor is also high (1 Hz). As sensor technology improves, these factors are expected to improve. The AOF algorithm is required to process the sensor measurements sequentially in real time. Thus, a batch algorithm is ruled out for this tracking scenario. As discussed previously, a PF is not considered for this problem due to its lack of state estimation accuracy and high computational cost. It has been observed in [
33,
34,
35] that when the measurement accuracy and data rate are high (which is true for the current problem), the UKF and CKF have nearly the same accuracy, and the accuracy of the EKF is somewhat lower. If the dimension of the state is
n, then the UKF and CKF have
and
sigma points and cubature points, respectively. As a result, the computational cost of the CKF is lower than that of the UKF. If
, then the first weight in the UKF becomes negative and the rest of the
weights are positive. On the contrary, each of the
weights in the CKF is positive and equal to
. This negative weight may cause a filter-calculated covariance matrix to be non-positive definite in some cases [
27]. The CKF was also successfully used in our previous work on AOF in [
9]. Hence, we chose the third-degree spherical–radial cubature rule-based CKF [
27] to estimate the seven-dimensional state of the maneuvering target. The CKFs using the Euler and TS2 approximations are called CKF1 and CKF2, respectively. Thus, we consider four CKF filters; CKF1P, CKF1C, CKF2P, and CKF2C, where the last letter in the filter refers to polar and Cartesian velocity states.
Notation convention: For clarity, we use italics to denote scalar quantities and boldface for vectors and matrices. A lower or upper-case Roman letter represents a name (e.g., “s” for “sensor,” “RMS” for “root mean square,” etc.). We use “:=” to define a quantity and denotes the transpose of the vector or matrix . The dimensional identity matrix, dimensional null matrix, and null matrix are denoted by , , and , respectively.
The paper is organized as follows.
Section 2 presents the dynamic models for the target.
Section 3 explains the discretization of target NCT models, and
Section 4 describes sensor dynamic and measurement models. A summary of the four CKF filters is given in
Section 5. Numerical simulations and results are presented in
Section 6. Finally,
Section 7 summarizes our contributions in the paper.
2. Target Dynamic Models
We assume that the IRST sensor trajectory is deterministic and the states of the sensors are known exactly at measurement times. To improve the observability of the target state, the IRST sensor performs maneuvers with a sequence of CV and constant turn (CT) motions [
5,
8,
31].
Two types of coordinates are commonly used for the NCT in the
-plane: Cartesian velocity and polar velocity-based models [
43,
44,
45,
46]. In addition to the 2D position and velocity, the turn-rate or angular velocity
is also estimated in the NCT model.
Let
denote the Cartesian state along the
Z-axis with position and velocity components
For the NCT model in the
-plane, we use
and
for state vectors where the angular velocity
is estimated. The velocity in
and
has Cartesian and polar coordinates, respectively. Let
and
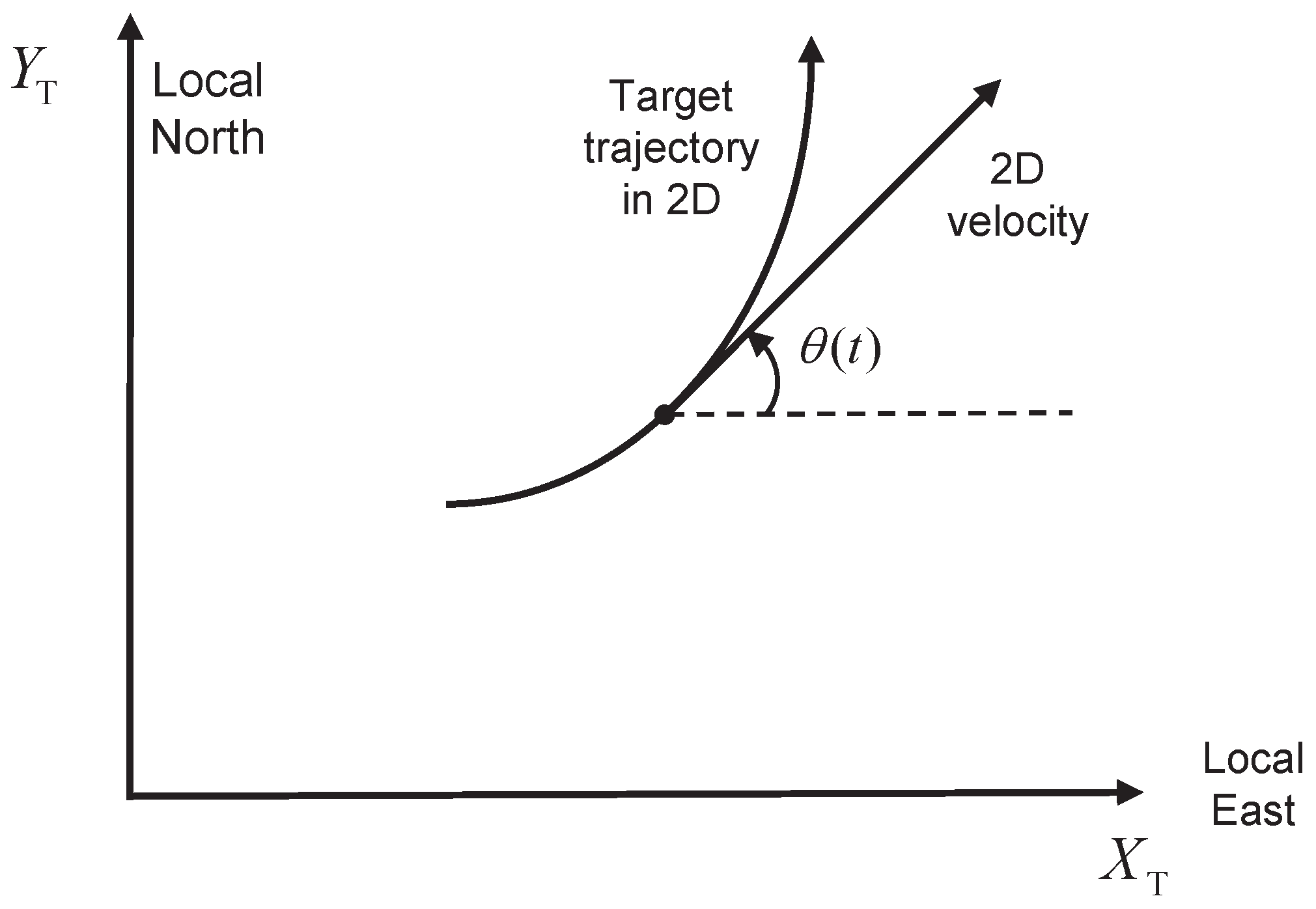
denote the speed and heading of the target in the
-plane. In this paper, the heading is defined as the angle of the velocity in the
-plane, measured from the
X-axis in the counter-clockwise direction, as shown in
Figure 1.
Then
and
are defined, respectively, by
Three-dimensional state vectors where angular velocity is estimated are defined, respectively, by
We assume that the measurement time interval is constant; i.e.,
for all
k. In this paper, we use the discretized continuous-time models [
22].
The discrete-time dynamic model for the NCV motion along the
Z-axis is given by
where
is the state transition matrix and
is a zero-mean white Gaussian process noise with covariance
,
where
is the power spectral density (PSD) of the continuous-time acceleration process noise along the
Z-axis [
22].
The time derivative of
is given by
Since
, (
10) can be written as
The time derivative of
is
In the constant turn (CT) model, the speed and turn rate are constant. The speed and turn rate can be modeled as nearly constant in the NCT motion. Examining (
12) and (
13), we find that for the NCT model, (
12) is more suitable than (
13), based on symmetry considerations. Using conventional models in the engineering literature [
22], for the NCT model, we may write
where
and
are continuous-time zero-mean white acceleration and angular acceleration process noises with power spectral densities
and
respectively, [
22]
where
is the Dirac delta function [
51]. We can write (
14)–(
16) mathematically rigorously by defining
where
and
are standard independent Wiener processes [
45,
48]
Then, conventionally, we can write
as [
23,
48]
We can write the time derivative of the polar state vector mathematically rigorously using the Itô stochastic differential equation (SDE) [
45,
48,
49]
where
We assume that the prior distribution of
is Gaussian,
The time derivative of
contains Cartesian accelerations
and
in (
13). It is necessary to transform them to derivatives of speed and angular velocity. The 2D Cartesian velocity is given by
and the Cartesian acceleration is
Using (
11), the Cartesian acceleration is expressed by
Using a similar approach, the Itô SDE [
45,
48,
49] for the Cartesian state is
where